Abstract
Forecasting multivariate time series is a pivotal task in controlling multi-sensor systems. The joint forecasting of all channels may be too complex, whereas forecasting the channels independently may cause important spatial inter-dependencies to be overlooked. In this paper, we improve the performance of single-channel forecasting algorithms by designing an interpretable front-end that extracts the spatial–temporal components from the input multivariate time series. Specifically, the multivariate samples are first segmented into equal-sized matrix symbols. The symbols are decomposed into the frequency-separated Intrinsic Mode Functions (IMFs) using a 2D Empirical-Mode Decomposition (EMD). The IMF components in each channel are then forecasted independently using relatively simple univariate predictors (UPs) such as DLinear, FITS, and TCN. The symbol size is determined to maximize the temporal stationarity of the EMD residual trend using Bayesian optimization. In addition, since the overall performance is usually dominated by a few of the weakest predictors, it is shown that the forecasting accuracy can be further improved by reordering the corresponding channels to make more correlated channels more adjacent. However, channel reordering requires retraining the affected predictors. The main advantage of the proposed forecasting framework for multivariate time series is that it retains the interpretability and simplicity of single-channel forecasting methods while improving their accuracy by capturing information about the spatial-channel dependencies. This has been demonstrated numerically assuming a 64-channel EEG dataset.
MSC:
62M20
1. Introduction
The accurate forecasting of a multivariate time series is crucial in many applications, including system control. For instance, forecasting multi-channel EEG signals enables anticipating an onset of epileptic seizures and identifying voluntary motor actions [1,2]. This can be used to devise timely therapeutic interventions, and to design the responsive brain–computer interfaces. Granger causality exploits forecasting to infer the causal associations among multivariate time series [3]. The performance gains of theoretically optimum multi-channel forecasting methods are difficult to realize in practice due to the inherent complexity of their designs, a lack of interpretability, and the issues with model overfitting [4,5]. These methods are also expensive to train, and the inferences are numerically costly. On the other hand, the single-channel forecasting schemes are easier to design, and they also have a lower computational complexity. Even though these schemes ignore the channel inter-dependencies, they can achieve a superior performance [6,7,8,9,10,11].
The DLinear decomposes the input time series into the trend and seasonal components, and then simple linear projections are used to predict the future values [6]. The LightTS replaces the attention originally introduced in transformers with compact temporal convolutions and gating mechanisms in order to capture the local sample dependencies [7]. It offers quick training times and robust short-term forecasts. The TIDE does not use attention nor convolutions, and instead creates multiple MLP paths with learnable time embedding between the encoding of past values and decoding of future values [8]. The TSMixer adopts the MLP-Mixer paradigm by linearly combining the temporal tokens from different channels [12]. The FITS uses a Fast Fourier Transform (FFT) to convert the input samples into the frequency domain [13], which enables choosing the most informative spectral components for predictions. The SparseTSF aims at forecasting the sparse periodic features of time series [9].
In general, multivariate time series can be decomposed into separate multi-scale components [14]. It allows for fine-tuning the forecasting algorithms into unique spatial–temporal dependencies of each component. The decomposition can be performed using, for example, the Fourier and wavelet transforms. The Singular Spectrum Analysis (SSA) yields the components that are linearly independent [15]. The auto-regressive (AR) models are commonly adopted in the literature to obtain the seasonal, non-seasonal, and trend components of linear time series [16]. The EMD decomposes time series into multiple intrinsic oscillatory modes called Intrinsic Mode Functions (IMFs) without any assumptions about the sample linearity or stationarity [17]. The EMD has shown that it can improve the prediction accuracy [18,19,20] by reducing the non-stationarity of the signal components [21,22,23]. The EMD can also be used adaptively to create stable IMF components [24,25,26]. A multi-stage EMD pre-processing was devised in [27] to extract more informative IMFs in order to improve the prediction accuracy. The 2D segmentation followed by 2D EMD is often used for semantic segmentation of images and videos [28], texture classification of images [29,30], and for making joint predictions in graph-based data models [31]. To the best of our knowledge, the 2D EMD was not previously considered for processing multivariate time series.
In this paper, the forecasting accuracy of multivariate time series using relatively simple but effective single-channel prediction algorithms is improved by creating an interpretable pre-processing front-end. The front-end extracts the spatial–temporal components, which are then predicted independently by the univariate predictors (UPs). The overall prediction scheme is referred to as the two-stage Symbol-EMD-UP. In particular, the input multivariate time series are first segmented into non-overlapping equal-sized 2D matrix symbols. The symbols are decomposed into the frequency-separated IMF components using the 2D EMD with bivariate spline interpolations. The actual prediction of each IMF component in each channel is performed independently, assuming the DLinear [6], the FITS [13], and the TCN [32], respectively. In addition, since the total forecasting accuracy is often dominated by a small number of the worst performing predictors, their accuracy is improved by reordering the channels in the corresponding 2D symbols and then retraining these predictors. This latter step defines the second stage of the proposed prediction scheme. Finally, the predicted IMF components are combined to obtain the same number of channels and time domain samples as the input multivariate time series. Thus, the predicted samples have the same spatial–temporal resolution as the input samples.
The size of 2D symbols in segmenting the input multivariate time series is chosen to maximize the temporal stationarity of their EMD residuals. The stationarity is measured by the augmented Dickey–Fuller (ADF) test [33], and the maximization is performed using Bayesian optimization. The channel reordering prior to the second-stage retraining of the weakest predictors aims to place more correlated channels closer together within the 2D symbols. Such a reordering can be formulated and solved as the Traveling Salesman Problem (TSP). Moreover, it is assumed that there are no missing data, so the time series to be forecasted are not sparse.
The numerical results are produced for the EEG dataset, assuming the standard as well as modifying the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) metrics. These results demonstrate that the proposed prediction architecture is very effective in capturing the spatial–temporal dependencies while maintaining the interpretability.
This paper reports the following contributions:
- An interpretable and low-complexity front-end for decomposing multivariate time series is proposed. The front-end captures the spatial–temporal inter-dependencies within the 2D data symbols without requiring complex multi-dimensional or deep learning methods for extracting relevant features. The front-end is followed by a bank of interpretable univariate (single-channel) predictors. The equal-sized segments avoid the need for optimizing the size of each 2D segment separately. In addition, 2D EMD with bivariate spline interpolations instead of the previously assumed 1D EMD is employed for extracting the spatial–temporal IMF components.
- It is shown that the overall prediction accuracy can be improved by reordering the channels, so that more correlated channels are put closer together. The channel reordering is formulated as the TSP. Since solving the TSP is computationally expensive, only the channels of the weakest UPs are reordered, and the corresponding predictors are retrained. Such a two-stage training extends other existing methods proposed in the literature.
- The improvements in the prediction accuracy due to the designed 2D symbol-EMD front-end with channel reordering are demonstrated numerically using a bank of the most common UPs, including DLinear, FITS, and TCN, respectively.
Furthermore, the following results were added to our conference version [34] of this paper. The channel reordering for the weakest predictors was proposed as a simple mechanism to further improve the overall forecasting accuracy. The TCN and the FITS single-channel predictors are now considered in addition to DLinear in our numerical experiments in order to show that the proposed front-end is effective with any UP. The numerical results are much more comprehensive, and they cover broader sets of parameter values, including evaluating different lengths of the look-back window and of the prediction horizon. The two new metrics, i.e., the MAE Reduction Rate (MAERR) and the RMSE Reduction Rate (RMSERR), are introduced as the relative reductions in the MAE and MSE values between two forecasting systems or configurations.
The remainder of this paper is organized as follows. Section 2 describes the key data processing modules, including the 2D EMD, Dlinear, FITS, and TCN single-channel predictors. The proposed two-stage Symbol-EMD-UP scheme is introduced in Section 3. Numerical results are presented in Section 4. Finally, the paper is concluded in Section 5.
2. Data Processing Modules
This section describes several data processing modules that are used to predict multivariate time series. The processing is performed on sample segments that are 2D matrices of equal sizes. Specifically, the 2D-EMD module decomposes the matrix inputs into a sum of the IMF matrix components and the residual matrix trend. The EMD is particularly effective when the input time series are non-linear and non-stationary. In case of linear and stationary time series, the decomposition and ARIMA modeling of the seasonal, trend, and residual noise components may be preferred.
The forecasting module is designed as the bank of independent single-channel predictors. Each predictor takes as the input a univariate time series of finite length representing the look-back window, and generates another univariate segment of predicted samples over a given forecasting horizon. In numerical simulations, the previously proposed DLinear, FITS, and TCN schemes were chosen as the predictors, since they are relatively simple, interpretable, and exploit different forecasting paradigms. In particular, the DLinear decomposes the univariate time series into a trend and a residual component. The FITS transforms the input samples into the frequency domain in order to leverage the spectral sparsity in making the predictions. The TCN learns temporal dependencies in the time series using causal and dilated convolutions.
2.1. A 2D-EMD Module
The EMD decomposes the signal into progressively lower-frequency IMF components and the residual trend using sifting. Thus, given a 2D matrix symbol, , of samples, the goal is to find m IMF components, , and the residual trend, , i.e.,
The sifting process to obtain decomposition (1) is performed recursively using the following steps [35]:
- Input normalization: The input samples are transformed to using the min–max normalization, i.e.,The normalization ensures consistent properties across space and time for extrema detection and envelope interpolation.
- Boundary extension: The normalized symbols are extended to using mirror-padding reflecting their values along the horizontal and vertical directions. This creates larger matrices in which the original samples are surrounded by their mirrored copies. It improves the accuracy of extrema detection near the original symbol boundaries, which yields smoother and more consistent IMF components.
- Extrema detection: The local maxima and minima, and , respectively, within the symbol are identified by comparing the samples with their neighboring values using a sliding 2D window. The extrema detection can be repeated multiple times in order to improve the robustness.
- Envelope construction: The extrema are interpolated in order to construct the upper and lower envelopes, and , respectively, using the bivariate splines , i.e.,
- Mean removal: The mean envelope is computed and subtracted, i.e.,The resulting symbol becomes the candidate IMF after one sifting iteration.
- The IMF criterion check: Steps 3–5 are performed repeatedly until the IMF condition is satisfied. In such a case, satisfying the IMF condition becomes the i-th IMF component, .
- Residual update and decomposition loops: The extracted IMF components are subtracted from the current residual until the remaining residual have no significant oscillatory modes, and the sifting process of extracting the IMF components can be terminated.
- Inverse (re-)normalization: At the final step, all extracted IMF components are re-normalized using an inverse min–max normalization in order to restore the scale of the original data samples.
The number of extracted IMF components can be also predefined, or it can be limited by the maximum number of sifting iterations. Alternative stopping criteria can evaluate the smoothness of the current envelope [36], the difference in means between two successive envelopes, the absolute value of the mean of the current envelope, and the current number of local extrema that are available for spline approximation.
The 2D-EMD described above is illustrated in Figure 1, assuming the data symbols of samples each. The color intensity signifies the sample amplitudes. The IMF components shown in Figure 1 are iteratively extracted from each symbol using sifting. The sifting identifies the local extrema in order to obtain the signal envelopes. The first component IMF 1 captures the fine-grained high-frequency textures. The other two components IMF 2 and IMF 3 contain increasingly coarser patterns of lower frequencies. Finally, the residual component represents a smooth trend without any obvious local extrema. It should be noted that this is a different strategy from traditional decomposition of the time series into seasonality, trend, and residual noise.
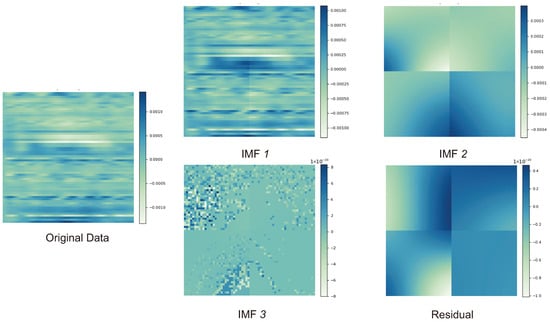
Figure 1.
An example of the 2D-EMD for data symbols.
The complexity of performing the 2D-EMD for a data symbol of samples is equal to
where k denotes the average number of sifting iterations. The term represents the complexity of element-wise operations in Steps 3 and 5. The term represents the complexity of finding the bivariate spline interpolation to obtain the upper and lower envelopes, with n denoting the number of local maxima and minima, respectively. Moreover, since the EMD only needs to be performed once for each data symbol, its complexity is acceptable.
It should be noted that the EMD and its 2D extension (i.e., 2D EMD) differ fundamentally from classical time series models, such as AR and random walk models, in both their formulation as well as the underlying assumptions. The AR and random walk models are parametric, and they are built upon defined stochastic structures. Specifically, the AR models exploit the defined linear relationships between the sequence values while assuming their Gaussianity and stationarity. The model parameters representing the temporal dependencies can be estimated from observations. On the other hand, the random walk model assumes independent and identically distributed zero-mean increments to model the sequence values. In contrast, the EMD adaptively decomposes the signal into a set of frequency-separated IMF components without imposing any requirements on the signal linearity and stationarity.
2.2. UP Modules
The UP modules DLinear, FITS, and TCN are considered for the downstream forecasting of individual IMF components in each time series channel. They were proposed previously in the literature, and they are briefly outlined here for convenience. These univariate predictors representing the distinct forecasting algorithms allow us to evaluate the proposed front-end for spatial–temporal feature extraction from multivariate time series, which improves the prediction accuracy and robustness of the standalone UPs.
The DLinear is a relatively simple linear framework for forecasting time series [6]. Despite its simple architecture, it can often achieve a superior performance over many different datasets, and the predictions are also interpretable and numerically efficient. The core idea is to decouple the input univariate time series X into the trend, , and the residual, , i.e.,
Each component is then predicted individually. It allows for balancing long-term trends with short-term variations. The overall prediction is obtained by linearly combining the predicted components as
where and denote the learnable weights for the residual and the trend, respectively. The principle of time series forecasting using DLinear is sketched in Figure 2.
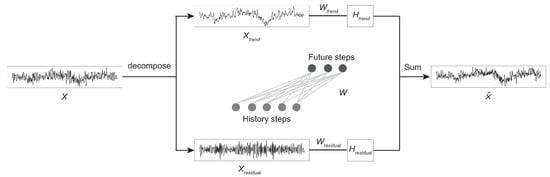
Figure 2.
The time series forecasting using DLinear.
The FITS is another lightweight linear architecture for forecasting time series [13]. The forecasted values are obtained in the frequency domain as indicated in Figure 3. In particular, the input samples are transformed to the frequency domain using FFT. The frequency domain representation can naturally capture non-linear dependencies and global periodic features. The frequency spectrum is interpolated to increase the frequency resolution. The interpolated spectrum is then passed through a learnable frequency mapping module such as a feedforward neural network. Finally, the predicted values are obtained by applying the inverse FFT.
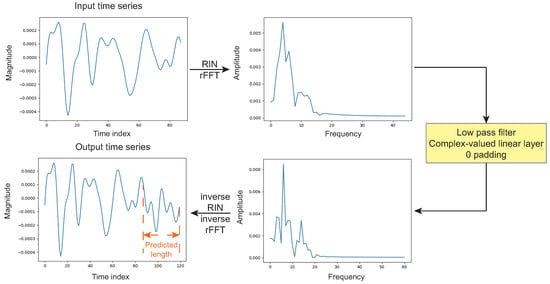
Figure 3.
The time series forecasting using FITS.
The TCN models the time series as a hierarchical structure of dilated causal convolution blocks, as shown in Figure 4 [32]. It enables learning the multi-scale temporal patterns, and enforces the strict temporal causality by ensuring that each output depends solely on its past inputs. In addition to stacked blocks of dilated convolutions, the layer normalizations, ReLU activations, and residual connections are used.
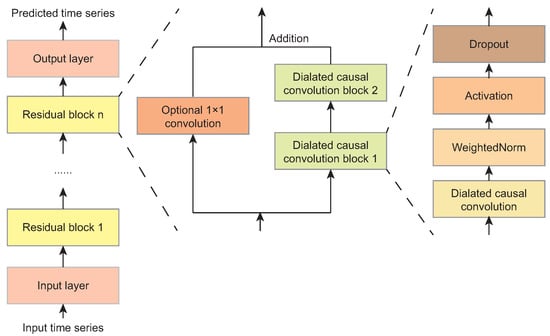
Figure 4.
The time series forecasting using the TCN.
3. A Two-Stage Symbol-EMD-UP
This section introduces the overall architecture of the proposed two-stage Symbol-EMD-UP for forecasting multivariate time series. The main motivation of this architecture is to improve the forecasting accuracy of the single-channel UP modules. This can be achieved by capturing the spatial dependencies within the data segments using the EMD. In particular, consider the vectors, , across W time series at time, t. Given the look-back window, , the objective is to predict the values over the horizon, , i.e.,
The samples are predicted in two stages. The objective of having the second stage is to improve the accuracy of the first stage by boosting the performance of the weak predictors. Thus, the input multivariate time series, , are first segmented into equal-sized data symbols. Each data symbol is then independently decomposed into m IMF components:
where .
Let denote the j-th univariate time series, . The UP modules learn the projection functions, , , to forecast the future values, i.e.,
Furthermore, and importantly, since the overall forecasting accuracy is usually dominated by a few weak predictors, in the second stage, a small number k of these predictors with the largest testing loss is retrained as follows. The basic idea is to reorder the corresponding input time series prior to the EMD. The reordered values at time t are denoted as , . Then, all steps performed for all W channels in the first stage are repeated, but now only for the k channels corresponding to the k selected predictors. The newly learned projection functions are denoted as . The final predicted outputs are obtained by summing up the corresponding predicted IMF components and the residual trends.
3.1. TSP-Based Channel Reordering
The aim of channel reordering is to place more correlated channels closer together, so the spatial coherence of channels is increased. Such a reordering can be formulated as the TSP problem [37]. In particular, within the context of channel reordering, the task is to visit each channel exactly once while the path cost is the accumulated correlations between consecutive channels; the correlation between the first and the last visited channels can be ignored. The diagram of the reordering process is depicted in Figure 5.
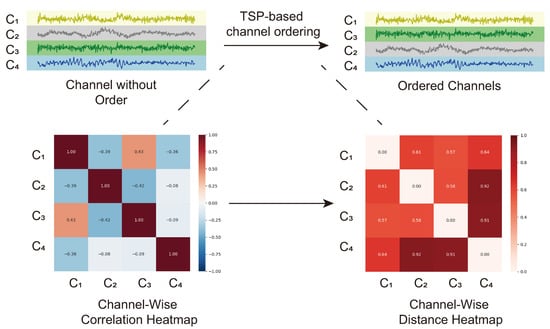
Figure 5.
The TSP-based channel reordering of multivariate time series.
Let be the data matrix of W channels and T temporal samples, and be the set of channel indices. Denote also to be the covariance matrix of the correlation coefficients between the channels. Define also the corresponding distance matrix having the elements, , where denotes the absolute value (i.e., larger correlations have smaller distances). The task is to find a permutation of the channel indices, , to minimize the total path cost (distance), i.e.,
Since this is known to be an NP-hard problem, we adopt a simple greedy algorithm to find an approximate solution. Thus, starting from an arbitrary channel, , the next channel is chosen among the unvisited channels as the one having the largest correlation (i.e., the smallest distance):
The TSP-based channel reordering is interpretable as making more correlated channels to be more adjacent, and it needs to be performed only once. Computing the distance matrix has the following complexity: . In addition, the greedy traversal to visit each channel exactly once has the quadratic complexity: . Hence, the total complexity of the TSP-based channel reordering is
3.2. The Overall Architecture
A block diagram of the two-stage Symbol-EMD-UP with channel reordering is shown in Figure 6. The input multivariate time series are usually first pre-processed to suppress the measurement noises, and to remove drifts and other undesirable artifacts. It is often performed by a purposely designed low-pass filter, employing the independent component analysis (ICA), and by subtracting a common average reference.
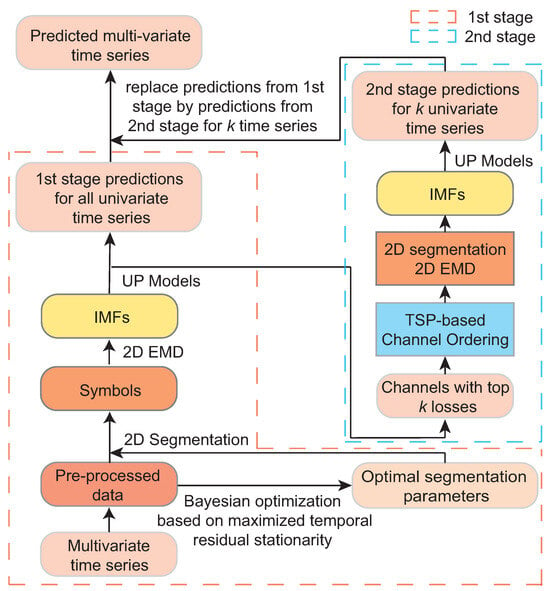
Figure 6.
A block diagram of the proposed two-stage Symbol-EMD-UP architecture for forecasting multivariate time series.
In the first stage, the pre-processed multivariate time series of samples are segmented into the 2D data symbols of equal-sized samples. A zero-padding can be considered in the vertical (across channels) and in the horizontal (temporal) directions. The sample symbolization allows for performing the 2D EMD more effectively on the individual symbols rather than on the whole time series. The extracted IMF components and the residual trend are the matrices of size samples as indicated by (1). The parameters and are determined, so that, given the number m of IMF components, the residual trend is approximately stationary. The rationale for maximizing the stationarity of the residual is that more stationary residual is easier to describe while the corresponding IMF components are more informative, which leads to more accurate predictions as observed in our numerical experiments.
The stationarity of the residual trends is averaged over n 2D data symbols, i.e.,
where is the fraction of rows (temporal residual trends) in the j-th data symbol that are stationary according to the ADF test. Since the average stationarity is affected by the symbol size, the Bayesian search (optimization) has been adopted to find the optimal-symbol-size parameters, and , to maximize (15); the search procedure is outlined in Figure 7.
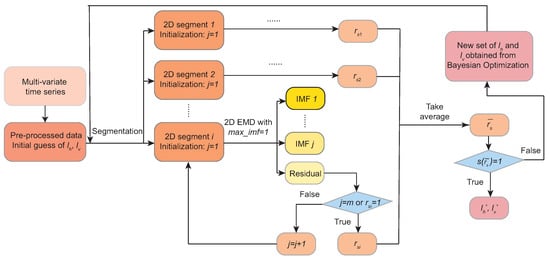
Figure 7.
The Bayesian optimization for finding the optimum symbol sizes, and , that maximize the average stationarity of the residual trends.
Finally, the rows of the extracted IMF component matrices are forecasted independently using their own pre-trained UP modules. Thus, there are UP modules required in total. In the second stage, as explained in the previous section, the channels corresponding to the k UPs with the largest testing losses are reordered, and these UPs are retrained again in order to improve the overall forecasting accuracy. In the last step, the row-by-row forecasted IMF components and the residual trends are summed up to obtain the W predicted horizons corresponding to the W look-back windows.
4. Numerical Experiments
Numerical experiments were performed using the publicly available EEG dataset [1]. It is a multivariate time series dataset consisting of EEG channels. The following subsections describe how the dataset was pre-processed, the performance evaluation metrics assumed, and the configuration of the experiments. Finally, the obtained results are presented and discussed.
The EEG dataset [1] contains the motor imagery (MI) signals, which is useful for developing brain–computer interfaces (BCIs) [38]. The time series are sampled at 512 samples per second (Hz). The actual sample values are reported in . A data subset for 10 subjects (participants), each containing 358,400 time samples over 64 channels, is considered. For each subject, there non-overlapping horizontal data segments of length samples.
The raw EEG signals are first cleaned up with the 4th-order Butterworth filter having passband frequencies between 0.5 and 70 Hz in order to remove the drifts and the spurious noises, and improve the signal-to-noise ratio. Other noises and non-brain-activity-related artifacts are eliminated by subtracting the common average reference, and subsequently, by using the ICA transform.
Additional insights into the forecasting performance can be obtained by examining how well the samples can be predicted in different frequency bands. Consequently, the original samples representing the ground-truth and the corresponding predicted signals were both filtered using the second-order Butterworth band-pass filter. The following canonical EEG bands were assumed: (1) the delta band (0.5–4 Hz), (2) the theta band (4–8 Hz), (3) the alpha band (8–13 Hz), (4) the beta band (13–30 Hz), and (5) the gamma band (30–40 Hz). The filtering is performed along the temporal axis for each channel individually.
4.1. Evaluation Metrics
Let and represent the pre-processed data, and the corresponding predicted samples, respectively, consisting of univariate time series as indicated by the double subscripts. The forecasting accuracy is evaluated considering the following two performance metrics:
Furthermore, in order to compare the prediction accuracy of two different architectures, or one model with two different configurations, the following metrics are also considered:
where and are the predicted samples of the two models considered. Thus, the metrics (17) express the reduction rate in the forecasting performance of model#2 compared to model#1. The reduction rates are unitless, or they can be expressed as a percentage change in the MAE or the RMSE values, respectively. It should also be noted that even though the Mean Absolute Percentage Error (MAPE) metric is commonly used for evaluating the performance of forecasting algorithms, our numerical results revealed that MAPE measurements tend to have a large variability, which makes it difficult to reliably evaluate and compare the performances. On the other hand, the MAE and RMSE values appear to be much more stable and consistent, and they show a clear improvement in the performance of the proposed scheme, so only these metrics are reported in this paper.
4.2. Experimental Setting
The univariate time series representing the IMF components, including the trend, are forecasted independently using DLinear, FITS, and TCN, respectively. In order to evaluate the impact of different data processing steps on the achieved forecasting accuracy, the baseline system employs only the bank of UPs immediately after the initial data pre-processing step. The second system adds the EMD step prior to the UP bank. The third system also divides the input multivariate time series into symbols as an extension of the second system. Finally, the fourth system represents the complete proposed two-stage Symbol-EMD-UP with channel reordering and with all the data processing steps included. In all evaluations, the EEG dataset is deterministically split into the training, validation, and testing datasets. Specifically, the first of samples are used for the UP training, the next of samples are used for the validation, and the last of samples are used for testing. The validation dataset is mainly used for selecting and fine-tuning the model parameters. The forecasting performance of different schemes is reported for the unseen test data. Such data splitting should be sufficient to avoid information leakage, even though it was not verified explicitly by performing the designated experiments.
The key parameter values are listed in Table 1. The horizontal length of the data symbols, , is chosen to maximize the temporal stationarity of the EMD residuals as discussed above. The optimum value is searched over the range, , where (s) is the sampling period. Such a range allows for exploring a sufficient number of temporal scales corresponding to fine as well as coarser time resolutions. For the vertical symbol size, , since there are only 64 channels available, only three possible vertical equal-sized partitions are considered. The Adam optimizer is used to find the learning rate for each model configuration within the range, . The training epoch is set to 100 samples, unless specified differently.

Table 1.
Key parameter values.
In order to decide on the number of IMF components, m, the fraction of the temporal residuals that are stationary is evaluated for several increasing values of m. The results of these experiments are shown in Figure 8. The stationarity ratio increases with m, even though its fluctuations also increase. For smaller values of m, the IMF components mainly capture the high-frequency but relatively stationary components, while the residual represents a low-frequency trend with transitions that are less stationary. This phenomenon causes the stationarity ratio to be smaller at the beginning of the curve in Figure 8. As m increases, more lower-frequency and non-stationary components are progressively separated into the IMF components, leaving the smoother residual. It leads to a steady rise in the values of the stationarity ratio, especially for .
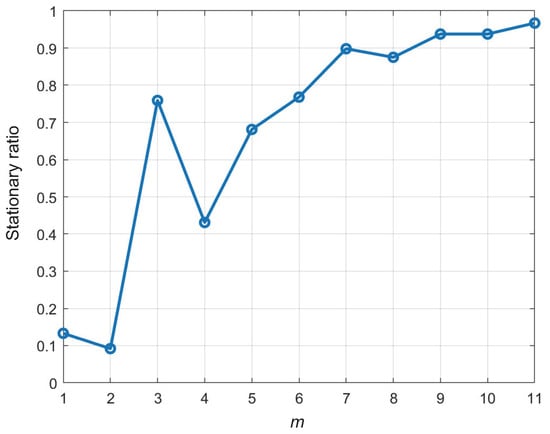
Figure 8.
A stationarity ratio of the temporal (horizontal) segments as a function of the number of IMF components, m.
The numerical examples presented below assume that . This value was chosen as it provides a substantial improvement in the stationarity of the IMF components, while requiring a small number of iterations in the EMD process. It is a good trade-off, ensuring that the extracted IMF components contain sufficient spatial information for subsequent independent forecasting by a bank of UPs. It also limits the number of less informative IMF components that would otherwise require the training and testing of a larger number of predictors for each channel.
In the numerical examples, the look-back window size is set to 88, 108, and 128 time steps, and the prediction horizon window is set to 32, 48, and 64 time steps, respectively. These values correspond to the short and medium sequences in the context of time series modeling and forecasting. The corresponding windows preserve fine-grained temporal and spatial information while ensuring that the model can discover the local temporal structures present in the data. In absolute terms, considering a sampling rate of 512 Hz, these windows represent the durations of only a few hundred milliseconds. These durations are sufficient to capture the essential neurophysiological dynamics, including the event-related potentials (ERPs) and the phase-locked responses.
For the FITS, the cut-off frequency for the frequency domain interpolation is set to 40 Hz following a series of empirical evaluations. The frequencies below this cut-off are usually associated with structured neural activities and other cognitive processes. These frequencies also tend to be more predictable and stable over time. In contrast, the high-frequency components are more difficult to model accurately, and their variability degrades the forecasting performance. The chosen cut-off value thus reflects a pragmatic trade-off between preserving information and signal structure while suppressing the high-frequency components that may hinder the model generalizations in forecasting.
In order to select the number of channels k to be reordered and predicted again, the fraction of stationary vertical data segments was evaluated for several values of k. Every data subset of k channels was tested for stationarity. The results of these experiments are reported in Figure 9 as a function of k. In particular, both curves show increasing trends as k increases. It reflects a natural tendency of the ADF test that when more channels are considered, their stationarity becomes more likely, since by combining more samples, the out-of-distribution variations are reduced. Nevertheless, the stationarity curve for channel reordering consistently stays above the curve without channel reordering except when . It clearly indicates that the reordering strategy considered enhances the stationarity. Even though larger values of k yield higher stationarity, has been chosen to produce the numerical results. Such a value provides a good trade-off between the improvement in forecasting accuracy, and the numerical complexity of the TSP-based channel reordering. Moreover, the difference in stationarity between the reordered and the original data for is comparable to that for . This suggests that the benefits of reordering may quickly level-off for larger values of k.
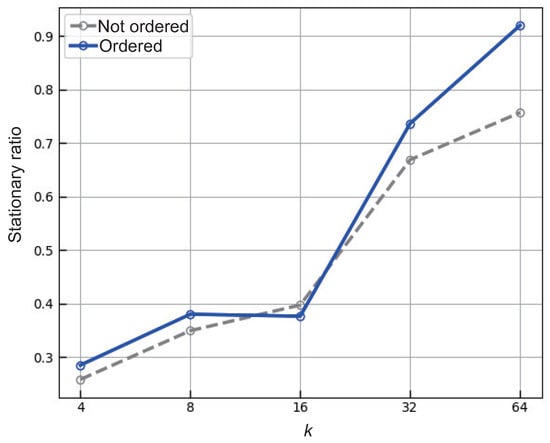
Figure 9.
A stationarity ratio of the vertical data segments as a function of the number of reordered channels, k.
4.3. Comparison of Forecasting Accuracy of Different Systems
Table 2, Table 3 and Table 4 report comprehensive evaluations of the forecasting performances of three baseline UP models, i.e., DLinear, FITS, and TCN, as well as the progressively enhanced systems in order to assess the effectiveness of each data processing module. Each system is trained and tested over the look-back window of 88, 108, and 128 samples, assuming the predicted horizons of 32, 48, and 64 samples, respectively. The performances are evaluated assuming the metrics defined in (16) and (17). The latter two metrics provide an intuitive insight into how much the MAE and the RMSE can be reduced by adopting more complex models. Note also that smaller MAE and RMSE values mean a better performance, whereas a larger improvement in the performance relative to a baseline system is indicated by larger MAERR and RMSERR values. The best performance values are highlighted in bold in the tables below.

Table 2.
Forecasting accuracies involving DLinear UP.

Table 3.
Forecasting accuracies involving FITS UP.

Table 4.
Forecasting accuracies involving TCN UP.
It can be observed from Table 4 that, for most configurations, the proposed two-stage Symbol-EMD-UP with channel reordering improved the forecasting performance of the simple banks of UPs. Specifically, the MAE and RMSE values are reduced by 1.81% and 1.58%, respectively, using two-stage Symbol-EMD-DLinear with ordering, by 1.68% and 1.89%, respectively, using two-stage Symbol-EMD-FITS with ordering, and by 2.91% and 2.94%, respectively, using two-stage Symbol-EMD-TCN with ordering. Such improvements can be explained as follows. The Symbol segmentation module enables finding more informative IMF components, i.e., to more effectively capture the information patterns embedded in the data. The EMD module leverages the frequency-specific characteristics of data symbols, thus avoiding learning the complex cross-frequency dependencies. This has a benign effect on performing the independent predictions for individual IMF components. The channel reordering module is followed by retraining the weakest performing predictors, which can substantially improve the overall forecasting accuracy. Moreover, reordering only a small number of channels appears to be sufficient for achieving a good performance.
It can be observed from Table 2, Table 3 and Table 4 that when the size of the look-back window is unchanged while the horizon increases, there is a noticeable increase in both MAE and RMSE as one might expect. In Table 2 and Table 3, the models utilizing DLinear and FITS offer consistent performance gains from integrating symbolization, 2D EMD, and channel reordering modules in most system configurations. The results in Table 4 confirm that the second stage has a significant effect on improving the overall forecasting performance, which is larger than any improvements achieved in the first stage. The TCN appears to always outperform the other two UPs considered, since it can more readily model and learn multi-scale dependencies in time series. On the other hand, DLinear and FITS have simpler structures, which make them more dependent on the spatial patterns extracted by the Symbol-EMD front-end.
In addition, it can be concluded from Table 5 that the two-stage Symbol-EMD-TCN with channel reordering has the best performance in terms of the MAERR and the RMSERR than the other two UP systems. It suggests that the TCN can benefit more from the Symbol-EMD front-end, especially in the second stage, since it can model the dependencies among reordered channels more effectively. Note also that when the look-back window is 88 or 128 samples, and the prediction horizon is 64 samples, the RMSERR values are negative for the two-stage Symbol-EMD-TCN with channel reordering.

Table 5.
Error reduction rates for the three UPs considered.
4.4. Forecasting Accuracy in Different Frequency Bands
It is also useful to evaluate the forecasting accuracy of different systems in five canonical EEG frequency bands. These results are reported in Figure 10, Figure 11 and Figure 12 using again the MAE and the RMSE metrics. The systems considered include the baseline system employing DLinear, FITS, and TCN predictors, respectively, and their enhanced counterparts, which employ the Symbol-EMD front-end, and possibly also the second stage with channel reordering. The ground-truth and the predicted time series data in the defined frequency bands are obtained by band-pass filtering as explained at the beginning of this section. The performance of the proposed two-stage Symbol-EMD-UP system with channel reordering is labeled (for simplicity) as “ours” in the figures.
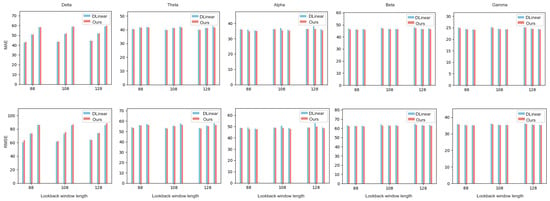
Figure 10.
The MAE and RMSE values for DLinear systems in different frequency bands.
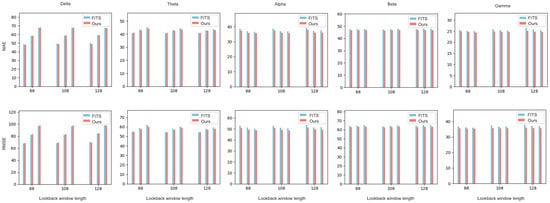
Figure 11.
The MAE and RMSE values for FITS systems in different frequency bands.
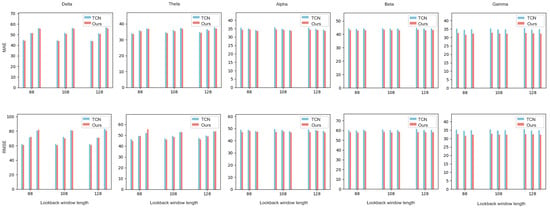
Figure 12.
The MAE and RMSE values for TCN systems in different frequency bands.
Table 6 reports the average MAERR and RMSERR values across all look-back window and horizon lengths, and the five frequency bands considered. It can be observed that the Symbol-EMD-DLinear with channel reordering exhibits larger MAE and RMSE values in the delta band compared to the baseline DLinear model, while consistently achieving smaller MAE and RMSE in the theta, alpha, beta, and gamma bands. Similar observations can be made when comparing the forecasting performance of the two-stage Symbol-EMD-FITS with channel reordering and the original FITS system. Although DLinear and FITS are well suited to model the signals in low-frequency bands, the noise induced by the 2D-EMD may eventually dominate. These results suggest that the proposed front-end may be less effective, or even detrimental, when modeling the time series data in the delta band. In the other four frequency bands, where the EEG signals exhibit more complex and rapidly changing oscillatory behaviors, the Symbol-EMD with channel reordering front-end enhances the effect of symbol segmentation and sample decomposition on forecasting, which is clearly measurable. In case of the TCN, the two-stage Symbol-EMD-TCN with channel reordering always achieves smaller MAE and RMSE values in all the frequency bands considered, including the delta band. This suggests that the convolutional architecture of the TCN benefits more effectively from the enhanced input representations produced by the Symbol-EMD with the channel reordering front-end. Thus, the TCN is more robust to the distortions possibly introduced by the front-end pre-processing stage, and it is also better equipped to extract meaningful features across all signal frequencies.

Table 6.
The error reduction rates (%) in different frequency bands.
4.5. Impact of Channel Reordering on Forecasting Accuracy
In order to investigate how channel reordering that is performed in the second stage affects the forecasting performance, Table 7, Table 8 and Table 9 report the MAERR and RMSERR values for the two-stage Symbol-EMD-UP, considering three different channel ordering strategies. In particular, the first TSP-based ordering was introduced in Section 3.1, and it is referred to herein as “more correlated channels more adjacent” (MCCMA) ordering. The second ordering is identical to the first one, except it makes “less correlated channels more adjacent” (LCCMA). The latter ordering method can be again formulated as the TSP and solved by a greedy algorithm. The third ordering simply sorts the channels in a descending order of their testing losses, and ignores channel correlations altogether; this ordering strategy is referred to as “not ordered” in the tables below.

Table 7.
The error reduction rates (%) for three channel reordering strategies and the two-stage Symbol-EMD-DLinear.

Table 8.
The error reduction rates (%) for three channel reordering strategies and the two-stage Symbol-EMD-FITS.

Table 9.
The error reduction rates (%) for three channel reordering strategies and the two-stage Symbol-EMD-TCN.
The empirical results reported in Table 7 and Table 8 for the three UPs considered demonstrate that, for most combinations of the look-back window and horizon lengths, the two-stage Symbol-EMD-UP framework benefits much more from the MCCMA ordering than from the other two ordering strategies. Even though only a small number of channels is selected for reordering in the second stage, the channel reordering has a clear observable effect on the forecasting accuracy. Consequently, we can conclude that channel reordering has a significant impact on the spatial patterns and information contained across multiple time series. For instance, the reordering affects the number and the locations of local extrema, which in turn influence the extraction of the IMF components. Moreover, placing highly correlated channels closer together causes the symbol matrices to be spatially smoother, which explains why it is beneficial for better separating the IMF components at different frequency scales. On the other hand, the other channel reordering strategies make the symbol matrices more discontinuous, which is equivalent to adding more noise to the samples. This makes extracting the modal structures and their forecasting more difficult.
5. Conclusions
A two-stage Symbol-EMD-UP with channel reordering was proposed for efficiently forecasting multivariate time series. The proposed scheme improves the performance of single-channel forecasting algorithms while retaining their interpretability. The basic idea is to create an interpretable front-end to effectively capture the spatial inter-dependencies across all data channels. In the first stage, the multivariate time series are segmented into equal-sized symbols. The data symbols are decomposed into a finite number of IMF components and the residual trend using the 2D EMD. The symbol size is optimized using Bayesian optimization to maximize the temporal stationarity of the residuals. Each IMF component is then independently predicted using a simple UP such as DLinear, FITS, and TCN. In the second stage, a small number of UPs with the largest testing errors are selected, and the corresponding channels are reordered to make more correlated channels to be more adjacent. The reordered channels undergo symbol segmentation again, and the EMD and the UP must be retrained.
The numerical results were produced for a publicly available EEG dataset. The improvements in the forecasting accuracy of the proposed scheme were evaluated for different combinations of the look-back window and prediction horizon lengths. Specifically, the MAE and RMSE were reduced by 1.81% and 1.58% with the two-stage Symbol-EMD-DLinear; by 1.68% and 1.89% with the two-stage Symbol-EMD-FITS; and by 2.91% and 2.94% with the two-stage Symbol-EMD-TCN, respectively. Among these models, the two-stage Symbol-EMD-TCN with channel reordering achieved the most consistent and the most substantial improvements in performance. The forecasting experiments were also carried out in different frequency bands corresponding to the five standard EEG bands. The TCN-based schemes had superior performance across all these bands, whereas the DLinear and FITS-based schemes struggled to achieve a good performance in the low-frequency delta band. This deficiency could be traced to the problem with performing the EMD for signals in the delta band, which affects the DLinear and the FITS, but not the TCN.
The channel reordering has a major impact on forecasting accuracy. It can be exploited in retraining weak predictors to boost the overall performance. A multi-stage forecasting step performed in several rounds could be implemented more effectively by reusing information from the previous stages as priors for predictors training at subsequent stages. In addition, the predictors can benefit greatly from specializing the forecasting algorithms to different additive components and frequency bands. Segmenting multivariate time series into equal-sized overlapping or non-overlapping data symbols not only supports effective implementations of the data processing algorithms, but it also appears to have a positive impact on the performance.
Future work may investigate the forecasting methods when the output spatial–temporal resolution of the predicted samples is different from the spatial–temporal resolution of the input samples. In addition, other strategies for designing spatial–temporal pre-processing could be investigated to improve not only forecasting performance, but also the training efficiency of state-of-the-art forecasting models, which often involve complex deep learning modules.
Author Contributions
Conceptualization, Y.Y. and P.L.; methodology, Y.Y., P.L., W.Z., Q.Z. and Y.G.; software, Y.Y., W.Z. and Q.Z.; validation, Y.Y.; formal analysis, Y.Y., W.Z. and Q.Z.; investigation, Y.Y., P.L., W.Z., Q.Z. and Y.G.; resources, Y.G.; data curation, Y.Y., W.Z. and Q.Z.; writing—original draft preparation, Y.Y.; writing—review and editing, P.L.; visualization, Y.Y.; supervision, P.L. and Y.G.; project administration, P.L. and Y.G.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a research grant from Zhejiang University.
Data Availability Statement
The data presented in this study are available in GigaScience at https://academic.oup.com/gigascience/article/6/7/gix034/3796323, reference number gix034.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cho, H.; Ahn, M.; Ahn, S.; Kwon, M.; Jun, S. EEG Datasets for Motor Imagery Brain Computer Interface. GigaScience 2017, 6, gix034. [Google Scholar] [CrossRef]
- Pankka, H.; Lehtinen, J.; Ilmoniemi, R.J.; Roine, T. Enhanced EEG Forecasting: A Probabilistic Deep Learning Approach. Neural Comput. 2025, 37, 793–814. [Google Scholar] [CrossRef] [PubMed]
- Diebold, F.X. Elements of Forecasting, 4th ed.; Thomson South-Western: Mason, OH, USA, 2006. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. Proc. NeurIPS 2021, 34, 22419–22430. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? Proc. AAAI 2023, 1248, 11121–11128. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Cao, W.; Bian, J.; Yi, X.; Zheng, S.; Li, J. Less Is More: Fast Multivariate Time Series Forecasting with Light Sampling-oriented MLP Structures. arXiv 2022, arXiv:2207.01186. [Google Scholar]
- Das, A.; Kong, W.; Leach, A.; Mathur, S.K.; Sen, R.; Yu, R. Long-Term Forecasting with TIDE: Time-Series Dense Encoder. arXiv 2023, arXiv:2304.08424. [Google Scholar]
- Lin, S.; Lin, W.; Wu, W.; Chen, H.; Yang, J. SparseTSF: Modeling Long-Term Time Series Forecasting with 1K Parameters. In Proceedings of the 41st ICML, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Han, L.; Ye, H.J.; Zhan, D.C. The Capacity and Robustness Trade-Off: Revisiting the Channel Independent Strategy for Multivariate Time Series Forecasting. IEEE Trans. Knowl. Data Eng. 2024, 36, 7129–7142. [Google Scholar] [CrossRef]
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do We Really Need Deep Learning Models for Time Series Forecasting? arXiv 2021, arXiv:2101.02118. [Google Scholar]
- Ekambaram, V.; Jati, A.; Nguyen, N.; Sinthong, P.; Kalagnanam, J. TSMixer: Lightweight MLP-Mixer Model for Multivariate Time Series Forecasting. In Proceedings of the 29th ACM CKDDM, Long Beach, CA, USA, 6–10 August 2023; pp. 459–469. [Google Scholar]
- Xu, Z.; Zeng, A.; Xu, Q. FITS: Modeling Time Series with 10K Parameters. In Proceedings of the 12th ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Duarte, F.S.; Rios, R.A.; Hruschka, E.R.; de Mello, R.F. Decomposing Time Series Into Deterministic and Stochastic Influences: A Survey. Digit. Signal Process. 2019, 95, 102582. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 3. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly Streamflow Prediction Using Modified EMD-Based Support Vector Machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Chen, Y.; Zhang, H.; Cheng, C. Annual Streamflow Time Series Prediction Using Extreme Learning Machine Based on Gravitational Search Algorithm and Variational Mode Decomposition. J. Hydrol. Eng. 2020, 25, 04020008. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Wan, X.; Xu, B.; Zhu, F.; Chen, J. Hydrological Time Series Forecasting via Signal Decomposition and Twin Support Vector Machine Using Cooperation Search Algorithm for Parameter Identification. J. Hydrol. 2022, 612, 128213. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Yin, Z.; Yang, L.; Singh, V.P. Two-Phase Extreme Learning Machines Integrated with the Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Algorithm for Multi-Scale Runoff Prediction Problems. J. Hydrol. 2019, 570, 167–184. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Ma, C.; Bai, Y. Improving the Prediction Accuracy of Monthly Streamflow Using a Data-Driven Model Based on a Double-Processing Strategy. J. Hydrol. 2019, 573, 733–745. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Q.; Chau, K.; Hu, H.; Zang, H.; Xu, D.M. An Enhanced Monthly Runoff Time Series Prediction Using Extreme Learning Machine Optimized by Salp Swarm Algorithm Based on Time Varying Filtering Based Empirical Mode Decomposition. J. Hydrol. 2023, 620, 129460. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Behboodi, A.; Bahrini, A. A novel hybrid model to forecast seasonal and chaotic time series. Expert Syst. Appl. 2024, 239, 122461. [Google Scholar] [CrossRef]
- Fan, G.; Wei, H.; Huang, H.; Hong, W. Application of ensemble empirical mode decomposition with support vector regression and wavelet neural network in electric load forecasting. Energy Sources Part B Econ. Plan. Policy 2025, 20, 2468687. [Google Scholar] [CrossRef]
- Zhong, B.; Yang, L.; Li, B.; Ji, M. Short-term power grid load forecasting based on VMD-SE-Bilstm-Attention hybrid model. Int. J.-Low-Carbon Technol. 2024, 19, 1951–1958. [Google Scholar] [CrossRef]
- Wu, B.; Wang, L. Two-stage decomposition and temporal fusion transformers for interpretable wind speed forecasting. Energy 2024, 288, 129728. [Google Scholar] [CrossRef]
- Liang, P.; Zhang, Y.; Ding, Y.; Chen, J.; Madukoma, C.S.; Weninger, T.; Shrout, J.D.; Chen, D.Z. H-EMD: A Hierarchical Earth Mover’s Distance Method for Instance Segmentation. IEEE Trans. Med. Imaging 2022, 41, 2582–2597. [Google Scholar] [CrossRef]
- Yang, L.; Lu, F.; Zhang, T.; Chen, J. Texture Feature Extraction of Image Based on 2D Hilbert-Huang Transform and Multifractal Analysis. In Proceedings of the ICICML, Chengdu, China, 3–5 November 2023; pp. 57–63. [Google Scholar] [CrossRef]
- Ma, P.; Ren, J.; Sun, G.; Zhao, H.; Jia, X.; Yan, Y.; Zabalza, J. Multiscale Superpixelwise Prophet Model for Noise-Robust Feature Extraction in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, R.; Xu, Z.; Lv, C.; Bi, R. Prediction of Soil Nutrients Based on Topographic Factors and Remote Sensing Index in a Coal Mining Area, China. Sustainability 2020, 12, 1626. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Dickey, D.A. 192-30: Stationarity Issues in Time Series Models. In Proceedings of the SUGI 30, Philadelphia, PA, USA, 10–13 April 2005; pp. 1–17. [Google Scholar]
- Yu, Y.; Loskot, P.; Zhang, W.; Zhang, Q.; Gao, Y. Joint Multivariate Time Series Forecasting Using Empirical Symbol Mode Decomposition Modeling. In Proceedings of the ICCCM, Okinawa, Japan, 11–13 July 2025; pp. 1–10. [Google Scholar]
- Koh, M.S.; Rodriguez-Marek, E.; Fischer, T.R. A New Two Dimensional Empirical Mode Decomposition for Images Using Inpainting. In Proceedings of the 10th ICSP, Beijing, China, 24–28 October 2010; pp. 13–16. [Google Scholar] [CrossRef]
- Laszuk, D. Python Implementation of Empirical Mode Decomposition Algorithm. GitHub Repository. 2017. Available online: https://github.com/laszukdawid/PyEMD (accessed on 5 July 2025).
- Déaz-Rós, D.; Salazar-González, J.J. Mathematical Formulations for Consistent Travelling Salesman Problems. Eur. J. Oper. Res. 2024, 313, 465–477. [Google Scholar] [CrossRef]
- Aggarwal, S.; Chugh, N. Review of Machine Learning Techniques for EEG Based Brain Computer Interface. Arch. Comput. Methods Eng. 2022, 29, 3001–3020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).