An Efficient Sparse Twin Parametric Insensitive Support Vector Regression Model

Abstract

This paper proposes a novel sparse twin parametric insensitive support vector regression (STPISVR) model, designed to enhance sparsity and improve generalization performance. Similar to twin parametric insensitive support vector regression (TPISVR), STPISVR constructs a pair of nonparallel parametric insensitive bound functions to indirectly determine the regression function. The optimization problems are reformulated as two sparse linear programming problems (LPPs), rather than traditional quadratic programming problems (QPPs). The two LPPs are originally derived from initial L1-norm regularization terms imposed on their respective dual variables, which are simplified to constants via the Karush–Kuhn–Tucker (KKT) conditions and consequently disappear. This simplification reduces model complexity, while the constraints constructed through the KKT conditions— particularly their geometric properties—effectively ensure sparsity. Moreover, a two-stage hybrid tuning strategy—combining grid search for coarse parameter space exploration and Bayesian optimization for fine-grained convergence—is proposed to precisely select the optimal parameters, reducing tuning time and improving accuracy compared to a singlemethod strategy. Experimental results on synthetic and benchmark datasets demonstrate that STPISVR significantly reduces the number of support vectors (SVs), thereby improving prediction speed and achieving a favorable trade-off among prediction accuracy, sparsity, and computational efficiency. Overall, STPISVR enhances generalization ability, promotes sparsity, and improves prediction efficiency, making it a competitive tool for regression tasks, especially in handling complex data structures.

1. Introduction

Since support vector machine (SVM) was first proposed by Vapnik et al. (1995) [1], it has become one of the most widely used machine learning algorithms, renowned for its excellent statistical properties and superior generalization performance. Support vector regression (SVR) [2,3,4,5,6,7,8], an extension of SVM for regression, applies the concept of support vectors (SVs) to handle regression tasks. By mapping samples from the input space into a high-dimensional feature space, SVR constructs a regression function with strong generalization capability. The SVs are then utilized to predict outcomes, effectively modeling nonlinear relationships within the data.

Although SVR has been successfully applied across various fields, it requires solving a large single quadratic programming problem (QPP) with three sets of constraints, each as many as the data points. As the dataset size grows and the feature dimensions increase, both the computational complexity and storage requirements of SVR escalate significantly, posing substantial challenges for large-scale data applications. To overcome these limitations, researchers have proposed numerous SVR variations from different perspectives [9,10,11,12,13], aiming to enhance its performance.

Among these variations, Peng [9] proposed twin support vector regression (TSVR), inspired by the concept of the twin support vector machine (TWSVM) [14]. TSVR indirectly optimizes the regression function through a pair of $ϵ$-insensitive down-bound and up-bound functions. TSVR fundamentally differs from classical SVR in that it solves two smaller-sized QPPs instead of a single large QPP, as required by traditional SVR. This strategy theoretically enables TSVR to operate faster than classical SVR [9]. However, in practice, the prediction speed of TSVR is noticeably slower than that of classical SVR due to the formulation of its augmented vectors [11]. Additionally, TSVR assumes a uniform noise level across the entire domain of the training data, which limits its applicability in more complex scenarios. In the same year, Hao [12] introduced a novel parametric-insensitive v-support vector regression (par-v-SVR) by incorporating a parametric-insensitive loss function into the framework of v-support vector regression (v-SVR) [13]. This approach is better suited for datasets with heteroscedastic noise compared to classical SVR or v-SVR. Nevertheless, despite this improvement, par-v-SVR still involves solving a large QPP, resulting in high computational complexity and a learning speed comparable to that of classical SVR.

Based on the twin parameter margin support vector machine (TPMSVM) [15], Peng [11] proposed the twin parametric-insensitive support vector regression (TPISVR), which successfully combines the advantages of both TSVR [9] and par-v-SVR [12]. The core strategy of TPISVR involves solving two smaller-sized QPPs, similar to TSVR, which significantly enhances its learning speed compared to par-v-SVR and classical SVR. At the same time, TPISVR effectively handles heteroscedastic noise structures, similar to par-v-SVR. An additional advantage of TPISVR is its parameters can control the fractions of SVs and errors of two bounds. Moreover, TPISVR achieves comparable generalization performance to par-v-SVR, TSVR, and SVR. However, similar to TSVR, TPISVR loses its sparsity due to the formulation of their augmented vectors [11], which results in slower prediction speed and suggests that its generalization ability still requires further improvement.

In recent years, sparse learning has emerged as a significant research direction in the fields of machine learning. Its primary objective is to optimize the computational efficiency of models while maintaining, or even enhancing, their predictive performance. This is particularly crucial for an algorithm where prediction speed is a decisive factor, especially in applications requiring real-time processing. As powerful tools for supervised learning, SVM, SVR, and their variations have attracted significant attention. The core idea behind these models is to reduce the number of SVs or features, enhance the sparsity of model solutions, and improve prediction speed. Researchers have explored various sparse methods from different perspectives, resulting in a range of innovative approaches aimed at improving operational efficiency, interpretability, and generalization ability. Among these, sparse regularization techniques have attracted particular attention due to their ability to induce sparsity [16,17,18,19,20]. Significant progress has been made by incorporating different sparse norms and integrating them with additional algorithmic strategies, thereby advancing the field of sparse learning [19,20,21,22,23,24,25]. For instance, Huang et al. [19] introduced a sparse learning algorithm for support vector machines (SVM) by incorporating a 0-pseudonorm regularization term. Although this method effectively promotes sparsity, it leads to significant computational challenges, requiring iterative reweighted optimization techniques to find approximate solutions. To improve sparsity and model interpretability, Bi et al. [20] proposed a two-stage sparse SVM framework that applies L1-norm regularization to both the primal weights and the dual variables. By reformulating the optimization as a linear programming problem (LPP), their method effectively reduces dimensionality and the number of SVs while improving generalization. However, representing the L1-norm requires introducing auxiliary variables, which increases the number of optimization variables and thus the overall algorithmic complexity. Nevertheless, the transformation of the original optimization problem into an LPP represents a powerful idea, as it enables efficient sparse model construction and effective variable selection within a well-understood optimization framework [26,27]. Building upon this foundation, Qu et al. (2024) [24] further investigated solution sparsity in the linear case. They proposed the Lin-STPMSVM model, which directly applies the L1-norm to the dual variables, offering a more efficient framework for sparse classification.

Despite significant advancements in sparsity research, real-world applications still face several key challenges, such as enhancing sparsity while maintaining model stability, balancing complexity and performance, and effectively handling complex data structures, including heteroscedastic noise, nonuniform distributions, and diverse sparsity requirements. Motivated by these challenges and inspired by prior work, we propose a sparse twin parametric insensitivity support vector regression model (STPISVR). Leveraging the strengths of the TPISVR framework, STPISVR introduces structural innovations to enhance solution sparsity and improve prediction efficiency.

The main contributions of this work are summarized as follows:

• An effective STPISVR model is introduced which encourages sparse solutions while retaining TPISVR’s ability for complex data structures, including heteroscedasticity.
• The optimization problems are reformulated as two sparse LPPs with constraints derived from the KKT conditions. One of these constraints corresponds to an L1-norm expression, which is shown to be a constant through further analysis of the KKT conditions. As a result, the explicit L1-norm regularization term is removed, and the resulting LPPs inherently produce sparse solutions due to their underlying geometric structure.
• This reformulation reduces computational complexity via two mechanisms: enhanced solution sparsity induced by the LPP structure and improved efficiency in solving LPPs instead of traditional QPPs.
• A two-stage hybrid parameter tuning strategy is adopted to improve both tuning accuracy and computational efficiency.
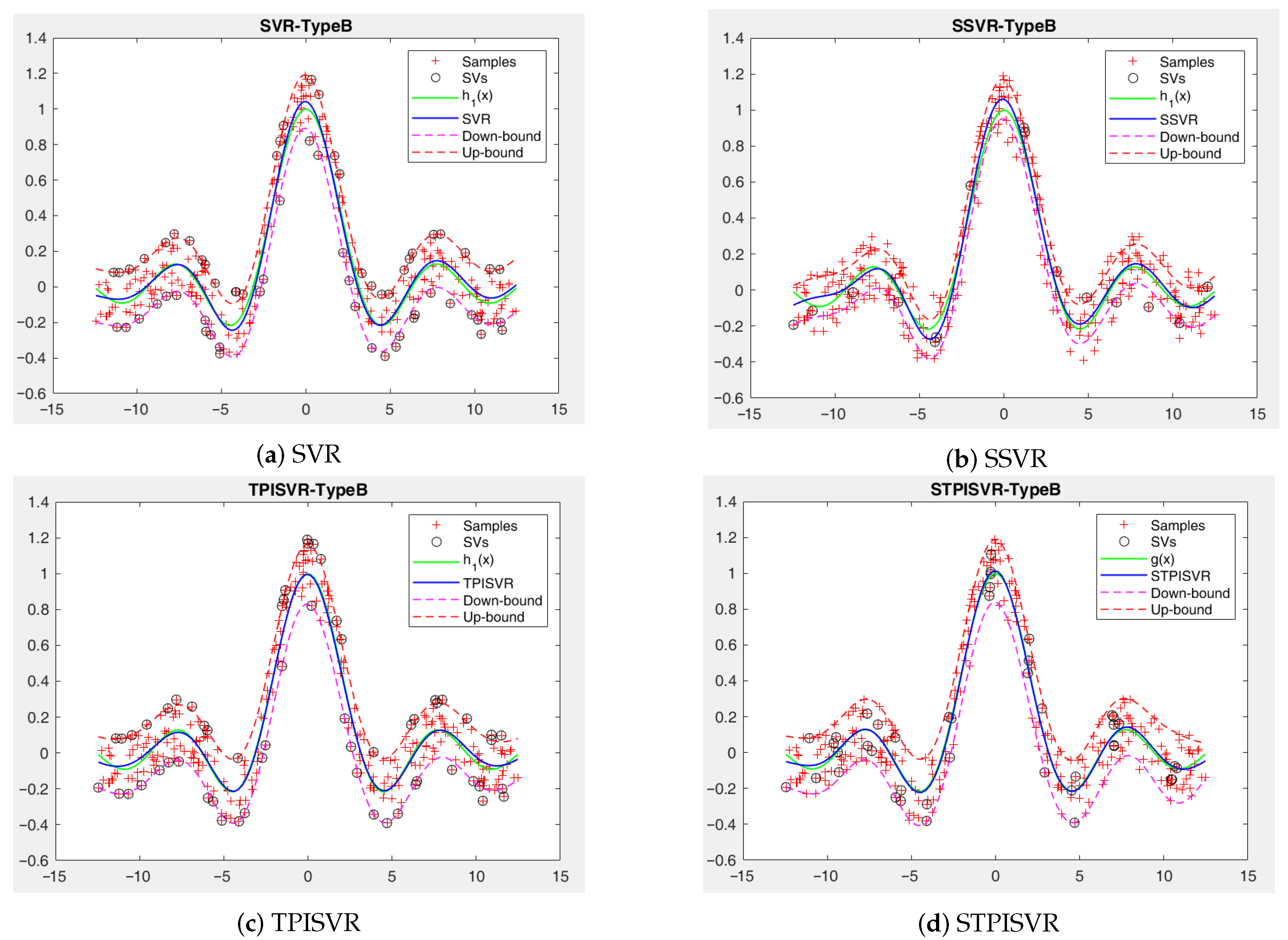
• Extensive experiments demonstrate that STPISVR significantly reduces SVs, enabling faster predictions without sacrificing accuracy, and achieves a superior trade-off among accuracy, sparsity, and computational efficiency, especially for complex data structures.

This paper is organized as follows: Section 2 provides a brief overview of related works; Section 3 introduces the STPISVR model and presents its relevant properties; Section 4 offers a discussion and comparison with several related models; in Section 5, we conduct numerical experiments on both synthetic and benchmark datasets to evaluate the performance of our sparse model; and finally, Section 6 presents conclusions and outlines directions for future research.

2. Related Works

In this section, we briefly review several related models that form the foundation for our proposed sparse method. For clarity and ease of reference,

Table 1. List of notations.

Notation	Description
$\mathbb{R}$	The real space
$\mathcal{H}$	The feature space
$|·|$	The cardinality of a set
${\parallel ·\parallel }_1$	The L1 norm: sum of absolute values of a vector’s components
${\parallel ·\parallel }_2$	The L2 norm: Euclidean norm of a vector
I	The index set of samples: $I=\{1,2,\dots ,|I\left|\right\}$
n	The dimension of samples
$x^p$	the pth sample, $x^p\in {\mathbb{R}}^{n\times 1},p=1,2,\dots ,\left|I\right|$
X	The samples matrix: $X=(x^1,x^2,\dots ,x^{\left|I\right|}{)}^{\mathrm{T}}\in {\mathbb{R}}^{\left|I\right|\times n}$ †
$y_p$	The response value of $x^p,p=1,2,\dots ,\left|I\right|$
Y	The response vector, $Y={(y_1,y_2,\dots ,y_{\left|I\right|})}^{\mathrm{T}}\in {\mathbb{R}}^{\left|I\right|\times 1}$
e	The vector of opportune dimensions with all components equal to 1
$w,w^d,w^u$	The normal vectors
$\phi (·)$	The mapping function from a original input space ${\mathbb{R}}^n$ to a feature space $\mathcal{H}$
$\phi \left(X\right)$	The mapping matrix: $\phi \left(X\right)={(\phi \left(x^1\right),\phi \left(x^2\right),\dots ,\phi \left(x^{\left|I\right|}\right))}^{\mathrm{T}}\in {\mathbb{R}}^{\left|I\right|\times n}$
$k(u,v)$	The kernel function: $k(u,v)=\phi {\left(u\right)}^{\mathrm{T}}\phi \left(v\right),u,v$ are all random n-dimensional vector
K	The kernel matrix: $K=\phi \left(X\right)\phi {\left(X\right)}^{\mathrm{T}}\in {\mathbb{R}}^{\left|I\right|\times \left|I\right|}$ with $k_{pq}=k(x^p,x^q),p,q\in I$
$K(X,x)$	The column vector: $K(X,x)={(k(x^1,x),k(x^2,x),\dots ,k(x^{\left|I\right|},x))}^{\mathrm{T}}\in {\mathbb{R}}^{\left|I\right|\times 1}$
${\xi }^{-},{\xi }^{+},{\xi }^d,{\xi }^u$	The slack variables
$\theta ,{\theta }_d,{\theta }_u$	The bias terms
$\rho ,{\rho }_d,{\rho }_u,v_d,v_u$	The regularization parameters
${\alpha }^{-},{\alpha }^{+}$	Lagrange multiplier vectors, the dual variables in SVR or SSVR
${\alpha }_p^{-}$	The pth element of ${\alpha }^{-},p\in I$
${\alpha }_q^{+}$	The qth element of ${\alpha }_q^{+}\in I$
${\alpha }^d,{\alpha }^u$	Lagrange multiplier vectors, the dual variables in TPISVR or STPISVR
${\alpha }_p^d$	The pth element of ${\alpha }^d,p\in I$
${\alpha }_q^u$	The qth element of ${\alpha }^u,q\in I$
$ϵ$	The insensitive tube parameter

Note: ^† The symbol ^T denotes the transpose of a matrix or vector.

lists some important notations used throughout this paper. In addition, all vectors in this article are assumed to be column vectors unless otherwise stated.

2.1. SVR Model

The classical SVR aims to determine a linear regression function in the feature space:

$$\begin{array}{c}\hfill f\left(x\right)=w^{\mathrm{T}}\phi \left(x\right)+\theta ,\end{array}$$

(1)

by introducing the kernel technique, the primal problem for classical SVR in nonlinear cases (for linear cases, the kernel function $\phi (·)$ reduces to the identity function; the other models discussed later follow a similar approach) [2,3,4,5,6,7] is given by:

$$\begin{array}{cc}\hfill \underset{w,\theta ,{\xi }^{+},{\xi }^{-}}{min}& {\displaystyle \frac{1}{2}}{\parallel w\parallel }_2^2+\rho e^{\mathrm{T}}({\xi }^{+}+{\xi }^{-})\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y-(\phi \left(X\right)w+\theta e\le ϵe+{\xi }^{+}),{\xi }^{+}\ge 0,\hfill \\ \hfill & (\phi \left(X\right)w+\theta e)-Y\le ϵe+{\xi }^{-},{\xi }^{-}\ge 0.\hfill \end{array}$$

(2)

By applying KKT conditions [5], the Wolfe dual problems [28] of SVR are

$$\begin{array}{cc}\hfill \underset{{\alpha }^{+},{\alpha }^{-}}{min}& {\displaystyle \frac{1}{2}}{({\alpha }^{+}-{\alpha }^{-})}^{\mathrm{T}}K({\alpha }^{+}-{\alpha }^{-})-Y^{\mathrm{T}}({\alpha }^{+}-{\alpha }^{-})+ϵe^{\mathrm{T}}({\alpha }^{+}+{\alpha }^{-})\hfill \\ \hfill \mathrm{subject} \mathrm{to}& e^{\mathrm{T}}({\alpha }^{+}-{\alpha }^{-})=0,0\le {\alpha }^{+},{\alpha }^{-}\le \rho e.\hfill \end{array}$$

(3)

After solving the above optimization problem, we can compute

$$\begin{array}{c}\hfill w=\phi {\left(X\right)}^{\mathrm{T}}({\alpha }^{+}-{\alpha }^{-})\end{array}$$

(4)

and

$$\begin{array}{c}\hfill \theta ={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{|{\mathcal{N}}_{+}|}}\sum _{p\in {\mathcal{N}}_{+}}\left(y_p-w^{\mathrm{T}}\phi \left(x^p\right)\right)+{\displaystyle \frac{1}{|{\mathcal{N}}_{-}|}}\sum _{q\in {\mathcal{N}}_{-}}\left(y_q-w^{\mathrm{T}}\phi \left(x^q\right)\right)\right),\end{array}$$

(5)

where $\mathcal{N}\pm$ are the index sets satisfying ${\alpha }_p^{+}\in (0,\rho ),p\in I$, or ${\alpha }_q^{-}\in (0,\rho ),q\in I$. Finally, the regression functions are given by:

$$\begin{array}{c}\hfill f\left(x\right)=w^{\mathrm{T}}\phi \left(x\right)+\theta ={({\alpha }^{+}-{\alpha }^{-})}^{\mathrm{T}}K(X,x)+\theta .\end{array}$$

(6)

2.2. TPISVR Model

The following two nonparallel functions in the feature space $\mathcal{H}$ are considered for the TPISVR model [11]:

$$\begin{array}{c}\hfill f_d\left(x\right)={\left(w^d\right)}^{\mathrm{T}}\phi \left(x\right)+{\theta }_d,f_u\left(x\right)={\left(w^u\right)}^{\mathrm{T}}\phi \left(x\right)+{\theta }_u.\end{array}$$

(7)

The function $f_d\left(x\right)$ and $f_u\left(x\right)$ are called the parametric insensitive down-bound function and up-bound function regression, respectively. The primal problems of TPISVR are as follows:

$$\begin{array}{cc}\hfill \underset{w^d,{\theta }_d,{\xi }^d}{min}& {\displaystyle \frac{1}{2}}{\parallel w^d\parallel }_2^2-{\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}(\phi \left(X\right)w^d+{\theta }_{d}e)+{\displaystyle \frac{{\rho }_d}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^d\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\ge \phi \left(X\right)w^d+{\theta }_{d}e-{\xi }^d,{\xi }^d\ge 0\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill \underset{w^u,{\theta }_u,{\xi }^u}{min}& {\displaystyle \frac{1}{2}}{\parallel w^u\parallel }_2^2+{\displaystyle \frac{v_u}{\left|I\right|}}{e}^{\mathrm{T}}(\phi \left(X\right)w^u+{\theta }_{u}e)+{\displaystyle \frac{{\rho }_u}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^u\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\le \phi \left(X\right)w^u+{\theta }_{u}e+{\xi }^u,{\xi }^u\ge 0.\hfill \end{array}$$

(9)

By introducing the Lagrangian function for (8) and (9), respectively, and incorporating the KKT conditions [11], we obtain the dual problems of TPISVR:

$$\begin{array}{cc}\hfill \underset{{\alpha }^d}{min}& {\displaystyle \frac{1}{2}}{\left({\alpha }^d\right)}^{\mathrm{T}}K{\alpha }^d-{\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^d+Y^{\mathrm{T}}{\alpha }^d\hfill \\ \hfill \mathrm{subject} \mathrm{to}& 0\le {\alpha }^d\le {\displaystyle \frac{{\rho }_d}{\left|I\right|}}e,e^{\mathrm{T}}{\alpha }^d=v_d\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill \underset{{\alpha }^u}{min}& {\displaystyle \frac{1}{2}}{\left({\alpha }^u\right)}^{\mathrm{T}}K{\alpha }^u-{\displaystyle \frac{v_u}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^u-Y^T{\alpha }^u\hfill \\ \hfill \mathrm{subject} \mathrm{to}& 0\le {\alpha }^u\le {\displaystyle \frac{{\rho }_u}{\left|I\right|}}e,e^{\mathrm{T}}{\alpha }^u=v_u.\hfill \end{array}$$

(11)

After optimizing the dual problems (10) and (11), we can compute

$$\begin{array}{c}\hfill w^d=\phi {\left(X\right)}^{\mathrm{T}}\left({\displaystyle \frac{v_d}{\left|I\right|}}e-{\alpha }^d\right),w^u=\phi {\left(X\right)}^{\mathrm{T}}\left(-{\displaystyle \frac{v_u}{\left|I\right|}}e+{\alpha }^u\right),\end{array}$$

(12)

and

$$\begin{array}{c}\hfill {\theta }_d={\displaystyle \frac{1}{|{\mathcal{N}}_d|}}\sum _{p\in {\mathcal{N}}_d}(y_p-{\left(w^d\right)}^{\mathrm{T}}\phi \left(x^p\right)),{\theta }_u={\displaystyle \frac{1}{|{\mathcal{N}}_u|}}\sum _{q\in {\mathcal{N}}_u}(y_q-{\left(w^u\right)}^{\mathrm{T}}\phi \left(x^q\right)),\end{array}$$

(13)

where ${\mathcal{N}}_d$ and ${\mathcal{N}}_u$ are the index sets satisfying ${\alpha }_p^d\in (0,{\displaystyle \frac{{\rho }_d}{\left|I\right|}}),p\in I$, and ${\alpha }_q^u\in (0,{\displaystyle \frac{{\rho }_u}{\left|I\right|}}),q\in I$, respectively. Then

$$\begin{array}{c}\hfill f_d\left(x\right)={\left(w^d\right)}^{\mathrm{T}}\phi \left(x\right)+{\theta }_d={\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}K(X,x)-{\left({\alpha }^d\right)}^{\mathrm{T}}K(X,x)+{\theta }_d\end{array}$$

(14)

and

$$\begin{array}{c}\hfill f_u\left(x\right)={\left(w^u\right)}^{\mathrm{T}}\phi \left(x\right)+{\theta }_u=-{\displaystyle \frac{v_u}{\left|I\right|}}{e}^{\mathrm{T}}K(X,x)+{\left({\alpha }^u\right)}^{\mathrm{T}}K(X,x)+{\theta }_u.\end{array}$$

(15)

Finally, the estimated regression function of TPISVR is as follows:

$$\begin{array}{c}\hfill f\left(x\right)={\displaystyle \frac{1}{2}}\left(f_d\left(x\right)+f_u\left(x\right)\right)={\displaystyle \frac{1}{2}}\left({\alpha }^u-{\alpha }^d+{\displaystyle \frac{v_d-v_u}{\left|I\right|}}{e}^{\mathrm{T}}\right)K(X,x)+{\displaystyle \frac{1}{2}}({\theta }_d+{\theta }_u).\end{array}$$

(16)

3. STPISVR

In this section, we introduce our STPISVR model and present some properties of it. For ease of comparison, we first propose the sparse SVR (SSVR) model, which will be formally shown in Equation (19). By incorporating the KKT conditions, we simplify the model formulation, making its interpretation more intuitive.

3.1. SSVR Model

We substitute (4) into the constraints of (2) first, and then, replace the first term ${\displaystyle \frac{1}{2}{\parallel w\parallel }_2^2}$ of the objective function in (2) with ${\displaystyle \frac{1}{2}(\parallel {\alpha }^{+}{\parallel }_1+\parallel {\alpha }^{-}{\parallel }_1)}$. Finally, we combine with the KKT conditions (see the constraints in (3)) to obtain

$$\begin{array}{cc}\hfill \underset{{\alpha }^{+},{\alpha }^{-},{\xi }^{+},{\xi }^{-},\theta }{min}& {\displaystyle \frac{1}{2}}\left(\parallel {\alpha }^{+}{\parallel }_1+{\parallel {\alpha }^{-}\parallel }_1\right)+\rho e^{\mathrm{T}}({\xi }^{+}+{\xi }^{-})\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y-K({\alpha }^{+}-{\alpha }^{-})-\theta e\le ϵe+{\xi }^{+},{\xi }^{+}\ge 0,\hfill \\ \hfill & K({\alpha }^{+}-{\alpha }^{-})+\theta e-Y\le ϵe+{\xi }^{-},{\xi }^{-}\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}({\alpha }^{-}-{\alpha }^{+})=0,0\le {\alpha }^{+},{\alpha }^{-}\le \rho e.\hfill \end{array}$$

(17)

Problem (17) is the embryonic form of our SSVR model. From the constraints $e^{\mathrm{T}}({\alpha }^{-}-{\alpha }^{+})=0$ and ${\alpha }^{+}\ge 0,{\alpha }^{-}\ge 0$, we have

$$\begin{array}{c}\hfill \parallel {\alpha }^{+}{\parallel }_1+{\parallel {\alpha }^{-}\parallel }_1=2e^{\mathrm{T}}{\alpha }^{+}.\end{array}$$

(18)

Thus, (17) can be rewritten as

$$\begin{array}{cc}\hfill \underset{{\alpha }^{+},{\alpha }^{-},{\xi }^{+},{\xi }^{-},\theta }{min}& e^{\mathrm{T}}{\alpha }^{+}+\rho e^{\mathrm{T}}({\xi }^{+}+{\xi }^{-})\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y-K({\alpha }^{+}-{\alpha }^{-})-\theta e\le ϵe+{\xi }^{+},{\xi }^{+}\ge 0,\hfill \\ \hfill & K({\alpha }^{+}-{\alpha }^{-})+\theta e-Y\le ϵe+{\xi }^{-},{\xi }^{-}\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}({\alpha }^{-}-{\alpha }^{+})=0,0\le {\alpha }^{+},{\alpha }^{-}\le \rho e.\hfill \end{array}$$

(19)

This optimization problem (19) defines the SSVR model used for comparison later. After solving this optimization problem, we can calculate w using Equation (4) without the need for additional computation of $\theta$, as $\theta$ has already been determined during the optimization process. Consequently, the final regression function of the SSVR is the same as that of the classical SVR.

Remark 1. 

In the primal problem (2) of SVR, the term ${\displaystyle \frac{1}{2}{\parallel w\parallel }_2^2}$ controls structural complexity. Similarly, in our SSVR model (17), the term ${\displaystyle \frac{1}{2}(\parallel {\alpha }^{+}{\parallel }_1+\parallel {\alpha }^{-}{\parallel }_1)}$ aims to minimize the number of nonzero elements in ${\alpha }^{+}$ and ${\alpha }^{-}$, thereby reducing structural complexity. Thus, both models share the same objective.

Remark 2. 

Unlike the classical SVR, which requires solving a QPP, our SSVR model is directly simplified into an LPP. Further analysis on this point will be provided in the subsequent sections.

3.2. STPISVR Model

As previously mentioned, the STPISVR model inherits the core of TPISVR by constructing a pair of nonparallel parametric insensitive bound functions, specifically the lower-bound and upper-bound regression functions. The final regression function remains consistent with Equation (16).

We now proceed to construct the STPISVR model. By substituting the first formula in (12) into both the second term of the objective function and the first constraint of problem (8), respectively, we obtain the following:

$$\begin{array}{c}\hfill -{\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}\left(\phi \left(X\right)w^d+{\theta }_{d}e\right)=v_d\left(-{\displaystyle \frac{v_d}{{\left|I\right|}^2}}{e}^{\mathrm{T}}Ke+{\displaystyle \frac{1}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^d-{\theta }_d\right)\end{array}$$

(20)

and

$$\begin{array}{c}\hfill Y\ge \phi \left(X\right)w^d+{\theta }_{d}e-{\xi }^d={\displaystyle \frac{v_d}{\left|I\right|}}Ke-K{\alpha }^d+{\theta }_{d}e-{\xi }^d.\end{array}$$

(21)

Combining (20), (21) with (8) and (10), and replacing the regularization term ${\displaystyle \frac{1}{2}{\parallel w^d\parallel }_2^2}$ with $\parallel {\alpha }^d{\parallel }_1$, we obtain the following optimization problem corresponding to (8):

$$\begin{array}{cc}\hfill \underset{{\alpha }^d,{\theta }_d,{\xi }^d}{min}& {\parallel {\alpha }^d\parallel }_1+v_d\left({\displaystyle \frac{1}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^d-{\theta }_d-{\displaystyle \frac{v_d}{{\left|I\right|}^2}}{e}^{\mathrm{T}}Ke\right)+{\displaystyle \frac{{\rho }_d}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^d\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\ge {\displaystyle \frac{v_d}{\left|I\right|}}Ke-K{\alpha }^d+{\theta }_{d}e-{\xi }^d,{\xi }^d\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^d=v_d,0\le {\alpha }^d\le {\displaystyle \frac{{\rho }_d}{\left|I\right|}}e.\hfill \end{array}$$

(22)

A similar procedure yields the following optimization problem corresponding to (9):

$$\begin{array}{cc}\hfill \underset{{\alpha }^u,{\theta }_u,{\xi }^u}{min}& {∥{\alpha }^u∥}_1+v_u\left({\displaystyle \frac{1}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^u+{\theta }_u-{\displaystyle \frac{v_u}{{\left|I\right|}^2}}{e}^{\mathrm{T}}Ke\right)+{\displaystyle \frac{{\rho }_u}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^u\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\le -{\displaystyle \frac{v_u}{\left|I\right|}}Ke+K{\alpha }^u+{\theta }_{u}e+{\xi }^u,{\xi }^u\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^u=v_u,0\le {\alpha }^u\le {\displaystyle \frac{{\rho }_u}{\left|I\right|}}e.\hfill \end{array}$$

(23)

Problems (22) and (23) represent the initial version of the STPISVR model.

Notably, in the optimization problem (22), the constraints ${\alpha }^d\ge 0$ and $e^{\mathrm{T}}{\alpha }^d=v_d$ allow us to easily obtain the following results:

$$\begin{array}{c}\hfill \parallel {\alpha }^d{\parallel }_1=e^{\mathrm{T}}{\alpha }^d=v_d.\end{array}$$

(24)

This term, thus, becomes a constant, independent of the optimization variable. By removing the constant term irrelevant to the optimization variables, problem (22) simplifies to the linear form:

$$\begin{array}{cc}\hfill \underset{{\alpha }^d,{\theta }_d,{\xi }^d}{min}& {\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^d-v_d{\theta }_d+{\displaystyle \frac{{\rho }_d}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^d\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\ge {\displaystyle \frac{v_d}{\left|I\right|}}Ke-K{\alpha }^d+{\theta }_{d}e-{\xi }^d,{\xi }^d\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^d=v_d,0\le {\alpha }^d\le {\displaystyle \frac{{\rho }_d}{\left|I\right|}}e.\hfill \end{array}$$

(25)

Similarly, we have

$$\begin{array}{c}\hfill {∥{\alpha }^u∥}_1=e^{\mathrm{T}}{\alpha }^u=v_u,\end{array}$$

(26)

and problem (23) simplifies to (27) using the same reasoning:

$$\begin{array}{cc}\hfill \underset{{\alpha }^u,{\theta }_u,{\xi }^u}{min}& {\displaystyle \frac{v_u}{\left|I\right|}}{e}^{\mathrm{T}}K{\alpha }^u+v_u{\theta }_u+{\displaystyle \frac{{\rho }_u}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^u\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\le -{\displaystyle \frac{v_u}{\left|I\right|}}Ke+K{\alpha }^u+{\theta }_{u}e+{\xi }^u,{\xi }^u\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^u=v_u,0\le {\alpha }^u\le {\displaystyle \frac{{\rho }_u}{\left|I\right|}}e.\hfill \end{array}$$

(27)

Problems (25) and (27) are our final STPISVR model. Once solved, we can calculate the values of $w^d$ and $w^u$ according to Equation (12), where ${\theta }_d$ and ${\theta }_u$ do not need to be recalculated, as they have already been obtained during the optimization process. After these values are obtained, we can then derive the down-bound and up-bound functions, as shown in (15), and final regression function, as given in (16).

Let us now revisit the initial version of the model (22), noting that (25) is just a simplified form derived from it. The first term $\parallel {\alpha }^d{\parallel }_1$ in the objective function is originally introduced to promote sparsity in the model, which in turn simplifies its structural complexity. As discussed in Remark 1, this simplification of structural complexity aligns with the role of the ${\displaystyle \frac{1}{2}{\parallel w^d\parallel }_2^2}$ term in the primal problem (8) of TPISVR, despite their different mathematical forms. However, during the derivation, this L1-norm regularization term in (22) is simplified to a constant via the KKT conditions, and therefore, disappears from the final optimization problem (25), which clearly leads to a more efficient reduction in optimization complexity. Nonetheless, it is important to note that the disappearance of this term does not affect the sparsity of the final model; the sparsity is effectively guaranteed by the linear programming structure and the constraints derived from the KKT conditions, which will be further analyzed in Section 4.1. The second term of the objective function in (22), derived from (20), aims to maximize the projection of the mean value of the training sample points on $f_d\left(x\right)$, causing $f_d\left(x\right)$ to be as large as possible. The third term of the objective function in (22) minimizes the sum of error variables, mitigating overfitting to the training samples. Based on (21) and (14), the first constraint in (22) can be rewritten as

$$\begin{array}{c}\hfill Y\ge f_d\left(X\right)-{\xi }^d,\end{array}$$

(28)

which means that the estimated value of the sample point x on $f_d\left(x\right)$ cannot exceed the response value of the sample point; otherwise, a nonnegative value ${\xi }_x^d$ is introduced to measure this error. The final two constraints on ${\alpha }^d$ are derived from KKT conditions.

Remark 3. 

The objective functions in (25) and (27) are linear, in contrasts to the dual QPPs in TPISVR.

Remark 4. 

The terms $\parallel {\alpha }^d{\parallel }_1$ and $\parallel {\alpha }^u{\parallel }_1$ in (22) and (23) may be replaced by other sparse norms.

Remark 5. 

In the linear case, where $\phi \left(X\right)=X$, the optimization problems (25) and (27) reduce to the following form:

$$\begin{array}{cc}\hfill \underset{{\alpha }^d,{\theta }_d,{\xi }^d}{min}& {\displaystyle \frac{v_d}{\left|I\right|}}{e}^{\mathrm{T}}X{X}^{\mathrm{T}}{\alpha }^d-v_d{\theta }_d+{\displaystyle \frac{{\rho }_d}{\left|I\right|}}{e}^T{\xi }^d\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\ge {\displaystyle \frac{v_d}{\left|I\right|}}X{X}^{\mathrm{T}}e-X{X}^{\mathrm{T}}{\alpha }^d+{\theta }_{d}e-{\xi }^d,{\xi }^d\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^d=v_d,0\le {\alpha }^d\le {\displaystyle \frac{{\rho }_d}{\left|I\right|}}e,\hfill \end{array}$$

(29)

and

$$\begin{array}{cc}\hfill \underset{{\alpha }^u,{\theta }_u,{\xi }^u}{min}& {\displaystyle \frac{v_u}{\left|I\right|}}{e}^{\mathrm{T}}X{X}^{\mathrm{T}}{\alpha }^u+v_u{\theta }_u+{\displaystyle \frac{{\rho }_u}{\left|I\right|}}{e}^{\mathrm{T}}{\xi }^u\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\le -{\displaystyle \frac{v_u}{\left|I\right|}}X{X}^{\mathrm{T}}e+X{X}^{\mathrm{T}}{\alpha }^u+{\theta }_{u}e+{\xi }^u,{\xi }^u\ge 0,\hfill \\ \hfill & e^{\mathrm{T}}{\alpha }^u=v_u,0\le {\alpha }^u\le {\displaystyle \frac{{\rho }_u}{\left|I\right|}}e.\hfill \end{array}$$

(30)

Next, we propose two modular algorithms for STPISVR: a training algorithm that learns the prediction function and records sparsity and training time (Algorithm 1) and a testing algorithm that evaluates performance and inference time (Algorithm 2). The detailed metric definitions are provided in Section 5.

Algorithm 1 STPISVR training algorithm.

Input: Training set $D=\{X,Y\}$; parameter combination $\theta =(v_d,v_u,{\rho }_d,{\rho }_u,\gamma$ (Gaussian kernel parameter)) Output: Prediction function $f\left(x\right)$; training time (Tr-time); number of SVs (Num-SVs) 1.   Start timer. 2.   Solve optimization problem (25) to obtain ${\alpha }^d$ and ${\theta }_d$. 3.   Solve optimization problem (27) to obtain ${\alpha }^u$ and ${\theta }_u$. 4.   Construct bound functions $f_d\left(x\right)$ and $f_u\left(x\right)$ using Equations (14) and (15), respectively. 5.   Compute final regression function $f\left(x\right)={\displaystyle \frac{1}{2}}\left(f_d\left(x\right)+f_u\left(x\right)\right)$ via Equation (16). 6.   Stop timer, record Tr-time. 7.   Count Num-SVs from ${\alpha }^d$ and ${\alpha }^u$. 8.   Return $f\left(x\right)$, Tr-time and Num-SVs.

Algorithm 2 STPISVR Testing Algorithm

Input: Test set $T=\{X_{\mathrm{test}},Y_{\mathrm{test}}\}$; trained prediction function $f\left(x\right)$ Output: Root mean squared error (RMSE); coefficient of determination ($R^2$); test time (Te-time); Zone Width between insensitive boundaes (ZoneWidth, if needed) 1.   Start timer. 2.   For each test sample $x_i$ in $X_{\mathrm{test}}$, Compute prediction ${\widehat{y}}_i=f\left(x_i\right)$. 3.   Calculate RMSE and $R^2$. 4.   Stop timer, record Te-time. 5.   Return RMSE, $R^2$, Te-time and ZoneWidth (if computed).

3.3. Properties of the STPISVR Model

To theoretically analyze the proposed STPISVR model given in (25) and (27), we present two results to help us further understand its behavior.

As is well known, setting the parameters of the model in machine learning algorithms is crucial for achieving optimal performance. The following important theorem will illustrate how the parameters control the fractions of SVs and errors. Before presenting the theorems, let us first define the following two key terms.

Definition 1. 

The fractions of down-SVs and up-SVs are defined as:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\left|I\right|}}\left|\right\{x^p:{\alpha }_p^d>0,p\in I\left\}\right|\mathrm{and}{\displaystyle \frac{1}{\left|I\right|}}\left|\{x^q:{\alpha }_q^u>0,q\in I\}\right|,\end{array}$$

(31)

respectively.

Definition 2. 

The fractions of down-errors and up-errors are:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\left|I\right|}}|\{x^p:f_d\left(x^p\right)<0,p\in I\}|\mathrm{and}{\displaystyle \frac{1}{\left|I\right|}}\left|\{x^q:f_u\left(x^q\right)>0,q\in I\}\right|,\end{array}$$

(32)

respectively.

Theorem 1. 

Let $f_d\left(x\right)$ and $f_u\left(x\right)$ be what the STPISVR obtains as the nondegenerate parametric insensitive down-bound and up-bound regression functions, respectively; then, the following statements hold:

(i)

${\displaystyle \frac{v_d}{{\rho }_d}}$ and ${\displaystyle \frac{v_u}{{\rho }_u}}$ are the lower bounds on the fractions of down-SVs and up-SVs, respectively.

(ii)

${\displaystyle \frac{v_d}{{\rho }_d}}$ and ${\displaystyle \frac{v_u}{{\rho }_u}}$ are the upper bounds on the fractions of down-errors and up-errors, respectively.

Proof. 

From problem (29), we have

$$\begin{array}{c}\hfill {\displaystyle 0\le {\alpha }_p^d\le \frac{{\rho }_d}{\left|I\right|},p\in I.}\end{array}$$

(33)

(i) Suppose the number of down-SVs is denoted as $s_d$. From problem (29), we have ${\displaystyle v_d=e^{\mathrm{T}}{\alpha }^d=\sum _{p\in I}{\alpha }_p^d\le s_d\frac{{\rho }_d}{\left|I\right|}}$. Therefore, we can deduce that ${\displaystyle \frac{v_d}{{\rho }_d}\le \frac{s_d}{\left|I\right|}}$. This shows that ${\displaystyle \frac{v_d}{{\rho }_d}}$ is a lower bound on the fraction of down-SVs.

Similarly, by the same reasoning, we can conclude that ${\displaystyle \frac{v_u}{{\rho }_u}}$ is a lower bound on the fraction of up-SVs. Thus, conclusion (i) is proved.

(ii) Suppose the number of all the points $x^p$ with $f_d\left(x^p\right)<0$ is $t_d$, where $p\in I$. Again, from problem (29), we have ${\displaystyle v_d=e^{\mathrm{T}}{\alpha }^d=\sum _{p\in I}{\alpha }_p^d\ge t_d\frac{{\rho }_d}{\left|I\right|}}$, and ${\displaystyle \frac{v_d}{{\rho }_d}\ge \frac{t_d}{\left|I\right|}}$ can be obtained immediately. Therefore, ${\displaystyle \frac{v_d}{{\rho }_d}}$ is an upper bound on the fraction of down-errors.

By the same token, we can obtain that ${\displaystyle \frac{v_u}{{\rho }_u}}$ is an upper bound on the fraction of up-errors. Thus, conclusion (ii) is also proved.    □

Remark 6. 

Theorem 1 states that the values of ${\displaystyle \frac{v_d}{{\rho }_d}}$$\left({\displaystyle \frac{v_u}{{\rho }_u}}\right)$ can control the fractions of down-SVs (or up-SVs) and errors.

Remark 7. 

Obviously, $v_d\le {\rho }_d$ and $v_u\le {\rho }_u$ for STPISVR. For an overlarge value of ${\displaystyle \frac{v_d}{{\rho }_d}\left(\frac{v_u}{{\rho }_u}\right)}$, the sparsity and errors of the model can get worse, even leading $f_d\left(x\right)\left(f_u\left(x\right)\right)$ to shift up (move down), we will see this point in the next theorem. However, if the value of ${\displaystyle \frac{v_d}{{\rho }_d}\left(\frac{v_u}{{\rho }_u}\right)}$ is too small, it may cause overfitting, which will affect the generalization ability of the model. Thus, for the STPISVR model, a very important work is still to set and determine the parameters as other machine learning algorithms.

To further explain the theoretical properties of our STPISVR model, we set $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$, which is a common practice in real applications. Now, we consider the following new optimization problem first:

$$\begin{array}{cc}\hfill \underset{{\alpha }^d,{\alpha }^u,{\theta }_d,{\theta }_u,{\xi }^d,{\xi }^u}{min}& 2v+{\displaystyle \frac{v}{\left|I\right|}}{e}^{\mathrm{T}}K({\alpha }^d+{\alpha }^u)+vs.({\theta }_u-{\theta }_d)-2{\displaystyle \frac{v^2}{{\left|I\right|}^2}}{e}^{\mathrm{T}}Ke+{\displaystyle \frac{\rho }{\left|I\right|}}{e}^T({\xi }^d+{\xi }^u),\hfill \\ \hfill \mathrm{subject} \mathrm{to}& Y\ge f_d\left(X\right)-{\xi }^d,{\xi }^d\ge 0,e^{\mathrm{T}}{\alpha }^d=v,0\le {\alpha }^d\le {\displaystyle \frac{\rho }{\left|I\right|}}e,\hfill \\ \hfill & Y\le f_u\left(X\right)+{\xi }^u,{\xi }^u\ge 0,e^{\mathrm{T}}{\alpha }^u=v,0\le {\alpha }^u\le {\displaystyle \frac{\rho }{\left|I\right|}}e,\hfill \end{array}$$

(34)

In this case, the objective function is the sum of the objective functions in (22) and (23), reflecting the results after combining (24) and (26), and the constraints are the unions of those in (22) and (23) when $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$. Clearly, problem (34) is optimized if both (25) and (27) (or (22) and (23)) are optimized.

For a data point $(x,y)$, we introduce

$$\begin{array}{c}\hfill g\left(x\right)={\displaystyle \frac{f_u\left(x\right)-f_d\left(x\right)}{2}},\end{array}$$

(35)

which represents half of the longitudinal distance between the down- and up-insensitive regression bounds at the sample point x, when $f_u\left(x\right)\ge f_d\left(x\right)$ (we will discuss other cases in Theorem 2), reflecting the size of the insensitive interval. The larger the value of $g\left(x\right)$, the wider the regression interval, and the stronger the robustness of the model to noise and outliers. Conversely, the smaller the value of $g\left(x\right)$, the narrower the regression interval, the stringent the model fits the data, and the more sensitive the model.

Substituting (14) and (15) into (35), we have

$$\begin{array}{c}\hfill g\left(x\right)=-{\displaystyle \frac{v}{\left|I\right|}}{e}^{\mathrm{T}}K(X,x)+{\displaystyle \frac{1}{2}}K{(X,x)}^{\mathrm{T}}({\alpha }^u+{\alpha }^d)+{\displaystyle \frac{1}{2}}({\theta }_u+{\theta }_d).\end{array}$$

(36)

Thus, problem (34) can be rewritten as:

$$\begin{array}{cc}\hfill \underset{{\alpha }^d,{\alpha }^u,{\theta }_d,{\theta }_u,{\xi }^d,{\xi }^u}{min}& 2v+2{\displaystyle \frac{v}{\left|I\right|}}{e}^{\mathrm{T}}g\left(X\right)+{\displaystyle \frac{\rho }{\left|I\right|}}{e}^{\mathrm{T}}({\xi }^d+{\xi }^u)\hfill \\ \hfill \mathrm{subject} \mathrm{to}& f\left(X\right)-Y\le g\left(X\right)+{\xi }^d,{\xi }^d\ge 0,e^{\mathrm{T}}{\alpha }^d=v,0\le {\alpha }^d\le {\displaystyle \frac{\rho }{\left|I\right|}}e,\hfill \\ \hfill & Y-f\left(X\right)\le g\left(X\right)+{\xi }^u,{\xi }^u\ge 0,e^{\mathrm{T}}{\alpha }^u=v,0\le {\alpha }^u\le {\displaystyle \frac{\rho }{\left|I\right|}}e.\hfill \end{array}$$

(37)

The following theorem will help us understand how to set the parameter range for STPISVR more precisely when $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$.

Theorem 2. 

Let $f_d\left(x\right)$ and $f_u\left(x\right)$ be the nondegenerate parametric insensitive down-bound and up-bound regression functions for STPISVR. Assuming $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$, then we have

(i)

$f_u\left(x\right)>f_d\left(x\right)$ for any data point $(x,y)$ if ${\displaystyle \frac{v}{\rho }<\frac{1}{2}}$.

(ii)

$f_u\left(x\right)<f_d\left(x\right)$ for any data point $(x,y)$ if ${\displaystyle \frac{v}{\rho }>\frac{1}{2}}$.

(iii)

$f_u\left(x\right)=f_d\left(x\right)$ for any data point $(x,y)$ if ${\displaystyle \frac{v}{\rho }=\frac{1}{2}}$.

Proof. 

For a data point $(x,y)$, when $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$, the empirical loss of the optimization problem (37) is

$$\begin{array}{c}\hfill 2vg\left(x\right)+\rho \left({\left({\xi }^d\right)}_x+{\left({\xi }^u\right)}_x\right),\end{array}$$

(38)

and the constraints are

$$\begin{array}{c}\hfill f\left(x\right)-y\le g\left(x\right)+{\left({\xi }^d\right)}_x,{\left({\xi }^d\right)}_x\ge 0,e^{\mathrm{T}}{\alpha }^d=v,0\le {\alpha }^d\le {\displaystyle \frac{\rho }{\left|I\right|}}e,\\ \hfill y-f\left(x\right)\le g\left(x\right)+{\left({\xi }^u\right)}_x,{\left({\xi }^u\right)}_x\ge 0,e^{\mathrm{T}}{\alpha }^u=v,0\le {\alpha }^u\le {\displaystyle \frac{\rho }{\left|I\right|}}e.\end{array}$$

(39)

From the KKT conditions, at least one of ${\left({\xi }^d\right)}_x$ and ${\left({\xi }^u\right)}_x$ must be equal to zero. For example, assume ${\left({\xi }^u\right)}_x=0$. Then, from (39), we have

$$\begin{array}{c}\hfill f\left(x\right)-y=g\left(x\right)+{\left({\xi }^d\right)}_x,{\left({\xi }^d\right)}_x\ge 0,\end{array}$$

(40)

$$\begin{array}{c}\hfill y-f\left(x\right)\le g\left(x\right).\end{array}$$

(41)

We have the following

(i) if ${\displaystyle \frac{v}{\rho }<\frac{1}{2}}$, we have $2v<\rho$, which causes $g\left(x\right)$ to be larger than ${\left({\xi }^d\right)}_x$ in order to minimize the empirical loss at point $(x,y)$; then, we have $g\left(x\right)>{\left({\xi }^d\right)}_x$, and $f_d\left(x\right)<f_u\left(x\right)$ by considering ${\left({\xi }^d\right)}_x\ge 0$.

(ii) if ${\displaystyle \frac{v}{\rho }>\frac{1}{2}}$, then $2v>\rho$, which causes $g\left(x\right)$ be less than ${\left({\xi }^d\right)}_x$ in order to minimize the empirical loss at point $(x,y)$. In this time, if $g\left(x\right)=0$, we have that ${\displaystyle \frac{\partial }{\partial g\left(x\right)}(2vg\left(x\right)+\rho {\left({\xi }^d\right)}_x)=2v-\rho =0}$, and this contradicts ${\displaystyle \frac{v}{\rho }>\frac{1}{2}}$. Thus, $g\left(x\right)<0$, and $f_d\left(x\right)>f_u\left(x\right)$.

(iii) if ${\displaystyle \frac{v}{\rho }=\frac{1}{2}}$, we have $f_d\left(x\right)=f_u\left(x\right)$. In this case, the STPISVR model degenerates into a general regression model with no insensitive parametric boundary regions.    □

Remark 8. 

Theorem 1 states that both the values of ${\displaystyle \frac{v_d}{{\rho }_d}}$ and ${\displaystyle \frac{v_u}{{\rho }_u}}$ should not exceed 1. From Theorem 2, we see more clearly that when $v_d=v_u=v$ and ${\rho }_d={\rho }_u=\rho$, ${\displaystyle \frac{v}{\rho }}$ should be less than ${\displaystyle \frac{1}{2}}$ in order to obtain reasonable insensitive down-bound function $f_d\left(x\right)$ and up-bound function $f_u\left(x\right)$; otherwise, $f_d\left(x\right)$ will shift up and $f_u\left(x\right)$ will move down.

Remark 9. 

According to (38), under the conditions of Theorem 2, when ${\displaystyle \frac{v}{\rho }\le \frac{1}{2}}$, STPISVR minimizes both $g\left(x\right)$ and ${\left({\xi }^d\right)}_x+{\left({\xi }^u\right)}_x$. On the one hand, it imposes that the parameter insensitive down-bound function and up-bound regression function are as close as possible; on the other hand, the sum of errors at each point x as small as possible. The optimization process aims to determine an optimal balance between these two goals.

4. Discussion and Comparison

To better understand our proposed sparse model, this section presents a discussion and comparison with several related algorithms regarding sparsity, prediction speed, and computational complexity.

4.1. Sparsity

As mentioned earlier, TPISVR loses sparsity due to its structure. In contrast, both SSVR and STPISVR are sparse models, achieving this by introducing the L1-norm of the dual variables as a regularization term. This results in fewer SVs compared to the traditional models, yielding sparser solutions. Although the L1-norm regularization term in STPISVR becomes a constant and does not explicitly appear in the final objective function, sparsity is preserved and even enhanced by the following mechanisms: (1) The optimization problems are ultimately formulated as LPPs with L1-norm equality constraints and box constraints; (2) According to linear programming theory, an optimal solution lies at a vertex of the feasible region, which, in high-dimensional spaces, is typically sparse—that is, many components of the optimization variables (i.e., the dual variables) are zero. Therefore, even without an explicit regularization term, the formulation and geometry of the problem naturally promote sparse solutions. Additionally, SSVR is based on SVR and simultaneously optimizes ${\alpha }^{+}$ and ${\alpha }^{-}$, whereas STPISVR is derived from TPISVR and optimizes ${\alpha }^d$ and ${\alpha }^u$ separately. Theoretically, SSVR is expected to yield sparser models than STPISVR. which is further supported by experimental results later.

4.2. Prediction Speed

The prediction speed of a machine learning algorithm is closely linked to its sparsity. Both SSVR and STPISVR benefit from sparsity due to having fewer SVs compared to the traditional models, SVR and TPISVR. This directly reduces the number of SVs, resulting in faster prediction speeds during the test phase.

In typical scenarios, we simplify the models by setting $v_d=v_u$ and ${\rho }_d={\rho }_u$ in both TPISVR and STPISVR, which allows the regressor (16) to be rewritten as:

$$\begin{array}{c}\hfill f\left(x\right)={\displaystyle \frac{1}{2}}({\alpha }^u-{\alpha }^d)K(X,x)+{\displaystyle \frac{1}{2}}({\theta }_d+{\theta }_u).\end{array}$$

(42)

From (6) and (42), it is clear that prediction speed depends primarily on the number of nonzero dual vectors, i.e., the number of SVs.

Although SSVR may be slightly faster than STPISVR due to its higher degree of sparsity, nevertheless, both models still outperform SVR and TPISVR in terms of prediction speed. Faster prediction speeds are particularly advantageous for real-time prediction tasks once the model is trained, as they enable more efficient and timely predictions. Thus, the sparse nature of SSVR and STPISVR results in faster prediction speeds, making these models well-suited for real-time applications after training.

4.3. Computational Complexity

The computational complexity of SVR and TPISVR is generally $O\left(\right|I{|}^3)$, with TPISVR typically being faster than SVR [11]. The complexities of STPISVR and SSVR are also $O\left(\right|I{|}^3)$.

In STPISVR, as shown in (25) and (27), all optimization variables are solved simultaneously without separately computing bias terms. Although STPISVR involves more constraints ($4\left|I\right|+1$) compared to TPISVR, the linearity of the objective function and the constant regularization term help control computational costs. In fact, solving QPPs is generally more computationally demanding than solving LPPs under similar conditions. For linear optimization, complexity depends on both the number of variables and constraints [29]. STPISVR’s each optimization problem involves $2\left|I\right|+1$ variables and $4\left|I\right|+1$ constraints—more constraints than in TPISVR. This increase in the number of constraints may leads to higher computational load as the training sample size grows. However, the linear objective in STPISVR provides an advantage over the quadratic form in TPISVR, keeping overall complexity manageable at $O\left(\right|I{|}^3)$ and ensuring practical feasibility for most real-world applications. This reflects a trade-off between the growth in linear constraints and the simplification from the linear objective. While more constraints increase computational burden, the simpler objective reduces complexity relative to quadratic formulations, maintaining scalability for large-scale problems.

By contrast, SSVR involves $4\left|I\right|+1$ variables and $8\left|I\right|+1$ constraints, significantly exceeding those of STPISVR, leading to higher computational costs —particularly for large sample sizes. Thus, SSVR is the most computationally expensive among the four algorithms during the training phase. Despite STPISVR’s slightly higher training cost compared to TPISVR, its reduced number of SVs results in faster and more efficient prediction during the testing phase. Therefore, STPISVR is well-suited for real-time prediction tasks. Ultimately, the improved sparsity of STPISVR offsets the additional training complexity, offering better generalization and prediction efficiency—making the slight increase in training cost a worthwhile trade-off.

5. Numerical Experiments

To validate the sparsity and generalization performance of the proposed STPISVR model, we compare the results of STPISVR, SVR, TPISVR, and SSVR across several synthetic datasets and 10 benchmark datasets. All experiments are conducted using MATLAB 2024A on a PC equipped with an Intel Core i7 processor and 4 GB of RAM. Since the training speed is not only related to the computational complexity of the model itself, but also closely related to the solver selected, selecting the appropriate solver for different models can speed up the training process. In this paper, we use Mosek 10.2 solver for solving QPPs, and Gurobi 12.0.1 solver for solving LPPs to ensure solver–model alignment and improve overall training efficiency.

Given the critical importance of parameter tuning, which directly influences model training and prediction performance, we employ a two-stage combinatorial tuning strategy with five-fold cross-validation at each stage. The tuning set is composed of 50% of the data randomly selected from the training set. In the first stage, we perform a grid search to select the top five parameter combinations based on performance. Then, leveraging the grid search results, we significantly narrow the parameter range and apply Bayesian optimization [30] for 200 iterations to identify the optimal parameter combination. This hybrid approach combines the broad filtering power of grid search with the precision of Bayesian optimization, yielding more reliable and accurate identification of optimal parameters. Moreover, this strategy helps address the challenge of parameter instability in sparse models, especially those involving L1-regularization. The effectiveness of this approach is further evaluated through ablation studies presented later. Once the optimal parameters are identified, the tuning data is reintegrated into the full training set to retrain the model and learn the final regressor.

Algorithm 3 outlines the two-stage parameter tuning procedure in detail.

For the synthetic datasets, unless otherwise specified, we always generate 10 distinct training sets and 10 corresponding test sets for each example. The models are trained and tested across these datasets, and the results are reported as the mean ± standard deviation over the 10 test sets. For the benchmark datasets, we apply 10-fold cross-validation on each dataset to train the models and assess generalization performance, with results also presented as the mean ± standard deviation across the 10 folds.

For consistency and simplicity, we set ${\rho }_d={\rho }_u=\rho$ for all models, and $v_d=v_u=v$ for both TPISVR and STPISVR. Across all models, at the grid search stage, $\rho$ is selected from the set $\{{10}^i\mid i=-2, -1, \dots , 4\}$, while $v/\rho$ for TPISVR and STPISVR is selected from the set $\{0.05, 0.1, 0.15, \dots , 0.5\}$. For nonlinear cases, the Gaussian kernel parameter is chosen from the set $\{2^{-8}, 2^{-7}, \dots , 2^8\}$. The insensitive tube parameter $ϵ$ for SVR and SSVR is selected from the set $\{0.01, 0.02, \dots , 0.2\}$.

Algorithm 3 Two-stage parameter tuning strategy for STPISVR.

Input: Full training set D; grid parameter space ${\Theta }_{\mathrm{grid}}=\left\{(v_d,v_u,{\rho }_d,{\rho }_u,\gamma )\right\}$; number of cross-validation folds K Output: Optimal parameter combination ${\theta }^{*}=(v_d^{*},v_u^{*},{\rho }_d^{*},{\rho }_u^{*},{\gamma }^{*})$ 1.   Randomly select 50% of D as tuning subset $D_{\mathrm{tuning}}$. 2.   Stage 1: Grid Search 3.   For each $\theta$ in ${\Theta }_{\mathrm{grid}}$: 4.       Perform K-fold cross-validation on $D_{\mathrm{tuning}}$: 5.          For each fold: 6.            Train STPISVR on training fold using Algorithm 1 with parameter $\theta$. 7.            Evaluate on validation fold using Algorithm 2 to obtain RMSE. 8.       Compute average RMSE over all folds. 9.   Select top 5 candidates with the lowest average RMSE. 10.   Stage 2: Bayesian Optimization 11.   Randomly split $D_{\mathrm{tuning}}$ into training set $D_{\mathrm{tuning}\_\mathrm{tr}}$ (40%) and validation set $D_{\mathrm{tuning}\_\mathrm{val}}$ (10%). 12.   Define Bayesian parameter search space ${\Theta }_{\mathrm{bayes}}$ based on the top 5 candidates from grid search. 13.   Initialize $best\_score$ using the lowest RMSE of a top candidate from grid search, and set ${\theta }^{*}$ accordingly. 14.   Set $no\_improve\_count=0$. 15.   Repeat for up to 200 iterations: 16.       Propose candidate parameter ${\theta }_{\mathrm{candidate}}$ via Bayesian optimization. 17.       Train STPISVR on $D_{\mathrm{tuning}\_\mathrm{tr}}$ using Algorithm 1 with ${\theta }_{\mathrm{candidate}}$. 18.       Evaluate on $D_{\mathrm{tuning}\_\mathrm{val}}$ using Algorithm 2 to obtain RMSE. 19.       If RMSE < $best\_score$: 20.            Update $best\_score\leftarrow$ RMSE, ${\theta }^{*}\leftarrow {\theta }_{\mathrm{candidate}}$, and reset $no\_improve\_count=0$. 21.       Else: 22.            Increment $no\_improve\_count$ by 1. 23.       Update Bayesian optimizer with $({\theta }_{\mathrm{candidate}},\mathrm{RMSE})$. 24.       If $no\_improve\_count\ge 20$, break loop. 25.   Return ${\theta }^{*}=(v_d^{*},v_u^{*},{\rho }_d^{*},{\rho }_u^{*},{\gamma }^{*})$.

In the following experiments, we evaluate the performance of the four algorithms using several key metrics: root mean squared error (RMSE), coefficient of determination ($R^2$), number of SVs (Num-SVs), training time (Tr-time), and test time (Te-time). Additionally, Zone Width between insensitive boundaries (ZoneWidth) is considered for TPISVR and STPISVR. The definitions of the RMSE, $R^2$, and ZoneWidth metrics are as follows:

$$\begin{array}{c}\hfill \mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{\left|I\right|}}\sum _{p=1}^{\left|I\right|}(y_p-{\widehat{y}}_p)},R^2=1-{\displaystyle \frac{{\displaystyle \sum _{p=1}^{\left|I\right|}}{(y_p-{\widehat{y}}_p)}^2}{{\displaystyle \sum _{p=1}^{\left|I\right|}}{(y_p-{\overline{y}}_p)}^2}},\\ \hfill \mathrm{ZoneWidth}={\displaystyle \frac{1}{\left|I\right|}}\sum _{p=1}^{\left|I\right|}|f_u\left(x^p\right)-f_d\left(x^p\right)|={\displaystyle \frac{1}{\left|I\right|}}\sum _{p=1}^{\left|I\right|}g\left(x^p\right),\end{array}$$

(43)

where $\widehat{y_p}=f\left(x^p\right),p\in I$, represents the regression value of the model for the pth sample $x^p,p\in I$, and ${\displaystyle \overline{y}=\frac{1}{\left|I\right|}\sum _{p=1}^{\left|I\right|}{y}_p}$ represents the mean of $y_p,p\in I$. RMSE reflects the square error of the regression model, and generally, $R^2\in [0, 1]$ is a measure of how well the model fits the dataset. Clearly, for a given method, the smaller the RMSE value and the larger the $R^2$ value, the better the prediction performance.

5.1. Synthesis Datasets

Example 1. 

The first example is on the regression estimation of the Sinc function, which is defined as:

$$\begin{array}{c}\hfill y=h_1\left(x\right)=Sinc\left(x\right)={\displaystyle \frac{sinx}{x}},x\in [-4\pi ,4\pi ].\end{array}$$

(44)

To effectively reflect the performance of our method, for a sample $x_p,p\in I$, two types of noises are introduced, and

$$\begin{array}{c}\hfill y_p=h_1\left(x^p\right)+e_p,x^p\sim U[-4\pi ,4\pi ],p\in I,\end{array}$$

(45)

where $e_p,p\in I$, represents noise. We consider two kinds of noises:

Type A: $e_p\sim N(0,0.1^2),p\in I$;

Type B: $e_p\sim U(-0.2,0.2),p\in I.$

For each type of noise, we graduate 10 independent groups of samples, each comprising 300 training samples in this example and 300 test samples according to (45) and the above two kind of noise distribution.

Figure 1 and Figure 2 (unless otherwise specified, all graphical results presented in this paper are obtained with the optimal parameters) illustrate the regression performance of SVR, SSVR, TPISVR, and STPISVR on one of the ten test sets in Example 1, corresponding to Type A and Type B, respectively. It is evident from Figure 1 and Figure 2 that SSVR and STPISVR utilize significantly fewer SVs than SVR and TPISVR. Among these methods, STPISVR achieves the best regressors under both cases. From Figure 1 and Figure 2, it is interesting to note that the SVs identified by SSVR and STPISVR are neither strictly beyond the upper or lower bounds, nor constrained to the boundaries as in the traditional methods. Instead, they represent prototype points of the dataset. This phenomenon arises because, during the optimization process, ${\alpha }^{-}$ and ${\alpha }^{+}$ in SSVR, as well as ${\alpha }^d$ and ${\alpha }^u$ in STPISVR, no longer act as simple dual variables, but take on more structural roles in optimization. This fundamental shift marks the key difference between our sparse models and conventional approaches.

Table 2. Results for Example 1.

Type of Noise	Evaluation Index	SVR	SSVR	TPISVR	STPISVR
Type A	RMSE	0.1085 ± 0.0053	0.1063 ± 0.0026	0.1110 ± 0.0043	0.1028 ± 0.0041
Noisy test	$R^2$	0.9010 ± 0.0146	0.9102 ± 0.0102	0.8965 ± 0.0143	0.9111 ± 0.0133
	Num-SVs	107.60 ± 7.8060	18.80 ± 1.0328	154.10 ± 3.6347	46.60 ± 1.5776
	Tr-time (s)	0.4377 ± 0.0435	0.2509 ± 0.0220	0.8406 ± 0.0253	0.3270 ± 0.0213
	Te-time (s)	0.0116 ± 0.0013	0.0028 ± 0.0008	0.0186 ± 0.0029	0.0060 ± 0.0012
Noiseless test	RMSE	0.0447 ± 0.0050	0.0377 ± 0.0035	0.0487 ± 0.0049	0.0366 ± 0.0049
	$R^2$	0.9815 ± 0.0038	0.9844 ± 0.0012	0.9781 ± 0.0034	0.9873 ± 0.0042
	Te-time (s)	0.0117 ± 0.0014	0.0021 ± 0.0004	0.0172 ± 0.0006	0.0051 ± 0.0005
Type B	RMSE	0.1281 ± 0.0040	0.1194 ± 0.0048	0.1261 ± 0.0045	0.1171 ± 0.0038
Noisy test	$R^2$	0.8645 ± 0.0143	0.8820 ± 0.0153	0.8648 ± 0.0169	0.8866 ± 0.0151
	Num-SVs	214.50 ± 11.3652	15.30 ± 0.9487	164.30 ± 4.3474	45.50 ± 1.7159
	Tr-time (s)	0.4605 ± 0.0423	0.2753 ± 0.0349	0.7615 ± 0.0324	0.3232 ± 0.0113
	Te-time (s)	0.0268 ± 0.0038	0.0026 ± 0.0005	0.0198 ± 0.0032	0.0059 ± 0.0009
Noiseless test	RMSE	0.0548 ± 0.0069	0.0277 ± 0.0055	0.0476 ± 0.0051	0.0140 ± 0.0036
	$R^2$	0.9719 ± 0.0073	0.9927 ± 0.0029	0.9787 ± 0.0056	0.9981 ± 0.0010
	Te-time (s)	0.0244 ± 0.0025	0.0022 ± 0.0006	0.0207 ± 0.0025	0.0048 ± 0.0004
Type A †	RMSE	0.1089 ± 0.0049	0.1076 ± 0.0030	0.1115 ± 0.0045	0.1070 ± 0.0040
Noisy test	$R^2$	0.9003 ± 0.0119	0.9033 ± 0.0111	0.8957 ± 0.0145	0.9065 ± 0.0143
	Num-SVs	173.00 ± 8.3267	17.00 ± 0.4714	138.50 ± 3.0277	101.50 ± 1.9579
	Tr-time (s)	0.4255 ± 0.0443	0.9490 ± 0.0558	0.8805 ± 0.0484	0.8482 ± 0.0442
	Te-time (s)	0.0198 ± 0.0032	0.0016 ± 0.0005	0.0170 ± 0.0025	0.0125 ± 0.0016
Noiseless test	RMSE	0.0448 ± 0.0065	0.0385 ± 0.0033	0.0503 ± 0.0047	0.0379 ± 0.0058
	$R^2$	0.9809 ± 0.0039	0.9838 ± 0.0013	0.9766 ± 0.0037	0.9864 ± 0.0034
	Te-time (s)	0.0191 ± 0.0023	0.0019 ± 0.0002	0.0167 ± 0.0011	0.0059 ± 0.0006

Note: ^† indicates the results obtained using grid search alone for parameter tuning.

reports the average test results from 10 groups for each method on Example 1. To better measure the model performance, experiments were also conducted using noiseless test sets for Type A and Type B. The samples of the noiseless test set are the same as those of the noise test set, but the response values are obtained by (44). It can be observed from Table 2 that STPISVR demonstrates the best overall performance across all test scenarios, achieving the lowest RMSE and the highest $R^2$ values among the four algorithms. While SSVR features the fewest SVs, which aligns with the analysis of its superior sparsity and the shortest prediction time, its predictive performance is inferior to that of STPISVR. The very small number of SVs may cause underfitting, resulting in poorer prediction performance. In terms of training time (in our experiments, the SVR model used MATLAB’s optimized ‘fitrsvm’ function; although SVR results are reported, its training time is excluded from comparisons, which applies to subsequent examples as well), in this example, STPISVR benefits from the computational efficiency of a linear model, resulting in significantly faster training time compared to TPISVR. Among all the methods, SSVR achieves the shortest training time; however, its prediction performance is inferior to STPISVR, although it still outperforms SVR. Overall, STPISVR demonstrates the best comprehensive performance. Furthermore, when compared specifically with TPISVR, STPISVR surpasses TPISVR across all evaluation metrics on this example. STPISVR not only utilizes fewer SVs but also achieves shorter training time and prediction time while consistently delivering superior predictive performance.

Table 2 also presents the results for Type A of Example 1 using only grid search, evaluated on both noisy and noiseless test sets. Compared to the hybrid two-stage tuning strategy, the hybrid approach consistently achieves better prediction accuracy and stability, highlighting the advantage of combining broad parameter search with local refinement.

To further evaluate the effectiveness of our proposed STPISVR model, we tested the four models on a dataset with a heteroscedastic structure. We consider the following function as our Example 2:

Example 2. 

$$\begin{array}{c}\hfill y=h_2\left(x\right)=0.2sin\left(2\pi x\right)+0.2x^2+0.3,x\in [0,1].\end{array}$$

(46)

For a sample point $x^p,p\in I=\{1,2,\dots ,200\}$, we set

$$\begin{array}{c}\hfill y_p=h_2\left(x^p\right)+e_p,e_p=\left(0.1{\left(x^p\right)}^2+0.05\right){ϵ}_p,p\in I,\end{array}$$

(47)

where $e_p,p\in I$ represents noise with the specified heteroscedastic structure. We consider the following two kind of noises:

Type C: $x_p=0.005p,{ϵ}_p\sim U(-1,1),p\in I.$

Type D: $x_p\sim U(0,1),{ϵ}_p\sim N(0,0.25),p\in I.$

For each type of noise, we again generate 10 groups of samples and each consisting of 200 training samples and 200 test samples in this example, and the training set and test set are generated in a manner similar to Example 1.

In Example 2, the performance of SVR, SSVR, TPISVR, and STPISVR on one of the ten test sets is depicted in Figure 3 and Figure 4, corresponding to Type C and Type D, respectively. It can be observed that SSVR and STPISVR exhibit greater sparsity, while TPISVR and STPISVR achieve better fitting results compared to SVR and SSVR. This outcome aligns with previous observations, as TPISVR and STPISVR are better suited for datasets with heteroscedastic structures.

Additional results are presented in

Table 3. Results for Example 2.

Type of Noise	Evaluation Index	SVR	SSVR	TPISVR	STPISVR
Type C	RMSE	0.0518 ± 0.0027	0.0520 ± 0.0022	0.0508 ± 0.0025	0.0505 ± 0.0023
Noisy test	$R^2$	0.7950 ± 0.0163	0.7950 ± 0.0170	0.8040 ± 0.0114	0.8070 ± 0.0104
	Num-SVs	133.10 ± 5.8395	4.30 ± 0.4830	43.0 ± 0.6667	26.0 ± 0.6667
	Tr-time (s)	0.2779 ± 0.0243	0.1143 ± 0.0202	0.5414 ± 0.0420	0.1721 ± 0.0946
	Te-time (s)	0.0096 ± 0.0012	0.0008 ± 0.0005	0.0036 ± 0.0007	0.0020 ± 0.0004
Noiseless test	RMSE	0.0146 ± 0.0029	0.0135 ± 0.0020	0.0097 ± 0.0021	0.0061 ± 0.0020
	$R^2$	0.9795 ± 0.0077	0.9827 ± 0.0056	0.9910 ± 0.0036	0.9962 ± 0.0021
	Te-time (s)	0.0093 ± 0.0010	0.0007 ± 0.0004	0.0035 ± 0.0011	0.0020 ± 0.0002
Type D	RMSE	0.0455 ± 0.0025	0.0447 ± 0.0024	0.0447 ± 0.0024	0.0445 ± 0.0025
Noisy test	$R^2$	0.8350 ± 0.0222	0.8410 ± 0.0213	0.8410 ± 0.0203	0.8419 ± 0.0222
	Num-SVs	78.90 ± 4.4083	6.20 ± 0.4216	117.50 ± 3.2745	78.70 ± 0.6749
	Tr-time (s)	0.2892 ± 0.0154	0.5111 ± 0.0322	0.5069 ± 0.0183	0.1587 ± 0.0174
	Te-time (s)	0.0052 ± 0.0005	0.0007 ± 0.0003	0.0081 ± 0.0011	0.0059 ± 0.0005
Noiseless test	RMSE	0.0116 ± 0.0020	0.0088 ± 0.0028	0.0087 ± 0.0031	0.0085 ± 0.0025
	$R^2$	0.9872 ± 0.0043	0.9923 ± 0.0055	0.9924 ± 0.0044	0.9928 ± 0.0037
	Te-time (s)	0.0052 ± 0.0005	0.0006 ± 0.0001	0.0073 ± 0.0008	0.0060 ± 0.0005

, including those on the noiseless test sets, as in Example 1. It can be seen that, similar to Example 1, STPISVR demonstrates the best overall prediction performance. Compared to TPISVR, STPISVR is sparser in several scenarios, exhibiting faster prediction speeds. Moreover, the training time of STPISVR is still lower than that of TPISVR on this example. SSVR performs well in terms of obtaining fewer SVs, having a shorter training time, and having a faster prediction time; however, in terms of generalization ability, it is inferior to both TPISVR and STPISVR. Notably, in this example, the prediction performance of TPISVR ranks second only to STPISVR. The reason is that both models are better suited for heteroscedastic datasets than SVR and SSVR, consistent with the results shown in Figure 3 and Figure 4.

To further demonstrate the overall performance of our STPISVR method, we continue the analysis using Example 2 (Type C), examining it from different perspectives. The results are reported in Figure 5, Figure 6 and Figure 7.

Figure 5 shows the relationships between the parameters $(\rho ,v)$ and the fraction of SVs and errors of STPISVR on Type C. Here, we present results for down-SVs and down-errors only, as up-SVs and up-errors exhibit similar patterns. In this figure, the kernel parameter is fixed at its optimal value. As can be seen from the three-dimensional graph of Figure 5, both the fraction of SVs and errors increase with the increase of $v/\rho$, but as $\rho$ increases, the fraction of SVs rises, while the fraction of errors decreases. To highlight the results effectively, we set $\rho =0.1$ and examine how $v/\rho$ affects the fraction of SVs and errors (see the two-dimensional graph in Figure 5). As suggested by Theorem 1, $v/\rho$ controls both the fraction of SVs and the errors well.

The relation between ($\rho ,v$) and the ZoneWidth for STPISVR are shown in Figure 6. When $v/\rho$ increases and is less than 0.5, the width values and its standard deviation decrease. Instead, when $v/\rho$ is larger than 0.5, the width increases. The reason is that if $v/\rho >0.5,f_u\left(x\right)$ moves down and $f_d\left(x\right)$ shift up, $f_u\left(x\right)<f_d\left(x\right)$. This confirms the results of Theorem 2. In addition, this example also shows that for smaller or larger $\rho$, the width of the parametric insensitive zone is relatively stable, stabilizing at larger or smaller values, respectively.

Figure 7 presents the relationship between $(\rho ,v)$ and RMSE and $R^2$, respectively, which further demonstrates that, over a large range of $\rho$, the RMSE stabilizes at a smaller value, while $R^2$ stabilizes at a larger value. These findings provide valuable guidance for setting appropriate parameter ranges to optimize the performance of our sparse regressor.

To investigate how the parameters of the STPISVR model influence the evaluation indicators, and more specifically, how different evaluation metrics change with increasing noise variance, we conduct an experiment using another type of noise (denoted as Type E) again for Example 2:

Type E: $x_p\sim U(0,1),{ϵ}_p\sim U(-a,a),p\in I,I=\{1, 2, \dots , 200\}$. Here, we set the value of a as $0.2, 0.4, 0.6, \dots , 2.0$, respectively, then the corresponding noise standard deviations of ${ϵ}_p$ are given by: ${\displaystyle \frac{2}{\sqrt{300}},\frac{3}{\sqrt{300}},\frac{4}{\sqrt{300}},\dots ,\frac{20}{\sqrt{300}}}$, respectively.

Figure 8 illustrates the impact of different noise variances on the evaluation indicators of the STPISVR model for heteroscedastic structured data. It is evident that the width of the parametric insensitive zone increases as the variance of ${ϵ}_p$ increases, whereas the proportion of SVs remains largely unaffected by changes in ${ϵ}_p$. This observation indicates that the STPISVR model can automatically adjust the width of the parametric insensitive zone in response to variations in noise variance. Additionally, when we use the noise test set, as noise intensity increases, the RMSE increases and $R^2$ decreases. However, the magnitude of these changes is relatively minor when using a noiseless test set, indicating that the model is robust against increasing noise intensity.

To study how evaluation metrics change with increasing training sample size, we concentrate our attention to the case where $a=2.0$, corresponding to the largest noise variance in Figure 8, and we increase our dataset size from 200 up to 2000 samples by 200 in each step. The test dataset with the size of 200 samples is fixed. The results are presented in Figure 9 and Figure 10.

Figure 9 illustrates the trends in RMSE, $R^2$, the proportion of SVs to training samples, training time, and test time of the four algorithms as the training sample size increases. From Figure 9, we observe that the RMSE ($R^2$) values of SVR, TPISVR, and STPISVR steadily decrease (increase) as the training sample size grows. Among these, STPISVR exhibits the best performance, followed by TPISVR. In contrast, the RMSE ($R^2$) values of SSVR fluctuate significantly, and even with larger sample sizes, its performance is worse than any other methods. Regarding sparsity, STPISVR exhibits a higher level of sparsity than TPISVR. As for training time, when the sample size remains below 1000, STPISVR continues to benefit from the computational efficiency due to the linearity of the model. Consistent with the results from previous examples, its training time remains lower than that of TPISVR and even outperforms the other algorithms. However, as the training sample size increases, its training time shows an upward trend; nonetheless, the overall computational cost remains acceptable. In contrast, TPISVR maintains a relatively stable increase in training time. For SSVR, previous examples have shown that it achieves the shortest training time due to the smaller sample size. However, in this case, when the sample size exceeds 400, its training cost rises significantly and continues to increase rapidly as the sample size grows. This result is largely consistent with our previous analysis of computational complexity. In terms of testing speed, STPISVR is significantly faster than TPISVR due to its higher sparsity. Moreover, as the sample size increases, the gap in test time between STPISVR and TPISVR widens further, highlighting the advantages brought by sparsity of STPISVR. Overall, STPISVR demonstrates the best performance on this example, striking a balance between accuracy, sparsity, and efficiency. It achieves a lower proportion of SVs and a faster prediction speed than TPISVR, though at the cost of higher computational complexity for larger-scale datasets. Nevertheless, this trade-off proves worthwhile, especially for regression tasks that require real-time predictions after training.

Figure 10 compares the trends of STPISVR and TPISVR on the parametric insensitive zone; the fraction of down-SVs and down-errors (results for up-SVs and up-errors are similar) decreases as the sample size increases. Moreover, to compare the trends of sparsity between TPISVR and STPISVR more clearly as the sample size increases, we also present the number of SVs of the two methods here. From Figure 10, we can highlight the following key aspects. First, the number of SVs for both methods increases with the training sample size. However, the difference between the two methods becomes more pronounced as the sample size grows, highlighting the sparsity advantage of STPISVR over TPISVR with larger datasets. Second, for STPISVR, the fractions of down-SVs and down-errors converge toward $y=0.0588$ (the optimal value of $v/\rho$ in STPISVR) from above and below, respectively, as the training sample size increases. A similar pattern is observed for TPISVR (converging to $y=0.0960$). This outcome further confirms the conclusion of Theorem 1. Third, the widths of the parametric insensitive zones remain relatively stable for both methods. However, the width for STPISVR is consistently a little larger than that of TPISVR, which contributes to the superior performance of STPISVR.

5.2. Benchmark Datasets

To further evaluate the performance of our sparse models, we conduct experiments using four algorithms on 10 publicly available benchmark datasets: Auto-mpg (D1), AutoPrice (D2), Boston (D3), Concrete (D4), Daily (D5), Machine (D6), Mcs (D7), Motorcycle (B8), Yacht (D9), and Stock1 (D10). For a fair comparison, all dataset features were rescaled to the range [0,1] before the experiment. The results on these benchmark datasets are presented in

Table 4. Results for 10 benchmark datasets.

Dataset	Evaluation Index	SVR	SSVR	TPISVR	STPISVR
D1	RMSE	0.7107 ± 0.0868	0.7121 ± 0.1000	0.7073 ± 0.0825	0.7034 ± 0.0548
(398 × 8)	$R^2$	0.4721 ± 0.1705	0.4519 ± 0.1373	0.4765 ± 0.0846	0.4897 ± 0.606
	Num-SVs	196.20 ± 5.1651	32.60 ± 3.0258	266.70 ± 5.5187	188.80 ± 4.4920
	Tr-time (s)	0.0215 ± 0.0074	0.3734 ± 0.0596	0.9445 ± 0.0260	0.5137 ± 0.1133
	Te-time (s)	0.0017 ± 0.0014	0.0003 ± 0.0002	0.0019 ± 0.0003	0.0015 ± 0.0002
D2	RMSE	0.3801 ± 0.2137	0.3741 ± 0.1654	0.3940 ± 0.1720	0.3712 ± 0.1163
(159 × 16)	$R^2$	0.7813 ± 0.1543	0.7958 ± 0.0944	0.7761 ± 0.1426	0.7983 ± 0.1179
	Num-SVs	79.60 ± 3.0258	52.80 ± 2.8206	106.50 ± 4.1433	37.10 ± 2.5582
	Tr-time (s)	0.0269 ± 0.0079	0.0868 ± 0.0125	0.5812 ± 0.0244	0.1352 ± 0.0806
	Te-time (s)	0.0010 ± 0.0006	0.0006 ± 0.0010	0.0006 ± 0.0005	0.0003 ± 0.0002
D3	RMSE	0.3911 ± 0.0928	0.3812 ± 0.1029	0.3556 ± 0.1025	0.3426 ± 0.0896
(506 × 14)	$R^2$	0.8412 ± 0.0516	0.8422 ± 0.0631	0.8516 ± 0.0853	0.8554 ± 0.0583
	Num-SVs	273.20 ± 5.3707	61.50 ± 2.9533	307.10 ± 5.3635	226.20 ± 3.3928
	Tr-time (s)	0.1777 ± 0.0215	0.8818 ± 0.0502	1.1177 ± 0.0544	0.8554 ± 0.0583
	Te-time (s)	0.0020 ± 0.0005	0.0009 ± 0.0005	0.0029 ± 0.0004	0.0018 ± 0.0004
D4	RMSE	0.3384 ± 0.0610	0.3372 ± 0.0533	0.4223 ± 0.0504	0.3902 ± 0.0465
(1030 × 9)	$R^2$	0.8783 ± 0.0491	0.8795 ± 0.0459	0.8173 ± 0.0489	0.8424 ± 0.0413
	Num-SVs	603.70 ± 7.3944	156.90 ± 4.0947	634.60 ± 12.1546	485.6 ± 4,8808
	Tr-time (s)	0.8718 ± 0.0904	9.4158 ± 0.3500	4.7170 ± 0.1532	3.1539 ± 0.2175
	Te-time (s)	0.0110 ± 0.0009	0.0036 ± 0.0009	0.0122 ± 0.0018	0.0103 ± 0.0009
D5	RMSE	0.1058 ± 0.0875	0.1108 ± 0.1047	0.1012 ± 0.1313	0.1013 ± 0.1299
(60 × 10)	$R^2$	0.9566 ± 0.0574	0.9536 ± 0.0863	0.9659 ± 0.0387	0.9657 ± 0.0361
	Num-SVs	36.90 ± 1.8529	11.60 ± 0.8433	39.00 ± 2.3570	23.80 ± 0.8756
	Tr-time (s)	0.0070 ± 0.0013	0.0102 ± 0.0019	0.5196 ± 0.0463	0.0805 ± 0.0021
	Te-time (s)	0.0007 ± 0.0004	0.0004 ± 0.0007	0.0003 ± 0.0004	0.0002 ± 0.0002
D6	RMSE	0.0878 ± 0.0686	0.0906 ± 0.0859	0.1816 ± 0.2815	0.1824 ± 0.1871
(209 × 7)	$R^2$	0.9880 ± 0.0046	0.9845 ± 0.0141	0.9549 ± 0.0536	0.9546 ± 0.0234
	Num-SVs	30.90 ± 1.5239	18.90 ± 1.2649	122.30 ± 19.3861	103.40 ± 1.2293
	Tr-time (s)	0.0664 ± 0.0330	0.1188 ± 0.0167	0.6926 ± 0.1372	0.1327 ± 0.0395
	Te-time (s)	0.0012 ± 0.0015	0.0004 ± 0.0005	0.0006 ± 0.0004	0.0004 ± 0.0002
D7	RMSE	0.5786 ± 0.1970	0.6029 ± 0.2414	0.5576 ± 0.2119	0.5362 ± 0.1878
(107 × 4)	$R^2$	0.5454 ± 0.1982	0.5429 ± 0.1541	0.5555 ± 0.2720	0.5569 ± 0.2134
	Num-SVs	73.30 ± 2.6331	10.40 ± 1.1738	49.10 ± 2.9364	33.70 ± 2.0248
	Tr-time (s)	0.0180 ± 0.0061	0.0215 ± 0.0061	0.5677 ± 0.0446	0.0861 ± 0.0026
	Te-time (s)	0.0009 ± 0.0007	0.0003 ± 0.0005	0.0004 ± 0.0005	0.0003 ± 0.0002
D8	RMSE	0.4619 ± 0.1120	0.4616 ± 0.1238	0.4531 ± 0.1012	0.4398 ± 0.0918
(133 × 2)	$R^2$	0.6967 ± 0.3489	0.6969 ± 0.2139	0.7055 ± 0.1560	0.8256 ± 0.2867
	Num-SVs	74.80 ± 2.4060	13.40 ± 0.6992	66.80 ± 1.6364	35.40 ± 0.8756
	Tr-time (s)	0.0138 ± 0.0267	0.0555 ± 0.0159	0.5382 ± 0.0209	0.1007 ± 0.0094
	Te-time (s)	0.0008 ± 0.0006	0.0004 ± 0.0004	0.0007 ± 0.0004	0.0004 ± 0.0002
D9	RMSE	0.1008 ± 0.0211	0.1391 ± 0.0223	0.1764 ± 0.0737	0.1692 ± 0.0663
(308 × 6)	$R^2$	0.9846 ± 0.0033	0.9705 ± 0.0054	0.9450 ± 0.0396	0.9613 ± 0.0405
	Num-SVs	73.20 ± 3.7947	61.10 ± 1.7029	156.00 ± 1.8257	85.00 ± 2.9814
	Tr-time (s)	0.0445 ± 0.0425	0.3344 ± 0.0564	0.8192 ± 0.0430	0.2916 ± 0.0124
	Te-time (s)	0.0008 ± 0.0005	0.0006 ± 0.0005	0.0010 ± 0.0004	0.0007 ± 0.0004
D10	RMSE	0.6999 ± 0.0780	0.6848 ± 0.0742	0.6681 ± 0.1020	0.6429 ± 0.0711
(536 × 8)	$R^2$	0.4870 ± 0.0834	0.5089 ± 0.0761	0.5343 ± 0.0808	0.5428 ± 0.0547
	Num-SVs	475.20 ± 2.5298	16.90 ± 1.1005	288.40 ± 2.7568	238.50 ± 1.3540
	Tr-time (s)	0.0378 ± 0.0162	0.5449 ± 0.0505	1.3134 ± 0.1316	0.5132 ± 0.0426
	Te-time (s)	0.0019 ± 0.0010	0.0005 ± 0.0004	0.0023 ± 0.0005	0.0020 ± 0.0002
D8 †	RMSE	0.4911 ± 0.1115	0.4759 ± 0.1057	0.4673 ± 0.1027	0.4464 ± 0.1179
(133 × 2)	$R^2$	0.5718 ± 0.4510	0.6161 ± 0.3490	0.6189 ± 0.5790	0.6572 ± 0.5867
	Num-SVs	102.20 ± 1.3160	11.00 ± 0.4714	43.20 ± 0.7888	32.50 ± 0.8498
	Tr-time (s)	0.3333 ± 0.0431	0.3548 ± 0.0323	0.5215 ± 0.0283	0.5054 ± 0.0165
	Te-time (s)	0.0017 ± 0.0015	0.0004 ± 0.0005	0.0006 ± 0.0004	0.0005 ± 0.0003

Note: ^† indicates the results obtained using grid search alone for parameter tuning.

.

As shown in Table 4, consistent with the results from synthetic datasets, the proposed STPISVR model achieves the best overall performance among the four methods. It records the lowest RMSE and highest $R^2$ values on 6 of the 10 benchmark datasets. If compared with TPISVR alone, from the values of RMSE and $R^2$, the predictive performance of STPISVR exceeds TPISVR in 8 out of 10 datasets, and is only slightly lower than TPISVR on the other 2 datasets (D5 and D6), i.e., it is almost the same as TPISVR.These results suggest that STPISVR is better suited for a wider range of scenarios.

Regarding the number of SVs, Table 4 reveals that STPISVR consistently requires fewer SVs than TPISVR across all datasets, even on dataset D2, which has the fewest SVs among the four algorithms. Similarly, SSVR achieves greater sparsity than SVR and proves to be the sparsest model on 9 out of the 10 datasets. This finding aligns with earlier theoretical analyses and results from synthetic datasets.

In terms of training time, STPISVR outperforms TPISVR in all 10 datasets, once again demonstrating its advantage in training speed for small and medium sized datasets. A closer examination reveals that on datasets D3, D4, and D10, the training time of SSVR exceeds that of STPISVR. Notably, the sample size of these three datasets surpasses 500, and in particular, the training time of SSVR on D4 is nearly three times that of STPISVR. These findings indicate that while SSVR is faster only for very small-scale datasets, it becomes computationally expensive and less efficient as the dataset size increases.

Among the 4 algorithms, SSVR achieves the shortest prediction time on 8 out of 10 datasets, which is naturally attributed to its high sparsity. Although STPISVR exhibits slightly lower sparsity than SSVR and has a more complex regression function, it still achieves the shortest prediction time on 5 of the 10 datasets. Moreover, in 3 cases, its mean training time matches that of SSVR while exhibiting lower variance, highlighting its greater stability. Compared to TPISVR, STPISVR consistently achieves a faster prediction speed, further emphasizing its computational efficiency. Additionally, for the dataset D8, we conducted an ablation comparing grid search alone with the hybrid two-stage tuning strategy, confirming the latter’s superiority in prediction accuracy and stability.

In summary, STPISVR consistently outperforms the other methods in terms of prediction accuracy, sparsity, training time, prediction speed, and overall stability across these datasets.

To provide a more intuitive understanding of these results, we graphically visualized the outcomes for the dataset D8 as Figure 11. The visualization highlights that both STPISVR and SSVR achieve greater sparsity. Additionally, STPISVR and TPISVR display a better data-fitting effect compared to SVR and SSVR on this heteroscedastic dataset. Overall, STPISVR demonstrates superior performance, combining the advantages of sparsity and predictive accuracy effectively.

6. Conclusions

In this paper, the STPISVR model is presented, an efficient sparse regression model that refines TPISVR by reformulating its primal problem into an equivalent optimization in the dual space. In contrast to TPISVR, STPISVR promotes sparsity explicitly by incorporating a 1-norm regularization term on the dual variable, which is subsequently simplified to a constant through the application of the KKT conditions. This reformulation enables direct optimization over the dual variables, reducing the complexity of the original QPPs to LPPs, thereby improving computational efficiency.

Theoretical analysis and experimental evaluations confirm that STPISVR outperforms traditional regression models by achieving higher sparsity, faster prediction speeds, and superior prediction performance. The model’s ability to balance sparsity and computational efficiency makes it particularly advantageous for a wider range of datasets, including those with heteroscedastic noise structures. Notably, the results highlight that while STPISVR retains the efficiency of a linear model on small- and medium-sized datasets, while maintaining manageable computational cost as data scale increases. Moreover, it consistently achieves a favorable trade-off between prediction accuracy and model simplicity.

Future work includes exploring alternative sparse regularization strategies, such as different norms, pseudo-norms, and their continuous nonlinear approximations, as well as adaptive penalties, to further enhance performance across diverse regression tasks. Additionally, the model evaluation will be extended to a broader range of large-scale, high-dimensional real-world datasets to gain deeper insights into its robustness and adaptability. Further theoretical investigations will be conducted to refine the model’s computational complexity and establish formal guarantees, such as statistical consistency and generalization bounds, to enhance its efficiency, robustness, and reliability. Finally, direct comparisons with state-of-the-art sparse regression models will be carried out to better demonstrate STPISVR’s practical advantages in various application scenarios.