Variational Bayesian Variable Selection in Logistic Regression Based on Spike-and-Slab Lasso
Abstract
1. Introduction
2. Bayesian Logistic Regression
2.1. Bayesian Logistic Regression Based on Pólya-Gamma Latent Variables
2.2. Bayesian Logistic Regression Based on Lower-Bound Approximation
2.3. Spike-and-Slab Lasso Prior
3. Variational Bayesian Variable Selection
- Input data: ;
- Initialize the variational parameters;
- Set iteration counter and maximum iteration T;
- While the convergence criterion is not met and :
- (a)
- Update and via and ;
- (b)
- Update for ;
- (c)
- Update and for and ;
- (d)
- Update from ;
- (e)
- Update for ;
- (f)
- Update and for and ;
- (g)
- Compute entropy of :
- (h)
- Check convergence: if the change of entropy between successive iterations is below a preset threshold (e.g., ), then stop.
- Output , , and .
4. Theoretical Results
5. Simulation Study and Actual Data Analysis
5.1. Simulation Study
5.2. Actual Data Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef]
- Casella, G.; Ghosh, M.; Gill, J.; Kyung, M. Penalized regression, standard errors, and Bayesian lassos. Bayesian Anal. 2010, 5, 369–411. [Google Scholar] [CrossRef]
- Hans, C. Bayesian lasso regression. Biometrika 2009, 96, 835–845. [Google Scholar] [CrossRef]
- Li, Q.; Lin, N. The Bayesian elastic net. Bayesian Anal. 2010, 5, 151–170. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Roková, V. Bayesian estimation of sparse signals with a continuous spike-and-slab prior. Ann. Stat. 2018, 46, 401–444. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Beauchamp, J.J. Bayesian variable selection in linear regression. J. Am. Stat. Assoc. 1988, 83, 1023–1032. [Google Scholar] [CrossRef]
- Castillo, I.; van der Vaart, A. Needles and straw in a haystack: Posterior concentration for possibly sparse sequences. Ann. Stat. 2012, 40, 2069–2101. [Google Scholar] [CrossRef]
- Roková, V.; George, E.I. The spike-and-slab lasso. J. Am. Stat. Assoc. 2018, 113, 431–444. [Google Scholar] [CrossRef]
- Bai, R.; Rockova, V.; George, E.I. Spike-and-slab meets lasso: A review of the spike-and-slab lasso. arXiv 2020, arXiv:2010.06451. [Google Scholar]
- Carbonetto, P.; Stephens, M. Scalable variational inference for bayesian variable selection in regression, and its accuracy in genetic association studies. Bayesian Anal. 2012, 7, 73–108. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J.; Liang, F. A variational algorithm for Bayesian variable selection. arXiv 2016, arXiv:1602.07640. [Google Scholar]
- Ray, K.; Szabó, B. Variational Bayes for high-dimensional linear regression with sparse priors. J. Am. Stat. Assoc. 2022, 117, 1270–1281. [Google Scholar] [CrossRef]
- MacKay, D.J.C. The evidence framework applied to classification networks. Neural Comput. 1992, 4, 720–736. [Google Scholar] [CrossRef]
- Jaakkola, T.S.; Jordan, M.I. Bayesian parameter estimation via variational methods. Stat. Comput. 2000, 10, 25–37. [Google Scholar] [CrossRef]
- Wang, C.; Blei, D.M. Variational inference in nonconjugate models. J. Mach. Learn. Res. 2013, 14, 1005–1031. [Google Scholar]
- Polson, N.G.; Scott, J.G.; Windle, J. Bayesian inference for logistic models using Pólya–Gamma latent variables. J. Am. Stat. Assoc. 2013, 108, 1339–1349. [Google Scholar] [CrossRef]
- Zhang, C.X.; Xu, S.; Zhang, J.S. A novel variational Bayesian method for variable selection in logistic regression models. Comput. Stat. Data Anal. 2019, 133, 1–19. [Google Scholar] [CrossRef]
- Ray, K.; Szabó, B.; Clara, G. Spike and slab variational Bayes for high dimensional logistic regression. Adv. Neural Inf. Process. Syst. 2020, 33, 14423–14434. [Google Scholar]
- Tang, Z.; Shen, Y.; Zhang, X.; Yi, N. The spike-and-slab lasso generalized linear models for prediction and associated genes detection. Genetics 2017, 205, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Wei, R.; Ghosal, S. Contraction Properties of Shrinkage Priors in Logistic Regression. J. Stat. Plan. Inference 2020, 207, 215–229. [Google Scholar] [CrossRef]
- Mcdermott, P.; Snyder, J.; Willison, R. Methods for Bayesian Variable Selection with Binary Response Data using the EM Algorithm. arXiv 2016, arXiv:1605.05429. [Google Scholar]
- Van De Vijver, M.J.; He, Y.D.; Va not Veer, L.J.; Dai, H.; Hart, A.A.; Voskuil, D.W.; Schreiber, G.J.; Peterse, J.L.; Roberts, C.; Marton, M.J.; et al. A Gene-Expression Signature as a Predictor of Survival in Breast Cancer. N. Engl. J. Med. 2002, 347, 1999–2009. [Google Scholar] [CrossRef]
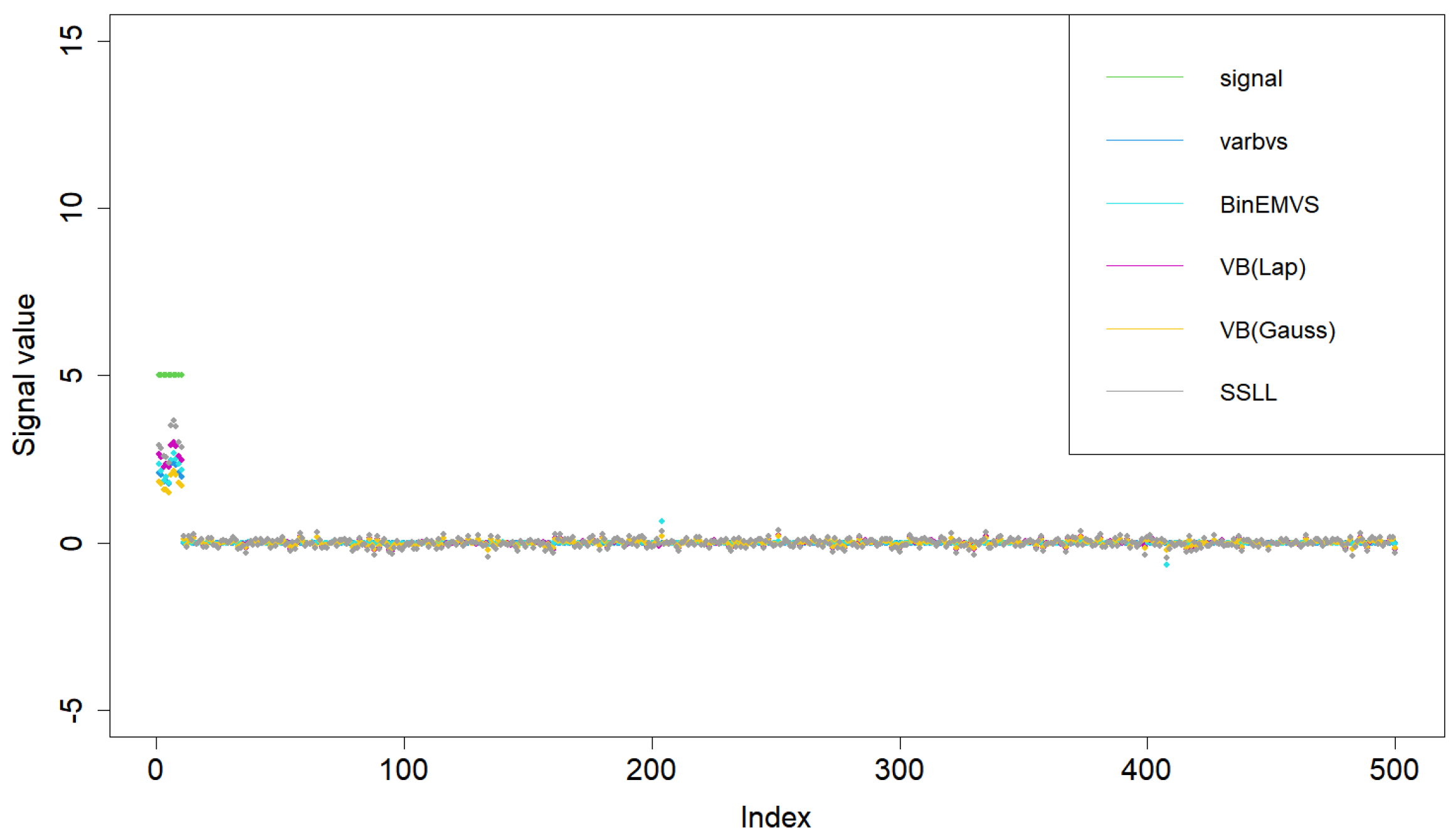
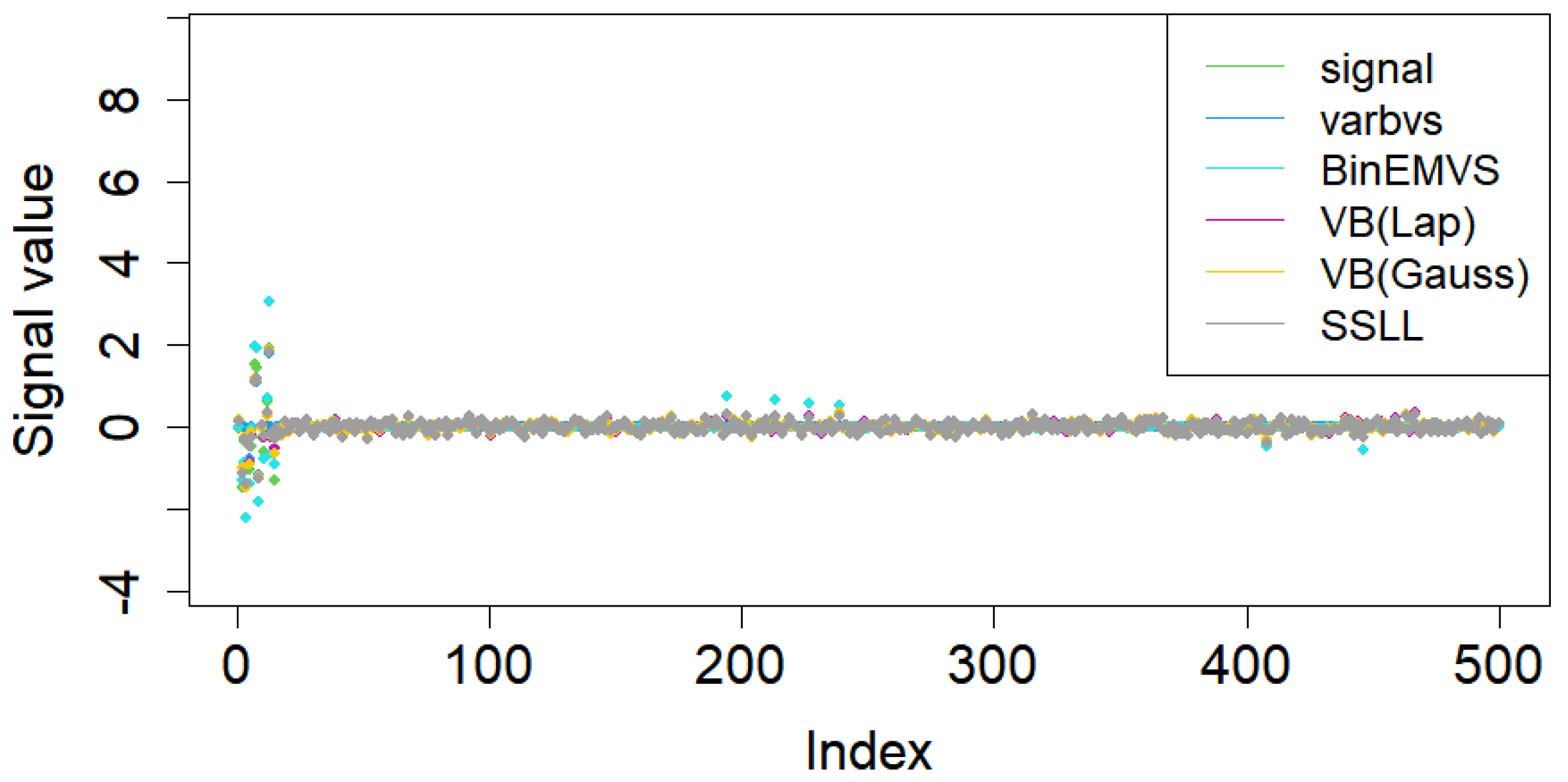
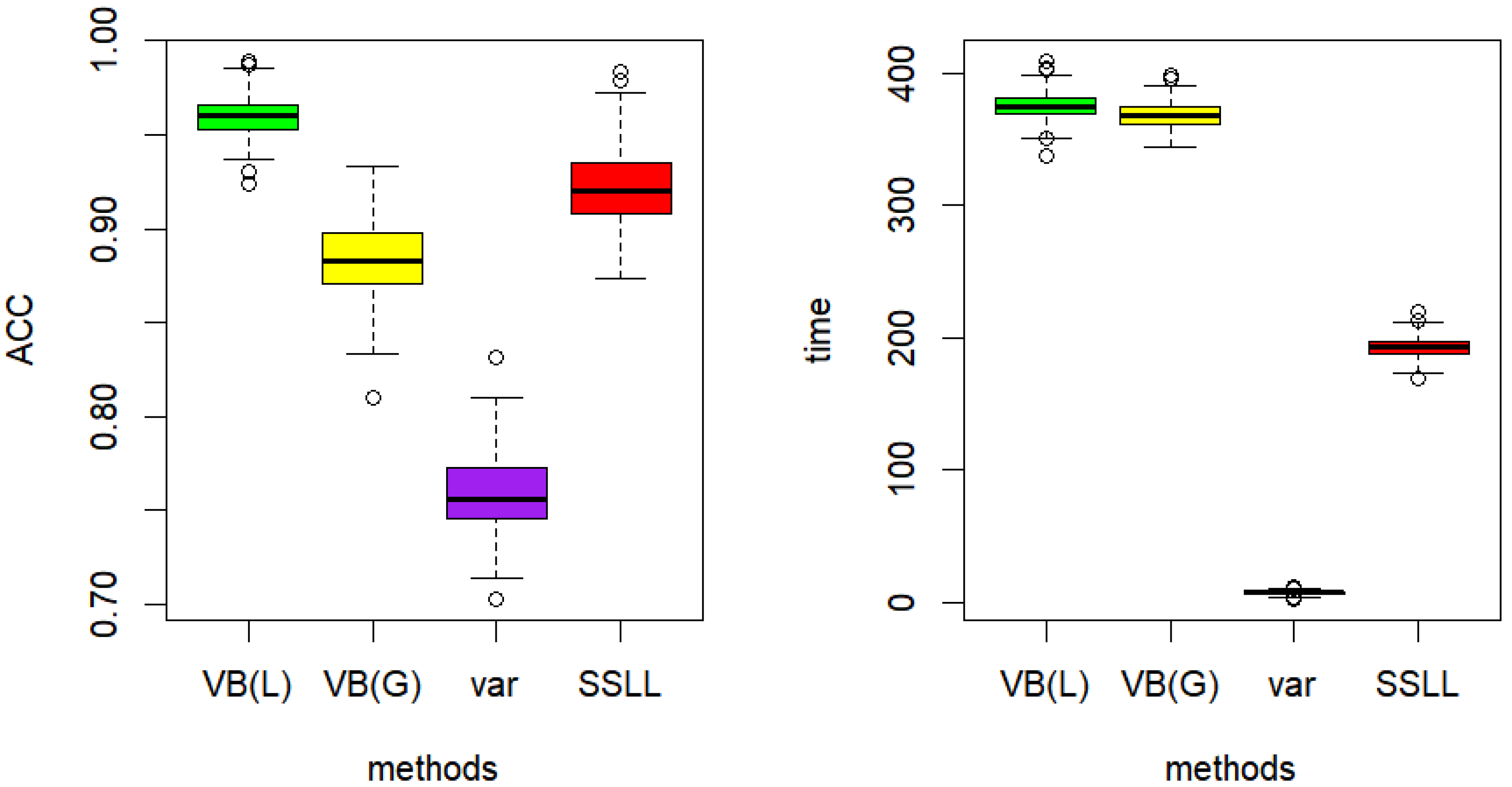

| Methods | TP | MSPE | T | |
|---|---|---|---|---|
| BinEMVS | 9.134 | 0.095 | 33.807 | |
| (0.00) | (0.011) | (0.001) | (10.196) | |
| VB (Lap) | 8.218 | 0.145 | 3.683 | |
| (0.00) | (0.050) | (0.001) | (0.033) | |
| VB (Gauss) | 10.841 | 0.150 | 3.087 | |
| (0.00) | (0.010) | (0.001) | (0.034) | |
| varbvs | 9.532 | 0.086 | 2.118 | |
| (0.00) | (0.000) | (0.000) | (0.053) | |
| SSLL | 7.012 | 0.113 | 1.165 | |
| (0.00) | (0.031) | (0.020) | (0.018) | |
| BL | 9.012 | 0.121 | 30.552 | |
| (0.00) | (0.052) | (0.031) | (1.325) |
| Methods | TP | MSPE | T | |
|---|---|---|---|---|
| BinEMVS | 0.80 | 3.231 | 0.258 | 40.028 |
| (0.00) | (0.178) | (0.003) | (0.945) | |
| VB (Lap) | 0.67 | 2.756 | 0.126 | 3.234 |
| (0.00) | (0.040) | (0.001) | (0.096) | |
| VB (Gauss) | 0.68 | 2.812 | 0.134 | 3.217 |
| (0.02) | (0.012) | (0.001) | (0.053) | |
| varbvs | 0.60 | 1.984 | 0.215 | 3.328 |
| (0.00) | (0.000) | (0.000) | (0.124) | |
| SSLL | 0.70 | 2.150 | 0.133 | 2.231 |
| (0.00) | (0.001) | (0.001) | (0.037) | |
| BL | 0.60 | 2.321 | 0.233 | 41.621 |
| (0.00) | (0.002) | (0.005) | (1.054) |
| Methods | TP | MSPE | T | |
|---|---|---|---|---|
| BinEMVS | ∖ | ∖ | ∖ | ∖ |
| ∖ | ∖ | ∖ | ∖ | |
| VB (Lap) | 1.00 | 10.623 | 0.031 | 383.532 |
| (0.00) | (0.050) | (0.001) | (10.033) | |
| VB (Gauss) | 1.00 | 15.247 | 0.136 | 367.145 |
| (0.00) | (0.010) | (0.002) | (9.623) | |
| varbvs | 1.00 | 29.126 | 0.212 | 7.856 |
| (0.00) | (0.000) | (0.000) | (0.522) | |
| SSLL | 1.00 | 14.217 | 0.075 | 175.144 |
| (0.00) | (0.031) | (0.030) | (0.312) | |
| BL | ∖ | ∖ | ∖ | ∖ |
| ∖ | ∖ | ∖ | ∖ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, W.; Yang, M.; Tian, M. Variational Bayesian Variable Selection in Logistic Regression Based on Spike-and-Slab Lasso. Mathematics 2025, 13, 2205. https://doi.org/10.3390/math13132205
Zhang J, Wang W, Yang M, Tian M. Variational Bayesian Variable Selection in Logistic Regression Based on Spike-and-Slab Lasso. Mathematics. 2025; 13(13):2205. https://doi.org/10.3390/math13132205
Chicago/Turabian StyleZhang, Juanjuan, Weixian Wang, Mingming Yang, and Maozai Tian. 2025. "Variational Bayesian Variable Selection in Logistic Regression Based on Spike-and-Slab Lasso" Mathematics 13, no. 13: 2205. https://doi.org/10.3390/math13132205
APA StyleZhang, J., Wang, W., Yang, M., & Tian, M. (2025). Variational Bayesian Variable Selection in Logistic Regression Based on Spike-and-Slab Lasso. Mathematics, 13(13), 2205. https://doi.org/10.3390/math13132205






