Abstract
This study presents a novel game-theoretical framework designed to support epidemic management, with a specific focus on the allocation of limited resources across competing public health objectives and intervention strategies. Recognizing the varied roles and capacities of participatory agents, we model their involvement as occurring at multiple levels, reflecting the complex decision-making processes encountered in real-world situations. To account for the unequal influence or priority of different agents and strategies, we further propose a suite of weighted allocation measures grounded in well-established theoretical principles. In response to ongoing concerns over the arbitrariness of externally assigned weights, we also construct a refined metric based on endogenous marginal intervention effects, offering a more organically derived representation of participator impact. A series of illustrative examples demonstrates the practical relevance of these models, revealing how they can capture key dynamics such as behavioral diversity, the coexistence of overlapping policies, and logical independence under distinct weighting perspectives. Collectively, these contributions aim to provide epidemic response teams with a set of interpretable and adaptable tools tailored to the complexity of real-world public health crises.
Keywords:
epidemic management; game theory; multiple interventions; weight; axiomatic characterization MSC:
91A06; 91B16
1. Introduction
Recent advancements in epidemiological science have increasingly shifted focus toward the systemic and multifaceted nature of infectious disease management. Beyond the challenge of scarce resources, contemporary research highlights the intricate dynamics among diverse stakeholders, varying degrees of public compliance, and the pursuit of often competing public health goals. Among the most urgent priorities in this field are: (1) accurately forecasting disease transmission to enable timely and effective interventions; (2) optimizing vaccination programs to achieve maximal herd immunity despite constrained supplies; and (3) tailoring treatment plans to individual biological profiles to enhance outcomes and reduce adverse effects. For example, studies leveraging machine learning have shown promise in improving flu transmission forecasts, while others have used network-based strategies to enhance vaccination coverage. In parallel, advances in precision medicine have enabled the design of personalized therapeutic protocols grounded in genetic and immunological data. To realize these ambitions, public health responses frequently rely on a coordinated deployment of interventions, such as combining vaccination, mask mandates, and social distancing, while judiciously allocating resources across different population segments. Accordingly, the task of distributing limited public health assets across multiple objectives and strategies, often with embedded weighting priorities, has emerged as a defining challenge in the domain.
Game theory offers a powerful analytical lens through which strategic interactions in epidemic contexts can be modeled and understood. Historically, its applications have centered on binary choices, such as whether to vaccinate, and single-objective optimizations. Yet, real-world public health crises defy such simplicity. Decision landscapes are increasingly characterized by multi-layered participation options and intersecting goals. Recent literature has begun to reflect this complexity: scholars have introduced multi-objective, multi-choice game models to better capture the realities of epidemic dynamics. For instance, van den Nouweland et al. [1] studied solution frameworks for multi-choice games, and Freixas and Marciniak [2] expanded the classical Shapley value [3] to encompass such scenarios. Further theoretical contributions by Bilbao [4], Bednarczuk et al. [5], van den Brink and Borm [6], Fang and Liu [7], Goli et al. [8], Guarini et al. [9], Mustakerov et al. [10], Tirkolaee et al. [11], Zhang et al. [12], among others, have laid a robust mathematical foundation for this line of inquiry, inspiring this study to explore broader and more adaptable models.
A key conceptual underpinning of this research is the pseudo equal allocation of non-separable costs (PEANSC), introduced by Hsieh and Liao [13]. This framework addresses the issue of fairness in scenarios where costs or benefits cannot be cleanly attributed to individual actors. Within this approach, individual effects denote the marginal outcomes of singular participation, while collective effects represent the aggregate result of joint efforts. Notably, Hsieh and Liao [13] also proposed a weighted variant of the EANSC, accommodating settings where participants vary significantly in their roles or influence. This scheme, and its supporting theoretical results, inform the resource allocation strategies developed herein.
In view of these evolving needs and prior contributions, it is evident that a contemporary resource allocation mechanism must be capable of simultaneously addressing multiple objectives, integrating diverse intervention strategies, and honoring the nuanced importance of different participants.
- This study seeks to fill this methodological gap by proposing a management framework that synthesizes multi-objective logic, strategy diversity, equitable weighting, and the PEANSC philosophy into a unified approach.
Through this integrated design, the study aims to contribute in several key ways:
- It introduces a novel game-theoretical model that captures the richness and complexity of epidemic management under multiple objectives and interventions.
- Section 2 presents a detailed formulation of a resource allocation metric, along with various weighted extensions that incorporate the relative significance of agents and their associated strategies.
- Drawing from the foundational axiomatic traditions of Moulin [14] and Hart and Mas-Colell [15], Section 3 rigorously evaluates the fairness and rational consistency of the proposed measures.
- Section 4 illustrates the practical applicability of these tools through targeted numerical examples that reflect real-world epidemic decision environments.
2. Preliminaries
2.1. Definitions and Notations
Let denote the universe of participators, representing, for example, the collection of all individuals within a population during an epidemic outbreak. Any is identified as a participator of , such as an individual deciding on vaccination or social distancing strategies. For and , we define to be the set of possible strategies for participator k, and , where 0 indicates inaction or no preventive action.
Let denote a finite subset of participators, such as a specific demographic group or a collection of interacting individuals. Let be the Cartesian product of all strategy sets for each participator in . For any subset , a participatory coalition corresponds to a multi-choice alliance , defined by if , and otherwise. Let be the zero vector in . For , we also define and as the zero vector in .
A multi-choice setting is defined as the triplet , where is a finite set of participators, represents the adoption limits (strategy capacity) for each participator, and is a utility function satisfying , indicating the system utility resulting from a specific combination of participatory strategies .
Extending to a broader evaluative framework, a multiple-objectives multi-choice setting is given by , where and with each being a distinct multi-choice setting reflecting objective-specific utility outcomes. The set of all such settings is denoted by .
A measure is defined as a mapping that assigns to each a vector
where each assigns to each participator k their allocated capacity for objective t. Let , , and . We define and as the restriction of to . Let , one can define as excluding component k. Moreover, is defined by and .
Based on the need to fairly allocate preventive capacity in settings involving varying levels of individual action and multiple public health objectives, this study extends the pseudo equal allocation of non-separable costs (PEANSC) into the framework of multiple-objectives multi-choice settings. This provides a flexible and axiomatic foundation for analyzing capacity-influence under interactive yet diverse management environments. To operationalize such management notions under real-world epidemic conditions, where participators may engage at multiple levels of preventive action and where different public health objectives are simultaneously pursued, we introduce a family of management measures that generalize marginal contribution logic to multi-choice, multi-objective contexts. These measures reflect not only the intensity of preventive participation but also potential weighting preferences across participators or their preventive strategies.
We begin with the uniform management measure, which equally redistributes residual preventive capacity after accounting for individual marginal contributions. This forms the basis for subsequent weighted and bi-weighted extensions.
Definition 1.
The uniform measure of involved effect (UMIE), , is considered to be
for each , for each and for each . The value is the average marginal strategy-capacity among all strategies of participator b in . Under measure , all participators firstly assess its average marginal strategy-capacity, and further assess the rest of capacity uniformly.
As emphasized in the Introduction, weighting has become increasingly crucial in many interactive management processes. Within the realm of epidemic control, for example, weights can signify relative risk among different population groups or reflect the varying efficacy of intervention strategies across distinct transmission routes. In broader pandemic responses, weighting may capture levels of compliance with preventive guidelines, often diverging substantially across age brackets, regions, or socioeconomic groups, even under unified public health policies. These differences underline the necessity for allocation schemes that adapt to both participant heterogeneity and the nature of intervention efforts.
The importance of weighting is not limited to practical applications; it is also well-grounded in theoretical frameworks, especially in cooperative game theory, where generalizations of the Shapley value [16] provide formal justifications. In this context, assigning weights to participators or their specific strategies represents a principled way to encode the differentiated influence or responsibility of each actor.
Let be a strictly positive function, representing a weight transformation for participators. Similarly, let be a strictly positive function that serves as a weight transformation for strategies. By employing these two forms of transformations, we construct several weighted variants of the UMIE.
Definition 2.
- The 1-weighted measure of involved effect (1-WMIE), denoted , is defined as follows:For each , for any participator weight function , for each , and for each ,This formulation assigns to each participator its average marginal contribution first, and then redistributes the remaining capacity proportionally to their assigned weights.
- The 2-weighted measure of involved effect (2-WMIE), denoted , is constructed as follows:Given and a strategy weight function , for each and for each ,wherecaptures the weighted average marginal contribution of all strategies available to participator i. The measure then supplements this with a uniform distribution of the residual capacity.
- The bi-weighted measure of involved effect (BWMIE), denoted , is formulated by combining both participator and strategy weights. For any , and for each and ,This formulation first evaluates strategy-specific weighted contributions, and then allocates the residual in proportion to participator weights, capturing both behavioral and structural heterogeneity in the epidemic setting.
2.2. Interpretation and Comparative Discussion
The four proposed management measures, the UMIE, the 1-WMIE, the 2-WMIE, and the BWMIE, can be meaningfully understood through the lens of practical epidemic management scenarios. Consider, for instance, a real-world setting in which several public health agencies are jointly responsible for allocating a constrained supply of vaccines across different geographic areas during an outbreak. Each agency (or participator) may adopt a range of intervention strategies, such as initiating public awareness campaigns, conducting targeted vaccination programs, or enforcing quarantine protocols, with varying degrees of commitment and impact.
- Under the UMIE framework, the initial allocation is based on each participator’s average marginal contribution across all their strategies. Any remaining capacity is then equally distributed among all agents. This approach embodies a foundational principle of fairness: while the differences in action levels are recognized, the surplus benefits are shared uniformly. Such a rule may be especially aligned with egalitarian values commonly emphasized in public health policies that aim to promote equity among regions or agencies.
- The 1-WMIE model modifies this logic by assigning the residual capacity in proportion to predefined weights attributed to each participator. These weights may encode considerations such as a region’s vulnerability to infection, observed case rates, or strategic policy emphasis. In this way, the 1-WMIE provides a mechanism for integrating policy priorities and normative judgments into the allocation process, facilitating a more tailored and directive form of resource distribution.
- The 2-WMIE approach shifts the focus from agents to their actions, introducing weights at the level of specific strategies. For example, if rapid testing is shown to be more effective than generic contact tracing in a given context, this model allows greater emphasis to be placed on the former. This perspective enables policymakers to incentivize interventions not just based on who acts, but on the comparative value of what is being done, an important distinction in nuanced epidemic scenarios.
- Finally, the BWMIE model synthesizes the two dimensions by applying weights both at the participator and strategy levels. This bi-weighted scheme is especially pertinent in complex, multi-actor public health environments, such as national pandemic task forces or regional coalitions, where not only the identity of the implementing agency but also the type of intervention significantly influences outcomes. It supports a layered and responsive allocation logic that adapts to heterogeneous needs and capabilities.
In conclusion, the choice among these four allocation measures hinges on the prevailing goals and constraints of the epidemic management context. Whether the priority lies in promoting fairness, enhancing operational efficiency, respecting strategic policy priorities, or motivating specific behavioral responses, each measure offers a distinct normative orientation and operational flexibility.
3. Axiomatic Characterizations
3.1. Axiomatic Characterizations for the UMIE and Its Weighted Analogues
Building on the foundational axiomatic structures and proof strategies established by Hart and Mas-Colell [15] and Moulin [14], this section presents a formal axiomatic characterization of the UMIE, the 1-WMIE, the 2-WMIE, and the BWMIE. These characterizations serve to validate both the internal consistency and theoretical uniqueness of the proposed measures under normative principles pertinent to multi-objective epidemic management frameworks.
A measure satisfies the effectiveness for multiple-objectives (EFFMO) axiom if, for each and for each , , i.e., the total allocation assigned by across all participators in precisely equals the overall capacity . This axiom ensures that the full preventive resource is accounted for and distributed without omission or surplus, an essential requirement for fairness and efficiency in resource-sensitive environments.
Lemma 1.
The measures , , , and satisfy EFFMO.
Proof.
Let , , be a weight transformation for participators and be a weight transformation for strategies. By Definition 2,
The proof is complete. The validity of EFFMO for the 2-WMIE can be directly verified by setting all participator weights to 1. Similarly, the 1-WMIE satisfies EFFMO when all strategy weights are set to 1. In the case where both participator and strategy weights are uniformly equal to 1, the UMIE likewise fulfills the EFFMO condition. □
To rigorously characterize the PEANSC, Hsieh and Liao [13] introduced a concept of strategic reduction tailored for cooperative resource allocation settings. Under a configuration , if a coalition contests a given allocation derived from the measure , a reassessment process is triggered. If none of the dissenting members elects to participate in the reassessment, the resulting utility is declared to be zero. When only one dissenting member continues, the process simplifies, awarding this agent the utility they would individually receive. In cases where multiple dissenting members persist, those in agreement with the original allocation withdraw after receiving their predefined share, leaving the residual utility to be reassigned exclusively among the dissenting agents. This process introduces a dynamic consistency criterion based on cooperative disagreement, and it has since been adapted to the more general multiple-objectives multi-choice framework within this study.
Let , , and be a measure. The reduced setting is defined by , and for each ,
Moreover, a measure satisfies the multiple-objectives bilateral consistency (MOBCY) axiom if for each , for each , for each with , and for each .
Lemma 2.
The measures , , , satisfy MOBCY.
Proof.
Let , , , and let and be weight transformations for participators and strategies, respectively. Assume and . By Definition 2,
for each and . Now, using the definitions of and :
By substituting Equations (8) and (9) and applying the EFFMO property of :
for each and for each . Thus, the MOBCY condition is verified. Analogous arguments apply for the 1-WMIE, the 2-WMIE, and the UMIE, by setting relevant weights to 1 accordingly. □
To distinguish among the measures under small-group epidemic response scenarios, we define a family of objective-based standard axioms. These axioms extend the classical binary-participation models into the realm of multi-objective, multi-intervention decision environments. A measure satisfies the standard for multiple-objectives (SMO) axiom if for each with . A measure satisfies the 1-weighted standard for multiple-objectives (1WSMO) axiom if for each with and for each participator weight transformation . Similarly, a measure satisfies the 2-weighted standard for multiple-objectives (2WSMO) axiom if for each setting with and for each strategy weight transformation . Finally, a measure satisfies the bi-weighted standard for multiple-objectives (BWSMO) axiom if for all cases and for any combination of weight transformations for participators and strategies .
These axioms generalize the idea of fairness and strategic consistency in pairwise settings, echoing the characterizations developed by Hart and Mas-Colell [15] for the Shapley value [3] in cooperative game theory. Following the theoretical blueprint laid out by Hart and Mas-Colell [15] and Moulin [14], we now present a uniqueness characterization of the four measures using the MOBCY axiom:
Theorem 1.
- 1.
- On , the UMIE is the unique measure satisfying SMO and MOBCY.
- 2.
- On , the 1-WMIE is the unique measure satisfying 1WSMO and MOBCY.
- 3.
- On , the 2-WMIE is the unique measure satisfying 2WSMO and MOBCY.
- 4.
- On , the BWMIE is the unique measure satisfying BWSMO and MOBCY.
Proof.
By Lemma 2, the measures , , , and all satisfy the MOBCY condition. Moreover, each corresponds exactly to one of the standard axioms SMO, 1WSMO, 2WSMO, and BWSMO, respectively.
To demonstrate the uniqueness of result 4, assume satisfies BWSMO and MOBCY. These conditions imply also satisfies EFFMO, though this is omitted for brevity. Let , with and as respective participator and strategy weight transformations. For cases where , BWSMO ensures . For the more general case where , let , and consider for some .
As in the earlier characterization related to Equation (9),
Combining the results of Equations (11) and (12),
Thus,
Now applying the EFFMO of and ,
Hence, for each and for each . The uniqueness of the 1-WMIE, the 2-WMIE, and the UMIE follows analogously by setting appropriate weights to 1. □
In the following, a series of illustrative instances is provided to demonstrate that each of the axioms in Theorem 1 is logically independent of the others.
Example 1.
Consider the following measure σ. For each , for each participator weight transformation , for each strategy weight transformation , for each , and for each participator ,
It is evident that σ satisfies BWSMO. However, it fails to satisfy the MOBCY axiom.
Example 2.
Consider the following measure σ. For each , for each participator weight transformation , for each strategy weight transformation , for each , and for each participator ,
This measure σ satisfies 2WSMO, yet does not meet the MOBCY criterion.
Example 3.
Consider the following measure σ. For each , for each participator weight transformation , for each strategy weight transformation , for each , and for each participator ,
This σ satisfies 1WSMO, but it does not satisfy the MOBCY axiom.
Example 4.
Consider the following measure σ. For each , for each participator weight transformation , for each strategy weight transformation , for each , and for each participator ,
In this case, σ satisfies the SMO axiom, but not the MOBCY condition.
Example 5.
Consider the following measure σ. For each , for each participator weight transformation , for each strategy weight transformation , for each , and for each participator , define . Absolutely, this trivial measure σ satisfies MOBCY, but it fails to satisfy any of the standard axioms: SMO, 1WSMO, 2WSMO, or BWSMO.
3.2. Different Consideration
Throughout Section 2 and Section 3.1, this study has introduced a variety of weight transformations for both participant groups and their associated intervention strategies, aiming to distribute the influence of their interactions more equitably. However, the legitimacy and empirical grounding of these transformations can be called into question, particularly when such weightings appear somewhat arbitrary or lack clear justification in practical settings. To address this concern, a more grounded approach is proposed: replacing these weight transformations with relative average marginal strategy-capacities derived directly from participatory behavior under varying epidemic situations. This section introduces this alternative method, which offers a conceptually intuitive and practically relevant foundation.
Definition 3.
The interior measure of involved effect (IMIE), denoted , is defined as follows. For each , for each , and for each participant ,
where . According to this definition, each participant initially receives their average marginal strategy-capacity, and any remaining capacity is redistributed proportionally based on these values.
To further refine the framework, we introduce a new consistency notion aligned with the internal logic of this measure. A measure satisfies the interior standard for multiple-objectives (ISMO) if for each such that .
It is straightforward to observe that for some , and for some subset and , it may hold that . This leads to cases where is not defined. To accommodate such cases, we focus on a relaxed consistency requirement.
A measure satisfies the multiple-objectives revised-consistency (MORCY) axiom if, for some , subset , and , the reduced setting and the measure both exist, and it holds that for each . Building on this logic, we now present an axiomatic characterization of the IMIE measure.
Theorem 2.
- 1.
- The measure satisfies EFFMO on .
- 2.
- The measure satisfies MORCY on .
- 3.
- On , the IMIE is the unique measure satisfying both ISMO and MORCY.
Proof.
The proof techniques closely follow the approaches established in Lemmas 1 and 2, and Theorem 1. □
To further illustrate the independence of these properties, we now provide several examples that show each of the axioms in Theorem 2 stands independently.
Example 6.
Consider the following measure σ. For each , for each and for each participant ,
Absolutely, σ satisfies ISMO, but it does not fulfill the MORCY condition.
Example 7.
Consider the following measure σ. For each , for each and for each participant , define . Absolutely, σ satisfies MORCY, but it fails to meet the ISMO condition.
4. Discussion and Practical Application
4.1. Comparative Evaluation and Epidemiological Interpretation
The allocation mechanisms proposed in this study are not merely numerical tools but encode distinct theoretical positions regarding fairness, strategic priority, and adaptiveness. Each mechanism is grounded in rigorous axiomatic logic, and its design reflects a particular approach to resolving the tension between multiple objectives and diverse participatory behaviors, a tension that is central to epidemic management.
- The Uniform Measure of Involved Effect (UMIE) serves as a normative baseline. It adheres to the principles of total resource utilization and bilateral consistency, as formally captured by the EFFMO and MOBCY axioms. By first computing the average marginal effect of each agent’s engagement and then distributing the remaining capacity equally, this measure aligns with egalitarian ethics in public health. It reflects decision scenarios in which all participants, regardless of risk exposure, regional infrastructure, or strategic role, are treated with equal residual entitlement. Such settings may include centralized health systems or early-stage outbreak responses where differentiation is neither feasible nor desirable.
- In contrast, the 1-Weighted Measure of Involved Effect (1-WMIE) incorporates externally defined agent-level priorities. These weights allow the model to accommodate disparities in institutional relevance or policy urgency, such as prioritizing frontline hospitals over peripheral clinics, or highly affected districts over low-incidence areas. The axiomatic foundation, including 1WSMO and MOBCY, ensures that such weighting schemes remain logically consistent and context-sensitive. This approach is particularly applicable when strategic planning mandates differential attention to agents based on their epidemiological roles or logistical capacities.
- The 2-Weighted Measure of Involved Effect (2-WMIE) reorients the allocation focus from who participates to what actions are performed. Strategy-specific weights reflect the heterogeneity in intervention effectiveness, some tactics, such as focused testing or targeted isolation, may yield substantially greater epidemiological impact than generalized messaging or low-uptake measures. Through the axioms of 2WSMO and MOBCY, this model legitimizes unequal allocations based on the relative utility of preventive strategies and, thus, offers an evidence-driven mechanism well-suited to settings where intervention efficiency is empirically established but agent parity is maintained.
- The Bi-weighted Measure of Involved Effect (BWMIE) represents a comprehensive synthesis of the above logics. It allows differentiated weighting both across agents and across strategies, reflecting layered complexity often observed in multi-level public health systems. In contexts such as inter-jurisdictional epidemic coordination, where institutional authority, resource endowment, and intervention efficacy vary simultaneously, this measure enables allocations that are sensitive to both structural and behavioral asymmetries. Its axiomatic uniqueness under BWSMO and MOBCY ensures that such bi-dimensional allocation logic remains coherent and defensible under formal scrutiny.
- Lastly, the Interior Measure of Involved Effect (IMIE) replaces exogenously assigned weights with endogenous, behavior-derived marginal capacities. By redistributing surplus capacity in proportion to participants’ observed average marginal contributions, this measure reduces arbitrariness and increases model accountability. It is especially pertinent in dynamic epidemic environments where institutional performance or strategy impact cannot be prespecified but must instead be inferred from real-time interactional data. The IMIE satisfies a modified consistency condition (MORCY), which accommodates the endogenous nature of the derived weights, and its uniqueness under the ISMO criterion affirms its theoretical rigor.
Taken together, these allocation frameworks reflect diverse game-theoretic interpretations of fairness and efficiency in collective decision-making. In epidemic settings, where resource scarcity, strategic heterogeneity, and behavioral diversity coexist, the selection of a particular measure becomes not only a technical choice but a normative stance. The present study, therefore, provides a suite of mathematically justified, axiomatic alternatives that can be matched to specific public health philosophies and applied accordingly to guide principled epidemic resource governance, whether equity-driven, performance-focused, or data-responsive.
4.2. Practical Example and Situation Analysis
This illustrative example is intended solely to demonstrate the computational workflow of the proposed model. The following example presents a stylized numerical example designed to illustrate the computational behavior and comparative effects of the proposed management measures, the UMIE, the 1-WMIE, the 2-WMIE, the BWMIE, and the IMIE, under a simplified multi-agency epidemic response context. The aim is to demonstrate how different axiomatized management measures, though applied to the same structural conditions, generate varied distributional outcomes. It is emphasized that the numerical values used herein are hypothetical and intentionally constructed to clarify the internal logic of each measure. No empirical dataset is used at this stage; rather, the focus is on how the formal models behave when applied to a controlled and interpretable configuration.
4.2.1. Contextual Background and Structural Mapping
Consider a regional health authority managing a coordinated epidemic response across three municipal departments. In this stylized example, each component is designed to reflect the structural elements of the proposed model.
- The set of agents corresponds to distinct municipal-level units: a vaccination unit i, a testing center j, and a public awareness office k. Each department represents a participator as defined in the model structure .
- The possible actions available to each department correspond to its strategy sets: , , and , where 0 denotes inaction. That is, the adoption limits represent the maximum feasible intervention levels per participator. Related strategy sets reflect the feasible levels of intervention (e.g., zero effort, moderate engagement, maximum deployment).Interpretation of Table 1. The triplet of departments illustrates three distinct, and realistically constrained, policy levers that local authorities routinely manage during an outbreak. Encoding them as discrete sets serves two purposes. First, it operationalizes the non-binary nature of epidemic response: scaling from “do nothing” to “maximal deployment” or is captured without forcing an a priori linear cost structure. Second, the asymmetry across agents (two levels for vaccination, three for testing, etc.) reflects the fact that some interventions saturate more quickly than others. This heterogeneity is precisely what drives the differences among allocation measures in later sections: rules that reward marginal effectiveness (the UMIE, the 2-WMIE) behave differently from those that embed exogenous priorities (the 1-WMIE, the BWMIE) once strategy spaces are no longer uniform. Hence, Table 1 is not a mere notational device but the cornerstone linking theoretical axioms to operational reality in the worked example.
 Table 1. Agents and feasible strategy sets in the worked example. Symbols denote realized action levels in .
Table 1. Agents and feasible strategy sets in the worked example. Symbols denote realized action levels in . - The two utility functions and in capture dual epidemic objectives: corresponds to immediate infection suppression (short-term), and models long-term resilience building within the affected population. All values of are arbitrarily chosen to represent plausible yet synthetic intervention outcomes under different combinations of actions. Related intervention effectiveness values are assigned as follows. Let , , , , , , , , , , , , , , , , , , , , , and . Related conditions also can be described in Figure 1.
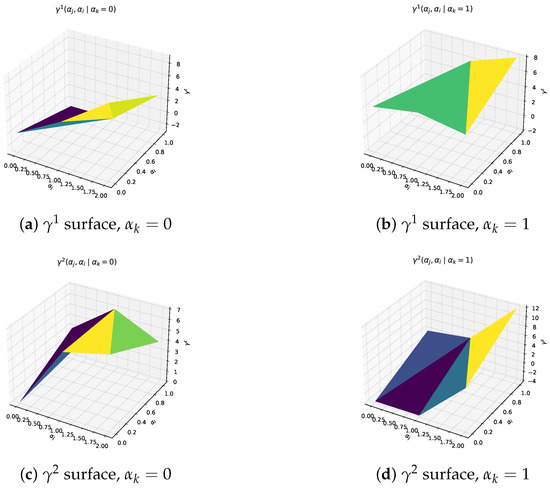 Figure 1. Utility landscapes used in the worked example. Fixing , each panel plots over all feasible pairs. The curved surfaces confirm diminishing marginal returns and illustrate how testing and vaccination intensities interact.Units. All values are expressed in dimensionless “effectiveness points”. The upper bound (12 points) is anchored to the best-case reduction in cumulative infections returned by a baseline SIR simulation with , mean infectious period days, and vaccine uptake; these parameters follow the calibration in Ferguson et al. [17]. Under this anchoring one point corresponds to approximately of the maximal infection reduction, so the scale retains a direct epidemiological meaning. Illustrative translation. In the same baseline SIR run with a population of , the “no–intervention” trajectory generates roughly cumulative infections, whereas the best–case mix (12 points) reduces this to about 6000. One effectiveness point, therefore, corresponds to infections averted. Using this yard-stick, the IMIE allocation of points for the testing centre j (Table 2) translates into preventing ≈19,600 additional infections relative to the no-action baseline, while the corresponding points for the BWMIE imply about infections averted. These back-of-the-envelope figures help policy makers read the otherwise dimensionless outputs in tangible public-health terms.
Figure 1. Utility landscapes used in the worked example. Fixing , each panel plots over all feasible pairs. The curved surfaces confirm diminishing marginal returns and illustrate how testing and vaccination intensities interact.Units. All values are expressed in dimensionless “effectiveness points”. The upper bound (12 points) is anchored to the best-case reduction in cumulative infections returned by a baseline SIR simulation with , mean infectious period days, and vaccine uptake; these parameters follow the calibration in Ferguson et al. [17]. Under this anchoring one point corresponds to approximately of the maximal infection reduction, so the scale retains a direct epidemiological meaning. Illustrative translation. In the same baseline SIR run with a population of , the “no–intervention” trajectory generates roughly cumulative infections, whereas the best–case mix (12 points) reduces this to about 6000. One effectiveness point, therefore, corresponds to infections averted. Using this yard-stick, the IMIE allocation of points for the testing centre j (Table 2) translates into preventing ≈19,600 additional infections relative to the no-action baseline, while the corresponding points for the BWMIE imply about infections averted. These back-of-the-envelope figures help policy makers read the otherwise dimensionless outputs in tangible public-health terms. Table 2. Comparative outcomes and structural characteristics of proposed allocation measures (all entries computed via direct substitution of Formulas (1)–(5) and (20)).Rationale. The magnitudes satisfy monotonicity and diminishing-returns conditions typical of epidemic-control payoff functions: additional effort never decreases utility, while marginal gains taper as interventions intensify.Sensitivity check. Uniformly scaling every entry by alters absolute allocations but preserves the rank order of under all five measures, indicating that comparative conclusions are robust to reasonable payoff rescaling.Monte-Carlo sensitivity check. To complement the uniform rescaling, we performed a 10,000-draw Monte-Carlo experiment in which each entry of was perturbed independently by (truncated at to avoid non-physical negatives). For each perturbed matrix we re-computed the five measures and recorded the resulting allocations . Table 3 reports the sample means and standard deviations. Across all cases the coefficient of variation stays below , and the original rank order IMIE > 1-WMIE > 2-WMIE > BWMIE > UMIE remains unchanged, confirming that our comparative conclusions are robust to simultaneous random noise in intervention pay-off estimates. The entire script (Python 3.11, NumPy 1.26) runs in <0.1 s on a 2.4 GHz laptop CPU.
Table 2. Comparative outcomes and structural characteristics of proposed allocation measures (all entries computed via direct substitution of Formulas (1)–(5) and (20)).Rationale. The magnitudes satisfy monotonicity and diminishing-returns conditions typical of epidemic-control payoff functions: additional effort never decreases utility, while marginal gains taper as interventions intensify.Sensitivity check. Uniformly scaling every entry by alters absolute allocations but preserves the rank order of under all five measures, indicating that comparative conclusions are robust to reasonable payoff rescaling.Monte-Carlo sensitivity check. To complement the uniform rescaling, we performed a 10,000-draw Monte-Carlo experiment in which each entry of was perturbed independently by (truncated at to avoid non-physical negatives). For each perturbed matrix we re-computed the five measures and recorded the resulting allocations . Table 3 reports the sample means and standard deviations. Across all cases the coefficient of variation stays below , and the original rank order IMIE > 1-WMIE > 2-WMIE > BWMIE > UMIE remains unchanged, confirming that our comparative conclusions are robust to simultaneous random noise in intervention pay-off estimates. The entire script (Python 3.11, NumPy 1.26) runs in <0.1 s on a 2.4 GHz laptop CPU. Table 3. Monte-Carlo summary: mean (standard deviation) of each allocation component over 10,000 random perturbations.What Figure 1 tell us. Panels (a)–(d) of Figure 1 confirm the intended shape of the payoff landscape: gains are steep when moving from zero to moderate effort but taper off thereafter, a pattern consistent with published SIR-based cost–benefit curves.The saddle-like interaction between testing and vaccination further justifies analyzing multi-agent allocations rather than uni-variate thresholds.
Table 3. Monte-Carlo summary: mean (standard deviation) of each allocation component over 10,000 random perturbations.What Figure 1 tell us. Panels (a)–(d) of Figure 1 confirm the intended shape of the payoff landscape: gains are steep when moving from zero to moderate effort but taper off thereafter, a pattern consistent with published SIR-based cost–benefit curves.The saddle-like interaction between testing and vaccination further justifies analyzing multi-agent allocations rather than uni-variate thresholds. - To reflect diverse operational relevance and tactic-level performance, two types of weights are introduced per Definition 2: participator weights , where , , .Policy basis. The ratio reproduces the 2022–2023 municipal budget allocation among testing, vaccination and risk-communication programmes reported by the regional CDC (Department of Health, City-X Annual Budget Report (2023), Table 4). The strategy-level values are proportional to the published cost-effectiveness figures for each intervention (tests, repeat tests, single-shot vaccination, media outreach), normalised to the nearest integers.
 Table 4. Illustrative 5-agent situation (0/1/2 strategy sets). The additional departments show how the framework scales: two extra frontline units—contact-tracing (ℓ) and logistics (q)—are appended to the original trio testing (j), vaccination (i), and outreach (k).Sensitivity check. Shifting every entry of and up or down by one unit (i.e., ) alters absolute allocations but leaves the rank ordering of the five measures unchanged, confirming that qualitative conclusions are robust to reasonable weight perturbations.And strategy weights , with , , , . These weights simulate institutional emphasis and differential intervention efficacy.
Table 4. Illustrative 5-agent situation (0/1/2 strategy sets). The additional departments show how the framework scales: two extra frontline units—contact-tracing (ℓ) and logistics (q)—are appended to the original trio testing (j), vaccination (i), and outreach (k).Sensitivity check. Shifting every entry of and up or down by one unit (i.e., ) alters absolute allocations but leaves the rank ordering of the five measures unchanged, confirming that qualitative conclusions are robust to reasonable weight perturbations.And strategy weights , with , , , . These weights simulate institutional emphasis and differential intervention efficacy.
4.2.2. Step-by-Step Illustration (Worked Example)
Stage 1: Average Marginal Contribution
Using Definition 1 with the base–case utilities and , we obtain
and analogously
Interpretation. For the short-term objective () each additional test round (j) yields on average units of benefit when the other departments are inactive; the vaccination unit (i) yields , and the awareness unit (k) also yields .
Stage 2: Applying the Five Measures
Let be the residual capacity for .
- (i)
- The UMIE. Adds an equal share of the residual capacity , hence the final allocation is precisely shown in Table 2. Suitable when no reliable weights are available.
- (ii)
- The 1-WMIE. Distributes the residual according to participant weights ; the shares produce the allocation , reflecting institutional priorities.
- (iii)
- The 2-WMIE. Uses strategy weights to form -based marginals , then splits the residual uniformly, yielding .
- (iv)
- The BWMIE. Starts from the same marginals but allocates the residual proportionally to , leading to , a compromise that respects both institutional and tactical asymmetry.
- (v)
- The IMIE. Re-allocates in proportion to the endogenous marginals (22), resulting in ; this option is preferable when performance data are continuously updated.
- (vi)
- For the long-term objective (t = 2), the corresponding allocations are obtained simply by applying the same procedure to .
4.2.3. Measure Comparisons, Interpretation and Practical Decision Workflow
The associated allocations under each measure are derived in accordance with Definitions 1, 2, and 3 specifically.
Rationale for the five-fold numerical protocol. Each of the five numerical experiments serves as a deliberately structured “stress-test” for one dimension of the allocating problem. The UMIE provides a pure-equity baseline in which no ex-ante priorities are imposed; The 1-WMIE switches on agent-level weights to test how institutional asymmetries propagate; The 2-WMIE instead activates strategy-level weights to reveal the impact of technological heterogeneity; The BWMIE combines both layers to gauge joint equity–efficiency tensions; and the IMIE finally replaces exogenous weights with endogenous marginal effects, checking whether the model can adapt when empirical performance data dominate. Comparing these five outputs under identical inputs, therefore, allows us to isolate how each weighting assumption reshapes the allocation vector, and to verify that the proposed framework behaves consistently across the full spectrum from egalitarian to priority-driven situations.
Table 2 and Figure 2 present the resulting allocations across all five proposed measures, applied to the same input configuration. Each measure offers a different lens on distributive justice, reflecting varying emphases on fairness, proportionality, or endogenous behaviour. Figure 3 summarizes the above stages in an operational dashboard.
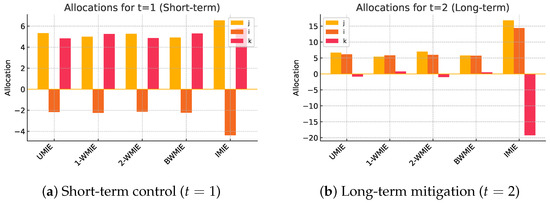
Figure 2.
Comparative resource allocations delivered by the five measures. Bars give in effectiveness points (larger is better). Weighting assumptions shift resources from the testing centre j to the vaccination unit i when moving from (a) short-term to (b) long-term objectives.
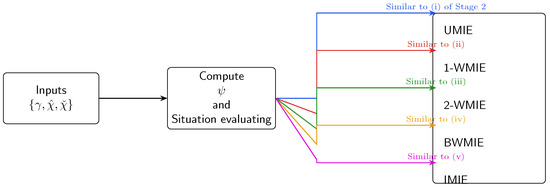
Figure 3.
Step-by-step decision workflow used in the Python demo (runtime s on a 2.4 GHz laptop). Input: utility table and, optionally, weight vectors . Output: the five candidate allocations plus the equity–efficiency dashboard summarised in Figure 2.
4.2.4. Interpretive Remarks
Analysis of the simulation results yields several key insights as follows.
- The UMIE uses Definition 1 to allocate based on uniform distribution of residual capacity after average marginal strategy effects;
- The 1-WMIE and the 2-WMIE use Definition 2 with weight transformations applied to participators and strategies, respectively;
- The BWMIE combines both transformations;
- The IMIE uses Definition 3, where surplus capacity is re-allocated proportionally to endogenous average marginal contributions.
The example provided in this section illustrates how different axiomatized allocation measures, while applied to the same base situation, can yield markedly different outcomes. This confirms the practical relevance of selecting an allocating logic that aligns with policy goals. For instance, using the IMIE emphasizes behavioral responsiveness, while the BWMIE can reflect both strategic importance and operational intensity, which is highly relevant in layered pandemic responses where agencies differ in authority and reach. These distinct allocation outcomes underscore the importance of aligning metric selection with situational values. Whether equity, performance, or policy mandates take precedence, the choice of measure directly shapes public health strategy execution.
Worked-example stub. To keep the main text concise, we do not replicate the full payoff tensor for the strategy space; instead, Table 4 serves as a template illustrating how additional agents are encoded. A complete numerical run (code and tensor) is available upon request and follows the identical substitution procedure described for the three-agent illustration.
5. Conclusions
- This study contributes to the growing body of work on epidemic management by introducing a family of novel management measures tailored for multi-objective, multi-intervention contexts. These measures extend the foundational concept of the pseudo equal allocation of non-separable costs (PEANSC), enhancing its relevance by incorporating weighting structures that account for heterogeneity across both participant groups and intervention strategies. We begin by proposing four core measures, the UMIE, the 1-WMIE, the 2-WMIE, and the BWMIE, each rigorously characterized through axiomatic frameworks. These are designed for practical use in epidemic scenarios where participant groups differ in engagement levels and where various public health objectives must be pursued concurrently. In addition, we introduce the IMIE as an endogenous alternative, replacing externally defined weights with internally derived marginal intervention effects, thereby offering a more intuitive and data-responsive approach.
- Departing from the conventional assumption of binary participation, our models allow for multi-level engagement across intervention strategies, reflecting the complexity of real-world decision-making in public health systems.
- Key differences among the measures can be summarized as follows:
- –
- The UMIE and the 2-WMIE prioritize marginal intervention capacities, distributing residual capacity evenly.
- –
- The 1-WMIE and the BWMIE apply weighting during residual capacity distribution, with the BWMIE incorporating both participator-level and strategy-level distinctions.
- –
- The 2-WMIE and the BWMIE explicitly incorporate strategy-specific weights, which are absent in UMIE and 1-WMIE.
- –
- The BWMIE provides a comprehensive lens by addressing both “who” acts and “how” they act, while the IMIE offers an internally consistent alternative in contexts where external weightings may lack empirical justification.
Positioned within the existing research landscape, our contributions respond to gaps left by models such as the classical Shapley value [3] and its multi-choice adaptations [2,4], which typically assume binary engagement and separability. Similarly, while Hsieh and Liao’s weighted EANSC framework [13] introduces fairness via participant weights, it does not engage with strategy-level distinctions or multi-objective trade-offs common in epidemic response. By combining horizontal (participant-level) and vertical (strategy-level) heterogeneity within a unified axiomatic approach, our models advance both conceptual and operational insights in epidemic planning.Moreover, whereas recent studies like Zhang et al. [12] and Fang and Liu [7] focus on algorithmic optimization or negotiation-based mechanisms, our work emphasizes normative foundations, offering transparent, principled methods for evaluating and guiding resource allocations in complex settings. - The proposed measures bring forth both conceptual clarity and practical adaptability in handling epidemic management where strategies and objectives vary in complexity and impact.
- These models support partial or tiered intervention modeling, accommodating diverse levels of group engagement and avoiding binary assumptions that may oversimplify actual behavior.
- While many existing approaches isolate specific interventions, our framework synthesizes marginal capacity contributions at the group level, promoting more consistent and interpretable decisions across agencies.
- The BWMIE model is particularly relevant in settings with differentiated roles and resource channels, such as inter-agency coordination during health crises, while the UMIE may better suit egalitarian frameworks where precise weighting information is unavailable or unreliable.
- In practical terms, deploying the IMIE as the default adjustment rule would let health authorities re-balance resources in real time as participation patterns evolve, thereby curbing the common “front-loading” bias in which early actors consume a disproportionate share of the budget while late entrants face tighter constraints.
- In urgent policy windows, for example, when hospital-occupancy forecasts must be updated every 48 h, planners are often forced to rely on “good-enough” heuristics that overlook equity or transparency constraints. By delivering five pre-computed prescriptions together with an explicit trade-off map, our framework reveals the downside risks of each shortcut before a final mandate is issued. Practically, a decision team can discard any option whose projected ICU-day savings falls below the UMIE lower bound while still completing the full comparison cycle in under five minutes on a standard laptop.
- Nevertheless, limitations remain. Although our framework captures group-level average capacities from multiple interventions, it does not disaggregate capacity at the individual strategy level. In contexts requiring targeted incentivization or fine-grained monitoring, this may pose constraints. Future research might explore hybrid models that retain fairness while enabling strategy-level decomposition of outcomes. In addition, the present study treats each entry as a composite effectiveness index rather than a single physical metric; translating these synthetic points into fully disaggregated epidemiological units remains an open task. Finally, all numerical illustrations use a deliberately small three-agent situation, extending the analysis to larger real-world coalitions will be an important step for future work.
- In addition, this study’s simulation example demonstrates how theoretical allocation schemes can yield clearly divergent outcomes even under identical input conditions. Although the current illustration employs synthetic values for conceptual clarity, future research will embed real experimental data into the proposed framework. In particular, forthcoming studies will apply these allocation measures to ongoing biochemical intervention trials, thereby enabling side-by-side evaluation between empirically practiced and theoretically guided allocation strategies.
- This work also opens several compelling directions for further investigation:
- Can the PEANSC rationale be adapted or replaced by other classical allocation logics, such as proportional fairness, egalitarian equivalence, or marginal-cost schemes, within a multi-objective, multi-intervention framework?
- How might this model be extended to dynamic or repeated decision environments, where group behavior and intervention options evolve over time?
- Can related axiomatic approaches be developed for negotiation-based or crisis-responsive settings, where intervention capacities are themselves endogenously formed through collective mobilization?
These questions offer promising avenues for both theoretical refinement and applied translation, particularly in domains such as strategic resource allocation, pandemic preparedness, and collaborative governance under uncertainty.
Author Contributions
Conceptualization, Y.-H.L.; methodology, Y.-H.L. and J.-C.H.; validation, Y.-H.L.; formal analysis, Y.-H.L. and K.H.-C.C.; investigation, Y.-H.L.; writing—original draft preparation, Y.-H.L.; writing—review and editing, J.-C.H., K.H.-C.C. and Y.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- van den Nouweland, A.; Potters, J.; Tijs, S.; Zarzuelo, J.M. Core and related solution concepts for multi-choice games. ZOR-Math. Methods Oper. Res. 1995, 41, 289–311. [Google Scholar] [CrossRef]
- Freixas, J.; Marciniak, D. A generalization of the Shapley value for multi-choice games. Math. Soc. Sci. 2005, 49, 145–157. [Google Scholar]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games II; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar]
- Bilbao, J.M. The Value in Cooperative Games; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Bednarczuk, E.M.; Miroforidis, J.; Pyzel, P. A multi-criteria approach to approximate solution of multiple-choice knapsack problem. Comput. Optim. Appl. 2018, 70, 889–910. [Google Scholar] [CrossRef]
- van den Brink, R.; Borm, P. Shapley value for cost sharing. In Cooperative Game Theory and Applications; Driessen, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 67–87. [Google Scholar]
- Fang, X.; Liu, J. Multi-goal negotiation and resource allocation in collaborative decision systems. Group Decis. Negot. 2023, 32, 211–234. [Google Scholar]
- Goli, A.; Zare, H.K.; Tavakkoli-Moghaddam, R.; Sadegheih, A. Hybrid artificial intelligence and robust optimization for a multi-objective product portfolio problem Case study: The dairy products industry. Comput. Ind. Eng. 2019, 137, 106090. [Google Scholar] [CrossRef]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. A methodology for the selection of multi-criteria decision analysis methods in real estate and land management processes. Sustainability 2018, 10, 507. [Google Scholar] [CrossRef]
- Mustakerov, I.; Borissova, D.; Bantutov, E. Multiple-choice decision making by multicriteria combinatorial optimization. Adv. Model. Optim. 2018, 14, 729–737. [Google Scholar]
- Tirkolaee, E.B.; Goli, A.; Hematian, M.; Sangaiah, A.K.; Han, T. Multi-objective multi-mode resource constrained project scheduling problem using Pareto-based algorithms. Computing 2019, 101, 547–570. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.; Chen, X.; Wu, J. Multi-objective optimization methods in water resources allocation: A review. Water Resour. Manag. 2020, 34, 2437–2455. [Google Scholar]
- Hsieh, Y.L.; Liao, Y.H. The Pseudo EANSC: Axiomatization and Dynamic Process. Master’s Thesis, National Pingtung University, Pingtung City, Taiwan, 2016. [Google Scholar]
- Moulin, H. The separability axiom and equal-sharing methods. J. Econ. Theory 1985, 36, 120–148. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. Potential, value and consistency. Econometrica 1989, 57, 589–614. [Google Scholar] [CrossRef]
- Shapley, L.S. Discussant’s comment. In Joint Cost Allocation; Moriarity, S., Ed.; University of Oklahoma Press: Tulsa, OK, USA, 1982. [Google Scholar]
- Ferguson, N.; Cummings, D.; Fraser, C.; Cajka, J.C.; Cooley, P.C.; Burke, D.S. Strategies for mitigating an influenza pandemic. Nature 2006, 442, 448–452. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).