1. Introduction
Graphs are powerful tools for modeling relationships and dependencies across diverse fields, including network analysis [
1,
2], transport optimization [
3,
4], natural language processing [
5,
6], pattern recognition [
7,
8,
9,
10], knowledge representation [
11,
12,
13], liver disease analysis [
14,
15], neuroscience [
16,
17,
18], and the construction of bioinformatics networks [
19,
20,
21,
22]. Algebraic hyperstructures were introduced by Marty in 1934 as a generalization of classical algebraic structures [
23]. They were extensively explored by Corsini [
24,
25,
26], and later by other authors [
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42]. The connection between algebraic hyperstructures and binary relations has been rigorously investigated [
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54], establishing a framework for representing and analyzing graph properties through hyperstructures [
55,
56,
57,
58,
59,
60,
61,
62,
63,
64]. In this direction, the introduction and investigation of algebraic hyperoperations deriving from directed graphs offer an integration of hypercompositional algebra with graph theory [
65,
66]. These graph hyperoperations exhibit characteristics dictated by the structure of their underlying graphs, which, in turn, define corresponding graph classes. This synergy provides novel insights and methodologies for analyzing complex graph properties [
67,
68,
69], further enriching the study of graph theory through the lens of algebraic hyperstructures.
In this paper, we extend these ideas by examining fuzzy graph hyperoperations. The concept of fuzzy graphs, first introduced by Rosenfeld in 1975 [
70], extends classical graph theory by incorporating fuzzy set theory to model uncertainty and imprecision in complex systems. A fuzzy graph is typically defined as a pair consisting of a fuzzy set of vertices and a fuzzy set of edges, with the constraint that the membership value of an edge cannot exceed the membership values of its connecting vertices [
71,
72]. By associating fuzzy membership values with nodes and edges, fuzzy graphs provide a robust framework for analyzing systems where interactions and elements exhibit inherent vagueness or ambiguity. This allows fuzzy graphs to represent partially connected vertices and varying strengths of relationships, making them particularly valuable in applications where traditional graph models fail to capture underlying complexities [
73,
74,
75,
76].
Fuzzy graphs have been applied across diverse domains, including social network analysis, bioinformatics, transportation systems, and more. In social network analysis, they model relationships with varying strength or certainty, such as trust or influence [
77,
78,
79,
80,
81]. In medical diagnosis, fuzzy graphs help identify uncertain symptom-disease correlations [
82]. In transportation systems, they facilitate traffic optimization by modeling routes with varying congestion levels or reliability [
83]. Additionally, fuzzy graphs have been used in pattern recognition to identify complex structures [
84,
85] and in disease spread modeling to address uncertainties in transmission dynamics [
86].
In this paper, we introduce hypercompositional structures on fuzzy graphs by extending classical path-based hyperoperations to a fuzzy framework. Building on the notion of
strongest strong paths—those that are both strength-optimal and composed exclusively of strong edges—we define two types of fuzzy hyperoperations: a
vertex-based and an
edge-based fuzzy path hyperoperation. These operations generalize classical crisp hyperoperations and are compatible with fuzzy graph topology. The proposed framework allows us to reason algebraically about fuzzy connectivity and uncertainty-aware navigation in networks, providing a rich theoretical foundation for applications in social systems, biological regulation, communication networks, and medical diagnostics [
74,
75,
76,
77,
78,
79,
81,
82,
86].
While classical fuzzy graph models typically focus on scalar-valued connectivity—such as determining the degree of reachability between two nodes using relational composition or -cut-based adjacency—they often do not preserve intermediate structural information, nor do they support compositional reasoning over sets of paths or substructures. In contrast, the vertex-based and edge-based fuzzy path hyperoperations introduced in this paper generate fuzzy subsets of vertices or edges lying on strongest strong paths, enabling the algebraic manipulation of connectivity regions rather than scalar summaries. This set-valued perspective permits the formalization of algebraic operations that are closed, associative, and structurally meaningful, thereby integrating fuzzy graph theory with hypercompositional algebra. Additionally, our framework supports the construction of quotient graphs that preserve directional strength semantics and admit interpretation as condensed fuzzy systems, offering advantages in modular analysis and abstraction. These features distinguish the proposed model from traditional fuzzy connectivity approaches and motivate its development as a foundational tool for uncertainty-aware reasoning in complex networks.
In the introduced framework, we develop a comprehensive set of structural and algebraic properties for the associated fuzzy hyperoperations. In particular, for the vertex fuzzy path hyperoperation, we prove associativity, thereby establishing a fuzzy hypersemigroup over the vertex set. We demonstrate reflexivity and -cut monotonicity, enabling threshold-sensitive reasoning. We characterize fuzzy strong cut vertices and edges, introduce a fuzzy distance function quantifying path strength, and analyze how these features behave under equivalence relations derived from mutual full-strength connectivity. By constructing quotient fuzzy graphs and establishing the closure properties of their equivalence classes, we derive coarse-grained models that preserve key connectivity semantics.
The paper is organized as follows.
Section 2 reviews algebraic hyperstructures and classical graph hyperoperations.
Section 3 extends these ideas to fuzzy graphs, defining fuzzy paths, strongest paths, and strongest strong paths.
Section 4 introduces vertex- and edge-based fuzzy path hyperoperations and proves their key algebraic properties.
Section 5 defines the mutual full-strength connectivity relation
and studies the quotient fuzzy graph.
Section 6 introduces a fuzzy distance function and examines its behavior on both the original and quotient graphs.
Section 7 presents application scenarios, including trust networks and biological systems.
Section 8 concludes the paper with a summary and future research directions.
2. Algebraic Background and Classical Graph Hyperoperations
We start with some necessary notions from hypercompositional algebra. Given a nonempty set
V, a
hyperoperation (
hyperproduct) on
V is a mapping
where
denotes the powerset of
V. As usual we set
We define the hyperproduct between two subsets
by
A
hypergroupoid is a pair
, where ★ is a hyperoperation on the set
V. Following [
37], a hypergroupoid
is called
Nonpartial: If the hyperproduct is nonempty for all .
Degenerative: If for all .
Weakly degenerative: If for all , with .
Total: If for all .
Commutative: If, for all , it holds that .
Weakly commutative: If, for all , it holds that .
A directed crisp graph (or simply graph) consists of a set of vertices (nodes) V and a set of edges . A subgraph of such a graph G is a graph with and , such that every edge in has both endpoints in .
Given a graph
, a
path P inside
G from a vertex
to a vertex
is a sequence of edges:
such that for every
i, it holds that
. In this case, we say that the path has length
m, and that the nodes
lie on the path
P and similarly for the edges in the sequence. Note that nodes and edges may appear more than once in a path. Given a path
P, we write
and
to express that vertex
v and edge
lie on
P, respectively. We denote a path
P from
to
by
If all nodes appear at most once in a path, the path is called simple. A cycle is a path that starts and ends at the same node. The empty sequence is a cycle from u to itself, containing only u.
The set of all nodes that lie in a path from
to
is denoted by
A graph G is called strongly connected if, for any two nodes and , there exists at least one path from to . A strongly connected subgraph of a graph G is called a Strongly Connected Component of G.
Given a graph
, the
path hyperoperation (see [
65,
66,
67,
68,
69]) is a mapping
defined by
The hyperstructure
is called the
path hypergroupoid corresponding to
G.
3. Fuzzy Graphs and Strongest Strong Paths
In this section we extend the definition of directed graphs to introduce fuzzy directed graphs, which incorporate the concept of partial membership for nodes and edges.
Fuzzy sets generalize traditional (crisp) sets, which allow only binary membership values of 0 or 1—an element either entirely belongs to the set or does not belong at all. By contrast, fuzzy sets capture a continuum of membership, enabling the representation of uncertain or imprecise data.
Formally, a fuzzy set is defined as a nonempty crisp set A paired with a function , known as membership function. For every element , the value represents the membership grade of s in the fuzzy set. This grade indicates the degree to which the element belongs to the set, where implies no membership, implies full membership, and intermediate values reflect partial membership. From this definition it is clear that crisp sets are a special case of fuzzy sets.
If
is a fuzzy set and
, then
denotes the fuzzy set obtained by taking the restriction of
to
B. Given a finite universal set
, the fuzzy set
can be denoted as
The set of all fuzzy sets that can be defined on a universe set
A is denoted by
. The
support of a fuzzy set
is defined as the crisp subset of
A containing all elements with a non-zero membership grade. Formally, the support of
, denoted as
, is given by
In other words, the support of a fuzzy set includes all elements of the universe
A that have a positive degree of membership.
The
-cut (or
-level set) of a fuzzy set
is a crisp subset of
A containing all elements whose membership grades are greater than or equal to a given threshold
, where
. The
-cut is a fundamental concept in fuzzy set theory, providing a way to analyze and approximate fuzzy sets using crisp subsets. It is particularly useful in applications where decision-making or reasoning is based on threshold levels. Formally, the
-cut of
, denoted as
, is defined as
and the
strict -cut of
, denoted as
, is
For
, the strict
-cut corresponds to the support of the fuzzy set, i.e.,
For any , we denote by the minimum of a and b and by their maximum.
A
fuzzy directed graph (or simply fuzzy graph) [
71] is a generalization of a directed crisp graph, where the nodes and the edges are characterized by membership functions that represent the degree of membership. Formally, a fuzzy graph is defined as a pair
where
- -
V is the set of vertices (nodes) of the graph.
- -
is the vertex membership function, which assigns to each vertex a membership grade , indicating the degree to which v belongs to the graph.
- -
is the edge membership function, which assigns to each pair of vertices a membership grade , indicating the degree of connectivity between u and v.
In addition, the following condition is required:
ensuring that the degree of membership of an edge cannot exceed the membership grades of its endpoints. Given a fuzzy graph
, the set
together with the edge membership function
, is called the edge set of
F and is denoted by
.
Given a fuzzy graph
, the
underlying crisp graph of
F is the graph
, where
is the underlying crisp vertex set and
is the underlying crisp edge set. A fuzzy graph
is called
complete if
for every
.
Now we introduce the concept of a
fuzzy path within a fuzzy graph. Given a fuzzy graph
and two nodes
, a fuzzy path
P of length
k, from the node
to the node
, is a sequence of edges
such that
for every
. We say that the vertices
and the edges
belong to the fuzzy path
P or, equivalently, that
F contains them. The set of all fuzzy paths from
v to
u, inside a fuzzy graph
F, is denoted by
. For every vertex
, the empty sequence
is a path from
u to itself, containing only the vertex
u and no edges.
Given a fuzzy graph and a set , a path in is path in F that does not contain any vertices from S, and similarly, given a set , a path in does not contain any edges from E.
The
strength of a path P inside a fuzzy graph
is denoted by
, and it is the minimum membership grade among all of the edges of
P, i.e.,
The
strength of connectedness between two nodes
u and
v of a fuzzy graph
F is defined as the maximum of the strengths of all paths
and is denoted by
. If no path exists between
u and
v, we set
.
A path
of a fuzzy graph
F is called a
strongest path of
F if
. Equivalently,
P is a strongest fuzzy path of
F if and only if
A fuzzy graph
is
strongly connected if for every
, it holds that
. An edge
is called
strong if
. A path consisting entirely of strong edges is called a
strong path. In general, a path may be the strongest without being strong and vice versa. Fuzzy paths that admit both properties are called
strongest strong paths (see [
72]). Formally we have
Intuitively, the strongest strong paths represent the most reliable routes in a fuzzy network, combining the optimal overall strength with the local edge optimality. The set of all strongest strong paths from
u to
v inside a fuzzy graph
F is denoted by
.
Fuzzy strong cuts were introduced for undirected fuzzy graphs in [
87] by employing the strongest strong paths. We define them in a similar way for directed fuzzy graphs as follows. Consider a fuzzy graph
with an underlying crisp graph
. A subset
is called a
fuzzy strong vertex cut set if for some vertices
, there exists
, but there exists no strongest strong path from
u to
v in
. In other words, this means that there is a strongest strong path
P from
u to
v inside
F if and only if we allow
P to go through the vertices of
M. If
, then
u is called a
fuzzy strong cut vertex of
F. A subset
is called a
fuzzy strong edge cut set if for some vertices
there exists
but there exists no strongest strong path from
u to
v in
. If
, then
is called a
fuzzy strong cut edge of
F.
Example 1. Consider the directed fuzzy graph of Figure 1, with vertices , vertex membership functionand edge membership function: The fuzzy paths from a to e are
with strength
with strength
with strength
with strength
with strength
The strength of connectedness between a and e is ; hence, the strongest paths from a to e are and . From these two only is strong. The path is not strong since it includes the edge , which is not strong because it holds . Thus, the only strongest strong path from a to e is . From this we can see that b and d are fuzzy strong cut vertices and that the edges are fuzzy strong cut edges of .
Figure 1.
The fuzzy graph of Example 1, with vertex memberships and edge weights shown.
Figure 1.
The fuzzy graph of Example 1, with vertex memberships and edge weights shown.
4. Fuzzy Hyperoperations and Structural Properties
A
fuzzy hypergroupoid is a pair
, where
V is a nonempty set and ★ is a binary fuzzy hyperoperation
Given a fuzzy graph
, we define a binary and a unary fuzzy hyperoperation as follows. The
vertex fuzzy path hyperoperation
is defined by setting
Hence,
is a fuzzy subset of
V with membership function
if
lies on some
, and 0 otherwise. Note that
yields a fuzzy subset where membership grades reflect the original vertex reliabilities of nodes participating in optimal signal transmission paths.
Intuitively, the vertex fuzzy path hyperoperation captures all nodes that lie on strongest strong paths from vertices v to u. It produces a fuzzy subset of vertices weighted by their original credibility scores , thereby modeling the spread or support of optimal communication under full-strength constraints. This operation generalizes binary connectivity to a graded, path-based relation central to our fuzzy algebraic framework.
The
edge fuzzy path hyperoperation is a unary hyperoperation on the set
defined by
Hence,
is a fuzzy subset of
with membership function
if
lies on some
, and 0 otherwise.
Remark 1. Although the domain of the edge fuzzy path hyperoperation is formally , which would suggest a binary operation in the classical sense, we interpret as a unary hyperoperation over the edge universe . This perspective aligns with the structural analogy to the vertex-based fuzzy path hyperoperation , which acts on the vertex set V. In this framework, the set serves as the domain and codomain of the hyperoperation, thereby justifying its classification as unary within the context of edge-based fuzzy algebraic structures.
The proposed fuzzy hyperoperations generalize classical graph hyperoperations while preserving their structure when applied to crisp graphs. The following proposition formally establishes this by showing that the vertex fuzzy path hyperoperation coincides with the classical path hyperoperation when all memberships are binary.
Proposition 1. The path hyperoperation and the vertex fuzzy path hyperoperation coincide for crisp graphs.
Proof. Let
be a directed crisp graph. The path hyperoperation
is defined as
Now consider the corresponding fuzzy graph
where
That is,
F is a crisp graph viewed as a fuzzy graph with binary membership functions. In this case, every existing path
P from
u to
v consists entirely of edges with membership 1. Therefore, each such path has strength
, the maximum possible and since
, all such paths are strongest.
To determine whether these paths are also
strong, recall that an edge
is called strong if
For all
, we have
. Thus, all edges in the graph are strong, and every path composed of such edges is also strong. Therefore, every path in the crisp graph is both strongest and strong, which means
The vertex fuzzy path hyperoperation is defined by
Since
for all
, this reduces to the crisp set
Thus,
. □
Given a fuzzy graph
and a set
, the
strongest fuzzy subgraph of
F generated by
M is the fuzzy graph
, where
and
A graph is called strongest if . We now give an example showing that even if a graph is strongest, not every path is a strongest strong path.
Example 2. Let be the fuzzy graph of Figure 2, with a vertex set and uniform vertex membership . Let the non-zero edge membership values beThe graph is strongest since each edge in the graph satisfiesThe pathshave strengthsTherefore, even though P is a path in a strongest graph, it is not a strongest strong path between and .
Figure 2.
The fuzzy graph of Example 2, illustrating that not every path in a strongest graph is a strongest strong path.
Figure 2.
The fuzzy graph of Example 2, illustrating that not every path in a strongest graph is a strongest strong path.
The following proposition provides a precise characterization of fuzzy strong cut edges by identifying them as those edges that appear in every strongest strong path between a given pair of vertices.
Proposition 2. Let be a strongest fuzzy graph. An edge is a fuzzy strong cut edge if and only if it appears in every strongest strong path between some pair of vertices .
Proof. (⇒) Suppose that is a fuzzy strong cut edge. By definition, there exist vertices such that
- (i)
,
- (ii)
, where .
This means that every strongest strong path from u to v in F must contain the edge . Otherwise, if there existed a path that did not include , then P would still be present in , contradicting the assumption that .
(⇐) Conversely, suppose that appears in every strongest strong path from u to v. Then, removing from F eliminates all such paths. That is, in the graph , we have . Hence, by definition, is a fuzzy strong cut edge. □
We now turn to a fundamental structural behavior of strongest strong paths in fuzzy graphs. In many practical contexts, especially in decision-making and network resilience, it is important to understand how the set of available paths changes as we impose stricter constraints on the strength of connections. This motivates the following proposition, which formalizes the monotonicity of the -cuts of the vertex fuzzy path hyperoperation.
Proposition 3. Let be a fuzzy graph, and let . If , thenwhere denotes the γ-cut of the fuzzy set , for any . Proof. By definition, the vertex fuzzy path hyperoperation
is a fuzzy subset of
V, with membership function
The
-cut of this fuzzy set is defined by
Now suppose
, and let
. Then
which implies
. Therefore,
□
An identity property of the vertex fuzzy path hyperoperation can be established on the diagonal.
Proposition 4. Let be a fuzzy directed graph. If F is acyclic, then for every , we havei.e., the fuzzy set resulting from the vertex fuzzy path hyperoperation on the diagonal contains only the node v with its original membership grade. Proof. Since F is acyclic, any path from v to v must be the trivial path , which is both strong and strongest by definition and, hence, belongs to . Since the only node appearing in is v, the fuzzy set is , as required. □
The following result highlights that the support of the fuzzy path hyperoperation is always contained within the classical path hyperoperation. In effect, the fuzzy vertex hyperoperation respects the topology of the underlying graph and supports hybrid models that combine both crisp and fuzzy structures.
Proposition 5. Let be a fuzzy graph, and let be its underlying crisp graph. Then, for any , we havewhere denotes the classical path hyperoperation in G. Proof. By definition,
is a fuzzy subset of
V such that
Thus, the support of
is the set of all nodes lying on some strongest strong path from
u to
v in
F:
Since all paths in
are also paths in the underlying crisp graph
G, we have
□
To assess the utility of a vertex in fuzzy connectivity without entirely removing it from the graph, we adopt a notion of structural removal. The following definition formalizes this operation.
Let
be a fuzzy graph and let
. We define the
structural removal of
v, denoted by
, as the fuzzy graph obtained by removing all edges incident to
v while keeping
v in the vertex set. Formally,
The presence of fuzzy strong cut vertices influences the composition of strongest strong paths in a fuzzy graph. Specifically, if a vertex lies on every such path between two nodes, then it serves as a critical connector whose structural removal partitions the path space. Hence, these nodes effectively segment the network into components that are joined solely through them.
Theorem 1. Let be a fuzzy graph and let be a fuzzy strong cut vertex. Then, there exist vertices such that
- (i)
,
- (ii)
,
- (iii)
v lies on every path in ,
- (iv)
The set is partitioned into components that are connected only through v.
Proof. By definition of a fuzzy strong cut vertex, there exist such that every path in contains v, and . Since each path in must pass through v, removing all edges incident to v (as in ) breaks the connectivity of each such path at the point that links these two components. □
We now establish a relationship between vertex and edge membership values along strongest strong paths. Specifically, the membership of any node appearing in such a path is bounded below by the minimal edge strength of that path.
Proposition 6. Let be a fuzzy graph and letbe a strongest strong path. Then, for any vertex that appears in P, we have Proof. Let
, and let
Since
P is a strongest strong path, each edge
is strong, so
Thus, for every
i, we have
. □
Remark 2. This result ensures that fuzzy path hyperoperations preserve minimum reliability thresholds—if a signal can traverse a path of strength α, then all intermediate nodes have reliability of at least α.
Corollary 1. Let be a fuzzy graph, and letbe a strongest strong path of strength α. Then, for every vertex that appears in P, we havei.e., . We now prove that the vertex fuzzy path hyperoperation is associative.
Proposition 7. Let be a fuzzy graph. Then, the vertex fuzzy path hyperoperation is associative; i.e., for all , Proof. Recall that for any
, the fuzzy set
is defined by
Let us compute both sides of the identity and show that they yield the same fuzzy set.
Left-hand side:
. Let
Then,
The above formula describes how to compute the left-hand side of the associativity identity using the definition of the vertex fuzzy path hyperoperation.
Here, is the fuzzy set of all vertices lying on some strongest strong path from u to v, with membership values inherited from . The support consists of all vertices that occur with positive membership in A.
For each such vertex , we compute , which includes all vertices lying on some strongest strong path from x to w. Taking the union over all such x yields the fuzzy set of vertices that lie on some strongest strong path from u to v and then from x to w.
Since the family of strongest strong paths is closed under concatenation when intermediate vertices are shared, this construction recovers all vertices lying on some strongest strong path from u to w through v, preserving the membership structure. This justifies the associativity of the operation .
Right-hand side:
. Let
Then,
In this case, for each y lying on a strongest strong path from v to w, we consider all strongest strong paths from u to y, and their union yields the same support and membership degrees as the LHS.
In both cases, the construction effectively accumulates all nodes lying on a strongest strong path from
u to
w. The union over all intermediate decompositions covers all such paths, and due to maximality in the strength selection of
, we do not introduce weaker paths. Hence,
□
Intuitively, this result reflects that fuzzy path composition is independent of grouping; hence, intermediate aggregation points do not affect the final reachability analysis.
The associativity of the vertex fuzzy path hyperoperation establishes a foundational algebraic structure over the fuzzy vertex set. Specifically, it ensures that forms a fuzzy hypersemigroup, a hypercompositional analogue of semigroups in which the operation yields fuzzy subsets rather than single elements. This result provides a robust algebraic framework for modeling compositional reasoning in systems with uncertainty, where reachability and influence propagate through multiple layers of interaction. It also enables the application of tools from hyperstructure theory to analyze the dynamics and resilience of fuzzy networks in a mathematically rigorous manner.
Corollary 2. Let be a fuzzy graph. Then, the structure forms a fuzzy hypersemigroup.
This algebraic structure opens the door to applying tools from hyperalgebra and fuzzy semigroup theory in the analysis of fuzzy graphs. It also connects the proposed hyperoperation to a broader mathematical context, enabling generalizations to fuzzy hypermonoids or hypergroupoids when identity or inverse properties are explored.
The following proposition highlights a fundamental structural property of the vertex fuzzy path hyperoperation. Path decomposition reflects the internal coherence of the hyperoperation and enables localized analysis of fuzzy connectivity through intermediate nodes.
Proposition 8 (Path Decomposition)
. Consider a fuzzy graph and vertices . If , then Proof. Suppose . Then, by definition, x lies on a path .
Since
by assumption, the path
P can be decomposed into two subpaths
each of which is a subpath of a strongest strong path. Because all edges in
P are strong and the overall path is the strongest, both
and
are themselves strongest strong paths.
Therefore, any vertex
must either belong to
or
, implying
Thus,
and since
x was arbitrary in
, we conclude that
□
The inclusion in the above proposition becomes an equality when the intermediate vertex is traversed by every strongest strong path between the two endpoints.
Proposition 9. Let be a fuzzy graph, and let . If every path in contains w, then Proof. From Proposition 8, we already know that
To prove the reverse inclusion, let
. Then, either
- (i)
x lies on a path , or
- (ii)
x lies on a path .
By the hypothesis, every path in
contains
w. Let
P be any such path; then,
P can be decomposed as
where
is a strongest strong path from
u to
w, and
is a strongest strong path from
w to
v. Since strongest strong paths from
u to
w and from
w to
v exist and include
x in at least one of them, then
x must lie on some
. Thus,
Therefore,
Combined with the earlier inclusion, this proves the equality
□
This result shows that under a strong centrality condition—where all strongest strong paths from u to v must pass through w—the fuzzy vertex path operation satisfies an exact decomposability property.
Proposition 10 (Edge Support Decomposition)
. Let be a fuzzy graph, and let . If for every , it holds that , then,with equality if every can be decomposed as with and . Proof. Let . Then, by definition, there exists a strongest strong path such that is an edge of P. By hypothesis, w lies on every such path P, so P contains w and can be written as the concatenation , where is a subpath from u to w, and is a subpath from w to v.
Since
P is a strongest strong path and all of its subpaths are also strongest strong paths, we have
and
. Hence, the edge
must appear in either
or
, which implies that
Therefore,
If, in addition, every
decomposes into a concatenation of paths in
and
, then the reverse inclusion holds, yielding equality. □
The following result formalizes the monotonicity of -cuts in the context of the edge fuzzy path hyperoperation.
Proposition 11 (Monotonicity of
-Cuts of the Edge Fuzzy Path Hyperoperation)
. Let be a fuzzy graph, and let . For any , denote by the γ-cut of the fuzzy set , defined asThen, Proof. Let
. By definition, there exists a strongest strong path
such that
and
. Since
, it follows that
as well. Thus,
also belongs to the
-cut:
Therefore, we conclude that
□
5. Equivalence Classes, Quotient Graphs, and Connectivity Structures
We now introduce a relation on the vertex set of a fuzzy graph that captures mutual full-strength connectivity. Let
be a fuzzy graph, we define the binary relation
by setting
if and only if there exists a path
P from
u to
v and a path
from
v to
u such that
and
. Equivalently,
The following proposition shows that is an equivalence relation on the set V.
Proposition 12. The relation is an equivalence relation on the vertex set V of the fuzzy graph .
Proof. We verify the three defining properties of an equivalence relation:
Reflexivity: For every , consider the trivial path from u to itself (i.e., a path of length zero). Since this path contains no edges, its strength is defined to be 1. Hence, .
Symmetry: Suppose . Then, by definition, there exists a path and a path such that both and . Therefore, by symmetry of the existence of such paths, .
Transitivity: Suppose and . Then, there exist paths
and , both with strength 1,
and , both with strength 1.
Let be the concatenation of paths from u to v and then from v to w. Similarly, define , a path from w to v and then from v to u.
Since each edge in and has a membership value of 1 (as their strengths are 1), all edges in have a membership value of 1, and thus . The same applies to .
Therefore, there exists a path from u to w and from w to u, both of strength 1, and so .
Hence, is reflexive, symmetric, and transitive, and it is, therefore, an equivalence relation. □
The equivalence relation partitions the vertex set V into disjoint subsets, each consisting of vertices that are mutually connected via paths of maximal edge strength. These equivalence classes can be viewed as the strongly connected components of the crisp digraph obtained by taking the -cut of the fuzzy graph at level .
Proposition 13. Let be a fuzzy graph, and let be the directed graph obtained by the α-cut at level , whereThen, the equivalence classes of the relation coincide with the strongly connected components of the crisp digraph . Proof. By definition, two vertices satisfy if and only if there exist paths and in F such that . This implies that every edge on these paths must have a membership value of 1, i.e., each edge belongs to . Therefore, u and v are connected by directed paths in both directions in the graph , which means they lie in the same strongly connected component of .
Conversely, if u and v lie in the same strongly connected component of , then there exist paths in from u to v and from v to u, consisting entirely of edges with a membership value of 1 in F, and, hence, of strength 1. Therefore, .
Thus, the equivalence classes of are exactly the strongly connected components of . □
The following proposition shows that the equivalence classes determined by the relation are -closed components.
Proposition 14. Given a fuzzy graph , every equivalence class under the relation is closed under ; that is, for all , we have Proof. Let and . By definition of the hyperoperation , this means that z lies on some strongest strong path P from u to w, and the strength of P is .
Since , we have by the definition of . Hence, the path P is a strongest strong path from u to w with strength 1. Therefore, every edge of P has a membership value of exactly 1.
Let
be the subpath of
P from
u to
z, and
the subpath from
z to
w. Since all edges in
P have a membership of 1, the same holds for
and
, and both have a strength of 1; hence,
Since
, there exists a strongest strong path
Q from
w to
u of strength 1. Consider the concatenation of the paths
and
Q. This forms a path
R from
z to
u, and all its edges have a membership of 1, i.e.,
Since
, we have
. But
and, hence,
. It follows that
□
Corollary 3. The vertex set of the quotient graph consists precisely of the maximal -closed subsets of V. That is, each equivalence class under is a maximal subset of V that is closed under the hyperoperation , and distinct classes are disjoint with respect to .
Proof. By the previous proposition, each equivalence class under is closed under . To show maximality, suppose there exists such that for some . Then, by the definition of , u lies on a strongest strong path of strength 1 between x and y. This implies , so , contradicting the assumption. Hence, no element outside can be generated by from elements inside it, and the class is maximal.
Distinct classes are disjoint by the definition of , and since each is -closed, the equivalence classes partition V into maximal -closed subsets, which form the vertex set of . □
Remark 3. The above corollary suggests that the quotient graph admits an interpretation as an algebraic reduction of the fuzzy graph F into its maximal -closed components, and one may view the quotient as the base set for an induced hyperstructure.
The relation
also admits a natural interpretation in terms of fuzzy connectivity measures. First, if
, then there exist bidirectional paths of strength 1 between
u and
v, which implies that the connection strengths satisfy
Moreover, in this case, any strongest strong path connecting
u and
v necessarily consists entirely of edges with membership value 1. As a result, every vertex lying on such a path inherits a membership of at least 1 under the vertex fuzzy path hyperoperation, and in fact retains its original membership value exactly. If no edge in the graph has a membership value of 1, then
reduces to the identity relation. Conversely, if all edges have a membership value of 1, then
coincides with classical strong connectivity. Therefore,
captures the top tier of certainty in fuzzy connectivity and can be used to isolate fully reliable components within a fuzzy network.
Let be a fuzzy graph, and let be the equivalence relation on V defined by mutual full-strength connectivity. The quotient fuzzy graph of F with respect to , denoted , is the fuzzy graph defined as follows:
- -
The vertex set
W is the set of equivalence classes of
V under
; that is,
- -
The fuzzy vertex membership function
is given by
- -
The fuzzy edge membership function
is defined by
The equivalence relation identifies groups of vertices that are mutually reachable through strongest strong paths, i.e., fully reliable and symmetric fuzzy connections. The corresponding quotient fuzzy graph abstracts each equivalence class as a single node and preserves the strongest interclass connections. This reduction simplifies the structure of the fuzzy graph while retaining essential path-based connectivity information, making it easier to analyze large or modular fuzzy systems.
Proposition 15. Let be a fuzzy graph; then, the quotient fuzzy graph is well-defined.
Proof. The vertex membership function is clearly well-defined since each equivalence class is nonempty and .
The edge membership function is also well-defined, since it considers all pairs
with
,
and selects the maximum of their membership grades:
We now verify that the fuzzy graph condition is preserved; that is,
Let
and
be such that
. Since
is a fuzzy graph, it satisfies
But by the definition of
, we have
and
; hence,
Therefore,
This shows that both and are well-defined and satisfy the fuzzy graph condition. Hence, the quotient is a well-defined fuzzy graph. □
The quotient fuzzy graph can be interpreted as the condensation of the fuzzy graph F at strength level 1. Each vertex of represents a maximal subset of vertices of F that are mutually connected by paths of strength 1, that is, an equivalence class under . The internal structure within each -class is collapsed into a single node, and the edges between classes reflect the strongest possible fuzzy connections between different full-strength components. In this way, provides a simplified representation of the overall connectivity of F among its fully reliable substructures.
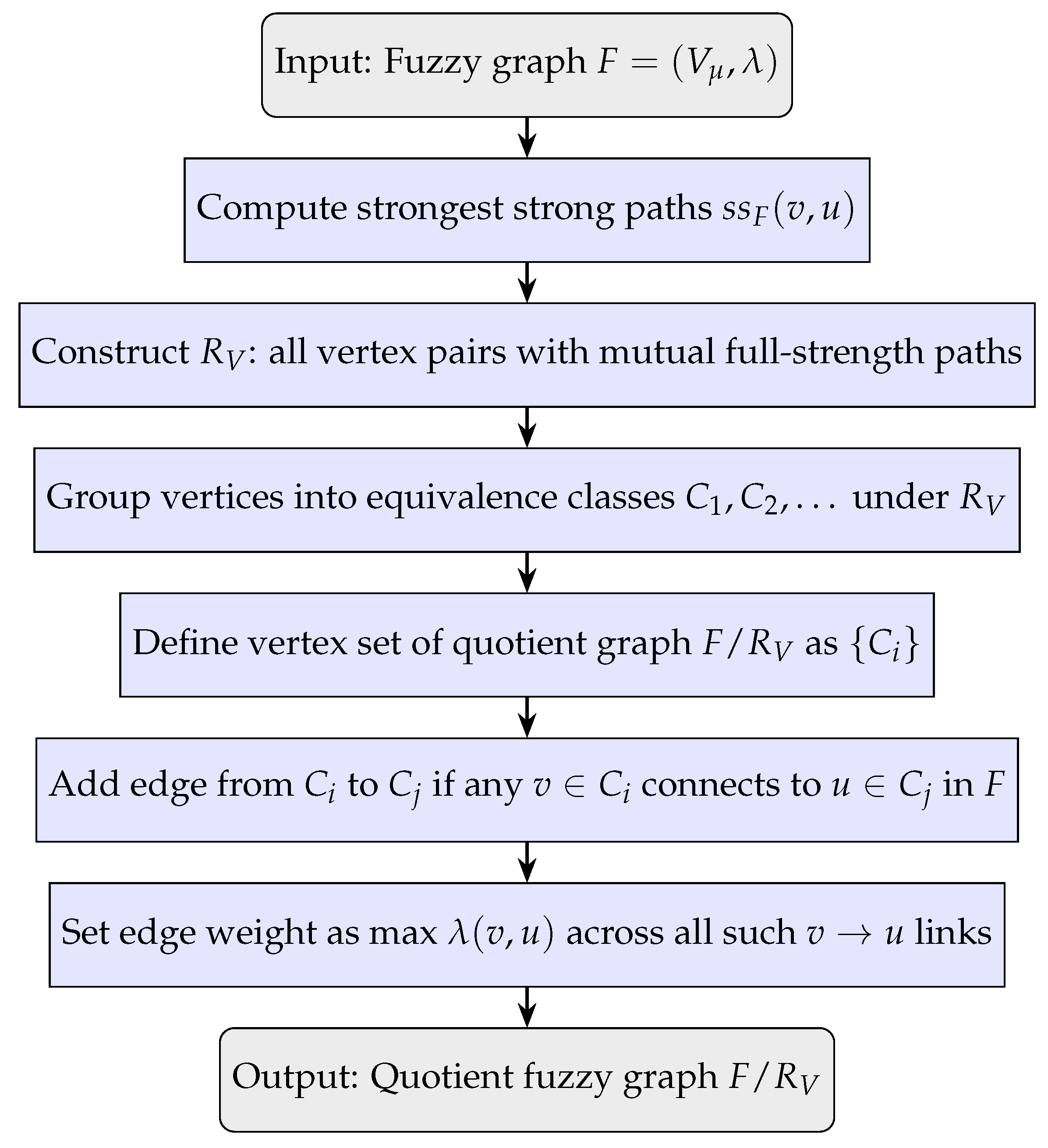
We illustrate the quotient fuzzy graph construction process using a flowchart in
Figure 3. The diagram outlines the key computational steps, starting from a fuzzy graph
, through the identification of mutual full-strength connectivity and equivalence classes to the construction of the resulting coarse-grained graph
. Each step preserves directional trust semantics and fuzzy strength while simplifying the graph’s structure.
Corollary 4. The quotient fuzzy graph is the condensation of the fuzzy graph F at strength level 1. Each vertex of corresponds to a maximal subset of vertices of F that are mutually connected by paths of strength 1, and the edges of represent the strongest fuzzy connections between different such subsets.
Remark 4. If all edges of a fuzzy graph have a membership value of 1, that is, if for all , then the relation becomes the universal relation on V. In this case, the quotient fuzzy graph consists of a single vertex representing the entire vertex set V and no edges. Thus, reduces to a fuzzy graph with one vertex whose membership is the maximum of all vertex memberships in F.
Example 3. Consider the fuzzy graph shown in Figure 4. The vertices form a fully strongly connected component via full-strength paths and define an equivalence class under , denoted . The maximum vertex membership in this class isSimilarly, and form strongly connected components, defining the classes and with The vertex , not reachable via any full-strength path from or to another vertex, forms its own singleton class , with . The quotient fuzzy graph , shown in Figure 5, has a vertex set . Each vertex is labeled with its corresponding membership value. An edge is drawn from to whenever there exists an edge from some vertex in to some vertex in in the original graph , and the membership of the edge in the quotient is defined as the maximum among those edges. In this case, there is an edge from to of strength 0.8, coming from . An edge from to arises from , with strength 0.6. Finally, an edge from to comes from , with strength 0.9.
We now introduce a fuzzy distance function based on the strength of the strongest strong path between two vertices in a fuzzy graph. This measure reflects the reliability or certainty of connection between nodes, i.e., the stronger the path, the shorter the distance.
Let
be a fuzzy graph. The
fuzzy distance function is defined by
where
denotes the strength of the strongest strong path from
u to
v.
Proposition 16. The function is a fuzzy semi-metric on V.
Proof. We verify the properties of a semi-metric.
- (i)
Non-negativity and boundedness. For all
, since
, we have
- (ii)
Identity of indiscernibles. Since the strongest strong path from a vertex to itself is the trivial path with strength 1, we have
However, does not imply ; it only implies that there exists a strongest strong path from u to v with maximum strength. Hence, the identity of indiscernibles holds only in one direction.
- (iii)
Symmetry does not hold in general. In directed fuzzy graphs, it is possible that
and, therefore,
Thus, is not symmetric unless F is symmetric.
□
This distance may be useful in applications where reliability or confidence of interaction is key, such as in fuzzy social networks, communication systems, and uncertain biological networks. Its inverse relation to connection strength makes it suitable for optimization, ranking, and clustering tasks in fuzzy environments.
The distance function on a fuzzy graph does not, in general, satisfy the identity of indiscernibles in the strong form. However, the quotient graph obtained by the equivalence relation admits this property. This is formalized in the following proposition.
Proposition 17. Let be a fuzzy graph, and let . The fuzzy distance function satisfies the identity of indiscernibles in the strong form: Proof. Assume . Then, , since the strongest strong path from a class to itself is trivially of strength 1.
Conversely, suppose
. By the construction of the quotient graph, any edge from a vertex in
to a vertex in
must have a strength that is strictly less than 1; otherwise,
u and
v would belong to the same
-class, contradicting the assumption. Therefore, every path from
to
in the quotient has a strength strictly less than 1, and, hence,
Thus,
implies
, completing the proof. □
6. Fuzzy Distance and Metric Interpretations
This interpretation extends naturally to the quotient graph , where each equivalence class represents a maximal hyperoperation-closed component. The quotient distance function thus captures the separation between these structurally aggregated units, measuring how distant entire hyperoperation closures are from one another in terms of fuzzy connectivity.
The fuzzy distance function can be interpreted in terms of the vertex fuzzy path hyperoperation . The value quantifies the extent to which the vertex v is reachable from u via high-strength paths. When , we have , so . If in addition, , then , and the two vertices lie on mutual full-strength strongest strong paths. In that case, they belong to the same equivalence class under , which is closed under .
In contrast, when , a strongest strong path from u to v may still exist, but its strength is strictly less than 1. In this case, v may still belong to , but mutual inclusion and equivalence are not guaranteed. Thus, the distance function reflects how close a pair of vertices is to being symmetrically and fully connected within a -closed structure, and it provides a graded measure of deviation from this ideal.
Proposition 18. Let be a fuzzy graph; then, for any vertices , the following are equivalent:
- (i)
and ,
- (ii)
,
- (iii)
and ,
- (iv)
u and v belong to the same equivalence class under .
Example 4. Consider the fuzzy graph shown in Figure 6, where each vertex is labeled by its fuzzy membership grade , and each edge is labeled by its membership value . Its equivalence classes with respect to areThe behavior of the vertex fuzzy path hyperoperation confirms the structural coherence of the equivalence classes under . Proposition 14 guarantees that each class is closed under . This aligns with the observation that within each class, all paths contributing to the hyperoperation closure are of full strength and remain entirely internal. Furthermore, Corollary 3 implies that each equivalence class can be viewed as a -closed component—meaning that for all .
The quotient graph is shown in Figure 7. For instance, the cycle , composed entirely of edges with strength 1, becomes condensed into the single node , and the resulting quotient graph shows the directional relationship among the classes with appropriate edge strengths preserved. The above example illustrates the interpretation of the fuzzy distance ; as established in Proposition 16, defines a fuzzy semi-metric on the vertex set V, capturing the loss of connectivity strength from one node to another. In the original graph, several pairs of distinct vertices satisfy , indicating that there exists a strongest strong path of full strength from u to v, though not necessarily reciprocally. Thus, while quantifies directed closeness, it lacks full symmetry and fails the strong form of identity of indiscernibles.
However, as Proposition 17 confirms, the induced distance on the quotient graph satisfies the identity of indiscernibles in its strong form. In the context of Example 4, this means that the distance between two quotient nodes is zero if and only if they correspond to the same equivalence class under . The quotient graph, therefore, provides a coarse-grained metric abstraction in which each node represents a maximal zero-distance component of the original graph.
In practice, this metric can be useful in applications such as information flow modeling, fault-tolerant communication networks, or biological regulatory analysis. The original distance function supports fine-grained ranking and uncertainty-aware navigation, while the quotient distance supports cluster identification and top-level structural reasoning.
7. Applications of Fuzzy Connectivity Structures
The fuzzy hyperoperational framework introduced in this paper provides an algebraic foundation for analyzing systems with partial, asymmetric, or uncertain connectivity. By combining strongest strong path analysis with hypercompositional operations, the proposed model captures local and global properties of interaction networks.
7.1. Trust-Aware Social Systems
We illustrate a simulated trust network modeled as a fuzzy graph with directional fuzzy path analysis. Consider a distributed decision-making system consisting of eight agents , where each agent is assigned a fuzzy credibility score and directional fuzzy trust scores toward others based on prior collaborative experience.
The credibility scores (vertex membership values) are as follows:
The directional trust scores (edge membership values) are as follows:
The resulting fuzzy graph
respects the structural constraint
and is visualized in
Figure 8. Using the vertex fuzzy path hyperoperation
, we compute the strongest strong paths and identify the equivalence classes under the mutual full-strength connectivity relation
:
Each class
forms a closed component under
, meaning that every pair of nodes within
is mutually reachable via full-strength paths. The corresponding quotient fuzzy graph
, shown in
Figure 9, has a vertex set
. It includes a single inter-class edge from
to
, derived from the link
of strength 0.6.
This abstraction highlights the formation of three coherent trust clusters, each internally robust in connectivity. The edge signifies a unidirectional trust influence from the first group toward the third. In applied contexts such as team formation or consensus protocols, the quotient graph offers a compact yet semantically meaningful representation, preserving the directionality and strength of trust dynamics in a coarse-grained manner.
The fuzzy distance function can now be applied to the trust network to quantify the absence or weakness of strong trust pathways between agents. In this context, the distance metric helps identify pairs of agents lacking reliable directional influence, cluster users based on proximity in trust propagation, and detect structural gaps or bottlenecks across classes. For example, the edge from to in the quotient graph highlights a weak inter-cluster trust dependency that may warrant strategic reinforcement. Thus, fuzzy distance not only complements hyperoperation-based reasoning but also enables applications in trust evaluation, decision-making optimization, and network resilience analysis.
7.2. Communication Networks
In communication networks or transportation systems, connections often vary in reliability or capacity due to physical limitations, congestion, or failures. Fuzzy graphs provide a natural way to model such uncertainties by allowing both nodes (e.g., stations or routers) and edges (e.g., links or routes) to have membership values representing their operational reliability.
Consider a communication backbone connecting eight relay nodes
, where
The edge membership values represent the current quality or bandwidth availability of the connection between two nodes:
The vertex fuzzy path hyperoperation yields the fuzzy set of relay nodes lying on strongest strong communication paths between and , respecting both the edge quality and node reliability. For instance, the strongest strong path from to traverses , with strength , and the involved nodes all have , as ensured by Proposition 6.
The equivalence relation
reveals clusters of fully bidirectional, high-confidence communication, such as
The quotient graph abstracts the relay infrastructure into a smaller graph with well-defined inter-cluster bandwidths. For instance, the path of strength 0.9 becomes an edge from to , and the link induces an edge from to of strength 0.8.
The fuzzy distance function supports diagnosing degraded or failing paths, identifying redundant versus critical infrastructure and prioritizing high-strength relay chains for robust routing.
7.3. Biological Systems
In systems biology and epidemiology, the spread of signaling cascades, protein activation, or infectious agents through complex biological or social networks is often non-uniform and uncertain. Nodes (e.g., proteins, genes, or individuals) may differ in their activation readiness or susceptibility, while connections (e.g., reactions or interactions) vary in reliability or strength due to biological noise, mutation, or behavioral diversity. Fuzzy graphs offer a rigorous framework for capturing these graded interactions.
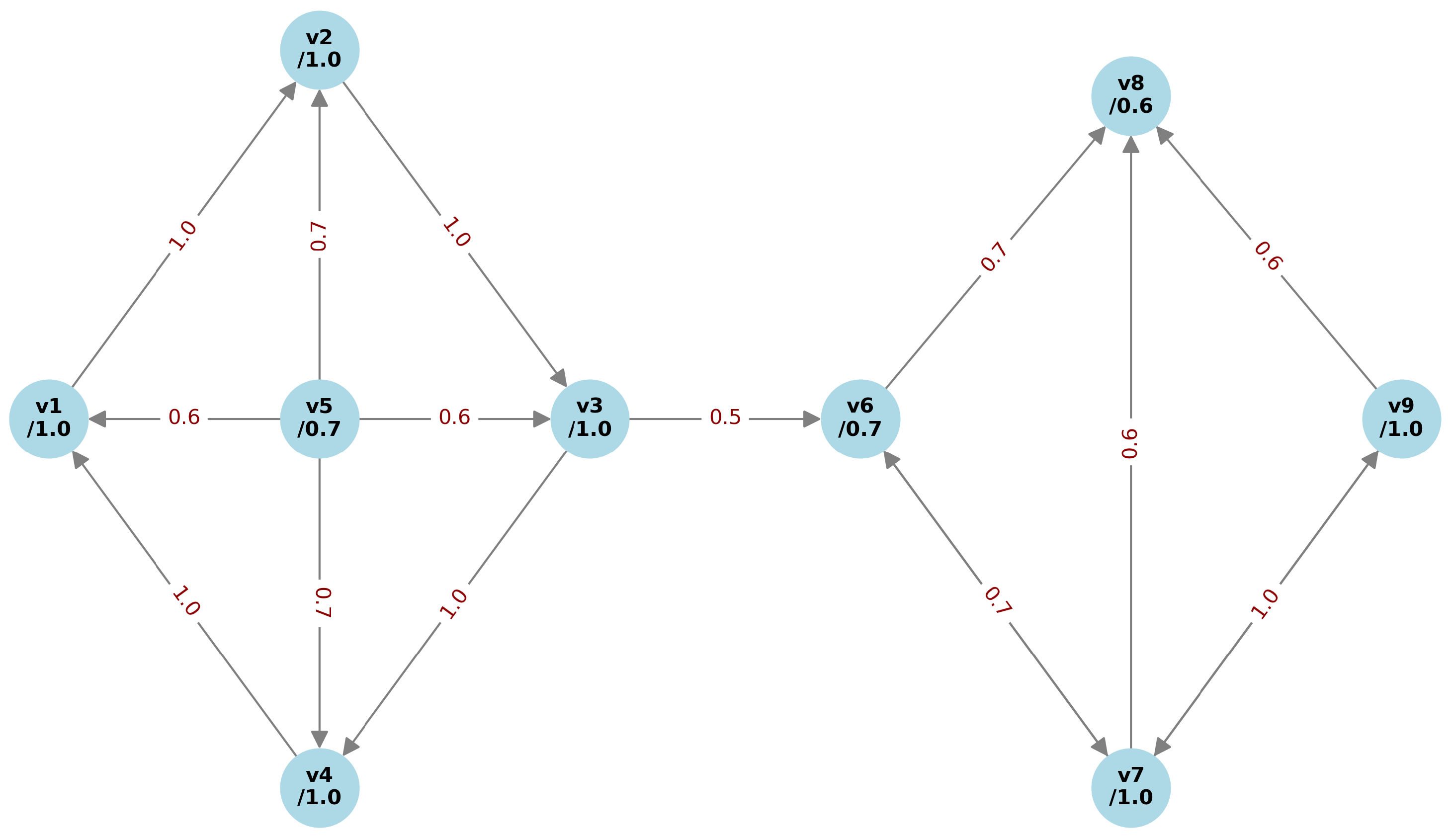
Consider a simplified biological network
representing signal transduction between nine molecular or cellular entities
. Node memberships
denote activation readiness or receptor density, and directed edge memberships
represent the likelihood or reliability of downstream activation from
u to
v. The graph is shown in
Figure 10 and satisfies all fuzzy graph consistency constraints.
The vertex fuzzy path hyperoperation identifies all biological units participating in the strongest strong signal paths between components and , where both transmission fidelity and local reactivity are preserved. For example, the strongest strong paths, without repeating nodes, from to are
since they both achieve the maximum possible strength
, and all edges in these paths are strong edges. Note also that all vertices lying in these paths have membership values
, complying with Proposition 6. The vertex fuzzy path hyperoperation
yields the fuzzy set
where each vertex that appears in any of the strongest strong paths retains its original membership value from the fuzzy graph
.
The equivalence relation
captures bidirectional full-strength signaling loops. In this case, five equivalence classes emerge:
These groups reflect integrated biological modules or compartments. The quotient fuzzy graph
shown in
Figure 11 reduces the system to 5 aggregate components and reveals dominant signal routes between them. The quotient model facilitates analysis of cross-module influence, redundancy, and critical weak points in the network.
In the quotient graph
, the only strongest strong path from the class of
to the class of
, i.e., from
to
is
Therefore, the vertex fuzzy path hyperoperation
yields the fuzzy set
This result captures the signal propagation pathway from the
module (containing
) through the integrated
module (
) and intermediate
module (
) to reach the target
module (
). In biological terms, this means that signal transmission from module
to
must pass through the integrated signaling hub
and regulatory checkpoint
, suggesting that these modules are critical for inter-compartment communication and represent potential therapeutic targets or regulatory control points in the biological system.
The introduced hyperoperational framework enables robust subsystem identification (via and ), failure impact analysis using fuzzy strong cut vertices and edges, and signal strength-based reachability (via fuzzy distances ). Such an approach supports targeted drug design, epidemiological intervention planning, and resilience testing in systems characterized by gradated structure and uncertain propagation.
8. Conclusions and Future Directions
In this paper, we introduce a novel framework of fuzzy graph hyperoperations based on the concept of strongest strong paths, which are both optimal in strength and entirely composed of strong edges. We define two key hyperoperations: the vertex-based fuzzy path hyperoperation and the edge-based fuzzy path hyperoperation , generalizing classical path-based operations in a fuzzy environment.
We prove that forms a fuzzy hypersemigroup and establish fundamental properties such as reflexivity and -cut monotonicity. These results allow for the analysis of fuzzy connectivity at varying levels of confidence. We also characterize structural features such as fuzzy strong cut vertices and edges, which identify points of vulnerability and resilience in fuzzy networks.
A fuzzy distance function is introduced to quantify directional closeness between vertices. While this function does not satisfy the strong identity of indiscernibles in general, its induced counterpart on the quotient graph respects this property. The construction of the quotient fuzzy graph , based on mutual full-strength connectivity, enables a semantically faithful abstraction that preserves the topology of the original graph.
To demonstrate the real-world relevance of the proposed framework, we present detailed examples from trust-aware social networks, communication infrastructures, and biological regulatory systems. These applications illustrate the interpretability and flexibility of our model in domains where uncertainty and asymmetric influence are intrinsic.
While the primary aim of this work is to establish a rigorous algebraic framework for fuzzy graph hyperoperations, it is important to consider their algorithmic realizability in applied settings. The construction of strongest strong paths and the evaluation of the fuzzy hyperoperations can be implemented using adaptations of fuzzy relation composition algorithms, particularly those relying on max–min and max–product transitive closures. For example, the equivalence classes under can be computed via a repeated composition of the fuzzy adjacency matrix until a fixed point is reached, with a worst-case time complexity of , where n is the number of vertices. Once is derived, the construction of quotient graphs proceeds in polynomial time, with each inter-class edge determined via constrained maximum search.
Furthermore, computing the fuzzy distance function for all vertex pairs can be achieved using a modified version of the Floyd–Warshall algorithm adapted for fuzzy conjunctions. These algorithmic pathways suggest that the proposed framework is not only mathematically elegant but also computationally tractable.
We envision extending this line of work by developing concrete implementations and integrating them into fuzzy trust modeling, social influence mapping, and graph-based neural architectures. Additional research directions merit further exploration, including developing efficient algorithms for large-scale fuzzy networks, extending to temporal fuzzy graphs where membership values evolve over time, formal development of fuzzy hypermonoid and fuzzy hypergroupoid structures, algorithmic implementations for the efficient computation of and , and exploring applications in machine learning where fuzzy hyperoperations could serve as novel graph neural network layers for uncertainty-aware deep learning architectures as well as application to recommendation systems, epidemic modeling, and robustness analysis in intelligent infrastructure.