Applications of the Calculus by the Transfer Matrix Method for Long Rectangular Plates Under Uniform Vertical Loads
Abstract
1. Introduction
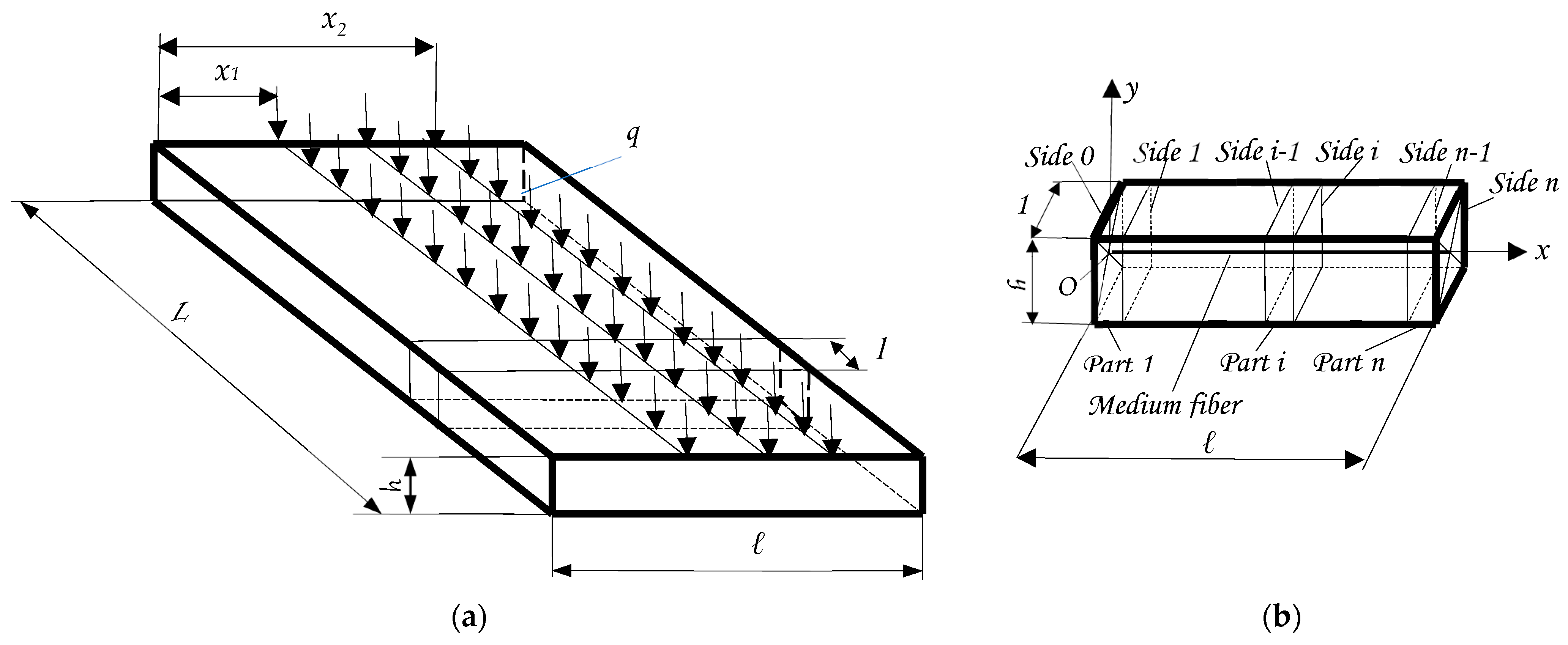
2. Analysis of Long Rectangular Plates Using TMM: A Brief Overview
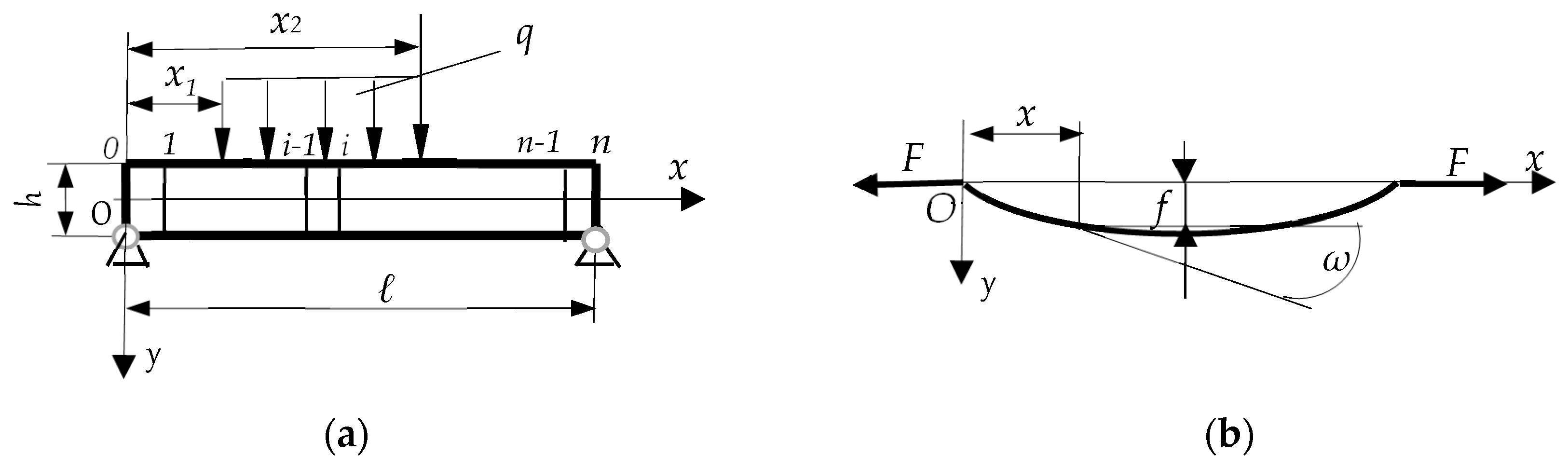
2.1. Analytical Approach for a Long Rectangular Plate
2.2. TMM-Based Calculation Algorithm for Long Rectangular Plates
3. Applications of the TMM for the Calculation of Long Rectangular Plates Under Uniform Loads Acting on Different Surfaces
- A uniform vertical load q, acting from section x1 to the right end of the unit beam, over a length of (l − x1), as shown in Figure 4;
3.1. Unit Beam Embedded at Both Ends, Subjected to a Uniform Vertical Load q Acting over a Length (x2 − x1) of the Beam, as Shown in Figure 3
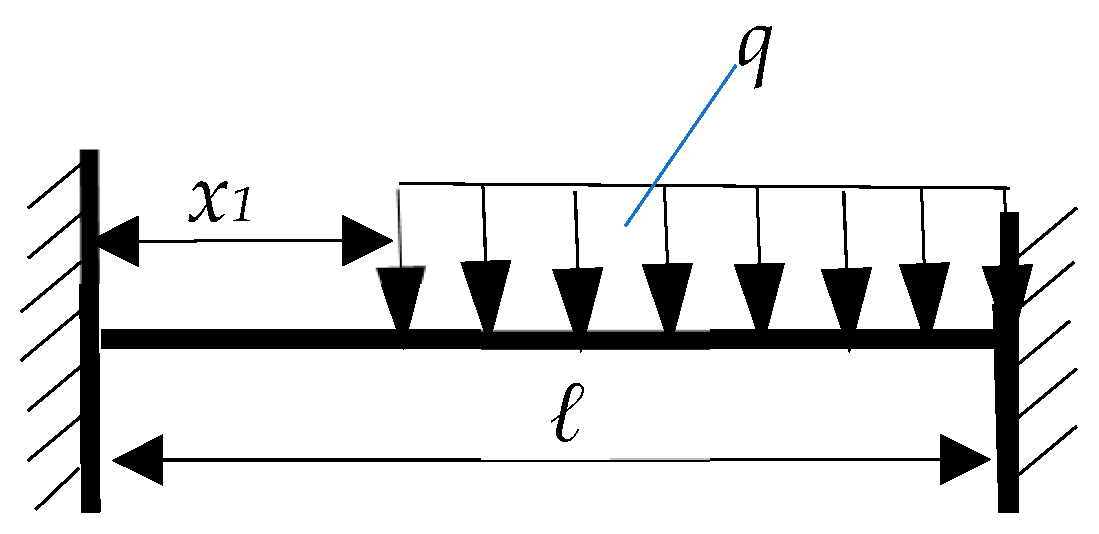
3.2. Unit Beam Embedded at the Two Edges Charged with Uniform Load q Which Acts from Section x1 to the Right End of the Beam, Along a Length (l − x1), as in Figure 4
3.3. Unit Beam Embedded at the Two Edges Charged with Uniform Load q Which Acts Along the Length x1, as in Figure 5
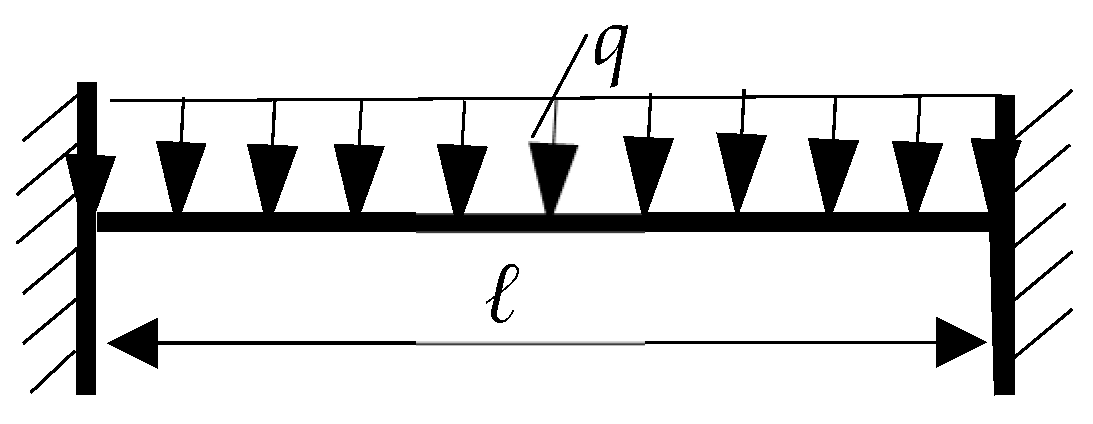
3.4. Unit Beam Embedded at the Two Edges Charged with Uniform Load q Which Acts Along the Entire Length l of the Beam, as in Figure 6
3.5. Unit Beam Embedded at the Two Edges Charged with Uniform Load q Which Acts Along the Length x1, as in Figure 7a,b
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TMM | Transfer Matrix Method |
| FEM | Finite Elements Method |
| E | Modulus of Elasticity or Young’s Modulus |
| I | Axial Moment of Inertia |
| EI | Bending Stiffness |
References
- Gery, P.-M.; Calgaro, J.-A. Les Matrices-Transfert dans le Calcul des Structures; Éditions Eyrolles: Paris, France, 1973. [Google Scholar]
- Suciu, M.; Tripa, M.-S. Strength of Materials; UT Press: Cluj-Napoca, Romania, 2024. [Google Scholar]
- Warren, C.Y. Roark’s Formulas for Stress & Strain, 6th ed.; McGraw Hill Book Company: New York, NY, USA, 1989. [Google Scholar]
- Opruţa, D.; Tripa, M.-S.; Codrea, L.; Boldor, C.; Dumea, D.; Gyorbiro, R.; Brisc, C.; Bărăian, I.; Opriţoiu, P.; Chereches, A.; et al. Calculus of Long Rectangular Plates Embedded in Long Borders with Uniform Vertical Load on a Line Parallel to the Long Borders. Mathematics 2025, 13, 993. [Google Scholar] [CrossRef]
- Codrea, L.; Tripa, M.-S.; Opruţa, D.; Gyorbiro, R.; Suciu, M. Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications. Mathematics 2023, 11, 3756. [Google Scholar] [CrossRef]
- Suciu, M. An Approach Using the Transfer Matrix Method (TMM) for Mandible Body Bone Calculus. Mathematics 2023, 11, 450. [Google Scholar] [CrossRef]
- Cojocariu-Oltean, O.; Tripa, M.-S.; Baraian, I.; Rotaru, D.-I.; SUCIU, M. About Calculus Through the Transfer Matrix Method of a Beam with Intermediate Support with Applications in Dental Restorations. Mathematics 2024, 12, 3861. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Arabi, E.; Masoodi, A.R. A triangular shell element for geometrically nonlinear analysis. Acta Mech. 2018, 229, 323–342. [Google Scholar] [CrossRef]
- Suciu, M. Calculus of Long Rectangle Plate Articulated on Both Long Sides Charged with a Linear Load Uniformly Distributed on a Line Parallel to the Long Borders through the Transfer-Matrix Method. EMSJ 2024, 8, 157–167. [Google Scholar] [CrossRef]
- Viebahn, N.; Pimenta, P.M.; Schröder, J. A simple triangular finite element for nonlinear thin shells: Statics, dynamics and anisotropy. Comput. Mech. 2017, 59, 281–297. [Google Scholar] [CrossRef]
- Sanchez, M.L.; Pimenta, P.M.; Ibrahimbegovic, A. A simple geometrically exact finite element for thin shells—Part 1: Statics. Comput. Mech. 2023, 72, 1119–1139. [Google Scholar] [CrossRef]
- Costa, J.C.; Pimenta, P.M.; Wriggers, P. Meshless analysis of shear deformable shells: Boundary and interface constraints. Comput. Mech. 2016, 57, 679–700. [Google Scholar] [CrossRef]
- Yessenbayeva, G.A.; Yesbayeva, D.N.; Syzdykova, N.K. On the finite element method for calculation of rectangular plates. Bull. Karaganda Univ. Math. Ser. 2019, 95, 128–135. [Google Scholar] [CrossRef]
- Yessenbayeva, G.A.; Yesbayeva, D.N.; Makazhanova, T.K. On the calculation of the rectangular finite element of the plate. Bull. Karaganda Univ. Math. Ser. 2018, 90, 150–156. [Google Scholar] [CrossRef]
- Yuhong, B. Bending of Rectangular Plate with Each Edges Arbitrary a Point Supported under a Concentrated Load. Appl. Math. Mech. 2000, 21, 591–596. [Google Scholar] [CrossRef]
- Ohga, M.; Shigematsu, T.; Kohigashi, S. Analysis of folded plate structures by a combined boundary element-transfer matrix method. Comput. Struct. 1991, 41, 739–744. [Google Scholar] [CrossRef]
- Ohga, M.; Shigematsu, T.; Hara, T. A Finite Element-Transfer Matrix Method for Dynamic Analysis of Frame Structures. J. Sound Vib. 1993, 167, 401–411. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Doudoumis, I.N. Elastic analysis and application tables of rectangular plates with unilateral contact support conditions. Comput. Struct. 2001, 79, 2559–2578. [Google Scholar] [CrossRef]
- Tuozzo, D.M.; Silva, O.M.; Kulakauskas, L.V.Q.; Vargas, J.G.; Lenzi, A. Time-harmonic analysis of acoustic pulsation in gas pipeline systems using the Finite Element Transfer Matrix Method: Theoretical aspects. Mech. Syst. Signal Process. 2023, 186, 109824. [Google Scholar] [CrossRef]
- Vijayasree, N.K.; Munjal, M.L. On an Integrated Transfer Matrix method for multiply connected mufflers. J. Sound Vib. 2012, 331, 1926–1938. [Google Scholar] [CrossRef]
- Delyavs’kyi, M.V.; Zdolbits’ka, N.V.; Onyshko, L.I.; Zdolbits’kyi, A.P. Determination of the stress-strain state in thin orthotropic plates on Winkler’s elastic foundations. Mater. Sci. 2015, 50, 782–791. [Google Scholar] [CrossRef]
- Lin, H.-C.; Lu, S.-C.; Huang, H.-H. Evaluation of a Hybrid Underwater Sound-Absorbing Metastructure by Using the Transfer Matrix Method. Materials 2023, 16, 1718. [Google Scholar] [CrossRef]
- Cretu, N.; Pop, M.-I.; Andia Prado, H.S. Some Theoretical and Experimental Extensions Based on the Properties of the Intrinsic Transfer Matrix. Materials 2022, 15, 519. [Google Scholar] [CrossRef]
- Verdière, K.; Panneton, R.; Elkoun, S.; Dupon, T.; Leclaire, P. Transfer matrix method applied to the parallel assembly of sound absorbing materials. J. Acoust. Soc. Am. 2013, 134, 4648–4658. [Google Scholar] [CrossRef]
- Rui, X.T.; Zhang, J.S.; Wang, X.; Rong, B.; He, B.; Jin, Z. Multibody system transfer matrix method: The past, the present, and the future. Int. J. Mech. Syst. Dyn. 2022, 2, 3–26. [Google Scholar] [CrossRef]
- Roi, X.T.; Wang, X.; Zhou, Q.B.; Zhang, J.S. Transfer matrix method for multibody systems (Rui method) and its applications. China Technol. Sci. 2019, 62, 712–720. [Google Scholar] [CrossRef]
- Gerges, S.N.Y.; Jordan, R.; Thieme, F.A.; Bento Coelho, J.L.; Arenas, J.P. Muffler Modeling by Transfer Matrix Method and Experimental Verification. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 132–140. [Google Scholar] [CrossRef]
- Revenko, V. Development of two-dimensional theory of thick plates bending on the basis of general solution of Lamé equations. Sci. J. Ternopil Natl. Tech. Univ. 2018, 89, 33–39. [Google Scholar] [CrossRef]
- Chevillotte, F.; Panneton, R. Coupling transfer matrix method to finite element method for analyzing the acoustics of complex hollow body networks. Appl. Acoust. 2011, 72, 962–968. [Google Scholar] [CrossRef]
- Fertis, D.; Lee, C. Equivalent systems for the analysis of rectangular plates of varying thickness. Dev. Theor. Appl. Mech. 1990, 15, 627–637. [Google Scholar]
- Volokh, K.Y. On the classical theory of plates. J. Appl. Math. Mech. 1994, 58, 1101–1110. [Google Scholar] [CrossRef]
- Meleshko, V.V.; Gomilko, A.M. On the bending of clamped rectangular plates. Mech. Res. Commun. 1994, 21, 19–24. [Google Scholar] [CrossRef]
- Revenko, V.P.; Revenko, A.V. Determination of Plane Stress-Strain States of the Plates on the Basis of the Three-Dimensional Theory of Elasticity. Mater. Sci. 2017, 52, 811–818. [Google Scholar] [CrossRef]
- Zveryayev, Y.M. Analysis of the hypotheses used when constructing the theory of beams and plates. J. Appl. Math. Mech. 2003, 67, 425–434. [Google Scholar] [CrossRef]
- Ahanova, A.S.; Yessenbayeva, G.A.; Tursyngaliev, N.K. On the calculation of plates by the series representation of the deflection function. Bull. Karaganda Univ. Math. Ser. 2016, 82, 15–22. [Google Scholar]
- Delyavskyy, M.; Rosinski, K. Solution of non-rectangular plates with macroelement method. AIP Conf. Proc. 2017, 1822, 020005. [Google Scholar]
- Kuliyev, S. Stress state of compound polygonal plate. Mech. Res. Commun. 2003, 30, 519–530. [Google Scholar] [CrossRef]
- Delyavskyy, M.; Sobczak-Piąstka, J.; Rosinski, K.; Buchaniec, D.; Famulyak, Y. Solution of thin rectangular plates with various boundary conditions. AIP Conf. Proc. 2023, 2949, 020023. [Google Scholar]
- Imrak, C.E.; Gerdemeli, I. An exact solution for the deflection of a clamped rectangular plate under uniform load. Appl. Math. Sci. 2007, 1, 2129–2137. [Google Scholar]
- Matrosov, A.V.; Suratov, V.A. Stress-strain state in the corner points of a clamped plate under uniformly distributed normal load. Mater. Phys. Mech. 2018, 36, 124–146. [Google Scholar]
- Moubayed, N.; Wahab, A.; Bernard, M.; El-Khatib, H.; Sayegh, A.; Alsaleh, F.; Dachouwaly, Y.; Chehadeh, N. Static analysis of an orthotropic plate. Phys. Procedia 2014, 55, 367–372. [Google Scholar] [CrossRef]
- Bhavikatti, S.S. Theory of Plates and Shells; New Age International Publishers: New Delhi, India, 2024; ISBN 978-81-224-3492-7. [Google Scholar]
- Grigorenko, Y.M.; Rozhok, L.S. Stress–strain analysis of rectangular plates with a variable thickness and constant weight. Int. Appl. Mech. 2002, 38, 167–173. [Google Scholar] [CrossRef]
- Altenbach, H. Analysis of homogeneous and non-homogeneous plates. In Lecture Notes on Composite Materials: Current Topics and Achievements; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–36. [Google Scholar]
- Fetea, M.S. Theoretical and comparative study regarding the mechanical response under the static loading for different rectangular plates. Ann. Univ. Oradea Fascicle Environ. Prot. 2018, 31, 141–146. [Google Scholar]
- Goloskokov, D.P.; Matrosov, A.V. Approximate analytical solutions in the analysis of thin elastic plates. AIP Conf. Proc. 2018, 1959, 070012. [Google Scholar]
- Kutsenko, A.; Kutsenko, O.; Yaremenko, V.V. On some aspects of implementation of boundary elements method in plate theory. Mach. Energetics 2021, 12, 107–111. [Google Scholar] [CrossRef]
- Niyonyungu, F.; Karangwa, J. Convergence analysis of finite element approach to classical approach for analysis of plates in bending. Adv. Sci. Technology. Res. J. 2019, 13, 170–180. [Google Scholar] [CrossRef]
- Orynyak, I.; Danylenko, K. Method of matched sections as a beam-like approach for plate analysis. Finite Elem. Anal. Des. 2024, 230, 104103. [Google Scholar] [CrossRef]
- Nikolić Stanojević, V.; Dolićanin, Ć.; Radojković, M. Application of Numerical methods in Solving a Phenomenon of the Theory of thin Plates. Sci. Tech. Rev. 2010, 60, 61–65. [Google Scholar]
- Vijayakumar, K. Review of a few selected theories of plates in bending. Int. Sch. Res. Not. 2014, 2014, 291478. [Google Scholar] [CrossRef]
- Surianinov, M.; Shyliaiev, O. Calculation of plate-beam systems by method of boundary elements. Int. J. Eng. Technol. 2018, 7, 238–241. [Google Scholar] [CrossRef]
- Sprinţu, I.; Fuiorea, I. Analytical solutions of the mechanical answer of thin orthotropic plates. Proc. Rom. Acad. Ser. A 2013, 14, 343–350. [Google Scholar]
- Pinto-Cruz, M.C. Optimized Transfer Matrix Approach for Global Buckling Analysis: Bypassing Zero Matrix Inversion. Period. Polytech. Civ. Eng. 2024, 69, 28–44. [Google Scholar] [CrossRef]
- ASTM E2611-09; Standard Test Method for Measurement of Normal Incidence Sound Transmission of Acoustical Materials Based on the Transfer Matrix Method. American Society for Testing and Materials: West Conshohocken, PA, USA, 2009. Available online: https://webstore.ansi.org/standards/astm/astme261109?srsltid=AfmBOopQ-dF-nYZAadkDHf4iJO5UNQICSyTG4_h7E3qEdeXFiXAN8MsP (accessed on 8 November 2024).
- Hakim, G.; Abramovich, H. The Behavior of Long Thin Rectangular Plates under Normal Pressure—A Thorough Investigation. Materials 2024, 17, 2902. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Chu, J.; Li, R. Analytic Solution for Buckling Problem of Rectangular Thin Plates Supported by Four Corners with Four Edges Free Based on the Symplectic Superposition Method. Mathematics 2024, 12, 249. [Google Scholar] [CrossRef]
- Hakim, G.; Abramovich, H. Multiwall Rectangular Plates under Transverse Pressure—A Non-Linear Experimental and Numerical Study. Materials 2023, 16, 2041. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brisc, C.-S.; Tripa, M.-S.; Boldor, I.-C.; Dumea, D.-M.; Gyorbiro, R.; Opriţoiu, P.-C.; Chifor, L.E.; Chereches, I.-A.; Mureşan, V.; Suciu, M. Applications of the Calculus by the Transfer Matrix Method for Long Rectangular Plates Under Uniform Vertical Loads. Mathematics 2025, 13, 2181. https://doi.org/10.3390/math13132181
Brisc C-S, Tripa M-S, Boldor I-C, Dumea D-M, Gyorbiro R, Opriţoiu P-C, Chifor LE, Chereches I-A, Mureşan V, Suciu M. Applications of the Calculus by the Transfer Matrix Method for Long Rectangular Plates Under Uniform Vertical Loads. Mathematics. 2025; 13(13):2181. https://doi.org/10.3390/math13132181
Chicago/Turabian StyleBrisc, Cosmin-Sergiu, Mihai-Sorin Tripa, Ilie-Cristian Boldor, Dan-Marius Dumea, Robert Gyorbiro, Petre-Corneliu Opriţoiu, Laurenţiu Eusebiu Chifor, Ioan-Aurel Chereches, Vlad Mureşan, and Mihaela Suciu. 2025. "Applications of the Calculus by the Transfer Matrix Method for Long Rectangular Plates Under Uniform Vertical Loads" Mathematics 13, no. 13: 2181. https://doi.org/10.3390/math13132181
APA StyleBrisc, C.-S., Tripa, M.-S., Boldor, I.-C., Dumea, D.-M., Gyorbiro, R., Opriţoiu, P.-C., Chifor, L. E., Chereches, I.-A., Mureşan, V., & Suciu, M. (2025). Applications of the Calculus by the Transfer Matrix Method for Long Rectangular Plates Under Uniform Vertical Loads. Mathematics, 13(13), 2181. https://doi.org/10.3390/math13132181







