DMET: Dynamic Mask-Enhanced Transformer for Generalizable Deep Image Denoising

Abstract

Different types of noise are inevitably introduced by devices during image acquisition and transmission processes. Therefore, image denoising remains a crucial challenge in computer vision. Deep learning, especially recent Transformer-based architectures, has demonstrated remarkable performance for image denoising tasks. However, due to its data-driven nature, deep learning can easily overfit the training data, leading to a lack of generalization ability. In order to address this issue, we present a novel Dynamic Mask-Enhanced Transformer (DMET) to improve the generalization capacity of denoising networks. Specifically, a texture-guided adaptive masking mechanism is introduced to simulate possible noise in practical applications. Then, we apply a masked hierarchical attention block to mitigate information loss and leverage global statistics, which combines shifted window multi-head self-attention with channel attention. Additionally, an attention mask is applied during training to reduce discrepancies between training and testing. Extensive experiments demonstrate that our approach achieves better generalization performance than state-of-the-art deep learning models and can be directly applied to real-world scenarios.

1. Introduction

Image denoising is a fundamental computer vision task aiming to restore clean images from noisy counterparts, and plays a crucial role in enhancing image quality in diverse applications. With the rapid development of deep learning, numerous deep neural networks have demonstrated remarkable performance in image denoising [1,2,3].

However, most methods suffer from a critical limitation, overfitting to the training noise distributions, which severely restricts generalization to unseen or real-world noise types [4,5]. Existing methods typically optimize pixel-wise similarity between denoised outputs and ground-truth images, inadvertently memorizing noise patterns instead of learning intrinsic image semantics. Consequently, these models struggle when confronted with noise types or levels outside their training distribution, which highlights a pressing need for generalizable denoising frameworks.

As real-world noise encompasses various types and distributions, the computer vision community aspires to develop a universal deep learning model with good generalization performance. To address this issue, recent efforts [6,7] have attempted to improve generalization ability by utilizing unsupervised training directly on the target noise or collecting training data more similar to those in the real world, while others [8] suppose the noise level of a specific type of noise is undetermined. However, these methods still encounter significant challenges in enhancing the generalization ability of the model [9,10,11]. They perform inefficiently when confronted with mismatched noise distribution or noise types unseen during training. Additionally, the above approaches also face the limitation that massive training data with various types and levels of noise are required.

Drawing inspiration from masked models that can learn the semantics and texture of images, a state-of-the-art network [12] based on Transformer with a masked training strategy efficiently enhances generalization ability, which enables it to learn to reconstruct the texture and semantics of images rather than overfitting to training noise. While this model has demonstrated superiority in denoising multiple noises, it employs uniform random masking to indiscriminately discard information across texture-rich and smooth regions. This leads to two key drawbacks: (1) excessive masking in detailed areas forces the model to hallucinate missing content; (2) insufficient masking in smooth regions allows overfitting to local noise patterns.

To leverage the strengths of masked training and address its limitations, this paper proposes a novel approach named Dynamic Mask-Enhanced Transformer (DMET). The DMET framework integrates texture-guided adaptive masking with a masked hierarchical attention mechanism to balance detail preservation and semantic recovery. Specifically, the proposed texture-guided adaptive masking dynamically adjusts masking probabilities based on local image complexity, which preserves fine details in texture-rich regions while enforcing robust semantic recovery in smooth areas to mitigate overfitting to noise patterns. Additionally, the masked hierarchical attention block combines shifted window multi-head self-attention (SW-MSA) for long-range dependencies and a channel attention block (CAB) to recover fine details lost during masking. An attention mask is applied during training to regularize feature learning and bridge training–testing discrepancies.

Although the DMET model is trained only with Gaussian noise, as shown in Figure 1, our method shows remarkable performance across diverse noise types, including salt-and-pepper noise, speckle noise, and Monte Carlo-rendered noise. The experimental results demonstrate that DMET possesses superior generalization performance compared to state-of-the-art models.

Figure 1. Visual comparison of denoised results across different noise types. Each row shows ground truth, noisy input, and output of our method (DMET) on (a) speckle noise (${\sigma }^2=$ 0.04), (b) salt-and-pepper noise ($d=$ 0.002), and (c) Monte Carlo noise (128 spp). The red box in the first column of the images outlines the region which is magnified in other three parallel images on the right for detailed visual comparison.

The main contributions of this work are summarized as follows:

• We propose a new Dynamic Mask-Enhanced Transformer for image denoising, dubbed DMET. The proposed model integrates texture-guided adaptive input masking and masked hierarchical attention masking to improve generalization across diverse noise types. The input mask adaptively corrupts pixels based on local texture complexity, while the attention mask regularizes feature learning to bridge the training–testing gap.
• We introduce a texture-guided adaptive masking mechanism that utilizes masking based on local texture complexity, enforcing robust semantic recovery in smooth regions while preserving details in texture-rich areas. Additionally, we also design a masked hierarchical attention block, which combines shifted window multi-head self-attention for long-range dependencies and channel attention to recover fine details. A texture-guided gating weight is further applied to dynamically fuse these features.
• We conduct extensive experiments on public datasets, and the results show that the proposed DMET can achieve competitive performance over state-of-the-art models. An ablation study and visualization analysis are also conducted to demonstrate the rationality of the proposed method.

The rest of this paper is structured as follows. In Section 2, we briefly review the related work. The overall architecture of the proposed method is introduced in Section 3. In Section 4, we show the experimental results and present a discussion. Finally, the conclusions and future expectations are presented in Section 5.

2. Related Work

In this paper, a model is proposed for an image denoising task with a generalization problem, which is closely related to channel attention and mask modeling. Therefore, in this section, we briefly review the existing studies on these research topics.

2.1. Image Denoising

Image denoising is one of the typical and most studied problems in image processing. Traditional methods rely on modeling image priors to restore the original content from noise-corrupted images [13,14,15,16]. These methods have shown robust generalization abilities across different noise types since they do not have strict constraints on the specific type of noise. However, these approaches have often been considered inadequate when it comes to complex textures or non-Gaussian noise.

Recently, because of the remarkable success of deep learning, convolutional neural networks (CNNs) have been widely introduced to image denoising tasks [17,18]. For example, DnCNN [8] utilizes a regularization method and specializes in denoising white Gaussian noise, while RNAN [19] applies a residual non-local attention network to image denoising. The above-mentioned models enhance their ability to learn effective image priors from extensive datasets. Subsequently, Transformers, a distinct class of neural architectures, have demonstrated remarkable advancements in vision tasks as well as the natural language processing domain [20]. Therefore, many models based on Transformer have emerged for image denoising [21,22]. Typically, Restormer [23], an efficient Transformer model capable of capturing long-range pixel interactions, and SwinIR [24], an improved variant of the Swin Transformer, have both achieved remarkable results. Compared to traditional denoising methods, deep learning models, particularly Transformers, can leverage large data priors and semantic context to recover fine image structures, making them more suitable for real-world and high-noise scenarios. However, one existing challenge of these models is their limited generalization ability. They struggle to adapt to unseen or diverse noise, resulting in performance degradation in real-world scenarios. It is significant to improve the generalization of deep models against various noise characteristics.

Recently, unsupervised denoising methods such as Noise2Void [25], Self2Self [26], and Neighbor2Neighbor [27] have also been proposed to address the lack of clean labels. These methods typically rely on internal statistics or self-supervised masking strategies to train denoisers using only noisy images. While promising in practical scenarios, they tend to underperform in PSNR and SSIM on synthetic datasets compared to supervised approaches. Moreover, their training objectives and paradigms differ fundamentally from those in our setting. In this work, we focus on enhancing the generalization ability of supervised models.

2.2. Generalization Problem

A common generalization issue in low-level vision tasks arises when the degradation in the testing phase differs from that encountered during the training phase [28]. Typically, deep denoising models are developed using Gaussian noise in the training phase. However, real-world noise predominantly follows non-Gaussian distributions. Consequently, models solely trained on Gaussian noise often fail to perform well in scenarios involving non-Gaussian noise.

There are three main categories of solutions to this problem. The first is “blind” denoising models [25] that train a denoiser using the noise level and noise as inputs to a CNN. These have benefited from the modeling capacity of CNNs and have shown the ability to learn a single-blind denoising model. However, their denoising performance is limited, and their results are not satisfactory on different types of noise. For example, DnCNN [8] is designed to handle Gaussian denoising with an unknown noise level. However, it requires training on a wide range of noise types and still fails to generalize to unseen noise distributions. Another category of solutions aims to make training datasets with noise modeling as close to reality as possible during development [6]. Although these methods can improve performance on certain noise types, they still struggle to generalize to out-of-distribution noise. The third approach applies masking operations [12] to guide the network to learn the textures of the image rather than the distribution of noise. However, to achieve significant effects across diverse noise types and levels, the mask ratio must be set to a high value, which inevitably results in the loss of information. In our work, we introduce a channel attention-based convolution block to involve more global information.

2.3. Channel Attention

The attention mechanism has emerged as a powerful technique for enhancing deep CNNs. The core principle behind attention is to selectively allocate visual emphasis to important information, resulting in enhanced computational efficiency and resource utilization. Among the various attention mechanisms, channel attention has particularly demonstrated its success in the field of computer vision. It allows networks to focus on essential channels or features, thereby enhancing overall CNN performance. Specifically, it utilizes scalars to represent and assess the significance of individual channels.

Recently, the incorporation of channel attention into convolution blocks has attracted a lot of interest, showing great potential for image denoising. The groundbreaking SE-Net [29] dynamically adjusts channel-wise feature responses by explicitly modeling the relationships between channels. CBAM [30] utilizes a 2D convolution operation to compute spatial attention and then combines spatial attention with channel attention to enhance the modeling ability of both spatial and channel dependencies. GE [31] investigates spatial extension by leveraging depth-wise convolution, which benefits the aggregation of features. Motivated by the above research, we take advantage of the capability of channel attention, enabling the effective utilization of global statistics. This allows us to introduce more pixel information into the network, enhancing its ability to capture relevant details and improve overall performance.

2.4. Mask Modeling

In the field of natural language processing, masked language modeling and its autoregressive counterparts have become highly appreciated methods for pre-training [32,33,34]. These methods typically obscure parts of the input sequence and train models to reconstruct missing content. Analogously, in computer vision, masked image modeling aims to learn robust visual representations by reconstructing corrupted images. Early inspirations for this approach can be traced to denoising auto-encoders [35]. Subsequent studies have leveraged the prediction of missing image regions to develop powerful visual encoders [36,37,38,39]. Notably, despite the inherent suitability of masked pre-training with low-level vision tasks, its successful adoption in these domains has been limited. Unlike high-level vision tasks, low-level applications require fine-grained detail recovery, which poses unique challenges for masked modeling.

Recently, Chen [12] proposed adding a mask module to the vision Transformer for image denoising, improving the generalization performance of deep learning-based image denoising models. It learns to reconstruct the texture and semantics of images rather than overfitting the noise pattern. However, randomly masking a substantial proportion of pixels can lead to information loss and potentially contribute to blurriness in the output.

3. Proposed Method

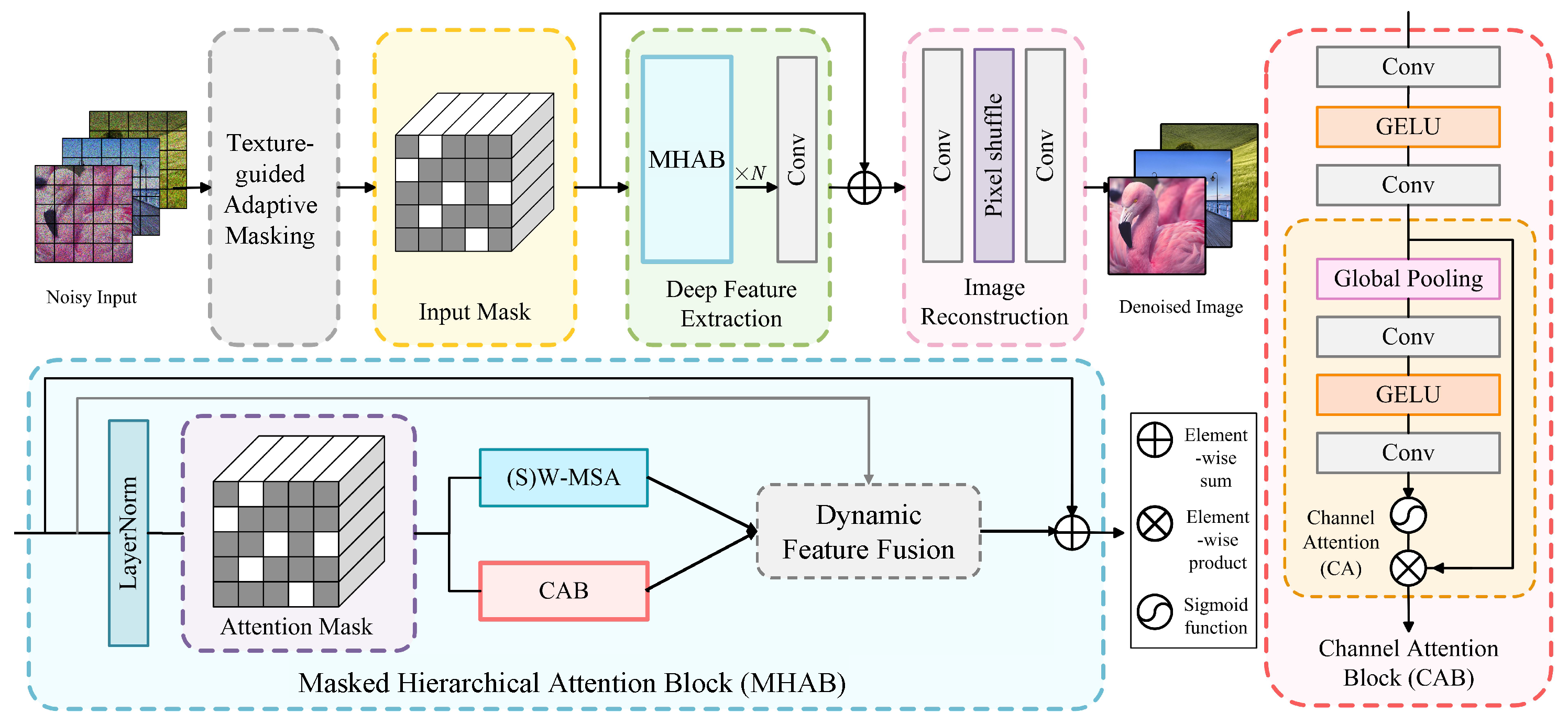
In this section, we propose a Dynamic Mask-Enhanced Transformer (DMET) model to improve the generalization capability of deep denoising models. Figure 2 shows the overall framework of the proposed method. As illustrated, DMET integrates texture-guided adaptive input masking, shifted window multi-head self-attention, and channel attention blocks into a unified architecture. The framework emphasizes robust feature learning through hierarchical masking and dynamic fusion, enabling superior generalization across diverse noise types. In the following, we elaborate on each component.

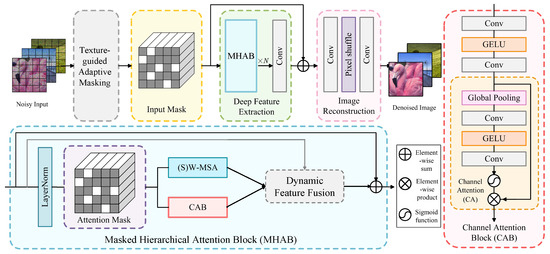
Figure 2. The overall architecture of the proposed Dynamic Mask-Enhanced Transformer (DMET) for image denoising, integrating texture-guided adaptive masking and masked hierarchical attention blocks.

3.1. Texture-Guided Adaptive Masking

Previous research has adopted mask training for image denoising. However, the existing models rely on fixed or uniformly random masking strategies, which may incur two main pitfalls. First, high masking ratios in texture-rich areas destroy fine details, forcing the model to hallucinate missing information and introducing artifacts. Second, low masking ratios in homogeneous areas allow the model to overfit to local noise patterns rather than learning robust semantic recovery. To mitigate these issues, we introduce texture-complexity-guided masking to dynamically adjust masking probabilities based on local image complexity. Specifically, for an input noisy image ${\mathit{I}}_N\in {\mathbb{R}}^{H\times W\times 3}$, the initial step in DMET is employing a convolution layer as shallow feature embedding, which enables 3-channel pixel mapping to a $\mathit{C}$-dimensional feature space. With ${\mathit{F}}_{emb}\in {\mathbb{R}}^{H\times W\times C}$, where $\mathit{H}$, $\mathit{W}$, and $\mathit{C}$ represent the image height, width, and channel number, respectively, we compute a texture complexity map $\mathcal{T}$ using gradient magnitude:

$$\mathcal{T}(i,j)={\displaystyle \frac{\left|\right|\nabla F_{\mathrm{embed}}(i,j){\left|\right|}_2}{max\left(\left|\right|\nabla F_{\mathrm{embed}}{\left|\right|}_2\right)+ϵ}},$$

(1)

where ∇ is the Sobel gradient operator, and $ϵ={10}^{-6}$ prevents division by zero. Higher values of $\mathcal{T}$ indicate richer textures.

Subsequently, the masking probability is inversely proportional to texture complexity:

$$P_{\mathrm{DM}}(i,j)=P_{\mathrm{base}}+\gamma ·(1-\mathcal{T}(i,j)),$$

(2)

where $P_{\mathrm{base}}$ is the base masking ratio and $\gamma$ scales the complexity weight. In our experiments, we choose 0.7 for $P_{\mathrm{base}}$ and 0.2 for $\gamma$. This ensures high masking ratios (up to $90\%$) in smooth regions to enforce semantic recovery while maintaining low masking ratios (down to $70\%$) in texture-rich regions to preserve details.

Then, a binary mask $\mathbf{M}$ is generated by sampling from $P_{\mathrm{DM}}$. To avoid abrupt transitions, Gaussian blur is applied to create smooth transitions between masked and unmasked regions. The masked image ${\tilde{I}}_N$ is generated by applying $\mathbf{M}$ to the original input image:

$${\tilde{I}}_N=I_N\odot \mathbf{M},$$

(3)

where ⊙ denotes element-wise multiplication. With the dynamic mask mechanism, pixels are adaptively masked based on the texture complexity to simulate possible noise or information loss in practical applications, thereby enhancing the generalization ability of the denoising model.

3.2. Masked Hierarchical Attention Block

The masked input ${\tilde{I}}_N$ is processed through a Transformer backbone enhanced with SW-MSA and CAB modules. A convolutional layer projects ${\tilde{I}}_N$ into a feature space ${\mathit{F}}_0\in {\mathbb{R}}^{H\times W\times C}$, preserving spatial relationships while reducing sensitivity to masked regions. Then, we employ shifted window multi-head self-attention (SW-MSA) to capture both local details and global structures by iteratively focusing on intra-window patterns and inter-window dependencies. The SW-MSA first divides ${\mathit{F}}_0$ into $\mathit{M}\times \mathit{M}$ non-overlapping windows. Each window is reshaped into a token sequence $\mathit{X}\in {\mathbb{R}}^{M^2\times C}$, where $M^2$ represents the number of tokens per window. Generally, the self-attention with the window is then computed by the following:

$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V,$$

(4)

$$\mathrm{Attention}(Q,K,V)=\mathrm{Softmax}(Q{K}^T/\sqrt{d}+B)V,$$

(5)

where ${\mathit{W}}_Q$, ${\mathit{W}}_K$ and ${\mathit{W}}_V$ are learnable weights, and $\mathit{B}\in {\mathbb{R}}^{M^2\times M^2}$ is a learnable relative positional encoding that captures spatial relationships between tokens. In alternating Transformer layers, the window grid is shifted diagonally by $M/2$ pixels. This shift enables tokens in previously isolated windows to interact, expanding the effective receptive field without increasing computational complexity.

To address the information loss caused by masking operations and enhance the network’s ability to emphasize significant channel-wise information, a channel attention block (CAB) is integrated in parallel with SW-MSA. As illustrated in Figure 2, the CAB integrates a channel attention (CA) module along with two standard convolution layers and a GELU activation function. The first convolution layer reduces the channel dimension, while the second convolution layer restores it to the original size. This bottleneck design balances efficiency and representational capacity. After the convolutional pathway, a channel attention mechanism dynamically recalibrates feature responses. The module aggregates spatial information via global average pooling, followed by a $1\times 1$ convolution and GELU activation to capture cross-channel interactions. A sigmoid function then generates channel-wise scaling factors, which are applied to the input feature to amplify critical channels.

While input masking corrupts pixel-level inputs, an attention mask is introduced in self-attention layers to regularize feature learning and bridge the training–testing discrepancy. With random mask tokens with an attention mask ratio $P_{\mathrm{AM}}$ in $\mathit{Q},\mathit{K},\mathit{V}$ during training, attention scores are computed only for unmasked tokens, which forces the model to rely on contextual relationships rather than overfitting to specific tokens.

3.3. Dynamic Feature Fusion

To harmonize the contributions of SW-MSA and CAB, we introduce a texture-guided fusion mechanism. A gating weight g is computed using the texture map $\mathcal{T}$:

$$g=\sigma \left({\mathrm{Conv}}_{1\times 1}\left(\mathcal{T}\right)\right),$$

(6)

where $\sigma$ is the sigmoid function. To ensure that texture-rich regions prioritize SW-MSA’s spatial attention, while smooth regions rely on CAB’s channel-wise refinement, we combine the SW-MSA and CAB outputs adaptively:

$$X_{fused}=g·X_{SW-MSA}+(1-g)·X_{CAB},$$

(7)

Finally, the fused feature is processed to generate a clean image by using the pixel-shuffle method.

4. Experimental Results and Discussion

4.1. Experimental Settings

The DMET model is implemented using the PyTorch 1.12.0 framework and trained on an RTX 4090 GPU. In our experiments, 800 images from the DIV2K dataset [40] and 2650 images from the Flickr2K dataset [41] are used for training. For testing, 100 images from Urban100 [42] and 68 images from CBSD68 [43] are employed. Each image is randomly cropped into $64\times 64$ patches, yielding approximately 450K patches. All experiments are conducted on RGB images. The model can also process grayscale images by treating them as single-channel inputs. To simulate real-world generalization challenges, we only utilize Gaussian noise with standard deviation of $\sigma =15$ to train the network. PSNR and SSIM are employed as evaluation metrics in all experiments. We use pixel-wise $L_1$ loss during training. For RGB images, the loss is computed per pixel across all three channels, then averaged over the entire image. The $L_1$ loss is defined as

$${\mathcal{L}}_{L_1}={\displaystyle \frac{1}{H\times W\times C}}\sum _{i=1}^H\sum _{j=1}^W\sum _{c=1}^C\left|{\widehat{I}}_{i,j,c}-I_{i,j,c}\right|,$$

(8)

where $\widehat{I}$ denotes the denoised image, I is the clean ground-truth image, and H, W, and C represent the height, width, and channel number ($C=$ 3 for RGB), respectively. This formulation ensures pixel-wise consistency and aligns with PSNR and SSIM, which are sensitive to pixel intensity differences. The Adam optimizer [42] is set to ${\beta }_1=0.9$ and ${\beta }_2=0.99$ to minimize $L_1$ pixel loss. Additionally, we set the learning rate to $1\times {10}^{-4}$ and the batch size to 8. Because the model is trained with Gaussian noise, we evaluate the generalization performance of the model on three other synthetic noises, including salt-and-pepper noise, speckle noise, and Monte Carlo (MC)-rendered image noise.

4.2. Quantitative Comparison

4.2.1. Generalization Performance

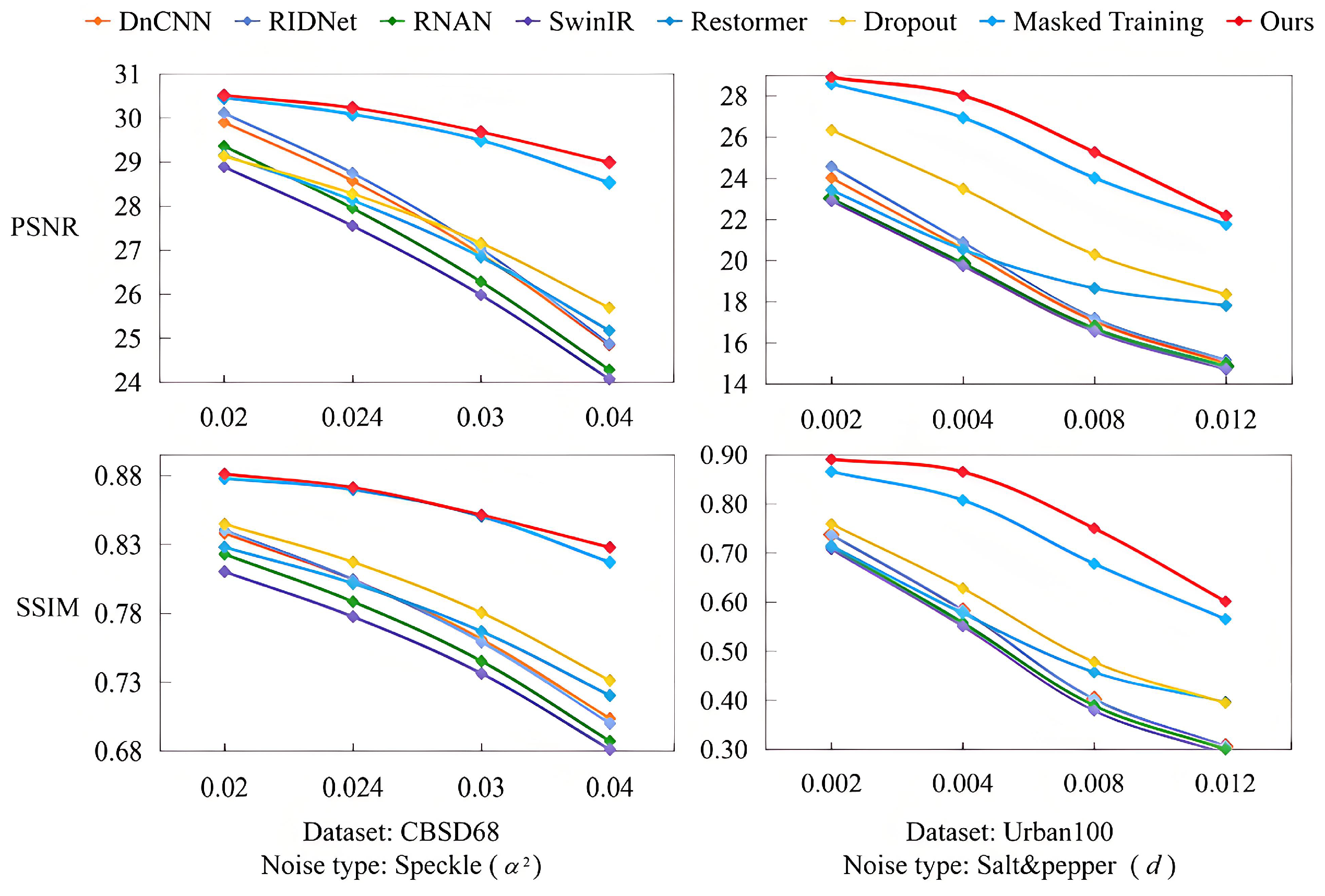
In order to assess generalization ability, our method is tested on multiple synthetic types of non-Gaussian noise, while the model is trained on images corrupted with single-level Gaussian noise. In this paper, we employ the the metrics PSNR and SSIM as criteria to compare our method with other state-of-the-art models. Seven recent models are compared with DMET. The first is DnCNN [8], which is a classical deep learning-based denoising method. The second model is RIDNet [44], which is efficient and capable of handling synthetic as well as real-world noise present in images. The third model is RNAN [19], which is a residual non-local attention network for image restoration. The fourth model is Restormer [23], which is an efficient Transformer model that can capture long-range pixel interactions. The fifth model is SwinIR [24], which is a strong baseline model for image restoration. The sixth model is Dropout [45], which applies the appropriate usage of dropout in SR networks. The seventh model is Masked Training [12], which utilizes a uniform masked training method to improve generalization performance. The experimental results show that our method achieves significant improvement compared to other models. Particularly, when the noise level increases, our model exhibits less performance degradation than other models, indicating its superior generalization ability. It is also demonstrated that our model possesses the potential to remove the unseen noise.

4.2.2. Evaluation on Speckle Noise

Speckles noise is a type of noise that is generated during the acquisition of medical images or tomography images. We employ different variances ${\sigma }^2$ to generate different levels of noise. Multiplicative noise is added following the equation $\mathit{J}=\mathit{I}+\mathit{n}\ast \mathit{I}$, where $\mathit{n}$ is uniformly distributed random noise with mean 0 and variance ${\sigma }^2$, and $\mathit{J}$ represents the noisy image. We validate the superiority of our denoising model for speckle noise on the CBSD68 [43] and Urban100 [42] datasets, and the experimental results are presented in Table 1 and Figure 3. Table 1 shows that DMET achieves 29.68 PSNR (${\sigma }^2$ = 0.03) and 28.99 PSNR (${\sigma }^2$ = 0.04) on the CBSD68 dataset, outperforming the masked training baseline by +0.19 dB and +0.46 dB, respectively. This improvement is attributed to the texture-guided adaptive masking, which preserves fine details in texture-rich regions (e.g., fabric patterns) while enforcing semantic recovery in smooth areas (e.g., sky regions). Although speckle noise is typically associated with domains such as medical imaging or synthetic aperture radar (SAR), in this study we apply it to natural-scene images to evaluate the cross-domain generalization capacity of DMET to multiplicative distortions. As shown in Figure 3, the model still demonstrates strong denoising performance for the example building image outside of its original domain, which further indicates the robust generalization ability of our model. To assess model performance across a wider range of multiplicative noise, we additionally tested ${\sigma }^2$ = 0.024 and 0.02, as shown in Figure 4. DMET maintains strong denoising performance and exhibits stability across varying noise intensities.

Table 1. Quantitative comparison of speckle noise denoising on CBSD68 dataset (${\sigma }^2=$ 0.03 and 0.04).

Dataset		CBSD68 [43]
Noise Type		Speckle
Metric	Method	${\mathit{\sigma }}^{\mathbf{2}}=$ 0.03	${\mathit{\sigma }}^{\mathbf{2}}=$ 0.04
PSNR ↑	DnCNN [8]	26.90	24.84
	RIDNet [44]	27.03	24.87
	RNAN [19]	26.28	24.28
	SwinIR [24]	25.98	24.07
	Restormer [23]	26.84	25.17
	Dropout [45]	27.16	25.69
	Masked Training [12]	29.49	28.53
	Ours	29.68	28.99
SSIM ↑	DnCNN [8]	0.7610	0.7035
	RIDNet [44]	0.7590	0.6999
	RNAN [19]	0.7451	0.6870
	SwinIR [24]	0.7362	0.6810
	Restormer [23]	0.7667	0.7202
	Dropout [45]	0.7804	0.7311
	Masked Training [12]	0.8502	0.8169
	Ours	0.8512	0.8277

Figure 3. Visual comparison of out-of-distribution speckle noise denoising results on CBSD68 dataset. A red box demarcates a randomly sampled region in the left panel. The panels on the right provide magnified visualizations of this region, enabling a visual comparison of the denoising performance across different models.

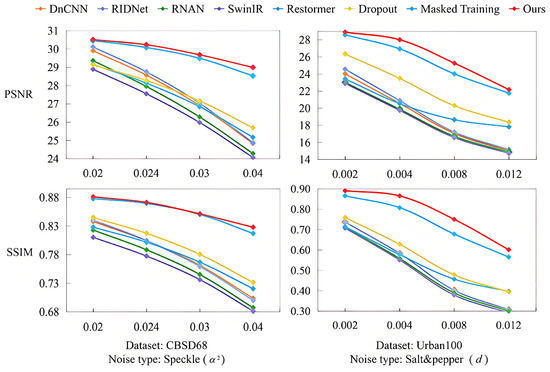
Figure 4. Performance comparisons under varying speckle and salt-and-pepper noise levels in terms of PSNR and SSIM. All models are trained only on Gaussian noise.

4.2.3. Evaluation on Salt-and-Pepper Noise

Salt-and-pepper noise, also known as impulse noise, can be caused by sharp and sudden disturbances in the image signal. Distinct noise levels correspond to varying noise densities, which can be quantified as d. Salt-and-Pepper noise is synthesized by randomly replacing a fraction d of the pixels with either 0 (pepper) or 255 (salt). We employ the CBSD68 [43] and Urban100 [42] datasets for testing with $d=$ 0.002 and $d=$ 0.004. These two noise levels represent light and moderate impulse noise, respectively. The results are shown in Figure 5 and Table 2. Our method achieves superior results compared to other methods in terms of PSNR and SSIM. Furthermore, as evident from Figure 5, our proposed method is able to generate effective denoising results when facing unseen noise. Although the Masked Training method [12] efficiently removes noise on the white background, there still exits obvious noise in the nearly black places. Compared with Masked Training, our proposed method not only demonstrates remarkable noise reduction capabilities on a white background but also excels at eliminating noise present in intricate textures. Additionally, Table 2 illustrates that DMET does not have the same magnitude of decline at the higher noise level as other methods. We also evaluated the model under more challenging impulse noise conditions, with higher noise densities of d = 0.008 and 0.012. The performance comparison is illustrated in Figure 4. Despite the increased corruption, DMET demonstrates graceful degradation and retains a clear advantage over competing methods.

Figure 5. Visual comparison of salt-and-pepper noise denoising results on Urban100 dataset. A red box demarcates a randomly sampled region in the left panel. The panels on the right provide magnified visualizations of this region, enabling a visual comparison of the denoising performance across different models. The spatially dispersed colored dots in the image represent MATLAB-simulated salt&pepper noise. Fewer colored dots correspond to higher reconstruction fidelity, which provides visual validation of model performance.

Table 2. Quantitative comparison of salt-and-pepper noise denoising results on Urban100 dataset ($d=$ 0.002 and $d=$ 0.004).

Dataset		Urban 100 [42]
Noise Type		Salt-and-Pepper
Metric	Method	$\mathit{d}=$ 0.002	$\mathit{d}=$ 0.004
PSNR ↑	DnCNN [8]	24.01	20.55
	RIDNet [44]	24.56	20.88
	RNAN [19]	23.01	19.87
	SwinIR [24]	22.90	19.74
	Restormer [23]	23.42	20.53
	Dropout [45]	26.33	23.48
	Masked Training [12]	28.58	26.93
	Ours	28.89	28.66
SSIM ↑	DnCNN [8]	0.7372	0.5828
	RIDNet [44]	0.7372	0.5835
	RNAN [19]	0.7132	0.5582
	SwinIR [24]	0.7075	0.5507
	Restormer [23]	0.7145	0.5772
	Dropout [45]	0.7591	0.6279
	Masked Training [12]	0.8655	0.8074
	Ours	0.8905	0.8804

4.2.4. Evaluation on Monte Carlo Rendering Noise

Monte Carlo (MC) integration is used ubiquitously in realistic image synthesis because of its flexibility and generality. As an integral part of the rendering process, the Monte Carlo denoising process is utilized as a post-processing step to effectively eliminate any noticeable remaining noise. We leverage a test dataset introduced by Firmino et al. [46], which specifically targets the evaluation of denoising algorithms applied to Monte Carlo-rendered images. The test dataset comprises images rendered at both 128 samples per pixel (spp) and 64 spp. Notably, a lower spp value leads to more pronounced noise in the rendered images. To ensure the compatibility of this test set with our model, we first apply tone mapping to convert the dataset into the sRGB color space. This step ensures that the images are in a format that is more conducive to human perception and visual assessment, facilitating a fair and accurate comparison of denoising performance. From Table 3, we can observe that DMET achieves superior average PSNR and SSIM values for the 64 spp and 128 spp settings. The key advantage is the proposed masked hierarchical attention block, which combines shifted window self-attention to capture spatial dependencies and channel attention to suppress impulse noise in both high-contrast edges and low-contrast regions.

Table 3. Quantitative evaluation of Monte Carlo-rendered noise denoising on MC [46] dataset (128 spp and 64 spp).

Dataset		MC [46]
Noise Type		Monte Carlo-Rendered
Metric	Method	128 spp	64 spp
PSNR ↑	DnCNN [8]	29.94	26.28
	RIDNet [44]	29.96	26.27
	RNAN [19]	29.86	26.26
	SwinIR [24]	24.98	24.59
	Restormer [23]	29.32	26.14
	Dropout [45]	28.85	26.10
	Masked Training [12]	30.62	28.25
	Ours	30.80	28.46
SSIM ↑	DnCNN [8]	0.7883	0.6779
	RIDNet [44]	0.7921	0.6788
	RNAN [19]	0.7825	0.6743
	SwinIR [24]	0.6598	0.5880
	Restormer [23]	0.7627	0.6651
	Dropout [45]	0.7753	0.6696
	Masked Training [12]	0.8500	0.7694
	Ours	0.8535	0.7822

4.3. Ablation Study

To systematically validate the incremental contributions of each component in the proposed DMET, we conduct ablation experiments on the CBSD68 dataset with speckle noise (${\sigma }^2=$ 0.04). Specifically, we analyze the contributions of the texture-guided adaptive masking (TAM), masked hierarchical attention block (MHAB), and dynamic feature fusion (DFF). The baseline model is a vanilla Transformer architecture with uniform random masking (URM) and no channel attention. Table 4 presents the experimental results. From the table, we can observe that adding TAM to the baseline model yields significant improvement (+0.78 dB PSNR, +0.0361 SSIM), which indicates that adaptive masking is critical for simulating realistic noise patterns and guiding the model to focus on texture-rich regions. The addition of MHAB further enhances performance (+0.43 dB PSNR, +0.0108 SSIM), demonstrating that hierarchical attention with channel-wise features improves the recovery of fine details from masked regions. Furthermore, the final boost in performance (+0.44 dB PSNR, +0.0154 SSIM) is provided by incorporating DFF. The adaptive fusion of spatial and channel features is confirmed to optimize the integration of multi-scale representations.

Table 4. The ablation studies of the effects of the proposed DMET components on generalization performance for speckle noise denoising.

Baseline	TAM	MHAB	DFF	PSNR ↑	SSIM ↑
✓				27.34	0.7654
✓	✓			28.12	0.8015
✓	✓	✓		28.55	0.8123
✓	✓	✓	✓	28.99	0.8277

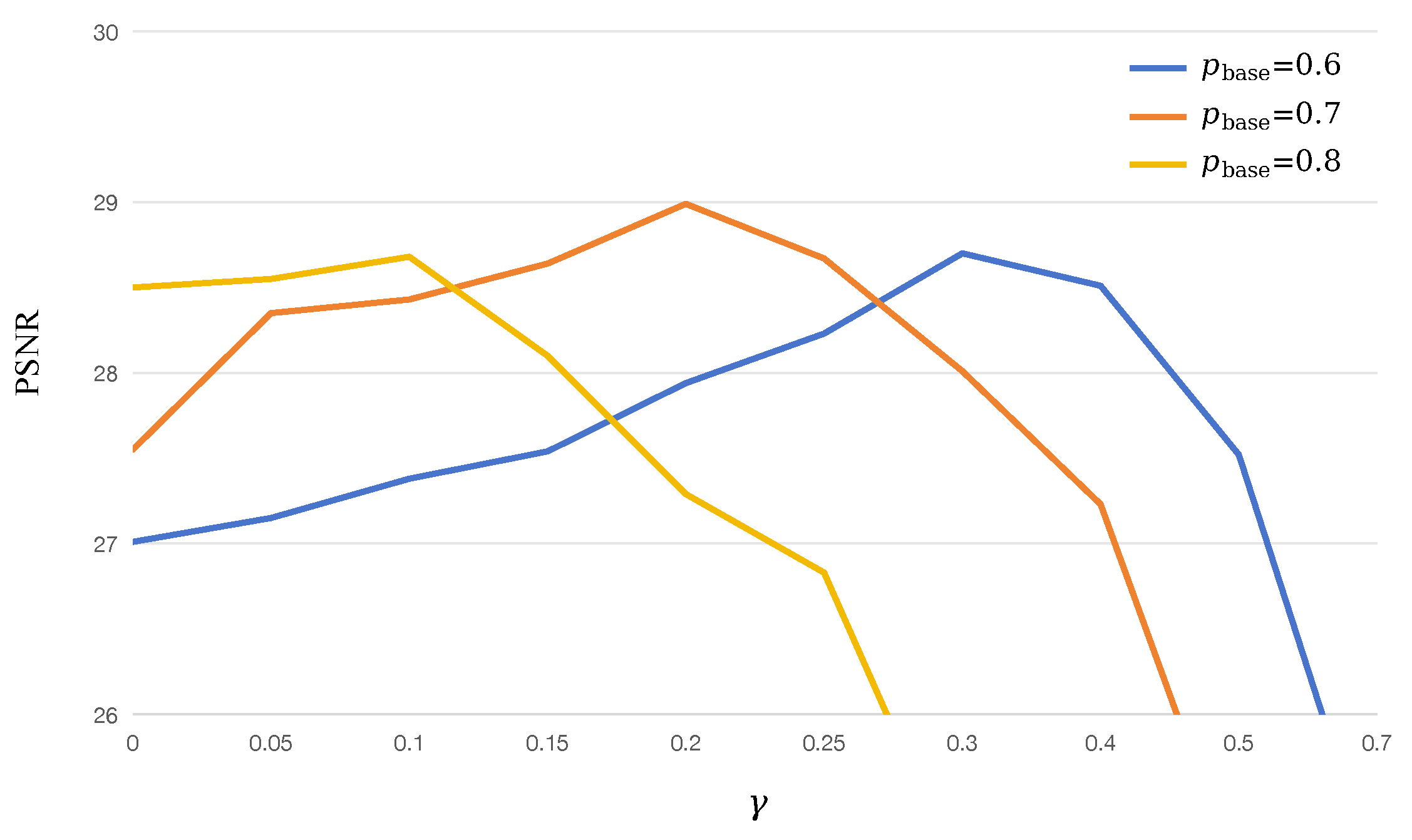
We also conduct an ablation study for the parameters $P_{\mathrm{base}}$ and $\gamma$ in the texture-guided adaptive masking mechanism. A previous study [12] demonstrated that the best performance is achieved with $75\%-85\%$ masking ratios. Therefore, we vary $\gamma$ to analyze how texture complexity influences masking probabilities with $P_{\mathrm{base}}=0.6,0.7,0.8$. Figure 6 shows the experimental results with different values of $P_{\mathrm{base}}$ and $\gamma$. As we can observe, the best performance is achieved with $P_{\mathrm{base}}=0.7$ and $\gamma =0.2$. This ensures high masking ratios (up to $90\%$) in smooth regions to enforce semantic recovery, and low masking ratios (down to $70\%$) in texture-rich regions to preserve details. Our search for the two parameters is limited to a narrow range based on empirical performance. Future work will explore broader search spaces or employ automated hyperparameter optimization to refine these selections.

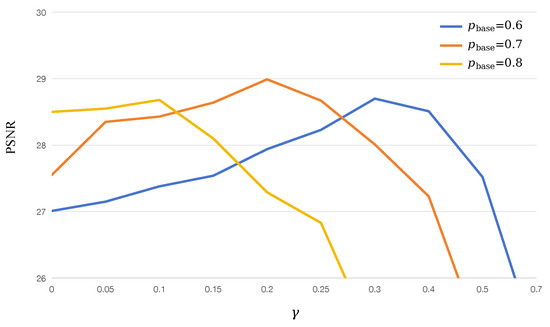
Figure 6. The PSNR performance of the proposed DMET on the CBSD68 dataset corrupted with speckle noise (${\sigma }^2$ = 0.04) under different $P_{\mathrm{base}}$ and $\gamma$.

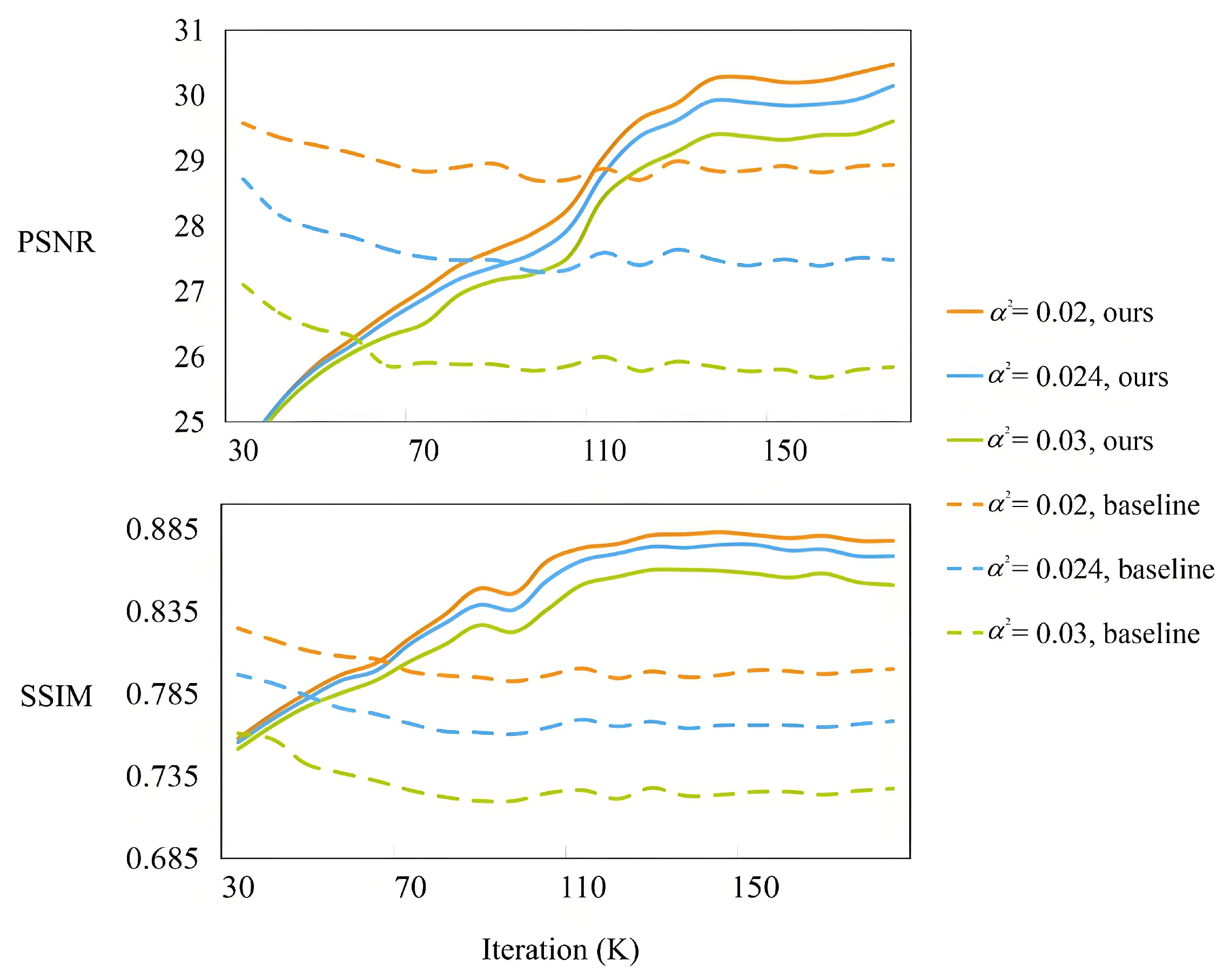
To further evaluate the robustness of DMET in mitigating overfitting, we compare the performance of the models over training epochs on speckle noise, as shown in Figure 7. Both models are trained on Gaussian noise only. The baseline model (without masking) suffers from an overfitting problem. In contrast, our proposed approach exhibits consistent improvement, indicating both better generalization and training stability. This further confirms the effectiveness of our dynamic masking strategy in enhancing overfitting resistance.

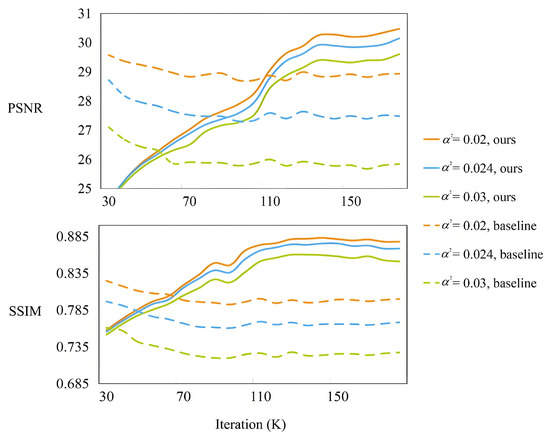
Figure 7. Comparison of testing curves under speckle noise for baseline and DMET, both trained on Gaussian noise.

4.4. Computational Complexity

To compare the computational complexity of our proposed DMET with the baseline models, we provide the number of parameters, inference time, and FLOPs in Table 5. The testing image is a color image with a size of 512 × 512. From the table, we can conclude that despite a moderate increase in parameter count, the overall efficiency of our model is outstanding.

Table 5. Efficiency comparisons with the baseline models in terms of parameter count, FLOPs, and inference time.

	DnCNN [8]	Restormer [23]	Mask [12]	Ours
Params (M)	0.67	26.1	0.88	1.43
FLOPs (G)	176.1	564.0	204.9	80.7
Infer.time (s)	0.034	0.415	2.239	0.621

5. Conclusions

In this paper, we present a novel Dynamic Mask-Enhanced Transformer (DMET) to improve the generalization performance of deep learning-based image denoising models. By incorporating texture-guided adaptive masking and a masked hierarchical attention mechanism, DMET effectively balances the reconstruction of masked regions and the preservation of critical details. The texture-guided adaptive masking enables the preservation of fine details in texture-rich regions and the enforcement of robust semantic recovery in smooth areas. Additionally, the integration of SW-MSA and CAB enables robust feature learning, while dynamic fusion ensures the optimal utilization of spatial and channel-wise information. Extensive experiments on unseen noise types, including speckle, salt-and-pepper, and Monte Carlo rendering noise, demonstrate that DMET achieves strong generalization ability, despite being trained only on Gaussian noise. The quantitative results across different noise levels show that our method consistently outperforms existing supervised baselines in both PSNR and SSIM. The ablation studies confirm that adaptive masking and hierarchical attention are key to this generalization. Although our current evaluations are based on natural-scene datasets, extending the validation to domain-specific images such as medical ultrasound or SAR remains an important next step. We plan to include such applications in future work to further verify the real-world robustness and generalization capability of the proposed DMET.

Despite these promising results, DMET still has several limitations. Under extremely high noise levels where structural semantics are severely degraded, the model may produce oversmoothed or hallucinated content, particularly in texture-ambiguous domains such as ultrasound imaging. In addition, like most supervised methods, DMET was trained on isolated noise types and has not been evaluated on mixed-noise scenarios that commonly occur in real-world applications. From a deployment perspective, the current model size and inference cost may limit its use in edge devices.

To address these limitations, future work will explore (1) confidence-aware fusion or uncertainty estimation to mitigate hallucination under severe corruption; (2) targeted data augmentation and robustness-aware training strategies for difficult modalities; (3) model evaluation on mixed-noise inputs such as combined speckle and impulse noise; and (4) pruning and quantization techniques to reduce model complexity and enable lightweight deployment on mobile platforms.