Anonymous and Traceable: A Dynamic Group Signature-Based Cross-Domain Authentication for IIoT

Abstract

As the Internet of Things (IoT) continues to evolve, the demand for cross-domain collaboration between devices and data sharing has grown significantly. Operations confined to a single trust domain can no longer satisfy this requirement, so cross-domain access to resources is becoming an inevitable trend in the evolution of the IIoT. Due to identity trust issues between different domains, authorized access is required before resources can be shared. However, most existing cross-domain authentication schemes face significant challenges in terms of dynamic membership management, privacy protection, and traceability. These schemes involve complex and inefficient interactions and fail to meet the dynamic and lightweight requirements of the IIoT. To address these issues, we propose a privacy-preserving and traceable cross-domain authentication scheme based on dynamic group signatures that enables efficient authentication. The scheme supports anonymous authentication via succinct proofs and incorporates a trapdoor mechanism to enable group managers to trace and revoke malicious identities. Additionally, our solution supports efficient joining and revoking of members and implements blacklist-based proof of non-membership. We formally prove the security of the proposed scheme. The experimental results demonstrate that the proposed scheme outperforms others in terms of computational cost and revocation overhead.

1. Introduction

The Industrial Internet of Things (IIoT) [1], as an important branch of the Internet of Things, connects various sensors, actuators, and other intelligent terminals deployed in production plants or equipment sites, thus realizing equipment interconnection, production optimization, and intelligent decision-making [2]. In IIoT architecture, devices are usually managed by different service providers or divided into separate administrative zones (e.g., manufacturing workshops and warehousing areas managed by different departments). A trust domain is a group of devices managed by the same service provider or in the same administrative zone [3]. Unified authentication protocols and access control policies within a single domain ensure secure connections between devices. However, as the IIoT evolves, the process of manufacturing products has become increasingly complex in industrial manufacturing, often requiring cross-domain collaboration. Unauthorized access to systems in another domain could leak production data and sensitive information, thus compromising the security and accuracy of manufacturing processes [4]. Therefore, in cross-domain resource sharing and collaboration, the accessed domain must verify the requesting devices in order to ensure data security. However, cross-domain authentication remains a major challenge for the current IIoT solutions.

First, IIoT devices in different domains that are frequently supplied by different suppliers or situated in different geographical locations [5] have limited shared trust. However, these devices must collaborate to accomplish critical production tasks [6]. If real-identity authentication is used, malicious nodes may intercept transmitted or stored data, exposing critical information such as industrial network topologies and device operational statuses. This could provide intelligence for targeted attacks. Therefore, it is necessary to provide anonymous cross-domain authentication. Additionally, anonymity must not preclude identity tracking and monitoring to prevent compromised devices from sending harmful data and disrupting production. Therefore, it is also necessary to implement identity tracking to achieve conditional privacy protection [7]. However, traditional solutions, such as certificate-based or identity-based cross-domain authentication, either fail to adequately address both aspects or involve significant implementation complexity [8].

In addition, some IoT devices may need to be dynamically migrated (e.g., introducing new devices and revoking old devices) during the production process in order to accomplish collaborative tasks, which requires cross-domain systems to accommodate this dynamism [9]. Many IIoT application scenarios (e.g., automation control and fault warning) are highly sensitive to data interaction latency. An efficient join or revoke process can complete secure initialization or revocation actions in the shortest possible time, preventing production interruptions and false alarms caused by authentication delays. Therefore, the joining or revocation of devices for cross-domain authentication should be realized efficiently. However, the current most commonly used revocation mechanism (certificate revocation lists) requires a complex process and suffers from high latency.

In order to address these challenges, we propose a cross-domain authentication scheme based on group signatures, which supports conditional privacy protection and efficient dynamic migration of IIoT devices [10]. Compared to PKI/IBC solutions, group signatures inherently support anonymity and traceability; compared to blockchain solutions, they have lower computational overhead. Our scheme can be applied to smart factory collaboration (such as automotive supply chains), preventing malicious cross-domain attacks while protecting device privacy, reducing the risk of industrial data leaks, and complying with privacy regulations such as GDPR. The main contributions are summarized as follows:

• We propose a cross-domain authentication scheme based on group signatures, in which the group signature is constructed using zero-knowledge proofs and dynamic accumulators. This allows devices to authenticate anonymously while enabling the group manager to identify and revoke the access rights of malicious devices as needed.
• Our scheme enables efficient dynamic membership management. It achieves O(1) time complexity for device enrollment and revocation. A lazy witness update algorithm is introduced to reduce the frequency of witness updates and computational overhead. Furthermore, we have designed a non-membership proof mechanism based on blacklists to verify the legitimacy of devices using fixed-size group elements, which significantly reduces storage and communication costs.
• We perform a security analysis of the proposed scheme to demonstrate its security and privacy-preserving properties. The experimental results show that our scheme has lower computational overhead and stronger dynamic adaptability than other schemes.

1.1. Related Work

We classify cross-domain authentication technologies into three categories: PKI/IBC-based technologies, blockchain-based technologies, and group signature-based technologies. PKI/IBC represents traditional technologies and is currently the most widely used. Blockchain technology is gradually being widely adopted due to its inherent transparency and immutability. Group signatures are also being used in the field of cross-domain authentication due to their excellent characteristics of anonymity and traceability.

1.1.1. Cross-Domain Authentication Based on PKI/IBC

Wang et al. [11] proposed a two-layer public key infrastructure (PKI) model to achieve scalability. However, the collapse of the global PKI layer could lead to severe system disruptions [12]. Millan et al. [13] analyzed the feasibility of the bridge CA (BCA) model, while Hu et al. [14] used PKI for authentication in all domains to form an integrated network and avoid single points of failure. Yuan et al. [15] enabled key agreement between PKI and identity-based cryptography (IBC) domains, but their protocol requires initialization with parameters from the same cryptographic setup. Chen et al. [16] presented XAuth, an efficient privacy-preserving cross-domain authentication scheme addressing slow response times caused by low blockchain throughput. Shen et al. [17] proposed an efficient blockchain-assisted authentication scheme that combines blockchain with IBC to enable identity verification and key agreement, ensuring device anonymity through pseudonyms [18] and security via periodic pseudonym updates.

1.1.2. Blockchain-Based Cross-Domain Authentication

Owing to the decentralization and tamper-proof characteristics of a blockchain, it can prevent single points of failure [8]. Therefore, more and more cross-domain authentication schemes have introduced blockchain. Yao et al. [19] and Li et al. [20] proposed blockchain-assisted lightweight anonymous authentication mechanisms for distributed scenarios and Wi-Fi access, respectively. Chen et al. [21] designed the Bidm system, which utilizes blockchain to maintain identity information across distinct trust domains, addressing the inefficiencies and implementation challenges of traditional decentralized identity management mechanisms. However, blockchain faces inherent performance limitations and lacks real-time processing capacity, making it insufficient as a standalone solution for cross-domain authentication. Therefore, our scheme only employs blockchain assistance to achieve tamper-resistant effects without involving extensive blockchain access.

1.1.3. Group Signature-Based Cross-Domain Authentication

Hwang et al. [22] proposed a novel group signature scheme with controlled linkability, featuring short signature lengths suitable for resource-constrained privacy-enhancing scenarios. Sudarsono et al. [23] designed an anonymous authentication system based on group signatures to preserve user anonymity during service access. Several researchers have applied group signatures to IIoT scenarios to protect node anonymity [24,25,26]. Yuan et al. [27] proposed a dynamic cross-domain authentication scheme, DCAGS-IoT, incorporating a Merkle tree-based user update algorithm with $O(logN)$ complexity. By integrating blockchain-stored registration lists, the scheme effectively identifies malicious user identities. However, these schemes suffer from complex designs, high computational overhead, and incomplete support for dynamic revocable group signatures.

In summary, PKI and IBC rely on centralized or hierarchical trust centers to achieve cross-domain permission control through certificate chains, but they face issues of complex certificate management and poor scalability. Blockchain utilizes distributed ledgers and smart contracts to achieve trust consensus without central nodes but is constrained by performance bottlenecks. Group signatures can protect device anonymity while supporting malicious identity tracking, but the existing schemes have issues regarding efficiency and design complexity. Our scheme designs a new group signature for cross-domain authentication, enabling efficient and secure cross-domain authentication.

1.2. Paper Outline

The remainder of this paper is structured as follows: Section 2 introduces the cryptographic primitives that support the proposed scheme. Section 3 describes the dynamic membership management mechanism designed for real-time device enrollment and revocation. Section 4 details the complete cross-domain authentication protocol. Subsequently, Section 5 conducts a formal security analysis of the proposed scheme. Section 6 verifies the practicality of the scheme through experimental comparison with existing schemes. Finally, Section 7 concludes this paper and summarizes its contributions.

2. Preliminaries

2.1. Bilinear Mappings

Let $G_1$ and $G_2$ be two additive cyclic groups of order q, and $G_T$ be a multiplicative cyclic group of the same order. A bilinear mapping is defined as a map $e:G_1\times G_2\to G_T$ satisfying the following three properties [28]:

• Bilinearity: For all $P_1\in G_1$, $P_2\in G_2$, and $a,b\in {\mathbb{Z}}_p^{\ast }$, the following holds:

  $$e(a{P}_1,b{P}_2)=e(ab{P}_1,P_2)=e(P_1,ab{P}_2)=e{(P_1,P_2)}^{ab}.$$
• Computability: For any $P_1\in G_1$ and $P_2\in G_2$, $e(P_1,P_2)$ can be efficiently computed.
• Non-degeneracy: There exist $P_1\in G_1$ and $P_2\in G_2$ such that $e(P_1,P_2)\ne 1$.

2.2. Dynamic Accumulator

The classical constructions of dynamic accumulators include the RSA-based dynamic accumulator under the strong RSA assumption [29] and the bilinear map-based dynamic accumulator under the q-SDH assumption [30]. Our scheme adopts the latter.

A dynamic accumulator generates a succinct binding commitment for a set of elements and produces a short membership or non-membership proof for any element in the set. These proofs can be publicly verified against the commitment. It satisfies the following properties:

Computability: For a member set $X=\{x_1,\dots ,x_n\}$, there exists a deterministic function $\mathrm{AccF}\left(X\right)\to \mathrm{ACC}$, where $\mathrm{ACC}=\left({\prod }_{x_i\in X}(x_i+x)\right)P_1$ and x is the group manager’s private key.

Efficient Verification: For any $x_i\in X$, a witness $W_i$ can be generated, which satisfies the verification equation $\mathrm{Verify}(\mathrm{Acc},x_i,W_i)=\mathrm{True}$.

Quasi-Commutativity: The order of element additions does not affect the final accumulated value, enabling witness updates via simple operations [31]:

$$f(f(u,x_1),x_2)=f(f(u,x_2),x_1).$$

2.3. Non-Interactive Zero-Knowledge Proof (NIZK)

The NIZK allows one party (the prover) to convince the other party (the verifier) that a statement is correct without revealing any information beyond the validity of the statement, and without requiring an interactive challenge [32]. Most NIZK systems require pre-generated global public parameters, leading to complex proof processes. Alternatively, the Fiat–Shamir heuristic [33] can transform interactive zero-knowledge proofs into non-interactive ones by leveraging the random oracle model (ROM). However, since ROM does not exist in practice, cryptographic hash functions (e.g., SHA-256) are commonly used to emulate ideal random functions. For example, the Schnorr protocol allows a prover to convince a verifier of possessing a private key x associated with the public key $y=g^{x}modp$ while preserving the confidentiality of x. By applying the Fiat–Shamir heuristic, the interactive Schnorr protocol can be converted into an NIZK through the following procedure:

• Proof Generation: The prover first selects a random number $r\in {\mathbb{Z}}_p^{\ast }$ and computes the commitment $R=g^{r}modp$. Subsequently, a hash-based challenge $c=H(R\Vert y)$ is generated using a cryptographic hash function $H(·)$. The prover then calculates the response $s=(r+c·x)modq$ and generates the signature $\sigma =(R,s)$ for transmission to the verifier.
• Verification: Upon receiving $\sigma$, the verifier extracts components R and s. The verification consists of two sequential checks: First, the hash equivalence $c\stackrel{?}{=}H(R\Vert y)$ must hold, ensuring the challenge consistency. Then, the algebraic relationship $g^s\stackrel{?}{=}R·y^c$ is verified to confirm the validity of the proof without requiring interaction.

2.4. Group Signatures

The concept of group signatures was first introduced by Chaum et al. in 1991 [34]. It allows any group member to sign messages on behalf of the group, enabling public verification without revealing the signer’s identity. When disputes arise over a signature, the group manager can identify the signing member. Formally, a group signature scheme is a tuple of probabilistic polynomial-time (PPT) algorithms:

• $Setup\left(1^{\lambda }\right)\to (gpk,gsk)$: On input security parameter $\lambda$, generate a group public key $gpk$ and a group manager’s secret key $gsk$.
• $Join(gpk,gmsk)\to (s{k}_i,cer{t}_i)$: Enable the group manager to enroll user i, issuing them a signing key $s{k}_i$ and a certificate $cer{t}_i$.
• $Sign(gpk,s{k}_i,m)\to \sigma$: Produce a group signature $\sigma$ on message m using member i’s key $s{k}_i$.
• $Verify(gpk,m,\sigma )\to (0/1)$: $\mathrm{Check}\mathrm{the}\mathrm{validity}\mathrm{of}\sigma \mathrm{under}gpk.$
• $Open(gmsk,m,\sigma )\to i$: Allow the group manager to reveal the identity i of the signer, if necessary.

Group signatures can be implemented in various ways as their construction methods depend on different cryptographic assumptions and application scenarios. To meet the needs of the IIoT in our scheme, we use NIZK and dynamic accumulator techniques to create group signatures.

3. Enhanced Dynamic Member Management

To satisfy the requirements of the IIoT, we introduce a dynamic membership management mechanism that supports device join and revocation in O(1) time. The mechanism also incorporates a lazy witness update strategy that allows batch witness updates to minimize computational resource consumption and operational costs. Furthermore, updates to the dynamic accumulator are synchronized with the blockchain, ensuring immutability and decentralization without the need for additional trusted third parties.

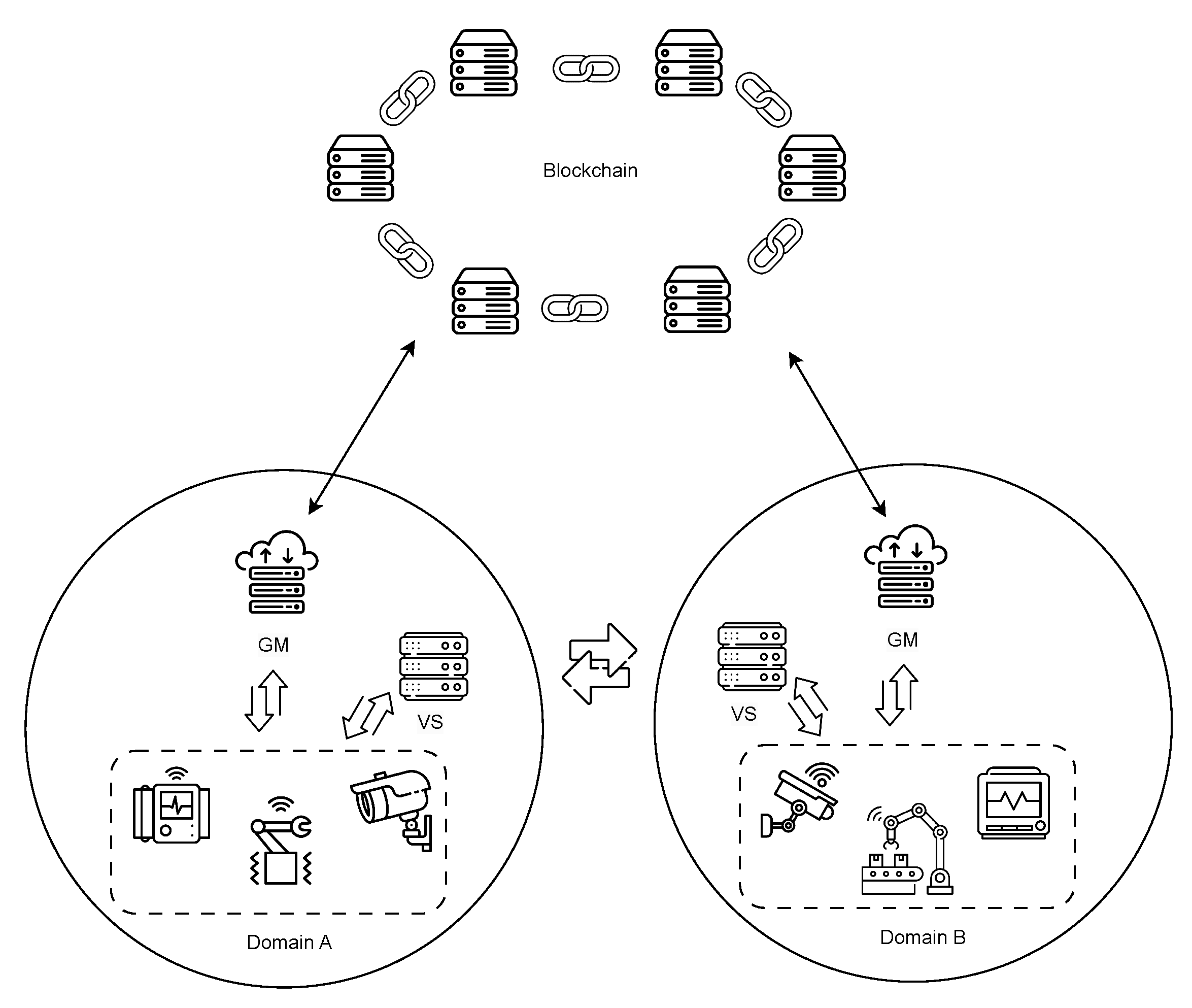
3.1. System Overview

Complex IIoT tasks usually require collaboration between multiple factories in different domains. The architecture of the entire system is shown in Figure 1, involving multiple participating entities:

• Devices: Devices play a key role in cross-domain authentication. Devices in different domains perform different tasks. However, most IIoT devices have limited resources, with memory capacities in the kilobyte range and clock frequencies in the megahertz range. These limitations make executing complex cryptographic algorithms infeasible. Each device has a unique and tamper-proof real identity $id$ (such as one embedded in a security chip when the device leaves the factory).
• Group Manager (GM): In each domain, group membership is maintained via a dynamic accumulator, and the GM is the sole trusted group administrator. The GM generates the system parameters required for cross-domain identity authentication and issues certificates and membership witnesses to devices when they join the group. Moreover, the GM tracks identities and revokes the access privileges of malicious devices.
• Verification Server (VS): The cross-domain authentication process requires multiple bilinear mappings for verification, but these mappings are computationally expensive and difficult for IIoT devices with limited resources to complete. The VS was introduced to enable devices to efficiently perform authentication and production operations. For multi-user concurrent authentication, VS can use GPU-accelerated bilinear interpolation calculations and asynchronous pipeline processing. It can also cache some fixed parameters to reduce calculations.

3.2. Initialization

Before crossing domains, each management domain must perform initialization operations, including sharing public information, such as elliptic curve parameters and hash functions, with cross-domain systems. The system parameters of this scheme are shown in

Table 1. Notations.

Notation	Description
$\lambda$	Security parameter
p	Large prime number
$G_1,G_2$	Additive cyclic group
$G_T$	Multiplicative cyclic group
$P_1$	Generator of group $G_1$
$P_2$	Generator of group $G_2$
H	Secure hash function
$C_i$	Group member certificate
$W_i$	Accumulator member witness
$w_y$	Blacklist non-membership witness
$P{K}_{GM}$	Public key of the group manager
x	Private key of the group manager

.

$\mathrm{Setup}\left(1^{\lambda }\right)\to (PP,gsk)$: In this stage, the GM performs the setup algorithm by providing a security parameter $\lambda$, which generates the group’s public parameters and group private key, thus creating the group.

Suppose $G_1$ and $G_2$ are additive cyclic groups, and $G_T$ is a multiplicative cyclic group. e is a bilinear mapping $e:G_1\times G_2\to G_T$, where $P_1$ and $P_2$ are generators of $G_1$ and $G_2$. Specifically, GM randomly selects x as group private key $gsk$ and public key $P{K}_{GM}=x{P}_1$, initializes accumulator value $AC{C}_0=P_2$, and chooses collision-resistant hash function $H:{\{0,1\}}^{\ast }\to {\mathbb{Z}}_p^{\ast }$. Moreover, it creates a list, $DeviceList$, which will save the device state information. The elements stored in $DeviceList$ are formatted as follows:

$$<num,id,uid{P}_1,flag,updateNum,W>,$$

where num is a serial number, and, for each device added, the corresponding num value is increased by 1.

After generating the required parameters, the GM issues parameters $PP=(P{K}_{GM},AC{C}_0,G_1,G_2,G_T,e,P_1,P_2,H)$. In addition, GM maintains a blacklist cumulative value $A_{\kappa }\left(X\right)$. If the identity of the malicious participant is traced in the tracking phase, it will be added to $A_{\kappa }\left(X\right)$ to prevent illegal devices from being added repeatedly. Concretely, it randomly selects $k\in {\mathbb{Z}}_p^{\ast }$ and computes $G_k=\left[k\right]P_1.$ For a blacklist $X=\{x_1,x_2,\dots ,x_n\},$ a polynomial is constructed as $f_X\left(k\right)={\prod }_{x\in X}(x+k)\mathrm{mod}p$, and the accumulator value is defined as $A_k\left(X\right)=f_X\left(k\right)·P_1=\left({\prod }_{x\in X}(x+k)\right)P_1$.

3.3. Design Details

$\mathrm{BNMP}(PP,X)\to (u_y,v_y)$: Traditional blacklist-based schemes require a centralized administrator to maintain and query the list. In such approaches, a device must submit its identity to the administrator, who then checks if the device is on the blacklist. However, this method results in linear growth in both query latency and storage consumption as the number of devices increases. To overcome these limitations, our scheme adopts a bilinear pairing-based dynamic accumulator [35], which enables compact non-membership proofs with constant communication overhead.

First, we consider a scenario where device $A_i$ in domain A requires cross-domain access to device $B_j$ in domain B. Device $A_i$ needs to generate a fixed-size witness $w_y=(u_y,v_y)$. To prove that the value $y\mathrm{is}\mathrm{not}\mathrm{in}X,\mathrm{the}\mathrm{device}\mathrm{first}\mathrm{calculates}$

$$u_y=-\prod _{x\in X}(x-y)\mathrm{mod}p,$$

(1)

and calculates polynomial ${\widehat{q}}_X\left(\kappa \right)$, which satisfies $f_X\left(\kappa \right)+u_y=(y+\kappa )·{\widehat{q}}_X\left(\kappa \right)$. Then, it calculates

$$v_y={\widehat{q}}_X\left(\kappa \right)·P_1.$$

(2)

$A_i$ utilizes $(v_y,u_y)$ as a non-membership proof for identity exclusion.

$\mathrm{JoinGroup}(DeviceLis{t}_A,A_i,PP)\to (C_i,W_i,nu{m}_i)$: After successfully executing the Join algorithm, device $A_i$ becomes a legitimate group member and acquires the corresponding group witness $W_i$ and group certificate $C_i$ to generate the group signature $\sigma$.

First, device $A_i$ sends its real identity $i{d}_i$ and non-membership witness $w_y=(u_y,v_y)$ to $G{M}_A$. Then, $G{M}_A$ verifies whether the equation is true:

$$e\left(v_y,y{P}_1+G_{\mathbf{k}}\right)\stackrel{?}{=}e\left(A_{\kappa }\left(X\right)+u_y{P}_1,P_1\right).$$

(3)

If the validation passes, $G{M}_A$ computes the group membership witness and membership certificate for $A_i$ and updates the accumulator value. Algorithm 1 details the specific steps.

Algorithm 1 JoinGroup Algorithm

Input:

$DeviceLis{t}_A$: Domain A’s device list

$A_i$: Device requesting to join

$PP$: Public parameters $(P{K}_{GM},AC{C}_0,G_1,G_2,G_T,e,P_1,P_2,H)$

$(u_y,v_y)$: Non-membership proof from $A_i$

Output:

$(C_i,W_i,nu{m}_i)$: Group certificate, witness, and sequence number

1:  Check $e(v_y,y{P}_1+G_{\kappa })\stackrel{?}{=}e(A_{\kappa }\left(X\right)+u_y{P}_1,P_1)$

2:  if verification passes then

3:        Compute $nu{m}_i=nu{m}_{i-1}+1$

4:        Compute $ui{d}_i=H(i{d}_i\Vert nu{m}_i)$

5:        Compute group certificate $C_i={(ui{d}_i+x)}^{-1}{P}_2$

6:        Update accumulator $AC{C}_A=(ui{d}_i+x)·AC{C}_A$

7:        Compute membership witness $W_i={(ui{d}_i+x)}^{-1}·AC{C}_A$

8:        Set element $updateNu{m}_i=nu{m}_i$

9:        Add record to $DeviceLis{t}_A$: $$\langle nu{m}_i,i{d}_i,ui{d}_i{P}_1,flag=1,updateNu{m}_i,W_i\rangle$$

10:       return $\{C_i,W_i,nu{m}_i\}$

11:  else

12:       return Join request rejected

13:  end if

$\mathrm{UpdateACC}(DeviceLis{t}_A,A_i,nu{m}_k,PP)\to \left(W_i^{\prime }\right)$: When device $A_i$ intends to initiate cross-domain authentication, it must first update its witness value to the latest value. The detailed steps are as follows:

• $A_i\mathrm{sends}\{nu{m}_i,ui{d}_i\}\mathrm{to}G{M}_A,\mathrm{requesting}\mathrm{an}\mathrm{update}\mathrm{of}\mathrm{its}\mathrm{witness}{W}_i.\mathrm{The}G{M}_A$ uses the value of $nu{m}_i$ to quickly locate the corresponding $updateNu{m}_i$ in $DeviceLis{t}_A$.
• If $updateNu{m}_i=k$, the records $\{l_1,\dots ,l_k\}$ in $DeviceLis{t}_A=\{l_1,\dots ,l_n\}$ represent the accumulator updates already processed by the device, while $\{l_{k+1},\dots ,l_n\}$ are newly added records not yet incorporated into the witness. Partition $\{l_{k+1},\dots ,l_n\}$ into two sublists: $lis{t}_0$ (entries with flag = 0) and $lis{t}_1$ (entries with flag = 1). The $G{M}_A$ computes the update factor $\delta$ as

  $$\delta =\prod _{i\in lis{t}_0}{(ui{d}_i+x)}^{-1}\prod _{j\in lis{t}_1}(ui{d}_j+x).$$
• Then, $G{M}_A$ updates the $W_i$ value of device $A_i$ to $W_i^{\prime }=\delta ·W_i$, sets $updateNu{m}_i=n$, and returns $W_i^{\prime }$ to $A_i$. Later updates for $A_i$ will directly start from the n-th record in $DeviceLis{t}_A$, ensuring efficient and lazy updates. For revoked devices, if $G{M}_A$ identifies that the witness value $W=\varnothing$, the update request is denied.

4. Complete Cross-Domain Authentication Scheme

Although the dynamic accumulator designed in the previous chapter can achieve authentication, directly exposing $W_i$ and $C_i$ risks information leakage (e.g., revealing access footprints). Therefore, we propose a dynamically revocable group signature scheme to solve this problem based on the dynamic accumulator in the previous chapter and combined with a non-interactive zero-knowledge proof. This solution enables cross-domain identity verification without disclosing specific values [36], such as $W_i$.

Assuming all domains have completed initialization and device $A_i$ has joined the member group of domain A, the requirement is for $A_i$ to authenticate across domains without disclosing its specific credentials, such as $ui{d}_i$, $W_i$, and $C_i$. The cross-domain authentication process consists of two stages: (1) cross-domain authentication, and (2) tracking and revocation. The following sections detail the design of these two parts.

4.1. Cross-Domain Authentication

In order to perform successful authentication, $A_i$ invokes the UpdateACC algorithm to update its membership witness. If $A_i$ continues to use an outdated witness, the signature generation will fail due to the witness’s expiration. Corresponding to steps 5–7 in Figure 2, device $A_i$ sends $(nu{m}_i,ui{d}_i)$ to $G{M}_A$. Then, $G{M}_A$ updates $w_i$ based on $DeviceLis{t}_A$ and returns it to $A_i$. Assuming the latest dynamic accumulator value of domain A is $AC{C}_{new}$, the update satisfies $AC{C}_{new}=W_i(ui{d}_i+x).$

This scheme adopts the Fiat–Shamir Transform to turn interactive zero-knowledge proofs into non-interactive versions. The cross-domain authentication phase corresponds to steps 8–12 in Figure 2. The specific group signature algorithm is designed as follows:

$\mathrm{Sign}(ui{d}_i,W_i,C_i,PP)\to (\sigma ,m)$: We use the Diffie–Hellman key exchange to enable secure communication between cross-domain devices because symmetric encryption has much lower computational costs than public-key encryption. First, $A_i$ sets m as its public key $p{k}_{A_i}=a{P}_1\in G_1$. During the commitment phase, $A_i$ selects a random number $r\in {\mathbb{Z}}_p^{\ast }$ to randomize associated parameters. Each selection of r must satisfy a uniform distribution; otherwise, secret information may be leaked. $A_i$ computes $T_1=r{P}_1\in G_1$ and further binds the user identifier $ui{d}_i$ with the group manager’s public key $P{K}_{GM}$ to generate $T_2=ui{d}_i{P}_1+rP{K}_{GM}\in G_1$.

Additionally, $A_i$ binds r with its witness $W_i$ and group certificate $C_i$ and sets $T_3=r{W}_i$ and $T_4=r{C}_i$. Since a distinct r is chosen for each proof generation, the resulting $T_3$ and $T_4$ are completely randomized, which obscures the link between the group certificate and the witness. This ensures the unlinkability of device identities and prevents signature correlation.

Next, $A_i$ generates two random numbers, ${\beta }_1,{\beta }_2\in {\mathbb{Z}}_p^{\ast },$ and computes $Y_1={\beta }_1{P}_1,Y_2={\beta }_{1}P{K}_{GM},Y_3={\beta }_2{P}_1.$ A timestamp, $\tau$, is generated to restrict the validity window of the signature and prevent replay attacks. The collision-resistant hash function SHA3-256 is used to generate a zero-knowledge challenge. The challenge value c is computed as follows:

$$c=H(m\Vert \tau \Vert T_1\Vert T_2\Vert T_3\Vert T_4\Vert Y_1\Vert Y_2\Vert Y_3),$$

where $H(·)$ is hash function. The security of the scheme relies on the collision resistance of $H(·)$; any weakness in the hash function could severely harm the entire system.

Finally, $A_i\mathrm{computes}{z}_1={\beta }_1+c·r\mathrm{and}{z}_2={\beta }_2+c·ui{d}_i$ and produces the signature $\sigma =\left(m,\tau ,T_1,T_2,T_3,T_4,Y_1,Y_2,Y_3,c,z_1,z_2\right).$ Then, $A_i$ sends $(\sigma ,m)$ to the verification server $V{S}_B$ in domain B. $V{S}_B$ retrieves domain A’s public parameters by invoking the blockchain’s smart contract and proceeds to execute the Verify algorithm to validate the signature.

$\mathrm{Verify}(m,\sigma ,PP)\to (0/1)$: The Verify algorithm verifies the validity of the signature. First, the verifier ($V{S}_B$) performs the challenge value verification by checking if the timestamp $\tau$ meets the requirements; i.e., it must be within the time window $\Delta t$ to prevent replay attacks. It reconstructs the challenge value $c^{\prime }=H(m\Vert \tau \Vert T_1\Vert T_2\Vert T_3\Vert T_4\Vert Y_1\Vert Y_2\Vert Y_3).$ $\mathrm{If}{c}^{\prime }\ne c$, abort the verification process. Then, it verifies whether the following equation holds:

$$e(c·P{K}_{GM}+z_2{P}_1-Y_3,T_3)\stackrel{?}{=}e{(T_1,AC{C}_{\mathrm{new}})}^c$$

(4)

$$e(c·P{K}_{GM}+z_2{P}_1-Y_3,T_4)\stackrel{?}{=}e{(T_1,P_2)}^c$$

(5)

$$Y_1\stackrel{?}{=}{z}_1{P}_1-c{T}_1,c{T}_1\stackrel{?}{=}{z}_1{P}_1-Y_1$$

(6)

$$z_2{P}_1+z_{1}P{K}_{GM}-c{T}_2\stackrel{?}{=}{Y}_2+Y_3.$$

(7)

If all verifications pass, the $V{S}_B$ transmits a response to $B_j$. Subsequently, $B_j$ selects its private key $b\in {\mathbb{Z}}_p^{\ast }$, generates its public key $p{k}_{B_j}=b{P}_1\in G_1$, and sends $p{k}_{B_j}$ to $A_i$. $A_i$ then computes $K_A=a·p{k}_{B_j}=ab{P}_1$, while $B_j$ computes $K_B=b·p{k}_{A_i}=ab{P}_1$. The shared session key is derived as $K=K_A=K_B$.

4.2. Tracking and Revoking Malicious Devices

In cross-domain authentication scenarios, malicious devices may compromise system security through replay attacks or data tampering. Our scheme incorporates an identity tracing mechanism that allows the $GM$ to trace the real identity of malicious devices when necessary. In other words, group devices can enjoy anonymity until the tracing authority locates them [37]. Figure 3 illustrates this process.

• $G{M}_A$ computes $ui{d}_i{P}_1=T_2-x{T}_1$ using its private key x and the values $T_1,T_2$ from the signature $\sigma$. Then, $G{M}_A$ queries $DeviceLis{t}_A$ with $ui{d}_i{P}_1$ to retrieve the real identity $i{d}_i$ of the malicious device $A_i$.
• After obtaining the tracing information, $G{M}_A$ sets $w_i=\varnothing$ in the $DeviceLis{t}_A$ and inserts the following record into $DeviceLis{t}_A$ to revoke $A_i$’s group membership:

  $$\langle num+1,i{d}_i,ui{d}_i{P}_1,flag=0,updateNu{m}_i=\varnothing ,w_i=\varnothing \rangle .$$
• Then, $G{M}_A$ updates the latest accumulator value as $ACC=ACC·{\left(ui{d}_i+x\right)}^{-1}$ and synchronizes the new $ACC$ to the blockchain.
• Additionally, $G{M}_A\mathrm{adds}{A}_i^{\prime }\mathrm{s}i{d}_i\mathrm{to}\mathrm{the}\mathrm{blacklist}\mathrm{cumulative}\mathrm{value}{A}_K\left(X\right),\mathrm{updating}$ it as $A_K\left(X\right)=(i{d}_i+k)·A_K\left(X\right).$

5. Security Analysis

5.1. Threat Model

In our scheme, the verification server is considered a semi-honest entity. This means that, while it faithfully executes the protocol, it may attempt to infer private information during protocol execution. In contrast, IIoT devices are treated as untrusted entities. They may collude with external attackers or other group members to achieve unauthorized authentication through various strategies. They might impersonate legitimate devices to succeed in authentication or generate authentication information that cannot be traced back to the attacker’s real identity. The group manager is the only honest entity, and, if corrupted, the security of the scheme will be compromised. In practical scenarios, since the group private key is typically well-protected, we consider that adversaries cannot obtain the group private key x.

In this paper, security analysis needs to prove properties such as anonymity and traceability to ensure that cross-domain authentication schemes can protect user privacy while resisting malicious tampering and forgery. At the same time, our scheme should also resist common malicious attacks (such as replay attacks and collusion attacks). In addition, we need to prove that the non-membership proof of the blacklist is unforgeable; otherwise, the revoked device will rejoin the system. We reduce these malicious capabilities to the q-SDH assumption and prove the reliability of the scheme.

5.2. Security Objectives

To ensure the safety of production processes, the cross-domain authentication of IIoT devices should satisfy the following security objectives:

• Anonymity: The proposed cross-domain scheme should ensure the confidentiality of IIoT devices’ identity information, thereby protecting their identity privacy and ensuring anonymity throughout the authentication process.
• Traceability: The scheme should prevent adversaries from generating untraceable signatures. In other words, all legitimate signatures must be traceable back to their respective signers.
• Unlinkability: The cross-domain authentication scheme should ensure that attackers cannot determine whether two messages originate from the same entity.
• Replay Resistance: The cross-domain authentication scheme should prevent attackers from reusing validated legitimate signatures to forge identities or compromise security.

We compared our scheme with three recent cross-domain authentication schemes [3,16,17], and the comparative results are shown in

Table 2. Comparison of security and functionality.

Properties	BASA [17]	XAuth [16]	CCAP [3]	Our Scheme
Dynamic Capability	×	×	×	✓
Anonymous Authentication	✓	✓	✓	✓
Identity Traceability	✓	×	✓	✓
Unlinkability	✓	✓	✓	✓
Collision Resistance	×	×	✓	✓
Replay Resistance	×	✓	✓	✓

.

5.3. Security Assumption

This section introduces the core security assumptions on which our scheme relies to prove its security.

The q-Strong Diffie–Hellman (q-SDH): Let $G=\langle g\rangle$ be a cyclic group of prime order p, and let $x\in {\mathbb{Z}}_p^{\ast }$ be a secret value. Under the q-SDH assumption, for any probabilistic polynomial-time (PPT) algorithm $\mathcal{A}$, given the set of elements $\left\{g^{x^i}\in G\mid 0\le i\le q\right\},$ it is computationally infeasible to output a pair $\left(s,g^{\frac{1}{x+s}}\right)$. Formally, the success probability of $\mathcal{A}$ satisfies

$$Pr\left[\mathcal{A}\left(g,g^x,g^{x^2},\dots ,g^{x^q}\right)\to \left(s,g^{\frac{1}{x+s}}\right)\right]\le ϵ,$$

where the probability is over the random choice of x in ${\mathbb{Z}}_p^{\ast }$ and the random bits consumed by $\mathcal{A}$.

5.4. Security Properties and Proofs

Theorem 1.

The proposed cross-domain authentication scheme satisfies correctness.

Proof. 

Before conducting the security analysis, we first prove the scheme’s correctness. If the device is legitimate and strictly adheres to the protocol, the scheme is correct. The proof proceeds as follows:

• Verification of non-membership proof: According to Equations (1) and (2), we can conclude that

  $$\begin{array}{cc}\hfill e(v_y,y{P}_1+G_k)& =e\left({\widehat{q}}_X\left(k\right)·P_1,(y+k)P_1\right)\hfill \\ & =e{(P_1,P_1)}^{{\widehat{q}}_X\left(k\right)·(y+k)}.\hfill \end{array}$$
  And continue to calculate

  $$\begin{array}{cc}\hfill e\left((f_X\left(k\right)+u_y)·P_1,P_1\right)& =e\left((y+k)·{\widehat{q}}_X\left(k\right)·P_1,P_1\right)\hfill \\ & =e{(P_1,P_1)}^{(y+k)·{\widehat{q}}_X\left(k\right)}.\hfill \end{array}$$
  Therefore, Equation (3) holds.
• Verification of the equation $e(c·P{K}_{GM}+z_2{P}_1-The{Y}_3,T_3)=e{(T_1,AC{C}_{\mathrm{new}})}^c:$
  The right $e{(T_1,AC{C}_{\mathrm{new}})}^c=e{(r{P}_1,AC{C}_{\mathrm{new}})}^c=e{(P_1,AC{C}_{\mathrm{new}})}^{rc}$. According to $z_2{P}_1-Y_3=z_2{P}_1-{\beta }_2{P}_1,\mathrm{and}c·ui{d}_i{P}_1=z_2{P}_1-{\beta }_2{P}_1$, we can prove

  $$\begin{array}{cc}\hfill e(cP{K}_{GM}+z_2{P}_1-Y_3,T_3)& =e(cP{K}_{GM}+cui{d}_i{P}_1,T_3)\hfill \\ & =e{(P{K}_{GM}+ui{d}_i{P}_1,w_i)}^{rc}.\hfill \end{array}$$
  Due to $e\left((ui{d}_i+x)P_1,w_i\right)=e(P_1,{\mathrm{ACC}}_{new})=e(ui{d}_i{P}_1+P{K}_{GM},w_i),$ Equation (4) is proven. Similarly, we can prove that Equation (5) also holds.
• We calculate $z_1{P}_1-Y_1=({\beta }_1+cr)P_1-{\beta }_1{P}_1=cr{P}_1=c{T}_1,$ and $z_1{P}_1-c{T}_1=({\beta }_1+cr)P_1-c\left(r{P}_1\right)={\beta }_1{P}_1=Y_1.$ Thus, Equation (6) holds.
• Based on the values of $T_1,z_1,z_2$, the following can be calculated:

  $$\begin{array}{cc}\hfill z_2{P}_1+z_{1}P{K}_{GM}-c{T}_2=& ({\beta }_2+cui{d}_i)P_1+({\beta }_1+cr)P{K}_{GM}-c(ui{d}_i{P}_1+rP{K}_{GM})\hfill \\ \hfill =& {\beta }_2{P}_1+{\beta }_{1}P{K}_{GM}\hfill \\ \hfill =& Y_2+Y_3.\hfill \end{array}$$
  So, Equation (7) holds.

Since all the above equations hold, our scheme satisfies correctness. In other words, if a signer possesses valid $(W_i,C_i)$ and correctly executes the sign algorithm to obtain the signature $\sigma$, the verification algorithm $Verify\left(\sigma \right)$ will always return 1. □

Theorem 2.

There exists an extractor for the proposal group signature scheme.

Proof. 

Assume an adversary $\mathcal{A}$ can generate two valid signatures $\sigma =(c,z_1,z_2,\dots )$ and ${\sigma }^{\prime }=(c^{\prime },z_1^{\prime },z_2^{\prime },\dots )$ for the same commitment $(T_1,T_2,T_3,T_4,Y_1,Y_2)$, where $c\ne c^{\prime }$. All verification equations hold. Define the differences as

$$\Delta c=c-c^{\prime },\Delta z_1=z_1-z_1^{\prime },\Delta z_2=z_2-z_2^{\prime }.$$

According to verification Equation (6), the two signatures share the same commitment. Since $Y_1$ remains identical for both c and $c^{\prime }$, substituting into the equations yields

$$Y_1=z_1{P}_1-c{T}_1,Y_1=z_1^{\prime }{P}_1-c^{\prime }{T}_1.$$

Thus, $\Delta z_1{P}_1=\Delta c{T}_1,T_1={\displaystyle \frac{\Delta z_1}{\Delta c}}{P}_1\sin \mathrm{ce}{T}_1=r{P}_1.$ Let $\widehat{r}={\displaystyle \frac{\Delta z_1}{\Delta c}}$ and we get

$${\widehat{W}}_i={\widehat{r}}^{-1}{T}_3,{\widehat{C}}_i={\widehat{r}}^{-1}{T}_4.$$

According to Equation (7) and $T_2=ui{d}_i{P}_1+rP{K}_{GM}$, we get

$$\Delta z_2{P}_1+\Delta z_{1}P{k}_{GM}=\Delta c{T}_2,{\widehat{uid}}_i={\displaystyle \frac{\Delta z_2}{\Delta c}}.$$

The tuple $({\widehat{W}}_i,{\widehat{C}}_i,\widehat{uid})$ is successfully extracted. □

Theorem 3.

The non-membership proof is unforgeable.

Proof. 

Under the q-SDH assumption over group G, for any probabilistic polynomial-time adversary $\mathcal{A},\mathrm{given}\mathrm{a}\mathrm{set}X\left(\right|X|\leqq q)\mathrm{and}\mathrm{the}\mathrm{set}{\{x^i·G\}}_{i=0}^q,\mathrm{it}\mathrm{is}\mathrm{infeasible}\mathrm{for}\mathcal{A}$ to produce a valid non-membership witness ${\widehat{w}}_y=(v_y,u_y)\mathrm{for}y\in X,$ except with negligible probability $O(1/p)$.

Assume $\mathcal{A}$ outputs a witness ${\widehat{w}}_y=(v_y,u_y)$. For $y\in X$, the equation $(y+k)·v_y=f_X\left(k\right)·G+u_y·G$ holds. Since $y\in X$, we have $(y+k)\mid f_X\left(k\right)$, and thus $f_X\left(k\right)=(y+k)·q\left(k\right)$. We can get

$$(y+k)·v_y=(y+k)·q\left(k\right)·G+u_y·G.$$

Dividing both sides by $(y+k)$ (noting $y+k\ne 0$): $v_y=q\left(k\right)·G+{\displaystyle \frac{u_y}{y+k}}·G.$ Since $u_y\ne 0$, rearranging terms yields

$${\displaystyle \frac{1}{y+k}}·G={\displaystyle \frac{1}{u_y}}·(v_y-q\left(k\right)·G).$$

The computation of ${\displaystyle \frac{1}{y+k}}·G$ would violate the q-SDH assumption, rendering the probability of forgery negligible. □

Theorem 4.

Under the q-SDH assumption, the proposed scheme satisfies traceability.

Proof. 

Assume there exists a probabilistic polynomial-time adversary $\mathcal{A}$ capable of forging a valid signature ${\sigma }^{\ast }=(T_1^{\ast },T_2^{\ast },T_3^{\ast },\dots )$. $\mathrm{When}{\sigma }^{\ast }\mathrm{is}\mathrm{forged}$, the tracing algorithm fails to recover the corresponding identity $i{d}^{\ast }$. We construct a challenger $\mathcal{C}$ that calls $\mathcal{A}$ to break the q-SDH assumption.

• Initialization:
  • $\mathcal{C}$ generates system parameters $PP=(P{K}_{GM}=x{P}_1,AC{C}_0=P_2,G_1,G_2,G_T,e,H)$ and publishes them.
  • $\mathcal{C}$ receives a q-SDH challenge tuple $(P_1,x{P}_1,x^2{P}_1,\dots ,x^q{P}_1)\in G_1$, where x is unknown.
• Query Phase: $\mathcal{A}$ adaptively interacts with $\mathcal{C}$ via the following oracles:
  • Device Enrollment: For any device $i{d}_i$, $\mathcal{C}$ random selection $ui{d}_i\in {\mathbb{Z}}_p$ generates a certificate $C_i={(ui{d}_i+x)}^{-1}{P}_2$ and updates the accumulator $ACC$.
  • Signature Generation: For any message m and device $i{d}_i$, $\mathcal{C}$ generates valid signatures using $C_i$ and $W_i$.
• Forgery Phase:
  • $\mathcal{A}\mathrm{outputs}\mathrm{a}\mathrm{forged}\mathrm{signature}{\sigma }^{\ast }=(T_1^{\ast },T_2^{\ast },T_3^{\ast },\dots ),\mathrm{where}{T}_2^{\ast }=ui{d}^{\ast }{P}_1+r^{\ast }P{K}_{GM}$ and $T_3^{\ast }=r^{\ast }{W}^{\ast }.$

If $ui{d}^{\ast }\notin DeviceList$, the adversary $\mathcal{A}$ must have forged a valid witness $W^{\ast }$ for an unregistered identity. However, $W^{\ast }$ must satisfy $W^{\ast }={(ui{d}^{\ast }+x)}^{-1}AC{C}_{new}$. This requires $\mathcal{A}$ to know ${(ui{d}^{\ast }+x)}^{-1}$, rendering the probability of untraceability negligible. □

Theorem 5.

The proposed scheme satisfies anonymity.

Proof. 

The proposed scheme achieves anonymity by leveraging group signatures combined with zero-knowledge proofs and randomized parameter binding. Specifically, during the signing phase, each device $A_i$ generates a signature $\sigma$ using randomized parameters r, $T_1=r{P}_1$, $T_2=ui{d}_i{P}_1+rP{K}_{GM}$, $T_3=r{W}_i$, and $T_4=r{C}_i$. The randomization via r ensures that distinct signatures generated by the same device are computationally indistinguishable from those generated by different devices. Furthermore, the zero-knowledge proof embedded in $\sigma$ conceals all identity-related parameters $(wi{d}_i,W_i,C_i)$ while proving their validity. This prevents adversaries from linking signatures to specific devices or correlating multiple signatures from the same device.

Formally, assume an adversary $\mathcal{A}$ attempts to distinguish two signatures ${\sigma }_0$ and ${\sigma }_1$ produced by devices $A_0$ and $A_1$, respectively. Due to the randomization of r, the distributions of $T_1$, $T_2$, $T_3$, and $T_4$ are statistically independent of $ui{d}_i$. Additionally, the zero-knowledge challenge c and responses $z_1$ and $z_2$ are derived from cryptographic hash functions and a random number, ensuring no leakage of identity information. Even if the adversary obtains multiple signatures, the unlinkability property guarantees that no polynomial-time adversary can determine whether two signatures originate from the same device with non-negligible advantage under the q-SDH assumption. Thus, the proposed scheme satisfies the anonymity requirement by rendering the signatures indistinguishable and untraceable to specific devices for all parties except the group manager. □

6. Experimental Evaluation

6.1. Experimental Setup

To evaluate the practicality of our scheme, we compare it with cross-domain schemes: CCAP [3], XAuth [16], and BASA [17]. We conducted the experiments on a server platform equipped with an Intel Xeon E5-2683 v3 processor and 225.5 GiB RAM, running Ubuntu 20.04.6 LTS. We used Python 3.9.5 as the programming language and used Charm-Crypto 3.9.4 as the core library. For elliptic curve operations, we utilized the SHA3-256 hash function and selected the MNT224 curve from Charm-Crypto for elliptic curve operations as it provides enhanced security over alternatives such as SS512 and MNT201.

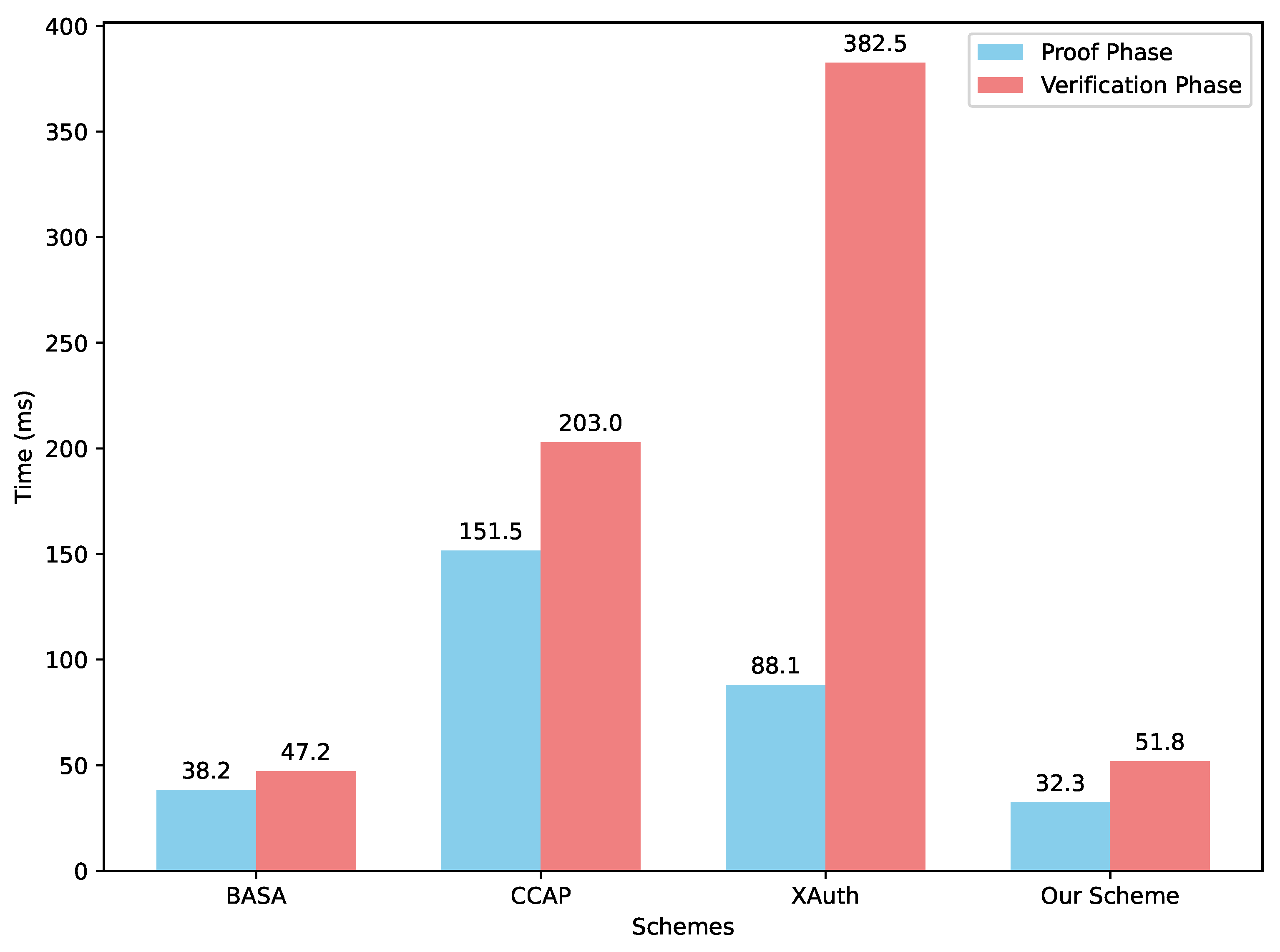
6.2. Computation Cost

The existing cross-domain authentication schemes commonly adopt various cryptographic primitives in their designs, including bilinear mappings, hash functions, scalar multiplication in additive groups, operations in multiplicative groups, and large-integer multiplication. The corresponding notations are summarized in

Table 3. Calculation notations.

Notation	Definition
$T_{BP}$	Bilinear mapping cost: $e:G_1\times G_2\to G_T$
$T_H$	Hash function cost
$T_{GADD}$	Group scalar multiplication cost: $a{P}_1$
$T_{GMUL}$	Group modular exponentiation cost: $g^a$
$T_{ABMUL}$	Large-integer multiplication cost: $a·b$

.

We analyze the theoretical computational costs of each scheme. Due to the large number of cryptographic operations involved in each scheme, we statistically compare only the time-consuming ones. Generally, the overhead of bilinear mappings significantly surpasses other operations, while the costs of hash functions and large-integer arithmetic are negligible. Notably, although XAuth does not explicitly use bilinear mappings, its zero-knowledge proof protocol invokes the Pinocchio protocol, which involves numerous time-consuming computational operations. A detailed comparison of these schemes is illustrated in

Table 4. Time-consuming cryptographic operations.

Scheme	Proof Phase	Verification Phase	Total Process
BASA [17]	$3T_{\mathrm{GMUL}}+1T_{\mathrm{BP}}$	$2T_{GMUL}+1T_{GADD}+2T_{BP}$	$5T_{GMUL}+1T_{GADD}+3T_{BP}$
CCAP [3]	$23T_{\mathrm{GMUL}}+6T_{\mathrm{BP}}$	$25T_{\mathrm{GMUL}}+7T_{\mathrm{BP}}$	$48T_{\mathrm{GMUL}}+13T_{\mathrm{BP}}$
XAuth [16]	$25T_{\mathrm{GMUL}}$	$17T_{\mathrm{GMUL}}+14T_{\mathrm{TBP}}$	$42T_{\mathrm{GMUL}}+14T_{\mathrm{TBP}}$
Our Scheme	$9T_{\mathrm{GADD}}$	$10T_{\mathrm{GADD}}+2T_{\mathrm{BP}}$	$19T_{\mathrm{GADD}}+2T_{\mathrm{BP}}$

.

All experiments were repeated 100 times to ensure data stability, with the averaged results shown in Figure 4. Our scheme achieves a time overhead of 32.3 ms in the proof phase and 51.8 ms in the verification phase, resulting in a total of 84.1 ms. This significantly outperforms CCAP (354.5 ms) and XAuth (470.3 ms).

6.3. Communication Cost

In this section, we compare the communication costs of cross-domain schemes. Specifically, a $G_1$ group element occupies 42 bytes, a $G_2$ group element requires 118 bytes, and a $G_T$ group element consumes 226 bytes. Large integers are represented using 28 bytes. A comparative analysis of the communication overhead across schemes is provided in Figure 5.

Based on the parameters defined above, the corresponding group elements in the following experimental analysis are uniformly calculated. In our scheme, the cross-domain authentication protocol transmits $\sigma =(m,\tau ,c,T_1,T_2,T_3,T_4,Y_1,Y_2,Y_3,z_1,z_2).$ The communication cost of $\sigma$ is $142\times 6+118\times 2+28\times 2+4=548$ bytes. Moreover, the total overhead is approximately 1.3 KB when including communication costs for witness updates, updating the latest accumulator values, and retrieving public parameters. In the XAuth, the cross-domain protocol adopts the Pinocchio protocol to generate proofs, occupying 42 + 8 × 42 = 378 bytes. Combined with parameter retrieval, the total overhead is about 1 KB. For CCAP, the proof $\pi$ requires 13 × 42 + 2 × 226 + 15 × 28 = 1400 bytes. Since CCAP adopts a threshold mechanism, proofs must be sent to verification servers in each domain. If there are t domains, the communication overhead can reach $1.4t$ KB. Given that threshold mechanisms typically require t > 2, we set t = 3 in this experiment. The BASA scheme incurs a proof communication cost of 1536 bytes, with additional parameters raising the total overhead to 1.9 KB.

6.4. Revocation Cost

In this section, we evaluate the dynamic migration capability of our scheme. Without loss of generality, we focus on measuring the device revocation time. To evaluate this performance, we simulate the average revocation time per device under different network scales (100–1000 devices). The comparison results are shown in Figure 6. Specifically, our scheme uses dynamic accumulators for membership management, in which device revocation only requires updating the corresponding accumulator, resulting in a constant time complexity of $O\left(1\right)$, independent of the total number of devices. The average revocation time per device in our scheme remains stable at 10.8 ms, which is lower than other schemes. Experimental data validates the efficiency and scalability of our solution in large-scale IIoT scenarios. Notably, the CCAP scheme preserves the original domain management mechanisms (e.g., PKI). When revoking a device, CCAP requires $O\left(t\right)$ decryption operations (t denotes the number of domains), leading to a linear increase in revocation time as t grows. In BASA, a blockchain-based cross-domain scheme, revocation is carried out by updating the relevant information file and recording the change on the blockchain. As a result, the revocation time increases with the number of devices.

7. Conclusions

In this paper, we propose a novel cross-domain authentication scheme based on group signatures to address the challenges of secure cross-domain authentication in the IIoT. To address the security issues related to cross-domain authentication, our scheme implements anonymous authentication while supporting the tracking and revocation of malicious devices through a trapdoor mechanism. By adopting a dynamic accumulator, our scheme supports constant-time member joining and revocation and adopts a lazy witness update algorithm to reduce computational overhead. Additionally, a blacklist-based non-membership proof mechanism further reduces storage and communication costs. Under the q-SDH assumption, we prove the correctness and security of the proposed scheme. The experimental results demonstrate that our scheme is exceedingly efficient and scalable.