Markov-Chain Perturbation and Approximation Bounds in Stochastic Biochemical Kinetics

Abstract

Markov chain perturbation theory is a rapidly developing subfield of the theory of stochastic processes. This review outlines emerging applications of this theory in the analysis of stochastic models of chemical reactions, with a particular focus on biochemistry and molecular biology. We begin by discussing the general problem of approximate modeling in stochastic chemical kinetics. We then briefly review some essential mathematical results pertaining to perturbation bounds for continuous-time Markov chains, emphasizing the relationship between robustness under perturbations and the rate of exponential convergence to the stationary distribution. We illustrate the use of these results to analyze stochastic models of biochemical reactions by providing concrete examples. Particular attention is given to fundamental problems related to approximation accuracy in model reduction. These include the partial thermodynamic limit, the irreversible-reaction limit, parametric uncertainty analysis, and model reduction for linear reaction networks. We conclude by discussing generalizations and future developments of these methodologies, such as the need for time-inhomogeneous Markov models.

1. Introduction

With the rapid development of systems biology during the last ~25 years, stochastic modeling has become an increasingly common methodology in quantitative molecular and cellular biology [1,2,3,4,5]. This methodology, particularly with its recent and promising focus on reaction networks [6,7,8], is indispensable in studies where the non-deterministic nature of molecular interactions (i.e., random fluctuations or “molecular noise”) can impact biological systems and processes. This is particularly important for systems containing a small number of molecules. As a classic example, we mention ion-channel studies, where single-channel recordings experimentally capture random interconversions between the states of only one protein molecule [9,10,11,12]. Another example is provided by gene-regulation studies, where a cell may contain as few as one or two dozen copies of a transcription factor (i.e., a protein regulating gene expression) [13,14,15]. As our third example, we mention recent studies of antibody binding with multiantigen substrates [16,17].

The most common mathematical tool in such studies is the formalism of continuous-time Markov chains (CTMCs) [1,18,19]. This formalism offers several significant advantages. Indeed, from the chemical physics point of view, it stands on a firm conceptual foundation and is known as the chemical master equation [20,21,22,23]. This is the appropriate methodology for modeling many quantitative phenomena on the mesoscopic scale (i.e., the scale between the macroscopic scale of deterministic equations and microscopic scale of quantum phenomena) [23]. Mathematically, the behavior of CTMCs can be described using systems of linear ordinary differential equations (ODEs) known as the forward Kolmogorov equations, and this allows one to use the powerful ODE theory to study CTMCs. At the same time, the coefficients of these linear equations can exhibit nonlinear dependencies on state variables (which often represent the numbers of molecules for different biochemical species in the system). As a result, the chemical master equation can be used to model arbitrarily complex phenomena in stochastic biochemical kinetics [24].

Going beyond biochemistry, the CTMC formalism can be applied to essentially any system consisting of interacting and interconverting elements (e.g., biological cells or organisms) considered as particles whose dynamics are measured in continuous time (physical time is continuous). The main necessary assumption is that of “memorylessness” of the system, i.e., that its future behavior is independent of the past given the present. In many cases, this assumption can be regarded as satisfied—at the very least, in the first approximation. This makes CTMCs a natural choice of modeling formalism in biological fields as diverse as epidemic modeling [25], ecology [26], and evolution [27]. In fact, biochemical kinetics-type models can be viewed as a universal formalism for stochastic phenomena; indeed, chemical kinetics has been called a “metalanguage” for mathematical modeling [24].

New mathematical developments are crucial for CTMC applications, because many of the analytic or numerical studies involving such models require rigorous and non-trivial methods for model approximation and simplification. The probabilistic nature and special structure of the chemical master equation necessitates the development of approximation methods tailored specifically to CTMCs in general and this equation in particular [28,29,30,31]. Importantly, approximations can be used not merely as a means of computational convenience, but as a systematic way to implement fundamental physics-based concepts, such as the thermodynamic limit [32]. Several relevant methodologies have been developed and are briefly reviewed in the next section. However, one general and powerful type of approximation has not yet received sufficient attention in the biokinetics context: approximation of one CTMC by another CTMC (possibly having a simpler structure) on the same state space. This may be the most straightforwardly formulated type of approximation problem, and the range of possible applications is vast.

Here, the main idea is that one CTMC can be regarded as an unperturbed Markov chain, whereas the other is regarded as a perturbed one. Given the magnitude of the perturbation in the CTMC parameters, we are interested in estimating (i.e., obtaining a bound on) the nearness of the two CTMCs’ outputs. The main advantage of this approach is twofold. First, it allows one to obtain explicit and computable perturbation and approximation bounds, which can elucidate the role of specific system parameters in shaping the accuracy of the approximation under study. Second, it provides one with an accuracy guarantee for that approximation. Fortunately, some interesting and insightful mathematics for it is available. The purpose of this review is to introduce this methodology and discuss some of its current and emerging applications.

2. Continuous-Time Markov Chains, Approximations, and Perturbation Bounds

2.1. Approximation Approaches for the Chemical Master Equation

The importance of approximations is illustrated by their diversity and by the depth of the underlying mathematical and computational approaches [20,29,33,34,35,36]. A classic example of approximation is the thermodynamic limit, where it is assumed that the volume of the reaction compartment, as well as the numbers of molecules for all the chemical species, tend to infinity (while the species’ concentrations approach finite limits) [33,37]. The limiting kinetics in such a system are described by a system of ODEs for the species’ concentrations. A related approach is diffusion approximation, which occupies an intermediate position between the master equation (i.e., the CTMC model) and the corresponding ODE model in the thermodynamic limit [37,38,39].

A more nuanced approach is related to the use of hybrid-modeling algorithms, where some of the molecular species follow ODE-driven kinetics, whereas others evolve according to a CTMC-type stochastic mechanism [40,41]. Such algorithms have been developed to address the need for faster numerical schemes to simulate stochastic chemical models with very large numbers of molecules. Theoretical justification for such algorithmic approaches was achieved by the introduction and analysis of partial thermodynamic limits, where only some of the chemical species in the reaction compartment are subjected to the infinite-volume and infinite-molecule-number limit [42,43]. The corresponding general theory is somewhat related to the type of perturbation analysis that we consider here. Yet, it only addresses one type of perturbations (specifically, partial thermodynamic limits) and the error bounds are qualitative (i.e., they indicate a convergence rate, but the associated constants are not explicitly computable) [42]. In this article, we will provide an example of fully quantitative perturbation analysis for the partial thermodynamic limit.

This review is focused on perturbations that modify a CTMC’s transition rates. By contrast, another prominent approach focuses on cases where model reduction results in a CTMC with a smaller state space. This approach, termed state-space truncation, plays a role in both general CTMC theory and stochastic modeling of (bio)chemical systems [44,45,46]. A related approach, also leading to a reduced state space, involves aggregation of several states of the original CTMC into one. Such state lumping has been characterized by explicit error bounds [47,48], and applications of those results to stochastic biomolecular systems would be of interest.

2.2. Continuous-Time Markov Chains and the Chemical Master Equation

In this subsection, we provide basic notation and assumptions pertaining to CTMCs; see, e.g., Ref. [19] for a background on Markov chain theory. Consider a CTMC denoted by $X=\{X\left(t\right), t\ge 0\}$ and defined on a finite state space $S=\{0,1,\dots ,N\}$ $(1\le N<\infty )$. For $X$ representing the kinetics of a well-mixed (bio)chemical system, $N<\infty$ implies that the total number of molecules of interest in the system is finite. This condition significantly simplifies the analysis but can, in principle, be relaxed. The temporal behavior of $X$ is a sequence of random jumps between its states, and a jump from state $i$ to state $j$ $(i\ne j)$ occurs at a rate $q_{ij}\ge 0$ (here assumed independent of time: we are analyzing time-homogeneous CTMCs). If the Markov chain models a chemical reaction, then the jumps between the states represent changes in the number of molecules in the system. Such changes are caused by random molecular collisions, which lead to random redistribution of energy, so that at some point some molecule(s) accumulate enough energy for a reaction to occur.

The matrix $\mathit{Q}=\left(q_{ij}\right)$ is the transition-rate matrix (also termed the generator) of $X$. (The off-diagonal entries of $\mathit{Q}$ are defined as described, and the diagonal entries are chosen so that all the row sums are equal to zero). The main characteristic of the chain $X$ is its state-probability vector $\mathit{p}\left(t\right)=\left(p_i\right(t\left)\right)$, $i\in S$ (following a common convention, here we regard vectors as row vectors, so matrices are multiplied by vectors via left multiplication). Here, $p_i\left(t\right)$ is the probability that the chain $X$ will be in state $i$ at time $t$. Given the initial condition $\mathit{p}\left(0\right)$, the state-probability vector can be determined by solving the forward Kolmogorov equation:

$${\displaystyle \frac{d\mathit{p}\left(t\right)}{dt}}=\mathit{p}\left(t\right)\mathit{Q}.$$

We will regard the chain $X$ as an unperturbed chain and will also consider a perturbed chain $\tilde{X}=\{\tilde{X}\left(t\right), t\ge 0\}$ with generator $\tilde{\mathit{Q}}$ and state-probability vector $\tilde{\mathit{p}}\left(t\right)$. Thus, $\mathit{E}≔\tilde{\mathit{Q}}-\mathit{Q}$ ($\mathit{E}\ne \mathbf{0}$), with entries $e_{ij}$, is the perturbation in the generator, and $\mathit{z}\left(t\right)≔\tilde{\mathit{p}}\left(t\right)-\mathit{p}\left(t\right)$ is the perturbation in the state-probability vector. To measure the magnitude of these perturbations, we will choose a norm for vectors and matrices. It will be convenient to use the $l_1$ norm for vectors ($‖\mathit{v}‖={\sum }_i\left|v_i\right|$); this is one of the most frequently used norms in both matrix analysis and probability theory (where it leads to the widely used total variation distance between distributions) [49]. For matrices, we will use the corresponding subordinate norm ($‖\mathit{A}‖=\underset{i}{\max }{\sum }_j\left|a_{ij}\right|$).

This choice of norm allows one to obtain informative bounds and even explicit expressions for the magnitude of the perturbation in the generator. Let ${\mathit{E}}_0$ be the matrix obtained from $\mathit{E}$ by replacing all the diagonal entries with zeros. It turns out that the norm of this matrix provides a straightforward way to gauge the perturbation magnitude, as we will show in the next two sections. This is made possible via the following Assertion 1 (see Ref. [50] for the proof).

Assertion 1.

For the generator perturbation, the following bound holds:

$$‖\mathit{E}‖\le 2‖{\mathit{E}}_0‖.$$

In this inequality, equality is achieved if, in every row of $\mathit{E}$, the non-zero off-diagonal entries (if they are present) are either all negative or all positive.

If the chain $X$ describes changes in the state of one biomolecule (e.g., its different conformations or activity levels), then the values of the transition rates $q_{ij}$ is all we need to know to study the dynamics of the system. However, often each element of the state space $S$ corresponds to the state of a multi-molecule and multi-species system, with each state represented by a vector whose entries reflect the numbers of molecules for the different molecular species in the reaction compartment. In this case, the transition rates are multi-variable functions of these numbers of molecules, and they also depend on the rate constants defining the rates of the corresponding biochemical reactions. If the Kolmogorov equation is written in a form that explicitly accounts for such multidimensional states, then this equation is the “canonical” chemical master equation for the system [20,21,32].

Importantly, however, even if we are modeling a multi-species molecular system, the use of the full multidimensional representation for the transition rates is not always necessary. Indeed, in some cases the state space of the chemical master equation can be reparametrized in a way that makes the system state depend on only one variable (e.g., the number of molecules for only one molecular species). One such example of general importance in biological modeling is birth–death processes, which are CTMCs with a tri-diagonal generator [51,52]. Birth–death processes can be used to model systems with one or more molecular species, and we will see examples of such models in the next section.

2.3. Markov Chain Convergence to Steady State

For the examples of perturbation and approximation results considered in this article, we need to make one additional assumption. Specifically, we will assume that the stationary distribution (also called the steady state) $\mathit{\pi }=\left({\pi }_i\right)$ of the unperturbed Markov chain $X$ is unique, which is equivalent to the uniqueness of an irreducible class of states for $X$. In applications, this is perhaps the most encountered situation. In the context of chemical reactions, a unique stationary distribution can be logically associated with the uniqueness of chemical equilibrium in the system. Even if the system is multistable, the stationary distribution can still be unique (in which case it is likely to be multimodal) [24].

One particularly important special case where such uniqueness holds is reversible Markov chains. Reversibility is essential for modeling biomolecular systems because it corresponds to the physical requirement of detailed balance [23,53]. By definition, the CTMC $X$ is reversible if it is irreducible (i.e., each state is reachable from each other state, implying ${\pi }_i>0$ for every $i\in S$) and, for all $i,j\in S$, the following reversibility condition holds:

$${\pi }_i{q}_{ij}={\pi }_j{q}_{ji}.$$

(1)

See, e.g., Refs. [53,54,55,56] for a background on reversibility in molecular systems. Importantly, note the difference between this definition and the definition of an (ir)reversible chemical reaction, which we will discuss in the next section.

In the general case, Equation (1) imposes certain constraints on the values of the transition rates and leads to equations that need to be solved to define the transition rates consistently [53,56]. However, in one special case the reversibility condition holds for arbitrary values of the transition rates: birth–death processes with all-positive birth and death rates (more generally, this holds for any CTMC whose transition graph is a tree [56]). The chain $X$ is a birth–death process if the only positive transition rates (i.e., off-diagonal entries of the generator) are the birth rates ${\lambda }_i≔q_{i,i+1}$ and the death rates ${\mu }_i≔q_{i,i-1}$, $i\in S$ (naturally, ${\lambda }_N={\mu }_0=0$).

The unique stationary distribution $\mathit{\pi }$ is the probability vector satisfying the equation $\mathit{\pi }\mathit{Q}=\mathbf{0}$. Importantly, the convergence to the stationary distribution is exponential: there exist positive real numbers $b, C$ such that

$$‖\mathit{p}\left(t\right)-\mathit{\pi }‖\le C{e}^{-bt} \mathrm{for} \mathrm{all} t\ge 0 \mathrm{and} \mathrm{all} \mathit{p}\left(0\right),$$

(2)

and this bound implies that $C\ge 1$. (Equation (2) can be proved in a number of ways; one way is to use the spectral decomposition for the solution of the Kolmogorov equation [57], which is analogous to the spectral decomposition for discrete-time Markov chains [58]). Convergence bounds of this type have been an active research topic, and many such results are available [49]. One relevant example is the following bound [57]:

$$‖\mathit{p}\left(t\right)-\mathit{\pi }‖\le K{e}^{-\lambda t},$$

(3)

where $\lambda$ is the spectral gap of the generator $\mathit{Q}$ (i.e., the smallest absolute non-zero real part among all the eigenvalues of $\mathit{Q}$) and $K=\kappa \left(\mathit{X}\right)-1$; here, $\kappa \left(\mathit{X}\right)≔‖\mathit{X}‖‖{\mathit{X}}^{-1}‖$ is the condition number of $\mathit{X}$, which is a matrix that diagonalizes $\mathit{Q}$. Equation (3) holds under the assumption that the generator $\mathit{Q}$ is diagonalizable. This assumption is not restrictive, because, for many matrices arising in applications (including all reversible Markov chains), the multiplicity of every eigenvalue equals 1, which is sufficient for diagonalizability. Because every square matrix is infinitely close to a matrix with distinct eigenvalues [59], this case may be regarded as the “most typical” in practice, which lends wide applicability to Equation (3). An additional advantage of Equation (3) is that it links the rate of convergence to the stationary distribution with the sensitivity of the spectral gap $\lambda$, because $\kappa \left(\mathit{X}\right)$ is known to be a condition number for the eigenvalues of the generator $\mathit{Q}$ [57].

The quantities $b$ and $C$ generally depend on the individual transition rates $q_{ij}$ in a complicated way. Would it be possible to obtain a convergence bound that depends on the $q_{ij}$ values in an explicit way? That would provide a formula with an analytical dependence on the rate constants for the reactions involved, which in turn could yield valuable insights. It turns out that this is indeed possible if the chain $X$ is a birth–death process.

If $X$ is a birth–death process, then it is defined by the set of birth rates ${\lambda }_i$ and death rates ${\mu }_i$. Consider the following quantity:

$$\alpha ≔\underset{0\le i<N}{\min }\left({\lambda }_i+{\mu }_{i+1}-{\lambda }_{i+1}-{\mu }_i\right).$$

If $\alpha >0$ then, combining Proposition 1 of Ref. [60] with the bound $‖{\mathit{p}}_1-{\mathit{p}}_2‖\le 2$ (which holds for any two probability vectors), we obtain the following convergence bound:

$$‖\mathit{p}\left(t\right)-\mathit{\pi }‖\le 8N{e}^{-\alpha t}.$$

(4)

Importantly, this bound can be generalized to the time-inhomogeneous case [60] and to the case of infinite state spaces [61,62], which are important next steps to take in the development of perturbation-analysis methodology. Interestingly, many such results were originally obtained in the context of queuing theory, and recently it became clear that queuing theory is applicable to stochastic biomolecular models [63,64]. This paradigm appears to be worthy of further exploration.

2.4. Perturbation Bounds for Continuous-Time Markov Chains

Perturbation theory for Markov chains in general is a growing field, and the results for CTMCs have recently been reviewed [49,65]. Whereas several approaches to bounding CTMC perturbations exist, we will illustrate the available options by discussing examples that we regard as particularly instructive. One such bound is provided by the following expression (with the quantities $b$ and $C$ taken from Equation (2)) [57]:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le ‖\mathit{z}\left(0\right)‖+b^{-1}\left(\log C+1\right)‖\mathit{E}‖.$$

(5)

The use of this perturbation bound has several direct advantages, as follows. (1) It has a very compact, easy-to-analyze form. (2) It is sharp in the sense that, in certain cases, equality is achieved in it [49]. (3) It has a logically clear interpretation, showing that the main determinant of the (in)sensitivity of $X$ to perturbations is its rate of exponential convergence to stationarity. (4) It is applicable to both short- and long-time dynamics; because it holds uniformly over $t\ge 0$, we do not need to be concerned about what time scale we are analyzing. (5) It holds for both small and large perturbation magnitudes. Indeed, in many practical problems, $‖\mathit{z}\left(0\right)‖$ and $‖\mathit{E}‖$ will be assumed to be small, but the bound itself holds with no restrictions on perturbation magnitudes. (6) It can be generalized to cases where the perturbation magnitude $‖\mathit{E}‖$ and/or the generator $\mathit{Q}$ can vary over time (i.e., to time-inhomogeneous CTMCs) [65].

The parameter $b$ is the main determinant of robustness, but Equation (5) requires another parameter (i.e., $C$) to be known. Would it be possible to obtain a perturbation bound as general as Equation (5) but requiring only one parameter to be determined? This can be achieved through the use of ergodicity coefficients [66]. Let $\mathit{P}\left(t\right)≔\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathit{Q}t\right)$, with entries $p_{ij}\left(t\right)$, be the transition-probability matrix of the chain $X$. Then the $l_1$ ergodicity coefficient of $\mathit{P}\left(t\right)$, denoted $\beta \left(t\right)$, is defined as follows:

$$\beta \left(t\right)≔\underset{‖\mathit{x}‖=1, \mathit{x}{1}^{\prime }=0}{\sup }‖\mathit{x}\mathit{P}\left(t\right)‖={\displaystyle \frac{1}{2}}\underset{i,j}{\max }\sum _k\left|p_{ik}\left(t\right)-p_{jk}\left(t\right)\right|,$$

where $\mathbf{1}$ is a row vector of all 1s and ${\mathbf{1}}^{\prime }$ is its transpose. Under the assumption of stationary-distribution uniqueness, the following perturbation bound holds [51]:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖<‖\mathit{z}\left(0\right)‖+{\displaystyle \frac{s}{1-\beta \left(s\right)}}‖\mathit{E}‖.$$

(6)

Here, the number $s>0$ is arbitrary, and its choice completely determines the magnitude of the bound for the given $\mathit{Q}$ and the given perturbation magnitudes. An extra benefit of this bound is that its condition number (i.e., $s/(1-\beta (s)$) also determines the robustness of the ergodicity coefficient $\beta \left(t\right)$ itself to perturbations in $\mathit{Q}$ [50].

In theory, not all time-homogeneous CTMCs have a unique stationary distribution. In cases of non-uniqueness, one could use a generic CTMC perturbation bound (uniform over a finite time interval) that only depends on a characteristic time of this CTMC’s temporal behavior, which can be estimated using the available heuristic or empirical knowledge about the modeled system [49]. Moreover, some chemical-reaction systems need to be modeled using CTMCs with an infinite state space (e.g., the famous Schlögl model [67,68]). One possibility is to use perturbation bounds developed specifically for birth–death processes on an infinite state space [62]. Another plausible approach is to use the concept of hierarchical (or combined) approximation: first, reduce the model to a finite state space using state-space truncation, and then apply a finite-state-space perturbation bound to the reduced model.

3. Approximations and Perturbations for Individual Biochemical Reactions

Biomolecular networks consist of elementary (or individual) reactions, each of which is characterized by a single rate constant or two rate constants—forward and reverse—if the reaction is reversible. Irreversible reactions run in only one direction (i.e., from the reactants to the products), whereas reversible reactions also run in the opposite direction. (See, e.g., Refs. [1,24,69] for a background on deterministic and stochastic biochemical kinetics). Elementary reactions are reactions such as irreversible decay of molecular species $A$ ($A\to \varnothing$), reversible isomerization between molecular species $A$ and $B$ ($A\rightleftharpoons B$), reversible dimerization ($2A\rightleftharpoons A_2$), and so on. Because ternary (or higher-order) molecular collisions generally are very rare, such elementary reactions are typically unimolecular or bimolecular in models that are truly mechanistic [24] (in phenomenological models, this rule can be relaxed, which is the case, e.g., for the Schlögl model [67,68]). Each of such reactions may look simple, but the molecular networks they form can be arbitrarily complex. Because individual reactions act as “building blocks” of biomolecular networks, some of the network properties are likely to be strongly influenced by individual reactions. The examples in this section illustrate how such reactions can be studied using perturbation bounds.

3.1. An Illustrative Example: The Formation and Dissociation of Binary Complexes

Our main example will be the reaction $A+B \begin{array}{c}{k}_{+}\\ \rightleftharpoons \\ k_{-}\end{array} AB$, which reflects formation and dissociation of binary complexes $AB$. This appears to be the first biochemical reaction that was analyzed using perturbation-type bounds [43]; now that new theoretical tools are available, it is well worth revisiting. This reaction is of utmost importance for molecular biology, exemplified by binding of ligands to cellular receptors [70] and binding of regulatory proteins (transcription factors) to DNA [71] (analyzed in some detail as an example in the next section). We can model the number of $AB$ complexes in the reaction compartment as a birth–death process, $Y^{\left(quad\right)}$, on the state space $S=\{0,1,\dots ,N\}$ (the designation “quad” is motivated by the birth rates being a quadratic function of the state of the process). This process is defined by birth rates ${\lambda }_i^{\left(quad\right)}=(k_{+}/V)(M-i)(N-i)$ and death rates ${\mu }_i^{\left(quad\right)}=k_{-}i$, $i\in S$. Here, $V$ is the volume of the reaction compartment; $k_{+}$ and $k_{-}$ are the forward and reverse reaction rate constants, respectively (assumed positive); $M$ and $N$ are the total numbers of molecules (i.e., either free or bound in a binary complex) of species $A$ and $B$, respectively (without loss of generality, we assume $M\ge N$). In addition to this model, let us introduce a simplified model, $Y^{\left(lin\right)}$, for the same reaction. This simplified model is a birth–death process with linear transition rates: ${\lambda }_i^{\left(lin\right)}=k_{+}a(N-i)$, where $a≔M/V$, and ${\mu }_i^{\left(lin\right)}=k_{-}i$. One valuable mathematical result about this process (regarded as the unperturbed chain $X$) is the following convergence bound [57]:

$$‖\mathit{p}\left(t\right)-\mathit{\pi }‖\le 8N{e}^{-(k_{+}a+k_{-})t},$$

(7)

which is a special case of Equation (4). We will use this bound in the perturbation analyses described below. It is interesting to note that, for the state probabilities of the $Y^{\left(quad\right)}$ process, analytic expressions are known, but they are so complex that they can hardly be used in practice [72]. By contrast, the analytic expressions for the process $Y^{\left(lin\right)}$ are considerably more tractable and useful even in the time-inhomogeneous case [73]. The process $Y^{\left(lin\right)}$, known as the Prendiville process in applied probability [73], is the continuous-time analog of the celebrated Ehrenfest model in statistical physics [74].

3.2. Partial Thermodynamic Limit

In the binary-complex formation reaction $A+B\rightleftharpoons AB$ introduced above, the species $A$ may often be present in excess amount ($M\gg N$), so that its concentration during the reaction changes very little and the model $Y^{\left(lin\right)}$ could be nearly as accurate as $Y^{\left(quad\right)}$. In that case, how close are the state probabilities of these two models? This question can be answered by considering the partial thermodynamic limit (originally termed “one-species thermodynamic limit” [43]) as $M,V\to \infty$ with the value of $a$ fixed. Resorting to perturbation analysis, regard the processes $Y^{\left(lin\right)}$ and $Y^{\left(quad\right)}$ as the unperturbed and perturbed chains, respectively; thus, using our notation introduced earlier, we can set $X=Y^{\left(lin\right)}$ and $\tilde{X}=Y^{\left(quad\right)}$. This allows us to write expressions for the transition-rate perturbations:

$$e_{i,i+1}={\tilde{q}}_{i,i+1}-q_{i,i+1}={\lambda }_i^{\left(quad\right)}-{\lambda }_i^{\left(lin\right)}=-{\displaystyle \frac{k_{+}}{V}}i\left(N-i\right); e_{i,i-1}={\mu }_i^{\left(quad\right)}-{\mu }_i^{\left(lin\right)}=0.$$

We can use these expressions to explicitly calculate the quantity $‖{\mathit{E}}_0‖$ in Assertion 1; the calculation follows straightforwardly from our definition of the matrix norm. Then, using Assertion 1, we obtain a bound on the generator-perturbation magnitude:

$$‖\mathit{E}‖=2‖{\mathit{E}}_0‖={\displaystyle \frac{{2k}_{+}}{V}}\underset{i=0,1,\dots ,N}{\max }i\left(N-i\right)\le {\displaystyle \frac{{2k}_{+}}{V}}\underset{x\in \left[0,N\right]}{\max }x\left(N-x\right)={\displaystyle \frac{k_{+}{N}^2}{2V}}$$

Combining this with the convergence bound in Equation (7) and the perturbation bound in Equation (5), and assuming $‖\mathit{z}\left(0\right)‖=0$ (for simplicity), we get an explicit bound quantifying the rate of convergence in the partial thermodynamic limit:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le \left(\log \left(8N\right)+1\right){\displaystyle \frac{k_{+}{N}^2}{2V\left(k_{+}a+k_{-}\right)}}.$$

Note that the left-hand side of this bound characterizes the sum of all the perturbations in the probabilities of the individual states. It could be more informative to use the normalized distance $‖\mathit{z}\left(t\right)‖/(N+1)$, which characterizes the average perturbation magnitude for a state probability. If this distance is used, then the dependency of the right-hand side of the approximation bound on $N$ becomes essentially linear (if we ignore the additional weak logarithmic dependence). This implies that the bound is informative when $N$ is sufficiently small compared to $V$, which is naturally satisfied because, by assumption, $V/M=1/a=O\left(1\right)$ and $N/M=o\left(1\right)$. The obtained approximation bound can be used to find the threshold value of $V$ beyond which the deviations between the quadratic and linear models can be neglected (i.e., the partial thermodynamic limit is practically achieved).

3.3. Irreversible-Reaction Limit

The approach from the previous subsection can be naturally extended to other types of approximations viewed as perturbations. Let us now consider the case where the simplified CTMC represents an irreversible reaction, i.e., where its forward or its reverse reaction rate is equal to zero. (Note the contrast between this notion of an irreversible chemical reaction and the definition of an irreversible Markov chain, which is simply a Markov chain for which the condition of reversibility in Equation (1) is not satisfied).

Consider the process${ Y}^{\left(lin\right)}$, for which one of the rate constants—say, $k_{-}$—is assumed very small. If we actually set it equal to zero, then the resultant process, denoted $Y^{\left(bir\right)}$, is a pure birth process with birth rates equal to those for the process ${ Y}^{\left(lin\right)}$ (i.e., the binary complexes $AB$ are formed but do not dissociate). To perform perturbation analysis, designate the processes $Y^{\left(bir\right)}$ and $Y^{\left(lin\right)}$as the unperturbed and perturbed chains $X$ and $\tilde{X}$, respectively. In a way similar to the above, we can write the expressions for the off-diagonal perturbation-matrix entries:

$$e_{i,i+1}=0; e_{i,i-1}{=\tilde{q}}_{i,i-1}-q_{i,i-1}={\mu }_i^{\left(lin\right)}-{\mu }_i^{\left(bir\right)}=k_{-}i.$$

Consequently (using Assertion 1), we have

$$‖\mathit{E}‖=2k_{-}\underset{i=0,1,\dots ,N}{\max }i=2k_{-}N.$$

(8)

For the unperturbed pure-birth process $Y^{\left(bir\right)}$, we can use the approach from Ref. [61] and obtain an explicit convergence bound:

$$‖\mathit{p}\left(t\right)-\mathit{\pi }‖\le 8N{e}^{-k_{+}at}$$

(9)

(note that this bound follows directly from Equation (7) by setting $k_{-}=0$). Combining Equation (9) with the expression in Equation (8) for the perturbation magnitude and with the perturbation bound in Equation (5) (and again, setting $‖\mathit{z}\left(0\right)‖=0$), we obtain the approximation bound

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le \left(\log \left(8N\right)+1\right){\displaystyle \frac{2k_{-}N}{k_{+}a}}.$$

(10)

If, as above, we prefer to use the normalized distance $‖\mathit{z}\left(t\right)‖/(N+1)$, then the right-hand side of the corresponding approximation bound will depend on $N$ only logarithmically. As should naturally be expected, this irreversible-reaction approximation is accurate not only when $k_{-}$ is near zero, but when it is small relative to $k_{+}a$.

In this particular example, we could have reversed our choice of unperturbed and perturbed chains by regarding the processes $Y^{\left(lin\right)}$ and $Y^{\left(bir\right)}$ as chains $X$ and $\tilde{X}$, respectively. Then, by taking steps analogous to the above, we would have arrived at the following approximation bound:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le \left(\log \left(8N\right)+1\right){\displaystyle \frac{2k_{-}N}{{(k}_{+}a+k_{-})}}.$$

Because the denominator on the right-hand side includes $k_{-}$, this bound is sharper than Equation (10), and therefore should be preferred. In this case, even though the unperturbed process has a more complex structure (birth–death rather than pure birth), the availability of an explicit convergence bound for it (Equation (7)) makes it possible for us to choose between the two ways to approach this problem.

3.4. Parametric Uncertainty Analysis

Continuing the analysis from the previous subsection, consider the pure birth process $Y^{\left(bir\right)}$ and assume that the value of its (forward) rate constant, $k_{+}$, is not known with certainty (typically due to a measurement error). More specifically, assume that the true parameter value, $k_{+}^{\left(true\right)}$, lies somewhere in the interval $[k_{+}-∆, k_{+}+∆]$, where $0<∆<k_{+}$. Let $Y^{\left(true\right)}$ be a pure birth process with birth and death rates ${\lambda }_i^{\left(true\right)}=k_{+}^{\left(true\right)}a(N-i)$ and ${\mu }_i^{\left(true\right)}={\mu }_i^{\left(bir\right)}=0$, respectively. How good is $Y^{\left(bir\right)}$ as an approximation to $Y^{\left(true\right)}$? Let us regard $Y^{\left(bir\right)}$ and $Y^{\left(true\right)}$ as the unperturbed and perturbed chains $X$ and $\tilde{X}$, respectively. Similarly to the above, we can write

$$e_{i,i+1}={\tilde{q}}_{i,i+1}-q_{i,i+1}={\lambda }_i^{\left(true\right)}-{\lambda }_i^{\left(bir\right)}=\left(k_{+}^{\left(true\right)}-k_{+}\right)a\left(N-i\right); e_{i,i-1}=0.$$

Therefore (by Assertion 1),

$$‖\mathit{E}‖=2a\left|k_{+}^{\left(true\right)}-k_{+}\right|\underset{i=0,1,\dots ,N}{\max }(N-i)\le 2a∆N.$$

Using our convergence bound in Equation (9) for $Y^{\left(bir\right)}$ and combining it with the perturbation bound in Equation (5) (with $‖\mathit{z}\left(0\right)‖=0$), we obtain the following approximation bound:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le \left(\log \left(8N\right)+1\right){\displaystyle \frac{2∆N}{k_{+}}}.$$

As we can see, the structure of this bound is somewhat similar to Equation (10). However, for the parametric uncertainty analysis (unlike the irreversible-reaction limit), we only have one reasonable choice of the unperturbed process: the one whose forward-reaction rate constant corresponds to the middle of the parameter-variation interval.

3.5. Other Approximations, Individual Reactions, and Reaction Networks

The approximations considered above give us a glimpse of the perturbation-type analyzes that are possible for stochastic models. The simplest possible perturbation modifies the value of only one off-diagonal entry of the generator matrix. But in principle, any combination of off-diagonal generator entries can be perturbed, and the resultant $‖\mathit{E}‖$ calculated or bounded. If we are using the perturbation bound in Equation (5), then the essential component is an informative convergence bound for the unperturbed CTMC. In the context of individual reactions, such bounds are known for the reactions $A+B\rightleftharpoons C$, $A+B\rightleftharpoons C+D$, $A+B\rightleftharpoons 2C$, and $A\rightleftharpoons 2C$ [60]. Using the same methodology, one could derive convergence bounds for many more reaction schemes that can be modeled as a birth–death process. Note that even a reaction network (i.e., a system of several individual reactions) can in certain situations be modeled by a birth–death process (e.g., if some of the biochemical species in the reaction compartment are present in excess amounts) [67,75,76]. Convergence bounds for some generalizations of birth–death processes are also available (e.g., Ref. [77]).

4. Linear Reaction Networks

A (bio)chemical reaction network is a system of several (potentially, many) individual reactions that are coupled (i.e., occur in the same reaction compartment and share some of the reactants). Perhaps the simplest example of a multi-species reaction network is a network in which each reaction rate is a linear function of only one species concentration (such reactions are also known as first-order reactions). Of these, the most basic example is a network of unimolecular reactions, i.e., reactions of the type $A\to B$ or $A\rightleftharpoons B$. More generally, some (or all) of the reactions involved may be pseudo-first-order, which means that their reaction rates may depend on some species concentrations that remain constant and thus are factored into the linear-reaction rate constant. See Refs. [1,69] for a basic background on linear reaction networks, and Refs. [78,79] for an advanced analysis.

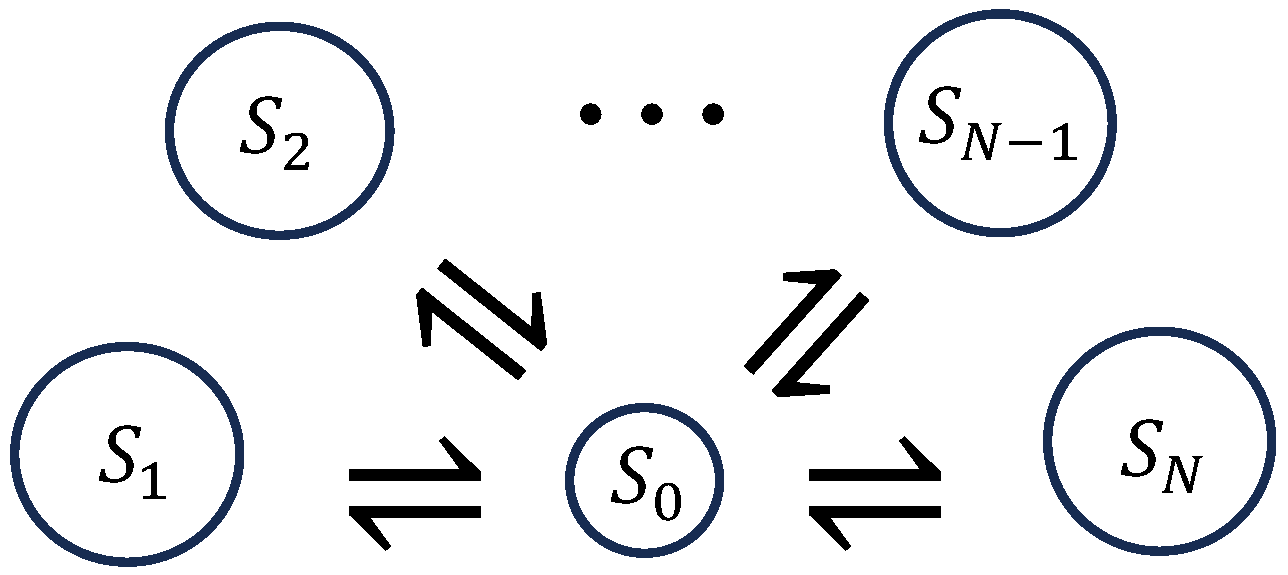
4.1. Networks of Unimolecular Reactions

Networks of unimolecular reactions represent several unimolecular chemical reactions occurring in the same reaction compartment. For such a network, we can have different numbers of distinct biochemical species, different numbers of molecules for each of them, and different patterns (i.e., topologies or “architectures”) of inter-species transitions. For example, the two reaction schemes in Figure 1 each represent a four-species unimolecular reaction network with participating species $A, B, C, D$, but their topologies are obviously different. Note that each of the topologies in Figure 1 represents a possible transition graph for an ion-channel model [9].

Assume that the reaction compartment can contain $N+1$ chemical species denoted $S_0, S_1,\dots , S_N.$ The canonical master-equation representation of the kinetics of the corresponding unimolecular reaction network is a CTMC whose states are $(N+1)$-dimensional vectors representing the numbers of molecules for each of the $N+1$ chemical species in the system [20,21,32]. Denote these counts by $n_0\left(t\right), n_1\left(t\right), \dots , n_N\left(t\right)$ (naturally, these numbers depend on the time variable, $t$). The structure of this CTMC’s generator reflects allowed transitions between states coded as $(N+1)$-dimensional vectors and, consequently, is rather involved. However, there is a much simpler way to represent the stochastic kinetics of such a chemical system.

Indeed, consider one of the molecules in the reaction compartment. Because all reactions are unimolecular, the molecule’s direct or indirect interconversions to and from all other possible molecular species can be represented by a much smaller CTMC—one with a “one-dimensional” state space $S=\{0, 1, \dots , N\}$, where state $i$ represents species $S_i$. The transition graph of this CTMC (i.e., the graph of possible one-step transitions between states [56]) has the same graph structure as the topology of the whole unimolecular reaction network, and the CTMC’s transition rates are equal to the rate constants of the corresponding unimolecular reactions. Thus, we can model all the possible random transitions of each molecule in the network using independent instances of the same CTMC (in this section, we will call it the core CTMC). Because all the molecules in the reaction compartment are assumed to behave independently from one another, we can then obtain a closed-form representation for the full probability distribution of all the molecule numbers in the reaction compartment via a multinomial-distribution formula [69,80]:

$$\mathit{P}\left\{n_0\left(t\right)=x_0, n_1\left(t\right)=x_1, \dots n_N\left(t\right)=x_N\right\}={\displaystyle \frac{K!}{x_0!x_1!\dots x_N!}}{p}_0^{x_0}\left(t\right)p_1^{x_1}\left(t\right)\dots p_N^{x_N}\left(t\right).$$

(11)

Here, the probability on the left-hand side is the probability that the numbers of molecules $n_0\left(t\right), n_1\left(t\right), \dots , n_N\left(t\right)$ will have the specific values $x_0, x_1,\dots , x_N$, respectively, and $K$ equals $x_0+x_1+\dots +x_N$ (i.e., the total number of molecules in the reaction compartment, which does not change). The values $p_i\left(t\right)$ are the probabilities that an individual molecule will be of species $S_i$ (equivalently, that the core CTMC will be in state $i$) at time $t$. The probabilities $p_i\left(t\right)$ do not explicitly depend on the initial state of each molecule, because the derivation of this formula assumes that all the molecules at time $t=0$ existed in the same state (i.e., were of the same chemical species). Obviously, this is a special case, but it is sufficient for our purposes.

4.2. Perturbation Analysis for Unimolecular Reaction Networks

Equation (11) shows that the full distribution of the numbers of molecules for all the chemical species in the reaction compartment depends on the reaction rate constants only via the probabilities $p_i\left(t\right)$ of the core CTMC. Therefore, if we wish to analyze the sensitivity of the reaction network to perturbations in the rate constants (the most common sensitivity-analysis problem), then it could be sufficient to analyze the sensitivity of the core CTMC. That, in turn, can be straightforwardly done using the array of available perturbation bounds, such as Equations (5) and (6) (setting $‖\mathit{z}\left(0\right)‖=0$), if the stationary distribution of the core CTMC is unique. Going beyond generic bounds, one could choose to use the bounds tailored to the specific situation at hand. For example, one could use a perturbation bound derived specifically for reversible CTMCs [81], because the core CTMC is likely to be reversible [53]. Another possible special case is the core CTMC that has a strongly accessible state (i.e., a state reachable from every other state in one transition). For such chains, perturbation bounds are available that directly and explicitly connect the chain’s sensitivity with the entries of its generator [82]. We consider a core CTMC with a strongly accessible state in the example below, which is taken from the domain of gene regulation. The general idea for this application has been introduced earlier [82], but here we present a more focused and detailed analysis.

4.3. A Biological Example: Competitive Transcription-Factor Binding to DNA

This molecular-biology example pertains to the basic mechanisms of gene-transcription regulation in a living cell (see, e.g., Refs. [14,83] for a relevant background). Briefly, for a DNA segment representing a functional gene, the transcription process is the synthesis of an mRNA molecule corresponding to the gene, which ultimately leads to the synthesis of the gene’s protein product. We will assume that the mRNA synthesis is possible only if a regulatory protein, known as a transcription factor (TF), is bound to the DNA upstream of the gene. (Thus, such a TF is a transcription activator; transcription repressors also exist and can be analyzed in an analogous way). TFs bind to special DNA sequences termed binding sites, and sometimes different TF species can bind with the same binding site (a phenomenon known as TF competition; see, e.g., Ref. [71]). We are interested in a quantitative analysis of mRNA-synthesis activation in this scenario.

Consider a reaction compartment containing DNA fragments, each of which can act as a binding site for $N$ distinct TF species; a binding site can be either free (unbound) or bound with one of the TFs. When the binding sites are free, they are regarded as species $S_0$; when they are bound with one of the TFs, the corresponding binary complexes are regarded as the distinct species $S_1, S_2, \dots , S_{N-1}, S_N$. We assume that the free (i.e., unbound) TFs are present in excess amounts at constant concentrations ${\tilde{a}}_1, {\tilde{a}}_2, \dots , {\tilde{a}}_{N-1}, {\tilde{a}}_N$, respectively, which do not change over time. (In effect, this means that the partial thermodynamic limit—discussed earlier in this article—is achieved with sufficient accuracy for the TF species $S_1, S_2, \dots , S_{N-1}, S_N$). The binding reaction rate constant for the $i$th TF is ${\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i$ (this is a pseudo-first-order reaction), and the corresponding unbinding rate constant is ${\tilde{k}}_{-}^{\left(i\right)}$ ($i=1,2,\dots ,N$); assume that all the rate constants are positive. The topology of this linear reaction network is shown in Figure 2. That topology is also the transition graph for the core CTMC $\tilde{X}$ with state space $S=\{0, 1, \dots , N\}$ and generator $\tilde{\mathit{Q}}$, which will be our focus in this subsection and will be regarded as the perturbed CTMC. For the generator entries, we have ${\tilde{q}}_{0i}={\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i$ and ${\tilde{q}}_{i0}={\tilde{k}}_{-}^{\left(i\right)}$ ($i=1,2,\dots ,N$); all the other off-diagonal entries are equal to zero. Note that the core CTMC replicates the binding–unbinding kinetics for one binding site.

In our example, the bound state of the binding site serves as the start signal for the mRNA synthesis initiation. Therefore, we are interested in a quantitative understanding of the bound-state kinetics given the binding and unbinding rate-constant values, which define the kinetics. Improved understanding can be achieved through a simplification of the postulated network topology (Figure 2) by identifying and eliminating the individual reactions that turn out to be less essential than others. Here, we will give two specific examples.

Example 1: permanent-activation approximation. Assume that the rate ${\tilde{k}}_{-}^{\left(N\right)}$ is quite small. This means almost irreversible binding with the $N$th TF, meaning that the chain $\tilde{X}$ will be spending most of its time in the state $S_N$. How close are these kinetics to those of a CTMC with essentially the same transition graph and one absorbing state, $S_N$? To assess that, introduce the unperturbed chain $X$ on the same state space and with generator $\mathit{Q}$ that is exactly like $\tilde{\mathit{Q}}$, except one thing: the unperturbed rate $k_{-}^{\left(N\right)}=0$. The kinetics of the chain $X$ consist of a transient after which the chain gets trapped in the absorbing state $S_N$; as a result, the gene controlled by the bound $N$th TF becomes permanently activated.

From this description, it follows that, in the perturbation matrix $\mathit{E}=\tilde{\mathit{Q}}-\mathit{Q}$, the only non-zero off-diagonal entry corresponds to the transition rates ${\tilde{q}}_{N0}={\tilde{k}}_{-}^{\left(N\right)}$ and $q_{N0}=0$: $e_{N0}={\tilde{q}}_{N0}-q_{N0}={\tilde{k}}_{-}^{\left(N\right)}$. Hence, for the matrix ${\mathit{E}}_0$ in Assertion 1, we have $‖{\mathit{E}}_0‖={\tilde{k}}_{-}^{\left(N\right)}$, which follows directly from our definition of matrix norm. Then, from Assertion 1, we obtain that $‖\mathit{E}‖=2{\tilde{k}}_{-}^{\left(N\right)}$. Using the perturbation bound in Equation (5), we thus obtain the following approximation bound:

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le 2\left(\log C+1\right){\displaystyle \frac{{\tilde{k}}_{-}^{\left(N\right)}}{b}}.$$

This bound shows that our permanent-activation approximation is accurate if the unbinding rate ${\tilde{k}}_{-}^{\left(N\right)}$ is small relative to the exponential-convergence parameter $b$ (which could be equal to, e.g., the spectral gap $\lambda$ of the unperturbed CTMC, if we are using Equation (3) together with Equation (5)).

Example 2: single-TF approximation. Let us now consider a different scenario. Assume that the binding rate constants, ${\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i$, for the first $N-1$ TFs (i.e., the ones corresponding to the states $S_1, S_2, \dots , S_{N-1}$) are quite small. That could result from small values of the corresponding ${\tilde{k}}_{+}^{\left(i\right)}$ (low intrinsic TF binding rate) or small values of ${\tilde{a}}_i$ (low TF abundance). A natural question that arises is: could we neglect the binding of those TFs by assuming that they cannot bind at all? That would significantly simplify the gene-regulation mechanism that we are investigating, because in that case the only significant regulator of the gene expression here would be the $N$th TF.

To assess the accuracy of this (single-TF) approximation, consider the unperturbed chain $X$ with generator $\mathit{Q}$, where $k_{+}^{\left(i\right)}{a}_i=0$ for $i=1,2,\dots ,N-1$, and all the other off-diagonal generator entries are the same as for $\tilde{\mathit{Q}}$. Thus, the only non-zero off-diagonal entries of the perturbation matrix $\mathit{E}$ are $e_{0i}={\tilde{q}}_{0i}-q_{0i}={\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i$, $i=1,2,\dots ,N-1$. Therefore, from the definition of ${\mathit{E}}_0$,

$$‖{\mathit{E}}_0‖=\sum _{i=1}^{N-1}\left|{\tilde{q}}_{0i}-q_{0i}\right|=\sum _{i=1}^{N-1}{\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i.$$

Now, from Assertion 1, we obtain that

$$‖\mathit{E}‖=2\sum _{i=1}^{N-1}{\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i\le 2(N-1)\underset{i=1,2,\dots ,N-1}{\max }{\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i.$$

Using this expression together with Equation (5), we obtain the approximation bound

$$\underset{t\ge 0}{\sup }‖\mathit{z}\left(t\right)‖\le 2(N-1)\left(\log C+1\right){\displaystyle \frac{\underset{i=1,2,\dots ,N-1}{\max }{\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i}{b}}.$$

Thus, if the ${\tilde{k}}_{+}^{\left(i\right)}{\tilde{a}}_i$ ($i=1,2,\dots , N-1$) are all of approximately the same small magnitude $\epsilon$, then the approximation accuracy will explicitly depend on ($N-1)\epsilon /b$(there may also be some implicit dependence on $N$ via $\log C$, but it is expected to be much weaker).

5. Generalizations and Related Topics

5.1. Extensions to General Reaction Networks

General reaction networks can contain first-order, pseudo-first-order, and non-first-order individual reactions. In the presence of non-first-order reactions, the general perturbation-analysis methodology for linear reaction networks (outlined in the previous section) is not applicable. Thus, development of a comprehensive perturbation analysis methodology applicable to both linear and non-linear networks is a problem in need of a solution. While an analytical solution would come as a welcome breakthrough, perhaps the first step would be to focus on algorithmic solutions. As one possibility, we imagine an algorithm that would decompose the network under study into a collection of individual reactions, each of which can be studied using, e.g., the perturbation-bound approaches discussed in this review. Such analysis would provide detailed information about the sensitivity of each individual reaction to perturbations in its forward and reverse reaction rates. These sensitivities could be compared with each other and, possibly, combined to provide network-level sensitivity information that takes the individual-reaction interconnections into account. This perturbation-bound-driven approach could then be compared and contrasted with existing sensitivity-analysis approaches, such as some version of variance-based sensitivity analysis [84] or analyses based on the use of derivatives [12,85,86].

5.2. The Need for Time-Inhomogeneous Markov Models

In all the examples considered so far, the generators of the CTMCs in question, as well as their perturbations, were time-independent, which corresponds to time-homogeneous CTMCs. Many aspects of the perturbation approaches that we discussed can be extended to the case of time-inhomogeneous CTMCs and their perturbations (i.e., cases where the generator matrix and/or its perturbation explicitly depends on time). Indeed, there are convergence bounds [61] and perturbation bounds [65,87] that are available in the literature for time-inhomogeneous CTMCs.

The necessity for the formalism of time-inhomogeneous CTMCs naturally arises from the needs of biological modeling. For example, sometimes the body temperature undergoes a noticeable change over time, which (according to the well-known Arrhenius equation) modulates all the rate constants for the biochemical reactions within the body (e.g., Ref. [88]). The most methodologically general way to account for such changes is to model the reactions using CTMCs with time-dependent transition rates. Another example: in a pseudo-first-order reaction, whose rate depends on the concentration of species present in excess amounts, the concentration of those species may change, as a function of time, due to some external (and unaccounted for) biochemical reactions. Furthermore, if our reaction compartment is a cell, then some of the reaction rates depend on the cell volume, which changes over time due to cell growth. All such processes are examples of nonequilibrium phenomena in biomolecular networks. These phenomena are attracting an increasing amount of attention in biophysics and mathematical cell biology [14,15], which includes research on sensitivity of biomolecular systems to perturbations [13]. Therefore, methodological and mathematical foundations for such research require continued development.

One stark example of nonequilibrium phenomena is provided by cellular signal transduction and control systems [89,90,91,92]. Living cells can sense the changing levels of extra- and intracellular signals (such as the concentrations of physiologically important substances) and use their molecular machinery to respond to such changes (e.g., by modulating the expression levels of certain genes). This type of modulation by a time-dependent external or internal signal is a clear example of a time-inhomogeneous perturbation, whose studies should thus be the natural next step in the mathematical analysis of perturbations in biomolecular systems. One promising approach is based on representing time-dependent perturbations as a sequence of “jumps” in the transition-rate values, followed by periods of convergence to the corresponding stationary distributions [93]. A new change in the incoming signal would cause a new “jump”, followed by convergence to a new steady state. Such piecewise-constant kinetics may provide a sufficiently accurate representation of reality, while preserving the conceptual simplicity and tractability of the mathematical techniques involved.

5.3. Tightness of the Perturbation Bounds

The perturbation bounds discussed in this review are upper bounds; due to their nature, they may overestimate the error in a CTMC’s state-probability vector for a given perturbation of the CTMC’s parameters. The question then becomes whether this presents a problem for practical applicability of the perturbation bounds. The answer appears to depend on the situation. As mentioned earlier, the bound in Equation (5) has recently been shown to be tight [49]. At the same time, other bounds might lose tightness when the size of the state space increases [43,81]. Yet, recently analyzed numerical examples suggest that perturbation bounds can indeed be quite informative [65,94]. Overall, a comprehensive numerical study focused on the tightness of CTMC perturbation bounds applied to biochemical models appears to be absent from the current literature. Such a study, investigating realistic models of natural systems and phenomena, would be a welcome addition to the current and emerging perturbation research.

6. Conclusions: Future Work

Here, our goal was to provide an overview of the existing and emerging applications of Markov chain perturbation theory in biochemical kinetics. We focused on the use of perturbation bounds, but that is not the only methodology in perturbation theory. Another powerful methodology—asymptotic expansions—together with its applications deserves a separate, focused overview [95,96]. Even for perturbation bounds, one review could not sufficiently cover all the relevant topics. Among the latter, we would like to mention three directions whose impact may be expected to grow. One is the interplay between mathematical approaches to perturbation bounds (such as the material presented in this review) and the recently emerged research on thermodynamic bounds for perturbations, which is rapidly gaining momentum in condensed-matter physics and biophysics [22,97,98,99]. This is paralleled by very recent, substantial use of stochastic-process perturbation bounds in other branches of quantum and statistical physics (see, e.g., Ref. [100] and the Supplementary Material in Ref. [101]), suggesting growing relevance of perturbation bounds to physical-sciences research in general.

Yet another direction is investigations of the relationship between perturbation bounds and statistical estimation of the CTMC parameters [102,103]. Very recent work suggested that the use of perturbation bounds may not be a very efficient way of obtaining confidence intervals for Markov-model characteristics [103]. At the same time, the amount of effort invested in accurate statistical estimation of model parameters should logically be linked to the sensitivity of the model’s behavior to changes in those parameters. Such questions may be relevant, e.g., for CTMC models of ion channels [9,11,12] and even for general CTMC modeling in biology [25,104]. Moreover, this logic can be extended, e.g., to hidden Markov models, given that they are also used in ion-channel modeling [105], and perturbation and approximation bounds for them are available [49,106]. Thus, possible connections between statistical procedures and perturbation analysis for stochastic models may deserve a deeper exploration.

The third direction is the focus on time-inhomogeneous Markov models, which we outlined in the previous section (perturbation analysis for infinite-state-space models is also very much of interest). Ongoing and future work in these and other directions will allow theoretical and applied researchers to realize the full potential of perturbation theory in stochastic modeling of molecular- and cellular-level biological phenomena.