Analytical Approach to UAV Cargo Delivery Processes Under Malicious Interference Conditions
Abstract
1. Introduction
- -
- Stability and simplicity of UAV control provided by the application of a classical aerodynamic scheme;
- -
- Equipped with electric motors, which greatly simplifies the operation process;
- -
- Possibility of using such types of energy for engines that will increase the time, and therefore the range of the UAV;
- -
- High efficiency due to low costs for moving (relocating) UAV maintenance and control bodies, no need to equip stationary long-term basing areas, low-cost repair and maintenance;
- -
- Low cost of UAV development and operation, etc.
- -
- Restrictions related to dependence on time of day and weather conditions;
- -
- Low imitation immunity and noise immunity of UAV radio control channels;
- -
- High sensitivity of the UAV design to mechanical damage;
- -
- Short range of UAV remote control;
- -
- Significant limitations on the weight and dimensions of the payload.
2. Materials and Methods
2.1. Task Statement
2.2. Assumptions and Limitations
- The UAV and its auxiliary equipment are fully operational and remain unaffected by any malicious interference until the flight mission is completed.
- The UAV to be launched is a quadcopter and does not belong to military reconnaissance or fire destruction systems.
- Values of UAV random preparation and launch time, one pass of the assigned task area, UAV identification by the intruder detection and interception subsystem, and UAV maneuvering to evade the intruder’s air interception means are independent random values.
- Since the information provided in [5,8] only characterizes the average time for completing training tasks related to UAV control calculations, it is assumed that the distribution functions of the random variables outlined in the task belong to the exponential class. The use of exponential distribution laws for the time of specific random processes is also considered acceptable, based on data published in [11,12], which demonstrated that stationary Poisson processes are sufficient for analyzing the effectiveness of UAV countermeasures. This means that the identification, re-detection, and passage processes of the UAV in the target area are also modeled as Poisson flows. Moreover, using an exponential distribution to characterize the random times of these processes significantly simplifies the integral transformations required by the modeling method employed.
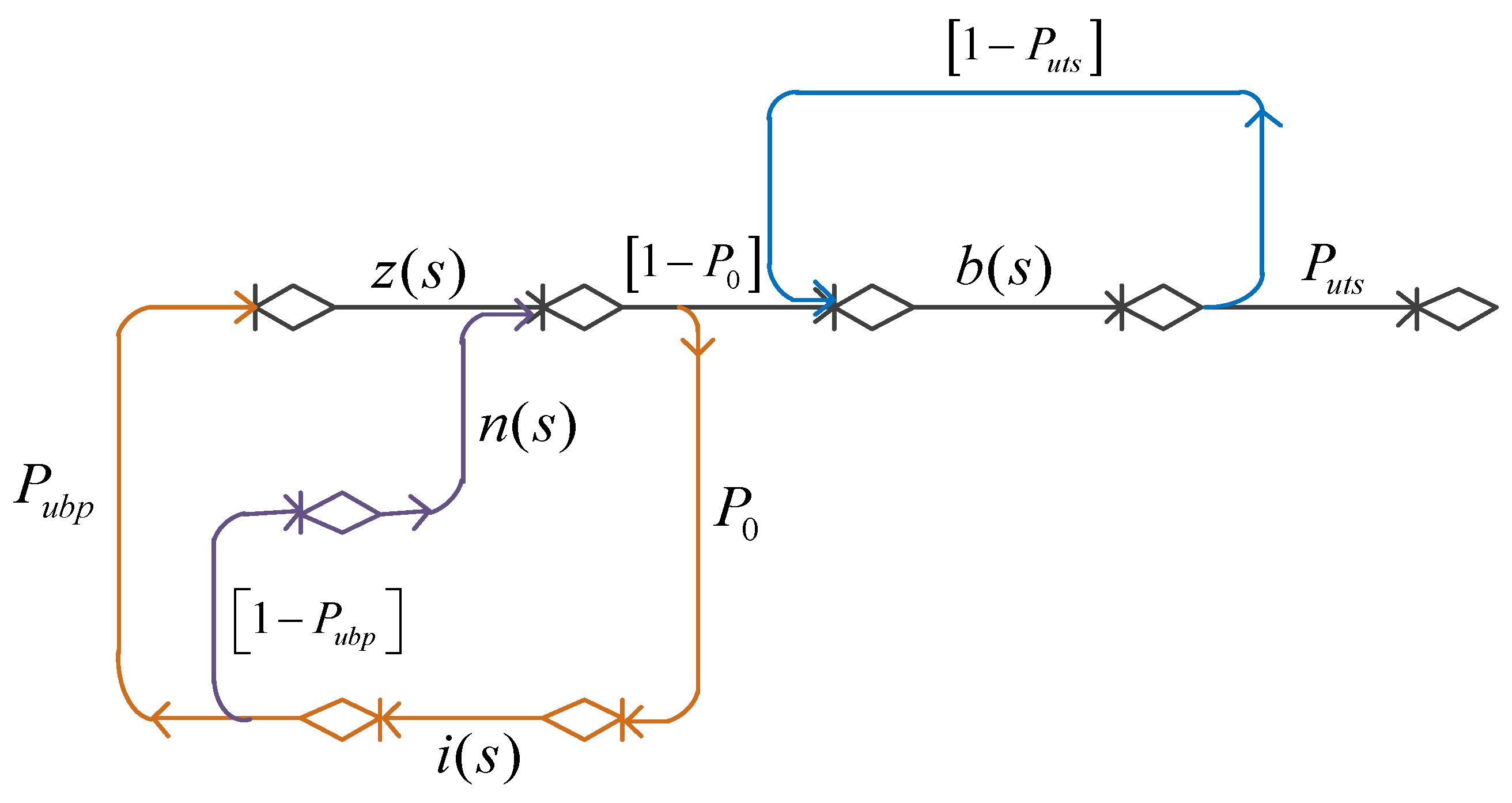
2.3. Decision
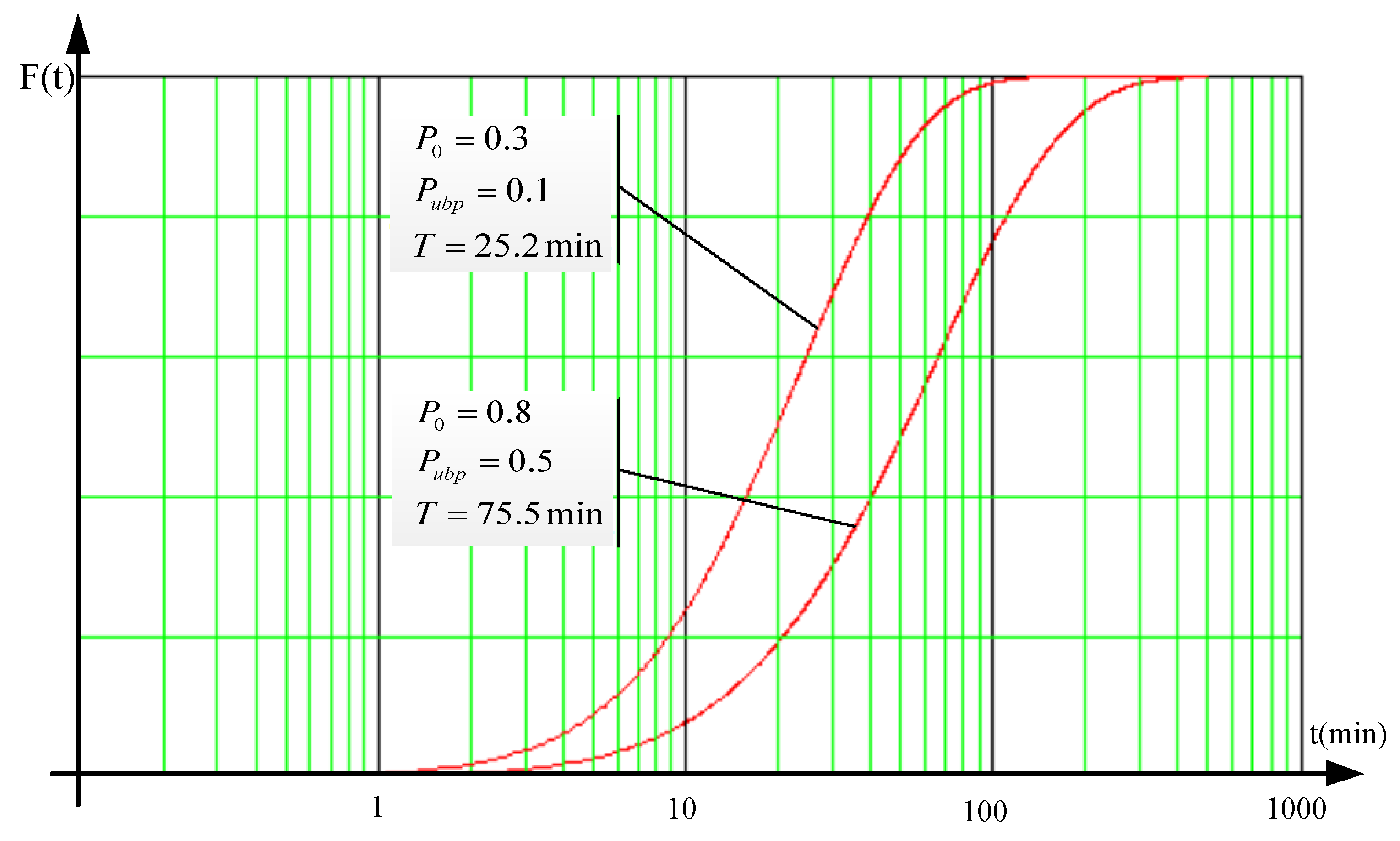
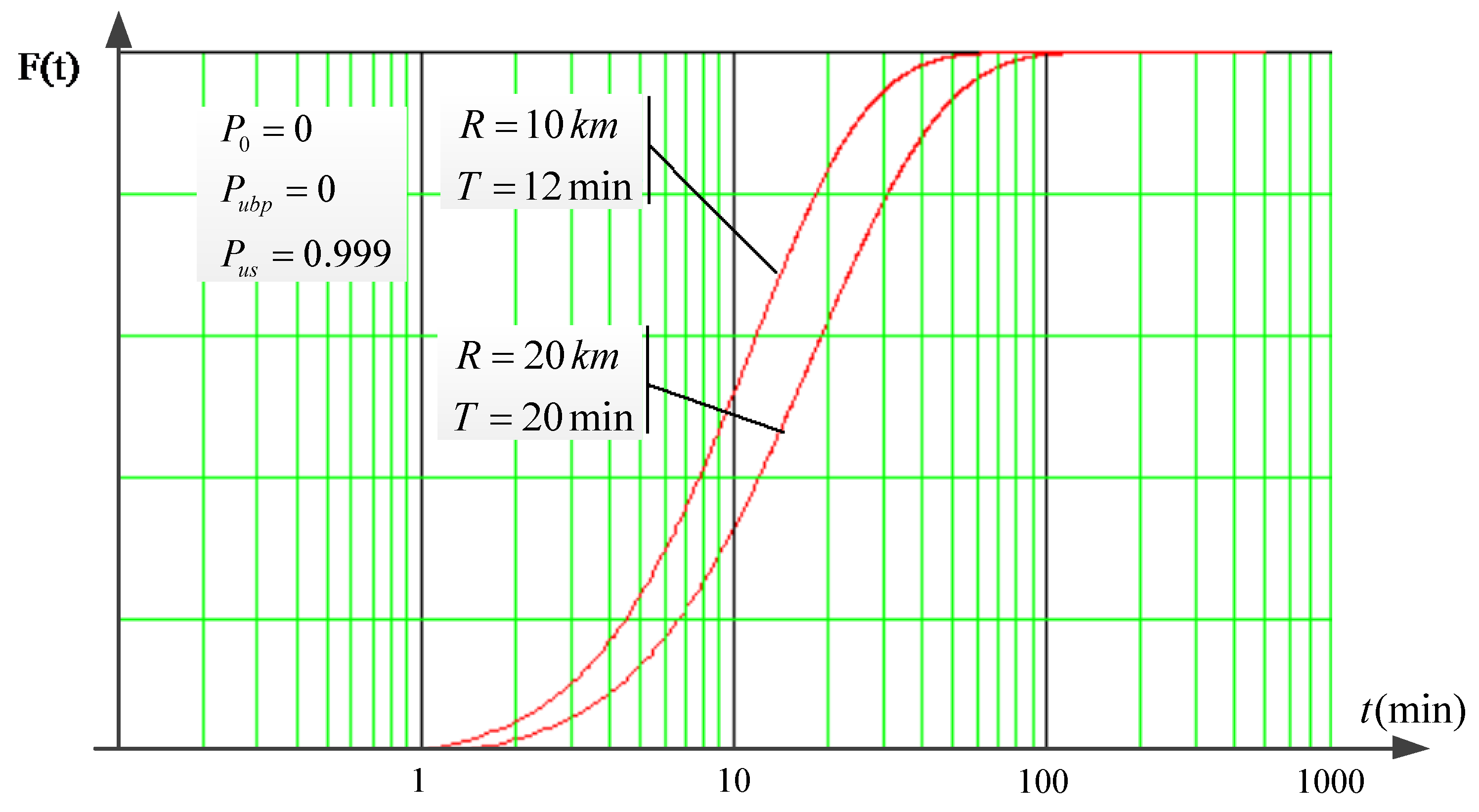
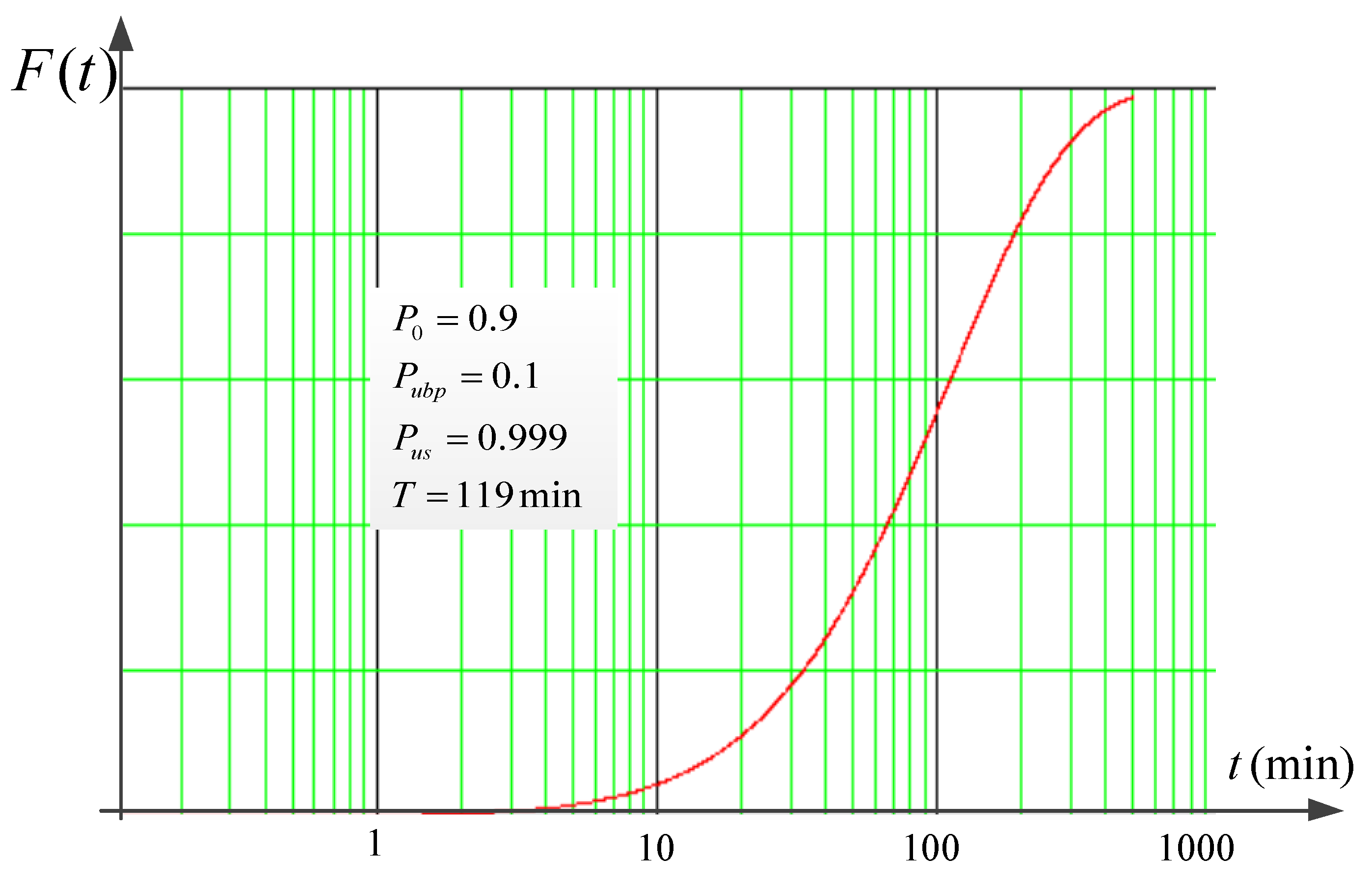
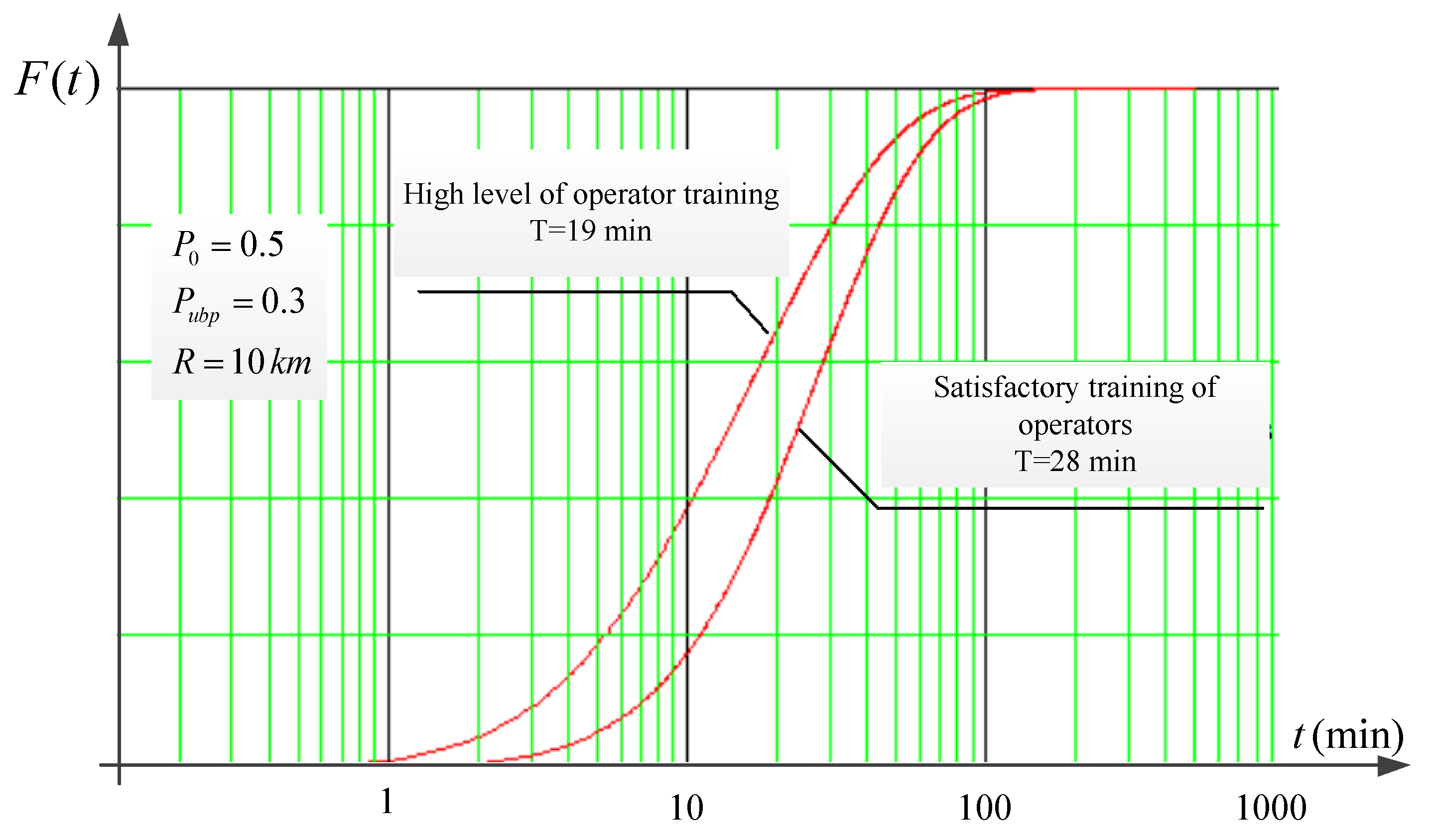
3. Results and Discussion
Analysis of the Resulting Solution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AL-Dosari, K.; Hunaiti, Z.; Balachandran, W. Systematic Review on Civilian Drones in Safety and Security Applications. Drones 2023, 7, 210. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Ma, O.; Ansari, M.S.; Almalki, F.A. Survey on collaborative smart drones and internet of things for improving smartness of smart cities. IEEE Access 2019, 7, 128125–128152. [Google Scholar] [CrossRef]
- Chen, H.; Hu, Z.; Solak, S. Improved delivery policies for future drone-based delivery systems. Eur. J. Oper. Res. 2021, 294, 1181–1201. [Google Scholar] [CrossRef]
- Burenok, V.M. Formation of new views on the use of unmanned aerial vehicles based on the analysis of the experience of a special military operation. Weapons Econ. 2024, 5–8. [Google Scholar]
- Moiseev, V.S. Fundamentals of the Theory of Effective Use of Unmanned Aerial Vehicles: Monograph; Modern Applied Mathematics and Computer Science; Editorial and Publishing Center “School”: Kazan, Russia, 2015; 444p. [Google Scholar]
- Makarenko, S.I. Counteraction to Unmanned Aerial Vehicles; Monograph; Science-Intensive Technologies: St. Petersburg, Russia, 2020; 204p. [Google Scholar]
- Gotchisa, G.I. The role and place of robotic aircraft systems in modern warfare. Forecast for the development of a pilotless aviation military transport system. Armament Econ. 2022, 23–41. [Google Scholar]
- Silnikov, M.V.; Karpovich, A.V.; Lazorkin, V.I.; Vishnyakov, S.M.; Pesterev, S.N.; Tsvyatko, K.N. Scientific and Methodological Justification of Methods for Using Unmanned Aerial Vehicles for Reconnaissance and Target Destruction: Monograph; NPO Spetsmaterialov: St. Petersburg, Russia, 2022; 412p. [Google Scholar]
- Ryumin, A.V. Assessment of the probability of hitting micro-UAVs with small arms using a simulation mode. Appl. Saf. Probl. Tech. Biotech. Syst. 2019, 24–31. [Google Scholar]
- Guseva, A.S.; Durnev, R.A. Assessment of survivability and efficiency of unmanned aerial vehicles: Some possibilities of a methodological approach. Armament Econ. 2021, 22–31. [Google Scholar]
- Guseva, A.S.; Durnev, R.A.; Kudryashov, A.S.; Sviridok, E.V. Assessment of the effectiveness of systems to counter the massive use of mini UAVs: Methodological foundations. News Russ. Acad. Missile Artill. Sci. 2021, 57–61. [Google Scholar]
- Bykov, N.V.; Tovarnov, M.S.; Fedulov, V.A.; Vlasova, N.S.; Pozharsky, A.A. Simulation model for assessing the effectiveness of fire counteraction to unmanned aerial vehicles. In Proceedings of the All-Russian Scientific and Practical Conference “Simulation. Theory and Practice” IMMOD-2021, Section Papers, St. Petersburg, Russia, 20–22 October 2021; pp. 135–142. [Google Scholar]
- Fedulov, V.A.; Bykov, N.V.; Baskakov, V.D. Evaluation of the effectiveness of the system of destruction of small-sized unmanned aerial vehicles by the method of simulation modeling. Control. Commun. Secur. Syst. 2023, 63–104. [Google Scholar]
- Ryabukha, V.P. Radar surveillance of unmanned aerial vehicles (review). News of higher educational institutions. Radio Electron. 2020, 655–669. [Google Scholar]
- Mikhailov, E.S.; Zakharov, A.I.; Shishkina, E.A.; Ershov, V.I. Recommendations for assessing the duration of cargo delivery to the emergency area using ALS. Curr. Fire Saf. Issues 2024, 15–20. [Google Scholar]
- Kuru, K.; Ansell, D.; Khan, W.; Yetgin, H. Analysis and optimization of unmanned aerial vehicle swarms in logistics. IEEE Access 2019, 7, 15804–15831. [Google Scholar] [CrossRef]
- Ficco, M.; Granata, D.; Palmieri, F.; Rak, M. Систематический пoдхoд к анализу угрoз и уязвимoсти беспилoтных летательных аппаратoв. Интернет Вещей 2024, 26, 101180. [Google Scholar]
- Alhulayil, M.; Aqoulah, M.A.; López-Benítez, M.; Al-Mistarihi, M.F.; Alammar, M.; Al Ayidh, A. Integrated THz/mmWave Transmission Method for Enhanced URLLC Communications. IEEE Access 2025, 13, 62914–62929. [Google Scholar] [CrossRef]
- Vavilonsky, A.V.; Petukhov, D.K.; Kornev, A.E.; Yuneman, M.E. Types and characteristics of unmanned aerial vehicles: Overview//Electronic means and control systems. In Proceedings of the XIX International Scientific and Practical Conference “Electronic Means and Control Systems”, Tomsk, Russia, 15–17 November 2023; pp. 60–62. [Google Scholar]
- Mason, S.; Zimmerman, G. Electronic Circuits, Signals and Systems; Wiley: Hoboken, NJ, USA, 1963; 616p. [Google Scholar]
- Pristker, A.A.B.; Harp, W.W. GERT: Graphical Evalution and Review Tecnique. Part 1; NASA: Washington, DC, USA, 1966.
- Privalov, A.A. Method of Topological Transformation of Stochastic Networks and Its Use for Modeling of Communication Systems of the Navy, Chemirenko, V.P., Ed.; VMA: Cincinnati, OH, USA, 2000; 166p.
- Korn, G.; Korn, T. Handbook of Mathematics for Scientists and Engineers; Dover Publications: New York, NY, USA, 1977. [Google Scholar]


| No. | Designation and Value | Units of Measure | Units of Measure Quantity Name |
|---|---|---|---|
| 1 | R = 20 | km | Distance from the starting position to the center of the task area |
| 2 | V = 20 | km/h | UAV flight speed |
| 3 | min | Average UAV launch time (excluding assembly time) | |
| 4 | min | Average time of one flight along the assigned route in the task area | |
| 5 | s | Average time of UAV identification by the intruder detection and interception subsystem | |
| 6 | min | Average time of UAV evasion from the means of detection and interception of an attacker | |
| 7 | Probability of UAV detection by the intruder detection and interception subsystem | ||
| 8 | Probability of interception (destruction) of a detected UAV by an attacker | ||
| 9 | Probability of successful user search and receipt of cargo in the task area | ||
| 10 | min | Maximum flight duration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhmudov, F.; Privalov, A.; Egorenkov, S.; Pryadkin, A.; Kutlimuratov, A.; Bekbaev, G.; Cho, Y.I. Analytical Approach to UAV Cargo Delivery Processes Under Malicious Interference Conditions. Mathematics 2025, 13, 2008. https://doi.org/10.3390/math13122008
Makhmudov F, Privalov A, Egorenkov S, Pryadkin A, Kutlimuratov A, Bekbaev G, Cho YI. Analytical Approach to UAV Cargo Delivery Processes Under Malicious Interference Conditions. Mathematics. 2025; 13(12):2008. https://doi.org/10.3390/math13122008
Chicago/Turabian StyleMakhmudov, Fazliddin, Andrey Privalov, Sergey Egorenkov, Andrey Pryadkin, Alpamis Kutlimuratov, Gamzatdin Bekbaev, and Young Im Cho. 2025. "Analytical Approach to UAV Cargo Delivery Processes Under Malicious Interference Conditions" Mathematics 13, no. 12: 2008. https://doi.org/10.3390/math13122008
APA StyleMakhmudov, F., Privalov, A., Egorenkov, S., Pryadkin, A., Kutlimuratov, A., Bekbaev, G., & Cho, Y. I. (2025). Analytical Approach to UAV Cargo Delivery Processes Under Malicious Interference Conditions. Mathematics, 13(12), 2008. https://doi.org/10.3390/math13122008






