Distributed Control Strategy for Automatic Power Sharing of Hybrid Energy Storage Systems with Constant Power Loads in DC Microgrids
Abstract
1. Introduction
- The primary control layer implements an enhanced P–V2 droop control mechanism utilizing adaptive virtual impedance instead of fixed droop coefficients. This strategic modification permits SCs to dynamically compensate for transient power fluctuations while BATs maintain steady-state power supply, collectively optimizing the system’s transient performance. Furthermore, this control scheme effectively eliminates the adverse impacts induced by CPLs;
- A secondary control method is proposed that achieves current sharing among multiple buses while maintaining voltage stabilization, thereby preventing excessive consumption in any individual unit and prolonging the system’s operational lifespan;
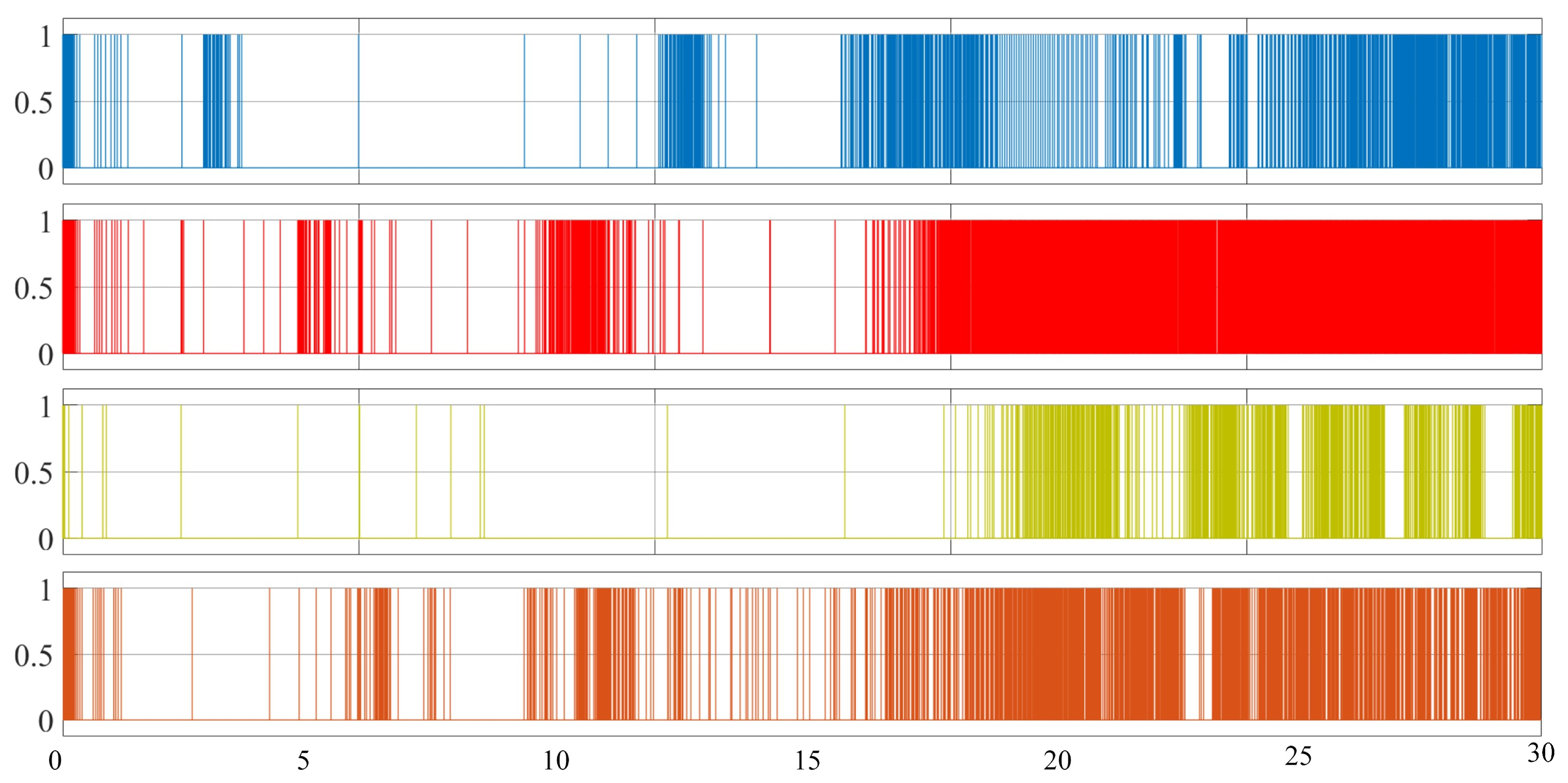
- The secondary control layer incorporates a dynamic event-triggered communication mechanism, which minimizes units communication and controller triggering frequencies by activating data transmission only during critical state deviations, thereby substantially reducing the system-wide communication overhead.
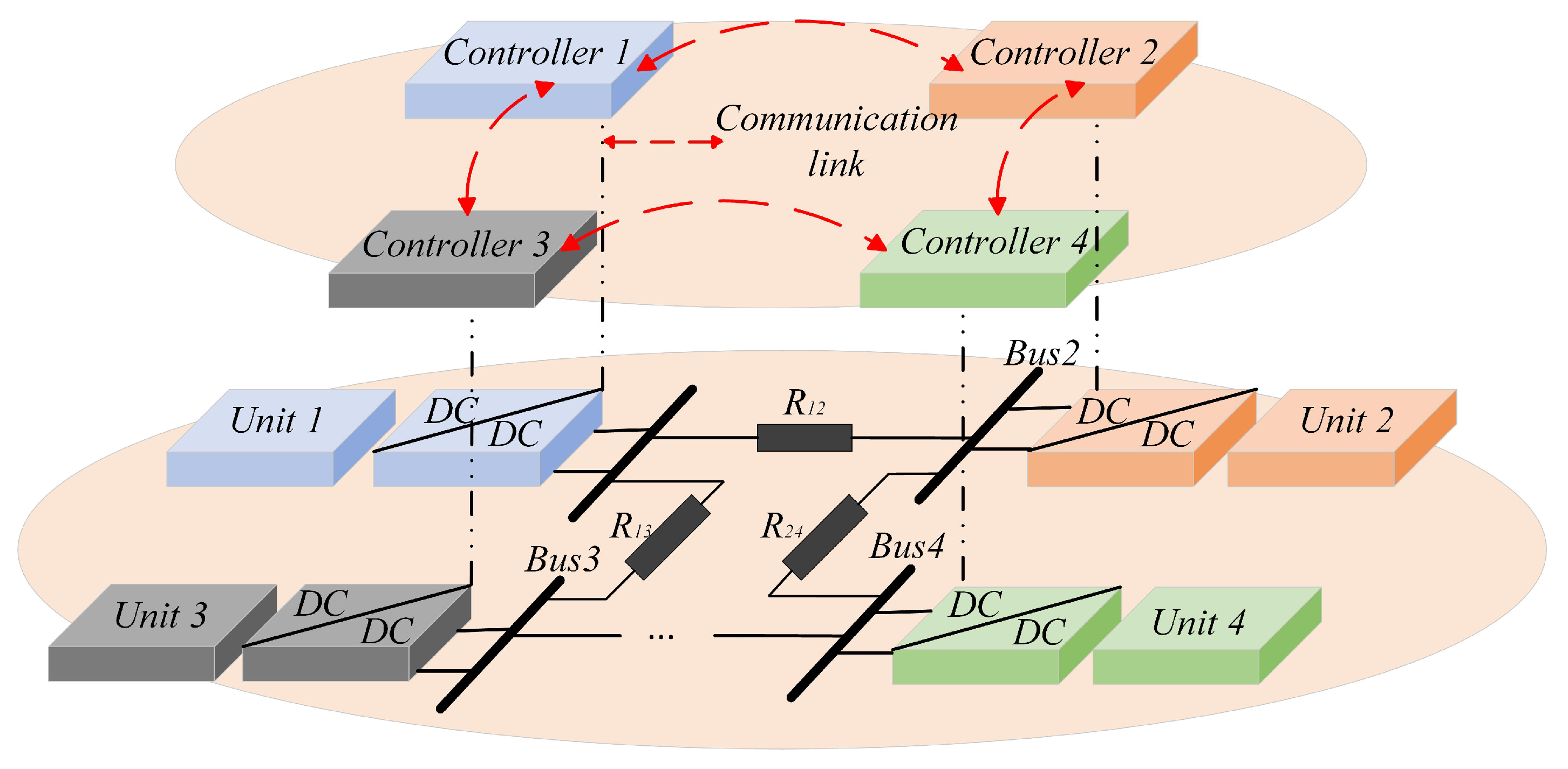
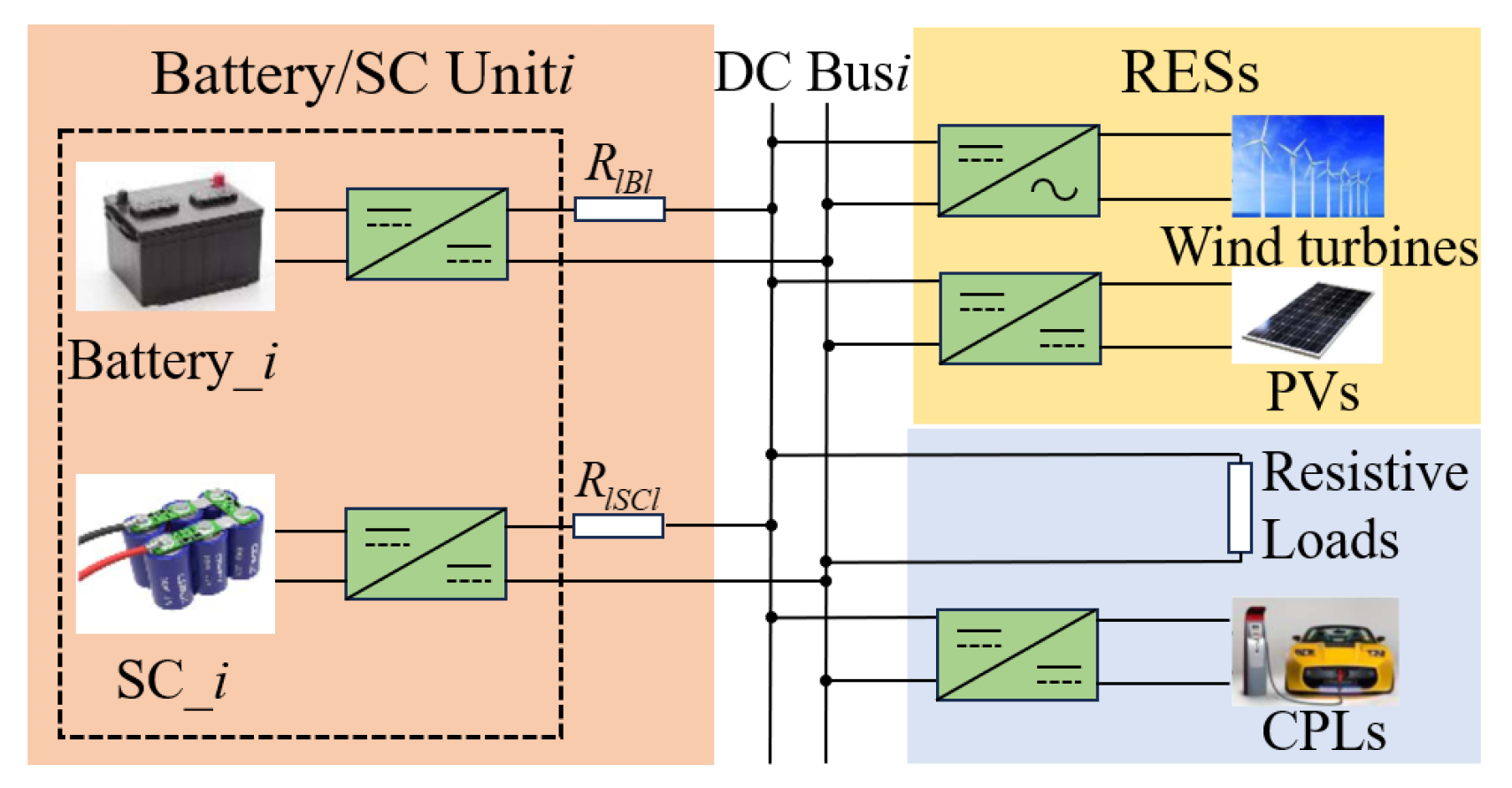
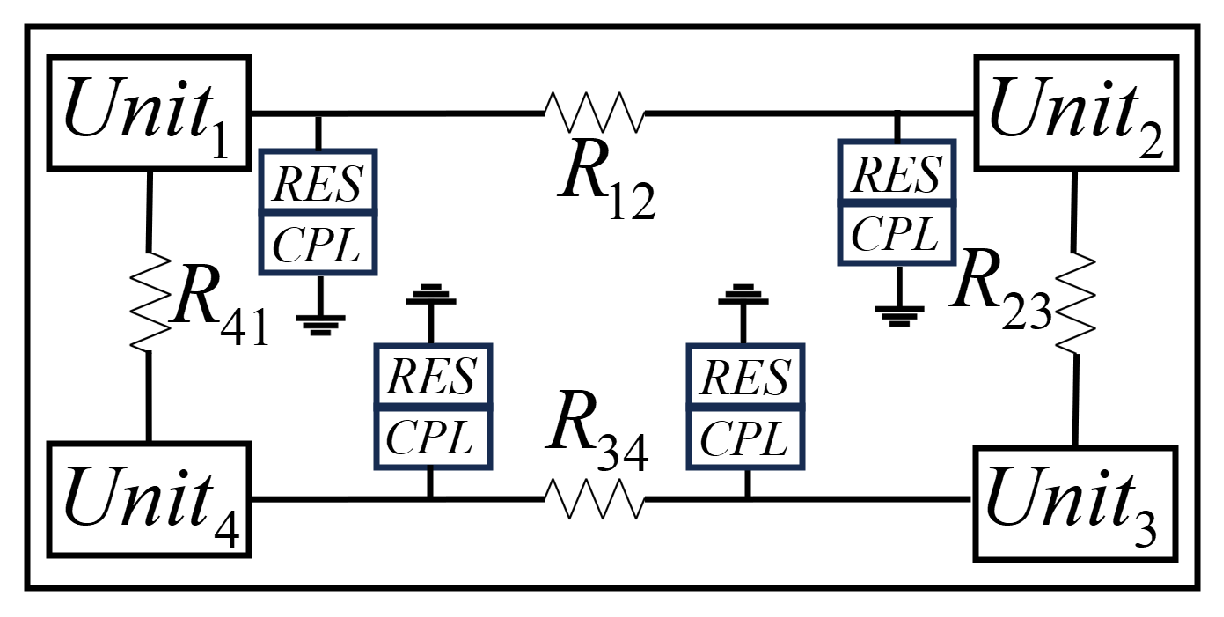
2. Problem Analysis and System Modeling
2.1. Nonlinearity in the Voltage–Current Relationship Caused by CPLs
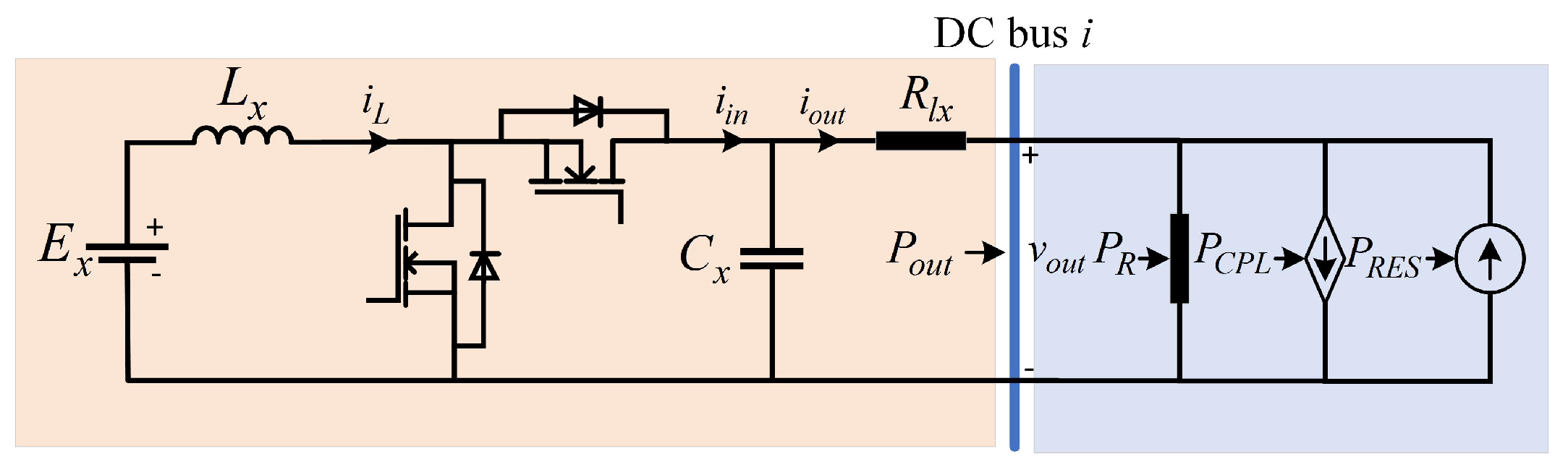
2.2. Modeling of the DC–DC Converter
3. The Proposed Controller Design
3.1. Primary Controller Design
3.2. Secondary Controller Design
4. Stability Analysis
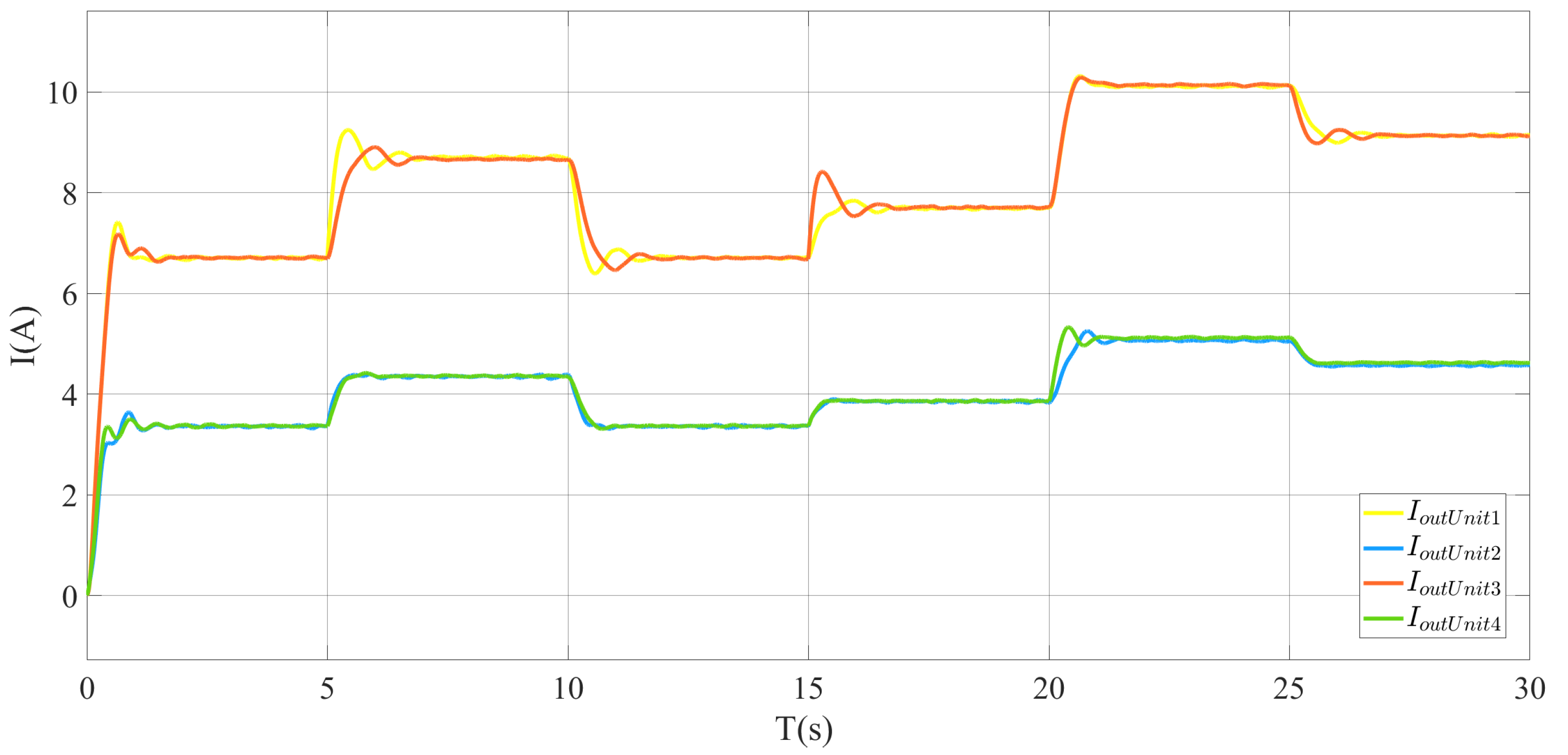
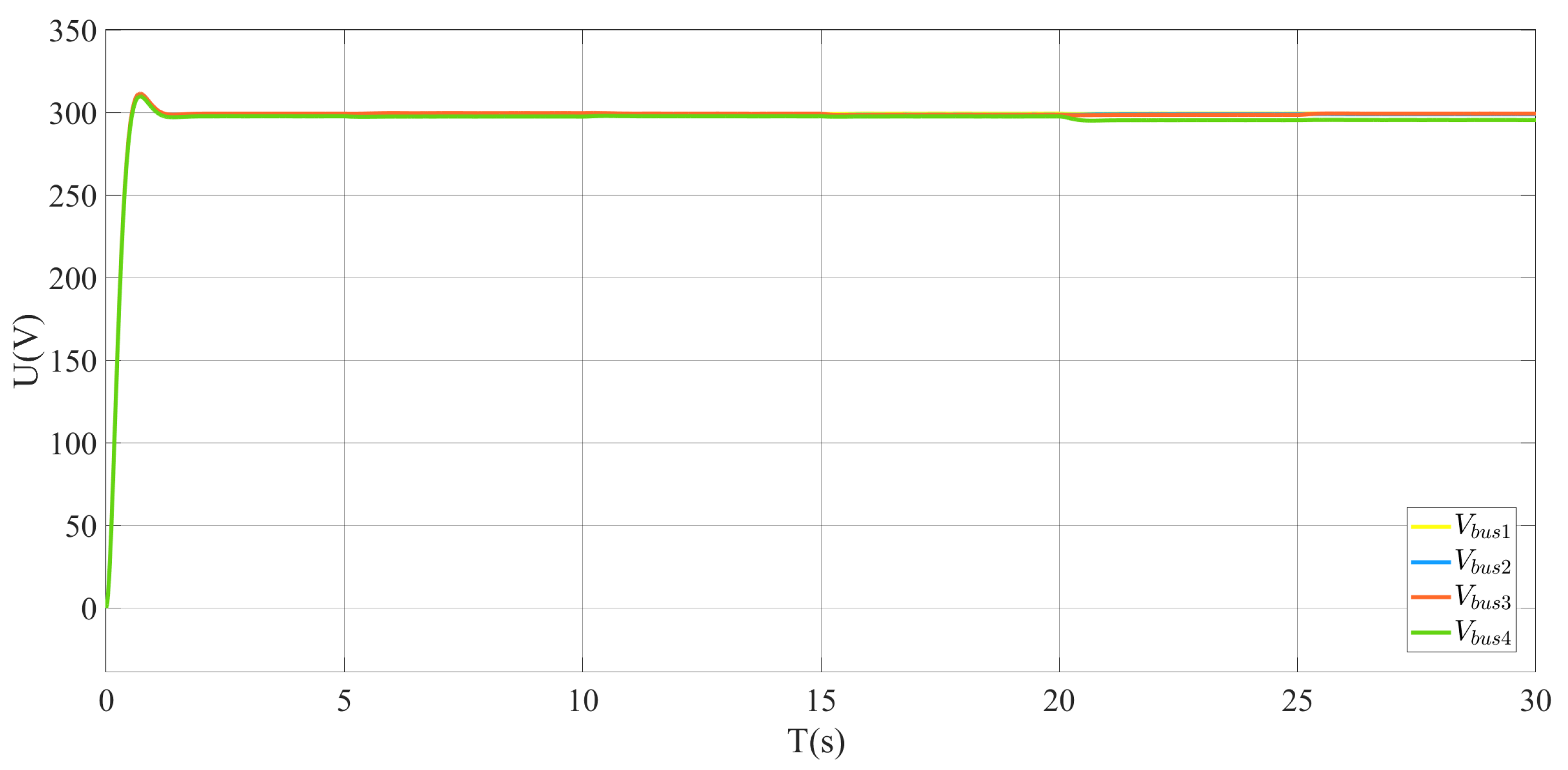
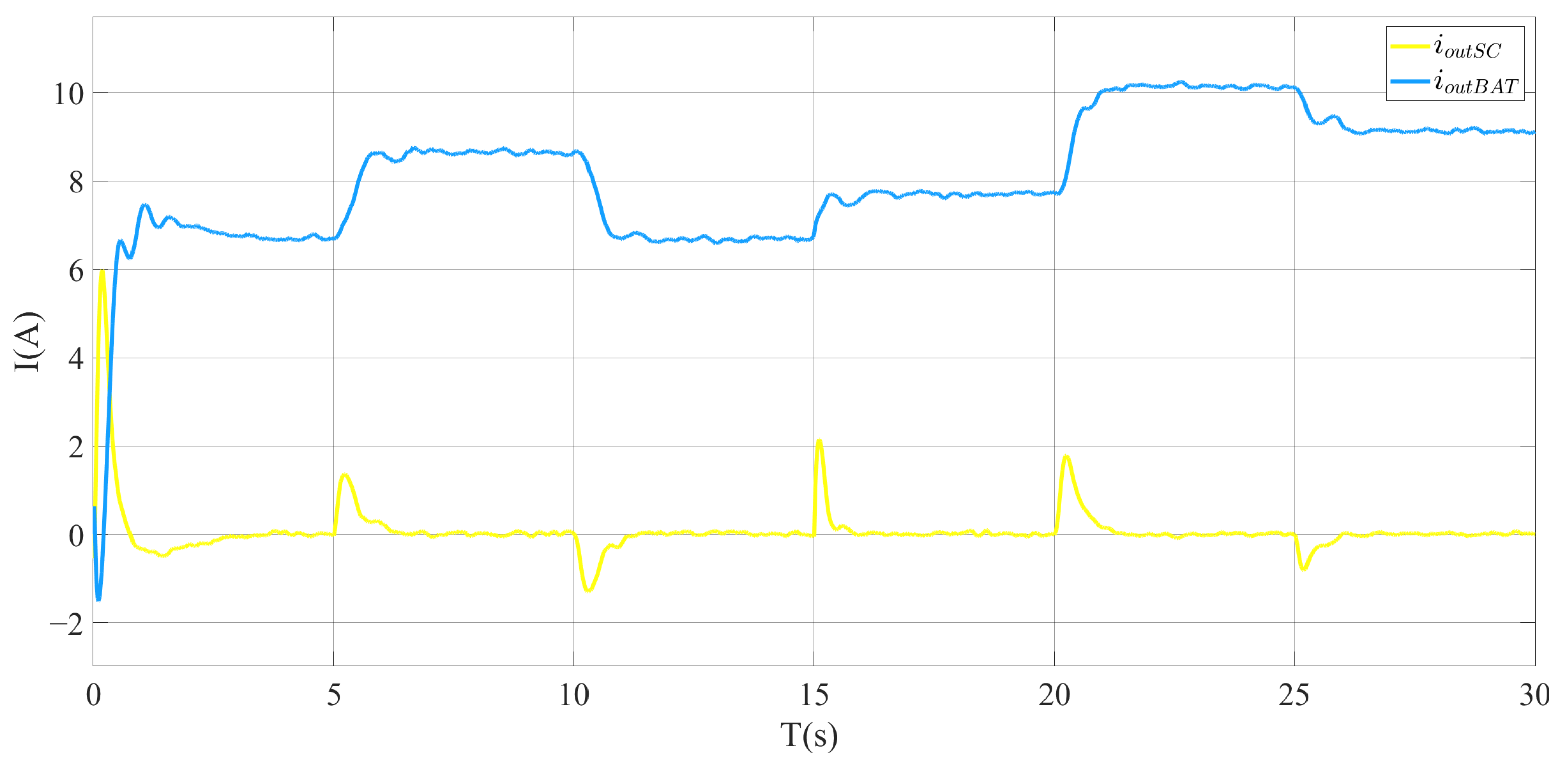
5. Simulation and Experimental Results
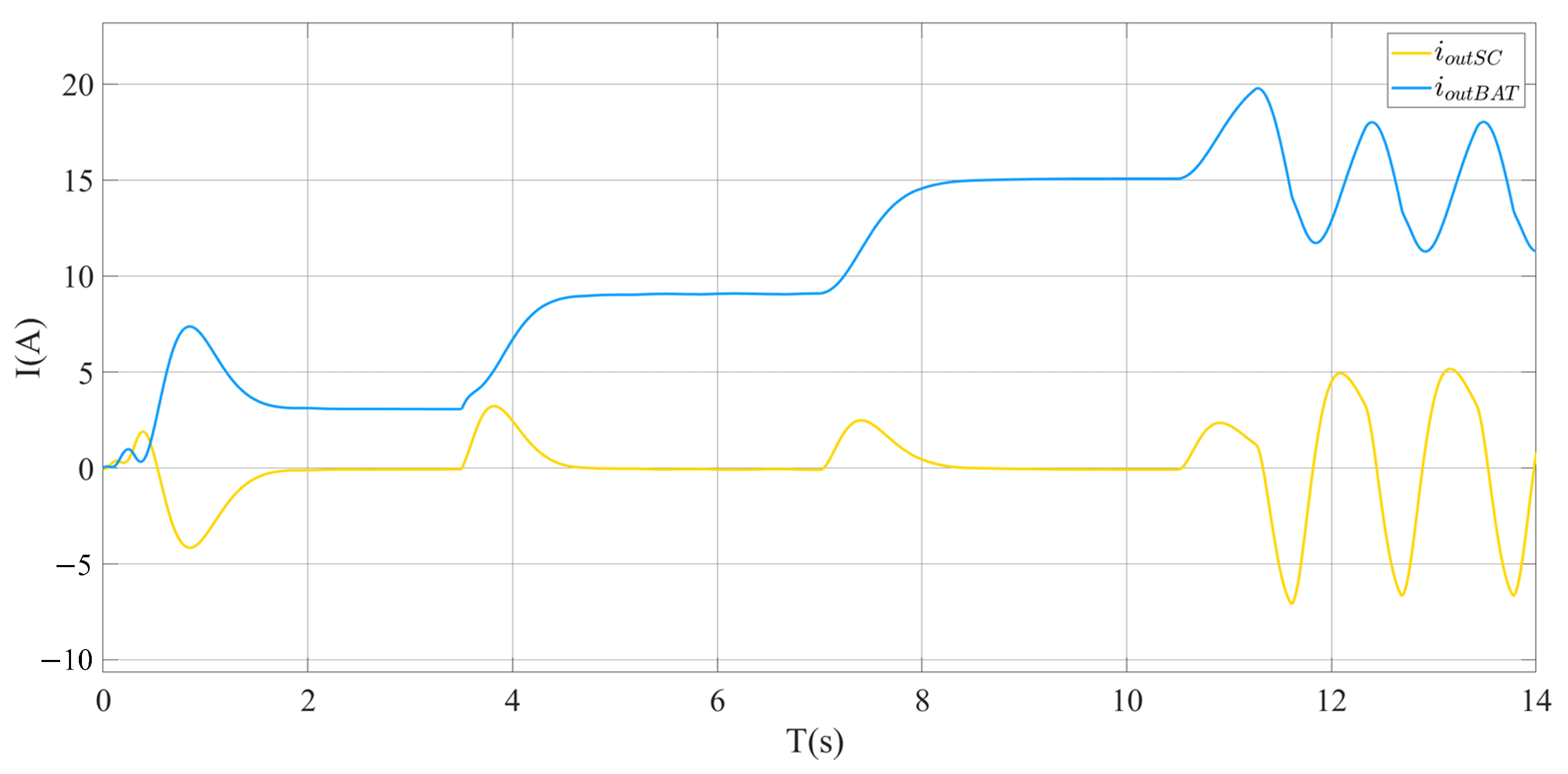
5.1. Simulation Results
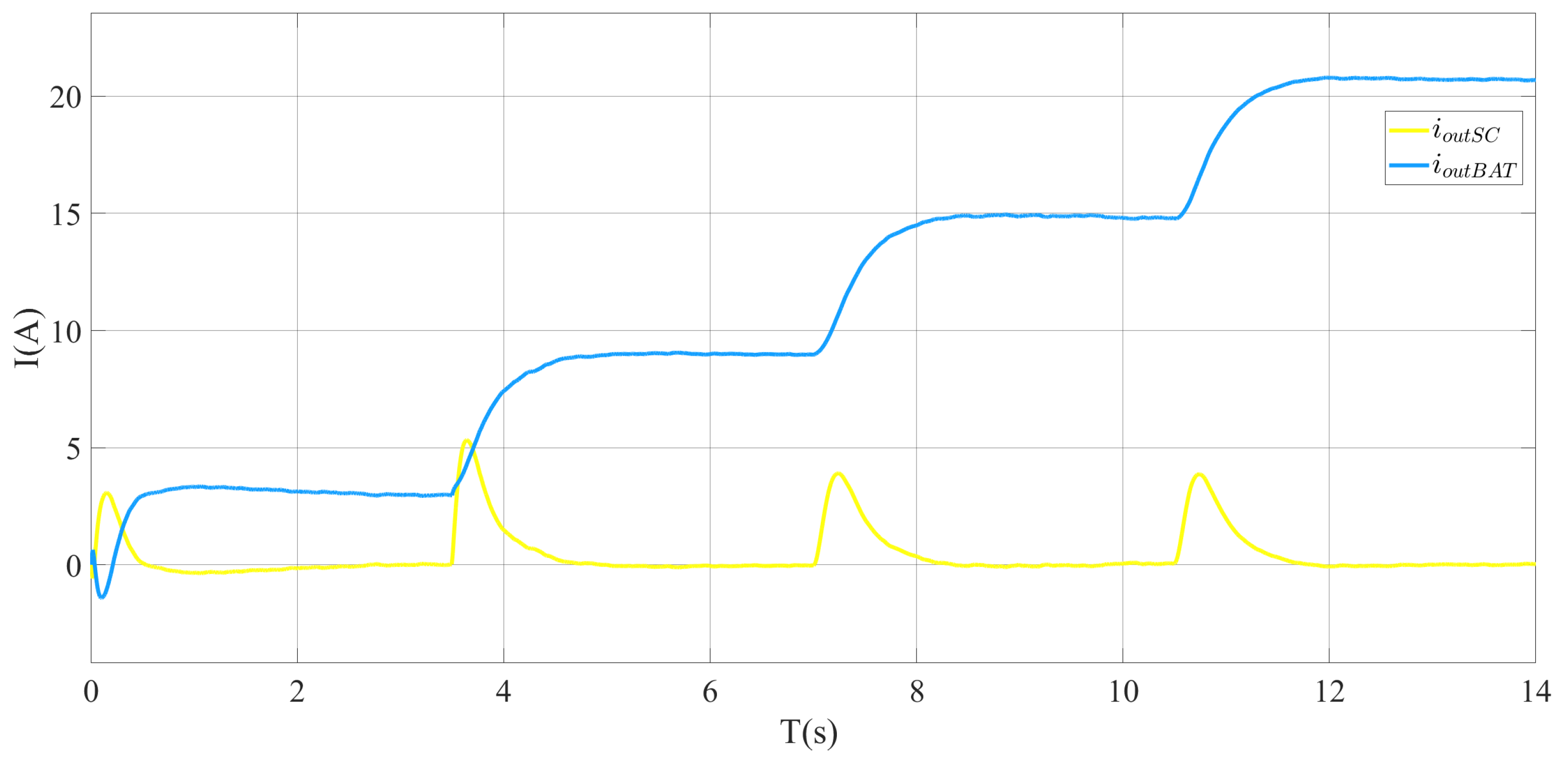
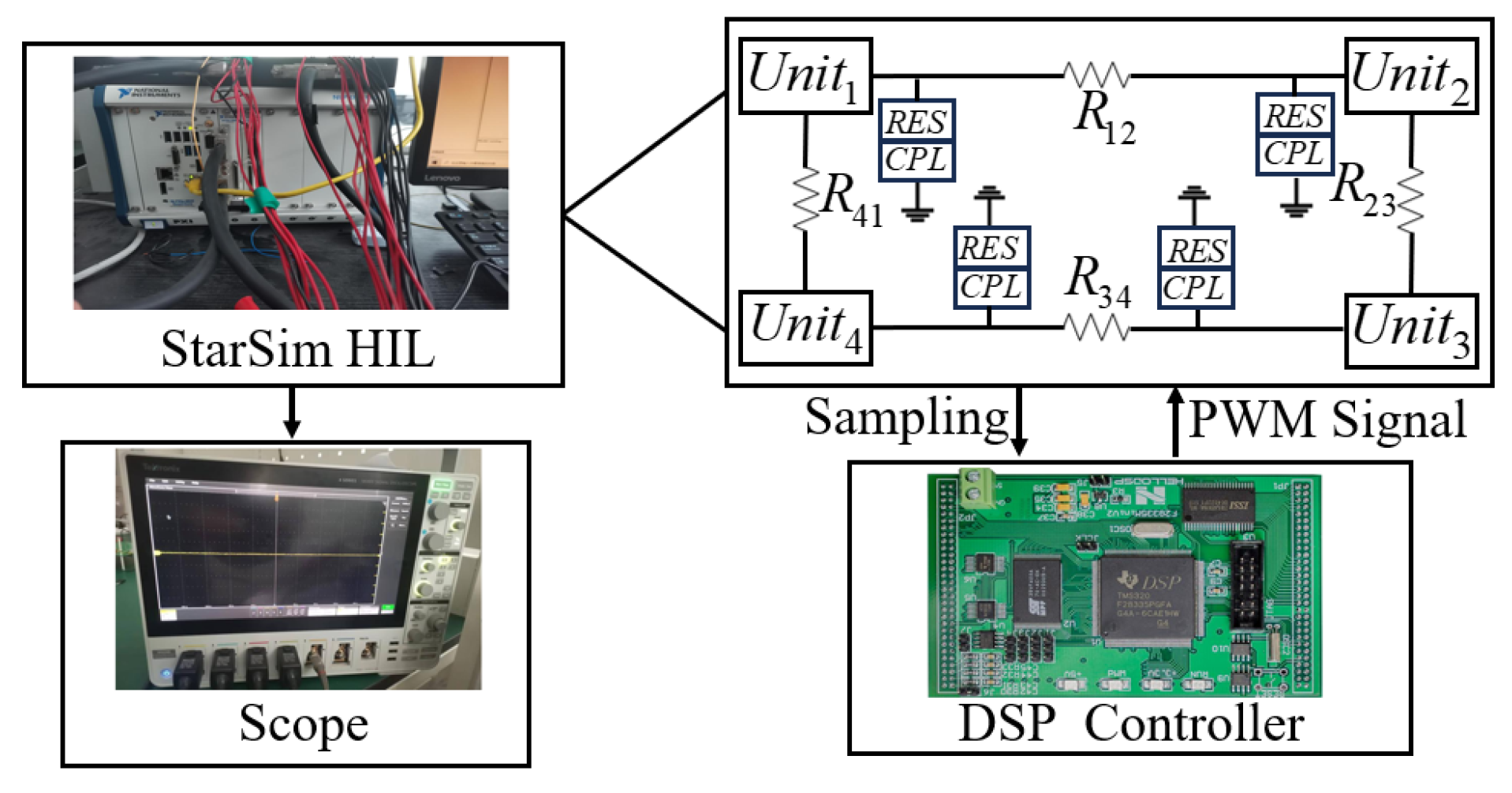
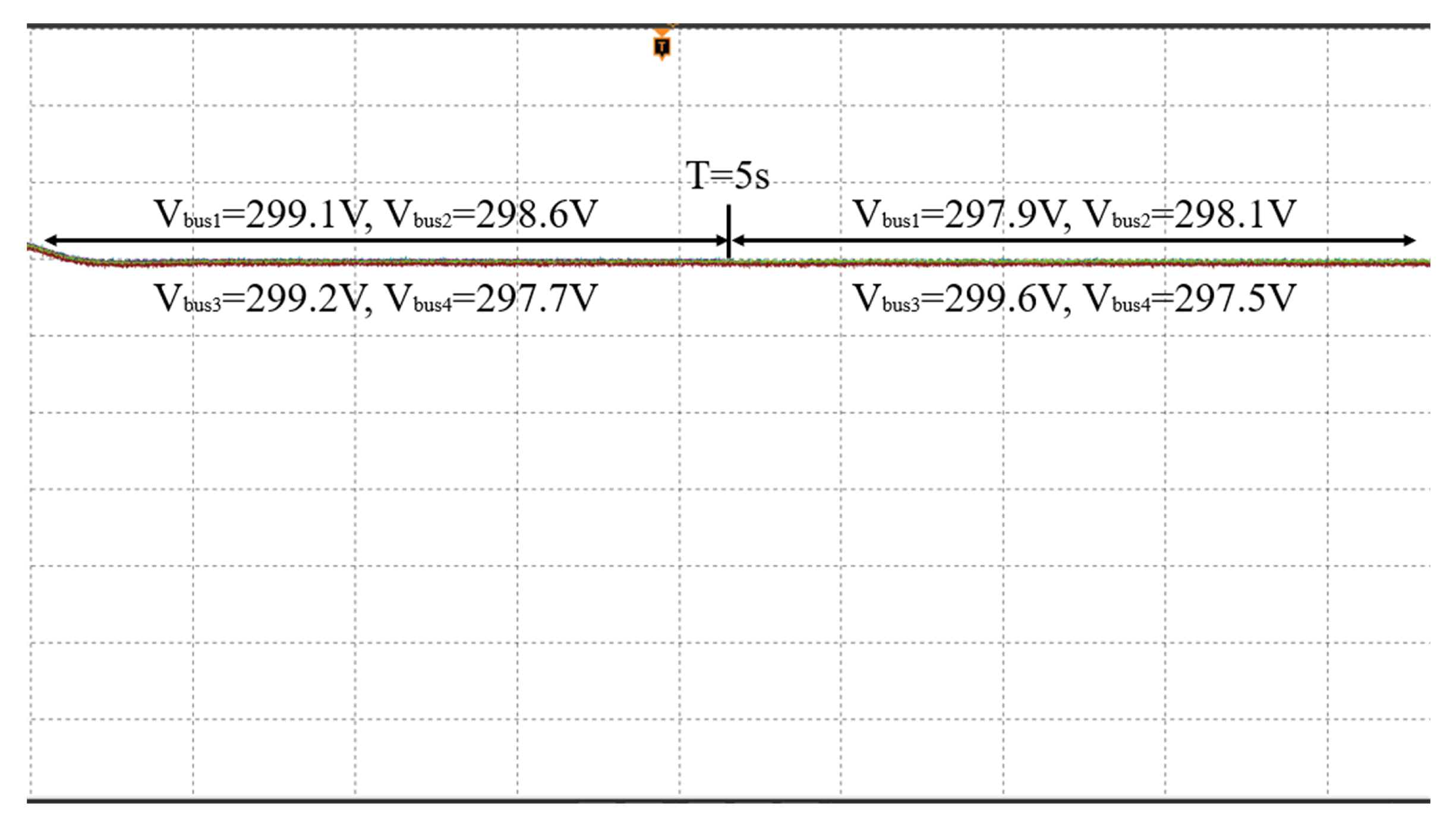
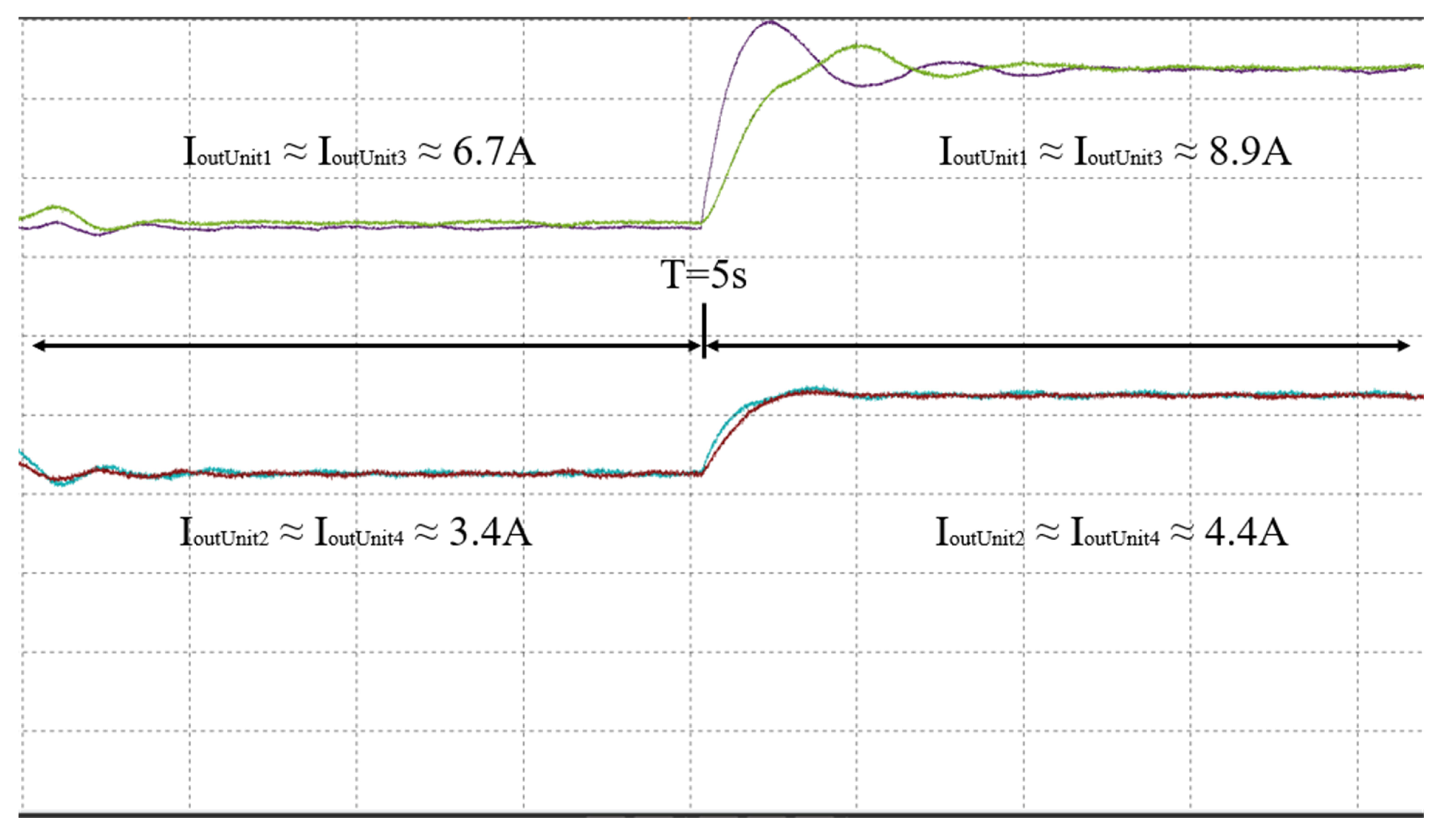
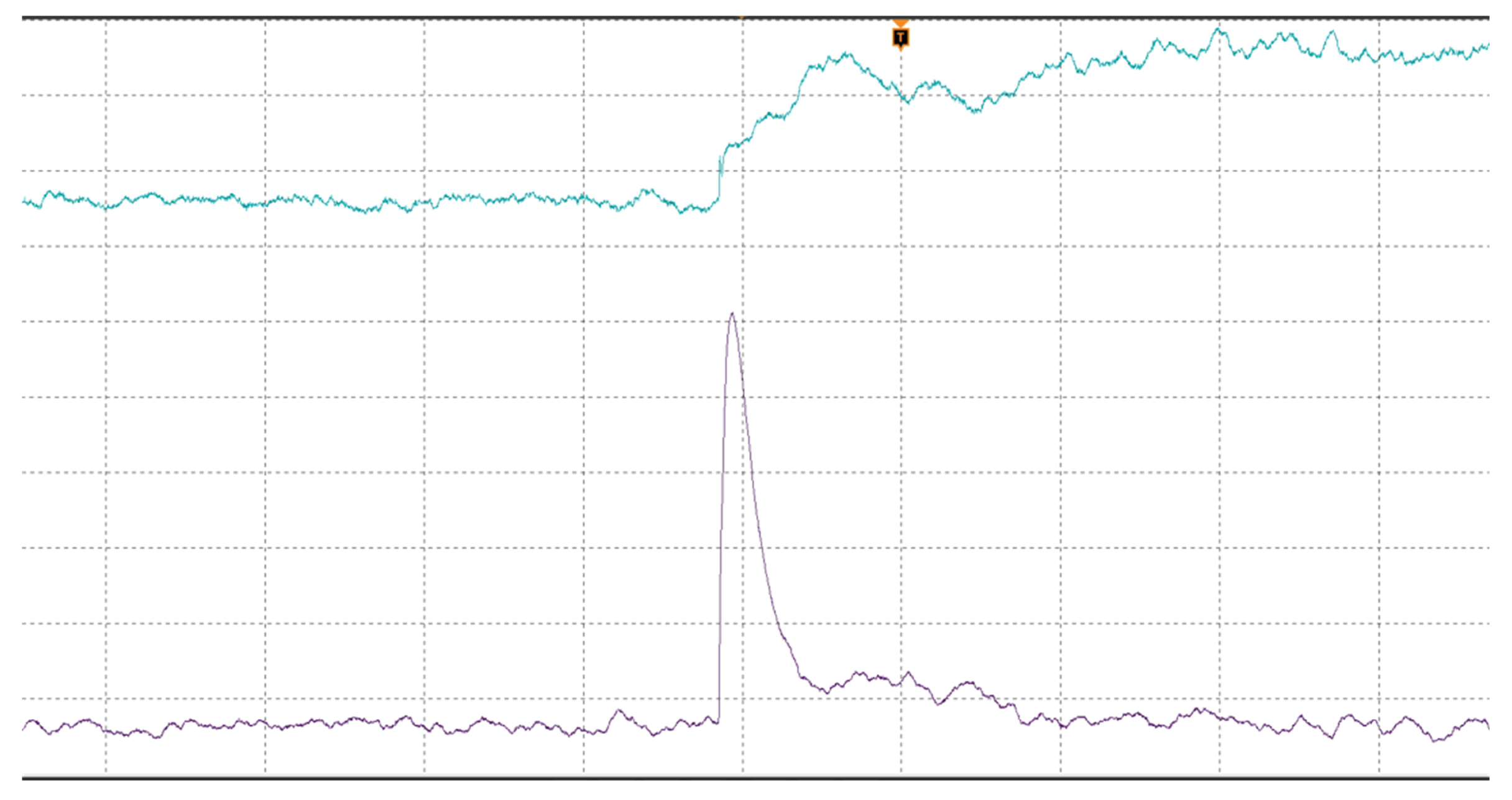
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HESS | Hybrid energy storage system |
| BAT | Battery |
| CPL | Constant power load |
| SC | Supercapacitor |
| RES | Renewable energy source |
| EFTO | Extended finite-time observer |
References
- Wang, R.; Sun, Q.; Hu, W.; Xiao, J.; Zhang, H.; Wang, P. Stability-Oriented Droop Coefficients Region Identification for Inverters within Weak Grid: An Impedance-Based Approach. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2258–2268. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, S.; Ma, J.; Jiang, Y.; Wang, P.; Liu, T.; Yang, Y. An Asymmetric Hybrid Phase-Leg Modular Multilevel Converter With Small Volume, Low Cost, and DC Fault-Blocking Capability. IEEE Trans. Power Electron. 2025, 40, 5336–5351. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Zhou, Y.; Zhang, Y.; Ukil, A. An Event-Triggered Deadbeat Control Considering Dynamic Power Loss Compensation for Hybrid Energy Storage System. IEEE Trans. Ind. Electron. 2023, 70, 6844–6855. [Google Scholar] [CrossRef]
- Kwon, M.; Choi, S. Control Scheme for Autonomous and Smooth Mode Switching of Bidirectional DC–DC Converters in a DC Microgrid. IEEE Trans. Power Electron. 2018, 33, 7094–7104. [Google Scholar] [CrossRef]
- Kotra, S.; Mishra, M.K. Design and Stability Analysis of DC Microgrid With Hybrid Energy Storage System. IEEE Trans. Sustain. Energy 2019, 3, 1603–1612. [Google Scholar] [CrossRef]
- Manandhar, U.; Ukil, A.; Gooi, H.B.; Tummuru, N.R.; Kollimalla, S.K.; Wang, B.; Chaudhari, K. Energy management and control for grid connected hybrid energy storage system under different operating modes. IEEE Trans. Smart Grid. 2019, 10, 1626–1636. [Google Scholar] [CrossRef]
- Tummuru, N.R.; Mishra, M.K.; Srinivas, S. Dynamic energy management of renewable grid integrated hybrid energy storage system. IEEE Trans. Ind. Electron. 2015, 62, 7728–7737. [Google Scholar] [CrossRef]
- Liu, B.; Zhuo, F.; Zhu, Y.; Yi, H. System operation and energy management of a renewable energy-based dc micro-grid for high penetration depth application. IEEE Trans. Smart Grid. 2015, 6, 1147–1155. [Google Scholar] [CrossRef]
- Cohen, I.J.; Wetz, D.A.; McRee, B.J.; Dong, Q.; Heinzel, J.M. Fuzzy logic control of a hybrid energy storage module for use as a high rate prime power supply. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3887–3893. [Google Scholar] [CrossRef]
- Feng, X.; Gooi, H.; Chen, S. Hybrid energy storage with multimode fuzzy power allocator for pv systems. IEEE Trans. Sustain. Energy 2014, 6, 389–397. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, J.; Wang, P.; Pan, X.; Wen, C. A decentralized control strategy for autonomous transient power sharing and state-of-charge recovery in hybrid energy storage systems. IEEE Trans. Sustain. Energy 2017, 8, 1443–1452. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, P.; Jiang, W.; Wang, P. A Decentralized Automatic Load Power Allocation Strategy for Hybrid Energy Storage System. IEEE Trans. Energy Convers. 2021, 36, 2227–2238. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Z.; Wang, J.; Zhang, X.; Wang, P. Decentralized Autonomous Energy Management Strategy for Multi-Paralleled Hybrid Energy Storage Systems in the DC Microgrid With Mismatched Line Impedance. IEEE Trans. Sustain. Energy 2024, 15, 1114–1126. [Google Scholar] [CrossRef]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 881–888. [Google Scholar]
- Wu, M.; Lu, D.D.C. A Novel Stabilization Method of LC Input Filter with Constant Power Loads Without Load Performance Compromise in DC Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4552–4562. [Google Scholar] [CrossRef]
- Cespedes, M.; Xing, L.; Sun, J. Constant-Power Load System Stabilization by Passive Damping. IEEE Trans. Power Electron. 2011, 26, 1832–1836. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L.; Wang, J. Stability Enhancement Based on Virtual Impedance for DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2015, 6, 2770–2783. [Google Scholar] [CrossRef]
- Narm, H.G.; Eren, S.; Karimi-Ghartemani, M. A Robust Controller with Integrated Plant Dynamics for Constant Power Loads in DC Microgrid. IEEE Trans. Power Electron. 2023, 38, 4419–4429. [Google Scholar] [CrossRef]
- Zhai, M.; Sun, Q.; Wang, R.; Wang, B.; Liu, S.; Zhang, H. Fully Distributed Fault-Tolerant Event-Triggered Control of Microgrids Under Directed Graphs. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3570–3579. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, L.; Zhao, H.; Zeng, H. Autonomous Voltage Regulation and Current Sharing in Islanded Multi-Inverter DC Microgrid. IEEE Trans. Smart Grid 2018, 9, 6429–6437. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed Cooperative Control of DC Microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Jinfeng, C.; Ke, J.; Zhenwen, X.; Rui, Z. Voltage Control Strategy of DC Microgrid Based on Discrete Consensus Algorithm. Zhejiang Electr. Power 2019, 38, 65–71. [Google Scholar]
- Liu, X.K.; He, H.; Wang, Y.W.; Xu, Q.; Guo, F. Distributed Hybrid Secondary Control for a DC Microgrid via Discrete-Time Interaction. IEEE Trans. Energy Convers. 2018, 33, 1865–1875. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Q.; Wen, C.; Wang, L.; Wang, P. Distributed Secondary Control for Power Allocation and Voltage Restoration in Islanded DC Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1857–1869. [Google Scholar] [CrossRef]
- Zhang, H.; Han, J.; Wang, Y.; Jiang, H. H∞ Consensus for Linear Heterogeneous Multiagent Systems Based on Event-Triggered Output Feedback Control Scheme. IEEE Trans. Cybern. 2019, 49, 2268–2279. [Google Scholar] [CrossRef]
- Huang, X.; Lin, W.; Yang, B. Global Finite-Time Stabilization of a Class of Uncertain Nonlinear Systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
| Symbol | Quantity | Nominal Value |
|---|---|---|
| bus voltage reference value | 300 V | |
| SC voltage reference value | 150 V | |
| Battery voltage reference value | 150 V | |
| switching frequency | 2 KHz | |
| L | inductance | 0.8 mH |
| C | capacitance | 2.2 mF |
| HES units’ line impedance | = 0.3 | |
| = 0.6 | ||
| = 0.8 | ||
| = 0.7 | ||
| Resistive Load | = 100 | |
| = 50 | ||
| = 80 | ||
| = 40 | ||
| Virtual Resistance Coefficient | , | |
| , | ||
| Virtual Inductance Coefficient | , | |
| , | ||
| 3 | ||
| 3 | ||
| 1 | ||
| k | Primary control gains | 2000 |
| 2000 | ||
| 10,000 | ||
| 0.5 | ||
| error gain | 20 | |
| 8 | ||
| 1 | ||
| Dynamic Event-triggered Control | 1.5 | |
| 0.5 | ||
| 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Zhou, H.; Huang, B. Distributed Control Strategy for Automatic Power Sharing of Hybrid Energy Storage Systems with Constant Power Loads in DC Microgrids. Mathematics 2025, 13, 2001. https://doi.org/10.3390/math13122001
Xia T, Zhou H, Huang B. Distributed Control Strategy for Automatic Power Sharing of Hybrid Energy Storage Systems with Constant Power Loads in DC Microgrids. Mathematics. 2025; 13(12):2001. https://doi.org/10.3390/math13122001
Chicago/Turabian StyleXia, Tian, He Zhou, and Bonan Huang. 2025. "Distributed Control Strategy for Automatic Power Sharing of Hybrid Energy Storage Systems with Constant Power Loads in DC Microgrids" Mathematics 13, no. 12: 2001. https://doi.org/10.3390/math13122001
APA StyleXia, T., Zhou, H., & Huang, B. (2025). Distributed Control Strategy for Automatic Power Sharing of Hybrid Energy Storage Systems with Constant Power Loads in DC Microgrids. Mathematics, 13(12), 2001. https://doi.org/10.3390/math13122001






