The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions

Abstract

In this paper, we focus on mean-field stochastic differential equations driven by G-Brownian motion (G-MFSDEs for short) with a drift coefficient satisfying the local one-sided Lipschitz condition with respect to the state variable and the global Lipschitz condition with respect to the law. We are concerned with the well-posedness and the numerical approximation of the G-MFSDE. Probability uncertainty leads the resulting expectation usually to be the G-expectation, which means that we cannot apply the numerical approximation for McKean–Vlasov equations to G-MFSDEs directly. To numerically approximate the G-MFSDE, with the help of G-expectation theory, we use the sample average value to represent the law and establish the interacting particle system whose mean square limit is the G-MFSDE. After this, we introduce the modified stochastic theta method to approximate the interacting particle system and study its strong convergence and asymptotic mean square stability. Finally, we present an example to verify our theoretical results.

1. Introduction

Mean-field stochastic differential equations (MFSDEs) (also referred to as stochastic McKean–Vlasov equations (MVSDEs)) were first introduced by Kac [1,2] to study the Boltzman equation for the particle density in diluted monatomic gases and the stochastic toy model for the Vlasov kinetic equation of plasma. Recently, Lions and Lasry [3], Huang et al. [4] and Bensoussan et al. [5] introduced mean-field game (MFG) theory to solve the existence of an approximate Nash equilibrium for differential games that have a large number of players. Subsequently, the MVSDEs and MFG theories have received widespread attention and played increasingly important roles in various fields, such as game theory, mathematical finance and the management of oil resources and complex networked systems. The well-posedness of MVSDEs with coefficients satisfying the global Lipschitz condition have been well studied in [6]. By truncating the coefficients in both the space and the distribution variables, Liu and Ma [7] obtained the existence and uniqueness of solutions to MVSDEs with coefficients satisfying local Lipschitz and linear growth conditions. Using an interpolated Euler-like sequence, Li et al. [8] established the existence and uniqueness of solutions to MVSDEs under local one-sided Lipschitz and uniform linear growth conditions. We refer the reader to [9,10] and the references therein for more results on the existence and uniqueness of solutions to MVSDEs under local Lipschitz conditions.

Most of the MVSDEs in [11] cannot be solved explicitly, so numerical methods are very important in practical applications. Compared with standard SDEs, the numerical simulation of MVSDEs always involves two steps: (1) approximating this distribution via the so-called interacting particle system; (2) proposing a stable numerical scheme to approximate the interacting particle system. Bossy and Talay [12] first investigated the Euler–Maruyama (EM) scheme for MVSDEs under the global Lipschitz condition. Budhiraja and Fan [13] studied the explicit Euler scheme for a specific MVSDE with a constant diffusion coefficient and a drift coefficient satisfying the global Lipschitz condition. Dos Reis et al. [14] showed that the implicit Euler scheme is convergent for MVSDEs with the drift term growing superlinearly and the diffusion term satisfying the global Lipschitz condition. Bao et al. [15] derived fully implementable first-order Milstein schemes for MVSDEs with a superlinearly growing drift term in the state component. More work on numerical approximations for MVSDEs can be found in [16,17,18,19,20] and the references therein.

In economy and finance, a vast number of applications require the modeling of Knightian uncertainty. Inspired by financial problems with uncertainty, Peng [21] introduced the theory of sublinear expectation and developed the theory of G-expectation; then, he proved that it can well characterize the Knightian uncertainty. In order to give a probabilistic interpretation of nonlocal PDEs of the mean-field type under the G-framework, Sun [22] introduced the mean-field backward stochastic differential equation driven by G-Brownian motion and studied its well-posedness. Recently, Xu et al. [23] established the existence and uniqueness of a solution for the G-MFSDEs under the global Lipschitz condition by applying the Banach fixed point theorem. Mao [24] pointed out that local Lipschitz-type conditions for classical SDEs ensure the existence and uniqueness of the local solution. Moreover, together with some growth conditions, such as linear growth conditions, monotone conditions or Khasminskii-type conditions, the local Lipschitz-type condition guarantees a global solution. We know that the local Lipschitz condition is more general than the global condition and the implicit scheme is more efficient than the explicit scheme for the stiff problem.

In this paper, we propose the modified stochastic theta method for the G-MFSDE whose drift coefficient satisfies the local Lipschitz condition with respect to the state variable and the global Lipschitz condition with respect to the law, and we then obtain the strong convergence and stability of the underlying scheme. Our main contributions and novelties can be summarized as follows: (I) due to the fact that the numerical approximation method for the McKean–Vlasov equations cannot be directly applied to G-MFSDEs, we use G-expectation theory and the sample average value to construct interacting particle systems whose mean square limits are G-MFSDEs, thereby numerically approximating the interacting particle systems; (II) we modify the stochastic theta method under the local one-sided Lipschitz condition to ensure that it is well-defined; furthermore, we use the modified stochastic theta method to approximate the interacting particle system and study the strong convergence and asymptotic mean square stability.

The paper is organized as follows. In Section 2, we briefly review some notations and results in the G-expectation framework. In Section 3, we study the well-posedness of the G-MFSDE under the local one-sided Lipschitz condition with respect to the state variable and establish the interacting particle system associated with it. In Section 4, we establish the modified stochastic theta method for the G-MFSDE and then study its strong convergence and stability. In Section 5, we present an example to verify the theoretical results.

2. Preliminaries

Let ${\mathbf{R}}^d$ be the space of d-dimensional real column vectors. Denote by $\mathbf{S}\left(d\right)$ the collection of all $d\times d$ symmetric matrices. Let $|·|$ represent the Euclidean norm in ${\mathbf{R}}^d$ or the trace norm in ${\mathbf{R}}^{d\times d}$. Let $\langle x,y\rangle$ be the inner product of $x,y\in {\mathbf{R}}^d$. Let $\Omega$ represent the nonempty sample space and ${\Omega }_t=\{\omega \left(·\wedge t\right):\omega \in \Omega \}$. Let $\mathcal{H}$ be the linear space of real-valued functions defined on $\Omega$ with $c\in \mathcal{H}$ for each constant c and $\left|X\right|\in \mathcal{H}$ if $X\in \mathcal{H}$. Denote by $\mathcal{B}(\Omega )$ the Borel $\sigma$ algebra on $\Omega$ and ${\mathcal{F}}_t=\mathcal{B}\left({\Omega }_t\right)$. Denote by $C_b(\Omega )$ all continuous elements in $B_b(\Omega )$ and $C_b\left({\Omega }_t\right)=C_b(\Omega )\cap L^0\left({\Omega }_t\right)$. Let $C_{b,L_{ip}}\left({\mathbf{R}}^{d\times n}\right)$ be the space of bounded and Lipschitz-continuous functions defined on ${\mathbf{R}}^{d\times n}$ and $C^{2,1}({\mathbf{R}}^d\times {\mathbf{R}}^d)$ be the space of continuously differentiable functions $f(x,y)$ defined on ${\mathbf{R}}^d\times {\mathbf{R}}^d$, which are twice-differentiable in x and once-differentiable in y. Let $\mathcal{P}\left({\mathbf{R}}^d\right)$ represent the space of all probability measures over $({\mathbf{R}}^d,\mathcal{B}\left({\mathbf{R}}^d\right))$ carrying the usual topology of weak convergence.

Definition 1 

([21]). A functional $\widehat{\mathbf{E}}:\mathcal{H}\to \mathbf{R}$ is called a sublinear expectation if, for any $X,Y\in \mathcal{H}$, it satisfies

(1) 

Monotonicity: $\widehat{\mathbf{E}}\left[X\right]\ge \widehat{\mathbf{E}}\left[Y\right]$ if $X\ge Y$;

(2) 

Constant preserving: $\widehat{\mathbf{E}}\left[C\right]=C$, $\forall C\in \mathbf{R}$;

(3) 

Subadditivity: $\widehat{\mathbf{E}}[X+Y]\le \widehat{\mathbf{E}}\left[X\right]+\widehat{\mathbf{E}}\left[Y\right]or\widehat{\mathbf{E}}\left[X\right]-\widehat{\mathbf{E}}\left[Y\right]\le \widehat{\mathbf{E}}[X-Y]$;

(4) 

Positive homogeneity: $\widehat{\mathbf{E}}\left[\lambda Y\right]=\lambda \widehat{\mathbf{E}}\left[Y\right]$, $\lambda \ge 0$.

We call the triple $(\Omega ,\mathcal{H},\widehat{\mathbf{E}})$ a sublinear expectation space.

Let $\Omega =C([0,\infty );{\mathbf{R}}^d)$ denote the space of all ${\mathbf{R}}^d$-valued continuous paths (${\omega }_t{)}_{t\ge 0}$ with ${\omega }_0=0$, equipped with the distance

$${\rho }_d({\omega }^1,{\omega }^2)=\sum _{i=1}^{\infty }{\displaystyle \frac{1}{2^i}}(\underset{t\in [0,i]}{max}|{\omega }_t^1-{\omega }_t^2|\wedge 1).$$

Given any $T>0$, we also define ${\Omega }_T=\{{\left({\omega }_{r\wedge T}\right)}_{r\ge 0}:\omega \in \Omega \}.$ Let $B_r\left(\omega \right)={\omega }_r$, $\omega \in \Omega$, $r\ge 0$, be the canonical process on $\Omega$. We introduce the space

$$\begin{array}{cc}\hfill L_{ip}\left({\Omega }_T\right)=& \left\{\phi (B_{r_1},B_{r_2}-B_{r_1},\cdots ,B_{r_n}-B_{r_{n-1}}):n\ge 1,0\le r_1<r_2<\cdots <r_n\le T,\right.\hfill \\ \hfill & \left.\phi \in C_{b,Lip}\left({\mathbf{R}}^{d\times n}\right)\right\}\hfill \end{array}$$

$L_{ip}(\Omega )={\bigcup }_{k=1}^{\infty }{L}_{ip}\left({\Omega }_k\right)$.

Definition 2. 

On the sublinear expectation space $(\Omega ,L_{ip}(\Omega ),\widehat{\mathbf{E}})$, the canonical process ${\left(B_r\right)}_{r\ge 0}$ is called G-Brownian motion if it satisfies

(1) 

$B_0=0$;

(2) 

$B_{r+s}-B_r\stackrel{d}{=}\sqrt{r}\xi$, for $s,r\ge 0$, where ξ is G-normally distributed;

(3) 

For all $0\le r_1\le \cdots \le r_d\le r<\infty$, the increments $B_{r+s}-B_r$ are independent of $B_{r_1},B_{r_2},\cdots ,B_{r_d}$.

Then, the sublinear expectation $\widehat{\mathbf{E}}[·]$ is called a G-expectation. More details regarding G-expectations and G-Brownian motion can be found in Peng [21], Hu-Peng [25] and Li-Peng [26].

For every $p\ge 1$, let $L_G^p(\Omega ,L_{ip}(\Omega ),\widehat{\mathbf{E}};{\mathbf{R}}^d)$ ($L_G^p(\Omega )$ for short) denote the completion of $L_{ip}(\Omega )$ under the norm ${\parallel ·\parallel }_p=(\widehat{\mathbf{E}}{|·|}^p{)}^{{\displaystyle \frac{1}{p}}}$. Additionally, denote by $L_G^p\left({\Omega }_t\right)$ the complete space of $L_{ip}\left({\Omega }_t\right)$ and $L_G^p\left({\Omega }_t\right)\subset L_G^p\left({\Omega }_T\right)\subset L_G^p(\Omega )$ for $0\le t\le T<\infty$.

Remark 1. 

In numerical simulations of mean-field stochastic differential equations, we only need to treat the linear expectation. The linear expectation operation follows the principle of additivity, which means that the expectation value of the sum of several random variables is equal to the sum of their respective expectation values. However, within the framework of sublinear expectation theory, the principle of additivity is no longer applicable. In a sublinear expectation space, the subadditivity and positive homogeneity make the study of the strong convergence and asymptotic mean square stability of the modified stochastic theta method for G-MFSDEs more complex than in a linear expectation space.

Lemma 1 

([25]). Let

$$\mathcal{P}=\{Pprobabilityon(\Omega ,\mathcal{B}(\Omega )):E_P\left[X\right]\le \widehat{\mathbf{E}}\left[X\right],forallX\in L_G^1(\Omega )\}.$$

Then, $\mathcal{P}\ne \varnothing$ is a convex, weakly compact subset of the space $\mathcal{P}\left({\mathbf{R}}^d\right)$ of all probability measures over $({\mathbf{R}}^d,\mathcal{B}\left({\mathbf{R}}^d\right))$ endowed with the topology of weak convergence, and

$$\widehat{\mathbf{E}}\left[\zeta \right]=\underset{P\in \mathcal{P}}{sup}{E}_P\left[\zeta \right],\zeta \in L_G^1(\Omega ).$$

(1)

We consider that the set $\mathcal{P}$ can represent $\widehat{\mathbf{E}}$.

Proposition 1 

([21]). The supremum in (1) is indeed a maximum, i.e., there exists a probability measure $P\in \mathcal{P}$ such that $\widehat{\mathbf{E}}\left[\zeta \right]=E_P\left[\zeta \right]$ for all $\zeta \in L_G^1(\Omega )$. Moreover, the set

$${\mathcal{P}}_{\left\{\zeta \right\}}=\left\{P\in \mathcal{P}:\widehat{\mathbf{E}}\left[\zeta \right]=E_P\left[\zeta \right]\right\}$$

is nonempty.

Now, we can define a Choquet capacity

$$\begin{array}{c}\hfill \mathcal{V}\left(A\right)=\underset{P\in \mathcal{P}}{sup}P\left(A\right)forA\in \mathcal{B}(\Omega ).\end{array}$$

Then, the notation of “quasi-surely” (q.s.) is defined as below.

Definition 3. 

A set $A\in \mathcal{B}(\Omega )$ is called polar if $\mathcal{V}\left(A\right)=0$. A property is said to hold quasi-surely if it holds outside a polar set.

We present an important proposition about conditional G-expectation $\widehat{\mathbf{E}}[·|{\Omega }_r]$, $r\in [0,T]$.

Proposition 2 

([21]).  The conditional expectation $\widehat{\mathbf{E}}[·|{\Omega }_r]$, $r\in [0,T]$ holds for each $X,Y\in L_G^1\left({\Omega }_r\right)$ if the following apply.

(1) 

If $X\ge Y$, then $\widehat{\mathbf{E}}\left[X\right|{\Omega }_r]\ge \widehat{\mathbf{E}}\left[Y\right|{\Omega }_r]$.

(2) 

$\widehat{\mathbf{E}}\left[\eta \right|{\Omega }_r]=\eta$, for each $r\in [0,\infty )$ and $\eta \in L_G^1\left({\Omega }_r\right)$.

(3) 

$\widehat{\mathbf{E}}\left[X\right|{\Omega }_r]-\widehat{\mathbf{E}}\left[Y\right|{\Omega }_r]\le \widehat{\mathbf{E}}[X-Y|{\Omega }_r]$.

(4) 

$\widehat{\mathbf{E}}\left[\eta X\right|{\Omega }_r]={\eta }^{+}\widehat{\mathbf{E}}\left[X\right|{\Omega }_r]+{\eta }^{-}\widehat{\mathbf{E}}[-X|{\Omega }_r]$ for each bounded $\eta \in L_G^1\left({\Omega }_r\right)$.

(5) 

$\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}\left[X\right|{\Omega }_r]\right|{\Omega }_s]=\widehat{\mathbf{E}}\left[X\right|{\Omega }_{r\wedge s}]$, in particular $\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}\left[X\right|{\Omega }_r]\right]=\widehat{\mathbf{E}}\left[X\right]$.

Define the space of simple processes

$$M_G^{p,0}\left([0,T]\right)=\left\{{\eta }_r=\sum _{j=0}^{n-1}{\xi }_{r_j}{I}_{[r_j,r_{j+1})}\left(r\right):0\le r_0<r_1<\cdots <r_n\le T,{\xi }_{r_j}\in L_G^p\left({\Omega }_{r_j}\right)\right\}.$$

We denote by $M_G^p\left([0,T]\right)$ the completion of $M_G^{p,0}\left([0,T]\right)$ under the norm ${\parallel \eta \parallel }_{M_G^p\left([0,T]\right)}={\left({\displaystyle \frac{1}{T}}{\int }_0^T\widehat{\mathbf{E}}{\left|{\eta }_r\right|}^{p}dr\right)}^{{\displaystyle \frac{1}{p}}}$. Let ${\left\{B_r\right\}}_{r\ge 0}$ be a one-dimensional G-Brownian motion with $G\left(a\right)={\displaystyle \frac{1}{2}}\widehat{\mathbf{E}}\left[a{B}_1^2\right]={\displaystyle \frac{1}{2}}({\overline{\sigma }}^2{a}^{+}-{\underline{\sigma }}^2{a}^{-})$, where $\widehat{\mathbf{E}}\left[B_1^2\right]={\overline{\sigma }}^2$, $-\widehat{\mathbf{E}}[-B_1^2]={\underline{\sigma }}^2$, $0\le \underline{\sigma }\le \overline{\sigma }<\infty$. One can see Definition 3.3.3 and (3.4.1) in Peng [21] for the definitions of the It$\widehat{o}$ integral and the quadratic variation process with G-Brownian motion. In the following, we present the lemmas used in the remainder of the paper.

Lemma 2. 

For each $0\le r\le T<\infty$, let the quadratic variation of G-Brownian motion ${\langle B\rangle }_r={\int }_0^r{v}_{s}ds$. Then, we have

$${\underline{\sigma }}^2(T-r)\le {\langle B\rangle }_T-{\langle B\rangle }_r\le {\overline{\sigma }}^2(T-r)q.s.$$

Moreover, ${\underline{\sigma }}^{2}dr\le d{\langle B\rangle }_r=v_{r}dr\le {\overline{\sigma }}^{2}dr$ q.s.

Lemma 3. 

For any $0\le s\le T<\infty$ and $p\ge 1$,

(1) 

$\widehat{\mathbf{E}}\left[{\int }_s^T{\eta }_{r}d{B}_r\right]=0$; $\widehat{\mathbf{E}}\left[\begin{array}{c}\hfill \left|{\int }_s^T{\eta }_{r}d{\langle B\rangle }_r\right|\end{array}\right]\le {\overline{\sigma }}^2\widehat{\mathbf{E}}{\int }_s^T\left|{\eta }_r\right|dr,\forall \eta \in M_G^1\left([0,T]\right)$,

(2) 

$\widehat{\mathbf{E}}\left[{\left({\int }_s^T{\eta }_{r}d{B}_r\right)}^2\right]=\widehat{\mathbf{E}}\left[{\int }_s^T{\eta }_r^{2}d{\langle B\rangle }_r\right],\forall \eta \in M_G^2\left([0,T]\right)$,

(3) 

$\widehat{\mathbf{E}}\left[{\int }_s^T|{\eta }_r{|}^{p}dr|\right]\le {\int }_s^T\widehat{\mathbf{E}}{\left|{\eta }_r\right|}^{p}dr$, $\forall \eta \in M_G^p\left([0,T]\right),p\ge 1.$

Lemma 4. 

For any $p\ge 1$, $s\in [0,T]$ and $\eta \in M_G^p\left([0,T]\right)$, we have

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{s\le u\le T}{sup}|{\int }_s^u{\eta }_{r}d{\langle B\rangle }_r{|}^p\right)\le {\overline{\sigma }}^{2p}{(T-s)}^{p-1}\widehat{\mathbf{E}}\left[{\int }_s^T{\left|{\eta }_r\right|}^{p}dr\right].\end{array}$$

Lemma 5. 

For any $p\ge 2$, $s\in [0,T]$ and $\eta \in M_G^p\left([0,T]\right)$, we have

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{s\le u\le T}{sup}|{\int }_s^u{\eta }_{r}d{B}_r{|}^p\right)\le {\overline{\sigma }}^p{(T-s)}^{{\displaystyle \frac{p}{2}}-1}\widehat{\mathbf{E}}\left[{\int }_s^T{\left|{\eta }_r\right|}^{p}dr\right].\end{array}$$

Proof. 

The proofs of Lemmas 3–5 follow from [21,24,27], and so we omit them here. □

3. The Well-Posedness of G-MFSDEs and the Stochastic Particle Method

This paper focuses on the following G-MFSDE:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dX\left(r\right)=b(X\left(r\right),\widehat{\mathbf{E}}\left[X\left(r\right)\right])dr+\iota (X\left(r\right),\widehat{\mathbf{E}}\left[X\left(r\right)\right])d{B}_r+h(X\left(r\right),\widehat{\mathbf{E}}\left[X\left(r\right)\right])d{\langle B\rangle }_r,\hfill \\ X\left(0\right)=\xi ,0\le r\le T<\infty ,\hfill \end{array}\right.\end{array}$$

(2)

where $b:{\mathbf{R}}^d\times {\mathbf{R}}^d\to {\mathbf{R}}^d$, $\iota :{\mathbf{R}}^d\times {\mathbf{R}}^d\to {\mathbf{R}}^d$ and $h:{\mathbf{R}}^d\times {\mathbf{R}}^d\to {\mathbf{R}}^d$ are Borel-measurable functions, $B_r$ is a one-dimensional G-Brownian motion, ${\langle B\rangle }_r$ is the quadratic variation process of $B_r$, $\widehat{\mathbf{E}}$ represents the G-expectation and $\xi$ is an ${\mathbf{R}}^d$-valued ${\mathcal{F}}_0$-measurable random variable. Note that the coefficients of (2) depend on the state process and their law, where the law is defined via the G-expectation.

3.1. Local One-Sided Lipschitz Condition

In practical applications, we often have some equations in which the drift coefficients are not global or local Lipschitz conditions. For example, $b\left(x\right)=x^3-{\left|x\right|}^{{\displaystyle \frac{1}{2}}}$ and $b\left(x\right)=x+x^2-x^3-{\left|x\right|}^{{\displaystyle \frac{1}{2}}}$ are not local Lipschitz, while it can be proven that $b\left(x\right)$ are local one-sided Lipschitz. So, in this paper, we are concerned with (2) under the local one-sided Lipschitz condition. We impose the following assumptions.

Assumption 1. 

For each $R>0$, there exists a positive constant $L_R$ with $L_R\le alogR$ for some constant a such that, for any $x,y\in {\mathbf{R}}^d$ with $\left|x\right|\vee \left|y\right|\le R$ and $z\in {\mathbf{R}}^d$,

$$\begin{array}{cc}\hfill \langle x-y,b(x,z)-b(y,z)\rangle \le & L_R{|x-y|}^2.\hfill \end{array}$$

Assumption 2. 

There exists a positive constant L such that, for any $x,y,u,v\in {\mathbf{R}}^d$,

$$\begin{array}{cc}\hfill {|b(y,u)-b(y,v)|}^2{\vee |\iota (x,u)-\iota (y,v)|}^2\vee {|h(x,u)-h(y,v)|}^2\le & L\left(\right|x-y{|}^2+|u-v{|}^2).\hfill \end{array}$$

Assumption 3. 

For any $y,u\in {\mathbf{R}}^d$, there exists a positive constant M such that

$$\begin{array}{c}\hfill \langle y,b(y,u)\rangle \le M\left(\right|y{|}^2+\left|u{|}^2\right),\end{array}$$

and

$$\begin{array}{c}\hfill \left|b\right(y,u\left)\right|\vee \left|\iota \right(y,u\left)\right|\vee \left|h\right(y,u\left)\right|\le M\left(\right|y|+|u\left|\right).\end{array}$$

Remark 2. 

The inequality in Assumption 2 shows that both the drift and diffusion coefficients are globally Lipschitz continuous in the law. In Assumption 3, we require growth conditions on both coefficients, which are essential in achieving the moment boundedness of (2) and analyzing the strong convergence and stability of the numerical solution.

Theorem 1. 

Let Assumptions 1–3 hold. Assume that $b(x,y)$, $\iota (x,y)$ and $h(x,y)$ belong to $M_G^2([0,T],{\mathbf{R}}^d)$ for any $x,y\in {\mathbf{R}}^d$. Then, G-MFSDE (2) subject to $X\left(0\right)=\xi$ has a unique strong solution ${\left\{X\left(t\right)\right\}}_{t\in [0,T]}$. Furthermore, for any $p\ge 2$, there exists a constant $C>0$ such that

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le t\le T}{sup}{\left|X\left(t\right)\right|}^p\right)<C.\end{array}$$

Proof. 

The proof of the existence and uniqueness of the solution in this theorem is similar to those in [8,23], so we omit it here. Thus, we only need to estimate the pth moment of the solution.

For each $R>0$, we define the stopping time

$${\tau }_R=inf\{r\in [0,T]:|X\left(r\right)|\ge R\}\wedge T.$$

The G-It$\widehat{o}$ formula yields

$$\begin{array}{cc}\hfill \underset{0\le r\le t\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^2\le & {\left|X\left(0\right)\right|}^2+2{\int }_0^{t\wedge {\tau }_R}\langle X\left(s\right),b(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle ds\hfill \\ & +2\underset{0\le r\le t\wedge {\tau }_R}{sup}{\int }_0^r\langle X\left(s\right),\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle d{B}_s\hfill \\ \hfill & +\underset{0\le r\le t\wedge {\tau }_R}{sup}{\int }_0^r\left({\iota }^T\iota \right)(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])d{\langle B\rangle }_s\hfill \\ \hfill & +2\underset{0\le r\le t\wedge {\tau }_R}{sup}{\int }_0^r\langle X\left(s\right),h(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle d{\langle B\rangle }_s.\hfill \end{array}$$

(3)

For any $p\ge 2$ and $t\in [0,T]$, we have

$$\begin{array}{cc}\hfill \underset{0\le r\le t\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\le & C_1\{{\left|X\left(0\right)\right|}^p+{\left({\int }_0^{t\wedge {\tau }_R}\langle X\left(s\right),b(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle ds\right)}^{{\displaystyle \frac{p}{2}}}\hfill \\ & +\underset{0\le r\le t\wedge {\tau }_R}{sup}{\left({\int }_0^r\langle X\left(s\right),\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle d{B}_s\right)}^{{\displaystyle \frac{p}{2}}}\hfill \\ \hfill & +\underset{0\le r\le t\wedge {\tau }_R}{sup}{\left({\int }_0^r\left({\iota }^T\iota \right)(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])d{\langle B\rangle }_s\right)}^{{\displaystyle \frac{p}{2}}}\hfill \\ \hfill & +\underset{0\le r\le t\wedge {\tau }_R}{sup}{\left({\int }_0^r\langle X\left(s\right),h(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\rangle d{\langle B\rangle }_s\right)}^{{\displaystyle \frac{p}{2}}}\},\hfill \end{array}$$

(4)

where $C_1$ is a constant dependent on p. Taking the G-expectation on both sides, it follows from the H$\ddot{o}$lder inequality, Assumption 3 and Lemmas 4 and 5 that

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le t\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\right)\le & C_2\{\widehat{\mathbf{E}}{\left|X\left(0\right)\right|}^p+\widehat{\mathbf{E}}{\int }_0^{t\wedge {\tau }_R}{\left|X\left(s\right)\right|}^{p}ds\hfill \\ \hfill & +\widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|X\left(s\right)\right|}^2{\left|\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{4}}}\hfill \\ \hfill & +\widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{2}}}\hfill \\ & +\widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|X\left(s\right)\right|}^2{\left|h(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{4}}}\},\hfill \end{array}$$

(5)

where $C_2$ is a constant. The Cauchy–Schwarz inequality yields

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|X\left(s\right)\right|}^2{\left|h(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{4}}}\hfill \\ \hfill \le & \widehat{\mathbf{E}}\left(\underset{0\le s\le t\wedge {\tau }_R}{sup}{\left|X\left(s\right)\right|}^{{\displaystyle \frac{p}{2}}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|h(X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{4}}}\right)\hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}\widehat{\mathbf{E}}\left(\underset{0\le s\le t\wedge {\tau }_R}{sup}{\left|X\left(s\right)\right|}^p\right)+C_3{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le r\le s\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\right)ds.\hfill \end{array}$$

A similar estimate holds for

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|X\left(s\right)\right|}^2{\left|\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{4}}}\end{array}$$

and

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}{\left({\int }_0^{t\wedge {\tau }_R}{\left|\iota (X\left(s\right),\widehat{\mathbf{E}}\left[X\left(s\right)\right])\right|}^{2}ds\right)}^{{\displaystyle \frac{p}{2}}}.\end{array}$$

Substituting these into (5) gives

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le t\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\right)\le & C_4\left(\widehat{\mathbf{E}}{\left|X\left(0\right)\right|}^p+{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le r\le s\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\right)ds\right)\end{array}$$

(6)

for some constant $C_4$. As ${\tau }_R\uparrow T$ a.s., the Gronwall inequality yields

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{\left|X\left(r\right)\right|}^p\right)\le \underset{R\to \infty }{lim}inf\widehat{\mathbf{E}}\left(\underset{0\le r\le T\wedge {\tau }_R}{sup}{\left|X\left(r\right)\right|}^p\right)\le C_5,\end{array}$$

where $C_5$ is a constant, which implies the desired result. □

3.2. The Interacting Particle System and Propagation of Chaos

For $N\ge 1$ and $i=1,2,\cdots ,N$. Let $({\xi }^1,B_t^1),({\xi }^2,B_t^2),\cdots ,({\xi }^N,B_t^N)$ be independent identically distributed (i.i.d.) of $(\xi ,B_t)$. We use the sample average value ${\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{X}^{i,N}\left(t\right)$ to approximate the G-expectation of $X^i\left(t\right)$. Thus, G-MFSDE (2) is obtained as the mean square limit of the system

$$\begin{array}{cc}\hfill d{X}^{i,N}\left(t\right)=& b(X^{i,N}\left(t\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right))dt+\iota (X^{i,N}\left(t\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right))d{B}_t^i\hfill \\ \hfill & +h(X^{i,N}\left(t\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right))d{\langle B^i\rangle }_t,t\ge 0,\hfill \end{array}$$

(7)

subject to the initial value $X^{i,N}\left(0\right)={\xi }^i$, $i=1,2,\cdots ,N$. We call (7) the interacting particle system associated with G-MFSDE (2).

We also introduce the following standard G-MFSDEs, called the noninteracting particle system,

$$\begin{array}{c}\hfill d{X}^i\left(t\right)=b(X^i\left(t\right),\widehat{\mathbf{E}}\left[X^i\left(t\right)\right])dt+\iota (X^i\left(t\right),\widehat{\mathbf{E}}\left[X^i\left(t\right)\right])d{B}_t^i+h(X^i\left(t\right),\widehat{\mathbf{E}}\left[X^i\left(t\right)\right])d{\langle B^i\rangle }_t,t\ge 0,\end{array}$$

(8)

subject to the initial value $X^i\left(0\right)={\xi }^i$, $i=1,2,\cdots ,N$.

When N becomes large, the solution of (7) approximates that of (2) in an appropriate sense, which is called the propagation of chaos. The pathwise propagation of chaos refers to the property

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}\underset{1\le i\le N}{sup}\widehat{\mathbf{E}}\left(\underset{t\in [0,T]}{sup}|X^{i,N}\left(t\right)-X^i\left(t\right){|}^2\right)=0,\end{array}$$

which plays a key role in the convergence analysis. More details regarding the stochastic particle method can be found in Carmona [28] and Sznitman [29].

The following lemma proves the propagation of chaos for the G-MFSDE under the local one-sided Lipschitz condition.

Lemma 6. 

Under Assumptions 1 and 2, it holds that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \underset{N\to \infty }{lim}}{\displaystyle \underset{i\le i\le N}{sup}}\widehat{\mathbf{E}}\left({\displaystyle \underset{0\le r\le T}{sup}}{|X^{i,N}\left(r\right)-X^i\left(r\right)|}^2\right)=0.\end{array}\end{array}$$

Proof. 

For any $1\le i\le N$ and $R>0$, define the stopping time ${\tau }_R^i=inf\{r\in [0,T]:|X^{i,N}\left(r\right)|\ge R\}\wedge inf\{r\in [0,T]:|X^i\left(r\right)|\ge R\}$; the G-It$\widehat{o}$ formula gives

$$\begin{array}{cc}\hfill & \underset{0\le r\le t}{sup}|X^{i,N}(r\wedge {\tau }_R^i)-X^i(r\wedge {\tau }_R^i){|}^2\hfill \\ \hfill \le & 2\underset{0\le r\le t}{sup}{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),b\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ \hfill & -b\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle ds\hfill \\ \hfill & +2\underset{0\le r\le t}{sup}{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),\iota \left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ \hfill & -\iota \left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle d{B}_s^i\hfill \\ \hfill & +\underset{0\le r\le t}{sup}{\int }_0^r|\iota \left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)-\iota \left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right){|}^{2}d{\langle B^i\rangle }_s\hfill \\ \hfill & +2\underset{0\le r\le t}{sup}{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),h\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ \hfill & -h\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle d{\langle B^i\rangle }_s.\hfill \end{array}$$

(9)

Denote

$$\begin{array}{cc}\hfill I_{1,R}\left(r\right)& =2{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),b\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ & -b\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle ds,\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{2,R}\left(r\right)& =2{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),\iota \left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ & -\iota \left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle d{B}_s^i,\hfill \end{array}$$

$$\begin{array}{c}\hfill I_{3,R}\left(r\right)={\int }_0^r|\iota (X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i))-\iota \left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right){|}^{2}d{\langle B^i\rangle }_s,\end{array}$$

and

$$\begin{array}{cc}\hfill I_{4,R}\left(r\right)& =2{\int }_0^r\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),h\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ & -h\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle d{\langle B^i\rangle }_s.\hfill \end{array}$$

Noting that $\widehat{\mathbf{E}}\left[{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{X}^{i,N}\left(t\right)\right]=\widehat{\mathbf{E}}\left[X^{i,N}\left(t\right)\right]$, it follows from Assumptions 1 and 2 that, for any $t\in [0,T]$,

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{I}_{1,R}(r\wedge {\tau }_R^i)\right)\hfill \\ \hfill \le & 2\widehat{\mathbf{E}}({\int }_0^t\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),b\left(X^{i,N}(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\hfill \\ \hfill & -b\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle ds)\hfill \\ \hfill & +2\widehat{\mathbf{E}}({\int }_0^t\langle X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i),b\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ \hfill & -b\left(X^{i,N}(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)\rangle ds)\hfill \\ \hfill \le & 2(L_R+L){\int }_0^t\widehat{\mathbf{E}}{|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|}^{2}ds.\hfill \end{array}$$

(10)

Using the Cauchy–Schwarz inequality, Lemma 5 and Assumptions 1 and 2, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{I}_{2,R}(r\wedge {\tau }_R^i)\right)\le & {\displaystyle \frac{1}{2}}\widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{|X^{i,N}(\wedge {\tau }_R^i)-X^i(r\wedge {\tau }_R^i)|}^2\right)\hfill \\ & +4{\overline{\sigma }}^2(L_R+L){\int }_0^t\widehat{\mathbf{E}}{|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|}^{2}ds.\hfill \end{array}$$

(11)

Similar to (11), with Lemma 4, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{I}_{3,R}(r\wedge {\tau }_R^i)\right)\le & {\overline{\sigma }}^2\widehat{\mathbf{E}}({\int }_0^t|\iota \left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)\hfill \\ & -\iota \left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right){|}^{2}ds)\hfill \\ \hfill \le & 2{\overline{\sigma }}^2(L_R+L){\int }_0^t\widehat{\mathbf{E}}{|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|}^{2}ds,\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}(\underset{0\le r\le t}{sup}& I_{4,R}(r\wedge {\tau }_R^i))\le 2{\overline{\sigma }}^2\widehat{\mathbf{E}}({\int }_0^t|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|\hfill \end{array}$$

$$\begin{array}{c}·|h\left(X^{i,N}(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)-h\left(X^i(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)|ds)\\ +2{\overline{\sigma }}^2\widehat{\mathbf{E}}({\int }_0^t|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|\hfill \\ ·|h\left(X^{i,N}(s\wedge {\tau }_R^i),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge {\tau }_R^i)\right)-h\left(X^{i,N}(s\wedge {\tau }_R^i),\widehat{\mathbf{E}}\left[X^i(s\wedge {\tau }_R^i)\right]\right)|ds)\hfill \\ \le 4{\overline{\sigma }}^2(1+L_R+L){\int }_0^{t\wedge {\tau }_R^i}\widehat{\mathbf{E}}{|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|}^{2}ds.\end{array}$$

(13)

Substituting (10)–(13) into (9), we have

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{|X^{i,N}(r\wedge {\tau }_R^i)-X^i(r\wedge {\tau }_R^i)|}^2\right)\hfill \\ \hfill \le & 2(2L_R+4{\overline{\sigma }}^2+10{\overline{\sigma }}^2{L}_R+2L+10{\overline{\sigma }}^{2}L){\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le s\le r}{sup}{|X^{i,N}(s\wedge {\tau }_R^i)-X^i(s\wedge {\tau }_R^i)|}^2\right)dr.\hfill \end{array}$$

Letting $R\to \infty$, the Gronwall inequality yields the desired assertion. □

Remark 3. 

We can see that (8) are standard G-MFSDEs and they serve as a bridge between the G-MFSDE and its interacting particle system. By Lemma 6, we can numerically approximate the G-MFSDE via numerically approximating its interacting particle system.

4. The Modified Stochastic Theta Method and Its Strong Convergence and Asymptotic Mean Square Stability

We know that the implicit scheme is more efficient than the explicit scheme for some stiff problems. We introduce the modified stochastic theta scheme to approximate G-MFSDE (2) in this section. The conclusions of the modified stochastic theta scheme can be extended to the explicit schemes.

For a positive integer n, define $\Delta =T/n$ and a partition $\{t_k=k\Delta :k=0,1,\cdots ,n\}$. Let $Y_0^{i,N,n}={\xi }^i$ and define

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}=& Y_k^{i,N,n}+\theta b\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\Delta +(1-\theta )b\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta \hfill \\ \hfill & +\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i+h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k,\hfill \end{array}$$

(14)

where ${\mu }_k^{Y,N,n}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{Y}_k^{i,N,n}$, $\Delta B_k^i=B_{k+1}^i-B_k^i$ and $\Delta {\langle B^i\rangle }_k=\langle B_{k+1}^i\rangle -\langle B_k^i\rangle$. Here, the parameter $\theta \in [0,1]$ impacts the implicitness of the numerical scheme. When $\theta =0$, the theta scheme is simplified to the EM scheme, and it is the backward EM scheme when $\theta =1$. Before we use an implicit scheme, we must make sure that it is well defined. It follows from the theory of monotone operators in [30] and Mao-Szpruch [31] that the drift term should satisfy

$$\begin{array}{c}\hfill \langle x-y,b(x,u)-b(y,u)\rangle \le {K|x-y|}^2,\end{array}$$

(15)

where K is a positive constant, and this condition can hardly be relaxed. In our Assumption 1, $L_R$ may tend to ∞ as $R\to \infty$, which means that the stochastic theta method (14) may be not well defined under the local one-sided Lipschitz condition. So, we need to modify the stochastic theta scheme with a truncated method.

4.1. The Modified Stochastic Theta Method

Choose a strictly decreasing function $\kappa :(0,1]\to (0,\infty )$ such that

$$\begin{array}{c}\hfill \underset{\Delta \to 0}{lim}\kappa (\Delta )=\infty ,L_{\kappa (\Delta )}{e}^{L_{\kappa (\Delta )}}\Delta \le 1,\mathrm{and}{\left(\kappa (\Delta )\right)}^2\Delta \le 1.\end{array}$$

(16)

We then face a question: does such a function exist? The answer is positive. For example, define $\kappa (\Delta )=ln{\Delta }^{-{\displaystyle \frac{1}{2}}}$; then, we can prove that $\kappa (\Delta )$ decreases strictly and tends to ∞ as $\Delta \to 0$. Let $L_{\kappa (\Delta )}=\kappa (\Delta )$, and we have $L_{\kappa (\Delta )}{e}^{L_{\kappa (\Delta )}}\Delta \le {\Delta }^{{\displaystyle \frac{1}{2}}}<1$ and ${\left(\kappa (\Delta )\right)}^2\Delta \le 1$.

We can also define a smooth, non-negative function $I_{\Delta }$ with compact support where

$$I_{\Delta }\left(y\right)=\left\{\begin{array}{c}1,for\left|y\right|\le \kappa (\Delta ),\hfill \\ 0,for\left|y\right|>\kappa (\Delta ).\hfill \end{array}\right.$$

It is easy to see that $I_{\Delta }\left(y\right)\le 1$ for all $y\in {\mathbf{R}}^d$, and $I_{\Delta }\left(y\right)$ is Lipschitzian with some constant $L_{I_{\Delta }}$.

Now, we define a truncated function by

$$b_{\Delta }(y,u)=I_{\Delta }\left(y\right)b(y,u).$$

It can be proven that the truncated function satisfies the following.

Lemma 7. 

Under Assumption 3, it holds that, for any $y,u\in {\mathbf{R}}^d$,

$$\begin{array}{c}\hfill \langle y,b_{\Delta }(y,u)\rangle \le {M\left(\right|y|}^2+{\left|u\right|}^2),and|b_{\Delta }(y,u)|\le M(\left|y\right|+\left|u\right|).\end{array}$$

(17)

Lemma 8. 

Under Assumptions 1–3, it holds that, for any $y,z$, $u\in {\mathbf{R}}^d$,

$$\begin{array}{c}\hfill \langle y-z,b_{\Delta }(y,u)-b_{\Delta }(z,u)\rangle \le {\overline{L}}_{\kappa (\Delta )}{|y-z|}^2,\end{array}$$

(18)

where ${\overline{L}}_{\kappa (\Delta )}=L_{\kappa (\Delta )}+2L_{I_{\Delta }}M\left|\kappa (\Delta )\right|$.

The proofs of Lemmas 7 and 8 are similar to those of Lemmas 2.2 and 2.3 in [32], so we omit the details here.

For $\theta \in [0,1]$, we apply the modified stochastic theta method to (7) to give

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}=& Y_k^{i,N,n}+\theta b_{\Delta }\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\Delta +(1-\theta )b_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta \hfill \\ & +\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i+h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k,\hfill \end{array}$$

(19)

With (16) and Lemma 8, the monotone operator implies that (19) is well defined. Considering the implicitness of the stochastic theta scheme, we set $\theta \Delta <{\displaystyle \frac{1}{12M}}$, where M is the constant defined in Assumption 3. Thus, we set ${\Delta }_1\in (0,{\displaystyle \frac{1}{12\theta M}})$ and choose the stepsize $\Delta \in (0,{\Delta }_1]$. We know that it is convenient to extend a discrete numerical solution to a continuous form. Fix any $T>0$, and denote $n={\displaystyle \frac{T}{\Delta }}$. We introduce two continuous-time step processes

$$Y_1^{i,N}\left(t\right)=\sum _{k=0}^{\infty }{Y}_k^{i,N,n}{\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right),Y_2^{i,N}\left(t\right)=\sum _{k=0}^{\infty }{Y}_{k+1}^{i,N,n}{\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right).$$

It is easy to get $Y_1^{i,N}\left(t_k\right)=Y_2^{i,N}\left(t_{k-1}\right)=Y_k^{i,N,n}$.

Denote by $Y^{i,N}\left(t\right)$ the continuous form of $Y_{t_k}^{i,N,n}$ with $Y^{i,N}\left(0\right)={\xi }^i$. Thus, the numerical solution of the modified stochastic theta method (19) can be extended to the continuous one,

$$\begin{array}{cc}\hfill Y^{i,N}\left(t\right)=& {\xi }^i+{\int }_0^t\left[(1-\theta )b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)+\theta b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\right]ds\hfill \\ \hfill & +{\int }_0^t\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i+{\int }_0^{t}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s,\hfill \end{array}$$

(20)

where

$$\begin{array}{c}\hfill {\mathcal{L}}_{{\overline{Y_1}}^N\left(t\right)}=\sum _{k=0}^{\infty }\left({\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{t_k}^{i,N,n}\right){\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right)\mathrm{and}{\mathcal{L}}_{{\overline{Y_2}}^N\left(t\right)}=\sum _{k=0}^{\infty }\left({\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right){\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right).\end{array}$$

Thus, we have $Y^{i,N}\left(t\right)=Y_k^{i,N,n}$ for any $t\in [t_k,t_{k+1}),k=0,1,\cdots ,n$. From now on, we use $C_i$, $i=7,8,\cdots ,28$ to denote different positive constants independent of $\Delta$.

Now, we turn to estimating the pth moment of the numerical solution.

Lemma 9. 

Let Assumption 3 hold. For $\theta \in [{\displaystyle \frac{1}{2}},1]$ and $p\ge 2$, it holds that

$$\underset{0\le k\le n}{sup}\widehat{\mathbf{E}}|Y_k^{i,N,n}{|}^p\le C_7\widehat{\mathbf{E}}{\left|\xi \right|}^p,$$

where $C_7$ is a positive constant.

Proof. 

From (20), we have

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}& ={\xi }^i+{\int }_0^{t_{k+1}}\left[(1-\theta )b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)+\theta b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\right]ds\hfill \\ \hfill & +{\int }_0^{t_{k+1}}\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i+{\int }_0^{t_{k+1}}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s.\hfill \end{array}$$

(21)

Noting that

$$\begin{array}{cc}\hfill {\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)ds=& {\int }_0^{t_k}{b}_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)ds+{\int }_{t_k}^{t_{k+1}}{b}_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)ds\hfill \\ \hfill ={\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds& -{\int }_0^{t_1}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds+b_{\Delta }\left(Y_{k+1}^{i,N,n},{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right)\Delta ,\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}=& {\xi }^i-\theta b_{\Delta }\left({\xi }^i,{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\xi }^i\right)\Delta +\theta b_{\Delta }\left(Y_{k+1}^{i,N,n},{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right)\Delta +{\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds\hfill \\ \hfill & +{\int }_0^{t_{k+1}}\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i+{\int }_0^{t_{k+1}}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s.\hfill \end{array}$$

(22)

It follows from the elementary inequality that

$$\begin{array}{cc}\hfill |Y_{k+1}^{i,N,n}{|}^2\le & 6\left\{\right|{\xi }^i{|}^2+{(\theta \Delta )}^2{\left|b_{\Delta }\left({\xi }^i,{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\xi }^i\right)\right|}^2+{(\theta \Delta )}^2|b_{\Delta }\left(Y_{k+1}^{i,N,n},{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right){|}^2\hfill \\ \hfill & +|{\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds{|}^2+|{\int }_0^{t_{k+1}}\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i{|}^2\hfill \\ \hfill & +\left|{\int }_0^{t_{k+1}}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s{|}^2\right\}.\hfill \end{array}$$

(23)

For any $p\ge 1$,

$$\begin{array}{cc}\hfill |Y_{k+1}^{i,N,n}{|}^{2p}\le & 6^{2p-1}\left\{\right|{\xi }^i{|}^{2p}+{(\theta \Delta )}^{2p}{\left|b_{\Delta }\left({\xi }^i,{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\xi }^i\right)\right|}^{2p}+{(\theta \Delta )}^{2p}|b_{\Delta }\left(Y_{k+1}^{i,N,n},{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right){|}^{2p}\hfill \\ \hfill & +|{\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds{|}^{2p}+|{\int }_0^{t_{k+1}}\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i{|}^{2p}\hfill \\ \hfill & +\left|{\int }_0^{t_{k+1}}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s{|}^{2p}\right\}.\hfill \end{array}$$

(24)

The H$\ddot{o}$lder inequality together with Lemmas 4 and 5 yields

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}{\left|Y_{k+1}^{i,N,n}\right|}^{2p}\right)\le 6^{2p-1}\{\widehat{\mathbf{E}}|{\xi }^i{|}^{2p}+{(\theta \Delta )}^{2p}\widehat{\mathbf{E}}{\left|b_{\Delta }\left({\xi }^i,{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\xi }^i\right)\right|}^{2p}\hfill \\ & +{(\theta \Delta )}^{2p}\widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}|b_{\Delta }\left(Y_{k+1}^{i,N,n},{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right){|}^{2p}\right)\hfill \\ \hfill & +\widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}|{\int }_0^{t_{k+1}}{b}_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)ds{|}^{2p}\right)\hfill \\ & +\widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}|{\int }_0^{t_{k+1}}\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i{|}^{2p}\right)\hfill \\ \hfill & +\widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}|{\int }_0^{t_{k+1}}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s{|}^{2p}\right)\}\hfill \\ \hfill \le & 6^{2p-1}\{\widehat{\mathbf{E}}{\left|\xi \right|}^{2p}+{(\theta \Delta )}^{2p}{\left(2M\right)}^{2p}\widehat{\mathbf{E}}{\left|\xi \right|}^{2p}+{(\theta \Delta )}^{2p}{\left(2M\right)}^{2p}\underset{0\le k\le n-1}{sup}\widehat{\mathbf{E}}{\left|Y_{k+1}^{i,N,n}\right|}^{2p}\hfill \\ \hfill & +{\left(2M\right)}^{2p}(T^{2p}+{\overline{\sigma }}^{2p}{T}^{p-1}+{\overline{\sigma }}^{4p}{T}^{2p-1})\sum _{k=0}^{n-1}\underset{0\le j\le k}{sup}\widehat{\mathbf{E}}{\left|Y_j^{i,N,n}\right|}^{2p}\}.\hfill \end{array}$$

(25)

We can choose a sufficiently small $\Delta \in (0,{\Delta }_1]$ such that ${(12\theta \Delta M)}^{2p}<{\displaystyle \frac{1}{2}}$. Then, (25) gives

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le k\le n}{sup}{\left|Y_k^{i,N,n}\right|}^{2p}\right)\hfill \\ \hfill \le & (6^{2p}+1)\widehat{\mathbf{E}}{\left|\xi \right|}^{2p}+2{\left(12M\right)}^{2p}(T^{2p}+{\overline{\sigma }}^{2p}{T}^{p-1}+{\overline{\sigma }}^{4p}{T}^{2p-1})\sum _{k=0}^{n-1}\underset{0\le j\le k}{sup}\widehat{\mathbf{E}}{\left|Y_j^{i,N,n}\right|}^{2p}.\hfill \end{array}$$

(26)

The discrete Gronwall inequality yields the desired result. □

Lemma 10. 

Let Assumption 3 hold. Then, for any $p\ge 2$, there exist two constants $C_8>0$ and $C_9>0$ such that

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le t\le T}{sup}{\left|Y^{i,N}\left(t\right)\right|}^p\right)\le C_8,\end{array}$$

(27)

and

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le k\le n-1}{sup}\underset{t_k\le t\le t_{k+1}}{sup}{|Y^{i,N}\left(t\right)-Y^{i,N}\left(t_k\right)|}^p\right)\le C_9{\Delta }^{{\displaystyle \frac{p}{2}}}.\end{array}$$

(28)

Proof. 

For any $p\ge 2$ and $t\in [0,T]$, it follows from (20) that

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}(\underset{0\le r\le t}{sup}& |Y^{i,N}{\left(r\right)|}^p)\le 4^{p-1}\widehat{\mathbf{E}}{\left|Y^{i,N}\left(0\right)\right|}^p+4^{p-1}\widehat{\mathbf{E}}(\underset{0\le r\le t}{sup}{\int }_0^r[(1-\theta )b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\hfill \end{array}$$

$$\begin{array}{c}+4^{p-1}\widehat{\mathbf{E}}{\left(\underset{0\le r\le t}{sup}{\int }_0^r\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i\right)}^p+\theta b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)]ds{)}^p\\ +4^{p-1}\widehat{\mathbf{E}}{\left(\underset{0\le r\le t}{sup}{\int }_0^{r}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s\right)}^p.\hfill \end{array}$$

(29)

The H$\ddot{o}$lder inequality together with Lemmas 4 and 5 yields

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{\left|Y^{i,N}\left(r\right)\right|}^p\right)\hfill \\ \hfill \le & 4^{p-1}\widehat{\mathbf{E}}|Y^{i,N}{\left(0\right)|}^p+8^{p-1}{t}^{p-1}{\int }_0^t[{(1-\theta )}^p\widehat{\mathbf{E}}{\left|b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\right|}^p\hfill \\ \hfill & +{\theta }^p\widehat{\mathbf{E}}{\left|b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\right|}^p]ds+4^{p-1}{\overline{\sigma }}^p{t}^{{\displaystyle \frac{p}{2}}-1}\widehat{\mathbf{E}}\left({\int }_0^t{\left|\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\right|}^{p}ds\right)\hfill \\ \hfill & +4^{p-1}{\overline{\sigma }}^{2p}{t}^{p-1}\widehat{\mathbf{E}}\left({\int }_0^t{\left|h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\right|}^{p}ds\right).\hfill \end{array}$$

Noting that

$$\begin{array}{c}\hfill Y_1^{i,N}\left(t\right)=\sum _{k=0}^{\infty }{Y}_k^{i,N,n}{\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right),Y_2^{i,N}\left(t\right)=\sum _{k=0}^{\infty }{Y}_{k+1}^{i,N,n}{\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right),\end{array}$$

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left|\left({\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right){\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right)\right|\le \widehat{\mathbf{E}}|Y_k^{i,N,n}|,\widehat{\mathbf{E}}\left|\left({\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right){\mathbf{1}}_{[t_k,t_{k+1})}\left(t\right)\right|\le \widehat{\mathbf{E}}\left|Y_{k+1}^{i,N,n}\right|,\end{array}$$

we obtain from Assumption 3 and Theorem 9 that

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le t\le T}{sup}{\left|Y^{i,N}\left(t\right)\right|}^p\right)\le C_{10}+C_{11}{\int }_0^T\widehat{\mathbf{E}}\underset{0\le k\le n}{sup}{\left|Y_k^{i,N,n}\right|}^{p}dt=C_8.\end{array}$$

Thus, (27) is proven. Now, we proceed to prove (28). By (20), we have

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{t_k\le t\le t_{k+1}}{sup}{|Y^{i,N}\left(t\right)-Y^{i,N}\left(t_k\right)|}^p\right)\hfill \\ \hfill \le & 3^{p-1}\widehat{\mathbf{E}}\left(\underset{t_k\le t\le t_{k+1}}{sup}|{\int }_{t_k}^t\left[(1-\theta )b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)+\theta b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\right]ds{|}^p\right)\hfill \\ \hfill & +3^{p-1}\widehat{\mathbf{E}}\left(\underset{t_k\le t\le t_{k+1}}{sup}|{\int }_{t_k}^t\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{B}_s^i{|}^p\right)\hfill \\ \hfill & +3^{p-1}\widehat{\mathbf{E}}\left(\underset{t_k\le t\le t_{k+1}}{sup}|{\int }_{t_k}^{t}h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)d{\langle B^i\rangle }_s{|}^p\right),\hfill \end{array}$$

Using the H$\ddot{o}$lder inequality and Lemmas 4 and 5, we arrive at

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{t_k\le t\le t_{k+1}}{sup}{|Y^{i,N}\left(t\right)-Y^{i,N}\left(t_k\right)|}^p\right)\hfill \\ \hfill \le & 3^{p-1}{\Delta }^{p-1}{\int }_{t_k}^{t_{k+1}}\widehat{\mathbf{E}}|(1-\theta )b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)+\theta b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right){|}^{p}ds\hfill \\ \hfill & +3^{p-1}{\overline{\sigma }}^p{\Delta }^{{\displaystyle \frac{p}{2}}-1}\widehat{\mathbf{E}}\left({\int }_{t_k}^{t_{k+1}}{\left|\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\right|}^{p}ds\right)\hfill \\ \hfill & +3^{p-1}{\overline{\sigma }}^{2p}{\Delta }^{p-1}\widehat{\mathbf{E}}\left({\int }_{t_k}^{t_{k+1}}{\left|h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\right|}^{p}ds\right)\hfill \\ \hfill \le & C_{12}{\Delta }^p+C_{13}{\Delta }^{{\displaystyle \frac{p}{2}}}\le C_{14}{\Delta }^{{\displaystyle \frac{p}{2}}},\hfill \end{array}$$

where $C_{12}$, $C_{13}$ and $C_{14}$ are positive constants. The desired assertion holds. □

4.2. The Strong Convergence

Define ${\tau }_{\Delta }=inf\{r\in [0,T]:|X^{i,N}\left(r\right)|\ge \kappa (\Delta )\},{\rho }_{\Delta }=inf\{r\in [0,T]:|Y^{i,N}\left(r\right)|\ge \kappa (\Delta )\},v_{\Delta }={\tau }_{\Delta }\wedge {\rho }_{\Delta }.$

Lemma 11. 

Let Assumptions 1–3 hold. Then, for any $T>0$ and $\theta \in [{\displaystyle \frac{1}{2}},1]$, it holds that

$$\mathcal{V}({\tau }_{\Delta }\le T)\le {\displaystyle \frac{C_{15}}{{\left(\kappa (\Delta )\right)}^p}},\mathcal{V}({\rho }_{\Delta }\le T)\le {\displaystyle \frac{C_{16}}{{\left(\kappa (\Delta )\right)}^p}},$$

where $C_{15}$ and $C_{16}$ are positive constants.

The proof can be completed with the Chebyshev inequality, so we omit the details here.

Lemma 12. 

Let Assumptions 1–3 hold. Then, for $\theta \in [{\displaystyle \frac{1}{2}},1]$, it holds that

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge v_{\Delta })-X^{i,N}(r\wedge v_{\Delta })|}^2\right)\le C_{21}{e}^{L_{\kappa (\Delta )}}\Delta ,\end{array}$$

where $C_{21}$ is a positive constant.

Proof. 

Denote $e\left(r\right)=Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)$. Applying the G-It$\widehat{o}$ formula to $|e(r\wedge v_{\Delta }){|}^2$, one has

$$\begin{array}{cc}\hfill & |e(r\wedge v_{\Delta }){|}^2\hfill \\ \le \hfill & 2{\int }_0^{r\wedge v_{\Delta }}\{〈Y^{i,N}\left(s\right)-X^{i,N}\left(s\right),(1-\theta )\left(b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right)\right)〉\hfill \\ \hfill & +〈Y^{i,N}\left(s\right)-X^{i,N}\left(s\right),\theta \left(b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right)\right)〉\}ds\hfill \\ \hfill & +2{\int }_0^{r\wedge v_{\Delta }}〈Y^{i,N}\left(s\right)-X^{i,N}\left(s\right),\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-\iota \left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right)〉d{B}_s^i\hfill \\ \hfill & +{\int }_0^{r\wedge v_{\Delta }}|\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-\iota \left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right){|}^{2}d{\langle B^i\rangle }_s\hfill \\ \hfill & +2{\int }_0^{r\wedge v_{\Delta }}〈Y^{i,N}\left(s\right)-X^{i,N}\left(s\right),h\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-h\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right)〉d{\langle B^i\rangle }_s\hfill \\ =\hfill & \sum _{i=1}^4{\Xi }_i\left(r\right).\hfill \end{array}$$

(30)

For any $0\le s\le r\wedge v_{\Delta }$, we have $|X^{i,N}\left(s\right)|\vee |Y^{i,N}\left(s\right)|\le \kappa (\Delta )$. Then, $b_{\Delta }\left(Y_k^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_k}}^N\left(s\right)}\right)=b\left(Y_k^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_k}}^N\left(s\right)}\right)$ for $0\le s\le r\wedge v_{\Delta }$ and $k=1,2$. Using the H$\ddot{o}$lder inequality, Lemma 10 and Assumptions 1 and 2, we have

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{\Xi }_1\left(r\right)\right)\hfill \\ \hfill \le & \widehat{\mathbf{E}}\left[{\int }_0^{t\wedge v_{\Delta }}2\right\{\langle Y_1^{i,N}\left(s\right)-X^{i,N}\left(s\right),(1-\theta )(b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\hfill \\ \hfill & +b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right))\rangle \hfill \\ \hfill & +\langle Y_2^{i,N}\left(s\right)-X^{i,N}\left(s\right),\theta (b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\hfill \\ \hfill & +b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right))\rangle \hfill \\ \hfill & +\langle Y^{i,N}\left(s\right)-Y_1^{i,N}\left(s\right),(1-\theta )(b_{\Delta }\left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)\hfill \\ \hfill & +b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right))\rangle \hfill \\ \hfill & +\langle Y^{i,N}\left(s\right)-Y_2^{i,N}\left(s\right),\theta (b_{\Delta }\left(Y_2^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)\hfill \\ \hfill & +b\left(X^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_2}}^N\left(s\right)}\right)-b\left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right))\rangle \}ds]\hfill \\ \hfill \le & C_{17}(L_{g(\Delta )}+L){\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le s\le r}{sup}{|Y^{i,N}(s\wedge v_{\Delta })-X^{i,N}(s\wedge v_{\Delta })|}^2\right)dr+C_{18}\Delta .\hfill \end{array}$$

(31)

Considering Lemma 5 and the Cauchy–SchwarX inequality, from Lemma 10, we have

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{\Xi }_2\left(r\right)\right)\hfill \\ \hfill \le & 2\overline{\sigma }\widehat{\mathbf{E}}{\left({\int }_0^{t\wedge v_{\Delta }}|Y^{i,N}\left(s\right)-X^{i,N}\left(s\right){|}^2|\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-\iota \left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right){|}^{2}ds\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill \le & 2\overline{\sigma }\widehat{\mathbf{E}}(\underset{0\le s\le t}{sup}{|Y^{i,N}(s\wedge v_{\Delta })-X^{i,N}(s\wedge v_{\Delta })|}^2\hfill \\ \hfill & ·{\int }_0^{t\wedge v_{\Delta }}|\iota \left(Y_1^{i,N}\left(s\right),{\mathcal{L}}_{{\overline{Y_1}}^N\left(s\right)}\right)-\iota \left(X^{i,N}\left(s\right),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(s\right)\right){|}^{2}ds{)}^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill \le & {\displaystyle \frac{1}{2}}\widehat{\mathbf{E}}\left(\underset{0\le s\le t}{sup}{|Y^{i,N}(s\wedge v_{\Delta })-X^{i,N}(s\wedge v_{\Delta })|}^2\right)\hfill \\ \hfill & +4(L_{g(\Delta )}+L){\overline{\sigma }}^2{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le u\le s}{sup}{|Y^{i,N}(u\wedge v_{\Delta })-X^{i,N}(u\wedge v_{\Delta })|}^2\right)ds.\hfill \end{array}$$

(32)

By Lemma 4, we derive that

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{\Xi }_3\left(r\right)\right)\hfill \\ \hfill \le & {\overline{\sigma }}^2\widehat{\mathbf{E}}\left({\int }_0^t|\iota \left(Y_1^{i,N}(s\wedge v_{\Delta }),{\mathcal{L}}_{{\overline{Y_1}}^N(s\wedge v_{\Delta })}\right)-\iota \left(X^{i,N}(s\wedge v_{\Delta }),{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}(s\wedge v_{\Delta })\right){|}^{2}ds\right)\hfill \\ \hfill \le & 2(L_{g(\Delta )}+L){\overline{\sigma }}^2{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le u\le s}{sup}{|Y^{i,N}(u\wedge v_{\Delta })-X^{i,N}(u\wedge v_{\Delta })|}^2\right)ds.\hfill \end{array}$$

(33)

Similarly,

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{\Xi }_4\left(r\right)\right)\hfill \\ \hfill \le & (1+2L_{g(\Delta )}+2L){\overline{\sigma }}^2{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le u\le s}{sup}{|Y^{i,N}(u\wedge v_{\Delta })-X^{i,N}(u\wedge v_{\Delta })|}^2\right)ds.\hfill \end{array}$$

(34)

Substituting (31)-(34) into (30), we have

$$\begin{array}{cc}\hfill & \widehat{\mathbf{E}}\left(\underset{0\le r\le t}{sup}{|Y^{i,N}(r\wedge v_{\Delta })-X^{i,N}(r\wedge v_{\Delta })|}^2\right)\hfill \\ \hfill \le & C_{19}{L}_{g(\Delta )}{\int }_0^t\widehat{\mathbf{E}}\left(\underset{0\le u\le s}{sup}{|Y^{i,N}(u\wedge v_{\Delta })-X^{i,N}(u\wedge v_{\Delta })|}^2\right)ds+C_{20}\Delta .\hfill \end{array}$$

(35)

The Gronwall inequality yields

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge v_{\Delta })-X^{i,N}(r\wedge v_{\Delta })|}^2\right)\le C_{21}{e}^{L_{g(\Delta )}}\Delta .\end{array}$$

(36)

□

Lemma 13. 

Let Assumptions 1–3 hold. For any $ϵ>0$ and $\theta \in [{\displaystyle \frac{1}{2}},1]$, there exists a ${\Delta }^{*}$ such that, for any $\Delta \in (0,{\Delta }^{*})$,

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)|}^2\right)<ϵ.\end{array}$$

(37)

Proof. 

Applying the Young inequality

$$X^{q}Y\le {\displaystyle \frac{q\eta X^p}{p}}+{\displaystyle \frac{p-q}{p{\eta }^{\frac{q}{p-q}}}}\begin{array}{c}\hfill Y^{{\displaystyle \frac{p}{p-q}}}\end{array},q<p,\eta >0,$$

for any $p>2$ and $\eta >0$, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}(\underset{0\le r\le T}{sup}|Y^{i,N}\left(r\right)& -X^{i,N}{\left(r\right)|}^2)\le \widehat{\mathbf{E}}\left({\mathbf{1}}_{\{{\tau }_{\Delta }>T,{\rho }_{\Delta }>T\}}\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)|}^2\right)\hfill \\ \hfill & +{\displaystyle \frac{2\eta }{p}}\widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)|}^p\right)+{\displaystyle \frac{p-2}{p{\eta }^{\frac{2}{p-2}}}}\mathcal{V}({\tau }_{\Delta }\le T\mathrm{or}{\rho }_{\Delta }\le T),\hfill \end{array}$$

(38)

which, together with Lemmas 1, 10 and 12, implies

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)|}^2\right)\le & \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge v_{\Delta })-X^{i,N}(r\wedge v_{\Delta })|}^2\right)\hfill \\ & +{\displaystyle \frac{2\eta C_{22}}{p}}+{\displaystyle \frac{2(p-2)C_{24}}{p{\eta }^{\frac{2}{p-2}}{\left(\kappa (\Delta )\right)}^p}}.\hfill \end{array}$$

For each $ϵ>0$, we can choose a sufficiently small $\eta$ such that

$${\displaystyle \frac{2\eta C_{23}}{p}}<{\displaystyle \frac{ϵ}{3}},$$

and a sufficiently large $\kappa (\Delta )$ with $\Delta$ sufficiently small to satisfy

$${\displaystyle \frac{2(p-2)C_{24}}{p{\eta }^{\frac{2}{p-2}}{\left(\kappa (\Delta )\right)}^p}}<{\displaystyle \frac{ϵ}{3}}\mathrm{and}{C}_{21}{e}^{L_{\kappa (\Delta )}}\Delta <{\displaystyle \frac{ϵ}{3}}.$$

Thus, the desired assertion holds. □

Now, we proceed to state the first main result of this section.

Theorem 2. 

Let Assumptions 1–3 hold. For any $ϵ>0$ and $\theta \in [{\displaystyle \frac{1}{2}},1]$, there exists a ${\Delta }^{*}$ such that

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}\underset{n\to \infty }{lim}\underset{0\le i\le N}{sup}\widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^i\left(r\right)|}^2\right)=0.\end{array}$$

(39)

Proof. 

The proof can be finished by the triangle inequality. □

Remark 4. 

The time discretization together with the stopping time arguments make it impossible to obtain the convergence rates of the numerical schemes for the G-MFSDEs with coefficients satisfying the local Lipschitz condition with respect to the state variable. Meanwhile, if $b,\iota$ and h satisfy the global Lipschitz condition, the convergence rate can be obtained by the triangle inequality; for example, we can choose sufficiently small Δ, η and L such that ${\displaystyle \frac{2\eta C_{23}}{p}}<C_{25}\Delta$, ${\displaystyle \frac{2(p-2)C_{24}}{p{\eta }^{\frac{2}{p-2}}{L}^p}}<C_{26}\Delta$ and $C_{21}{e}^L\Delta <C_{27}\Delta$. Thus, with the Glivenko–Cantelli theorem, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^i\left(r\right)|}^2\right)=& \widehat{\mathbf{E}}\left(\underset{0\le r\le T}{sup}{|Y^{i,N}\left(r\right)-X^{i,N}\left(r\right)+X^{i,N}\left(r\right)-X^i\left(r\right)|}^2\right)\hfill \\ \hfill \le & C_{28}\Delta +C_{29}{N}^{-1/2}+C_{30}{\Delta }^{1/2}.\hfill \end{array}$$

4.3. Asymptotic Mean Square Stability

As is known, stability properties are crucial in the automatic control of stochastic systems. In this section, we study the asymptotic mean square stability of the numerical solution of the modified stochastic theta scheme for the interacting particle system. We first introduce the asymptotic mean square stability of the numerical solution.

Definition 4. 

The numerical solution of the modified stochastic theta scheme (19) is said to be asymptotically mean-square-stable if

$$\underset{k\to \infty }{lim}\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2=0$$

holds for some sufficiently small Δ, θ and any $i\in \{1,2,\cdots ,N\}$.

To study the numerical stability, we impose an extra assumption.

Assumption 4. 

There exist two constants $a_1$, $a_2>0$ such that, for any $x,u\in {\mathbf{R}}^d$,

$$2x^{T}b(x,u)\le -a_1{\left|x\right|}^2+a_2{\left|u\right|}^2.$$

Now, we proceed to state the second main result of this section.

Theorem 3. 

Let Assumptions 3 and 4 hold with $0<a_2<a_1$ and $4M{\overline{\sigma }}^2+2a_2-1<2a_1$. Choose a $\theta <{\displaystyle \frac{|4M{\overline{\sigma }}^2+4M+2a_2-1|}{2a_1+4M}}$. Then, for any $i\in \{1,2,\cdots ,N\}$, there exists a step size ${\Delta }_{*}\in \left(0,min\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{(2a_1+4M)\theta -4M{\overline{\sigma }}^2-4M2a_2}}\}\right)$ small enough such that, for any $\Delta \in (0,{\Delta }_{*})$, the numerical solution $Y_k^{i,N,n}$ is asymptotically stable in the mean square sense, i.e.,

$$\underset{k\to \infty }{lim}\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2=0,$$

where the constraint on ${\Delta }_{*}$ is given in the proof.

Proof. 

Squaring both sides of (19), it follows from Assumption 4 that

$$\begin{array}{cc}\hfill & {\left(Y_{k+1}^{i,N,n}\right)}^2+{(\theta \Delta )}^2{b}_{\Delta }^2\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\hfill \\ \hfill =& {\left(Y_k^{i,N,n}\right)}^2+2\theta \Delta {\left(Y_{k+1}^{i,N,n}\right)}^T{b}_{\Delta }\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)+{\left((1-\theta )\Delta b_{\Delta }^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\right)}^2\hfill \\ & +{\left(\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\right)}^2+{\left(h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k\right)}^2\hfill \\ \hfill & +2{\left(Y_k^{i,N,n}\right)}^T(1-\theta )\Delta b_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)+2{\left(Y_k^{i,N,n}\right)}^T\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\hfill \\ \hfill & +2{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k+2{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\Delta {\langle B^i\rangle }_k\hfill \\ \hfill & +2(1-\theta )\Delta b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\left(\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i+h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k\right)\hfill \\ \hfill \le & {\left(Y_k^{i,N,n}\right)}^2+2\theta \Delta \left(-a_1|Y_{k+1}^{i,N,n}{|}^2+a_2{\left|{\mu }_{k+1}^{Y,N,n}\right|}^2\right)+{\left((1-\theta )\Delta b_{\Delta }^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\right)}^2\hfill \\ \hfill & +{\left(\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\right)}^2+{\left(h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k\right)}^2\hfill \\ \hfill & +2(1-\theta )\Delta \left(-a_1|Y_k^{i,N,n}{|}^2+a_2{\left|{\mu }_k^{Y,N,n}\right|}^2\right)+2{\left(Y_k^{i,N,n}\right)}^T\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\hfill \\ \hfill & +2{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k+2{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\Delta {\langle B^i\rangle }_k\hfill \\ \hfill & +2(1-\theta )\Delta b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\left(\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i+h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k\right).\hfill \end{array}$$

(40)

Considering that $Y_k^{i,N,n}$ is ${\mathcal{F}}_{t_k}$ measurable, by Proposition 2, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}\left[{\iota }^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\left(|\Delta B_k^i{|}^2-{\overline{\sigma }}^2\Delta \right)\right]& =\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}\left[{\iota }^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\left(|\Delta B_k^i{|}^2-{\overline{\sigma }}^2\Delta \right)\right|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[{\iota }^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[{(\Delta B_k^i)}^2-{\overline{\sigma }}^2\Delta |{\mathcal{F}}_{t_k}]\right]=0.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[{\left(Y_k^{i,N,n}\right)}^T\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i]& =\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}[{\left(Y_k^{i,N,n}\right)}^T\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i]\right|{\mathcal{F}}_{t_k}]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[{\left(Y_k^{i,N,n}\right)}^T\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta B_k^i|{\mathcal{F}}_{t_k}]\right]=0.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)& \Delta B_k^i]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i]\right|{\mathcal{F}}_{t_k}]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\iota \left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta B_k^i|{\mathcal{F}}_{t_k}]\right]\hfill \\ & =0.\hfill \end{array}$$

By Lemma 2, we have

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k]& =\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}[{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill & \le {\overline{\sigma }}^2\Delta \widehat{\mathbf{E}}\left[{\left(Y_k^{i,N,n}\right)}^{T}h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\right].\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h(Y_k^{i,N,n},& {\mu }_k^{Y,N,n})\Delta {\langle B^i\rangle }_k]\hfill \\ \hfill =& \widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill =& \widehat{\mathbf{E}}\left[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill \le & {\overline{\sigma }}^2\Delta \widehat{\mathbf{E}}\left[b_{\Delta }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\right].\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h(Y_k^{i,N,n},& {\mu }_k^{Y,N,n})\Delta B_k^i\Delta {\langle B^i\rangle }_k]\hfill \\ \hfill =& \widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}[{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill =& \widehat{\mathbf{E}}\left[{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta B_k^i\Delta {\langle B^i\rangle }_k|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill \le & {\overline{\sigma }}^2\Delta \widehat{\mathbf{E}}\left[{\iota }^T\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)h\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[\Delta B_k^i|{\mathcal{F}}_{t_k}]\right]=0.\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{\mathbf{E}}[h^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)({|\Delta {\langle B^i\rangle }_k|}^2& -{\overline{\sigma }}^2{\Delta }^2\left)\right]=\widehat{\mathbf{E}}\left[\widehat{\mathbf{E}}\left[h^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\left(|\Delta {\langle B^i\rangle }_k{|}^2-{\overline{\sigma }}^2{\Delta }^2\right)\right|{\mathcal{F}}_{t_k}]\right]\hfill \\ \hfill & =\widehat{\mathbf{E}}\left[h^2\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\widehat{\mathbf{E}}[{(\Delta {\langle B^i\rangle }_k)}^2-{\overline{\sigma }}^2{\Delta }^2|{\mathcal{F}}_{t_k}]\right]\le 0.\hfill \end{array}$$

These together with (40) yield that

$$\begin{array}{cc}\hfill (1+2\theta \Delta a_1-2\theta \Delta a_2)\widehat{\mathbf{E}}{\left|Y_{k+1}^{i,N,n}\right|}^2\le & 2\widehat{\mathbf{E}}|Y_k^{i,N,n}{|}^2+4{(1-\theta )}^2{\Delta }^{2}M\widehat{\mathbf{E}}|Y_k^{i,N,n}{|}^2+4M{\overline{\sigma }}^2\Delta \widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2\hfill \\ \hfill & +8M{\overline{\sigma }}^4{\Delta }^2\widehat{\mathbf{E}}|Y_k^{i,N,n}{|}^2+2(1-\theta )\Delta a_2\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2\hfill \\ \hfill & +(1-\theta )\Delta \left(4M\widehat{\mathbf{E}}|Y_k^{i,N,n}{|}^2+4M{\overline{\sigma }}^4{\Delta }^2\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2\right).\hfill \end{array}$$

(41)

For $4M{\overline{\sigma }}^2+2a_2-1<2a_1$ and $\theta <{\displaystyle \frac{|4M{\overline{\sigma }}^2+4M+2a_2-1|}{2a_1+4M}}$, we can choose a sufficiently small ${\Delta }_{*}\in \left(0,min\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{(2a_1+4M)\theta -4M{\overline{\sigma }}^2-4M2a_2}}\}\right)$ such that, for $\Delta \in (0,{\Delta }_{*})$,

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}|Y_{k+1}^{i,N,n}{|}^2\le C_{*}\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2,\end{array}$$

where $C_{*}={\displaystyle \frac{2+4{(1-\theta )}^2{\Delta }^{2}M+4M{\overline{\sigma }}^2\Delta +8M{\overline{\sigma }}^4{\Delta }^2+2(1-\theta )\Delta a_2(1-\theta )\Delta \left(4M+4M{\overline{\sigma }}^4{\Delta }^2\right)}{1+2\theta \Delta a_1-2\theta \Delta a_2}}<1$. Owing to this, it can be obtained by iteration that

$$\underset{k\to \infty }{lim}\widehat{\mathbf{E}}{\left|Y_k^{i,N,n}\right|}^2=0.$$

The proof is completed. □

Remark 5. 

From Theorem 3, we know that Assumptions 3 and 4 can lead the numerical solution of the modified stochastic theta method to be asymptotically mean-square-stable, whereas the moment exponential stability can be obtained only when we impose some extra assumptions due to the sublinearity of the G-expectation.

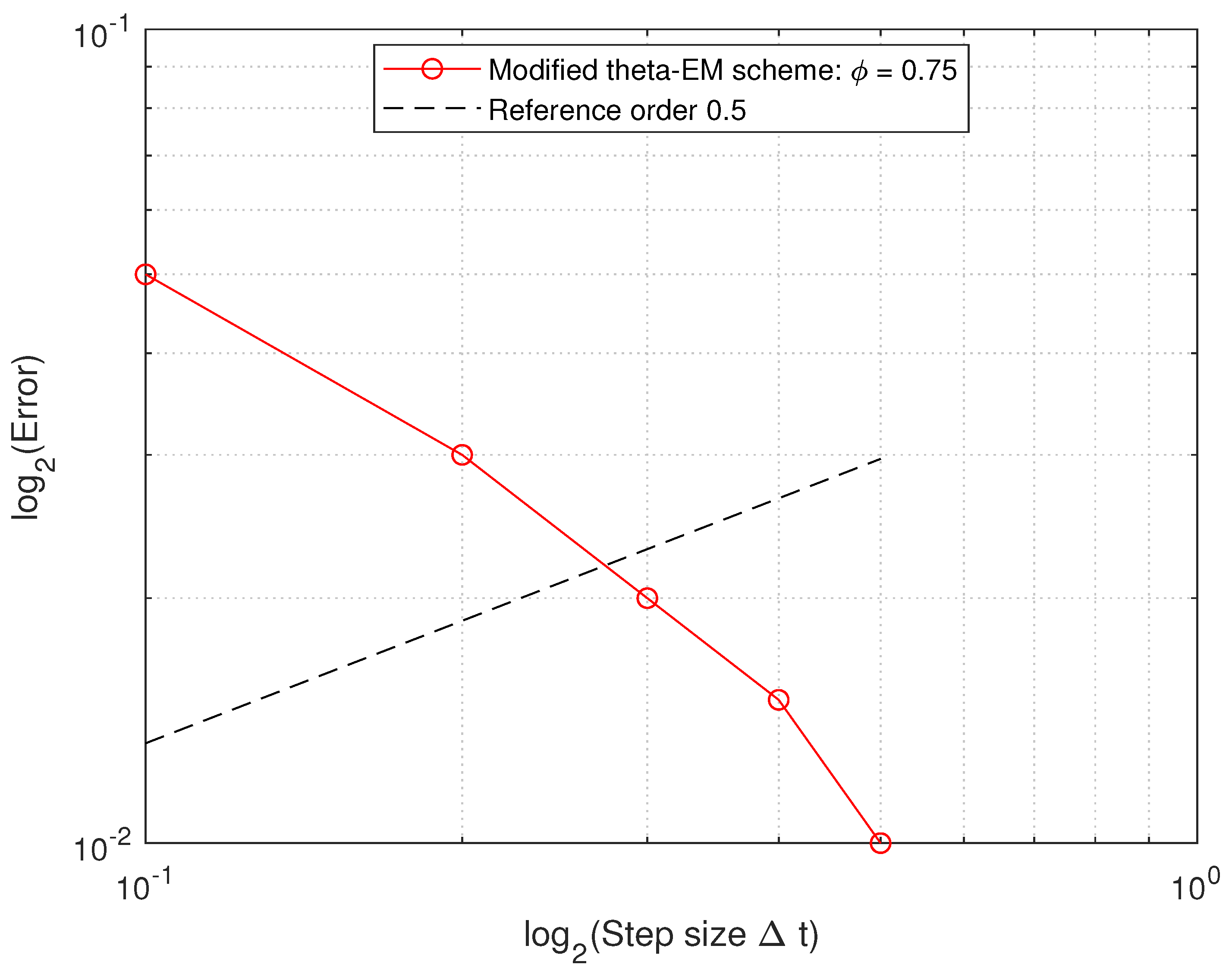
5. The Numerical Example

We perform a numerical experiment to demonstrate our theoretical results.

Example 1. 

Assume that $B\left(t\right)$ is a one-dimensional G-Brownian motion $B\left(t\right)$∼$N(0;[{\underline{\sigma }}^2,{\overline{\sigma }}^2]t)$ and consider

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dX\left(t\right)=\left(-X\left(t\right)-X^3\left(t\right)+2\widehat{\mathbf{E}}X\left(t\right)\right)dt+\left(2X\left(t\right)+\widehat{\mathbf{E}}X\left(t\right)\right)dB\left(t\right)\hfill \\ +\left(X\left(t\right)+\widehat{\mathbf{E}}X\left(t\right)\right)d\langle B\rangle \left(t\right),t\in [0,T],\hfill \\ X\left(0\right)=1,\hfill \end{array}\right.\end{array}$$

(42)

where $b(x,u)=-x-x^3+2u$, $\iota (x,u)=2x+u$ and $h(x,u)=x+u$.

For any integer $R\ge \sqrt{2}$ and $x,y,u\in \mathbf{R}$ with $\left|x\right|\vee \left|y\right|\le R$ and $a=42$,

$$\begin{array}{cc}\hfill \langle x-y,b(x,u)-b(y,u)\rangle & =\langle x-y,-x+y-x^3+y^3\rangle \le 42logR{|x-y|}^2,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {|\iota (x,u)-\iota (y,u)|}^2& ={|2x-2y|}^2\le 4{|x-y|}^2,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {|h(x,u)-h(y,u)|}^2& ={|x-y|}^2\le 2{|x-y|}^2.\hfill \end{array}$$

(45)

Therefore, $L_R=42logR$. For any $u,v\in \mathbf{R}$,

$$\begin{array}{cc}\hfill \left|b\right(x,u)-b(x,v\left)\right|& \le 2|u-v|,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill \left|\iota \right(x,u)-\iota (x,v\left)\right|=\left|h\right(x,u)& -h(x,v)|\le |u-v|.\hfill \end{array}$$

(47)

So, we may choose $L=2$ such that Assumptions 1 and 2 hold. It follows from Theorem 1 that (42) admits a unique solution ${\left\{X\left(t\right)\right\}}_{0\le t\le T}$, which satisfies

$$\begin{array}{c}\hfill \widehat{\mathbf{E}}\left(\underset{0\le t\le T}{sup}{\left|X\left(t\right)\right|}^p\right)<\infty ,p\ge 2.\end{array}$$

(48)

We have the interacting particle system

$$\begin{array}{cc}\hfill d{X}^{i,N}\left(t\right)=& \left(-X^{i,N}\left(t\right)-{\left(X^{i,N}\left(t\right)\right)}^3+{\displaystyle \frac{2}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right)\right)dt+(2X^{i,N}\left(t\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right))dB\left(t\right)+\left(X^{i,N}\left(t\right)+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{X}^{i,N}\left(t\right)\right)d\langle B\rangle \left(t\right),t\in [0,T],\hfill \end{array}$$

(49)

subject to $X^{i,N}\left(0\right)=1$, $i=1,2,\cdots ,N$.

The modified stochastic theta method for the interacting particle system yields

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}=& Y_k^{i,N,n}+\theta I_{\Delta }\left(Y_{k+1}^{i,N,n}\right)\left(-Y_{k+1}^{i,N,n}-{\left(Y_{k+1}^{i,N,n}\right)}^3+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right)\Delta \hfill \\ & +(1-\theta )I_{\Delta }\left(Y_k^{i,N,n}\right)\left(-Y_k^{i,N,n}-{\left(Y_k^{i,N,n}\right)}^3+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta \hfill \\ \hfill & +\left(2Y_k^{i,N,n}+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta B_k+\left(Y_k^{i,N,n}+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta {\langle B\rangle }_k,\hfill \end{array}$$

(50)

with the initial value $Y_0^{i,N,n}=1$.

We can verify that the conditions of Theorem 2 hold under (43)–(47), i.e., the numerical solution of the modified stochastic theta scheme for (42) converges to that of (49). We can also verify that

$$2x^{T}b(x,u)\le {\displaystyle \frac{-3}{2}}{\left|x\right|}^2+2u^2,$$

and, thus, the numerical solution is asymptotically mean-square-stable.

Now, we proceed to the numerical approximation. As it is difficult to obtain the analytic solutions of G-MFSDE (42) and the non-interacting particle system, we use the solution of the EM method with $M=2^{10}$ as a reference solution. In addition, we use the maximum sample average of the absolute error between the solution of (50) and the reference solution at time t to approximate the error between the exact solution and the corresponding numerical solution. That is, for a proper constant N,

$$\mathcal{E}\approx \widehat{\mathcal{E}}=\underset{1\le k\le M}{max}{\displaystyle \frac{1}{N}}\sum _{i=1}^N|Y^{i,N,M}\left(t_M^k\right)-Y_k^{i,N,n}|,$$

where $Y^{i,N,M}\left(t_M^k\right)$ is the k-th iteration of the EM scheme with step size $T/M$ and $Y_k^{i,N,n}$ is the k-th iteration of (50) with step size $T/n$.

Set $T=1$ and choose $N=100$. We use the step size $\Delta =2^{-10}$ and $n=M=2^{10}$ to compute the numerical solution $Y_k^{i,N,n}$. Let ${\mathcal{L}}_{Y_{t_k}^{i,N,n}}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{Y}_k^{i,N,n}$. We choose a sequence of random variables ${\zeta }_n^k=B\left(r_k\right)-B\left(r_{k-1}\right)\sim N(0,[{\underline{\sigma }}^2,{\overline{\sigma }}^2]\Delta )$, $k=1,\cdots ,n$, and the uniform step points ${\sigma }_s(s=1,\cdots ,I)$ with $\underline{\sigma }={\sigma }_1<{\sigma }_s<\cdots <{\sigma }_I=\overline{\sigma }$, based on which we can simulate the G-Brownian motion $\left(B\right(r),r\in [0,T\left]\right)$. Thus, ${\zeta }_n^{ks}(k=1,2\cdots ,n;s=1,2,\cdots ,I)$ obeys the classical normal distribution $N(0,{\sigma }_s^2\Delta )$. In accordance with the modified stochastic theta method (49), we have

$$\begin{array}{cc}\hfill Y_{k+1}^{i,N,n}=& Y_{t_k}^{i,N,n}+\theta I_{\Delta }\left(Y_{k+1}^{i,N,n}\right)\left(-Y_{k+1}^{i,N,n}-{\left(Y_{k+1}^{i,N,n}\right)}^3+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right)\Delta \hfill \\ & +(1-\theta )I_{\Delta }\left(Y_k^{i,N,n}\right)\left(-Y_k^{i,N,n}-{\left(Y_k^{i,N,n}\right)}^3+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta \hfill \\ \hfill & +\left(2Y_k^{i,N,n}+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right){\zeta }_n^{ks}\Delta +\left(Y_k^{i,N,n}+{\displaystyle \frac{1}{N}}\sum _{i=1}^N{Y}_k^{i,N,n}\right){\sigma }_s^2\Delta ,\hfill \end{array}$$

for $1\le s\le I$. Taking $I=100$, and $[{\underline{\sigma }}^2,{\overline{\sigma }}^2]=[0.2,0.5]$, we plot the numerical results in the following figure. From Figure 1, we can observe that the convergence of the modified stochastic theta scheme is close to the theoretical prediction.

Remark 6. 

Mean-field stochastic differential equations driven by G-Brownian motion have broad applications. In the field of mathematical finance, this type of stochastic differential equation simulates a large number of mutually influencing asset price dynamics and is applicable to systemic risk analysis, nonlinear volatility models, asset pricing and stable portfolio optimization. In the field of complex systems and network dynamics, this type of stochastic differential equation can be used to model the cognitive uncertainty of environmental parameters. In the field of nonlinear filtering and control, this type of stochastic differential equation can be used to solve the optimal control problems with fuzziness. The modified stochastic theta scheme for mean-field stochastic differential equations driven by G-Brownian motion provides a stable and convergent method for the numerical simulation of this type of stochastic differential equation under the local one-sided Lipschitz condition and provides an effective tool for the stability analysis of this type of stochastic differential equation.

6. Conclusions

In this paper, we have shown the strong convergence and asymptotic mean square stability of the stochastic theta method for the G-MFSDE under the local one-sided Lipschitz condition. We have used the sample average value to represent the G-expectation and introduced the interacting particle system to approximate the G-MFSDE. To guarantee the well-posedness of the G-MFSDE under the local one-sided Lipschitz condition, we introduce the modified stochastic theta method and show that the solution of the modified stochastic theta scheme for the non-interacting particle system strongly converges to the exact solution. Moreover, we have generalized the local Lipschitz condition to the global Lipschitz condition and obtained the convergence rate.

In this manuscript, we only consider the drift coefficient satisfying the local one-sided Lipschitz condition, and we only truncate the drift coefficient. We know that the diffusion term impacts the convergence. We will consider both the drift and diffusion coefficients satisfying local one-sided Lipschitz conditions and truncate the drift and diffusion coefficients in the future. This will be a new direction for our future work.