The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions
Abstract
1. Introduction
2. Preliminaries
- (1)
- Monotonicity: if ;
- (2)
- Constant preserving: , ;
- (3)
- Subadditivity: ;
- (4)
- Positive homogeneity: , .
- (1)
- ;
- (2)
- , for , where ξ is G-normally distributed;
- (3)
- For all , the increments are independent of .
- (1)
- If , then .
- (2)
- , for each and .
- (3)
- .
- (4)
- for each bounded .
- (5)
- , in particular .
- (1)
- ; ,
- (2)
- ,
- (3)
- ,
3. The Well-Posedness of G-MFSDEs and the Stochastic Particle Method
3.1. Local One-Sided Lipschitz Condition
3.2. The Interacting Particle System and Propagation of Chaos
4. The Modified Stochastic Theta Method and Its Strong Convergence and Asymptotic Mean Square Stability
4.1. The Modified Stochastic Theta Method
4.2. The Strong Convergence
4.3. Asymptotic Mean Square Stability
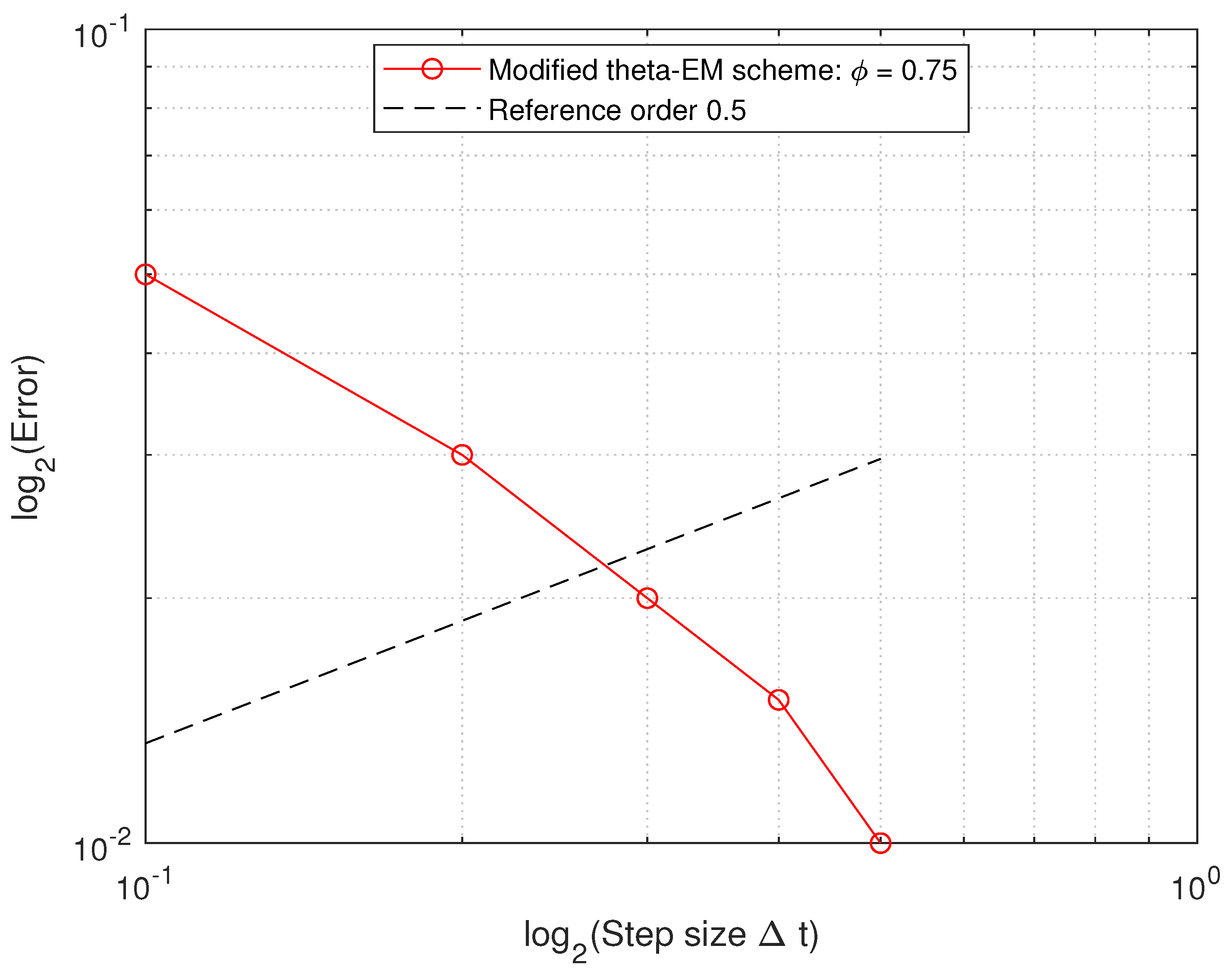
5. The Numerical Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kac, M. Foundations of kinetic theory. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 26–31 December 1954; University California Press: Berkeley, CA, USA, 1955; Volume III, pp. 171–197. [Google Scholar]
- Kac, M. Probability and Related Topics in Physical Sciences; Inter-Science Publishers: London, UK, 1959. [Google Scholar]
- Lasry, J.M.; Lions, P.L. Mean-field games. Jpn. J. Math. 2007, 2, 229–260. [Google Scholar] [CrossRef]
- Huang, M.; Malham, R.P.; Caines, P.E. Large population stochastic dynamic games: Closed-loop McKean-Vlasov systems and the nash certainty equivalence principle. Commun. Inf. Syst. 2006, 6, 221–252. [Google Scholar]
- Bensoussan, A.; Frehse, A.; Yam, P. Mean Field Games and Mean Field Type Control Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wang, F. Distribution dependent SDEs for Landau type equations. Stoch. Proc. Appl. 2018, 128, 595–621. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, J. Existence, uniqueness and exponential ergodicity under Lyapunov conditions for McKean-Vlasov SDEs with Markovian switching. J. Differ. Equ. 2022, 337, 138–167. [Google Scholar] [CrossRef]
- Li, Y.; Mao, X.; Song, Q.; Wu, F.; Yin, G. Strong convergence of Euler-Maruyama schemes for McKean-Vlasov stochastic differential equations under local Lipschitz conditions of state variables. IMA J. Numer. Anal. 2022, 43, 1001–1035. [Google Scholar] [CrossRef]
- Adams, D.; Dos Reis, G.; Ravaille, R.; Salkld, W.; Tugaut, J. Large deviations and exit-times for reflected McKean-Vlasov equations with self-stabilizing terms and superlinear drifts. Stoch. Process. Appl. 2022, 146, 264–310. [Google Scholar] [CrossRef]
- Hammersley, W.R.P.; Ika, D.; Szpruch, U. Weak existence and uniqueness for McKean-Vlasov SDEs with common noise. Ann. Probab. 2019, 49, 527–555. [Google Scholar] [CrossRef]
- Li, Z.; Xu, L.; Yan, L. McKean-Vlasov stochastic differential equations driven by the time-changed Brownian motion. J. Math. Anal. Appl. 2023, 527, 127336. [Google Scholar] [CrossRef]
- Bossy, M.; Talay, D. A stochastic particle method for the McKean-Vlasov and the Burgers equation. Math. Comp. 1997, 66, 157–192. [Google Scholar] [CrossRef]
- Budhiraja, A.; Fan, W.T.L. Uniform in time interacting particle approximations for nonlinear equations of Patlak-Keller-Segel type. Electron. J. Probab. 2016, 22, 1–37. [Google Scholar] [CrossRef]
- Dos Reis, G.; Engelhardt, S.; Smith, G. Simulation of McKean-Vlasov SDEs with super-linear growth. IMA J. Numer. Anal. 2022, 42, 874–922. [Google Scholar] [CrossRef]
- Bao, J.; Reisinger, C.; Ren, P.; Stockinger, W. First-order convergence of Milstein schemes for McKean-Vlasov equations and interacting particle systems. Proc. R. Soc. A 2021, 477, 20200258. [Google Scholar] [CrossRef] [PubMed]
- Gobet, E.; Pagliarani, S. Analytical approximations of non-linear SDEs of McKean-Vlasov type. J. Math. Anal. Appl. 2018, 466, 71–106. [Google Scholar] [CrossRef]
- Kumar, C.; Neelima, C. On explicit Milstein-type scheme for McKean-Vlasov stochastic differential equations with super-linear drift coefficient. Electron. J. Probab. 2021, 26, 1–32. [Google Scholar] [CrossRef]
- Neelima, S.; Biswas, C.; Kumar, G.; dos Reis, G.; Reisinger, C. Well-posedness and tamed Euler schemes for McKean-Vlasov equations driven by Lévy noise. arXiv 2010, arXiv:2010.08585. [Google Scholar]
- Hong, W.; Li, S.; Sun, X. Diffusion approximation for multi-scale McKean-Vlasov SDEs through different methods. J. Differ. Equ. 2025, 414, 405–454. [Google Scholar] [CrossRef]
- Jian, J.; Song, Q.; Wang, X.; Zhang, Z.; Zhao, Y. On modified Euler methods for McKean–Vlasov stochastic differential equations with super-linear coefficients. Automatica 2025, 177, 112284. [Google Scholar] [CrossRef]
- Peng, S. Nonlinear expectations and stochastic calculus under uncertainty. arXiv 2010, arXiv:1002.4546v1. [Google Scholar]
- Sun, S. Mean-field backward stochastic differential equations driven by G-Brownian motion and related partial differential equations. Math. Methods Appl. Sci. 2020, 43, 7484–7505. [Google Scholar] [CrossRef]
- Xu, M.; Yang, F.; Yin, W. Mean-field stochastic differential equations driven by G-brownian motion. Discrete Contin. Dyn. Syst. Ser. S 2023, 16, 924–936. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Horwood: Chichester, UK, 2007. [Google Scholar]
- Hu, M.; Peng, S. On representation theorem of G-expectations and paths of G-Brownian motion. Acta Math. Appl.-Sin.-Engl. Ser. 2009, 25, 539–546. [Google Scholar] [CrossRef]
- Li, X.; Peng, S. Stopping times and related Itô’s calculus with G-Brownian motion. In Stochastic Processes and Their Applications; Elsevier: Amsterdam, The Netherlands, 2009; Volume 121, pp. 1492–1508. [Google Scholar]
- Gao, F. Pathwise properties and homeomorphic flows for stochastic differential equations driven by G-Brownian motion. Stoch. Proc. Appl. 2009, 119, 3356–3382. [Google Scholar] [CrossRef]
- Carmona, R. Lectures of BSDEs. Stochastic Control, and Stochastic Differential Games with Financial Applications, SIAM, 2016. Available online: https://epubs.siam.org/doi/pdf/10.1137/1.9781611974249.fm (accessed on 27 April 2025).
- Sznitman, A.S. Topics in propagation of chaos. In École d’Éde Probabilités de Saint-Flour XIX-1989; Hennequin, P.L., Ed.; Lecture Notes in Math; 1991; Volume 1464, pp. 165–251. [Google Scholar]
- Zeidler, E. Nonlinear Functional Analysis and its Applications II; Springer: New York, NY, USA, 1990. [Google Scholar]
- Mao, X.; Szpruch, L. Strong convergence rates for backward Euler-Maruyama method for non-linear dissipative-type stochastic differential equations with super-linear diffusion coefficients. Stochastics 2013, 85, 144–171. [Google Scholar] [CrossRef]
- Li, T.; Yuan, C. A note on strong convergence of implicit scheme for SDEs under local one-sided Lipschitz conditions. Int. J. Comput. Math. 2020, 98, 238–251. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Yuan, H. The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions. Mathematics 2025, 13, 1993. https://doi.org/10.3390/math13121993
Zhao P, Yuan H. The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions. Mathematics. 2025; 13(12):1993. https://doi.org/10.3390/math13121993
Chicago/Turabian StyleZhao, Pengfei, and Haiyan Yuan. 2025. "The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions" Mathematics 13, no. 12: 1993. https://doi.org/10.3390/math13121993
APA StyleZhao, P., & Yuan, H. (2025). The Modified Stochastic Theta Scheme for Mean-Field Stochastic Differential Equations Driven by G-Brownian Motion Under Local One-Sided Lipschitz Conditions. Mathematics, 13(12), 1993. https://doi.org/10.3390/math13121993





