A New Generalization of q-Truncated Polynomials Associated with q-General Polynomials

Abstract

This article presents the theory of trivariate q-truncated Gould–Hopper polynomials through a generating function approach utilizing q-calculus functions. These polynomials are subsequently examined within the framework of quasi-monomiality, leading to the establishment of fundamental operational identities. Operational representations are then derived, and q-differential and partial differential equations are formulated for the trivariate q-truncated Gould–Hopper polynomials. Summation formulae are presented to elucidate the analytical properties of these polynomials. Finally, graphical representations are provided to illustrate the behavior of trivariate q-truncated Gould–Hopper polynomials and their potential applications.

1. Introduction

The Gould–Hopper polynomials, as a generalization of the Hermite polynomials, exhibit a rich set of mathematical properties that make them particularly useful in various analytical contexts. These polynomials possess orthogonality relations, recurrence formulas, and generating functions that facilitate their application in solving complex mathematical problems. Their connection to harmonic oscillators in quantum mechanics has led to significant advancements in the understanding of quantum systems, particularly in the study of energy levels and wave functions. Moreover, Gould–Hopper polynomials have proven invaluable in the development of numerical methods for approximating solutions to certain classes of differential equations [1]. The versatility of the Gould–Hopper polynomials extends beyond theoretical physics and pure mathematics. In applied mathematics, these polynomials have found applications in signal processing, where they are used to analyze and filter complex waveforms. In addition, their properties make them suitable for use in computational algorithms, particularly in the field of numerical analysis. The study of Gould–Hopper polynomials continues to be an active area of research, with ongoing investigations into their higher-order generalizations and potential applications in emerging fields, such as quantum computing and information theory.

The generating function defines the bivariate truncated polynomials (or simply, 2VTP), represented by the notation $e_w^{\left(r\right)}(\zeta ,\eta )$ [2]:

$${\displaystyle \frac{e^{\zeta t}}{1-\eta t^r}}=\sum _{w=0}^{\infty }{e}_w^{\left(r\right)}(\zeta ,\eta ){\displaystyle \frac{t^w}{w!}},$$

(1)

where

$$e_w^{\left(r\right)}(\zeta ,\eta )=w!\sum _{k=0}^{\left[{\displaystyle \frac{w}{r}}\right]}{\displaystyle \frac{{\eta }^k{\zeta }^{w-rk}}{(w-rk)!}}.$$

(2)

Very recently, in [3], Özat et al. articulated the structure of truncated exponential-based general Appell polynomials by utilizing the framework of two-variable general Appell polynomials as follows:

$$A\left(t\right)e^{\zeta t}\psi \left(\eta ,t\right){\displaystyle \frac{1}{1-\gamma t^m}}={\sum _{j=0}^{\infty }}_{e^{\left(m\right)}}{T}_j(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^n}{n!}}.$$

Furthermore, the authors derived explicit and determinant representations, as well as lowering and raising operators, recurrence relations, differential equations, and several summation formulas for these polynomials.

Quantum calculus, alternatively termed q-calculus, has emerged as a domain of significant scholarly interest. As q approaches $1^{-}$, this field converges with classical calculus. In recent scientific discourse, the applications of quantum calculus have extended across numerous disciplines, including mathematical sciences, quantum physics and mechanics, quantum algebra, approximation theory, and operator theory. The foundations of q-calculus were established by F.H. Jackson in the early 20th century, presenting a robust alternative to classical analysis through the introduction of q-analogues of differentiation and integration. This formalism has been rigorously extended in the comprehensive work of Andrews, Askey, and Roy [4], and further enriched by Askey’s exploration of q-Laguerre polynomial limits [5]. The algebraic and operational structures of q-polynomials began to take shape with Cigler’s operator-based identities [6], paving the way for the formulation of q-Appell families. Subsequently, Ernst [7] provided a modern comprehensive treatment that systematized q-calculus, thereby establishing it as a coherent field in its own right. In recent decades, q-polynomials have emerged as central tools in quantum algebra and theoretical physics, as demonstrated by Florenini and Vinet’s work on the interplay between quantum algebra and q-specific functions [8]. Additionally, the construction of multidimensional q-Hermite polynomials by Wani et al. [9] expanded the applicability of q-polynomials to higher-dimensional and multi-variable domains. These developments have culminated in a growing interest in truncated polynomial families, particularly those based on q-exponential functions, leading to the formulation of truncated exponential-based Appell polynomials and their generalizations. Building on this rich context, this study introduces a novel class of three-variable q-truncated Gould–Hopper polynomials, establishing new recurrence relations, operational identities, and q-differential structures that contribute to the ongoing expansion of the q-polynomial framework. Assume $0<q<1$. The q-shifted factorial ${(\gamma ;q)}_v$ is defined as:

$${(\vartheta ;q)}_u=\prod _{w=0}^{u-1}(1-q^w\vartheta ),(u\in \mathbb{N}),{(\vartheta ;q)}_0=1.$$

(3)

The q-analogue of a number $\gamma$ is given by

$${\left[\vartheta \right]}_q={\displaystyle \frac{1-q^{\vartheta }}{1-q}},0<q<1;\vartheta \in \mathbb{C}.$$

(4)

The q-factorial is given by

$${\left[\vartheta \right]}_q!=\left\{\begin{array}{ccc}\prod _{w=1}^{\vartheta }{\left[w\right]}_q,\vartheta \ge 1& & \\ & & \\ 1,& \vartheta =0& \end{array}\right..$$

(5)

The following equality holds:

$${(\tau \pm \gamma )}_q^v=\sum _{s=0}^v{\left({\displaystyle \genfrac{}{}{0pt}{}{v}{s}}\right)}_q{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{v-s}{2}}\right)}{\tau }^s{(\pm \gamma )}^{v-s},$$

(6)

where

$${\left({\displaystyle \genfrac{}{}{0pt}{}{\vartheta }{w}}\right)}_q={\displaystyle \frac{{\left[\vartheta \right]}_q!}{{\left[\vartheta -w\right]}_q!{\left[w\right]}_q!}}.$$

Thefollowing equalities hold:

$$e_q\left(\tau \right)=\sum _{w=0}^{\infty }{\displaystyle \frac{{\tau }^w}{{\left[w\right]}_q!}},0<q<1,$$

(7)

and

$$E_q\left(\tau \right)=\sum _{w=0}^{\infty }{\displaystyle \frac{q^{\left(\genfrac{}{}{0pt}{}{w}{2}\right)}{\tau }^w}{{\left[j\right]}_q!}},0<q<1.$$

(8)

The following equality holds:

$$e_q\left(\tau \right)E_q\left(\varphi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{(\tau +\varphi )}_q^n}{{\left[n\right]}_q!}}.$$

(9)

Hence,

$$e_q\left(\tau \right)E_q(-\tau )=1.$$

(10)

q-derivative of $h\left(\tau \right)$ is defined by

$${\widehat{D}}_{q,\tau }h\left(\tau \right)={\displaystyle \frac{h\left(q\tau \right)-h\left(\tau \right)}{\tau \left(1-q\right)}},0<q<1,\tau \ne 0.$$

(11)

In particular, we have

$${\widehat{D}}_{q,\tau }{\tau }^w={\left[w\right]}_q{\tau }^{w-1},$$

(12)

$${\widehat{D}}_{q,\tau }{e}_q\left(\alpha \tau \right)=\alpha e_q\left(\alpha \tau \right),\alpha \in \mathbb{C},$$

(13)

and

$${\widehat{D}}_{q,\tau }^w{e}_q\left(\alpha \tau \right)={\alpha }^w{e}_q\left(\alpha \tau \right),w\in \mathbb{N},\alpha \in \mathbb{C},$$

(14)

where ${\widehat{D}}_{q,\tau }^w$ denotes the $w^{th}$ order q-derivative with respect to $\tau$.

The q-derivative concerning the product of the functions $f\left(\tau \right)$ and $g\left(\tau \right)$ has been thoroughly examined in the existing literature:

$${\widehat{D}}_{q,\tau }\left(h\left(\tau \right)k\left(\tau \right)\right)=h\left(\tau \right){\widehat{D}}_{q,\tau }k\left(\tau \right)+k\left(q\tau \right){\widehat{D}}_{q,\tau }h\left(\tau \right)$$

(15)

and

$${\widehat{D}}_{q,\tau }\left({\displaystyle \frac{h\left(\tau \right)}{k\left(\tau \right)}}\right)={\displaystyle \frac{k\left(q\tau \right){\widehat{D}}_{q,\tau }h\left(\tau \right)-h\left(q\tau \right){\widehat{D}}_{q,\tau }k\left(\tau \right)}{k\left(\tau \right)k\left(q\tau \right)}}.$$

(16)

The q-integral of a function $h\left(\tau \right)$ is introduced as

$${\int }_0^{a}h\left(\tau \right)d_q\tau =(1-q)a\sum _{w=0}^{\infty }{q}^{w}h\left(a{q}^w\right).$$

(17)

By virtue of (17), we get

$${\int }_0^{\tau }{\lambda }^w{d}_q\lambda =(1-q)\tau \sum _{n=0}^{\infty }{\tau }^w{q}^{n(w+1)}$$

$$={\displaystyle \frac{{\tau }^{w+1}(1-q)}{1-q^{w+1}}}={\displaystyle \frac{{\tau }^{w+1}}{{[w+1]}_q}},w\in \mathbb{N}\bigsqcup \left\{0\right\}.$$

(18)

In particular ${\widehat{D}}_{q,\tau }^{-1}\left\{1\right\}=\tau$, and then

$${\left({\widehat{D}}_{q,\tau }^{-1}\right)}^r\left\{1\right\}={\displaystyle \frac{{\tau }^r}{{\left[r\right]}_q!}},r\in \mathbb{N}\bigsqcup \left\{0\right\}.$$

(19)

The q-Gould–Hopper polynomials can be defined following the generating function [10]

$$e_q\left(\zeta t\right)e_q\left(\eta t^m\right)=\sum _{w=0}^{\infty }{H}_{w,q}^{\left(m\right)}(\zeta ,\eta ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

(20)

and series definition

$$H_{w,q}^{\left(m\right)}(\zeta ,\eta )={\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w}{m}}\right]}{\displaystyle \frac{{\eta }^k{\zeta }^{w-mk}}{{\left[k\right]}_q!{[w-mk]}_q!}}.$$

(21)

The operational identity of q-Gould–Hopper polynomials $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ is as follows:

$$H_{w,q}^{\left(m\right)}(\zeta ,\eta )=e_q\left(\eta D_{q,\zeta }^m\right)\left\{{\zeta }^w\right\}.$$

(22)

The $r^{th}$-order bivariate q-truncated exponential polynomials denoted by $e_{w,q}^{\left(r\right)}$ are defined by the following generating function [11]

$${\displaystyle \frac{e_q\left(\zeta t\right)}{1-\gamma t^r}}=\sum _{w=0}^{\infty }{E}_{w,q}^{\left(r\right)}\left(\zeta ,\gamma \right){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(23)

In a recent study, Alam et al. [12] defined and examined the bivariate q-general polynomials denoted as $p_{\theta ,q}(\zeta ,\eta )$, which are defined by:

$$e_q\left(\gamma \delta \right){\varphi }_q(\nu ,\delta )=\sum _{\theta =0}^{\infty }{p}_{\theta ,q}(\gamma ,\nu ){\displaystyle \frac{{\delta }^{\theta }}{{\left[\theta \right]}_q!}},(p_{0,q}(\gamma ,\nu )=1),$$

(24)

where ${\varphi }_q(\nu ,\delta )$ has (at least) the formal series expansion

$${\varphi }_q(\nu ,\delta )=\sum _{\theta =0}^{\infty }{\varphi }_{\theta ,q}\left(\nu \right){\displaystyle \frac{{\delta }^{\theta }}{{\left[\theta \right]}_q!}},({\varphi }_{0,q}\left(\nu \right)\ne 0).$$

(25)

In this article, we introduce the concept of trivariate q-truncated Gould–Hopper polynomials, employing a generating function methodology that integrates q-calculus functions. We obtain these within the quasi-monomiality framework, enabling the establishment of fundamental operational identities for these polynomials. The investigation proceeds to derive operational representations and formulate both q-differential and partial differential equations for these polynomials. To enhance understanding of their analytical characteristics, summation formulas are constructed. The article concludes by presenting graphical depictions that showcase the behavior of three-variable q-truncated Gould–Hopper-based polynomials.

2. New Generalization of q-Truncated Polynomials

In this section, we introduce a new generalization of q-truncated polynomials and obtain the series definition, recurrence relation, and explicit formula for these polynomials. We begin with the following definition as follows.

Utilizing the relations (23) and (24), we introduce the new generalization of q-truncated polynomials ${}_{p}E_{\omega ,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$ in the following form:

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)=\sum _{w=0}^{\infty }{}_{p}E_{\omega ,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}},(p_{0,q}(\zeta ,\eta )=1),$$

(26)

where ${\varphi }_q(\eta ,\delta )$ has (at least) the formal series expansion

$${\varphi }_q(\eta ,\delta )=\sum _{\upsilon =0}^{\infty }{\varphi }_{\upsilon ,q}\left(\eta \right){\displaystyle \frac{{\delta }^{\upsilon }}{{\left[\upsilon \right]}_q!}},({\varphi }_{0,q}\left(\eta \right)\ne 0).$$

(27)

Theorem 1.

The following series definition for ${}_{p}E_{\omega ,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$ holds true:

$${}_{p}E_{\omega ,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )=\sum _{\omega =0}^{\upsilon }{\left({\displaystyle \genfrac{}{}{0pt}{}{\upsilon }{\psi }}\right)}_q{\varphi }_{\psi ,q}\left(\eta \right)E_{\upsilon -\psi ,q}^{\left(r\right)}(\zeta ,\gamma ).$$

(28)

Proof. 

Upon simplification of the left-hand side of Equation (26) through the applications of Equations (23) and (27), we get the assertion (28). □

Theorem 2.

The following q-recurrence formula for the new generalization of q-truncated polynomials ${}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$ holds true:

$${}_{p}E_{w+1,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )=\zeta {}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )+\sum _{k=0}^w{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{k}}\right)}_q{}_{p}E_{w-k,q}^{\left(r\right)}(q\zeta ,\eta ,\gamma ){\beta }_{k,q}$$

$$+{\left[r\right]}_q{\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w-r+1}{r}}\right]}{\displaystyle \frac{q^{w-kr-r+1}{\gamma }^{k+1}{}_{p}E_{w-kr-r+1,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )}{{[w-kr-r+1]}_q!}},$$

(29)

where

$${\displaystyle \frac{{\varphi }_q^{\prime }(\eta ,t)}{{\varphi }_q(\eta ,t)}}=\sum _{k=0}^{\infty }{\beta }_{k,q}{\displaystyle \frac{t^k}{{\left[k\right]}_q!}}.$$

(30)

Proof. 

By taking the q-partial derivative with respect to t on both sides of Equation (26) and employing Equations (15) and (16), we have

$$\sum _{w=0}^{\infty }{}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )w{\displaystyle \frac{t^{w-1}}{{\left[w\right]}_q!}}={\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(q\zeta t\right){\displaystyle \frac{{\varphi }_q^{\prime }(\eta ,t)}{{\varphi }_q(\eta ,t)}}{\varphi }_q(\eta ,t)+\zeta {\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)$$

$$+\left({\displaystyle \frac{{\left[r\right]}_q\gamma t^{r-1}}{1-\gamma t^r}}\right)\left({\displaystyle \frac{1}{1-\gamma q^r{t}^r}}\right)e_q\left(q\zeta t\right){\varphi }_q(\eta ,t)$$

(31)

Now, using Equations (26) and (30) in Equation (31), we get

$$\sum _{w=0}^{\infty }{}_{p}E_{w+1,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$=\sum _{w=0}^{\infty }{}_{p}E_{w,q}^{\left(r\right)}(q\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}\sum _{k=0}^{\infty }{\beta }_{k,q}{\displaystyle \frac{t^k}{{\left[k\right]}_q!}}+\zeta \sum _{w=0}^{\infty }{}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$+{\left[r\right]}_q\sum _{w=0}^{\infty }{\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w-r+1}{r}}\right]}{\displaystyle \frac{q^{w-kr-r+1}{\gamma }^{k+1}{}_{p}E_{w-kr-r+1,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )}{{[w-kr-r+1]}_q!}}{\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(32)

which, upon rearranging the series and subsequently equating the corresponding powers of t on both sides of the resultant equation, yields the assertion (29). □

Theorem 3.

The following explicit summation formula for ${}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$ in terms of the product of $p_{w,q}(\zeta ,\eta )$ and $E_{w,q}^{\left(r\right)}(\zeta ,\eta )$ holds true:

$${}_{p}E_{w,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )=\sum _{s=0}^w\sum _{k=0}^{w-s}{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{s}}\right)}_q{\left({\displaystyle \genfrac{}{}{0pt}{}{w-s}{k}}\right)}_q{(-u)}^s{p}_{w-k-s,q}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ).$$

(33)

Proof. 

Consider the product of the generating function (24) of $p_{w,q}(\zeta ,\eta )$ and the generating function (23) of $E_{w,q}^{\left(r\right)}(\zeta ,\eta )$ in the following form:

$${\displaystyle \frac{e_q\left(ut\right)}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)=\sum _{w=0}^{\infty }\sum _{k=0}^{\infty }{p}_{w,q}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^{w+k}}{{\left[w\right]}_q!{\left[k\right]}_q!}}.$$

(34)

In the r.h.s. of Equation (34), using the following identity,

$$\sum _{w=0}^{\infty }\sum _{k=0}^{\infty }A(k,w)=\sum _{w=0}^{\infty }\sum _{k=0}^{w}A(k,w-k),$$

(35)

we get

$${\displaystyle \frac{e_q\left(ut\right)}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)=\sum _{w=0}^{\infty }\sum _{k=0}^w{p}_{w-k,q}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^{w+k}}{{[w-k]}_q!{\left[k\right]}_q!}},$$

(36)

which, on shifting the $e_q\left(ut\right)$ to the l.h.s. and using the series definition of the exponential, becomes

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)=\sum _{w=0}^{\infty }\sum _{s=0}^{\infty }\sum _{k=0}^w{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{k}}\right)}_q{(-u)}^s{p}_{w-k,q}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^{w+s}}{{\left[w\right]}_q!{\left[s\right]}_q!}}.$$

(37)

Again, using Equation (35) in the r.h.s of Equation (37), we get

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right){\varphi }_q(\eta ,t)=\sum _{w=0}^{\infty }\sum _{s=0}^w\sum _{k=0}^{w-s}{\left({\displaystyle \genfrac{}{}{0pt}{}{w-s}{k}}\right)}_q{(-u)}^s{p}_{w-k-s,q}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^w}{{[w-s]}_q!{\left[s\right]}_q!}}.$$

(38)

Finally, using the equation generating function (26) in the l.h.s. of Equation (38) and equating the coefficients of like powers of t in the resultant equation, we get assertion (33). □

3. Applications

In this section, we introduce trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ i.e., ${\varphi }_q(\eta ,t)=e_q\left(\eta t^m\right)$ in (26) and obtain their series definition, recurrence relation, explicit formulas, and operational identities. Therefore, we define the trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$.

Here, we define the trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ of order r by means of the following generating function:

$${\displaystyle \frac{e_q\left(\zeta t\right)e_q\left(\eta t^m\right)}{1-\gamma t^r}}=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(39)

In other words, we note that

$$e_q\left(\eta {\widehat{D}}_{q,\zeta }^m\right){\displaystyle \frac{e_q\left(\zeta t\right)}{1-\gamma t^r}}=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(40)

Remark 1.

For $\gamma =1$, the following consequence of Equation (39) is deduced.

Corollary 1.

For the bivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ of order r, we use the following generating function:

$${\displaystyle \frac{e_q\left(\zeta t\right)e_q\left(\eta t^m\right)}{1-t^r}}=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(41)

Remark 2.

Letting $\eta =0$ and $\gamma =1$ in (39), the trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ of order r reduce the q-truncated exponential polynomials of order r, and the following generating function is used [10]

$${\displaystyle \frac{e_q\left(\zeta t\right)}{1-t^r}}=\sum _{w=0}^{\infty }{e}^{\left(r\right)}\left(\zeta \right){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(42)

Remark 3.

As $q\to 1^{-}$, Equation (39) reduces to the trivariate truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_w^{\left(m\right)}(\zeta ,\eta ,\gamma )$ of order r, the following generating function is used:

$${\displaystyle \frac{e^{\zeta t+\eta t^m}}{1-\gamma t^r}}=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_w^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{w!}}.$$

(43)

Theorem 4.

The three variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ of order r satisfy the following addition formula:

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta +\delta ,\eta ,\gamma )=\sum _{k=0}^w{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{k}}\right)}_q{\delta }^k{}_{e^{\left(r\right)}}H_{w-k,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ).$$

(44)

Proof. 

By changing $\zeta$ by $\zeta +\delta$ in (39), it follows that

$${\displaystyle \frac{e_q\left(\zeta t\right)e_q\left(\eta t^m\right)}{1-\gamma t^r}}{e}_q\left(\delta t\right)=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta +\delta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(45)

Using Equations (7) and (39) in the l.h.s. of the above equation, we have

$$\sum _{w=0}^{\infty }\sum _{k=0}^{\infty }{\delta }^k{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^{w+k}}{{\left[w\right]}_q!{\left[k\right]}_q!}}=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta +\delta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}},$$

which, on rearranging the series and then equating the similar powers of t on both sides, yields assertion (44). □

Theorem 5.

The trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ are defined by the series

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )={\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w}{m}}\right]}{\displaystyle \frac{{\gamma }^k{e}_{w-mk,q}^{\left(r\right)}(\zeta ,\gamma )}{{\left[k\right]}_q!{\left[w-mk\right]}_q!}}$$

(46)

and

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )={\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w}{r}}\right]}{\displaystyle \frac{{\eta }^k{H}_{w-rk,q}^{\left(m\right)}(\zeta ,\gamma )}{{\left[w-rk\right]}_q!}}.$$

(47)

Proof. 

In view of Equations (7), (20), and (23), we can easily obtain the assertions (46) and (47). □

Theorem 6.

The following q-recurrence formula for the trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ holds true:

$${}_{e^{\left(r\right)}}H_{w+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=\zeta {}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )+{\left[w\right]}_q!\eta \sum _{m=0}^{w-1}{\displaystyle \frac{{}_{e^{\left(r\right)}}H_{w-m+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )}{{\left[w-m+1\right]}_q}}{T}_{(\eta ;m)}{T}_{\zeta }$$

$$+{\left[r\right]}_q{\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w-r+1}{r}}\right]}{\displaystyle \frac{q^{w-kr-r+1}{\gamma }^{k+1}{}_{e^{\left(r\right)}}H_{w-kr-r+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )}{{[w-kr-r+1]}_q!}}.$$

(48)

Proof. 

Taking the q-partial derivative with respect to t in both sides of Equation (39) and using Equations (15) and (16), we have

$$\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )w{\displaystyle \frac{t^{w-1}}{{\left[w\right]}_q!}}=\zeta {\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^m\right)+\eta t^{m-1}{T}_{(\eta ;m)}{\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(q\zeta t\right)e_q\left(\eta t^m\right)$$

$$+\left({\displaystyle \frac{{\left[r\right]}_q\gamma t^{r-1}}{1-\gamma t^r}}\right)\left({\displaystyle \frac{1}{1-\gamma q^r{t}^r}}{e}_q\left(q\zeta t\right)e_q\left(q\eta t^m\right)\right).$$

(49)

Now, by using Equations (24) and (39) in Equation (49), we get

$$\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$=\zeta \sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}+{\left[w\right]}_q!\eta \sum _{w=0}^{\infty }\sum _{m=0}^{w-1}{\displaystyle \frac{{}_{e^{\left(r\right)}}H_{w-m+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )}{\left[w-m+1\right]}}{T}_{(\eta ;m)}{T}_{\zeta }{\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$+{\left[r\right]}_q\sum _{w=0}^{\infty }{\left[w\right]}_q!\sum _{k=0}^{\left[{\displaystyle \frac{w-r+1}{r}}\right]}{\displaystyle \frac{q^{w-kr-r+1}{\gamma }^{k+1}{}_{e^{\left(r\right)}}H_{w-kr-r+1,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )}{{[w-kr-r+1]}_q!}}{\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(50)

which, upon rearranging the series and subsequently equating the corresponding powers of t on both sides of the resultant equation, yields the assertion (48). □

Theorem 7.

The higher derivative formula for the trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ holds true:

$${\widehat{D}}_{q,t}^k{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )={\displaystyle \frac{{\left[w\right]}_q!}{{[w-k]}_q!}}{}_{e^{\left(r\right)}}H_{w-k,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ).$$

(51)

Proof. 

Taking the $k^{th}$ order q-partial derivative with respect to $\zeta$ on both sides of the generating function (39) and then using Equation (14) in the l.h.s., it follows that

$$\sum _{w=0}^{\infty }{\widehat{D}}_{q,t}^k{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}=t^k{\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^m\right)=\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^{w+k}}{{\left[w\right]}_q!}}.$$

(52)

Upon rearranging the aforementioned series and subsequently comparing the corresponding powers of t on both sides of the resulting equation, we obtain the assertion (51). □

The explicit summation formula for the ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ by using generating functions of q-GHP $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ are derived by proving the following theorem.

Theorem 8.

The following explicit summation formula for ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ in terms of the product of $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ and $e_{w,q}^{\left(r\right)}(\zeta ,\eta )$ holds true:

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=\sum _{s=0}^w\sum _{k=0}^{w-s}{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{s}}\right)}_q{\left({\displaystyle \genfrac{}{}{0pt}{}{w-s}{k}}\right)}_q{(-u)}^s{H}_{w-k-s}^{\left(m\right)}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ).$$

(53)

Proof. 

Consider the product of generating function (20) of $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ and generating function (23) of $E_{w,q}^{\left(r\right)}(\zeta ,\eta )$ in the following form:

$${\displaystyle \frac{e_q\left(ut\right)}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^r\right)=\sum _{w=0}^{\infty }\sum _{k=0}^{\infty }{H}_{w,q}^{\left(m\right)}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^{w+k}}{{\left[w\right]}_q!{\left[k\right]}_q!}}.$$

(54)

In the r.h.s. of Equation (54), using the following identity,

$$\sum _{w=0}^{\infty }\sum _{k=0}^{\infty }A(k,w)=\sum _{w=0}^{\infty }\sum _{k=0}^{w}A(k,w-k),$$

(55)

we get

$${\displaystyle \frac{e_q\left(ut\right)}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^r\right)=\sum _{w=0}^{\infty }\sum _{k=0}^w{H}_{w-k,q}^{\left(m\right)}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^{w+k}}{{[w-k]}_q!{\left[k\right]}_q!}},$$

(56)

which, on shifting the $e_q\left(ut\right)$ to the l.h.s. and using the series definition of the exponential, becomes

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^r\right)=\sum _{w=0}^{\infty }\sum _{s=0}^{\infty }\sum _{k=0}^w{\left({\displaystyle \genfrac{}{}{0pt}{}{w}{k}}\right)}_q{(-w)}^s{H}_{w-k,q}^{\left(m\right)}(\zeta ,\gamma )e_{k,q}^{\left(r\right)}(w,\eta ){\displaystyle \frac{t^{w+s}}{{\left[w\right]}_q!{\left[s\right]}_q!}}.$$

(57)

Again, using Equation (55) in the r.h.s of Equation (57), we get

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^r\right)=\sum _{w=0}^{\infty }\sum _{s=0}^w\sum _{k=0}^{w-s}{\left({\displaystyle \genfrac{}{}{0pt}{}{w-s}{k}}\right)}_q{(-u)}^s{H}_{w-k-s,q}^{\left(m\right)}(\zeta ,\eta )E_{k,q}^{\left(r\right)}(u,\gamma ){\displaystyle \frac{t^w}{{[w-s]}_q!{\left[s\right]}_q!}}.$$

(58)

Finally, using the equation-generating function (39) in the l.h.s. of Equation (58) and equating the coefficients of like powers of t in the resultant equation, we get assertion (53). □

4. Monomiality Characteristic

The concept of monomiality is a fundamental tool for the examination of exceptional polynomials and their characteristics. Initially introduced by J.F. Steffensen [13], this idea was later expanded into the field of quasi-monomiality by Dattoli and his colleagues [14,15,16]. In the realm of q-polynomials, Zayed et al. [17] further advanced the principle of monomiality. This advancement offers a comprehensive methodology for investigating the quasi-monomiality of specific q-special polynomials. Researchers have widely applied monomiality frameworks to develop and assess hybrid families of special polynomials [18]. The two q-operators ${\widehat{M}}_q$ and ${\widehat{P}}_q$, called q-multiplicative and q-derivative operators, respectively, for a q-polynomial set $p_{w,q}\left(\zeta \right)$$(w\in \mathbb{N},\zeta \in \mathbb{C})$ are realized by [17]

$$\widehat{M_q}\left\{p_{w,q}\left(\zeta \right)\right\}=p_{w+1,q}\left(\zeta \right),$$

(59)

and

$$\widehat{P_q}\left\{p_{w,q}\left(\zeta \right)\right\}={\left[w\right]}_q{p}_{w-1,q}\left(\zeta \right).$$

(60)

The operators $\widehat{M_q}$ and $\widehat{P_q}$ satisfy the following commutation relation:

$$[\widehat{M_q},\widehat{P_q}]=\widehat{P_q}\widehat{M_q}-\widehat{M_q}\widehat{P_q}.$$

(61)

The properties of the polynomials $p_{w,q}\left(\zeta \right)$ can be deduced from those of the $\widehat{M_q}$ and $\widehat{P_q}$ operators. If $\widehat{M_q}$ and $\widehat{P_q}$ possess a differential realization, then the polynomials $p_{w,q}\left(\zeta \right)$ satisfy the differential equation

$$\widehat{M_q}\widehat{P_q}\left\{p_{w,q}\left(\zeta \right)\right\}={\left[w\right]}_q{p}_{w,q}\left(\zeta \right),$$

(62)

and

$$\widehat{P_q}\widehat{M_q}\left\{p_{w,q}\left(\zeta \right)\right\}={[w+1]}_q{p}_{w,q}\left(\zeta \right).$$

(63)

In view of (59) and (60), we have

$$[\widehat{M_q},\widehat{P_q}]={[w+1]}_q-{\left[w\right]}_q.$$

(64)

From (59), we have

$${\widehat{M_q}}^r\left\{p_{w,q}\right\}=p_{w+r,q}\left(\zeta \right).$$

(65)

In particular, we have

$$p_{w,q}\left(\zeta \right)={\widehat{M_q}}^w\left\{p_{0,q}\right\}={\widehat{M_q}}^w\left\{1\right\},$$

(66)

where $p_{0,q}\left(\zeta \right)=1$ is the q-sequel of the polynomial $p_{w,q}\left(\zeta \right)$. Also, the generating function of $p_{w,q}\left(\zeta \right)$ can be obtained as

$$e_q\left(\widehat{M_q}t\right)\left\{1\right\}=\sum _{w=0}^{\infty }{p}_{w,q}\left(\zeta \right){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}.$$

(67)

The q-dilatation operator $T_z$, which acts on any function of the complex variable z in the following manner [19]

$$T_z^{k}f\left(z\right)=f\left(q^{k}z\right),k\in \mathbb{R},0<q<1,$$

(68)

satisfies the property

$$T_z^{-1}{T}_z^{1}f\left(z\right)=f\left(z\right).$$

(69)

The q-derivative of the q-exponential function $e_q\left(\eta t^m\right)$ is given as [17]

$${\widehat{D}}_{q,t}{e}_q\left(\eta t^m\right)=\eta t^{m-1}{T}_{(\eta ;m)}{e}_q\left(\eta t^m\right)$$

(70)

where

$$T_{(\eta ;m)}={\displaystyle \frac{1-q^m{T}_{\eta }^m}{1-q{T}_{\eta }}}=1+q{T}_{\eta }+\cdots +q^{m-1}{T}_{\eta }^{m-1}.$$

In the subsequent theorem, we elucidate the q-monomial attributes of the three-variable q-truncated Gould–Hopper polynomials, represented by the notation ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$.

Theorem 9.

The trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ are quasi-monomials under the following q-multiplicative and q-derivative operators:

$${\widehat{M}}_{3VqTGHP}=\zeta +\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)}{T}_{\zeta }+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^{r-1}}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta },$$

(71)

or, alternatively

$${\widehat{M}}_{3VqTGHP}=\zeta T_{\eta }+\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)}+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^{r-1}}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta }$$

(72)

and

$${\widehat{P}}_{3VqTGHP}={\widehat{D}}_{q,\zeta },$$

(73)

respectively, where $T_{\zeta }$ and $T_{\eta }$ denote the q-dilatation operators given by Equation (68).

Proof. 

Taking the q-derivatives on both sides of Equation (39) with respect to t by using Equations (15) and (16), we obtain

$$\sum _{w=1}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\widehat{D}}_{q,t}{\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$={\displaystyle \frac{1}{1-\gamma t^r}}{\widehat{D}}_{q,t}\left(e_q\left(\zeta t\right)e_q\left(\eta t^m\right)\right)+e_q\left(q\zeta t\right)e_q\left(q\eta t^m\right){\widehat{D}}_{q,t}{\displaystyle \frac{1}{1-\gamma t^r}},$$

(74)

which, on using Equations (15) and (16) by taking $f_q\left(t\right)=e_q\left(\eta t\right)e_q\left(\eta t^m\right)$ and $g\left(t\right)={\displaystyle \frac{1}{1-\gamma t^r}}$ and then simplifying the resultant equation by using Equations (16), (68), and (74) in the left-hand side, results in

$$\left(\zeta +\eta t^{m-1}{T}_{(\eta ;m)}{T}_{q,\zeta }+{\displaystyle \frac{{\left[r\right]}_q\gamma t^{r-1}}{1-q^r\gamma t^r}}{T}_{\zeta }{T}_{\eta }\right){\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^m\right)$$

$$=\sum _{w=1}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^{w-1}}{{[w-1]}_q!}}.$$

(75)

Therefore, by Equation (75), we get

$$\left(\zeta +\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)}{T}_{q,\zeta }+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^{r-1}}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta }\right){\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t^m\right)$$

$$=\sum _{w=1}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^{w-1}}{{[w-1]}_q!}},$$

(76)

which on using (39) gives

$$\left(\zeta +\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)}{T}_{q,\zeta }+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^{r-1}}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta }\right)\sum _{w=0}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$=\sum _{w=1}^{\infty }{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^{w-1}}{{[w-1]}_q!}}.$$

(77)

Comparing the coefficients of t on both sides of Equation (77) and then from a view of Equation (59), the resultant equation gives assertion (71).

Using Equation (16), again by taking $f_q\left(t\right)=e_q\left(\eta t^m\right)$ and $g_q\left(t\right)=e_q\left(\eta t\right)$ and following the same steps as in the proof of statement of Equation (71), we arrive at assertion (72).

In view of (60), we note that Equation (51) (for $k=1$) proves assertion (73). □

Theorem 10.

The following q-differential equation for ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ holds true:

$$\left(\zeta {\widehat{D}}_{q,\zeta }+\eta {\widehat{D}}_{q,\zeta }^m{T}_{(\eta ;m)}{T}_{\zeta }+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^r}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta }-{\left[w\right]}_q\right){}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0,$$

(78)

and

$$\left(\zeta {\widehat{D}}_{q,\zeta }{T}_{\eta }+\eta {\widehat{D}}_{q,\zeta }^m{T}_{(\eta ;m)}+{\displaystyle \frac{{\left[r\right]}_q\gamma {\widehat{D}}_{q,\zeta }^r}{1-q^r\gamma {\widehat{D}}_{q,\zeta }^r}}{T}_{\zeta }{T}_{\eta }-{\left[w\right]}_q\right){}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0.$$

(79)

Proof. 

Using (71)–(73) in (62), we get the assertions (78) and (79). □

We now establish the following result for operational identities of the trivariate q-truncated Gould–Hopper polynomials:

Theorem 11.

The trivariate q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ satisfy the following respective operational identities:

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=e_q\left(\eta {\widehat{D}}_{q,\zeta }^m\right)\left\{e_{w,q}^{\left(r\right)}(\zeta ,\gamma )\right\},$$

(80)

or, equivalently

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta +l,\gamma )=e_q\left(l{\widehat{D}}_{q,\zeta }^m\right)\left\{{}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )\right\}$$

(81)

and

$$E_q\left(-\eta {\widehat{D}}_{q,\zeta }^m\right){}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=e_{w,q}^{\left(r\right)}(\zeta ,\gamma ),$$

(82)

where ${\widehat{D}}_{q,\zeta }^m$ is the $m^{th}$ q-derivative operator.

Proof. 

In view of Equation (14), we have

$${\widehat{D}}_{q,\zeta }^m{\zeta }^w={\displaystyle \frac{{\left[w\right]}_q!}{{[w-mr]}_q!}}{\zeta }^{w-mr}.$$

(83)

Utilizing the preceding equation of the formula (39), we acquire

$${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=\sum _{r=0}^{\infty }{\displaystyle \frac{{\left(\eta {\widehat{D}}_{q,\zeta }^m\right)}^r}{{\left[r\right]}_q!}}{e}_{w,q}^{\left(r\right)}(\zeta ,\gamma ).$$

(84)

Utilizing the expression (5) on the r.h.s. of the preceding equation, we arrive at the statement (80). Again, by a similar method (80) and using (5), we get the assertion (81). Operating $E_q\left(-\eta {\widehat{D}}_{q,\zeta }^m\right)$ on both sides of Equation (80) and using Equation (10), we obtain (82). □

5. Distribution of Zeros and Graphical Representation

This section examines specific zero values of the three-variable q-truncated Gould–Hopper polynomials (3VqTGHP) and presents corresponding graphical representations.

The definition of the three-variable q-truncated Gould–Hopper polynomials is recalled from (39).

A few of them are as follows:

$$\begin{array}{l}{}_{e^{\left(3\right)}}H_{0,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )=1,\\ {}_{e^{\left(3\right)}}H_{1,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )=\zeta ,\\ {}_{e^{\left(3\right)}}H_{2,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^2,\\ {}_{e^{\left(3\right)}}H_{3,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^3+\gamma {\left[3\right]}_q!,\\ {}_{e^{\left(3\right)}}H_{4,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^4+\gamma \zeta {\left[4\right]}_q!,\\ {}_{e^{\left(3\right)}}H_{5,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^5+\eta {\left[5\right]}_q!+{\displaystyle \frac{\gamma {\zeta }^2{\left[5\right]}_q!}{{\left[2\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{6,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^6+{\gamma }^2{\left[6\right]}_q!+\zeta \eta {\left[6\right]}_q!+{\displaystyle \frac{\gamma {\zeta }^3{\left[6\right]}_q!}{{\left[3\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{7,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^7+{\gamma }^2\zeta {\left[7\right]}_q!+{\displaystyle \frac{{\zeta }^2\eta {\left[7\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^4{\left[7\right]}_q!}{{\left[4\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{8,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^8+\gamma \eta {\left[8\right]}_q!+{\displaystyle \frac{{\gamma }^2{\zeta }^2{\left[8\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{{\zeta }^3\eta {\left[8\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^5{\left[8\right]}_q!}{{\left[5\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{9,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^9+{\gamma }^3{\left[9\right]}_q!+\gamma \zeta \eta {\left[9\right]}_q!+{\displaystyle \frac{{\gamma }^2{\zeta }^3{\left[9\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{{\zeta }^4\eta {\left[9\right]}_q!}{{\left[4\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^6{\left[9\right]}_q!}{{\left[6\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{10,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^{10}+{\gamma }^3\zeta {\left[10\right]}_q!+{\displaystyle \frac{\gamma {\zeta }^2\eta {\left[10\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{{\eta }^2{\left[10\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{{\gamma }^2{\zeta }^4{\left[10\right]}_q!}{{\left[4\right]}_q!}}\\ +{\displaystyle \frac{{\zeta }^5\eta {\left[10\right]}_q!}{{\left[5\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^7{\left[10\right]}_q!}{{\left[7\right]}_q!}},\\ {}_{e^{\left(3\right)}}H_{11,q}^{\left(5\right)}(\zeta ,\eta ,\gamma )={\zeta }^{11}+{\gamma }^2\eta {\left[11\right]}_q!+{\displaystyle \frac{{\gamma }^3{\zeta }^2{\left[11\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{\zeta {\eta }^2{\left[11\right]}_q!}{{\left[2\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^3\eta {\left[11\right]}_q!}{{\left[3\right]}_q!}}+{\displaystyle \frac{{\gamma }^2{\zeta }^5{\left[11\right]}_q!}{{\left[5\right]}_q!}}\\ +{\displaystyle \frac{{\zeta }^6\eta {\left[11\right]}_q!}{{\left[6\right]}_q!}}+{\displaystyle \frac{\gamma {\zeta }^8{\left[11\right]}_q!}{{\left[8\right]}_q!}}.\end{array}$$

We investigated the beautiful zeros of the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$ by using a computer. We plot the zeros of the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$, for $w=50$ (Figure 1).

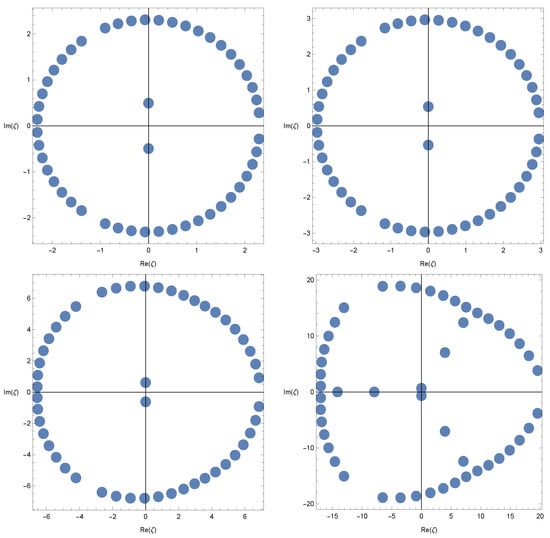
Figure 1. Zeros of ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$.

In Figure 1 (top-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{1}{10}}$. In Figure 1 (top-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{5}{10}}$. In Figure 1 (bottom-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{7}{10}}$. In Figure 1 (bottom-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{9}{10}}$.

Stacks of zeros of the three variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$ for $1\le w\le 50$, forming a 3D structure, are presented (Figure 2).

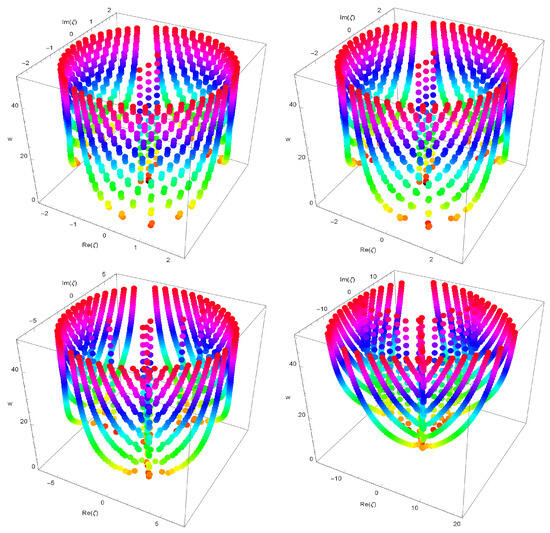
Figure 2. Zeros of ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$.

In Figure 2 (top-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{1}{10}}$. In Figure 2 (top-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{5}{10}}$. In Figure 2 (bottom-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{7}{10}}$. In Figure 2 (bottom-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{9}{10}}$.

We also investigated the beautiful zeros of the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$ by using a computer. We plotted the zeros of the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$, for $m=5,r=3,$ $\eta =2,\gamma =9,$ and $q={\displaystyle \frac{9}{10}}$ (Figure 3).

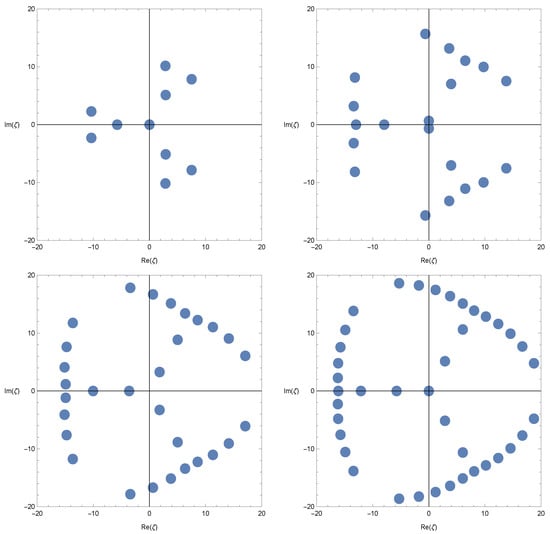
Figure 3. Zeros of ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$.

In Figure 3 (top-left), we choose $w=10$. In Figure 3 (top-right), we choose $w=20$. In Figure 3 (bottom-left), we choose $w=30$. In Figure 3 (bottom-right),we choose $w=40$.

Plots of the real zeros of the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$ for $1\le w\le 50$ are presented (Figure 4).

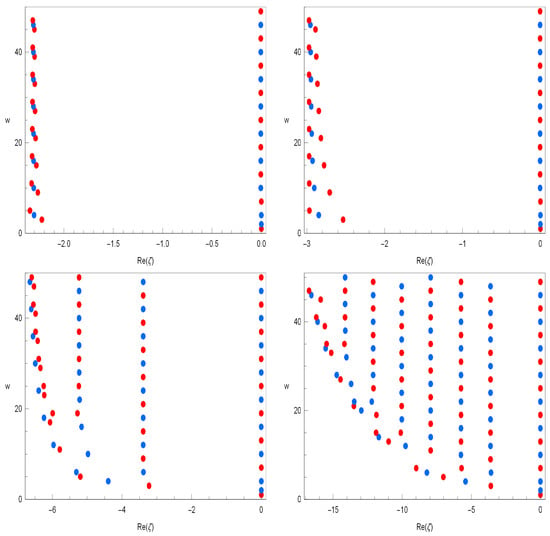
Figure 4. Real zeros of ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$.

In Figure 4 (top-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{1}{10}}$. In Figure 4 (top-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{5}{10}}$. In Figure 4 (bottom-left), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{7}{10}}$. In Figure 4 (bottom-right), we choose $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{9}{10}}$.

Next, we calculated an approximate solution satisfying the three-variable q-truncated Gould–Hopper polynomials ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$ for $m=5,r=3,\eta =2,\gamma =9,$ and $q={\displaystyle \frac{9}{10}}$. The results are given in Table 1.

Table 1. Approximate solutions of ${}_{e^{\left(r\right)}}H_{w,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )=0$.

Degree w	$\mathit{\zeta }$
1	0
2	$0,0$
3	$-3.5919,1.7959-3.1107i,1.7959+3.1107i$
4	$-5.4217,0,2.7108-4.6953i,2.7108+4.6953i$
5	$-7.0232,-0.00026-0.64979i,$
	$-0.00026+0.64979i,3.5119-6.0476i,3.5119+6.0476i$
6	$-8.2145,-3.5772,1.7867-3.3121i,$
	$1.7867+3.3121i,4.1092-7.0175i,4.1092+7.0175i$
7	$-8.9891,-5.7073,0,2.8387-5.3076i,$
	$2.8387+5.3076i,4.5096-7.5441i,4.5096+7.5441i$
8	$-8.6179-0.3656i,-8.6179+0.3656i,0.00166-0.64978i,$
	$0.00166+0.64978i,3.2576-7.8239i,3.2576+7.8239i,$
	$5.3586-7.1990i,5.3586+7.1990i$
9	$-9.6110-1.6439i,-9.6110+1.6439i,-3.6101,$
	$1.8083-3.2740i,1.8083+3.2740i,3.0110-9.2019i,$
	$3.0110+9.2019i,6.5968-7.5264i,6.5968+7.5264i$
10	$-10.3505-2.2864i,-10.3505+2.2864i,-5.7541,$
	$-0.0028880,2.8410-10.1594i,2.8410+10.1594i,$
	$2.8844-5.1257i,2.8844+5.1257i,7.5036-7.8530i,$
	$7.5036+7.8530i$

6. Conclusions and Some Remarks

Firstly, here we will list quasi-monomials under the following q-multiplicative and q-derivative operators for q-Gould–Hopper polynomials $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ (see Equation (20)):

Theorem 12.

The bivariate q-Gould–Hopper polynomials $H_{w,q}^{\left(m\right)}(\zeta ,\eta )$ are quasi-monomials under the following q-multiplicative and q-derivative operators:

$${\widehat{M}}_{2VqGHP}=\zeta T_{\eta }+\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)},$$

(85)

or, alternatively

$${\widehat{M}}_{2VqGHP}=\zeta +\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)}{T}_{\zeta }$$

(86)

and

$${\widehat{P}}_{2VqGHP}={\widehat{D}}_{q,\zeta },$$

(87)

respectively, where $T_{\zeta }$ and $T_{\eta }$ denote the q-dilatation operators given by Equation (68).

Proof. 

Taking q-derivative on both sides of Equation (20) with respect to t by using Equations (15) and (16), we obtain

$$\sum _{w=1}^{\infty }{H}_{w,q}^{\left(m\right)}(\zeta ,\eta ){\widehat{D}}_{q,t}{\displaystyle \frac{t^w}{{\left[w\right]}_q!}}$$

$$=e_q\left(q\eta t^m\right){\widehat{D}}_{q,t}\left(e_q\left(\zeta t\right)\right)+e_q\left(\zeta t\right){\widehat{D}}_{q,t}{e}_q\left(\eta t^m\right),$$

(88)

which, on using Equation (15) by taking $f_q\left(t\right)=e_q\left(\eta t\right)$ and $g\left(t\right)=e_q\left(\eta t^m\right)$ and then simplifying the resultant equation by using Equations (15), (20), (39), (59), and (60), allows us to easily obtain the assertions (85)–(87). □

We introduced the ${}_{e^{\left(r\right)}}H_{n,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$ in Section 2. Now, we will find the generating function of $H_{n,q}^{\left(m\right)}(\zeta ,\eta )$-based $e_{n,q}^{\left(r\right)}(\zeta ,\eta )$ and represent it as trivariate Gould–Hopper truncated exponential polynomials, denoted by ${}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$. For this, by replacing $\zeta$ by the multiplicative operator ${\widehat{M}}_{qH}$ of q-GHP $H_{n,q}^{\left(m\right)}(\zeta ,\eta )$ and $\eta$ by $\gamma$ in the generating function of $e_{n,q}^{\left(r\right)}(\zeta ,\eta )$, we have

$${\displaystyle \frac{e_q\left({\widehat{M}}_{qH}t\right)}{1-\gamma t^r}}=\sum _{n=0}^{\infty }{e}_{n,q}^{\left(r\right)}\left({\widehat{M}}_{qH}\right),\gamma ){\displaystyle \frac{t^n}{{\left[n\right]}_q!}},$$

(89)

which, on using the relation (85) in the l.h.s. and denoting the resultant in the r.h.s. by ${}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$, that is

$$e_{n,q}^{\left(r\right)}\left({\widehat{M}}_{qH}\right),\gamma )=e_{n,q}^{\left(r\right)}(\zeta T_{\eta }+\eta {\widehat{D}}_{q,\zeta }^{m-1}{T}_{(\eta ;m)})={}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ),$$

(90)

we get

$${\displaystyle \frac{1}{1-\gamma t^r}}\sum _{n=0}^{\infty }{H}_{n,q}^{\left(m\right)}(\zeta ,\eta ){\displaystyle \frac{t^n}{{\left[n\right]}_q!}}=\sum _{n=0}^{\infty }{}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^n}{{\left[n\right]}_q!}}.$$

(91)

Now, using generating function (20) of $H_{n,q}^{\left(m\right)}(\zeta ,\eta )$ in the l.h.s., we get

$${\displaystyle \frac{1}{1-\gamma t^r}}{e}_q\left(\zeta t\right)e_q\left(\eta t\right)=\sum _{n=0}^{\infty }{}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma ){\displaystyle \frac{t^n}{{\left[n\right]}_q!}},$$

(92)

which is the generating function of ${}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$.

From the generating functions (39) and (92), we observe that

$${}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )={}_{e^{\left(r\right)}}H_{n,q}^{\left(m\right)}(\zeta ,\eta ,\gamma ).$$

(93)

In view of the above relation, we conclude that all the properties of the ${}_{H^{\left(m\right)}}e_{n,q}^{\left(r\right)}(\zeta ,\eta ,\gamma )$ can be deduced from the corresponding ones for ${}_{e^{\left(r\right)}}H_{n,q}^{\left(m\right)}(\zeta ,\eta ,\gamma )$.

The q-monomiality concept plays a pivotal role in the study of special polynomials, providing a powerful framework for analyzing their properties and relationships. This paper delves into a comprehensive examination of trivariate q-truncated Gould–Hopper polynomials, employing the q-monomiality principle as the primary analytical tool. Through this approach, this research uncovers and elucidates multiple characteristics of these newly introduced polynomials, contributing to the broader understanding of polynomial theory within the q-calculus domain.

The study extends beyond theoretical exploration by investigating specific instances of these polynomials, thereby bridging the gap between abstract concepts and practical applications. Furthermore, the research encompasses the computation of zeros for these polynomial types, accompanied by visual representations that enhance the interpretation and comprehension of their behavior. By providing this detailed analysis and practical insights, the paper establishes a solid foundation for future research endeavors. Scholars can build upon these findings to further explore and uncover the intricate properties of various polynomials when examined through the lens of the q-monomiality principle, potentially leading to new discoveries and applications in mathematical analysis and related fields.

The subclasses of p-valent $\kappa$-uniformly convex and star-like functions, as defined through the q-derivative operator, hold significant applicability within the analytic theory of univalent and multivalent functions [20]. Furthermore, the results presented herein can contribute to the theory of multivalent functions by offering novel coefficient bounds and structural insights for the subclasses under investigation.