Abstract
Value-at-Risk (VaR) estimation using the GARCH model is an important topic in financial data analysis. It allows for an increase in the accuracy of risk assessment by controlling time-varying volatility. In this paper, we enhance this feature by exploring the functional path of the financial data. More precisely, we study the nonparametric estimation of the multi-functional VaR function using the local linear method, construct an estimator, and establish its stochastic consistency. The derived asymptotic result provides a rigorous mathematical foundation that permits boosting the use of the VaR function in financial data analysis. Furthermore, an empirical analysis is performed in order to examine the efficiency of the proposed algorithm. Additionally, a real data application is created to highlight the multi-functionality of the VaR estimation for multi-asset risk management.
Keywords:
Asymmetric least squares; value at risk; coherent risk measures; expected shortfall; expectile regression; prediction markets; decision making; big-data analysis MSC:
62G08; 62G10; 62G35; 62G07; 62G32; 62G30; 62H12
1. Introduction
With rapid technological developments enabling the digital control of financial activities, real-time analysis of financial risks is becoming essential. However, it is well known that standard instruments obtained from multivariate parametric statistics cannot be used to solve this problem. Instead, in this paper, we propose using multi-functional data to develop a new data-driven approach that is capable of managing multi-financial risks in real time. Specifically, we assess market risk through the estimation of the VaR-function using multi-functional co-variate functions.
It is well-documented that financial volatility is an important factor in investment decisions. It permits us to offer a dynamic and robust measure of financial risk. This subject has been widely considered in the statistical literature. The first study was introduced by [1]. He considered the autoregressive conditional heteroscedasticity (ARCH) model. Such a concept was generalized by [2] to the (GARCH) model. The functional version of the GARCH model was introduced by [3]. He stated the necessary conditions for the existence of a strictly stationary solution of the process and established the consistency of the estimators. We return to [4] for an illustrative study showing the potentiality of the functional GARCG to fit the high-frequency data. An alternative estimation-based quasi-likelihood approach was introduced by [5]. They proved the asymptotic normality of the constructed estimator. We return to [6] or [7] for more relevant studies on the topic. As a counterpart, VaR estimation is often constructed from the quantile function, which has been widely studied in mathematical statistics. In particular, estimation using quantile regression is a dominant approach because it makes it possible to fit the dynamics of quantiles. The first significant result on this subject was developed in [8]. In the latter reference, the problem of estimating the VaR was carried out under the conditional autoregressive structure. In addition, certain advances in risk management using the Conditional Autoregressive Value-at-Risk (CAVaR) models were obtained by numerous authors in the past (see, for example, [9] or [10]). Other alternative methods for estimating the CAVaR models are proposed in the literature. We cite, for example, the GARCH approach used in [11], the conditional Extreme Value (EV) method considered in [12], or the conditional Copula algorithm in [13]. For a comparative study between the three approaches using different stock market indices, we cite [14]. The authors of the last reference propose combining the GARCH, Copula, and EV functions to estimate the VaR of a given portfolio. Recently, the authors of [15] estimated the VaR under GARCH asymmetry models using the GARCH-EVT approach. This approach was applied to the financial time series on Kenya’s currency exchange rate. In functional data analysis, the estimation of quantile regression was introduced by the authors of [16]. They used the B-spline smoothing approach to study a linear model of regression on quantiles when the explanatory variable is Hilbertian. They established the -convergence rate of the estimate. In the nonparametric context, the authors of [17] established the almost complete convergence of a kernel estimator of the quantile regression when the observations are i.i.d. [18] established the convergence of the same estimator but in the dependent case. More recent investigations into quantile regression can be found in [19,20,21,22] and references therein. Despite the importance of multivariate functional data, the literature on the subject is limited. All the existing studies treat the unconditional quantile (see, [23,24] or [25]). Thus, the estimation of the conditional VaR-function using the local linear method is a challenging issue in functional statistics (see [26,27] for more information on the subject).
Value-at-Risk (VaR) in functional statistics (FVAR) allows us to tackle a more complex structure. Specifically, it permits us to analyze risk when the data comes in the form of entire curves. In financial markets, where prices fluctuate in milliseconds and risk evolves continuously, traditional Value-at-Risk (VaR) models often fail to follow the dynamic nature of modern trading. FVaR is more adequate for this situation. The literature on this topic is still limited. The first result on this model was developed by the authors of [28]; they proved the almost complete consistency of the local constant estimation of the FVAR model. The authors of [29] employed functional data modeling in financial risk management and applied their models to China’s stock market. The authors of [30] estimated the conditional VaR as a functional linear quantile regression model and used their linear estimator for FVAR to analyze the intra-day return curves. The authors of [31] considered the nonparametric estimation of the functional expected shortfall regression as an alternative risk tool to the FVAR function. We refer to [32,33,34] for more alternative nonparametric functional models to FVAR risk models.
Estimation using multivariate functional data is a challenging issue in functional statistics. Clearly, the multivariate functional data analysis allows us to explore the complex relationships between multiple functional variables that the univariate methods fail to model. The multivariate functional data involves the usual structure in applied areas, namely, in finance, where there are potential interactions between different trajectories of the portfolios. The second novelty of this contribution is to analyze financial risk using the nonparametric functional GARCH model. This consideration is motivated by the popularity of the GARCH model as a principal tool to forecast the variability of asset returns over time. It models the time-varying volatility, which is crucial in risk management. The combination of both of these structures is pivotal for financial risk. It permits us to enhance the accuracy of the prediction of fluctuations in financial dynamics by taking into account the multiple interactions of related financial movements. In the mathematical component of the paper, we construct an estimator of the dynamic VaR function using local linear estimation. Furthermore, we demonstrate the Borel convergence of the estimator within a multifunctional GARCH framework. It is widely recognized that local linear estimation provides a substantial benefit compared to local constant estimation, as it helps in minimizing the bias term. Thus, the local linear estimation method offers a more precise forecasting tool for managing financial risk. To measure the accuracy of the new estimator, we detail its convergence rate and describe it under broad assumptions that encompass the essential elements of the contributions, such as the functionality and correlation of the data, the nonparametric nature of the model, and the various parameters involved in the estimator. To illustrate real-world applicability, we examine the feasibility of our algorithm using simulated and real financial market data. The computational analysis of this contribution reveals the strong ability of the estimator to detect risk fluctuations.
This paper is organized as follows. In the next section, we define our statistical framework, and then we discuss the principal motivations to pursue this subject. We state the main results in Section 3. An empirical analysis is presented in Section 4. It contains illustrative examples covering different features of multivariate functional generalized autoregressive conditional heteroscedasticity(MFGARCH). A real data application is given in Section 5. In Section 6, we give a general conclusion and list some research perspectives allowing for further investigations in this area of statistics. The last section is an appendix (Appendix A) devoted to the demonstration of the intermediate results.
2. Statistical Framework Models and Estimators
In this paper, we introduce an innovative functional approach to analyze risk in multi-asset financial risk. Therefore, we consider, as price trajectories of n-sample portfolios of m financial assets. Assume that are multivariate functional GARCH processes (MFGARCH) defined by
Such a functional modelization allows us to more accurately model complex market dynamics. Specifically, we focus on the functional version of the dynamic conditional correlation GARCH, introduced by [35], for which
where ⊙ is the pointwise product, is a vector of independent functional random variables, and is the conditional covariance matrix, which has the following volatility decomposition,
where is the time-varying correlation matrix, and is a functional diagonal matrix defined by
The diagonal is
where and are linear operators. This formulation generalizes the univariate functional GARCH process (introduced by [36]) to the multivariate setting. It permits us to highlight the time-varying nature of covariances and correlations of multiple assets in a continuous time. This situation is more realistic than the standard case. Indeed, in financial markets, the connections between assets are always in continuous change. This feature is not covered by the traditional method. Instead, the functional approach completely overlooks the market dynamics. Similar to [36], the strict stationarity and the ergodicity of the MFGARCH is related to the Lyapunov exponent of the sequence of matrix of operators by
where are operators mapping . Typically, we assume the following:
- PO1:
- The top Lyapunov exponent of the sequence is such that
We point out that if , we obtain, from (4), the Nadaraya–Watson estimator. In this work, we aim to establish the convergence rate of the estimator to . Such a result constitutes a good mathematical support for the practical use of as a financial risk tool.
3. Notations, Assumptions and Comments
Now, to derive the claimed asymptotic result, we first denote, using C and , some strictly positive constants and, for , we define the ball
Moreover, for , we use to represent the -algebra generated by , … and for the -algebra generated by . We consider the following assumptions:
- PO2:
- The processes satisfies
- PO3:
- There exists such that, for all and , we have
- PO4:
- The kernel is a positive and differentiable function, which is supported within such thatis a positive definite matrix.
- PO5:
- where .
Comments on the Hypotheses
All the considered assumptions are fairly mild in the nonparametric functional statistic. They permit us to involve a larger class of financial times series data. In fact, the MFGARCH with the DCC-mode is crucial in finance. It allows us to analyze the time-varying correlations between multiple financial assets. The exploration of the functional nature of this kind of process is very interesting for portfolio optimization or risk management. The functional structure is characterized by the assumption PO2 that highlights the ergodicity property of the functional data. Clearly, this assumption is less restrictive to the assumption introduced by [38]. Indeed, unlike [38], in PO2, the decomposition of the concentration functions is not required. Thus, it is not necessary to use the Onsager–Machlup function (see [39]). The conditions PO3–PO5 are also standard, and they are assumed by several works in this area of functional time series data (see [38]).
4. Results
Our primary result is given in the following theorem. It deals with the Borel almost completely (a.co.) (see [40]).
Theorem 1.
Assume that PO1–PO4 are satisfied, and if , then we have
Comments on the results: Clearly, this theorem gives a more robust version of stochastic convergence (BC-mode) that surpasses the usual almost-sure or probability consistencies. Although milder assumptions are adequate for these, more typical forms of consistency would support the practical application of our estimator; we emphasized this mathematical broadness. The BC-mode is not only encompasses these easy forms but also highlights a crucial trade-off between theoretical assurances and imposed assumptions. Therefore, our contribution lies in this dual guarantee: strong theoretically results that simultaneously advance practical applications in this field of financial risk management.
Proof of the Main Result
The proof is based on the application of the second part of Lemma 1 in [41]. Indeed, we apply the cited Lemma on the triplet defined by
- The vectorial sequence of functionswhere
- The vectorial sequence
- The sequence .
Since the function is a monotone and increasing function, then the first condition of Lemma 1 in [41] is satisfied. So, Theorem 1 is a consequence of the following lemmas.
Lemma 1.
Under assumptions PO1–PO5, we have
Lemma 2.
Under assumptions PO1–PO5, and if , then, we have
with
and
5. Empirical Data Analysis
The DCC model is a popular version of Multivariate GARCH models. It was popularized in financial risk assessment through its time-varying correlations, which reflect the usual situations in practice. Thus, the generalization of DCC in MFGARCH modeling is very interesting in practice. It permits us to enhance and improve the accuracy of risk detection by exploring the dynamic nature of financial markets and the time-varying volatility. Moreover, in this context of multi-functional data analysis, the VaR-function has a crucial role. It is used to quantify the extreme loss or the extreme gain of multiple financial assets and highlight the complex dependencies between different factors in financial time series data. The main aim of this section is to examine the computationablity of the estimator using an artificial data drown from the DCC-MFGARCH process. In fact, the computationablity of the is related to the determination of the different parameters used in the estimator. In this context of local linear smoothing, the choice of the smoothing parameter is a critical issue. Furthermore, in quantile regression, there exist many rules to select this parameter. A popular one is the cross-validation approach used by [40]. In this empirical analysis, we compare the cited rule to two other algorithms. The first one is the cross-validation method used by [42], for which the bandwidth is selected as
where denotes the local empirical , computed from a neighbourhood of closest functionals to (we used different neighbour sizes (4, 6, 10, 14, and 20)). Also, is the conditional VaR estimator at . The second rule (approach) is proposed by [43]. Its optimal bandwidth is given by
Finally, we recall that the optimal bandwidth according to the cross-validation of [40] is
The three rules are optimized over , a subset of positive real numbers , for which the ball centered at with radius contains exactly k observation neighbors of . The comparative study will be performed through a multi-variate functional GARCH process generated using the algorithm (1). We put , and and the independent functional random variables are generated using the mfdata R-code (Version 4.2.2) in the R-package fda.usc. The operator and are defined by
where and
with These operators are considered in order to incorporate the theoretical assumption, namely, the postulate PO1. The generated MFGARCH represents the day-dynamic of portfolios containing two financial assets. The price trajectories of the two assets are plotted in Figure 1.
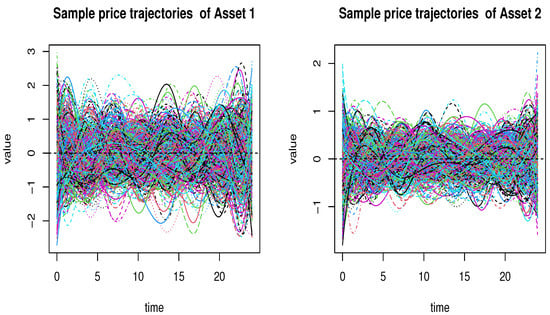
Figure 1.
The MFGARCH covariate.
The curve of the dynamic correlations between the two components is displayed in Figure 2.
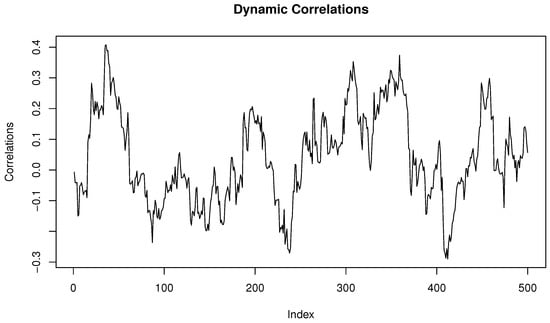
Figure 2.
The curve of the dynamic correlations.
Now, the output variable is , which repesents the mean of the daily variations of the two assets. We examine the reliability and the behavior of by using the quadratic kernel on and the metric associated to the spline basis functions. Next, the three selectors of the smoothing parameters are optimized over selected values of . Finally, the efficiency of the VaR- estimation is checked using the backtesting measure,
The obtained results are summarized in Table 1. It gives EQ−values for the three selectors based on the three values of and various sample sizes .

Table 1.
The for different selectors.
We observe that the estimator has a good behavior compared to the three proposed selectors. However, it is clear that the rule (5) is more adequate than the other rules. So, despite the complexity of the considered structure, it appears that the computation of is not very difficult. Moreover, its behaviour is less affected by the order of the threshold , and the performance of the estimator is improved with respect to the sample size n.
6. Real Data Application
In this section, we highlight the importance of the nonparametric estimation of the VaR function in multi-functional time series data. In particular, we emphasize the local linear estimation of the VaR function by comparing it to the constant local estimator defined by
We point out that the local constant is a particular case of the local linear approach. Moreover, it is well documented that the local linear approach reduces the bias term in the local constant one. Thus, our principal purpose in this section is to highlight the superiority of the local linear approach over the local constant approach in financial risk management. Recall that the main feature of the present contribution is the multifunctionality of the data, allowing us to analyze the risk of multiple assets. Thus, we consider the daily price of a portfolio containing high values of three cryptocurrencies: Biconomy, Bitcoin, and BinaryX. The data are available on the website https://stooq.com/db/h/ (accessed on 8 March 2025). We consider the data of weeks (from 18/11/2024 to 08/01/2025) with a frame of 5 mins. In order to examine the main characteristics of financial time series data, including volatility, skewness, kurtosis, and/or normality, we display the initial time series in Figure 3, Figure 4 and Figure 5.
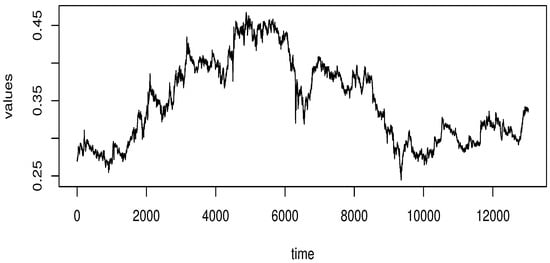
Figure 3.
The function of Biconomy.
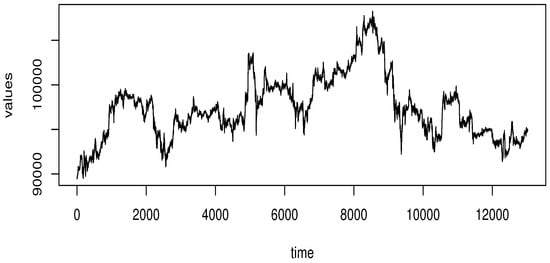
Figure 4.
The function of Bitcoin.
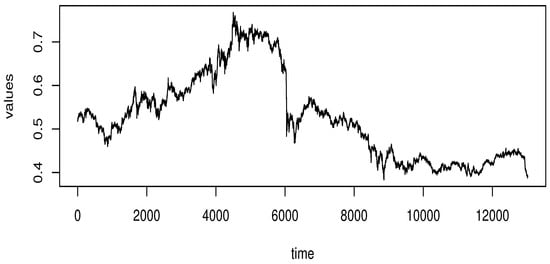
Figure 5.
The function BinaryX.
Biconomy is an important cryptocurrency market. The popularity of this cryptocurrency is justified by its simplicity as a decentralized application. It is based on simplifying Web3 interactions and cross-chain transfers. Biconomy is a creative solution and is playing a big role in making cryptocurrencies more accessible for regular users.
Bitcoin is one of the leading cryptocurrency markets. It is characterized by its rapid expansion and high volatility. As the first and most accessible digital currency, Bitcoin’s price movements often shape the overall market sentiment and serve as a crucial benchmark for assessing risks in crypto investments.
BinaryX (BNX) is a cryptocurrency platform known for its unpredictable price that increases and decreases, which defies general market trends. By including these three cryptocurrencies in our analysis, we specifically test our model’s ability to handle these sudden and isolated price explosions that can make or break a portfolio’s risk profile overnight. On the other hand, this type of high-frequency data requires special treatment because classical methods of multivariate statistics are unreliable in this situation. Usually, we are interested in the log-return, defined by
and we predict the extreme return at a time T given the process for
To compare the effectiveness of the two risk measures and , we divide the studied financial time series data into two parts: the learning sample (400 of observations) and the testing sample (100 of observations). The learning sample is used to select the main parameters of the estimator, whereas the testing sample is used to asses the behavior of the financial risks and . So, for this comparison study, we keep the same strategies for selecting the principal parameters, such as and kernel. In particular, we select the smoothing parameter using the following cross-validation rule:
where are the conditional VaR estimators ( and ) at without this observation. Similar to the simulated data case, the subset of the positive real numbers for which the ball centered at with radius contains exactly k observation neighbors of . The integer k is varied in . Next, the metric is the PCA-metric (see [44]) associated with the eigenvectors of the three largest eigenvalues. Finally, we point out that we used the quadratic kernel on (0,1). To examine the efficiency of both approaches, we repeat the splitting process between learning and testing samples (60 times) and plot the box plot of the backtesting measure,
In fact, the use of backtesting measure is common in financial risk analysis. It permits us to evaluate VaR’s conditional coverage via violation ratios—the proportion of observed returns breaching estimated quantiles. From the technical point of view, this backtesting measure helps traders validate whether their risk models can be trusted when markets turn volatile. Figure 6 and Figure 7 display the obtained boxplots for two values of .
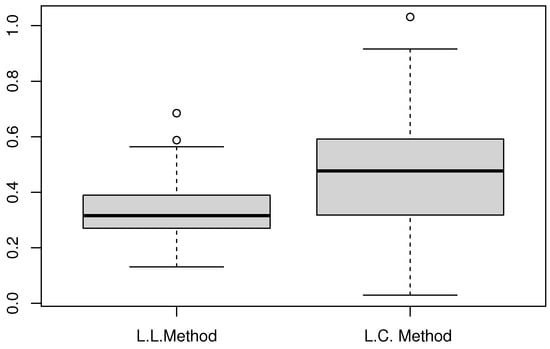
Figure 6.
Comparison of .
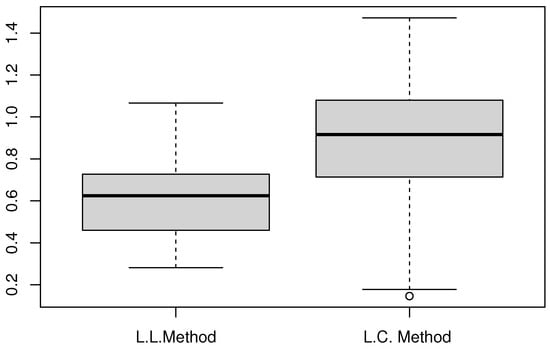
Figure 7.
Comparison of .
As expected, the local linear is more appropriate than the local constant . This statement is confirmed by the interquartile values. Typically, the IQR of the (L.L. Method) is versus for (L.C. Method). Our findings validate the theoretical results that state that the local linear estimation outperforms local constant methods by significantly reducing bias. This gain is more important in functional statistics because the local linearity constitutes a structural aspect relating the functionality of the model to the functionality of the data. It highlights the importance of the functional structure on the performance of the estimator.
7. Conclusions
The digitalization of financial transactions make real-time financial risk management an inevitable issue for both investors and financial institutions. The real time analysis of financial risk is the principal motivation of this contribution. In pursuit of this aim, we introduced a statistical algorithm combining the VaR function and the multi-GARCH with high-frequency data. Moreover, to overcome the limitation of the parametric approach, we employed the nonparametric local linear method. Unlike standard parametric approaches, which rely on restrictive linearity assumptions for modeling dynamics, our proposed method focuses on the general case without such constraints. From a theoretical point of view, we constructed an estimator of the local linear estimator of the VaR function and established its Borel convergence rate. The computational part demonstrates the easy implementation of the local linear VaR and proves that this estimator outperforms traditional kernel estimator in real-world financial applications. Through the conducted empirical analysis, we confirm two principal advantages of the proposed approach, which include its superior risk forecasting accuracy and computational efficiency. These advantages make it practical for making daily trading decisions regarding multiple assets. However, implementing this approach requires careful tuning of critical parameters, particularly the bandwidth and the distance metric , where the current methods still rely heavily on expert judgement rather than automatic selection. The parameter selection challenge currently limits the model’s implementation and highlights a crucial need for future work to develop data-driven methods to automate these choices. In addition, our contribution opens multiple promising research directions, including three particularly exciting directions: (1) adapting the framework for complex data structures (spatial markets or incomplete datasets); (2) extending it to alternative risk measures, like Expected Shortfall, that better capture tail risk; and (3) enhancing the multifunctional model’s predictive power by considering other functional time series cases. For risk managers, these advancements could eventually provide more risk models capable of incorporating the functional nature of the financial data.
Author Contributions
The authors contributed approximately equally to this work. Formal analysis, Z.C.-E.; validation, F.A.; writing—review & editing, I.M.A. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R358), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia; and the Deanship of Scientific Research and Graduate Studies at King Khalid University through the Research Groups Program under grant number RGP1/118/46.
Data Availability Statement
The data used in this study are available through the link https://stooq.com/db/h/ (accessed on 8 March 2025).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In order to simplify the demonstration of the preliminary results, we put
Proof of Lemma 1.
First, set
and
Then,
where
Observe, for , that
Using the same ideas,
From the exponential inequality of martingale difference to obtain for all , we have
Taking , then,
Under (PO2), we have
and similarly,
Therefore,
and
Next, the first component of is
Similarly, for the second component of , we have
We conclude that
□
Proof of Lemma 2.
We show that
and
References
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. A conditionally heteroskedastic time series model for speculative prices and rates of return. Rev. Econ. Stat. 1987, 69, 542–547. [Google Scholar] [CrossRef]
- Hormann, S.; Horvath, L.; Reeder, R. A functional version of the ARCH model. Econom. Theory 2013, 29, 267–288. [Google Scholar] [CrossRef]
- Yoon, J.E.; Kim, J.M.; Hwang, S.Y. Functional ARCH (fARCH) for high-frequency time series: Illustration. Korean J. Appl. Stat. 2017, 30, 983–991. [Google Scholar]
- Cerovecki, C.; Francq, C.; Hörmann, S.; Zakoïan, J.M. Functional GARCH models: The quasi-likelihood approach and its applications. J. Econom. 2019, 209, 353–375. [Google Scholar] [CrossRef]
- Sun, H.; Yu, B. Volatility asymmetry in functional threshold GARCH model. J. Time Ser. Anal. 2020, 41, 95–109. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Liu, J. A Functional Garch Model with Multiple Constant Parameters. Comput. Econ. 2025, 1–25. [Google Scholar] [CrossRef]
- Engle, R.F.; Manganelli, S. CAViaR: Conditional autoregressive value at risk by regression quantiles. J. Bus. Econ. Stat. 2004, 22, 367–381. [Google Scholar] [CrossRef]
- Kuester, K.; Mittnik, S.; Paolella, M.S. Value-at-risk prediction: A comparison of alternative strategies. J. Financ. Econom. 2006, 4, 53–89. [Google Scholar] [CrossRef]
- Sun, P.; Lin, F.; Xu, H.; Yu, K. Estimation of value-at-risk by L p quantile regression. Ann. Inst. Stat. Math. 2025, 77, 25–59. [Google Scholar] [CrossRef]
- Lux, M.; Härdle, W.K.; Lessmann, S. Data driven value-at-risk forecasting using a SVR-GARCH-KDE hybrid. Comput. Stat. 2020, 35, 947–981. [Google Scholar] [CrossRef]
- Herrera, R.; Schipp, B. Value at risk forecasts by extreme value models in a conditional duration framework. J. Empir. Financ. 2013, 23, 33–47. [Google Scholar] [CrossRef]
- Huang, J.J.; Lee, K.J.; Liang, H.; Lin, W.F. Estimating value at risk of portfolio by conditional copula-GARCH method. Insur. Math. Econ. 2009, 45, 315–324. [Google Scholar] [CrossRef]
- Brooks, C.; Chris, A.D.; Clare, J.W.; Dalle Molle, W.; Gita, P. A comparison of extreme value theory approaches for determining value at risk. J. Empir. Financ. 2005, 12, 339–352. [Google Scholar] [CrossRef]
- Kim, T.H.; White, H. On more robust estimation of skewness and kurtosis. Financ. Res. Lett. 2004, 1, 56–73. [Google Scholar] [CrossRef]
- Cardot, H.; Crambes, C.; Sarda, P. Quantile regression when the covariates are functions. Nonparametric Stat. 2005, 17, 841–856. [Google Scholar] [CrossRef]
- Ferraty, F.; Laksaci, A.; Vieu, P. Estimating some characteristics of the conditional distribution in nonparametric functional models. Stat. Inference Stoch. Process. 2006, 9, 47–76. [Google Scholar] [CrossRef]
- Dabo-Niang, S.; Laksaci, A. Nonparametric quantile regression estimation for functional dependent data. Commun. Stat.-Theory Methods 2012, 41, 1254–1268. [Google Scholar] [CrossRef]
- Messaci, F.; Nemouchi, N.; Ouassou, I.; Rachdi, M. Local polynomial modelling of the conditional quantile for functional data. Stat. Methods Appl. 2015, 24, 597–622. [Google Scholar] [CrossRef]
- Ling, N.; Yang, Y.; Peng, Q. Partial linear quantile regression model with incompletely observed functional covariates. J. Nonparametric Stat. 2025, 1–27. [Google Scholar] [CrossRef]
- Mutis, M.; Beyaztas, U.; Karaman, F.; Lin Shang, H. On function-on-function linear quantile regression. J. Appl. Stat. 2025, 52, 814–840. [Google Scholar] [CrossRef] [PubMed]
- Beyaztas, U.; Tez, M.; Lin Shang, H. Robust scalar-on-function partial quantile regression. J. Appl. Stat. 2024, 51, 1359–1377. [Google Scholar] [CrossRef]
- Kong, D.; Xue, K.; Yao, F.; Zhang, H.H. Partially functional linear regression in high dimensions. Biometrika 2016, 103, 147–159. [Google Scholar] [CrossRef]
- Kim, J.M.; Ha, I.D. Vine copula MFPCA residual control chart for sparse multivariate functional data. Commun. Stat.-Simul. Comput. 2025, 1–21. [Google Scholar] [CrossRef]
- Agarwal, G.; Sun, Y. Bivariate Functional Quantile Envelopes with Application to Radiosonde Wind Data. Technometrics 2020, 63, 199–211. [Google Scholar] [CrossRef]
- Bouanani, O.; Bouzebda, S. Limit theorems for local polynomial estimation of regression for functional dependent data. AIMS Math. 2024, 9, 23651–23691. [Google Scholar] [CrossRef]
- Berrahou, N.E.; Bouzebda, S.; Douge, L. The Bahadur Representation for Empirical and Smooth Quantile Estimators Under Association. Methodol. Comput. Appl. Probab. 2024, 26, 17. [Google Scholar] [CrossRef]
- Ferraty, F.; Quintela-Del-Río, A. Conditional VAR and expected shortfall: A new functional approach. Econom. Rev. 2016, 35, 263–292. [Google Scholar] [CrossRef]
- Cai, T. Financial risk management based on functional data analysis. J. Discret. Math. Sci. Cryptogr. 2018, 21, 1397–1400. [Google Scholar] [CrossRef]
- Rice, G.; Wirjanto, T.; Zhao, Y. Forecasting value at risk with intra-day return curves. Int. J. Forecast. 2020, 36, 1023–1038. [Google Scholar] [CrossRef]
- Ait-Hennani, L.; Kaid, Z.; Laksaci, A.; Rachdi, M. Nonparametric estimation of the expected shortfall regression for quasi-associated functional data. Mathematics 2022, 10, 4508. [Google Scholar] [CrossRef]
- Almanjahie, I.M.; Abood, H.; Bouzebda, S.; Alshahrani, F.; Laksaci, A. Nonparametric expectile shortfall regression for functional data. Demonstr. Math. 2025, 58, 20250125. [Google Scholar] [CrossRef]
- D’Ambra, L.; Castellano, R.; D’Urso, P.; De Iaco, S. Statistical methods for decision making in public sector: From the quality assessment to the citizen satisfaction. Ann. Oper. Res. 2024, 342, 1369–1377. [Google Scholar] [CrossRef]
- Litimein, O.; Laksaci, A.; Ait-Hennani, L.; Mechab, B.; Rachdi, M. Asymptotic normality of the local linear estimator of the functional expectile regression. J. Multivar. Anal. 2024, 202, 105281. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Küchnert, S. Functional arch and GARCH models: A Yule–Walker approach. Electron. J. Stat. 2020, 14, 4321–4360. [Google Scholar]
- Francq, C.; Zakoian, J.M. GARCH Models: Structure, Statistical Inference and Financial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Laib, N.; Louani, D. Rates of strong consistencies of the regression function estimator for functional stationary ergodic data. J. Stat. Plan. Inference 2011, 141, 359–372. [Google Scholar] [CrossRef]
- Bogachev, V.I. Gaussian Measures; American Mathematical Society: Rhode Island, USA, 1998; Volume 62. [Google Scholar]
- Ferraty, F. Nonparametric Functional Data Analysis; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Al-Awadhi, F.A.; Kaid, Z.; Laksaci, A.; Ouassou, I.; Rachdi, M. Functional data analysis: Local linear estimation of the L 1-conditional quantiles. Stat. Methods Appl. 2019, 28, 217–240. [Google Scholar] [CrossRef]
- Iglesias-Pérez, M.C. Strong representation of a conditional quantile function estimator with truncated and censored data. Stat. Probab. Lett. 2003, 65, 79–91. [Google Scholar] [CrossRef]
- Yuan, M. GACV for quantile smoothing splines. Comput. Stat. Data Anal. 2006, 50, 813–829. [Google Scholar] [CrossRef]
- Benhenni, K.; Ferraty, F.; Rachdi, M.; Vieu, P. Local smoothing regression with functional data. Comput. Stat. 2007, 22, 353–369. [Google Scholar] [CrossRef]
- Rachdi, M.; Laksaci, A.; Demongeot, J.; Abdali, A.; Madani, F. Theoretical and practical aspects of the quadratic error in the local linear estimation of the conditional density for functional data. Comput. Stat. Data Anal. 2014, 73, 53–68. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).