Proper 3-Dominating Sets in Graphs

Abstract

A dominating set is a classic concept that is widely used in road safety, disaster rescue operations, and chemical graphs. In this paper, we introduce a variation of the dominating set: the proper 3-dominating set. For a proper 3-dominating set D of graph $G,$ any vertex outside D is adjacent to at least three vertices inside D, and there exists one vertex outside D that is adjacent to three vertices inside D. For graph $G,$ the proper 3-domination number is the minimum cardinality among all proper 3-dominating sets of $G.$ We find that a graph with minimum degree at least 3 or one for which there exists a subgraph with some characteristic always contains a proper 3-dominating set. Further, we find that when certain conditions are met, some graph products, such as the joint product, strong product, lexicographic product, and corona product of two graphs, have a proper 3-dominating set. Moreover, we discover the bounds of the proper 3-domination number. For some special graphs, we get their proper 3-domination numbers.

1. Introduction

In general, we use the standard terminology and notation of graph theory (see [1]). In this paper, the graph is simple, connected, and undirected. Let G be a connected graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right).$ If there exists an edge $xy\in E\left(G\right)$ in the graph $G,$ then x is a neighbor of $y.$ The notation $N_G\left(x\right)$ denotes the set of all neighbors of vertex x in $G.$ Let $N_G\left[x\right]=N_G\left(x\right)\cup \left\{x\right\}.$ $d_G\left(x\right)$ is written as the degree of vertex x in $G,$ abbreviated as $d\left(x\right).$ We have $d\left(x\right)=|N_G\left(x\right)|.$ The minimum degree of G is denoted by $\delta \left(G\right).$ A star graph $S_n$ with n vertices is a tree where one vertex is called the central vertex, which has degree $n-1,$ and the other $n-1$ vertices have degree 1. The symbols $P_n,C_n,$ and $K_n$ represent a path, a cycle, and a complete graph of n vertices, respectively. The notation $K_{m,n}$ represents a complete bipartite graph with $m+n$ vertices.

If a graph $G^{\prime }$ satisfies $V\left(G^{\prime }\right)\subseteq V\left(G\right)$ and $E\left(G^{\prime }\right)\subseteq E\left(G\right),$ then the graph $G^{\prime }$ is a subgraph of $G.$ Suppose that $Ø\ne V^{\prime }\subseteq V\left(G\right).$ The induced subgraph $G\left[V^{\prime }\right]$ of a graph G is formed by a subset $V^{\prime }$ of the vertex set $V\left(G\right),$ and all the edges in G whose two end vertices are in $V^{\prime }.$

A subset $D\subseteq V\left(G\right)$ is said to be a dominating set of a graph G if every vertex outside D has at least one neighbor in $D.$ For more details about the domination of graphs, see [2,3]. A subset $S\subseteq V\left(G\right)$ is called a p-dominating set if every vertex outside S has at least p neighbors in $S,$ where p is any integer satisfying $p\ge 1.$ If $p=1,$ then the p-dominating set agrees with the classical dominating set. For $p=2,$ the 2-dominating set was studied in [4,5,6,7,8]. The p-domination number ${\gamma }_p\left(G\right)$ is the minimum cardinality among all p-dominating sets of $G.$ When $p=1,$${\gamma }_1\left(G\right)$ is also written as $\gamma \left(G\right).$ For the graph $G,$ a p-dominating set of minimum cardinality is denoted as a ${\gamma }_p\left(G\right)$-set or a ${\gamma }_p$-set of $G.$ If vertex $x\in V\left(G\right)\setminus D$ has at least p neighbors in the set $D,$ then we say that vertex x is dominated by at least p vertices in $D.$ If vertex $x\in V\left(G\right)\setminus D$ has fewer than p neighbors in the set $D,$ then we say that vertex x is not dominated by p vertices in $D.$ By definition, for any positive integer $h<p,$ we know that a p-dominating set is also an h-dominating set. Then, a 4-dominating set is also a 3-dominating set, and we have $\gamma \left(G\right)\le {\gamma }_2\left(G\right)\le {\gamma }_3\left(G\right)\le {\gamma }_4\left(G\right).$ For some results on the p-domination number, see [9,10,11]. As a generalization of domination, Harary and Haynes [12] introduced the concept of k-tuple domination. For k-tuple domination, see [13,14]. When $k=2,$ k-tuple domination is called double domination, which was studied in [15,16,17].

Dominating sets and their variants have extensive applications in the real world. The literature indicates that dominating sets and dominating parameters have applications in many fields, such as road safety, vehicular ad hoc communications, disaster rescue operations, and air/land/navy defense (see [18]). Moreover, dominating sets and their variants have been used in wireless networks [19] and chemical graphs [20]. From an algorithmic perspective, domination and its variants in graphs have been studied in [19,21,22].

We give an application problem for the p-domination number. A company needs to promote a new product. Suppose there are n potential customers for this new product. The company needs to select some salespeople from these n potential customers. None of these salespeople will buy the new product. We refer to the rest, excluding the salespeople, as target customers. If a salesperson knows a certain target customer, they will promote the product to the customer. We represent n potential customers as n vertices. If two potential customers know each other, then the vertices corresponding to the two potential customers are adjacent. This forms a graph G with n vertices. If each target customer is approached about the product by at least p salespeople, the company needs to know the minimum number of salespeople. That is, the company needs to know the p-domination number of the graph $G.$

Bednarz and Pirga [23] introduced the concept of proper 2-dominating sets. Similar to [23], a proper 3-dominating set is defined as follows:

Definition 1. 

A subset $D\subset V\left(G\right)$ is said to be a proper 3-dominating set if it is a 3-dominating set but not a 4-dominating set.

We use $\overline{3}$-dset to denote a proper 3-dominating set. The proper 3-domination number ${\gamma }_{\overline{3}}\left(G\right)$ is the minimum cardinality among all proper 3-dominating sets of $G.$ For a graph $G,$ a proper 3-dominating set of cardinality ${\gamma }_{\overline{3}}\left(G\right)$ is called a ${\gamma }_{\overline{3}}\left(G\right)$-set or a ${\gamma }_{\overline{3}}$-set of $G.$ D is a proper 3-dominating set if every vertex outside the set D has at least three neighbors in the set D and there exists a vertex outside the set D that has exactly three neighbors in the set $D.$ In the 3-dominating set $D^{\prime },$ if there exists a vertex outside $D^{\prime }$ that is dominated by three vertices in the set $D^{\prime },$ then this set $D^{\prime }$ cannot be a 4-dominating set. Thus, the existence of such a vertex fundamentally distinguishes a 3-dominating set from a 4-dominating set. For the graph G, let $U_1=\left\{u\right|d\left(u\right)=1\mathrm{and}u\in V\left(G\right)\},U_2=\left\{u\right|d\left(u\right)=2\mathrm{and}u\in V\left(G\right)\}.$ For proper dominating sets related to secondary domination, see [24,25].

Referring to [23], we present an example of the application of $\overline{3}$-dset. Suppose there are n places prone to natural disasters. In order to provide assistance to the residents in places affected by these disasters, rescue stations are to be established at m points (distinct from the n places). Suppose the residents in these n places can seek help from at least three rescue stations. In order to reduce costs by minimizing the number of rescue stations, where should the rescue stations be established? This problem is equivalent to finding a minimum 3-dominating set. Furthermore, if the minimum 3-dominating set is a minimum $\overline{3}$-dset, then it determines the weakest places from which only three rescue stations can be reached.

Proposition 1 

(Lemma 1 [23]). Suppose k is an integer satisfying $k\ge 2.$ In any connected graph, each vertex of degree $h<k$ belongs to a $(h+i)$-dominating set, where i is any integer satisfying $1\le i\le k.$

According to Proposition 1, in any connected graph, each vertex of degree 1 and 2 belongs to a 3-dominating set. Next, this paper considers what properties of graphs have a proper 3-dominating set, as well as the proper 3-domination number of some special graphs.

For convenience, we give the list of symbols in Table 1.

Table 1. List of symbols.

Symbol	Description
G	A connected graph
$V\left(G\right)$	The vertex set of G
$E\left(G\right)$	The edge set of G
$N_G\left(x\right)$	The set of all neighbors of vertex x in G
$N_G\left[x\right]$	$N_G\left[x\right]=N_G\left(x\right)\cup \left\{x\right\}$
$d_G\left(x\right)$	The degree of vertex x in G
$d\left(x\right)$	The abbreviation of $d_G\left(x\right)$
$\delta \left(G\right)$	The minimum degree of G
$S_n$	The star graph with n vertices
$P_n$	A path of n vertices
$C_n$	A cycle of n vertices
$K_n$	A complete graph of n vertices
$K_{m,n}$	A complete bipartite graph with $m+n$ vertices
$G\left[V^{\prime }\right]$	The induced subgraph of G by the subset $V^{\prime }\subseteq V\left(G\right)$
${\gamma }_p\left(G\right)$	The minimum cardinality among all p-dominating sets of G
$\gamma \left(G\right)$	${\gamma }_1\left(G\right)$
${\gamma }_{\overline{p}}\left(G\right)$	The minimum cardinality among all proper p-dominating sets of G
$U_i$	$U_i=\{u\mid d\left(u\right)=i\mathrm{and}u\in V\left(G\right),i=1,2.\}$

2. Main Results

Lemma 1. 

Let G be a connected graph with n vertices, where $n\ge 4.$ If there exists a vertex v in the graph G satisfying $d\left(v\right)=3,$ then G has a $\overline{3}$-dset.

Proof. 

Let $D=V\left(G\right)\setminus \left\{v\right\},$ then $\left\{v\right\}=V\left(G\right)\setminus D.$ Since $d\left(v\right)=3,$ then $|N_G\left(v\right)\cap D|=3.$ So, D is a $\overline{3}$ -dset. □

Lemma 2. 

Let G be a connected graph with n vertices, where $n\ge 5.$ If $\delta \left(G\right)\ge 4,$ then G has a $\overline{3}$-dset.

Proof. 

Let $\delta \left(G\right)=\delta .$ Let x be the vertex of minimum degree in the graph G, and $d\left(x\right)=\delta .$ Assume that $N_G\left(x\right)=\{u_1,u_2,\cdots ,u_{\delta }\}.$ Let $D=(V\left(G\right)\setminus N_G\left[x\right])\cup \{u_1,u_2,u_3\}.$ It can be seen that the vertices in D are $u_1,u_2,u_3,$ and all vertices in $V\left(G\right)\setminus N_G\left[x\right].$ Then, $V\left(G\right)\setminus D=\left\{x\right\}\cup \{u_4,u_5,\cdots ,u_{\delta }\}.$ For any vertex in $V\left(G\right)\setminus D,$ we consider the number of its neighbors in $D.$ Since $|V\left(G\right)\setminus D|=|\left\{x\right\}\cup \{u_4,u_5,\cdots ,u_{\delta }\}|=\delta -4+2=\delta -2,$ then $|N_G\left(u_i\right)\cap (V\left(G\right)\setminus D)|=|N_G\left(u_i\right)\cap (\{u_4,u_5,\cdots ,u_{\delta }\}\cup \left\{x\right\})|\le \delta -3,$ where $4\le i\le \delta .$ That is, the vertex $u_i$ has no more than $\delta -3$ neighbors outside $D.$ Since $d\left(u_i\right)\ge \delta ,$ we have $|N_G\left(u_i\right)\cap D|\ge 3,$ where $4\le i\le \delta .$ Furthermore, we have $N_G\left(x\right)\cap D=\{u_1,u_2,u_3\}.$ So, $|N_G\left(x\right)\cap D|=3,$ and D is a $\overline{3}$-dset. □

Corollary 1. 

Let G be a connected graph, and let $V^{\prime }\subset V\left(G\right)$ and $G\left[V^{\prime }\right]$ be connected. For the graph $G\left[V^{\prime }\right],$ suppose x is a vertex of minimum degree. For any vertex $y\in V\left(G\right)\setminus V^{\prime },$ x is not adjacent to $y.$ If $\delta \left(G\left[V^{\prime }\right]\right)\ge 4,$ then G has a $\overline{3}$-dset.

Proof. 

We have $\delta \left(G\left[V^{\prime }\right]\right)=d\left(x\right).$ Let $d\left(x\right)=h.$ Assume that $N_G\left(x\right)=\{u_1,u_2,\cdots ,u_h\}.$ Let $D=(V\left(G\right)\setminus N_G\left[x\right])\cup \{u_1,u_2,u_3\}.$ Then, $V\left(G\right)\setminus D=\left\{x\right\}\cup \{u_4,u_5,\cdots ,u_h\}.$ Similar to the proof of Lemma 2, we have $|N_G\left(u_i\right)\cap D|\ge 3,$ where $4\le i\le h.$ Moreover, $|N_G\left(x\right)\cap D|= |\{u_1,u_2,u_3\}| =3.$ Then, D is a $\overline{3}$-dset. □

Theorem 1. 

Let G be a connected graph with n vertices, where $n\ge 4.$ If $\delta \left(G\right)\ge 3,$ then G has a $\overline{3}$-dset.

Proof. 

If $\delta \left(G\right)=3,$ then there exists a vertex v in the graph G satisfying $d\left(v\right)=3.$ Then, according to Lemma 1, G has a $\overline{3}$-dset. If $\delta \left(G\right)\ge 4,$ according to Lemma 2, G has a $\overline{3}$-dset. □

Referring to the definition of the joint product of two graphs $G,H$ in [26], we give the following definition.

Definition 2. 

The joint product of two graphs G,H, denoted by $G+H,$ is a graph with vertex set $V(G+H)=V\left(G\right)\cup V\left(H\right)$ and edge set $E(G+H)=E\left(G\right)\cup E\left(H\right)\cup \left\{uv\right|u\in V\left(G\right)\mathit{and}$$v\in V\left(H\right)\}.$

For definitions of the two fundamental graph products (strong and lexicographic), see [27,28]. Next, we repeat these definitions.

Definition 3. 

The strong product of two graphs G,H, denoted by $G⊠H,$ is a graph with vertex set $V(G⊠H)=V\left(G\right)\times V\left(H\right),$ and $(u,u^{\prime })$ and $(v,v^{\prime })$ are adjacent if and only if one of the following conditions holds:

(1) $u=v$ and $u^{\prime }{v}^{\prime }\in E\left(H\right)$;

(2) $u^{\prime }=v^{\prime }$ and $uv\in E\left(G\right)$;

(3) $uv\in E\left(G\right)$ and $u^{\prime }{v}^{\prime }\in E\left(H\right)$.

Definition 4. 

The lexicographic product of two graphs $G,H,$ denoted by $G\circ H,$ is a graph with vertex set $V(G\circ H)=V\left(G\right)\times V\left(H\right),$ and $(u,u^{\prime })$ and $(v,v^{\prime })$ are adjacent if and only if one of the following conditions holds:

(1) $u=v$ and $u^{\prime }{v}^{\prime }\in E\left(H\right)$;

(2) $uv\in E\left(G\right)$.

Corollary 2. 

Let $G,H$ be two connected graphs with vertex numbers $m,n$, respectively, where $m\ge 3,n\ge 3.$ Then, each graph of $G+H,$ $G⊠H$, and $G\circ H$ has a $\overline{3}$-dset.

Proof. 

Suppose that $V\left(G\right)=\{u_1,u_2,\cdots ,u_m\}$ and $V\left(H\right)=\{v_1,v_2,\cdots ,v_n\}.$ Since G is a connected graph, any vertex u in G satisfies $d\left(u\right)\ge 1.$ Moreover, $n\ge 3.$ So, the vertex u in $G+H$ satisfies $d\left(u\right)\ge 4.$ Similarly, any vertex v in H satisfies $d\left(v\right)\ge 1.$ The vertex v in $G+H$ satisfies $d\left(v\right)\ge 4.$ Then, any vertex x in $G+H$ satisfies $d\left(x\right)\ge 4.$ That is, $\delta (G+H)\ge 4.$ Then, according to Theorem 1, $G+H$ has a $\overline{3}$-dset. Next, we consider $G⊠H$ and $G\circ H.$ For any vertex $(u_1,v_1)\in V(G⊠H)$ or $(u_1,v_1)\in V(G\circ H),$ assume that $u_1{u}_2\in E\left(G\right)$ and $v_1{v}_2\in E\left(H\right).$

For $G⊠H,$ according to Definition 3, $(u_1,v_1)$ is adjacent to $(u_1,v_2)$, $(u_2,v_1)$, and $(u_2,v_2).$ Therefore, for any vertex $(u_1,v_1)$ in $G⊠H$, the degree of $(u_1,v_1)$ is greater than or equal to $3.$ So, $G⊠H$ has a $\overline{3}$-dset.

For $G\circ H,$ according to Definition 4, $(u_1,v_1)$ is adjacent to $(u_1,v_2)$, $(u_2,v_1)$, and $(u_2,v_2).$ Therefore, for any vertex $(u_1,v_1)$ in $G\circ H$, the degree of $(u_1,v_1)$ is greater than or equal to $3.$ So, $G\circ H$ has a $\overline{3}$-dset. □

Theorem 2. 

Let G be a connected graph. Then, G has a $\overline{3}$-dset if and only if one of the following conditions holds:

(1) There is a vertex u that satisfies $d\left(u\right)=3$;

(2) There is a vertex v that satisfies $d\left(v\right)\ge 4.$ Let $S\subseteq N_G\left(v\right),$$\left|S\right|=d\left(v\right)-3$ and $D=V\left(G\right)\setminus (S\cup \{v\left\}\right).$ Moreover, for any vertex $x\in S,$ $|N_G\left(x\right)\cap D|\ge 3$ holds.

Proof. 

If G has a vertex u satisfying $d\left(u\right)=3,$ according to Lemma 1, the conclusion clearly holds. Next, we consider the case where G has a vertex v that satisfies $d\left(v\right)\ge 4.$ Since $D=V\left(G\right)\setminus (S\cup \{v\left\}\right),$ then $V\left(G\right)\setminus D=S\cup \left\{v\right\}.$ For any vertex $x\in S,$ we have $|N_G\left(x\right)\cap D|\ge 3.$ Furthermore, we have $|N_G\left(v\right)\cap D|=3.$ Then, D is a $\overline{3}$-dset.

For a graph $G,$ we assume that any vertex u of G satisfies $d\left(u\right)\ne 3.$ If any vertex w satisfies $d\left(w\right)\le 2,$ then G does not have a $\overline{3}$-dset. Since the graph G has a $\overline{3}$-dset, there exist vertices in the graph G with degree greater than or equal to $4.$ Suppose that $D_1$ is a $\overline{3}$-dset of $G.$ We have $U_1\cup U_2\subseteq D_1.$ Then, for any vertex $w\in V\left(G\right)\setminus D_1,$ we have $|N_G\left(w\right)\cap D_1|\ge 3.$ Moreover, there exists a vertex v that satisfies $|N_G\left(v\right)\cap D_1|=3,$ where $v\in V\left(G\right)\setminus D_1.$ Let $S=N_G\left(v\right)\setminus D_1$ and $D=V\left(G\right)\setminus (S\cup \{v\left\}\right).$ Then, we have $\left|S\right|=d\left(v\right)-3$ and $D_1\subseteq D.$ We have $|N_G\left(v\right)\cap D|=3.$ Moreover, for any vertex $x\in S,$ we have $|N_G\left(x\right)\cap D|\ge 3.$ □

Theorem 3. 

Let G be a connected graph. If there exists a vertex v in G satisfying the following conditions, then G has a $\overline{3}$-dset:

(1) $d\left(v\right)\ge 4$ and $|N_G\left(v\right)\cap (U_1\cup U_2)| \le 3$;

(2) For any vertex $x\in N_G\left(v\right),$ $y\in N_G\left(v\right),$ x is not adjacent to $y.$

Proof. 

Assume that $d\left(v\right)=i$ and $N_G\left(v\right)=\{u_1,u_2,\cdots ,u_i\},$ where $i\ge 4.$ Since $d\left(v\right)\ge 4,$ $i\ge 4.$ Since $|N_G\left(v\right)\cap (U_1\cup U_2)| \le 3,$ suppose that $d\left(u_j\right)\ge 3,$ where j is any integer that satisfies $4\le j\le i.$ If there is a vertex $u\in N_G\left(v\right)$ and $d\left(u\right)=3,$ according to Lemma 1, G has a $\overline{3}$-dset. Next, we consider the case where $d\left(u_j\right)\ge 4,$ where j is any integer satisfying $1\le j\le i.$ So, we consider $d\left(u_j\right)\ge 4,$ where j is any integer satisfying $4\le j\le i.$

If $|N_G\left(v\right)\cap (U_1\cup U_2)| =0,$ then $N_G\left(v\right)\cap (U_1\cup U_2)=Ø.$ If $|N_G\left(v\right)\cap (U_1\cup U_2)| =s$ and $1\le s\le 3,$ then $N_G\left(v\right)\cap (U_1\cup U_2)=\{u_1,u_2,\cdots ,u_s\},$ where $1\le s\le 3.$ Let $D=V\left(G\right)\setminus (\{u_4,u_5,\cdots ,u_i\}\cup \left\{v\right\}).$ Then, $V\left(G\right)\setminus D=\{u_4,u_5,\cdots ,u_i\}\cup \left\{v\right\}.$ For any j satisfying $4\le j\le i,$ since $d\left(u_j\right)\ge 4,$ $u_j$ has at least three neighbors within $D.$ That is, for any j satisfying $4\le j\le i,$ $|N_G\left(u_j\right)\cap D| \ge 3.$ Furthermore, we have $|N_G\left(v\right)\cap D|=|\{u_1,u_2,u_3\}| =3.$ Then, v has three neighbors within $D.$ So, D is a $\overline{3}$-dset. □

Theorem 3 requires this condition to be satisfied. That is, for a vertex v satisfying $d\left(v\right)\ge 4,$ any two neighbors x and y of v are not adjacent. If G is a tree, then this condition holds. In Theorem 4, we consider the case where G is a tree.

Theorem 4. 

Let G be a tree with n vertices, where $n\ge 4.$ Then, G has a $\overline{3}$-dset if and only if there exists a vertex v in G satisfying one of the following conditions:

(1) $d\left(v\right)=3$;

(2) $d\left(v\right)\ge 4$ and $|N_G\left(v\right)\cap (U_1\cup U_2)| \le 3.$

Proof. 

If the tree G has a vertex v that satisfies $d\left(v\right)=3,$ according to Lemma 1, the conclusion clearly holds. Next, we consider the case where the tree G has a vertex v that satisfies $d\left(v\right)\ge 4$ and $|N_G\left(v\right)\cap (U_1\cup U_2)| \le 3.$ For any vertex $x\in N_G\left(v\right),$$y\in N_G\left(v\right),$ since G is a tree, x is not adjacent to $y.$ Then, according to Theorem 3, G has a $\overline{3}$-dset.

For a tree $G,$ suppose that every vertex v of G satisfies $d\left(v\right)\ne 3.$ If every vertex v satisfies $d\left(v\right)\le 2,$ then G does not have a $\overline{3}$-dset. Since the tree G has a $\overline{3}$-dset, there exist vertices in the tree G with degree greater than or equal to $4.$ Suppose D is a $\overline{3}$-dset of $G.$ Then, we have $U_1\cup U_2\subseteq D.$ If any vertex v satisfies $d\left(v\right)\ge 4$ and $|N_G\left(v\right)\cap (U_1\cup U_2)| \ge 4,$ then v is dominated by at least four vertices in D, where $v\in V\left(G\right)\setminus D.$ So, G does not have a $\overline{3}$-dset. Thus, if the tree G has a $\overline{3}$-dset, the tree G has a vertex v that satisfies $d\left(v\right)=3$ or a vertex v that satisfies $d\left(v\right)\ge 4$ and $|N_G\left(v\right)\cap (U_1\cup U_2)| \le 3.$ □

Theorem 5. 

Let G be a connected graph with n vertices, where $n\ge 4.$ If G has a $\overline{3}$-dset, then ${\gamma }_3\left(G\right)\le {\gamma }_{\overline{3}}\left(G\right)\le {\gamma }_3\left(G\right)+2.$

Proof. 

Suppose that D is a ${\gamma }_3$-set of $G.$ Then, ${\gamma }_3\left(G\right)=\left|D\right|.$ By definition, we have ${\gamma }_3\left(G\right)\le {\gamma }_{\overline{3}}\left(G\right)$. If D is a ${\gamma }_{\overline{3}}$-set of $G,$ then ${\gamma }_3\left(G\right)={\gamma }_{\overline{3}}\left(G\right).$ Next, consider the case where D is not a ${\gamma }_{\overline{3}}$-set of $G.$ If D is not a ${\gamma }_{\overline{3}}$-set of $G,$ every vertex in $V\left(G\right)\setminus D$ is dominated by at least four vertices in $D.$ Then, D is a 4-dominating set. Furthermore, since ${\gamma }_4\left(G\right)\le \left|D\right|={\gamma }_3\left(G\right)$ and $\left|D\right|={\gamma }_3\left(G\right)\le {\gamma }_4\left(G\right),$ we have ${\gamma }_3\left(G\right)={\gamma }_4\left(G\right)=\left|D\right|.$ Then, D is a ${\gamma }_4$-set of $G.$ Since $U_1\cup U_2\subseteq D$, suppose that $D^{\prime }$ is a ${\gamma }_{\overline{3}}$-set of $G.$ Then, $U_1\cup U_2\subseteq D^{\prime }.$ Next, we prove that $D\ne U_1\cup U_2.$

If $D=U_1\cup U_2$, then each vertex in $V\left(G\right)\setminus D$ is dominated by at least four vertices in $D.$ If $\left|D\right|=n-1,$ the vertex in $V\left(G\right)\setminus D$ is dominated by at least four vertices in $D.$ So, the graph G does not have a $\overline{3}$-dset. Suppose that $\left|D\right|\le n-2.$ We have ${\gamma }_3\left(G\right)<{\gamma }_{\overline{3}}\left(G\right).$ That is, $\left|D\right|<|D^{\prime }|.$ If we add s vertices $u_1,u_2,\cdots ,u_s$ to $D,$ then $D^{\prime }=D\cup \{u_1,u_2,\cdots ,u_s\},$ where s is an integer satisfying $1\le s\le n-1-\left|D\right|.$ Since each vertex in $V\left(G\right)\setminus D$ is dominated by at least four vertices in $D,$ each vertex in $V\left(G\right)\setminus D^{\prime }$ is dominated by at least four vertices in $D^{\prime }.$ So, G does not have a $\overline{3}$-dset. Then, $D\ne U_1\cup U_2.$ Therefore, there exists at least one vertex u in D satisfying $d\left(u\right)\ge 3.$ We consider three cases.

Case 1: $|N_G\left(u\right)\cap D|=0.$

Since $d\left(u\right)\ge 3,$ u is adjacent to at least three vertices in $V\left(G\right)\setminus D.$ Suppose that u is adjacent to three vertices $x,y,z$ in $V\left(G\right)\setminus D.$ Let $D_1=(D\setminus \left\{u\right\})\cup \{x,y,z\}.$ Since every vertex in $V\left(G\right)\setminus D$ is dominated by at least four vertices in $D,$ every vertex in $V\left(G\right)\setminus D_1$ is dominated by at least three vertices in $D_1.$ Moreover, u is dominated by three vertices in $D_1.$ So, $D_1$ is a $\overline{3}$-dset. We have $|D_1|=|D|+2.$ That is, ${\gamma }_{\overline{3}}\left(G\right)\le {\gamma }_3\left(G\right)+2.$

Case 2: $|N_G\left(u\right)\cap D| =1.$

Since $d\left(u\right)\ge 3,$ u is adjacent to at least two vertices in $V\left(G\right)\setminus D.$ Suppose that u is adjacent to two vertices $w_1,w_2$ in $V\left(G\right)\setminus D.$ Let $D_2=(D\setminus \left\{u\right\})\cup \{w_1,w_2\}.$ Then, u is dominated by three vertices in $D_2,$ and every vertex in $V\left(G\right)\setminus D_2$ is dominated by at least three vertices in $D_2.$ So, $D_2$ is a $\overline{3}$-dset. We have $|D_2|=|D|+1.$ That is, ${\gamma }_{\overline{3}}\left(G\right)\le {\gamma }_3\left(G\right)+1.$

Case 3: $|N_G\left(u\right)\cap D| \ge 2.$

Suppose that $\{u_1,u_2,u_3\}\subseteq N_G\left(u\right)\cap D.$ Then, $D\setminus \left\{u\right\}$ is a 3-dominating set, which contradicts D as a ${\gamma }_3$-set. So, we have $|N_G\left(u\right)\cap D| =2.$ Since $d\left(u\right)\ge 3,$ we assume that u is adjacent to $v,$ where $v\in V\left(G\right)\setminus D.$ Let $D_3=(D\setminus \left\{u\right\})\cup \left\{v\right\}.$ Then, u is dominated by three vertices in $D_3,$ and every vertex in $V\left(G\right)\setminus D_3$ is dominated by at least three vertices in $D_3.$ So, $D_3$ is a $\overline{3}$-dset, and ${\gamma }_{\overline{3}}\left(G\right)={\gamma }_3\left(G\right).$ □

We give examples of graphs that satisfy ${\gamma }_{\overline{3}}\left(G_1\right)={\gamma }_3\left(G_1\right),$${\gamma }_{\overline{3}}\left(G_2\right)={\gamma }_3\left(G_2\right)+1,$ and ${\gamma }_{\overline{3}}\left(G_3\right)={\gamma }_3\left(G_3\right)+2.$

Example 1. 

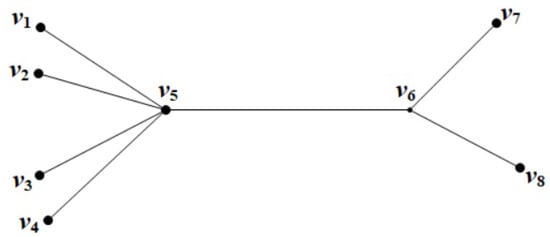
The graph $G_1$ is shown in Figure 1. The set $\{v_1,v_2,v_3,v_4,v_6,v_7,v_8\}$ is a ${\gamma }_3\left(G_1\right)$-set and also a ${\gamma }_4\left(G_1\right)$-set. Furthermore, the set $\{v_1,v_2,v_3,v_4,v_5,v_7,v_8\}$ is a ${\gamma }_{\overline{3}}\left(G_1\right)$-set. We have ${\gamma }_3\left(G_1\right)={\gamma }_{\overline{3}}\left(G_1\right)=7.$ So, ${\gamma }_{\overline{3}}\left(G_1\right)={\gamma }_3\left(G_1\right).$

Figure 1. The graph $G_1$.

Example 2. 

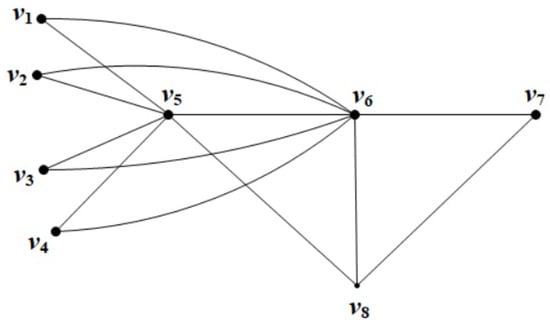
The graph $G_2$ is shown in Figure 2. The set $\{v_1,v_2,v_3,v_4,v_7,v_8\}$ is a ${\gamma }_3\left(G_2\right)$-set and also a ${\gamma }_4\left(G_2\right)$-set. Furthermore, the set $\{v_1,v_2,v_3,v_4,v_5,v_6,v_7\}$ is a ${\gamma }_{\overline{3}}\left(G_2\right)$-set. We have ${\gamma }_3\left(G_2\right)=6,{\gamma }_{\overline{3}}\left(G_2\right)=7.$ So, ${\gamma }_{\overline{3}}\left(G_2\right)={\gamma }_3\left(G_2\right)+1.$

Figure 2. The graph $G_2$.

Example 3. 

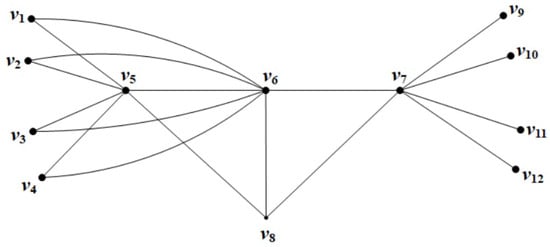
The graph $G_3$ is shown in Figure 3. The set $\{v_1,v_2,v_3,v_4,v_8,v_9,v_{10},v_{11},v_{12}\}$ is a ${\gamma }_3\left(G_3\right)$-set and also a ${\gamma }_4\left(G_3\right)$-set. Furthermore, the set $\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_9,v_{10},v_{11},v_{12}\}$ is a ${\gamma }_{\overline{3}}\left(G_3\right)$-set. We have ${\gamma }_3\left(G_3\right)=9,{\gamma }_{\overline{3}}\left(G_3\right)=11.$ So, ${\gamma }_{\overline{3}}\left(G_3\right)={\gamma }_3\left(G_3\right)+2.$

Figure 3. The graph $G_3$.

Referring to [27,29], we give the following definition.

Definition 5. 

The corona product of two graphs G,H, denoted by $G\odot H,$ is the graph obtained by taking a copy of G and $\left|V\right(G\left)\right|$ copies of H and joining the i-th vertex of G to every vertex in the i-th copy of $H.$

We consider the corona product $P_5\odot S_4$ of the two graphs $P_5$ and $S_4$, as shown in Figure 4.

Figure 4. The graph $P_5\odot S_4$.

Theorem 6. 

Let $G,H$ be two connected graphs with vertex numbers $m,n$, respectively, where $m\ge 2$ and $n\ge 4.$ If H has a $\overline{3}$-dset, then $G\odot H$ also has a $\overline{3}$-dset, and ${\gamma }_{\overline{3}}(G\odot H)\le m{\gamma }_{\overline{3}}\left(H\right).$

Proof. 

Let $V\left(G\right)=\{u_1,u_2,\cdots ,u_m\}$ and $V\left(H\right)=\{v_1,v_2,\cdots ,v_n\}.$ Let D be a ${\gamma }_{\overline{3}}$-set of H. We can assume that $D=\{v_1,v_2,\cdots ,v_j\}.$ Then, $\left|D\right|=j,$ where $3\le j\le n-1.$ Every vertex in $V\left(H\right)\setminus D$ is dominated by at least three vertices in $D,$ and at least one vertex $x\in V\left(H\right)\setminus D$ is dominated by three vertices in $D.$

For $1\le i\le m,$ let $H_i$ denote the i-th copy of $H,$ where each vertex of $H_i$ is connected to the i-th vertex of $G.$ Suppose that $V\left(H_i\right)=\{v_{i,1},v_{i,2},\cdots ,v_{i,n}\}.$ The vertex $u_i$ in G is labeled as the vertex $v_{i,0}$ in $G\odot H,$ where $1\le i\le m.$ Then, $V(G\odot H)={\cup }_{i=1}^{i=m}V\left(H_i\right)\cup \{v_{1,0},v_{2,0},\cdots ,v_{m,0}\}={\cup }_{i=1}^{i=m}\{v_{i,1},v_{i,2},\cdots ,v_{i,n}\}\cup \{v_{1,0},v_{2,0},\cdots ,v_{m,0}\}.$ Let $D_i=\{v_{i,1},v_{i,2},\cdots ,v_{i,j}\}.$ Then, $D^{\prime }={\cup }_{i=1}^{i=m}{D}_i={\cup }_{i=1}^{i=m}\{v_{i,1},v_{i,2},\cdots ,v_{i,j}\}.$ We have $V(G\odot H)\setminus D^{\prime }=\left({\cup }_{i=1}^{i=m}(V\left(H_i\right)\setminus D_i)\right)\cup \{v_{1,0},v_{2,0},\cdots ,v_{m,0}\}.$ Then, every vertex in $V\left(H_i\right)\setminus D_i$ is dominated by at least three vertices in $D_i,$ and at least one vertex $y\in V\left(H_i\right)\setminus D_i$ is dominated by three vertices in $D_i.$ $v_{k,0}$ is adjacent to $v_{k,1},v_{k,2},\cdots ,v_{k,j}$. Then, $v_{k,0}$ is dominated by j vertices in $D_k,$ where $1\le k\le m.$ Then, $D^{\prime }$ is a $\overline{3}$-dset of $G\odot H.$ So, ${\gamma }_{\overline{3}}(G\odot H)\le mj=m{\gamma }_{\overline{3}}\left(H\right).$ □

Suppose that G is a connected graph with m vertices, where $m\ge 2.$ Let H be a star graph with four vertices, that is, H is $S_4$. We have ${\gamma }_{\overline{3}}\left(S_4\right)=3.$ Then, the upper bound of ${\gamma }_{\overline{3}}(G\odot H)$ can be reached. We have ${\gamma }_{\overline{3}}(G\odot H)={\gamma }_{\overline{3}}(G\odot S_4)=3m$. For example, in Figure 4, ${\gamma }_{\overline{3}}(P_5\odot S_4)=15,$ and the 15 larger nodes constitute a ${\gamma }_{\overline{3}}(P_5\odot S_4)$-set.

Theorem 7. 

Let $m,n$ be positive integers. Then, the following statements apply:

(1) 

${\gamma }_{\overline{3}}\left(K_n\right)=3,\mathit{where}n\ge 4.$

(2) 

$\begin{array}{c}\hfill {\gamma }_{\overline{3}}\left(K_{m,n}\right)=\left\{\begin{array}{cc}3,\hfill & \mathit{where}m=3,n\ge m.\hfill \\ 6,\hfill & \mathit{where}m\ge 4,n\ge m.\hfill \end{array}\right.\end{array}$

(3) 

${\gamma }_{\overline{3}}(K_m+K_n)=3,\mathit{where}m\ge 3,n\ge 3.$

(4) 

${\gamma }_{\overline{3}}(K_m⊠K_n)=3,\mathit{where}m\ge 3,n\ge 3.$

(5) 

${\gamma }_{\overline{3}}(K_m\circ K_n)=3,\mathit{where}m\ge 3,n\ge 3.$

Proof. 

(1) For $n\ge 4,$ ${\gamma }_{\overline{3}}\left(K_n\right)=3$ is obvious, so we omit the proof.

(2) Let $F_1=\{w_1,w_2,\cdots ,w_m\}$ and $F_2=\{z_1,z_2,\cdots ,z_n\}.$ Let $V\left(K_{m,n}\right)=F_1\cup F_2=\{w_1,w_2,\cdots ,w_m\}\cup \{z_1,z_2,\cdots ,z_n\}$ and $E\left(K_{m,n}\right)=\left\{w_i{z}_j\right|\mathrm{where}1\le i\le m,1\le j\le n\}.$ If $m=3,n\ge 3,$ then $\{w_1,w_2,w_3\}$ is a ${\gamma }_{\overline{3}}\left(K_{m,n}\right)$-set. We consider $m\ge 4,n\ge m.$ Let D be a ${\gamma }_{\overline{3}}\left(K_{m,n}\right)$-set. Since at least one vertex $x\in V\left(K_{m,n}\right)\setminus D$ is dominated by three vertices in $D,$ we have $|D\cap F_1| =3$ or $|D\cap F_2| =3.$ Suppose that $|D\cap F_1| =3$. Then, each vertex in $F_1\setminus D$ is dominated by at least three vertices in $D\cap F_2.$ Since D is a ${\gamma }_{\overline{3}}\left(K_{m,n}\right)$-set, we have $|D\cap F_2| =3.$ Similarly, suppose that $|D\cap F_2| =3$. Then, we have $|D\cap F_1| =3.$ So, $\left|D\right| =6.$ Let $D=\{w_1,w_2,w_3,z_1,z_2,z_3\}.$ Then, D is a ${\gamma }_{\overline{3}}\left(K_{m,n}\right)$-set.

In (3)–(5), let $V\left(K_m\right)=\{u_1,u_2,\cdots ,u_m\}$ and $V\left(K_n\right)=\{v_1,v_2,\cdots ,v_n\},$ where $m\ge 3,n\ge 3.$

(3) For $K_m+K_n,$$\{u_1,u_2,u_3\}$ is a ${\gamma }_{\overline{3}}$-set.

(4) Suppose that any two distinct vertices $(u_i,v_j)\in V(K_m⊠K_n)$ and $(u_s,v_t)\in V(K_m⊠K_n).$ If $i=s,j\ne t,$ $v_j{v}_t\in E\left(K_n\right),$ then $(u_i,v_j)$ is adjacent to $(u_s,v_t)$ in $K_m⊠K_n.$ If $i\ne s,j=t,$ $u_i{u}_s\in E\left(K_m\right),$ then $(u_i,v_j)$ is adjacent to $(u_s,v_t)$ in $K_m⊠K_n.$ If $i\ne s,j\ne t,$ then $u_i{u}_s\in E\left(K_m\right),$$v_j{v}_t\in E\left(K_n\right).$ So $(u_i,v_j)$ is adjacent to $(u_s,v_t)$ in $K_m⊠K_n.$ Then, in graph $K_m⊠K_n,$ $(u_i,v_j)$ is adjacent to $(u_s,v_t).$ Let $D=\{(u_1,v_1),(u_2,v_2),(u_3,v_3)\}.$ For any vertex $(u_i,v_j)\in V(K_m⊠K_n)$ and $(u_i,v_j)\notin D,$$(u_i,v_j)$ is adjacent to $(u_1,v_1),(u_2,v_2),$ and $(u_3,v_3).$ Therefore, $D=\{(u_1,v_1),(u_2,v_2),(u_3,v_3)\}$ is a ${\gamma }_{\overline{3}}(K_m⊠K_n)$-set.

(5) Suppose that any two distinct vertices $(u_i,v_j)\in V(K_m\circ K_n)$ and $(u_s,v_t)\in V(K_m\circ K_n).$ If $i=s,j\ne t,$ $v_j{v}_t\in E\left(K_n\right),$ then $(u_i,v_j)$ is adjacent to $(u_s,v_t)$ in $K_m\circ K_n.$ If $i\ne s,$ $u_i{u}_s\in E\left(K_m\right),$ then $(u_i,v_j)$ is adjacent to $(u_s,v_t)$ in $K_m\circ K_n.$ Let $D=\{(u_1,v_1),(u_2,v_2),(u_3,v_3)\}.$ For any vertex $(u_i,v_j)\in K_m\circ K_n$ and $(u_i,v_j)\notin D,$ $(u_i,v_j)$ is adjacent to $(u_1,v_1),(u_2,v_2),$ and $(u_3,v_3).$ Therefore, for $K_m\circ K_n,$$D=\{(u_1,v_1),(u_2,v_2),(u_3,v_3)\}$ is a ${\gamma }_{\overline{3}}$-set. □

Theorem 8. 

Suppose that $S_m,S_n$ are star graphs, where m and n are positive integers that satisfy $m\ge 3$ and $n\ge m.$ Let $V\left(S_m\right)=\{u_1,u_2,\cdots ,u_m\}$ and $E\left(S_m\right)=\left\{u_1{u}_i\right|i=2,3,\cdots ,m\}.$ Let $V\left(S_n\right)=\{v_1,v_2,\cdots ,v_n\}$ and $E\left(S_n\right)=\left\{v_1{v}_i\right|i=2,3,\cdots ,n\}.$ Then,

$${\gamma }_{\overline{3}}(S_m+S_n)=\left\{\begin{array}{cc}3,\hfill & \mathit{where}3\le m\le 4,n\ge m,\hfill \\ 4,\hfill & \mathit{where}m\ge 5,n\ge m.\hfill \end{array}\right.$$

Proof. 

Suppose that D is a ${\gamma }_{\overline{3}}$-set of $S_m+S_n.$ If $m=3$ and $n\ge 3,$ then $D=\{u_1,u_2,u_3\}$ is a ${\gamma }_{\overline{3}}$-set. If $m=4$ and $n\ge 4,$ then $D=\{u_2,u_3,u_4\}$ is a ${\gamma }_{\overline{3}}$-set. If $m\ge 5$ and $n\ge m$, suppose that $|D\cap V(S_m\left)\right| =3$. Then, there exists at least one vertex in $V\left(S_m\right)\setminus D$ that is not dominated by three vertices in $D.$ Similarly, if $|D\cap V(S_n\left)\right| =3,$ there exists at least one vertex in $V\left(S_n\right)\setminus D$ that is not dominated by three vertices in $D.$ Suppose that $|D\cap V(S_m\left)\right| =2$ and $|D\cap V(S_n\left)\right| =1$. Then, there exists at least one vertex in $V\left(S_m\right)\setminus D$ that is not dominated by two vertices in $D\cap V\left(S_m\right).$ Thus, there exists at least one vertex in $V\left(S_m\right)\setminus D$ that is not dominated by three vertices in $D.$ Similarly, if $|D\cap V(S_m\left)\right| =1$ and $|D\cap V(S_n\left)\right| =2,$ there exists at least one vertex in $V\left(S_n\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right|\ge 4.$ Then, $D=\{u_1,u_2,v_1,v_2\}$ is a ${\gamma }_{\overline{3}}$-set. □

In Lemma 3 and Theorem 9 below, the notation $C_i$ represents a cycle of length i, where $i=m,n$. Suppose that $m\ge 3$ and $n\ge m.$ Let $V\left(C_m\right)=\{u_1,u_2,\cdots ,u_m\}$ and $E\left(C_m\right)=\left\{u_{i-1}{u}_i\right|i=2,3,\cdots ,m\}\cup \left\{u_m{u}_1\right\}.$ Let $V\left(C_n\right)=\{v_1,v_2,\cdots ,v_n\}$ and $E\left(C_n\right)=\left\{v_{i-1}{v}_i\right|i=2,3,\cdots ,n\}\cup \left\{v_n{v}_1\right\}.$

Lemma 3. 

Let $m,n$ be positive integers. Then,

$${\gamma }_{\overline{3}}(C_m+C_n)\ge \left\{\begin{array}{cc}4,\hfill & \mathit{where}m\ge 4,n\ge m,\hfill \\ 5,\hfill & \mathit{where}m\ge 7,n\ge m,\hfill \\ 6,\hfill & \mathit{where}m\ge 10,n\ge m.\hfill \end{array}\right.$$

Proof. 

Suppose that D is a ${\gamma }_{\overline{3}}$-set of $C_m+C_n.$ Let $|D\cap V(C_m\left)\right|=a$ and $|D\cap V(C_n\left)\right|=b.$ Suppose that $3\le a\le m-1$ and $b\le 2.$ If there exists one vertex x in $V\left(C_m\right)\setminus D$ that is not dominated by $3-b$ vertices in $V\left(C_m\right)\cap D$, then x is not dominated by three vertices in $D.$ Let $|D\cap V(C_m\left)\right|=b$ and $|D\cap V(C_n\left)\right|=a.$ Then, there exists one vertex y in $V\left(C_n\right)\setminus D$ that is not dominated by $3-b$ vertices in $V\left(C_n\right)\cap D.$ So, y is not dominated by three vertices in $D.$

Let $m\ge 4$ and $n\ge m.$ Suppose that $\left|D\right| =3.$ If $|D\cap V(C_m\left)\right| =3$, then, since every vertex $v\in V\left(C_m\right)$ has $d\left(v\right)=2,$ there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by three vertices in $D.$ Let $|D\cap V(C_m\left)\right| =2$ and $|D\cap V(C_n\left)\right| =1.$ Suppose that $D\cap V\left(C_n\right)=\left\{v_1\right\}.$ Then, $v_3$ is not dominated by three vertices in $D.$ If $|D\cap V(C_m\left)\right| =1$ and $|D\cap V(C_n\left)\right| =2$, suppose that $D\cap V\left(C_m\right)=\left\{u_1\right\}.$ Then, $u_3$ is not dominated by three vertices in $D.$ So, $\left|D\right|\ge 4.$

If $m\ge 7$ and $n\ge m$, we have $\left|D\right| \ge 4.$ Suppose that $\left|D\right| =4.$ If $|D\cap V(C_m\left)\right| =4$, then for any vertex $v\in V\left(C_m\right),$ we have $d\left(v\right)=2.$ Then, each vertex in $V\left(C_m\right)\setminus D$ is not dominated by three vertices in $D.$ If $|D\cap V(C_m\left)\right| =3$ and $|D\cap V(C_n\left)\right| =1$, then there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by two vertices in $D\cap V\left(C_m\right).$ So, there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(C_m\left)\right| =2$ and $|D\cap V(C_n\left)\right| =2$, then there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by one vertex in $D\cap V\left(C_m\right)$, and there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right| \ge 5.$

If $m\ge 10$ and $n\ge m$, we have $\left|D\right| \ge 5.$ Suppose that $\left|D\right| =5.$ If $|D\cap V(C_m\left)\right| =5$, then each vertex in $V\left(C_m\right)\setminus D$ is not dominated by three vertices in $D.$ If $|D\cap V(C_m\left)\right| =4$ and $|D\cap V(C_n\left)\right| =1$, then there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by two vertices in $D\cap V\left(C_m\right).$ So, there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(C_m\left)\right| =3$ and $|D\cap V(C_n\left)\right| =2$, then there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by one vertex in $D\cap V\left(C_m\right)$, and there exists at least one vertex in $V\left(C_m\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right| \ge 6.$ □

Theorem 9. 

Let $m,n$ be positive integers. Then,

$${\gamma }_{\overline{3}}(C_m+C_n)=\left\{\begin{array}{cc}3,\hfill & \mathit{where}m=3,n\ge 3,\hfill \\ 4,\hfill & \mathit{where}4\le m\le 6,n\ge m,\hfill \\ 5,\hfill & \mathit{where}7\le m\le 9,n\ge m,\hfill \\ 6,\hfill & \mathit{where}m\ge 10,n\ge m.\hfill \end{array}\right.$$

Proof. 

Suppose that D is a ${\gamma }_{\overline{3}}$-set of $C_m+C_n.$

Case 1: $m=3,n\ge 3.$

Then, $D=\{u_1,u_2,u_3\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 2: $4\le m\le 6,n\ge m.$

According to Lemma 3, we have $\left|D\right| \ge 4.$ If $m=4$ and $n\ge 4,$ then $D=\{u_1,u_2,u_3,v_1\}$ is a ${\gamma }_{\overline{3}}$-set. If $5\le m\le 6$ and $n\ge m,$ then $D=\{u_1,u_3,u_5,v_1\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 3: $7\le m\le 9,n\ge m.$

According to Lemma 3, we have $\left|D\right| \ge 5.$ Then, $D=\{u_1,u_4,u_7,v_1,v_2\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 4: $m\ge 10,n\ge m.$

According to Lemma 3, we have $\left|D\right|\ge 6.$ Then, $D=\{u_1,u_2,u_3,v_1,v_2,v_3\}$ is a ${\gamma }_{\overline{3}}$-set. □

In Lemma 4 and Theorem 10 below, the notation $P_i$ represents a path of i vertices, where $i=m,n$. Suppose that $m\ge 3$ and $n\ge m.$ Let $V\left(P_m\right)=\{u_1,u_2,\cdots ,u_m\}$ and $E\left(P_m\right)=\left\{u_{i-1}{u}_i\right|i=2,3,\cdots ,m\}.$ Let $V\left(P_n\right)=\{v_1,v_2,\cdots ,v_n\}$ and $E\left(P_n\right)=\left\{v_{i-1}{v}_i\right|i=2,3,\cdots ,n\}.$

Lemma 4. 

Let $m,n$ be positive integers. Then,

$${\gamma }_{\overline{3}}(P_m+P_n)\ge \left\{\begin{array}{cc}4,\hfill & \mathit{where}m\ge 4,n\ge m,\hfill \\ 5,\hfill & \mathit{where}m=6,n\ge 7,\hfill \\ 5,\hfill & \mathit{where}m\ge 7,n\ge m,\hfill \\ 6,\hfill & \mathit{where}m\ge 10,n\ge m.\hfill \end{array}\right.$$

Proof. 

Suppose that D is a ${\gamma }_{\overline{3}}$-set of $P_m+P_n.$ Let $|D\cap V(P_m\left)\right|=a$ and $|D\cap V(P_n\left)\right|=b.$ Suppose that $3\le a\le m-1$ and $b\le 2.$ If there exists one vertex x in $V\left(P_m\right)\setminus D$ that is not dominated by $3-b$ vertices in $V\left(P_m\right)\cap D$, then x is not dominated by three vertices in $D.$ Let $|D\cap V(P_m\left)\right|=b$ and $|D\cap V(P_n\left)\right|=a.$ Then, there exists one vertex y in $V\left(P_n\right)\setminus D$ that is not dominated by $3-b$ vertices in $V\left(P_n\right)\cap D.$ So, y is not dominated by three vertices in $D.$

Let $m\ge 4,n\ge m.$ Suppose that $\left|D\right|=3.$ If $|D\cap V(P_m\left)\right|=3.$ For any vertex $v\in V\left(P_m\right),$ we have $d\left(v\right)\le 2,$ so there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(P_m\left)\right|=2$ and $|D\cap V(P_n\left)\right|=1$, there exists at least one vertex in $V\left(P_n\right)\setminus D$ that is not adjacent to the vertex in $V\left(P_n\right)\cap D.$ Then, there exists at least one vertex in $V\left(P_n\right)\setminus D$ that is not dominated by three vertices in $D.$ Similarly, if $|D\cap V(P_m\left)\right|=1$ and $|D\cap V(P_n\left)\right|=2,$ then there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right|\ge 4.$

If $m=6,n\ge 7$ or $m\ge 7,n\ge m$, we have $\left|D\right|\ge 4.$ Suppose that $\left|D\right|=4.$ If $|D\cap V(P_m\left)\right|=4,$ then there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(P_m\left)\right|=3$ and $|D\cap V(P_n\left)\right|=1,$ then there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by two vertices in $D\cap V\left(P_m\right).$ Then, there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(P_m\left)\right|=2$ and $|D\cap V(P_n\left)\right|=2,$ then there exists at least one vertex in $V\left(P_n\right)\setminus D$ that is not dominated by one vertex in $D\cap V\left(P_n\right).$ Then, there exists at least one vertex in $V\left(P_n\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right|\ge 5.$

If $m\ge 10,n\ge m$, we have $\left|D\right|\ge 5.$ Suppose that $\left|D\right|=5.$ If $|D\cap V(P_m\left)\right|=5.$ Then, there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(P_m\left)\right|=4$ and $|D\cap V(P_n\left)\right|=1,$ then there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by two vertices in $D\cap V\left(P_m\right).$ Then, there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ If $|D\cap V(P_m\left)\right|=3$ and $|D\cap V(P_n\left)\right|=2,$ then there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by one vertex in $D\cap V\left(P_m\right).$ Then, there exists at least one vertex in $V\left(P_m\right)\setminus D$ that is not dominated by three vertices in $D.$ So, $\left|D\right|\ge 6.$ □

Theorem 10. 

Let $m,n$ be positive integers. Then,

$${\gamma }_{\overline{3}}(P_m+P_n)=\left\{\begin{array}{cc}3,\hfill & \mathit{where}m=3,n\ge 3,\hfill \\ 4,\hfill & \mathit{where}4\le m\le 5,n\ge m,\hfill \\ 4,\hfill & \mathit{where}m=6,n=6,\hfill \\ 5,\hfill & \mathit{where}m=6,n\ge 7,\hfill \\ 5,\hfill & \mathit{where}7\le m\le 9,n\ge m,\hfill \\ 6,\hfill & \mathit{where}m\ge 10,n\ge m.\hfill \end{array}\right.$$

Proof. 

Suppose that D is a ${\gamma }_{\overline{3}}$-set of $P_m+P_n.$

Case 1: $m=3,n\ge 3.$

Then, $D=\{u_1,u_2,u_3\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 2: $4\le m\le 5,n\ge m.$

According to Lemma 4, we have $\left|D\right|\ge 4.$ If $m=4$ and $n\ge m,$ then $D=\{u_1,u_3,u_4,v_1\}$ is a ${\gamma }_{\overline{3}}$-set. If $m=5$ and $n\ge m,$ then $D=\{u_1,u_3,u_5,v_1\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 3: $m=6,n=6.$

Then, $D=\{u_2,u_5,v_2,v_5\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 4: $m=6,n\ge 7.$

According to Lemma 4, we have $\left|D\right|\ge 5.$ Then, $D=\{u_2,u_3,u_5,v_1,v_2\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 5: $7\le m\le 9,n\ge m.$

If $7\le m\le 8$ and $n\ge m,$ then $D=\{u_2,u_5,u_7,v_1,v_2\}$ is a ${\gamma }_{\overline{3}}$-set. If $m=9$ and $n\ge m,$ then $D=\{u_2,u_5,u_8,v_1,v_2\}$ is a ${\gamma }_{\overline{3}}$-set.

Case 6: $m\ge 10,n\ge m.$

According to Lemma 4, we have $\left|D\right|\ge 6.$ Then, $D=\{u_1,u_2,u_3,v_1,v_2,v_3\}$ is a ${\gamma }_{\overline{3}}$-set. □

3. Conclusions

In this paper, we introduced the concept of proper 3-dominating sets in graphs and studied the characteristics of graphs with such sets. We found several sufficient conditions for graphs with proper 3-dominating sets. Corollary 2 and Theorem 6 show that there are proper 3-dominating sets in some graph products.

For a connected graph G with a $\overline{3}$-dset, we found the relationship between ${\gamma }_3\left(G\right)$ and ${\gamma }_{\overline{3}}\left(G\right).$ That is, ${\gamma }_3\left(G\right)\le {\gamma }_{\overline{3}}\left(G\right)\le {\gamma }_3\left(G\right)+2.$ However, for $i=0,1,2,$ the structure of the graph satisfying ${\gamma }_{\overline{3}}\left(G\right)={\gamma }_3\left(G\right)+i$ is still unknown, which we will examine in future work. In addition, for some joint products of two special graphs, we obtained their proper 3-domination numbers. It is also meaningful to calculate the proper 3-domination numbers of the strong product, lexicographic product, and corona product of two graphs. From an algorithmic perspective, it is also possible to consider studying the minimum $\overline{3}$-dset and the proper 3-domination number of the graph.