Dual Impact of Information Complexity and Individual Characteristics on Information and Disease Propagation

Abstract

With frequent interactions between social media platforms, the dissemination of information and the interaction of opinions on the internet have become increasingly complex and diverse. This increase in information complexity not only affects the formation of public opinion but may also exacerbate the spread of diseases. Based on multilayer complex networks and combined with the Deffuant-I model, this paper explores the dual impact of information complexity and individual characteristics on both information and disease propagation. Through systematic simulation experiments, this paper analyzes the mechanisms of information complexity, individual compromise, and cognitive ability in the evolution of propagation. This study shows that the interactive effects of individual characteristics and information complexity have a significant impact on disease spread. This research not only provides a new theoretical perspective for understanding complex information dissemination but also offers valuable insights for public policymakers in promoting social harmony and addressing public health emergencies.

1. Introduction

With the rapid development of the internet, big data, and intelligent technologies, social media platforms have gradually emerged as important arenas for information dissemination. The ways in which people access information, the channels through which it spreads, and the modes of dissemination have undergone profound changes. The rise in social media platforms has not only attracted a large number of users but also prompted traditional media and government agencies to join these platforms in order to expand their reach, further accelerating the rapid growth of online platforms. In this interconnected, multi-platform communication landscape, each individual can become both a producer and a disseminator of information. With mobile devices, individuals can easily switch between platforms to share, comment, and create content. This has made the interaction of opinions and the evolution of information on social platforms increasingly complex and difficult to predict. This complexity primarily stems from the individuals—the main agents of information dissemination and diffusion. Each person, based on their unique social background, education level, and cognitive ability, exhibits significant differences in how they receive, interpret, and react to information. Furthermore, individual reactions are not isolated; instead, they are influenced by multiple factors, particularly the interplay of information complexity, public opinion, and individual characteristics. Against this backdrop, information complexity and individual traits have had a profound impact on the spread and evolution of events. These factors not only determine the speed at which information spreads across networks but also influence the outcome of the event’s evolution to a certain extent.

As information spreads, complex content often diffuses rapidly through social media platforms. Over time, changes, misunderstandings, or distortions in the content may lead to shifts in or the exacerbation of public opinion, potentially triggering social panic or disorder. Individual cognitive ability, information reception preferences, and social background play a crucial role in information dissemination. They influence how individuals accept and respond to information, which in turn affects the disease transmission behavior of the broader social group. For example, an individual’s understanding and adoption of health information determines the implementation of preventive measures, which have a critical impact on the speed and scope of disease spread. Therefore, studying the role of information complexity and individual characteristics in the dissemination process can not only help us understand the underlying mechanisms of event evolution but also provide theoretical support and practical guidance for addressing public health emergencies and guiding social opinion. This paper aims to explore how information complexity and individual characteristics affect disease propagation, particularly examining the roles of individual compromise and cognitive ability in information dissemination, opinion formation, and disease spread. By analyzing the influence of these factors on the disease propagation process, this paper seeks to reveal the interrelationship between information dissemination, opinion interaction, and disease spread in the mobile internet environment, as well as explore how the modulation of individual characteristics and information complexity can enhance the effectiveness of information dissemination and improve the spread of health-related information.

2. Research Overview

In epidemic modeling, the seminal SIR model proposed by Kermack and McKendrick in 1927 offered the first mathematical framework for disease transmission dynamics in populations [1], forming the foundation for later models like SIS and SEIR. As complex network theory evolved, structures such as small-world [2], scale-free [3], and ER random networks [4] were introduced to simulate realistic contact patterns. Keeling and Eames explored how network features, especially clustering, influence local outbreaks and incorporated behavioral factors [5]. Newman applied generating functions to analyze disease spread over arbitrary degree distributions [6], while Pastor-Satorras revealed the “absence of epidemic threshold” in scale-free networks [7]. Molloy and Reed developed methods to construct networks with specified degree sequences [8], and Boguná demonstrated how degree assortativity elevates transmission risk [9]. Barabási [10] and Barrat et al. [11] further synthesized the relationship between network topology and epidemic dynamics, jointly laying the dual foundation of differential-equation-based and network-based epidemic theory.

In real-world contexts, epidemics are closely linked to the spread of information through news, social me-dia, and rumors. These information flows influence individual behavioral responses, which in turn reshape epidemic trajectories. Funk et al. pioneered awareness–epidemic coupled models and demonstrated how information diffusion suppresses outbreaks [12]. Granell et al. constructed a multiplex SIS–UAU framework, identifying threshold conditions under which awareness can inhibit disease spread [13]. Wang et al. unified diverse behavior–epidemic models and analyzed feedback effects from interventions [14]. Zhan et al. modeled double-layered heterogeneous networks, showing how behavioral delay and transmission priority affect epidemic size [15]. Chen et al. introduced a tripartite model incorporating awareness, epidemic status, and activity levels [16], while Hong et al. simulated competing information sources and strategic behavioral adaptation under trust heterogeneity [17]. Xian et al. explored selective exposure effects in media perception [18], and Zhang et al. proposed a self-awareness mechanism in which infected individuals actively spread alerts [19]. Bauch and Galvani embedded behavioral game theory into epidemiology, analyzing vaccine hesitancy and social contagion [20], and Funk and Salathé provided a foundational review summarizing these coupling models [21]. Collectively, these studies highlight the transition from single-layer epidemic modeling to integrated “epidemic–information–behavior” coevolution frameworks.

Information diffusion not only transforms how individuals acquire knowledge but also profoundly shapes the process of opinion formation and evolution. The Deffuant-I model proposed by Deffuant et al. introduces a confidence bound as an interaction threshold, revealing how individual heterogeneity in tolerance levels influences opinion aggregation and polarization [22,23]. Lorenz provided a systematic review of related models, highlighting the significant role of multidimensional information structures and network topologies in shaping opinion dynamics outcomes [24]. Further studies incorporated opinion dynamics into electoral modeling, showing that complexity in information preferences and transmission paths can trigger voter polarization [25]. Mäs and Flache demonstrated that even without explicit negative influence mechanisms, selective information exposure and homophily are sufficient to cause group polarization [26]. The Hegselmann–Krause model offers an alternative mean-field perspective, analyzing how initial opinion distributions relate to convergence patterns [27].

In addition, scholars have focused on the disruptive effects of biased information sources and trust mechanisms on opinion evolution. Acemoglu et al. revealed systemic misinformation pathways under heterogeneous trust, emphasizing the coupled effect of perception heterogeneity and bias reinforcement [28]. Flache et al. summarized the key frontiers in opinion dynamics, advocating for the integration of structural heterogeneity, transmission mechanisms, and learning behaviors into modeling frameworks [29]. In reality, algorithm-driven information filtering exposes individuals primarily to content that aligns with their existing views, thereby intensifying cognitive closure and social fragmentation [30]. Sîrbu et al. expanded model boundaries by incorporating media influence, emotional fluctuations, and memory effects, showing how external stimuli can destabilize internal opinion states [31]. Collectively, these studies demonstrate that information complexity (e.g., multiple sources) and individual heterogeneity (e.g., tolerance levels) are indispensable for understanding opinion evolution dynamics and serve as crucial theoretical foundations for constructing future models coupling epidemics, information, and opinion formation.

In existing research on epidemic–information co-propagation [12,13,14,15,16,17,18,19,20,21], scholars have primarily focused on how information dissemination within social networks influences the spread of infectious diseases, leading to the development of various “information–epidemic” coupled models. These studies are mainly based on mechanisms such as dynamic transmission paths, cognitive delays, and the diffusion of misinformation, aiming to reveal the complex interactions between information flow and disease transmission. However, several limitations remain in the current literature. First, most models simplify “information” into binary states (e.g., “received/not received” or “true/false”), overlooking the inherent structural complexity of information itself and its differentiated impacts on individual responses. This simplification makes it difficult to explain the substantial variation in the real-world effectiveness of information interventions [12,14,18]. Second, some studies only examine direct pathways such as “information influences behavior” or “misinformation induces panic,” without capturing how information shapes opinion dynamics, which in turn indirectly affects behavioral decisions and epidemic progression [15,19,21]. Third, behavioral evolution in many models is typically governed by homogeneous parameters, ignoring individual differences in cognitive capacity, willingness to compromise, and other psychological–behavioral traits. This limits the models’ ability to account for behavioral diversity and the emergence of societal polarization [13,17,20]. To address these limitations, this study constructs a comprehensive “information–opinion–behavior–epidemic” coupled model. By introducing two key dynamic factors, information complexity and individual heterogeneity, this framework offers a theoretical and methodological advancement over previous studies.

3. Information-Driven Multilayer Propagation Model Construction

3.1. Overview of the Information-Driven Multilayer Propagation Model

In today’s social media landscape the patterns of cross-platform information interaction and dissemination have become increasingly complex, characterized by high interconnectivity and accelerated spread. To better capture and understand these dynamics, this study proposes an Information-Driven Multilayer Propagation Model (IDMPM) by integrating multilayer complex network theory with the Deffuant-I opinion dynamics model. This framework enables the exploration of how information complexity and individual heterogeneity jointly influence the intertwined processes of information dissemination and disease diffusion.

The model is composed of the following two primary layers: the information layer, which captures the acquisition and evolution of individuals’ knowledge and opinions on social media platforms; and the contact layer, which simulates the physical spread of disease through interpersonal interactions. It is important to clarify that while individuals in both layers represent the same agents, their behaviors, interactions, and relational structures may differ across layers. For simplicity, this study assumes that individuals’ characteristics and social networks across different platforms are statistically independent, i.e., there are no direct cross-layer connections. Although this assumption simplifies the modeling process, it offers a novel analytical lens to dissect the interplay between information and disease dynamics in digital social environments.

Within the information layer, individuals can exist in one of the following three states: U (Unaware): The individual has not yet encountered any relevant information. A (Aware): The individual has received the information but remains neutral, without forming a strong opinion. O (Opinionated): The individual has formed a clear and firm stance through information interaction or opinion exchange. Transitions between these states are influenced by individual traits such as cognitive ability, willingness to compromise, and exposure to diverse information. The Deffuant-I model is used to simulate the opinion exchange process, where interactions between individuals can lead to convergence or divergence of viewpoints depending on their confidence thresholds.

In the contact layer, individuals are classified into the following two states: S (susceptible): The individual is healthy but at risk of infection. I (infected): The individual is infected and capable of transmitting the disease. Disease spreads through interpersonal contact, where an infected individual has a certain probability of infecting a susceptible individual. Additionally, due to external interventions or natural immunity, infected individuals may transition back to the susceptible state. This multilayer structure sets the foundation for modeling how information flows and evolving opinions may shape real-world behavior and, subsequently, epidemic trajectories.

3.2. Construction of the Information-Driven Multilayer Propagation Model

The IDMPM integrates two interconnected dynamical layers, the information layer and the contact layer. In the information layer, individuals receive information via social platforms. Their state transitions follow a three-step process of Unaware (U)→Aware (A)→Opinionated (O). Individuals progress from being unaware of the information to receiving it, and eventually to forming distinct attitudes or stances after cognitive processing or social interaction. In the contact layer, individuals exist in either the susceptible (S) or infected (I) state. Infected individuals can transmit the disease to susceptible ones with a certain probability, leading to their transition into the infected state. Conversely, infected individuals may also recover, returning to a susceptible state, depending on the simulation parameters.

Crucially, the opinions and attitudes formed in the information layer directly influence behavioral decisions in the contact layer—such as whether to adopt preventive measures or engage in risky interactions—which, in turn, affect the disease spread. The complexity of information (e.g., its multidimensionality, ambiguity, or overload) and individual psychological characteristics (e.g., cognitive capacity, openness to opposing views, and compromise threshold) are key factors that shape both layers’ dynamics. By simulating the interplay between informational influence and physical contagion, this multilayer model offers a novel perspective for understanding the co-evolutionary dynamics of information diffusion and epidemic propagation in networked societies.

Based on this analysis of the propagation process and considering the heterogeneity of nodes in the network, this study combines the Deffuant-I model to analyze the propagation dynamics in the multilayer model. In this multilayer propagation model, the dissemination in the information layer is influenced by individual cognitive ability, information complexity, and opinion interactions, while the dissemination in the contact layer depends on individuals’ infection status and epidemic prevention decisions. Through multilayer coupling individuals are affected not only by external information in both information and disease propagation processes but also by varying propagation behaviors resulting from the heterogeneity of individual characteristics. This multilayer coupled propagation model provides new insights into understanding information diffusion and epidemic spread in complex social networks and uncovers the mutual promotion mechanism between information dissemination and disease transmission. Based on the assumptions above, the propagation model of the multilayer network is as follows:

(1)

Propagation in the information layer:

$$\mathrm{U}\mathrm{S}+\mathrm{A}\mathrm{S}\stackrel{p_i}{\to }\mathrm{A}\mathrm{S}+\mathrm{A}\mathrm{S};\mathrm{U}\mathrm{S}+\mathrm{A}\mathrm{I}\stackrel{{\mathrm{p}}_{\mathrm{i}}}{\to }\mathrm{A}\mathrm{S}+\mathrm{A}\mathrm{I},$$

(1)

$$\mathrm{A}\mathrm{S}+\mathrm{O}\mathrm{S}\stackrel{p_o}{\to }\mathrm{O}\mathrm{S}+\mathrm{O}\mathrm{S};\mathrm{A}\mathrm{S}+\mathrm{O}\mathrm{I}\stackrel{p_o}{\to }\mathrm{O}\mathrm{S}+\mathrm{O}\mathrm{I},$$

(2)

$$\mathrm{A}\mathrm{I}+\mathrm{O}\mathrm{S}\stackrel{p_o}{\to }\mathrm{O}\mathrm{I}+\mathrm{O}\mathrm{S};\mathrm{A}\mathrm{I}+\mathrm{O}\mathrm{I}\stackrel{p_o}{\to }\mathrm{O}\mathrm{I}+\mathrm{O}\mathrm{I}.$$

(3)

(2)

Propagation in the contact layer:

$$\mathrm{U}\mathrm{S}+\mathrm{A}\mathrm{I}\stackrel{{\beta }^U}{\to }\mathrm{U}\mathrm{I}+\mathrm{A}\mathrm{I}\stackrel{1}{\to }\mathrm{A}\mathrm{I}+\mathrm{A}\mathrm{I},$$

(4)

$$\mathrm{A}\mathrm{S}+\mathrm{A}\mathrm{I}\stackrel{{\beta }^A}{\to }\mathrm{A}\mathrm{I}+\mathrm{A}\mathrm{I},$$

(5)

$$\mathrm{O}\mathrm{S}+\mathrm{A}\mathrm{I}\stackrel{{\beta }^O}{\to }\mathrm{O}\mathrm{I}+\mathrm{A}\mathrm{I},$$

(6)

$$\mathrm{U}\mathrm{S}+\mathrm{O}\mathrm{I}\stackrel{{\beta }^U}{\to }\mathrm{U}\mathrm{I}+\mathrm{O}\mathrm{I}\stackrel{1}{\to }\mathrm{A}\mathrm{I}+\mathrm{O}\mathrm{I},$$

(7)

$$\mathrm{A}\mathrm{S}+\mathrm{O}\mathrm{I}\stackrel{{\beta }^A}{\to }\mathrm{A}\mathrm{I}+\mathrm{O}\mathrm{I},$$

(8)

$$\mathrm{O}\mathrm{S}+\mathrm{O}\mathrm{I}\stackrel{{\beta }^O}{\to }\mathrm{O}\mathrm{I}+\mathrm{O}\mathrm{I}.$$

(9)

(3)

Recovery of nodes:

$$\mathrm{A}\mathrm{S}\stackrel{\upsilon }{\to }\mathrm{U}\mathrm{S};\mathrm{O}\mathrm{S}\stackrel{\mathsf{\omega }}{\to }\mathrm{A}\mathrm{S};\mathrm{O}\mathrm{I}\stackrel{\mathsf{\omega }}{\to }\mathrm{A}\mathrm{I},$$

(10)

$$\mathrm{A}\mathrm{I}\stackrel{\sigma }{\to }\mathrm{A}\mathrm{S};\mathrm{O}\mathrm{I}\stackrel{\sigma }{\to }\mathrm{O}\mathrm{S}.$$

(11)

In constructing the Information-Driven Multilayer Network Propagation Model, we analyze the propagation dynamics by integrating the Deffuant-I model. The model consists of two layers, the information layer and the contact layer. Propagation in the information layer is influenced by individual cognitive abilities, information complexity, and opinion interactions, while propagation in the contact layer depends on the individual’s infection status and transmission rate. Through multilayer coupling, individuals are affected not only by external information in both information and disease transmission processes but also exhibit different propagation behaviors due to the heterogeneity of individual characteristics. The mutual promotion mechanism between information dissemination and disease transmission provides new insights into understanding information diffusion and epidemic spread within complex social networks. Next, we define the key variables and formulas in the model to analyze the propagation process.

(1)

Propagation in the Information Layer

In the information layer some nodes are initially assigned a starting amount of information, typically a random value from a continuous range (e.g., [0,1]). Suppose a node i in the “unaware” state encounters a neighbor node j who is “aware.” The probability of node i acquiring information from node j is as follows:

$$p_i=\lambda {\gamma }_i,\mathrm{ }$$

(12)

where $\lambda$ represents the basic information propagation rate and ${\gamma }_i$ represents the cognitive ability of individual i.

For node i and its neighbor j to interact with information, the amount of information at time t for node i is denoted as $I_i\left(t\right)$, and the amount of information at time t for node j is $I_j\left(t\right)$. After the information interaction the amount of information for node i at time t + 1 can be expressed as follows:

$$I_i\left(t+1\right)=I_i\left(t\right)+\lambda {\gamma }_i\left|I_j\left(t\right)-I_i\left(t\right)\right|,$$

(13)

where ${\gamma }_i$ represents the cognitive ability of individual i. This formula describes how node i acquires information from all of its neighbors and updates its information based on its cognitive ability.

When the accumulated information value of node i in the information layer exceeds a certain threshold, at time t, when it encounters a node j with an opinion, there is a certain probability $p_o$ that node i will form an opinion value $O_i\left(t\right)$. The probability and the opinion value are defined by the following formulas:

$$p_o=\alpha e^{-I_i\left(t\right)}[1-\left|O_i\left(t\right)-O_j\left(t\right)\right|],\mathrm{ }$$

(14)

$$O_i\left(t\right)={\displaystyle \frac{I_i\left(t\right)\times {\mu }_i}{{\gamma }_i+\varphi }}+\epsilon ,\mathrm{ }$$

(15)

where $p_o$ represents the probability that an individual forms an opinion after encountering a neighbor who already holds one. $O_i\left(t\right)$ and $O_j\left(t\right)$ represent the opinion values of individual i and individual j at time t, respectively. $\alpha$ represents the base opinion propagation rate. $I_i\left(t\right)$ denotes the information amount possessed by node i at time t. ${\gamma }_i$ represents the cognitive ability of individual i. ${\mu }_i$ represents the compromise degree of individual i, reflecting how much the individual is willing to accept the opinions of neighbors. A larger ${\mu }_i$ indicates that the individual is less likely to change their opinion, while a smaller ${\mu }_i$ indicates that the individual is more likely to accept the opinion of others. $\varphi$ represents the information complexity. $\epsilon$ is a constant bias term, representing the individual’s fundamental position or preference when no other factors are influencing them. Equations (14) and (15) describe the probability and resulting opinion value when node i transitions from having no opinion to forming an explicit opinion.

When two nodes interact in the opinion layer, the opinion value of node i at time t is $O_i\left(t\right)$. The opinion interaction between node i and its neighbor j can be described as follows:

$$O_i\left(t+1\right)=O_i\left(t\right)+p_o\times (1-u_i)\times {\gamma }_i\times \Theta ({\delta }_{opi}-|O_i\left(t\right)-O_j\left(t\right)\left|\right)\times \left[O_i\left(t\right)-O_j\left(t\right)\right],$$

(16)

where Θ is the Heaviside step function, which indicates that opinion interaction between the two nodes will only occur when the difference in their opinion values is smaller than a certain threshold ${\delta }_{opi}$.

Therefore, for a node i in the information layer its state transitions can be described as follows:

(a)

Transition from U to A: A non-informed node U encounters an informed neighbor node j and, with probability p_i, acquires information, transitioning to an informed node A.

(b)

Transition from A to O: An informed node A encounters a neighbor node j with a stance and, with probability p_o, acquires a stance, transitioning to a node with a stance O.

(c)

Transition from A to U: An informed node A may, due to reasons such as forgetting, revert to a non-informed state U with probability υ.

(d)

Transition from O to A: A node with a stance O may, for reasons such as abandoning a stance, revert to an informed state A with probability ω.

(2)

Contact Layer Transmission

The disease transmission in the contact layer is triggered by the contact between an infected individual I and a susceptible individual S. After the infected individual I comes into contact with the susceptible individual S, the disease may spread, and the susceptible individual will transition to an infected state with a certain probability. However, if the information and opinions acquired from the information layer have a suppressive effect on disease transmission then the probability of disease transmission can be expressed by the following formula:

$$p_D=\beta \left(1-{\displaystyle \frac{1}{1+{\epsilon }_1{I}_i\left(t\right)}}\right)e^{[-{\epsilon }_2{O}_i(t\left)\right]},$$

(17)

where $\beta$ represents the base disease transmission rate, and ${\epsilon }_1$ and ${\epsilon }_2$ represent the adjustment parameters.

However, since the state of node i in the information layer is divided into three types, no information (U), has information (A), and has a stance (O), the transmission probabilities in the contact layer are different for each state. For the no-information node i, the transmission probability is as follows:

$${\beta }^U=\beta .$$

(18)

For a node i with information, where its information value is A, the transmission probability is as follows:

$${\beta }^A=\beta \left(1-{\displaystyle \frac{1}{1+{\epsilon }_1{I}_i\left(t\right)}}\right).\mathrm{ }$$

(19)

For a node i with an opinion, where its opinion value is O, the transmission probability is as follows:

$${\beta }^O=\beta \left(1-{\displaystyle \frac{1}{1+{\epsilon }_1{I}_i\left(t\right)}}\right)e^{[-{\epsilon }_2{O}_i(t\left)\right]}.$$

(20)

Therefore, for a node i in the contact layer the state transitions can be described as follows:

(a)

The transition of node i from susceptible (S) to infected (I): A susceptible node S becomes infected upon encountering an infected neighboring node j, with a certain probability of ${\beta }^U$, ${\beta }^A$, and ${\beta }^O$, and may also receive information with probability, leading to the transition from S to I.

(b)

The transition of node i from infected (I) to susceptible (S): An infected node i may recover, due to factors such as recovery or immunity, with a certain probability σ, thereby transitioning back to the susceptible state S.

4. Analysis of Multilayer Propagation Evolution Driven by Information

Based on the analysis above, in the information-driven multilayer propagation model each individual can be in one of five general states: no information and not infected (US), known information and not infected (AI), known information and infected (AS), no information but infected (OS), and known information and infected (OI). According to mean-field theory analysis [16,17], we can classify the individuals in the model based on their degree (degree in the information layer and contact layer). In the information-driven multilayer propagation evolution model, the number of propagating sources of individuals with degrees k and l in the information and contact layers at a certain time t can be expressed as follows: US(k, l, t), AI(k, l, t), AS(k, l, t), OS(k, l, t), and OI(k, l, t). At time t, the densities of these five states in the overall population are, respectively, ${\rho }^{\mathit{US}}(k,l,t)$, ${\rho }^{\mathit{AI}}(k,l,t)$, ${\rho }^{\mathit{AS}}(k,l,t)$, ${\rho }^{\mathit{OS}}(k,l,t)$, and ${\rho }^{\mathit{OI}}(k,l,t)$, and they satisfy certain relationships as shown in the following:

$${\rho }^{\mathit{US}}(k,l,t)+{\rho }^{\mathit{AI}}(k,l,t)+{\rho }^{\mathit{AS}}(k,l,t)+{\rho }^{\mathit{OS}}(k,l,t)+{\rho }^{\mathit{OI}}(k,l,t)=1.$$

(21)

Assume that at time t the number of individuals with known information connected to an individual propagating source is $\mathrm{g}(\mathrm{g}\le \mathrm{k})$, the number of individuals with opinions connected to the individual propagating source is $\mathrm{e}(\mathrm{e}\le \mathrm{k})$, and the number of infected individuals connected to the individual propagating source is $\mathrm{h}(\mathrm{h}\le \mathrm{l})$. The probabilities of the individual propagating source’s neighbors containing g individuals with information, e individuals with opinions, and h infected individuals are, respectively, as follows:

$$N_i^A\left(g,h,t\right)=C_k^g{\theta }_1{\left(k,l,t\right)}^g{\left[1-{\theta }_1\left(k,l,t\right)\right]}^{k-g},\mathrm{ }$$

(22)

$$N_i^O\left(g,h,t\right)=C_k^e{\theta }_2{\left(k,l,t\right)}^e{\left[1-{\theta }_2\left(k,l,t\right)\right]}^{k-e},\mathrm{ }$$

(23)

$$N_i^I\left(g,h,t\right)=C_l^h{\theta }_3{\left(k,l,t\right)}^h{\left[1-{\theta }_3\left(k,l,t\right)\right]}^{l-h},\mathrm{ }$$

(24)

where ${\theta }_1(k,l,t)={\sum }_{k^{\prime }}P\left(k^{\prime }\right|k\left)\right[{\rho }^{AS}(k^{\prime },l,t)+{\rho }^{AI}(k^{\prime },l,t)]$ and ${\theta }_1(k,l,t)$ represents the probability that a randomly selected propagating source with degree ${\theta }_1(k,l,t)$ in the multilayer network propagation model has an edge connected to an individual with information. ${\theta }_2(k,l,t)={\sum }_{k^{\prime }}P\left(k^{\prime }\right|k\left)\right[{\rho }^{\mathrm{OS}}(k^{\prime },l,t)+{\rho }^{\mathrm{OI}}(k^{\prime },l,t)]$ where ${\theta }_2(k,l,t)$ represents the probability that a randomly selected propagating source with degree ${\theta }_2(k,l,t)$ in the multilayer network propagation model has an edge connected to an individual with an opinion. ${\theta }_3(k,l,t)={\sum }_{l^{\prime }}P\left(l^{\prime }\right|l\left)\right[{\rho }^{AI}(k,l^{\prime },t)+{\rho }^{OI}(k,l^{\prime },t)]$ where ${\theta }_3(k,l,t)$ represents the probability that a randomly selected propagating source with degree ${\theta }_3(k,l,t)$ in the multilayer network propagation model has an edge connected to an individual infected with the disease. $P\left(k^{\prime }\right|k)$ and $P\left(l^{\prime }\right|l)$ represent the degree correlation distribution functions for the information layer and the contact layer, respectively, in the multilayer network propagation model.

At time t, when randomly selecting an individual propagating source i with degree $(k,l)$ in the multilayer network propagation model, among the neighbors connected to propagating source i, there are g individuals with information, e individuals with opinions, and h individuals infected with the disease. Therefore, the probability that individual propagating source iii does not acquire information within the time period t is $(1-p_i\Delta t{)}^g$, the probability that it does not acquire an opinion is $\left[\right(1-p_i\Delta t\left)\right(1-p_o\Delta t){]}^e$, the probability that it acquires information but does not participate in disease transmission is $(1-{\beta }^A\Delta t{)}^h$, the probability that it acquires an opinion but does not participate in disease transmission is $(1-{\beta }^O\Delta t{)}^h$, and the probability that it does not acquire information and does not participate in disease transmission is $(1-{\beta }^U\Delta t{)}^h$. Let $r_i$ represent the probability that an individual i with degree $(k,l)$ ultimately remains in the state of no information. Let $m_i$ represent the probability that an individual i with degree $(k,l)$ ultimately remains in the state of having information but no opinion. $q_i^A$ represents the probability that an individual propagating source i with degree $(k,l)$ ultimately remains in the state of having information but not infected with the disease. $q_i^O$ represents the probability that an individual propagating source i with degree $(k,l)$ ultimately remains in the state of having an opinion but not infected with the disease. $q_i^U$ represents the probability that an individual propagating source with degree $(k,l)$ ultimately remains in the state of no information and not infected with the disease.

Therefore, the propagation probability of an individual propagating source in an active state is as follows:

$$q_i^U=\sum _{h=0}^l{C}_l^h(1-{\beta }^U\Delta t{)}^h{\theta }_2(k,l,t{)}^h[1-{\theta }_2(k,l,t){]}^{l-h},\mathrm{ }$$

(25)

$$q_i^A=\sum _{h=0}^l{C}_l^h(1-{\beta }^A\Delta t{)}^h{\theta }_2(k,l,t{)}^h[1-{\theta }_2(k,l,t){]}^{l-h},$$

(26)

$$q_i^O=\sum _{h=0}^l{C}_l^h(1-{\beta }^O\Delta t{)}^h{\theta }_2(k,l,t{)}^h[1-{\theta }_2(k,l,t){]}^{l-h},$$

(27)

$$r_i=\sum _{g=0}^k{C}_k^g(1-p_i\Delta t{)}^g{\theta }_1(k,l,t{)}^g[1-{\theta }_1(k,l,t){]}^{k-g},\mathrm{ }$$

(28)

$$m_i=\sum _{e=0}^k{C}_k^e\left[\right(1-p_i\Delta t\left)\right(1-p_o\Delta t\left){]}^e{\theta }_3\right(k,l,t{)}^e[1-{\theta }_3(k,l,t){]}^{k-e},$$

(29)

Based on the model’s propagation and states, it can be analyzed that the state US has a probability of changing to state AS at each time step with a probability of $1-r_i$, and a probability of changing to state UI with a probability of $1-q_i^U$. On the other hand, state AS has a probability of changing to state US with a probability of $\upsilon$. State AS has a probability of changing to state OS with a probability of $1-m_i$, and a probability of changing to state OI with a probability of $1-q_i^O$. Furthermore, state OS has a probability of changing to state US with a probability of $\omega$. Based on the above analysis, the five overall states with degree $(k,l)$, US, AI, AS, OS, and OI, change over the time period $[t,t+\Delta t]$ as shown in the following Equation (30):

$$\left\{\begin{array}{l}\begin{array}{c}\mathrm{U}\mathrm{S}\left(k,l,t+\Delta t\right)=US\left(k,l,t\right)-\mathrm{U}\mathrm{S}\left(k,l,t\right)\left(1-r_i\right)-\mathrm{U}\mathrm{S}\left(k,l,t\right)r_i\left(1-q_i^U\right)\\ +\upsilon \sigma \Delta tAI\left(k,l,t\right)+\upsilon q_i^U\Delta tAS\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}\mathrm{A}\mathrm{S}\left(k,l,t+\Delta t\right)=\mathrm{A}\mathrm{S}\left(k,l,t\right)-\upsilon \Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)-\left(1-\upsilon \right)\left(1-m_i\right)\Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)\\ -\left(1-\upsilon \right)m_i{q}_i^A\Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)+\mathrm{U}\mathrm{S}\left(k,l,t\right)\left(1-r_i\right)m_i{q}_i^A+\sigma \left(1-\upsilon \right)m_i\Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)\\ +\omega q_i^A\Delta t\mathrm{O}\mathrm{S}\left(k,l,t\right)+\sigma \omega \Delta t\mathrm{O}\mathrm{I}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}\mathrm{A}\mathrm{I}\left(k,l,t+\Delta t\right)=\mathrm{A}\mathrm{I}\left(k,l,t\right)-\upsilon \Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)-\left(1-\upsilon \right)\left(1-m_i\right)\Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)\\ -\sigma \left(1-\upsilon \right)m_i\Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)+\mathrm{U}\mathrm{S}\left(k,l,t\right)r_i\left(1-q_i^U\right)+\mathrm{U}\mathrm{S}\left(k,l,t\right)\left(1-r_i\right)m_i{q}_i^A\\ +\left(1-\upsilon \right)m_i\left(1-q_i^A\right)\Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)+\omega \left(1-q_i^A\right)\Delta t\mathrm{O}\mathrm{S}\left(k,l,t\right)+\omega \left(1-\sigma \right)\Delta t\mathrm{O}\mathrm{I}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}\mathrm{O}\mathrm{S}\left(k,l,t+\Delta t\right)=\mathrm{O}\mathrm{S}\left(k,l,t\right)-\omega \Delta t\mathrm{O}\mathrm{S}\left(k,l,t\right)-\left(1-\omega \right)\left(1-q_i^O\right)\Delta t\mathrm{O}\mathrm{S}\left(k,l,t\right)\\ +\left(1-r_i\right)\left(1-m_i\right)q_i^O\mathrm{U}\mathrm{S}\left(k,l,t\right)+\left(1-\upsilon \right)\left(1-m_i\right)\sigma \Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)\\ +\left(1-\upsilon \right)\left(1-m_i\right)q_i^O\Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)+\sigma \left(1-\omega \right)\Delta t\mathrm{O}\mathrm{I}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}\mathrm{O}\mathrm{I}\left(k,l,t+\Delta t\right)=\mathrm{O}\mathrm{I}\left(k,l,t\right)-\omega \Delta t\mathrm{O}\mathrm{I}\left(k,l,t\right)-\sigma \left(1-\omega \right)\Delta t\mathrm{O}\mathrm{I}\left(k,l,t\right)\\ +\left(1-r_i\right)\left(1-m_i\right)\left(1-q_i^O\right)\mathrm{U}\mathrm{S}\left(k,l,t\right)+\left(1-\upsilon \right)\left(1-m_i\right)\left(1-\sigma \right)\Delta t\mathrm{A}\mathrm{I}\left(k,l,t\right)\\ +\left(1-\upsilon \right)\left(1-m_i\right)\left(1-q_i^O\right)\Delta t\mathrm{A}\mathrm{S}\left(k,l,t\right)+\left(1-\omega \right)\left(1-q_i^O\right)\Delta t\mathrm{O}\mathrm{S}\left(k,l,t\right).\end{array}\end{array}\right.$$

(30)

From Equation (30), a nonlinear dynamic system can be obtained. At a steady-state this system yields ${\rho }^{\mathrm{A}\mathrm{I}}\ll 1$. Using mean-field approximation for analysis and eliminating higher-order terms, we can obtain the result when $\Delta t\to 0$, which is shown as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{\displaystyle \frac{\partial {\rho }^{\mathit{US}}\left(k,l,t\right)}{dt}}=r_i{q}_i^U{\rho }^{\mathit{US}}\left(k,l,t\right)+\upsilon \sigma {\rho }^{\mathit{AI}}\left(k,l,t\right)+\upsilon q_i^U{\rho }^{\mathit{AS}}\left(k,l,t\right)\\ \end{array},\\ \begin{array}{c}{\displaystyle \frac{\partial {\rho }^{\mathit{AS}}\left(k,l,t\right)}{dt}}=(1-\upsilon )m_i{\rho }^{\mathit{AS}}\left(k,l,t\right)+(1-r_i)m_i{q}_i^{A}l{\rho }^{\mathit{US}}\left(k,l,t\right)\\ +\sigma (1-\upsilon )m_i{\rho }^{\mathit{AI}}\left(k,l,t\right)+\omega q_i^A{\rho }^{\mathit{OS}}\left(k,l,t\right)+\sigma \omega {\rho }^{\mathit{OI}}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}{\displaystyle \frac{\partial {\rho }^{\mathit{AI}}\left(k,l,t\right)}{dt}}=(1-\upsilon )(1-\sigma )m_i{\rho }^{\mathit{AI}}\left(k,l,t\right)+r_i(1-q_i^U){\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-r_i)m_i{q}_i^A{\rho }^{\mathit{US}}\left(k,l,t\right)+(1-\upsilon )(1-q_i^A)m_i{\rho }^{\mathit{AS}}\left(k,l,t\right)\\ +\omega (1-q_i^A){\rho }^{\mathit{OS}}\left(k,l,t\right)+\omega (1-\sigma ){\rho }^{\mathit{OI}}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}{\displaystyle \frac{\partial {\rho }^{\mathit{OS}}\left(k,l,t\right)}{dt}}=(1-\omega )q_i^O{\rho }^{\mathit{OS}}\left(k,l,t\right)+(1-r_i)(1-m_i)q_i^O{\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-\upsilon )(1-m_i)\sigma {\rho }^{\mathit{AI}}\left(k,l,t\right)+(1-\upsilon )(1-m_i)q_i^O{\rho }^{\mathit{AS}}\left(k,l,t\right),\\ \end{array}\\ \begin{array}{c}{\displaystyle \frac{\partial {\rho }^{\mathit{OI}}\left(k,l,t\right)}{dt}}=(1-\upsilon )(1-\omega ){\rho }^{\mathit{OI}}\left(k,l,t\right)+(1-r_i)(1-m_i)(1-q_i^O){\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-\upsilon )(1-m_i)(1-\sigma ){\rho }^{\mathit{AI}}\left(k,l,t\right)+(1-\upsilon )(1-m_i)(1-q_i^O){\rho }^{\mathit{AS}}\left(k,l,t\right)\\ +(1-\omega )(1-q_i^O){\rho }^{\mathit{AS}}\left(k,l,t\right).\end{array}\end{array}\right.$$

(31)

In real life, whether in the information layer or the contact layer, the connection relationships between individual propagators exhibit heterogeneity, meaning that most individual propagators have few connections, while only a small number have a large number of connections. This heterogeneity has an important impact on the multilayer network propagation model. After considering the correlation between the degrees of individual propagators in the multilayer network propagation model, it can be assumed that the degree distributions of both the information layer and the contact layer follow a power-law distribution. This means that the average degree $〈k〉=\sum _{k}kP\left(k\right)$ in the network can be represented in the power-law form $P\left(k\right)=k^{-\gamma }$. At the same time, it can be assumed that the degree between any two nodes in the network is uncorrelated, which means that the degree–degree correlation function can be represented by the following Equations (32) and (33) [32,33,34]:

$$P\left(k^{\prime }|k\right)={\displaystyle \frac{k^{\prime }P\left(k^{\prime }\right)}{〈k〉}},\mathrm{ }$$

(32)

$$P\left(l^{\prime }|l\right)={\displaystyle \frac{l^{\prime }P\left(l^{\prime }\right)}{〈l〉}}.\mathrm{ }$$

(33)

When the system is in a steady state, when $∆t\to \infty$, Equation (34), which is as follows, holds:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathsf{\partial }{\rho }^{\mathit{US}}\left(k,l,t\right)}{dt}}=0,\\ {\displaystyle \frac{\mathsf{\partial }{\rho }^{\mathit{AS}}\left(k,l,t\right)}{dt}}=0,\\ {\displaystyle \frac{\mathsf{\partial }{\rho }^{\mathit{AI}}\left(k,l,t\right)}{dt}}=0,\\ {\displaystyle \frac{\mathsf{\partial }{\rho }^{\mathit{OS}}\left(k,l,t\right)}{dt}}=0,\\ {\displaystyle \frac{\mathsf{\partial }{\rho }^{\mathit{OI}}\left(k,l,t\right)}{dt}}=0,\end{array}\right.$$

(34)

From Equations (31) and (34), Equation (31) can be rewritten as Equation (35), which is as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{r}_i{q}_i^U{\rho }^{\mathit{US}}\left(k,l,t\right)+\upsilon \sigma {\rho }^{\mathit{AI}}\left(k,l,t\right)+\upsilon q_i^U{\rho }^{\mathit{AS}}\left(k,l,t\right)=0\\ \end{array},\\ \begin{array}{c}(1-\upsilon )m_i{\rho }^{\mathit{AS}}\left(k,l,t\right)+(1-r_i)m_i{q}_i^{A}l{\rho }^{\mathit{US}}\left(k,l,t\right)\\ +\sigma (1-\upsilon )m_i{\rho }^{\mathit{AI}}\left(k,l,t\right)+\omega q_i^A{\rho }^{\mathit{OS}}\left(k,l,t\right)+\sigma \omega {\rho }^{\mathit{OI}}\left(k,l,t\right)=0\\ \end{array},\\ \begin{array}{c}(1-\upsilon )(1-\sigma )m_i{\rho }^{\mathit{AI}}\left(k,l,t\right)+r_i(1-q_i^U){\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-r_i)m_i{q}_i^A{\rho }^{\mathit{US}}\left(k,l,t\right)+(1-\upsilon )(1-q_i^A)m_i{\rho }^{\mathit{AS}}\left(k,l,t\right)\\ +\omega (1-q_i^A){\rho }^{\mathit{OS}}\left(k,l,t\right)+\omega (1-\sigma ){\rho }^{\mathit{OI}}\left(k,l,t\right)=0,\\ \end{array}\\ \begin{array}{c}(1-\omega )q_i^O{\rho }^{\mathit{OS}}\left(k,l,t\right)+(1-r_i)(1-m_i)q_i^O{\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-\upsilon )(1-m_i)\sigma {\rho }^{\mathit{AI}}\left(k,l,t\right)+(1-\upsilon )(1-m_i)q_i^O{\rho }^{\mathit{AS}}\left(k,l,t\right)=0\\ \end{array},\\ \begin{array}{c}(1-\upsilon )(1-\omega ){\rho }^{\mathit{OI}}\left(k,l,t\right)+(1-r_i)(1-m_i)(1-q_i^O){\rho }^{\mathit{US}}\left(k,l,t\right)\\ +(1-\upsilon )(1-m_i)(1-\sigma ){\rho }^{\mathit{AI}}\left(k,l,t\right)+(1-\upsilon )(1-m_i)(1-q_i^O){\rho }^{\mathit{AS}}\left(k,l,t\right)\\ +(1-\omega )(1-q_i^O){\rho }^{\mathit{AS}}\left(k,l,t\right)=0,\end{array}\end{array}\right.$$

(35)

Therefore, by using the elimination method, the steady-state solution ${\rho }^{\mathit{AI}}\left(k,l,t\right)+{\rho }^{\mathit{OI}}\left(k,l,t\right)=f(r_i,m_i,q_i^U,q_i^A,q_i^O,\upsilon ,\omega ,\sigma )$ obtained is a function of the parameter $r_i,m_i,q_i^U,q_i^A,q_i^O,\upsilon ,\omega ,\sigma$. Combining Equations (12)–(28), it can be seen that $r_i,m_i,q_i^U,q_i^A,q_i^O,\upsilon ,\omega ,\sigma$ is ultimately related to the parameter $\lambda ,\beta ,\alpha ,I_i,O_i,{\gamma }_i,{\mu }_i,\varphi$, and the final result is related to the parameter $\lambda ,\beta ,\alpha ,I_i,O_i,{\gamma }_i,{\mu }_i,\varphi$. A comprehensive analysis shows that in the information-driven multilayer propagation evolution model the number of infections involved in network propagation is related to the individual’s cognitive ability, degree of compromise, and information complexity.

5. Simulation Results and Numerical Analysis

5.1. Simulation Parameter Design

This section aims to explore how different individuals influence information propagation and opinion interaction in a complex social network, and how they, in turn, affect the evolution mechanism of online public opinion. To validate the previous discussion, we conducted a series of systematic simulation experiments using Python 3.12 and constructed an information-driven multilayer propagation evolution model based on the theories of scale-free networks and small-world networks [34]. In this model, the upper layer represents information while the lower layer represents opinions. It is important to note that the nodes in these two layers actually represent the same individuals, and there are interlayer connections between the corresponding nodes. In this co-evolutionary propagation model each dimension contains 5000 nodes. In each iteration of the model, the information layer adds a node with six edges, while the contact layer adds a node with three edges. The output results of each iteration are based on the average of 50 iterations.

5.2. Simulation Results Analysis

(1)

Impact Analysis of Information Complexity

In the current era of mobile big data dominated by social media, we observe the significant phenomenon that virtually every real-world event is rapidly reflected and amplified on virtual networks. This characteristic of instant propagation is largely due to the widespread adoption and application of mobile internet and Internet of Things technologies. In fact, online public opinion not only quickly forms around a specific event but also generates a massive and complex amount of information within a short period. The generation of such complex information is driven by the following two factors: the acceleration of information dissemination speed and the interaction and collision of opinions among individuals within the network.

Based on this, we will next explore the impact of information complexity on disease propagation. Information complexity refers to the complexity and diversity of information that individuals process and exchange, directly affecting the efficiency of information dissemination and the interaction methods between individuals. Changes in information complexity may alter propagation paths, thereby impacting the speed and scope of infection diffusion. Therefore, understanding how information complexity functions during the propagation process is crucial for revealing the underlying mechanisms of dissemination and designing effective intervention strategies.

In the following section we will further analyze the specific impact of information complexity on the propagation process using experimental results. Some of the parameter settings are as follows: information volume is set within the range [0,1], opinion value is set within the range [0,1], information and opinion thresholds are set within the range [0,1], the information dissemination rate is denoted as $\lambda =0.6$, opinion interaction rate is denoted as $\alpha =0.3$, disease transmission rate is denoted as $\beta =0.3$, recovery rate is denoted as $\sigma =0.1$, information recovery rate is denoted as $\nu =0.1$, individual cognitive ability is denoted as $\gamma =0.5$, and individual compromise level is denoted as $\mu =0.5$. The results obtained from the experiments are shown in Figure 1, which illustrates the impact of information complexity on evolution.

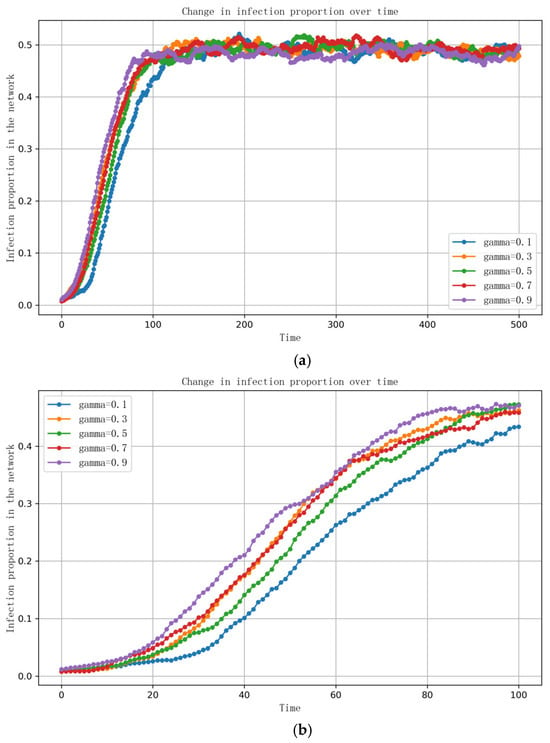
Figure 1a,b illustrate the impact of information complexity on the number of infections within the network. As shown in Figure 1a, the number of infections gradually stabilizes after time step 100, and the distinctions among different levels of information complexity become increasingly blurred in the later stages. This trend may be attributed to the saturation of infection spread across the network, where most nodes have already reached a stable state and the influence of complexity begins to converge.

In contrast, Figure 1b focuses on the early stage of the diffusion process (time range 0–100), where the impact of information complexity is more pronounced. The results indicate that higher information complexity leads to a faster increase in the number of infections, suggesting that complex information may accelerate the early spread of infection across the network.

Overall, when the information complexity reaches 0.9 the infection grows at the fastest rate, indicating a strong propagation effect. Conversely, at a complexity level of 0.1 the infection spreads most slowly, showing a more moderate growth. In the intermediate range of 0.3 to 0.7 the infection growth rate falls between the two extremes. These findings suggest that information complexity has a nonlinear effect on the diffusion process, potentially influencing the trajectory of infection by affecting individual comprehension difficulty, the degree of opinion divergence, and the speed of consensus formation during the early stages of spread.

(2)

Impact of Individual Compromise Level Analysis

Due to the vast and complex information in the network, the transmission process becomes more intricate. The role of individual sources in the formation of public opinion is particularly important, especially their level of compromise toward opinions. This factor not only influences the speed of information transmission but also determines the direction and depth of public opinion. For example, when opinion leaders or well-known individuals post viewpoints on social media their acceptance and compromise toward certain opinions or positions can significantly affect the views of a large number of followers, thus accelerating or altering the direction of public opinion. Therefore, this section focuses on analyzing the impact of individual compromise on the evolution of public opinion in a multilayer network.

Some of the parameter settings are as follows: information volume is set within the range [0,1], opinion value is set within the range [0,1], information and opinion thresholds are set within the range [0,1], the information dissemination rate is denoted as $\lambda =0.6$, opinion interaction rate is denoted as $\alpha =0.3$, disease transmission rate is denoted as $\beta =0.3$, recovery rate is denoted as $\sigma =0.1$, information recovery rate is denoted as $\nu =0.1$, individual cognitive ability is denoted as $\gamma =0.5$, and the information complexity level is denoted as $\phi =0.5$. The experimental results are shown in Figure 2, which illustrates the influence of individual compromise levels in the information layer on the evolutionary process.

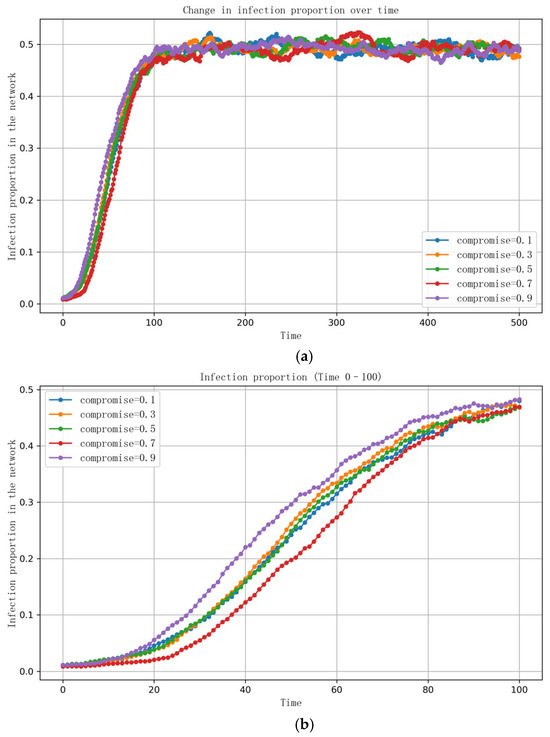
Figure 2a,b illustrate the influence of individual compromise levels on the evolution of infections within the network. In Figure 2a, as the simulation progresses to 500 time steps the number of infections steadily increases and eventually stabilizes. The differences between various compromise levels become less distinct over time. This is likely because the network reaches a saturation point where most individuals have already transitioned to an infected or stable state, and the diffusion process enters a balanced phase. Consequently, the marginal effect of compromise diminishes in the later stages. Figure 2b, which focuses on the early stage of the simulation (0–100 steps), shows more pronounced differences in infection dynamics across different compromise levels.

The results suggest that the influence of compromise is most evident during the initial phase of the spread. Overall, when the compromise level is high (e.g., 0.9), infections spread more rapidly and reach a higher final number. This indicates that high compromise may, paradoxically, accelerate transmission. One possible reason is that individuals with high compromise are more susceptible to diverse and conflicting information, which hinders the formation of consistent opinions and weakens the resistance to infection propagation. In contrast, individuals with low compromise are more likely to form localized consensus due to smaller opinion differences, enabling more coherent information interpretation and thus mitigating further spread. Therefore, the effect of compromise on diffusion is nonlinear as moderate or low levels can help to promote consensus and suppress infection, while excessively high compromise may weaken opinion stability and increase vulnerability to widespread contagion.

(3)

Analysis of the Impact of Individual Cognitive Ability

In previous sections, we have discussed in detail how individual compromise and information complexity affect the transmission of network public opinion crises. Similarly, individual cognitive ability is also a critical factor influencing information understanding and dissemination. Cognitive ability can be understood as an individual’s capacity to process, interpret, and apply information. This includes processes such as information filtering, decoding, internalization, and reflection. An individual with high cognitive ability may find it easier to recognize and understand complex information, think critically, and form their own opinions and stances based on this understanding. In contrast, individuals with lower cognitive abilities are more likely to be misled or biased, or to hold simplified or one-sided views of information. Therefore, we will analyze the specific impact of individual cognitive ability on transmission next and explore its role in information dissemination and the spread of infection.

Some of the parameter settings are as follows: information volume is set within the range [0,1], opinion value is set within the range [0,1], information and opinion thresholds are set within the range [0,1], the information dissemination rate is denoted as $\lambda =0.6$, opinion interaction rate is denoted as $\alpha =0.3$, disease transmission rate is denoted as $\beta =0.3$, recovery rate is denoted as $\sigma =0.1$, information recovery rate is denoted as $\nu =0.1$, individual compromise level is denoted as $\mu =0.5$, and the information complexity level is denoted as $\phi =0.5$. The results from the experiment are shown in Figure 3, which illustrates the impact of individual cognitive ability on the evolution process.

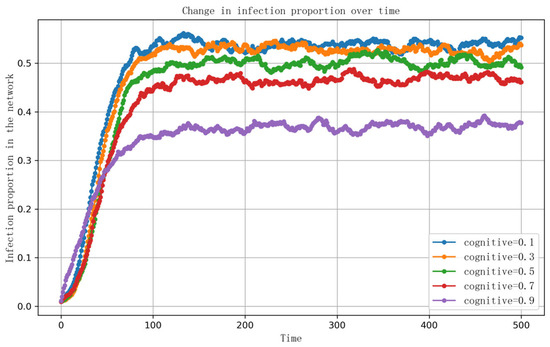
Figure 3 clearly illustrates the impact of individual cognitive ability on transmission. Over time, as the transmission progresses the number of infections in the network gradually stabilizes. The differences in cognitive ability among individuals start to become apparent, especially in the variation in transmission across individuals with different cognitive abilities. Individuals with lower cognitive abilities often lack the capacity to effectively judge and filter information, making them more susceptible to influence, which leads to the spread of infections. Specifically, there is a negative correlation between individual cognitive ability and the number of infections in the transmission process. Individuals with lower cognitive ability are more easily misled and influenced due to their weaker capacity to process and understand information about disease transmission, resulting in a higher number of infections. On the other hand, individuals with stronger cognitive abilities are better able to analyze, process, and respond to information, thus reducing their own infection risk and playing a role in suppressing the overall transmission in the network. This result demonstrates that individual cognitive ability plays a crucial role in both information dissemination and the spread of infections.

6. Conclusions

This study constructs an information-driven multilayer propagation model (IDMPM) to investigate the joint effects of information complexity and individual heterogeneity on information dissemination and epidemic spread within social media environments. The model incorporates heterogeneous factors such as information complexity, individual compromise levels, and cognitive abilities, which makes it more aligned with the real-world characteristics of diverse information flows and substantial individual differences compared to prior studies that simplify information into binary states or assume homogeneous behavioral responses [12,14,18].

The main contributions of this paper are reflected in the following three aspects:

First, the paper develops a multilayer coupled framework of “information–opinion–behavior–epidemic”. Specifically, the Deffuant-I model is introduced at the information layer to simulate how individuals interact with their neighbors after receiving multidimensional information, thereby dynamically evolving their cognitive judgments and attitudinal preferences. This enables the analysis of how opinion evolution indirectly influences epidemic dynamics, addressing a key gap in previous “information–epidemic” models that failed to consider opinion formation as an intermediary mechanism [15,19,21].

Second, the model introduces mechanisms for both information complexity and individual heterogeneity. At the information level, multidimensional variables are used to represent the complexity of the information itself; at the individual level, parameters such as compromise degree and cognitive ability are employed to dynamically adjust thresholds for opinion change and behavioral response. Compared to existing models [12,13,14,17,20] the proposed framework has stronger explanatory power for simulating significant differences in intervention effects and highly diversified individual responses observed in reality.

Third, the study conducts large-scale dynamic simulations to analyze the interactive effects of information complexity and individual heterogeneity. Results show that when information complexity is high and individual compromise levels are low, opinion evolution tends to become polarized, which weakens the consistency of preventive behavior and enlarges the scale of epidemic spread. This finding provides important insights for designing more effective information intervention strategies.

Nonetheless, the model has certain limitations. It currently does not account for adaptive behavioral feedback mechanisms that may arise under public health interventions or shifting social sentiment. In addition, the parameterization of cognitive ability and compromise thresholds is based on abstract settings rather than empirical data from social media, limiting its immediate applicability in real-world policy design. Future research can expand on this work by incorporating the dynamic evolution of real-world social networks, emotional and multi-source heterogeneous information, and optimizing behavioral rule settings based on empirical evidence. These enhancements would improve the model’s explanatory power and practical relevance for information governance and public health communication during sudden crises.