Online Multi-Layer FDR Control

Abstract

When hypotheses are tested in a stream and real-time decision-making is needed, online sequential hypothesis testing procedures are needed. Furthermore, these hypotheses are commonly partitioned into groups by their nature. For example, RNA nanocapsules can be partitioned based on the therapeutic nucleic acids (siRNAs) being used, as well as the delivery nanocapsules. When selecting effective RNA nanocapsules, simultaneous false discovery rate control at multiple partition levels is needed. In this paper, we develop hypothesis testing procedures which control the false discovery rate (FDR) simultaneously for multiple partitions of hypotheses in an online fashion. We provide rigorous proofs for their FDR or modified FDR (mFDR) control properties and use extensive simulations to demonstrate their performances.

1. Introduction

In early-stage drug development research, lead compounds are often selected in an online fashion for the next-stage experiment (i.e., from discovery to an in vitro study or from in vitro to in vivo studies) [1]. Because the data enters in a stream or in batches, and real-time decision-making is desirable, online sequential hypothesis testing procedures need to be adopted. Furthermore, hypotheses in drug discovery are commonly partitioned into groups by their nature, and multiple partitioning methods are simultaneously of interest. For example, in developing innovative RNA nanocapsules to treat cancer metastasis, therapeutic nucleic acids (siRNAs) as well as delivery nanocapsules are designed [2,3]. At each step of the screening, a decision needs to be made whether to follow up on a particular combination of an siRNA and nanocapsule. In this case, these combinations are naturally partitioned according to their siRNA and nanocapsule formulations. Ideally, to select the candidate lead compounds, we are interested in controlling the false positives in terms of both the siRNA and nanocapsule formulations. We are interested in other potential partitions, for example, based on experiments in different cancer types [4].

Beyond drug development, the need for multi-layer false discovery rate (FDR) control also arises in many modern applications. In real-time A/B testing on online platforms, experiments are often run concurrently across user segments, device types, or product categories, and the results arrive continuously [5,6]. Similar challenges also exist in genomics, where hypotheses (e.g., gene expressions or mutations) may be partitioned by biological pathways or genomic regions and tested sequentially in large-scale screening studies [7]. These situations require statistical methods that can make decisions in an online fashion while still simultaneously controlling the FDR across multiple layers of structures. Motivated by these examples, we aimed to develop a hypothesis testing procedure that controls the FDR simultaneously for multiple partitions of hypotheses in an online fashion.

Mathematically, at time $t\in \mathbb{N}$, we observe a stream of null hypotheses, $H_{i\left(t\right)j\left(t\right)}$, where $i\left(t\right)\in \mathbb{N}$ denotes the index for the siRNA being tested at time t, and $j\left(t\right)\in \mathbb{N}$ denotes the index for the nanocapsule being tested at time t. $H_{i\left(t\right)j\left(t\right)}$ indicates a hypothesis with respect to the siRNA $i\left(t\right)$ and nanocapsule $j\left(t\right)$.

We define two partition-level null hypotheses, $H_{i\left(t\right)}^1$ and $H_{j\left(t\right)}^2$, such that

$$H_{i\left(t\right)}^1\mathrm{is}\mathrm{true}\iff H_{i\left(t\right)j}\mathrm{is}\mathrm{true}\mathrm{for}j\in {\cup }_{u=1}^t\left\{j\left(u\right)\right\},$$

$$H_{j\left(t\right)}^2\mathrm{is}\mathrm{true}\iff H_{ij\left(t\right)}\mathrm{is}\mathrm{true}\mathrm{for}i\in {\cup }_{u=1}^t\left\{i\left(u\right)\right\},$$

where $H_{i\left(t\right)}^1$ is the partition-level hypothesis with respect to the siRNAs, and $H_{i\left(t\right)}^2$ is the partition-level hypothesis with respect to the nanocapsules. $H_{i\left(t\right)j}$ is the hypothesis where the siRNA index $i\left(t\right)$ is fixed at time t and varies over the nanocapsule indices j, and $H_{ij\left(t\right)}$ is a hypothesis where the nanocapsule index $j\left(t\right)$ is fixed at time t and varies over the siRNA indices i. At time t, we make a decision on whether to reject $H_{i\left(t\right)j\left(t\right)}$ based on its corresponding test statistic and p-value, as well as the history information on the previous hypotheses (statistics, p-values, and decisions); i.e., we let ${\delta }_t=1$ if we reject $H_{i\left(t\right)j\left(t\right)}$, and ${\delta }_t=0$ if we accept $H_{i\left(t\right)j\left(t\right)}$. Our goal is to control the group-level FDR with both partitions according to the siRNA and according to the nanocapsules, which we denote as ${\mathrm{FDR}}^1\left(t\right)$ and ${\mathrm{FDR}}^2\left(t\right)$. Let

$${\widehat{S}}^1\left(t\right)=\{i\left(u\right):{\delta }_u=1\},{\widehat{S}}^2\left(t\right)=\{j\left(u\right):{\delta }_u=1\},$$

$${\mathrm{FDR}}^1\left(t\right)=\mathbb{E}\left[{\displaystyle \frac{|{\widehat{S}}^1\left(t\right)\cap H_{i\left(t\right)}^1|}{|{\widehat{S}}^1\left(t\right)|\vee 1}}\right],{\mathrm{FDR}}^2\left(t\right)=\mathbb{E}\left[{\displaystyle \frac{|{\widehat{S}}^2\left(t\right)\cap H_{j\left(t\right)}^2|}{|{\widehat{S}}^2\left(t\right)|\vee 1}}\right],$$

where ${\widehat{S}}^1\left(t\right)$ and ${\widehat{S}}^2\left(t\right)$ denote the sets of rejected hypotheses at time t grouped by the siRNA and nanocapsule partitions, respectively; $H_{i\left(t\right)}^1$ and $H_{j\left(t\right)}^2$ denote the corresponding sets of true null hypotheses for the siRNA and nanocapsule partitions, respectively. ∨ is the maximum operator: $|{\widehat{S}}^1\left(t\right)|\vee 1=max(|{\widehat{S}}^1\left(t\right)|,1)$.

To control the FDR for individual online hypotheses, Foster and Stine (2008) [8] introduced the $\alpha$-investing framework, a foundational method for online FDR control. This approach treats significance thresholds as a budget, namely $\alpha$-wealth, which is spent to test hypotheses and “spent” upon discoveries (i.e., rejected null hypotheses). This method controls the modified FDR (mFDR) and is sensitive to test ordering. The modified false discovery rate (mFDR) is an alternative measure defined by the ratio between the expected number of false discoveries and the expected number of discoveries. To address these limitations, Javanmard and Montanari (2018) [9] proposed two alternative procedures, LOND (Levels based On Number of Discoveries) and LORD (Levels based On Recent Discoveries), to provide finite-sample FDR control under dependency structures. In LOND, the significance level at each step is scaled according to the number of previous rejections. The LORD procedure, on the other hand, updates the significance thresholds after each discovery, allowing for greater adaptability. Both methods depends on independent p-values. More recently, these methods have been further extended for improved power and relaxed dependence assumptions for the p-values [10,11,12].

For FDR control in grouped or structured hypotheses, such as genes grouped by biological pathways or drug compounds tested across cancer types, Ramdas and Barber (2019) [13] developed the p-filter, a method for multi-partitioned data settings where hypothesis testing occurs across distributed or federated environments. The p-filter maintains a dynamic filtration level that propagates across data partitions, enabling asynchronous hypothesis testing while preserving FDR guarantees. Ramdas et al. (2019) [14] developed the DAGGER method, which controls the FDR in hypothesis testing structured using directed acyclic graphs, where nodes represent hypotheses with parent–child dependencies. DAGGER processes hypotheses top-down, ensuring that a node is rejected only if its parents are rejected, and guarantees FDR control under the independence or positive or arbitrary dependence of p-values.

In many practical applications related to drug discovery, as we described in the Introduction, there is a need to control the FDR at multiple partition levels simultaneously in an online fashion; there is no existing method for this kind of setting. We aimed to address this gap by developing an FDR control method to control the group-level FDR defined based on multiple structures or partitions (multiple layers) in an online fashion. In our setting, not only do the hypotheses enter sequentially, but the group membership of the hypothesis entering each layer is also not predefined. We developed a novel framework that integrates online FDR control with multi-layer structured testing capabilities to provide theoretically guaranteed FDR control in multi-layer online testing environments. The main contributions of this paper are summarized below:

• We present multi-layer $\alpha$-investing, LOND, and LORD algorithms for controlling the FDR in online multiple-layer problems.
• We provide theoretical guarantees for the multi-layer $\alpha$-investing, LOND, and LORD methods.
• We demonstrate the numerical FDR control’s performance and the power of our methods over an extensive range of simulation settings.

The rest of this paper is structured as follow. In Section 2, we provide a mathematical formulation of the online multi-layer hypothesis testing problem. In Section 3, we illustrate the multi-layer $\alpha$-investing, LOND, and LORD algorithms. In Section 4, we show our main theoretical results, that the multi-layer $\alpha$-investing method simultaneously controls the mFDR in different layers and the multi-layer LOND and LORD simultaneously control the FDR and mFDR in different layers. In Section 5, we demonstrate the performance of our methods with the results from extensive simulation studies.

2. Model Framework

Now we formulate the problem for more general scenarios. From now on, we use the following notations. Suppose we have a series of (unlimited) null hypotheses, $H_i^0$s, $i\in \mathbb{N}$, and M partitions of the space $\mathbb{N}$, denoted as $A_1^m,\cdots ,A_{G_m}^m\subseteq \mathbb{N}$ for $m=1,\cdots ,M$. We call these M different partitions “layers” of hypotheses. We can define the group-level null hypotheses in layer m at time t as

$$H_{A_g^m}^0\left(t\right)={\cap }_{j\in A_g^m\cap \left[t\right]}{H}_j^0,\mathrm{where}g=1,\cdots ,G_m,$$

where [t] = $\{1,2,\dots ,t\}$. We also define a group index for the ith hypothesis in the mth layer as $g_i^m$, i.e., $i\in A_{g_i^m}^m$.

In the online setting, $H_i^0$s come in sequentially, and the corresponding test statistics $z_i$s and associated p-values $p_i$s are also observed sequentially. For each $H_i^0$ we need to make the decision ${\delta }_i$ whether to reject it based on $z_i$, $p_i$, and the available history information; i.e., ${\delta }_i=1$ if we reject $H_i^0$, and ${\delta }_i=0$ if we accept $H_i^0$. At time t (t is discretized), we have three different types of history information:

• All information, ${\mathcal{F}}_t^a=\{z_i,p_i,{\delta }_i,i=1,\cdots ,t\}$.
• All decisions, ${\mathcal{F}}_t^d=\{{\delta }_i,i=1,\cdots ,t\}$.
• A summary of decisions, for example, $D_t={\sum }_{i=1}^t{\delta }_i$.

Now, we define decisions at the group level using decisions at the individual level. At the individual level, we define the rejection set at time t as $\widehat{S}\left(t\right)=\{i:{\delta }_i=1\}\cap \left[t\right]$. Since the decision whether to reject a group will change over time, we use ${\delta }_g^m\left(t\right)$ to denote the decision for group g ($g\in \{1,\cdots ,G_m\}$) in layer m at time t, where

$${\delta }_g^m\left(t\right)=1\mathrm{if}\widehat{S}\left(t\right)\cap A_g^m\ne \varnothing \mathrm{and}{\delta }_g^m\left(t\right)=0\mathrm{otherwise}.$$

So for the mth partition, the group-level selected sets at time t are

$${\widehat{S}}^m\left(t\right)=\{g\in \{1,\cdots ,G_m\}:{\delta }_g^m\left(t\right)=1\}.$$

Similarly, we denote the truth about $H_i$ at the individual level by ${\theta }_i$; ${\theta }_i=0$ when $H_i^0$ should be accepted, while ${\theta }_i=1$ when $H_i^0$ should be rejected. We can obtain the true set $S\left(t\right)=\{i:{\theta }_i=1\}\cap \left[t\right]$ and

$${\theta }_g^m\left(t\right)=1\mathrm{if}S\left(t\right)\cap A_g^m\ne \varnothing \mathrm{and}{\theta }_g^m\left(t\right)=0\mathrm{otherwise}.$$

For the mth partition, the group-level true null set at time t is $S^m\left(t\right)=\{g\in \{1,\cdots ,G_m\}:{\theta }_g^m\left(t\right)=1\}$.

Now we can define the time-dependent false discovery rate (FDR) and modified false discovery rate (mFDR) for each layer separately. For the mth layer, we have

$${\mathrm{FDR}}^m\left(t\right)=\mathbb{E}\left[{\displaystyle \frac{V^m\left(t\right)}{R^m\left(t\right)\vee 1}}\right]\mathrm{and}{\mathrm{mFDR}}_{\eta }^m\left(t\right)={\displaystyle \frac{\mathbb{E}{V}^m\left(t\right)}{\mathbb{E}{R}^m\left(t\right)+\eta }},$$

where $V^m\left(t\right)=|{\widehat{S}}^m\left(t\right)\cap {\left(S^m\left(t\right)\right)}^c|$ and $R^m=|{\widehat{S}}^m\left(t\right)|$.

3. Algorithms

3.1. Multi-Layer $\alpha$-Investing

In this section, we illustrate the generalized $\alpha$-investing algorithm for the multi-layer setting.

A multi-layer $\alpha$-investing procedure is an adaptive sequential hypothesis testing procedure. Suppose that the overall target FDR is $\alpha$ for every layer. For each time point, t ($t=1,\cdots ,N$ where we allow $N\to \infty$), and partition layer, m ($m=1,\cdots ,M$), we define the significance level ${\alpha }_t^m$, the spending function ${\varphi }_t^m$, and the rewarding function ${\psi }_t^m$ that satisfy the assumptions in Theorem 1 and Lemma 1 in Section 4 (a simple choice is an alpha-investing [8] procedure with ${\alpha }_t^m=\alpha$, ${\varphi }_t^m={\displaystyle \frac{\alpha }{1-\alpha }}$, and ${\psi }_t^m={\varphi }_t^m+\alpha$). Each hypothesis, $H_i^0$, will be rejected if its p-values, $p_i^m$s, pass the corresponding thresholds ${\alpha }_i^m$s for all those ms for which a decision is still pending (that is, $\forall m$s s.t. ${\delta }_{g_i^m}^m(i-1)=0$). The wealth function $W^m\left(t\right)$ is initialized at $\alpha \eta$ and then updated under the following rule: at time $t=i$, if the hypothesis $H_i^0$ is rejected, then we gain a reward, ${\psi }_i^m$, for all the layers tested in this round. In the meantime, no matter whether $H_i^0$ is rejected, we spend ${\varphi }_i^m$ for those layers that are tested in this round. In other words, we can write $W^m\left(i\right)$ as

$$W^m\left(i\right)=\left\{\begin{array}{cc}{W}^m(i-1)+{\psi }_i^m-{\varphi }_i^m,\hfill & {\delta }_{g_i^m}^m(i-1)=0,{\delta }_{g_i^m}^m\left(i\right)=1\hfill \\ W^m(i-1)-{\varphi }_i^m,\hfill & {\delta }_{g_i^m}^m(i-1)=0,{\delta }_{g_i^m}^m\left(i\right)=0\hfill \end{array}\right.$$

This procedure simultaneously controls the mFDR in all the layers. We state the multi-layer $\alpha$-investing algorithm in Algorithm 1.

Algorithm 1 Multi-layer $\alpha$-investing.

1: Initialize ${\delta }_g^m=0$ and $W^m\left(0\right)=\alpha \eta$, for $m=1,\cdots ,M$ and all $g\in \{1,\cdots ,G_m\}$.   2: while${min}_m{W}^m\left(i\right)>0$ and $i\le N$ do   3:    ${\delta }_i=1$   4:    for $m=1,\cdots ,M$ do   5:      if ${\delta }_{g_i^m}^m=0$ then   6:         if $p_i^m\ge {\alpha }_i^m$ then   7:           ${\delta }_i=0$, break   8:         end if   9:      end if 10:    end for 11:    if ${\delta }_i=1$ then 12:      for $m=1,\cdots ,M$ do 13:         if ${\delta }_{g_i^m}^m=0$ then 14:           ${\delta }_{g_i^m}^m=1$ and $W^m\left(i\right)=W^m(i-1)+{\psi }_i^m-{\varphi }_i^m$ 15:         end if 16:      end for 17:    else 18:      for $m=1,\cdots ,M$ do 19:         if ${\delta }_{g_i^m}^m=0$ then 20:           $W^m\left(i\right)=W^m(i-1)-{\varphi }_i^m$ 21:         end if 22:      end for 23:    end if 24:    $i=i+1$ 25: end while

Remark: The statistics $p_i^m$s are also allowed to just be individual $p_i$s for all the layers or a combined score which is a function of all the $p_j$s s.t. $j\le i$ and $g_j^m=g_i^m$.

3.2. Multi-Layer LOND and LORD

In this section, we generalize the LOND and LORD algorithms to a multi-layer setting.

To extend the LOND algorithm to a multi-layer setting, we set the significance level for the hypothesis at time i in layer m to be ${\beta }_i^m(R^m(i-1)+1)$, where

$$\left\{{\beta }_i^m:\sum _{i=1}^{\infty }{\beta }_i^m=\alpha \right\}\mathrm{for}m=1,\cdots ,M$$

are M predefined infinite sequences that sum to 1, and $R^m(i-1)=|{\widehat{S}}^m(i-1)|$. Each hypothesis, $H_i^0$, will be rejected if its p-value, $p_i^m$, passes the threshold ${\beta }_i^m(R^m(i-1)+1)$ for all those ms for which a decision is still pending ($\forall m$s s.t. ${\delta }_{g_i^m}^m(i-1)=0$). We state the multi-layer LOND algorithm in Algorithm 2, and we will show that the multi-layer LOND algorithm can simultaneously control the multi-layer FDR and mFDR at level $\alpha$ in the next section.

Remark: Since in layer m, we did not need to test a hypothesis at every time point, $t=1,\cdots ,i$, in fact, we only performed ${\kappa }_i^m$ tests, where ${\kappa }_i^m=i-{\sum }_{j=1}^i{\delta }_{g_j^m}^m\left(i\right)+{\sum }_{j=1}^{G_m}{\delta }_j^m\left(i\right)$; we can improve the method by setting the significance level for the hypothesis at time i in layer m to be ${\beta }_{{\kappa }_i^m}^m(R^m+1)$. By doing this, the power is increased and the multi-layer FDRs are still controlled. We will show this improvement through a simulation in Section 4 but omit the theoretical proof of it.

To extend the LORD algorithm to the multi-layer setting, we set M predefined sequences, $\{{\beta }_j^m:{\sum }_{j=1}^{\infty }{\beta }_j^m=\alpha \}$. For the hypothesis at time i in layer m, we use the significance level ${\alpha }_i^m={\beta }_{{\zeta }_i^m}^m$, where ${\zeta }_i^m={\kappa }_i^m-{\kappa }_{{\tau }_i^m}^m+1$, ${\tau }_i^m=max\{j<i:{\delta }_{g_j^m}^m(j-1)=0,{\delta }_{g_j^m}^m\left(j\right)=1\}$, and ${\kappa }_i^m=i-{\sum }_{j=1}^i{\delta }_{g_j^m}^m\left(i\right)+{\sum }_{j=1}^{G_m}{\delta }_j^m\left(i\right)$. Define ${\zeta }_i^m={\kappa }_i^m-{\kappa }_{{\tau }_i^m}^m+1$. We can show that the modified LORD algorithm simultaneously controls the multi-layer FDR and mFDR at level $\alpha$. We state the multi-layer LORD algorithm in Algorithm 3.

Algorithm 2 Multi-layer LOND.

1: Select sequences ${\sum }_{j=1}^{\infty }{\beta }_j^m=\alpha$ and initial $R^m=0$, and ${\delta }_g^m=0$, for $m=1,\cdots ,M$ and all $g\in \{1,\cdots ,G_m\}$.   2: while  $i\le N$  do   3:    ${\delta }_i=1$   4:    for $m=1,\cdots ,M$ do   5:      if ${\delta }_{g_i^m}^m=0$ then   6:         if $p_i^m\ge {\beta }_i^m(R^m+1)$ then   7:           ${\delta }_i=0$, break   8:         end if   9:      end if 10:    end for 11:    if ${\delta }_i=1$ then 12:      for $m=1,\cdots ,M$ do 13:         if ${\delta }_{g_i^m}^m=0$ then 14:           $R^m=R^m+1$, ${\delta }_{g_i^m}^m=1$ 15:         end if 16:      end for 17:    end if 18:    $i=i+1$ 19: end while

Algorithm 3 Multi-layer LORD.

1: Select sequences ${\sum }_{g=1}^{\infty }{\beta }_g^m=\alpha$ and initial ${\zeta }^m=1$   2: while  $i\le N$  do   3:    ${\delta }_i=1$   4:    for $m=1,\cdots ,M$ do   5:      if ${\delta }_{g_i^m}^m=0$ then   6:         if $p_i^m\ge {\beta }_{{\zeta }^m}^m$ then   7:           ${\delta }_i=0$, break   8:         end if   9:      end if 10:    end for 11:    if ${\delta }_i=1$ then 12:      for $m=1,\cdots ,M$ do 13:         if ${\delta }_{g_i^m}^m=0$ then 14:           ${\zeta }^m=1$ and ${\delta }_{g_i^m}^m=1$ 15:         end if 16:      end for 17:    else 18:      for $m=1,\cdots ,M$ do 19:         if ${\delta }_{g_i^m}^m=0$ then 20:           ${\zeta }^m={\zeta }^m+1$ 21:         end if 22:      end for 23:    end if 24:    $i=i+1$ 25: end while

4. Theoretical Results

We will show that multi-layer $\alpha$-investing method simultaneously controls the mFDR in different layers and the multi-layer LOND and LORD simultaneously control both the FDR and mFDR in different layers. First we introduce one preliminary assumption; this assumption is weaker than the independence assumption across the tests.

Assumption 1.

$\forall m\in \{1,\cdots ,M\}$, and for all the layers that need to be tested at time j,

$$\begin{array}{cc}\hfill \forall {\theta }_j=0& :P_{\theta }({\delta }_{g_j^m}^m\left(j\right)=1|{\mathcal{F}}_{j-1})\le {\alpha }_j^m,\hfill \\ \hfill \forall {\theta }_j=1& :P_{\theta }({\delta }_{g_j^m}^m\left(j\right)=1|{\mathcal{F}}_{j-1})\le {\rho }_j^m.\hfill \end{array}$$

Remark: This assumption is a simple extension of Assumption 2.2 in the paper of Aharoni and Rosset (2014) [15] regarding the generalized $\alpha$-investing method. It requires that the level and power traits of a test hold even given the history of rejections. This is somewhat weaker than requiring independence. In particular, ${\rho }_j^m\le 1,\forall m\in \{1,\cdots ,M\}$ is the maximal probability of rejection for any parameter value in the alternative hypothesis, which quantifies the “best power”.

Next we state the theoretical $mFDR$ control guarantee for the multi-layer generalized $\alpha$-investing procedure.

Theorem 1.

Under Assumption 1, if $0\le {\psi }_j^m\le min({\displaystyle \frac{{\varphi }_j^m}{{\rho }_j^m}}+\alpha ,{\displaystyle \frac{{\varphi }_j^m}{{\alpha }_j^m}}+\alpha +1)$, then a multi-layer generalized α-investing procedure simultaneously controls the $mFD{R}_{\eta }^m$ for all the layers, $m=1,\cdots ,M$.

The proof of Theorem 1 is postponed to Appendix A. One key step is to establish a submartingale, as stated in the following lemma.

Lemma 1.

Under Assumption 1 and the multi-layer α-investing procedure, the stochastic processes $A^m\left(j\right)=\alpha R^m\left(j\right)-V^m\left(j\right)+\alpha \eta -W^m\left(j\right)$, $m=1,\cdots ,M$ are submartingales with respect to ${\mathcal{F}}_j$.

Next, we state the $FDR$ and $mFDR$ control guarantees for the multi-layer LOND and LORD methods.

Theorem 2.

Suppose that conditional on $R^m(i-1)=|{\widehat{S}}^m(i-1)|$, $m=1,\cdots ,M$, we have

$$\forall {\theta }_i\in \Theta ,\forall m=1,\cdots ,M,$$

$${\mathbb{P}}_{{\theta }_i=0}\left({\delta }_{g_i^m}^m\left(i\right)=1|R^m(i-1),{\delta }_{g_i^m}^m(i-1)=0\right)\le \mathbb{E}\left({\alpha }_i^m|R^m(i-1),{\delta }_{g_i^m}^m(i-1)=0\right),$$

where ${\alpha }_i^m={\beta }_i^m(R^m(i-1)+1)$ and ${\delta }_i^m$ are given by the LOND algorithm. Then this rule simultaneously controls the multi-layer FDRs and mFDRs at levels less than or equal to α; i.e.,

$$\forall n\ge 1,\forall m=1,\dots ,M,{\mathrm{FDR}}^m\left(n\right)\le \alpha \mathrm{and}{\mathrm{mFDR}}^m\left(n\right)\le \alpha .$$

Theorem 3.

Suppose that conditional on the history of decisions in layer m, ${\mathcal{F}}_t^m=\sigma \left\{{\delta }_{g_i^m}^m\left(i\right),\right.$$\left.i=1,\dots ,t\right\}$, we have $\forall \theta \in \Theta ,\forall m=1,\dots ,M$ that need to be tested at time i:

$${\mathbb{P}}_{{\theta }_i=0}\left({\delta }_{g_i^m}^m\left(i\right)=1\mid {\mathcal{F}}_t^m\right)\le \mathbb{E}\left({\alpha }_i^m\mid {\mathcal{F}}_t^m\right).$$

Then, the LORD rule simultaneously controls the multi-layer mFDR to ensure it is less than or equal to α; i.e., ${\mathrm{mFDR}}_1^m\left(n\right)\le \alpha \mathrm{for}\mathrm{all}n\ge 1.$ Further, it simultaneously controls the multi-layer FDR at every discovery. More specifically, letting $d_k^m$ be the time of the kth discovery in layer m, we have the following for all $k\ge 1$:

$$\underset{\theta \in \Theta }{sup}{\mathbb{E}}_{\theta }\left({\mathrm{FDP}}^m\left(d_k^m\right)·\mathbb{I}(d_k^m<\infty )\right)\le \alpha ,\forall m=1,\dots ,M.$$

All the proofs of Lemma 1 and Theorems 1–3 are in Web Appendix A.

5. Numerical Studies

We conducted extensive simulations to evaluate the performance of our proposed multi-layer methods in various scenarios. We simulated data from a two-layer model with different settings to evaluate the proposed methods. For each setting, we compared the FDR and mFDR control and power at both the group and individual levels. For all simulations, we set the target FDR level at $\alpha =0.1$ and ran 100 repeats.

5.1. Simulation of Group Structures

We considered three types of group structures: the first two were balanced, while the third was unbalanced. For the balanced structure, we denoted G as the number of groups and the number of hypotheses per group as n. Therefore, the total number of features was $N=nG$. The three types of group structures are described below:

• Balanced Block Structure: The features came in group by group; i.e., all the features from the first groups came in, then all the features from the second group followed, and so on.
• Balanced Interleaved Structure: The first feature was from group 1, the second feature was from group 2,⋯, the nth feature was from group n, the $(n+1)$th feature was from group 1, and so on.
• Unbalanced Structure: The features were randomly assigned to be in either the current group or a new group by some random mechanism. To be more specific, we fixed the total number of features as N and denoted the membership of the tth feature as $G\left(t\right)$, letting

  $$\mathbf{P}(G\left(t\right)=g|G(t-1)=g)=1-p_1,\mathbf{P}(G\left(t\right)=g^{\prime }|G(t-1)=g)={\displaystyle \frac{p_1}{G-1}},$$

  where $g^{\prime }\ne g\in \{1,\cdots ,G\}$.

5.2. Simulation of True Signals

We considered three signal structures:

• Fixed Pattern: The first $s\%$ of groups were true groups. Within the true groups, the first $k\%$ of features were the true features.
• Random Pattern: The true groups and true signals were randomly sampled. We first randomly sampled $s\%$ of the total groups to be true groups. Then within each true group, we randomly sampled $k\%$ of the features as the true features.
• Markov Pattern: The signals were from a hidden Markov model. We considered a Markov model with two hidden states: a stationary state and an eruption state. In the stationary state, ${\theta }_i\sim Binomial(N,0.5)$; in the erruption state, $\mathbf{P}({\theta }_i=0|{\theta }_{i-1}=0)=\mathbf{P}({\theta }_i=1|{\theta }_{i-1}=1)=0.9$. At each step, the probability that the signal remained in the same state as the previous step was 0.9, and it had a probability of 0.1 of changing to the other state.

5.3. Simulation of Signal Strength

We considered three types of signal strength settings:

• Constant Strength: The signal strengths were equal; the p-values for the true signals were from a two-sided test with z-statistics from $\mathcal{N}(1.5\beta ,1)$.
• Increasing Strength: The signal strengths were increasing; the p-values were from a two-sided test with z-statistics from $\mathcal{N}({\beta }_t,1)$, where ${\beta }_t=\beta (1+t/t_{TOL})$. Here t is the number of true signals until that moment, and $t_{TOL}$ is the total number of true signals in the simulation.
• Decreasing Strength: The signal strengths were decreasing; the p-values were from a two-sided test with z-statistics from $N({\beta }_t,1)$, where ${\beta }_t=\beta (2-t/t_{TOL})$, with t and $t_{TOL}$ defined the same as in (2).

All the simulation designs satisfied Assumption 1 by construction. Specifically, under the null hypothesis (${\theta }_i=0$), p-values were generated independently from the Uniform $(0,1)$ distribution. This guaranteed that the probability of rejection at each step was less than or equal to the target significance level ${\alpha }_i^m$ (i.e., $\mathbb{P}(p_j\le {\alpha }_j^m)={\alpha }_j^m$), satisfying the first condition of Assumption 1. Under the alternative hypothesis (${\theta }_i=1$), p-values were generated from two-sided tests using normally distributed test statistics with non-zero means. These distributions were stochastically smaller than the null distribution, which led to a higher probability of rejection. However, this probability was still finite and bounded above by one, ensuring that the second condition of Assumption 1 was satisfied with a constant ${\rho }_i^m\le 1$. Moreover, our simulation generated data sequentially and independently, making the conditional probability bounds in Assumption 1 valid under the filtration ${\mathcal{F}}_{i-1}$. Therefore, both conditions of Assumption 1 were met in all the simulation settings, ensuring that the theoretical guarantees in Theorems 1–3 were applicable.

We compared seven methods for each setting: the original $\alpha$-investing (GAI), original LORD (LORD), original LOND (LOND), multi-layer $\alpha$-investing (ml-GAI), multi-layer LORD (ml-LORD), multi-layer LOND (ml-LOND), and modified multi-layer LOND (ml-LOND_m) methods.

5.4. Simulation Results

Our baseline configuration used the following parameters: 20% true groups ($s=20$), 50% true signals within true groups ($k=100$), 20 groups in total ($G=20$), 10 features per group ($n=10$), a Balanced Block Structure, Fixed Pattern, and a Constant Strength. We varied the signal strength parameter $\beta$ to examine how the methods performed across different effect sizes.

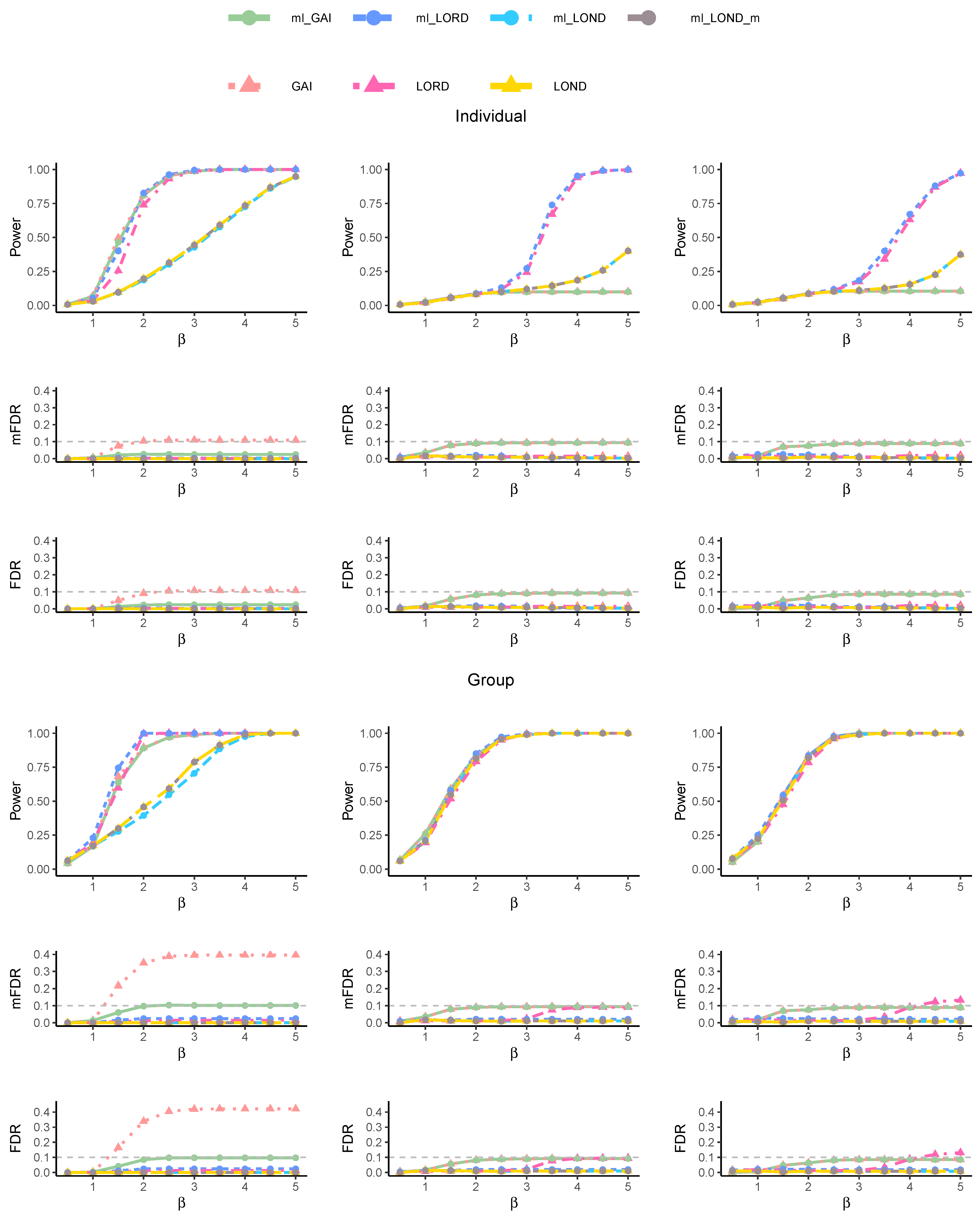
Figure 1 shows the power, FDR, and mFDR for both the individual and group layers under different group structures. For the Balanced Block Structure, all the methods successfully maintained FDR and mFDR control at both the individual and group levels except GAI. For GAI, both the group-level FDR and mFDR exceeded 0.4 when $\beta$ exceeded 2.0. The ml-LORD and LORD methods exhibited the highest power at both levels. As $\beta$ increased beyond 4.5, the power of all the methods approached 1.0. For the Balanced Interleaved Structure, we observed that the LORD methods (both LORD and ml-LORD) significantly outperformed all other methods in terms of power at both the individual and group levels. Importantly, all the multi-layer methods maintained FDR and mFDR control at both levels. The Unbalanced Structure demonstrated results largely consistent with those of the Balanced Interleaved Structure. However, a slight exceedance of the 0.1 threshold was observed for the LORD procedure when $\beta$ reached 0.5.

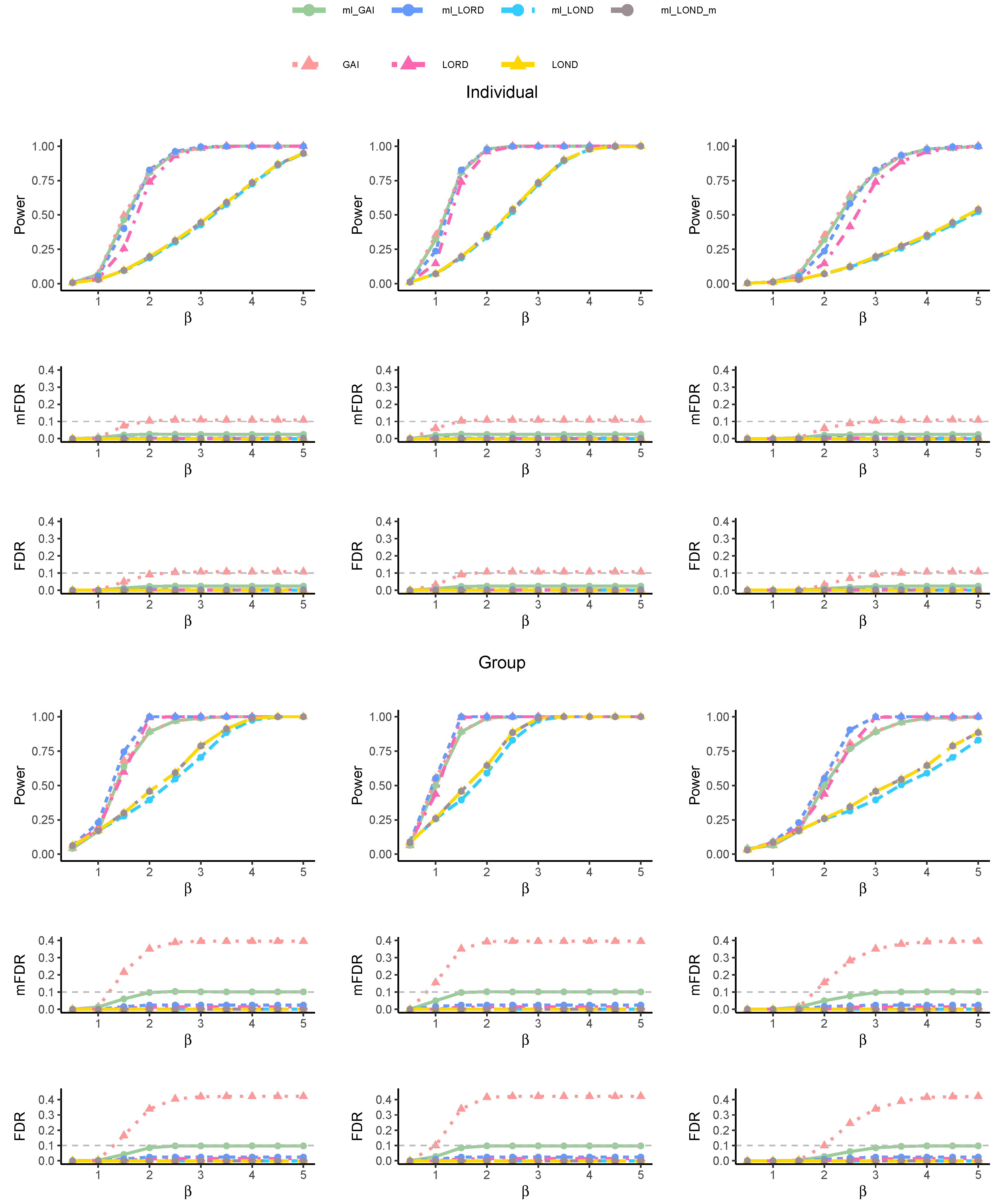
Figure 2 illustrates the performance metrics across different true signal patterns. All the methods controlled both the individual and group FDR and mFDR in the Fixed Pattern and Markov Pattern. However, LORD failed to control both the group-level mFDR and FDR for a Random Pattern when $\beta$ exceeded 3. In terms of power, both LORD and ml-LORD obviously had better performance than the other methods in these three patterns.

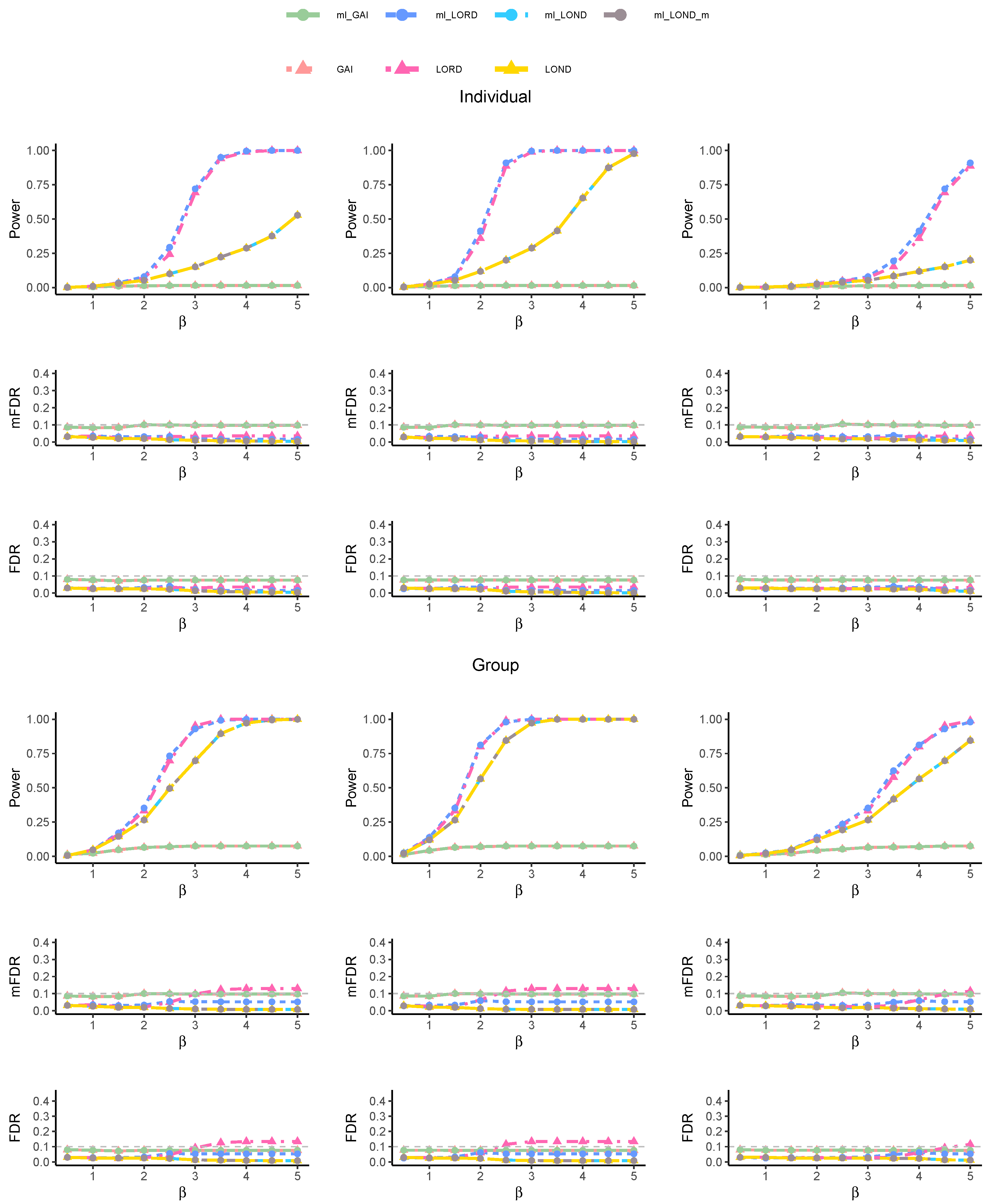
Figure 3 shows the impact of different signal strength patterns on the power and FDR control. The GAI method failed to control both the group-level mFDR and FDR across the three patterns. In contrast, all the multi-layer methods successfully controlled both the mFDR and FDR. Regarding power, all the versions of the LOND procedure (LOND, ml-LOND, and ml-LOND_m) exhibited lower power compared to the $\alpha$-investing (GAI, ml-GAI) and LORD (LORD, ml-LORD) methods. Among the three patterns, the ml-LORD method demonstrated the best overall performance, as it consistently achieved the highest power while maintaining FDR control. Furthermore, Figure 4 shows the results with a reduced number of true signals ($k=50$). Most methods continued to control both the FDR and mFDR. However, a slight exceedance of the 0.1 threshold was observed for the LORD method when the effect size $\beta$ exceeded 3.0.

Our extensive simulation studies highlighted the advantages of using multi-layer FDR control methods over the original ones. Under a Balanced Block Structure, the GAI procedure failed to maintain group-level FDR control. In more complex scenarios, such as the Random Pattern setting, the LORD method also failed to adequately control the group-level FDR. In contrast, all the multi-layer methods consistently maintained valid control of both the FDR and mFDR across all the settings. In terms of power, the modified multi-layer LORD method slightly outperformed the original LORD approach while maintaining comparable FDR control.

All the simulation results are consistent with theoretical results showing that the multi-layer $\alpha$-investing method simultaneously controls the mFDR in multiple layers (Theorem 1) and the multi-layer LOND and LORD procedures achieve the simultaneous control of both the FDR and mFDR across layers (Theorems 2 and 3). These findings demonstrate that multi-layer methods not only ensure more reliable FDR/mFDR control, particularly at the group level, but also deliver better statistical power compared to the original methods.

6. Discussion

In summary, we propose three methods that simultaneously control the mFDR or FDR for multiple layers of groups (partitions) of hypotheses in an online manner. The mFDR or FDR controls were theoretically guaranteed and demonstrated with simulations. These methods fill an important gap in drug discovery when we need to control the FDR in drug screening for multiple layers of features (i.e., siRNAs, nanocapsules, target cell lines, etc.). For example, when screening siRNA–nanocapsule combinations, our methods allow researchers to make statements about both the efficacy of specific combinations and the general performance of specific siRNAs or nanocapsules across all the combinations tested, which can accelerate the identification of promising candidates and reduce false leads. In addition, the proposed algorithms for the methods are also computationally efficient. The computational overhead of our multi-layer methods is minimal compared to that of the original methods. This makes our methods highly scalable, even for large-scale screening applications involving thousands of hypotheses across multiple layers.

A challenge we face is that the power of these methods reduces as the number of layers increases. We can potentially increase the power by adding more assumptions and estimating the pattern of the true signals and the correlation between the p-values more accurately. The modified multi-layer LOND method (${\mathrm{ml}-\mathrm{LOND}}_m$) shows an effective example. It had better power performance than the multi-layer LOND method in the simulation; developing such methods with theoretical guarantees will be the subject of our future work.

Another limitation lies in the assumption of independence or weak dependence among p-values across different layers. In real-world settings, particularly in high-throughput biological studies or multi-modal drug screenings, their characteristics are often correlated. Our multi-layer online frameworks do not assume independence across multiple characteristics because the key assumptions are based on the conditional distribution conditioned on the history information. The construction of statistics for such scenarios is a practical challenge. Some extensions of the conditional permutation test [16] can be explored as a future direction.