Fast Implementation of Generalized Koebe’s Iterative Method
Abstract
1. Introduction
2. The Circular Ring with Circular Holes Map
3. Conformal Mappings from Unbounded Simply Connected Domains onto the Unit Disk
4. Conformal Mappings from Unbounded Doubly Connected Domains onto a Circular Ring
5. Generalized Koebe’s Iterative Method
5.1. Initializations
5.2. Iterations
5.2.1. Step I
5.2.2. Step II
5.3. The Interior Points
5.4. The Inverse Circular Map
5.5. Computational Complexity
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crowdy, D.G. Solving Problems in Multiply Connected Domains; SIAM: Philadelphia, PA, USA, 2020. [Google Scholar]
- Schiffer, M. Recent advances in the theory of conformal mapping, appendix to: R. Courant. In Dirichlet’s Principle, Conformal Mapping, and Minimal Surfaces; Interscience Publishers: New York, NY, USA, 1950. [Google Scholar]
- Henrici, P. Applied and Computational Complex Analysis; John Wiley: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Koebe, P. Abhandlungen zur Theorie der konformen Abbildung, IV. Abbildung mehrfach zusammenhängender schlichter Bereiche auf Schlitzbe-reiche. Acta Math. 1918, 41, 305–344. [Google Scholar] [CrossRef]
- Wen, G.C. Conformal Mapping and Boundary Value Problems; American Mathematical Society: Providence, RI, USA, 1992. [Google Scholar]
- Crowdy, D. Conformal slit maps in applied mathematics. ANZIAM J. 2012, 53, 171–189. [Google Scholar]
- Nasser, M.M.S. Numerical conformal mapping via a boundary integral equation with the generalized Neumann kernel. SIAM J. Sci. Comput. 2009, 31, 1695–1715. [Google Scholar] [CrossRef]
- Nasser, M.M.S. Numerical conformal mapping of multiply connected regions onto the second, third and fourth categories of Koebe’s canonical slit domains. J. Math. Anal. Appl. 2009, 382, 47–56. [Google Scholar] [CrossRef]
- Nasser, M.M.S. Numerical conformal mapping of multiply connected regions onto the fifth category of Koebe’s canonical slit regions. J. Math. Anal. Appl. 2013, 398, 729–743. [Google Scholar] [CrossRef]
- Nasser, M.M.S.; Al-Shihri, F.A.A. A Fast Boundary Integral Equation Method for Conformal Mapping of Multiply Connected Regions. SIAM J. Sci. Comput. 2013, 35, A1736–A1760. [Google Scholar] [CrossRef]
- Koebe, P. Über die Uniformisierung der algebraischen Kurven. II. Math. Ann. 1910, 69, 1–81. [Google Scholar] [CrossRef]
- Marshall, D. Conformal welding for finitely connected regions. Comput. Methods Funct. Theory 2011, 11, 655–669. [Google Scholar] [CrossRef]
- Benchama, N.; DeLillo, T.; Hrycak, T.; Wang, L. A simplified Fornberg-like method for the conformal mapping of multiply connected regions–Comparisons and crowding. J. Comput. Appl. Math. 2007, 209, 1–21. [Google Scholar] [CrossRef]
- DeLillo, T.K.; Elcrat, A.R.; Pfaltzgraff, J.A. Schwarz–Christoffel mapping of multiply connected domains. J. Anal. Math. 2004, 94, 17–47. [Google Scholar] [CrossRef]
- Kropf, E.; Yin, X.; Yau, S.; Gu, X. Conformal parameterization for multiply connected domains: Combining finite elements and complex analysis. Eng. Comput. 2014, 30, 441–455. [Google Scholar] [CrossRef]
- Gu, X.; Zeng, W.; Luo, F.; Yau, S. Numerical computation of surface conformal mappings. Comput. Methods Funct. Theory 2011, 11, 747–787. [Google Scholar] [CrossRef]
- Luo, W.; Dai, J.; Gu, X.; Yau, S. Numerical conformal mapping of multiply connected domains to regions with circular boundaries. J. Comput. Appl. Math. 2010, 233, 2940–2947. [Google Scholar] [CrossRef]
- Nasser, M.M.S. Fast computation of the circular map. Comput. Methods Funct. Theory 2015, 15, 187–223. [Google Scholar] [CrossRef]
- Nasser, M.M.S. PlgCirMap: A MATLAB toolbox for computing conformal mappings from polygonal multiply connected domains onto circular domains. SoftwareX 2020, 11, 100464. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y.; Zeng, W.; Gu, X. Canonical conformal mapping for high genus surfaces with boundaries. Comput. Graph. 2012, 36, 417–426. [Google Scholar] [CrossRef]
- Wegmann, R. Fast conformal mapping of multiply connected regions. J. Comput. Appl. Math. 2001, 130, 119–138. [Google Scholar] [CrossRef]
- Zeng, W.; Yin, X.; Zhang, M.; Luo, F.; Gu, X. Generalized Koebe’s method for conformal mapping multiply connected domains. In Proceedings of the SIAM/ACM Joint Conference on Geometric and Physical Modeling, San Francisco, CA, USA, 5–8 October 2009; pp. 89–100. [Google Scholar]
- Wegmann, R. Methods for numerical conformal mapping. In Handbook of Complex Analysis: Geometric Function Theory; Kühnau, R., Ed.; Elsevier B. V.: Amsterdam, The Netherlands, 2005; Volume 2, pp. 351–477. [Google Scholar]
- Wegmann, R.; Nasser, M.M.S. The Riemann-Hilbert problem and the generalized Neumann kernel on multiply connected regions. J. Comput. Appl. Math. 2008, 214, 36–57. [Google Scholar] [CrossRef]
- Nasser, M.M.S. Fast solution of boundary integral equations with the generalized Neumann kernel. Electron. Trans. Numer. Anal. 2015, 44, 189–229. [Google Scholar]
- Nasser, M.M.S.; Murid, A.H.M.; Ismail, M.; Alejaily, E.M.A. Boundary integral equations with the generalized Neumann kernel for Laplace’s equation in multiply connected regions. Appl. Math. Comput. 2011, 217, 4710–4727. [Google Scholar] [CrossRef]
- Atkinson, K.E. The Numerical Solution of Integral Equations of the Second Kind; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Greengard, L.; Gimbutas, Z. FMMLIB2D: A MATLAB Toolbox for Fast Multipole Method in Two Dimensions, Version 1.2. 2019. Available online: https://github.com/zgimbutas/fmmlib2d (accessed on 1 February 2024).
- Sangawi, A.W.K.; Murid, A.H.M.; Lee, K.W. Conformal mappings of bounded multiply connected regions onto circular and parallel slits regions and their inverses using a GUI. ScienceAsia 2017, 43S, 79–89. [Google Scholar] [CrossRef]


| Method | Steps | Time (sec) | Roundness Error e(C) |
|---|---|---|---|
| Zeng et al. [22] | 5 | 486 | 0.143825 |
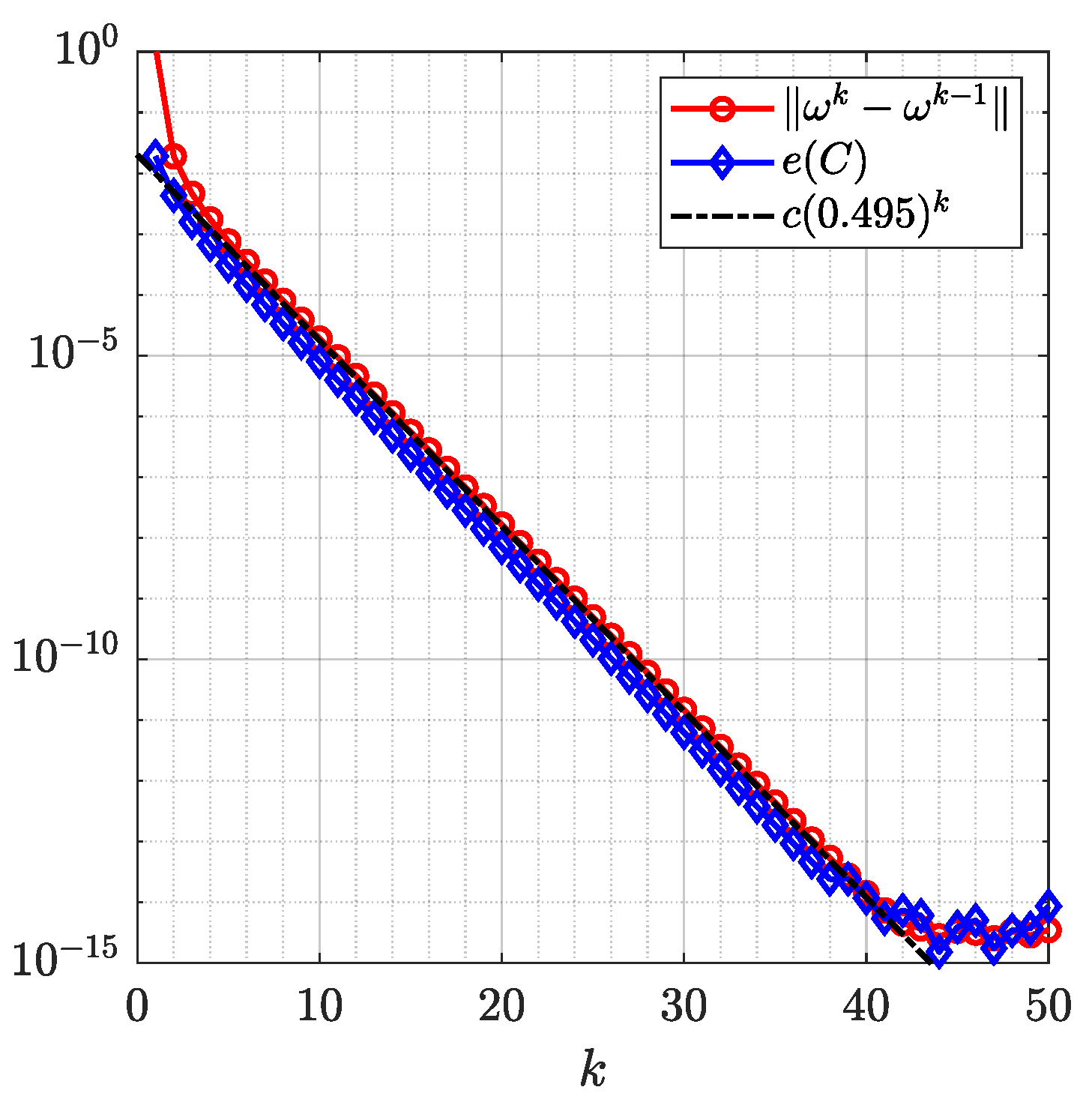
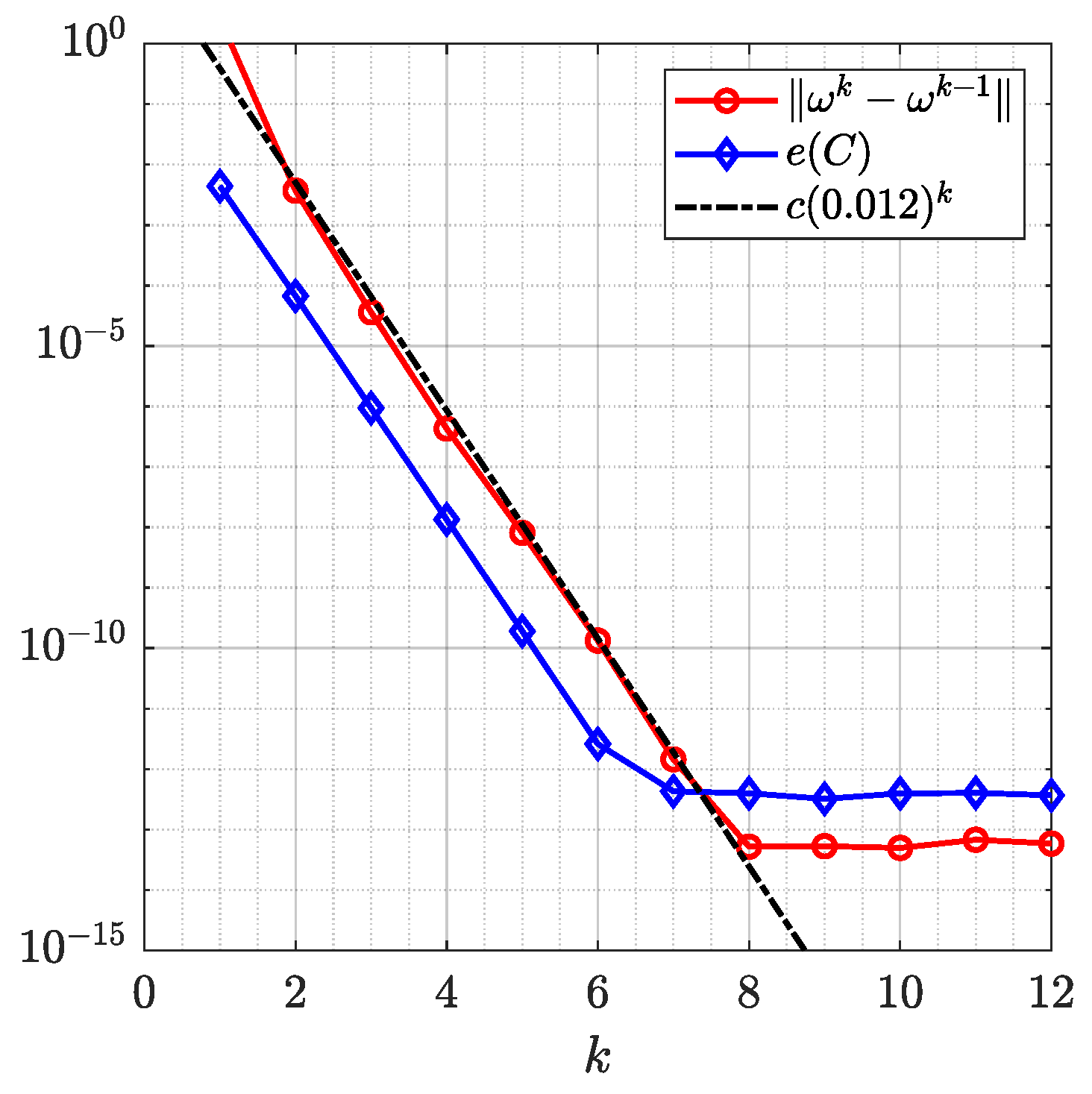
| Our method | 2 | 1.62 | 0.009606 |
| Example | m | n | Iterations | Time (s) |
|---|---|---|---|---|
| 1 | 2 | 1024 | 12 | 6.20 |
| 2 | 3 | 1024 | 10 | 7.45 |
| 3 | 2 | 1024 | 50 | 25.84 |
| 4 | 99 | 1024 | 12 | 1259.67 |
| 5 | 3 | 4096 | 15 | 13.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.W.; Murid, A.H.M.; Nasser, M.M.S.; Yeak, S.H. Fast Implementation of Generalized Koebe’s Iterative Method. Mathematics 2025, 13, 1920. https://doi.org/10.3390/math13121920
Lee KW, Murid AHM, Nasser MMS, Yeak SH. Fast Implementation of Generalized Koebe’s Iterative Method. Mathematics. 2025; 13(12):1920. https://doi.org/10.3390/math13121920
Chicago/Turabian StyleLee, Khiy Wei, Ali H. M. Murid, Mohamed M. S. Nasser, and Su Hoe Yeak. 2025. "Fast Implementation of Generalized Koebe’s Iterative Method" Mathematics 13, no. 12: 1920. https://doi.org/10.3390/math13121920
APA StyleLee, K. W., Murid, A. H. M., Nasser, M. M. S., & Yeak, S. H. (2025). Fast Implementation of Generalized Koebe’s Iterative Method. Mathematics, 13(12), 1920. https://doi.org/10.3390/math13121920





