CAG-MoE: Multimodal Emotion Recognition with Cross-Attention Gated Mixture of Experts

Abstract

Multimodal emotion recognition faces substantial challenges due to the inherent heterogeneity of data sources, each with its own temporal resolution, noise characteristics, and potential for incompleteness. For example, physiological signals, audio features, and textual data capture complementary yet distinct aspects of emotion, requiring specialized processing to extract meaningful cues. These challenges include aligning disparate modalities, handling varying levels of noise and missing data, and effectively fusing features without diluting critical contextual information. In this work, we propose a novel Mixture of Experts (MoE) framework that addresses these challenges by integrating specialized transformer-based sub-expert networks, a dynamic gating mechanism with sparse Top-k activation, and a cross-modal attention module. Each modality is processed by multiple dedicated sub-experts designed to capture intricate temporal and contextual patterns, while the dynamic gating network selectively weights the contributions of the most relevant experts. Our cross-modal attention module further enhances the integration by facilitating precise exchange of information among modalities, thereby reinforcing robustness in the presence of noisy or incomplete data. Additionally, an auxiliary diversity loss encourages expert specialization, ensuring the fused representation remains highly discriminative. Extensive theoretical analysis and rigorous experiments on benchmark datasets—the Korean Emotion Multimodal Database (KEMDy20) and the ASCERTAIN dataset—demonstrate that our approach significantly outperforms state-of-the-art methods in emotion recognition, setting new performance baselines in affective computing.

1. Introduction

The detection and computational analysis of human emotions represents a critical paradigm in understanding interpersonal dynamics and social cognition across both intimate and professional contexts [1]. The fundamental importance of this research has driven systematic investigations into emotion recognition systems and the rise of a specialized field dedicated to the algorithmic identification and classification of emotional states through multimodal behavioral markers, including textual expressions, facial configurations, and vocal characteristics. The domain has experienced significant research momentum and industrial investment in recent years, yielding substantial methodological breakthroughs and theoretical advancements [2,3,4,5,6,7]. Emotion recognition can be applied across various fields, such as medical diagnostics [8,9,10], sentiment analysis [11], misinformation detection [12,13], and human–computer dialogue systems [14,15,16], and opens the possibility of fostering more adaptive, intelligent, and empathetic interactions [17]. As Human–Computer Interaction (HCI) technologies advance [18], emotion recognition capabilities are anticipated to become an essential component of next-generation intelligent systems, enhancing their ability to process and respond to human emotional states in real time.

Multimodal emotion recognition has become a crucial research domain within artificial intelligence, driven by the increasing demand for systems capable of understanding and interpreting human affective states with greater depth and accuracy. Unlike unimodal approaches that rely on a single source of information, multimodal emotion recognition integrates diverse data streams such as facial expressions, vocal intonations, textual semantics, and physiological signals to provide a holistic representation of emotional states. This fusion of heterogeneous modalities helps capture the intricate and multi-faceted nature of human emotions, allowing for the extraction of complementary and reinforcing information that enhances prediction accuracy and robustness. The synergistic interaction between modalities effectively addresses the inherent limitations of isolated data sources. While facial expressions provide crucial visual indicators, without further context, their interpretation can be ambiguous; similarly, vocal features offer valuable affective cues but are susceptible to environmental noise and inter-speaker variability. Textual semantics contribute essential contextual information but lack the paralinguistic signals crucial for comprehensive emotion analysis. Physiological measurements, including electrodermal activity and heart rate variability, provide objective quantification of emotional arousal, substantially enriching the overall affective representation. The integration of these complementary modalities enables emotion recognition models to better account for expressive variations and contextual ambiguities, resulting in more reliable affective computing systems. Contemporary deep learning architectures have demonstrated remarkable efficacy in leveraging multimodal data, significantly advancing the state-of-the-art in emotion recognition performance.

Prior techniques in this domain have evolved significantly with the advent of deep learning, particularly through transformer-based models [19,20,21,22] that have revolutionized sequential data processing. Early approaches based on Recurrent Neural Networks (RNNs) [23,24] and Convolutional Neural Networks (CNNs) [25,26,27] were constrained by their inability to capture long-range dependencies and by limited parallelization. Transformer architectures have since been adapted for multimodal tasks, excelling at the extraction of high-level semantic representations from audio, text, and physiological signals [28]. In emotion recognition, these models capture nuanced prosodic features, semantic relationships, and intricate temporal dynamics. Their parallel processing capability not only accelerates training but also enhances model robustness, with benchmark evaluations consistently demonstrating superior performance compared to traditional methods [23]. Moreover, transformer-based cross-modal attention mechanisms further refine the fusion of heterogeneous data, giving these systems a more holistic understanding of emotional states. This shift to transformer-based methods represents a significant leap in efficiency and accuracy by capturing complex interdependencies across modalities. Their ability to fuse diverse information streams into unified representations is critical for handling the varied temporal resolutions and feature dimensions of multimodal data. Additionally, the modularity of transformers allows for the seamless integration of dynamic fusion components, such as cross-modal attention layers, which adjust to the reliability of each input source.

Despite these advances, existing approaches exhibit notable limitations that hinder their broader applicability. Many conventional models rely on static fusion strategies, either early or late fusion approaches that lack the flexibility to dynamically adjust the importance of each modality based on the context. Such rigid methods often lead to suboptimal performance, especially when the quality or reliability of individual modalities fluctuate. Additionally, transformer-based methods, while powerful, tend to be computationally demanding and are sometimes inadequate in handling the noise and redundancy present in heterogeneous datasets. Furthermore, the absence of mechanisms to promote expert specialization within the fusion process restricts the ability of existing models to fully exploit the unique characteristics of each modality.

To address these challenges, we propose a novel Mixture of Experts (MoE) framework that synergistically combines transformer-based sub-expert networks with a dynamic gating mechanism and cross-modal attention. Our approach, CAG-MoE (Cross-Attention Gated Mixture of Experts) assigns dedicated sub-experts to process each modality, capturing their unique features and temporal dynamics. A dynamic gating network employing a Top-k sparse activation strategy selectively fuses the most informative expert outputs, while an auxiliary diversity loss function encourages specialization among the experts. The incorporation of cross-modal attention further refines feature integration by enabling adaptive information exchange across modalities. Evaluations on the Korean Emotion Multimodal Database (KEMDy20) [29] and the ASCERTAIN [30] dataset demonstrate that our framework not only overcomes the limitations of previous approaches but also achieves state-of-the-art performance, paving the way for more robust and efficient emotion recognition systems that are better suited to real-world applications.

Our work makes the following key contributions:

• A novel Mixture of Experts (MoE) framework that utilizes dedicated transformer-based sub-expert networks to extract rich, modality-specific features from physiological signals, audio, and textual data.
• A dynamic gating mechanism incorporating Top-k sparse activation and auxiliary diversity loss to selectively and efficiently fuse expert outputs, thereby promoting specialization and reducing computational overhead.
• A cross-modal attention module that facilitates adaptive information exchange across heterogeneous modalities, enhancing the overall robustness and discriminative capability of the fused representations.
• Extensive evaluations on the Korean Emotion Multimodal Database (KEMDy20) and the ASCERTAIN dataset demonstrate that our approach significantly outperforms state-of-the-art methods, establishing new performance benchmarks in multimodal emotion recognition.

The remainder of this paper is structured as follows: Section 2 reviews related work, providing an overview of existing approaches and their limitations. Section 3 defines our methodology, highlighting the problem statement and describing the proposed framework with details on its architecture and components. Section 4 describes the experimental setup, benchmark datasets, evaluation metrics, and results, demonstrating the effectiveness of the proposed model. Finally, the conclusions and future research directions are discussed.

2. Literature Review

In this section, we provide an overview of the most relevant research efforts and methodologies related to our work, emphasizing their key contributions while identifying gaps or limitations. We then contextualize our approach in relation to these studies, highlighting how our solution extends, refines, or diverges from previous findings. This analysis establishes a foundation for understanding the advancements that have shaped the field and the rationale behind the proposed methodology.

2.1. Multimodal Emotion Recognition

Humans primarily rely on visual (facial expressions) auditory (vocal cues), and cognitive modalities to convey affective states. Attempts to classify both dimensional emotions such as valence (pleasantness) and arousal (intensity) and categorical emotions (e.g., happy, sad, and disgust) using multimodal input data have been extensively studied in prior works [31,32,33]. Large-scale benchmark challenges, including the AVEC series [34,35], the MuSe challenge [36], and the ABAW challenge, have further driven advancements in multimodal affect recognition. Emotion recognition is a complex task that requires modeling of dynamic interactions and relationships between modalities. Prior studies, such as [37,38], have explored the relationship between emotion and social context, highlighting the evolving nature of emotional expression in human interactions. To address these dynamics, various deep learning approaches have been proposed. DialogueRNN [39] employs a Recurrent Neural Network (RNN) with an attention mechanism to capture long-term dependencies and interaction patterns between speakers. DialogueGCN [40] extends this approach by utilizing a Graph Convolutional Network (GCN) to propagate and aggregate information across nodes and edges, enabling more effective handling of long-range dependencies and multi-turn interactions. These models illustrate the importance of structured representations in emotion recognition. In the multimodal emotion recognition domain, effective fusion of diverse modalities has been a key research focus [41,42,43,44]. LR-GCN [45], for instance, introduces a latent relationship representation mechanism to model the interactions between multimodal features, improving its overall recognition performance. While these models excel in unimodal and bimodal settings, robust integration of heterogeneous signals remains a challenge, particularly for physiological, audio, and textual modalities.

2.2. Integrated Multimodal Fusion

A crucial aspect of multimodal emotion recognition is the fusion strategy used to integrate diverse modality-specific features into a unified and discriminative representation. In general, tightly coupled interactions between modalities enhance the modeling of mutual dependencies. In [46], the authors leveraged a transformer-based model to fuse audiovisual modalities at the model level, where encoded features from both modalities were mapped into a shared semantic space to generate intermediate multimodal emotional representations. Similarly, Pepino et al. [47] explored various fusion techniques for emotion classification using acoustic and textual features, demonstrating that combining these modalities improved performance across datasets, albeit with marginal differences among the evaluated fusion methods. Deep learning-based fusion strategies have also been extensively studied for emotion recognition. Prasad et al. [48] proposed a framework that integrates textual and acoustic data for enhanced classification. Sebastian et al. [49] examined the use of Long Short-Term Memory (LSTM) networks and Convolutional Neural Networks (CNNs) in text-based emotion recognition. Their approach utilized pretrained word embeddings for LSTMs and discourse-level descriptors for CNN-based speech emotion recognition, demonstrating the effectiveness of hierarchical feature extraction. Beyond simple concatenation, models have increasingly adopted interaction-driven fusion mechanisms. Guang et al. [50] introduced a word-level interaction module within dual LSTM networks to explicitly model the dynamic interplay between audio and text features, leading to the development of the WISE framework, which effectively captures fine-grained dependencies in speech emotion recognition. Lian et al. [51] proposed a conversational transformer network for multimodal emotion recognition, incorporating word-level lexical features alongside fragment-level acoustic representations to preserve any temporal dependencies within the discourse. Moreover, recent work such as [52] demonstrates innovative strategies for fusing heterogeneous inputs in a different context. Unlike these methods that primarily focus on visual defect detection under few-shot conditions, our approach extends these ideas into the realm of affective computing by dynamically integrating diverse multimodal signals in real time, ensuring both scalability and robustness. Our approach extends this line of research by introducing a Mixture of Experts (MoE) framework that dynamically activates specialized transformer-based sub-experts, leverages a sparse gating mechanism, and employs cross-modal attention to optimize the fusion of physiological, audio, and textual data. Given the success of expert-based architectures in improving model efficiency and interpretability, we now turn to a discussion of prior works on Mixture of Experts (MoE) models and their applications in deep learning.Yang et al. [53] introduced an auxiliary tool for automatic depression detection based on multimodal purification fusion. The authors used a constraint gating strategy to inject doctors’ constraints into depression data in order to guide and constrain the learning process. Then, they introduced text and audio encoders to extract unpurified features from preprocessed depression data. Afterward, they adopted multimodal purification refinement to extract unintersected common and specific features from unpurified features, generating purified features. Meanwhile, they leveraged a multiperspective contrastive learning (MCL) strategy to enhance unpurified and purified features to further proposed a transformer for multimodal fusion. In another study [54], the authors proposed a two-stage framework to enable humanoid robots to generate authentic and expressive facial expressions using action unit (AU)-guided synthesis. In the first stage, they introduced a weakly supervised learning approach that disentangles expression-related features in a latent space to generate realistic facial expression images. In the second stage, these synthesized expressions were transferred to a robot through a specialized motor command mapping network, ensuring physically accurate and expressive facial movements. Furthermore, in [55], the authors proposed a cross-modality attention-based convolutional neural network (CM-CNN) for facial expression recognition, aiming to improve performance under challenging conditions such as pose and illumination variations and weak emotional intensities. Instead of directly combining complementary image modalities (gray-scale, LBP, and depth), they introduced a cross-modality attention fusion network to enhance spatial correlations between modalities. The model was trained using an improved focal loss to focus on subtle expressions. Their approach achieved competitive accuracy across multiple benchmark datasets.

2.3. Mixture of Experts

Recent advances in Mixture of Experts (MoE) architectures have significantly enhanced the scalability and specialization of deep neural networks. For instance, Fedus et al. [56] introduced the switch transformer, which employs a dynamic gating mechanism to activate only a subset of expert networks for each input. This sparse activation not only improves computational efficiency but also enables the model to learn highly specialized representations. Similarly, Lepikhin et al. [57] presented the GShard framework, which distributes parameters across multiple experts and leverages conditional computation to achieve superior performance in large-scale language modeling tasks. These innovations underscore the potential of MoE frameworks in dynamically allocating computational resources to tackle diverse aspects of complex data. Beyond language modeling, the MoE paradigm has been successfully extended to multimodal learning tasks where integrating heterogeneous data is critical. Recent studies have demonstrated that dynamically routing information through specialized sub-networks can significantly improve performance in tasks such as image–text retrieval, audio–visual speech recognition, and affective computing [58]. By selectively engaging different experts based on input characteristics, these models not only enhance interpretability but also provide a modular and scalable approach to multimodal fusion. This dynamic expert selection is central to our proposed framework, which integrates transformer-based sub-experts with a sparse dynamic gating mechanism and cross-modal attention to robustly fuse physiological, audio, and textual modalities.

3. Methodology

3.1. Proposed Method Overview and Novel Contributions

We propose a novel architecture for emotion recognition that extends the Mixture of Experts (MoE) paradigm to dynamically and adaptively fuse heterogeneous multimodal data. Our design, depicted in Figure 1, is motivated by the need to capture the complementary yet diverse information present in physiological signals, audio features, and textual data. Unlike conventional static fusion methods that rely on fixed integration strategies, our method leverages a synergistic combination of modules designed to overcome key limitations in multimodal fusion. Our approach consists of the following core components:

• Dynamic Sub-Expert Processing: Instead of a single processing unit per modality, our architecture deploys a bank of $K_m$ transformer encoder-based sub-experts for each input modality $X^{\left(m\right)}$. Each sub-expert $f_{{\theta }^{(m,k)}}$ is structured as a deep transformer module comprising multiple layers of multi-head self-attention followed by position-wise feed-forward networks, residual connections, and layer normalization. This design allows each sub-expert to learn distinct, specialized representations of the modality-specific data, thereby capturing subtle temporal and contextual patterns that are often lost in conventional feature extractors. This flexibility facilitates diversity among the experts, which is then exploited by our dynamic gating mechanism.
• Adaptive Gating with Sparse Activation: To robustly integrate the outputs of multiple sub-experts, we introduce an adaptive gating network that assigns weights to the sub-expert outputs based on the input characteristics. A key innovation in our approach is the application of a Top-k sparsity constraint to the gating weights, ensuring that only the most relevant expert outputs contribute to the final representation. This mechanism not only improves computational efficiency by reducing redundant calculations but also enhances model interpretability and robustness by prioritizing informative features. Quantitatively, our gating network achieves significant reductions in computational complexity while preserving or even enhancing performance compared to static fusion strategies.
• Cross-Modal Attention Mechanism: Recognizing that each modality contains complementary information, our framework incorporates a cross-modal attention module that allows one modality to refine its representation using context from the others. Specifically, for every modality m, we project its feature $H^{\left(m\right)}$ into a query space, while the remaining modalities $H^{\left(n\right)}$ ($n\ne m$) are projected into key and value spaces. The scaled dot-product attention mechanism is then applied, and the multi-head extension aggregates a richer set of inter-modal dependencies. This dynamic attention process not only mitigates the shortcomings of early and late fusion techniques but also quantitatively improves performance by robustly integrating noisy or incomplete data.
• Global Fusion and Final Classification: Finally, a global fusion network aggregates the refined modality-specific features obtained from the cross-modal interaction module. A global gating network computes a weight vector over modalities to balance their contributions adaptively. This hierarchical fusion strategy, which combines dynamic expert selection, adaptive gating, and cross-modal attention, enables our model to learn more discriminative features and achieve higher accuracy compared to traditional methods.

Novelty and Advantages: Our contributions are threefold:

• Adaptive and Scalable Fusion: By combining multiple transformer-based sub-experts with a gating mechanism, our model can scale flexibly with increasing data modalities while preserving computational efficiency.
• Robust Cross-Modal Integration: The incorporation of a cross-modal attention mechanism allows each modality to be enhanced by information from others, overcoming the limitations of static fusion methods where interactions between modalities are fixed and not contextually adaptive.
• Rigorous Theoretical and Empirical Validation: We provide detailed theoretical analyses of the sparse activation and diversity regularization components, and our extensive experiments on benchmark datasets (KEMDy20 and ASCERTAIN) demonstrate quantitative improvements in key performance metrics over state-of-the-art static fusion approaches.

This hybrid architecture, which synergistically combines dynamic sub-expert processing, adaptive gating with sparse activation, and robust cross-modal attention, directly addresses the challenges associated with multimodal emotion recognition.

3.2. Problem Setting

We consider the task of multimodal emotion recognition as a supervised learning problem in which each sample consists of multiple heterogeneous input modalities $\{X^{\left(1\right)},X^{\left(2\right)},\dots ,X^{\left(M\right)}\}$ (e.g., physiological signals, audio features, and text) and a corresponding emotion label $y\in \{1,2,\dots ,C\}$. Formally, given a training dataset ${\left\{(X_i^{\left(1\right)},X_i^{\left(2\right)},\dots ,X_i^{\left(M\right)},y_i)\right\}}_{i=1}^N$, the objective is to learn a mapping $F_{\Theta }:\mathcal{X}\to {\Delta }^C$ (where $\mathcal{X}=X^{\left(1\right)}\times X^{\left(2\right)}\times \dots \times X^{\left(M\right)}$ and ${\Delta }^C$ is the C-dimensional probability simplex) such that $F_{\Theta }(X_i^{\left(1\right)},X_i^{\left(2\right)},\dots ,X_i^{\left(M\right)})={\mathbf{p}}_i$ approximates the true emotion distribution by minimizing a loss function, typically the cross-entropy loss:

$${\mathcal{L}}_{\mathrm{CE}}=-\sum _{i=1}^N\sum _{c=1}^C{y}_{i,c}log{p}_{i,c}.$$

(1)

The problem is further complicated by the need to effectively align and fuse these modalities, which have distinct temporal resolutions and feature dimensions, to capture complementary cues essential for accurate emotion prediction.

3.3. Input Data Modalities

In our approach, the input comprises several heterogeneous modalities: physiological signals alongside audio features, facial and textual data. Each modality provides complementary information crucial for robust emotion recognition. In this section, we rigorously define the mathematical formulation, sampling characteristics, and preprocessing procedures applied to each modality.

3.3.1. Mathematical Formulation

$$\mathcal{X}=\{X^{\left(1\right)},X^{\left(2\right)},X^{\left(3\right)},X^{\left(4\right)},X^{\left(5\right)}\}$$

(2)

where the index $m\in \{1,2,3,4,5\}$ corresponds to the following modalities:

• $X^{\left(1\right)}$ represents Electrodermal Activity (EDA),
• $X^{\left(2\right)}$ represents skin temperature,
• $X^{\left(3\right)}$ represents facial expression,
• $X^{\left(4\right)}$ represents audio,
• $X^{\left(5\right)}$ represents text.

3.3.2. Physiological Signals

We recorded physiological samples for electrodermal activity and skin temperature as continuous time-series data at a specified sampling frequency (e.g., 128 Hz), yielding $T^{\prime }=T\times f$ time points for each modality over a duration $T.$ We then performed a series of preprocessing steps: first, we applied low-pass filtering to remove high-frequency noise and artifacts; next, we standardized each signal to zero mean and unit variance to minimize inter-subject variability; and finally, we resampled signals of differing rates to a common temporal resolution using interpolation. This combined approach ensures both consistency and comparability across the physiological modalities.

3.3.3. Audio Features

We processed the audio modality by first converting the raw audio waveform $a\left(t\right)$, where $t\in [0,T]$, into a time–frequency representation, typically using the Short-Time Fourier Transform (STFT). This procedure yields an audio feature matrix $X^{\left(4\right)}\in {\mathbb{R}}^{T_a\times D_a}$, where $T_a$ is the number of time frames (which may differ from $T^{\prime }$ in the physiological modalities) and $D_a$ represents the dimensionality of the audio feature vector. In terms of preprocessing, we first perform denoising via spectral subtraction to attenuate ambient noise. Next, we segment the raw waveform using a sliding window approach to compute the spectrogram for each segment. Finally, when synchronization with physiological signals is required, the audio frames are temporally aligned with those signals by resampling, ensuring that all modalities remain synchronized for subsequent analyses.

3.3.4. Text Sequences

The text modality captures linguistic content that is relevant to the emotional context (e.g., transcribed speech), where each textual input is tokenized into a sequence of discrete symbols drawn from a fixed vocabulary. Formally, we represent the text input as $X^{\left(5\right)}\in {\mathbb{Z}}^L$, with L indicating the length of the tokenized sequence. In practice, each token is subsequently mapped to a dense embedding vector through an embedding lookup table, which is learned during training. For preprocessing, we normalize the text by converting it to lowercase and removing punctuation to reduce variability; we then apply subword tokenization using Byte-Pair Encoding (BPE) to handle out-of-vocabulary words effectively; and finally, we pad all token sequences to a uniform length L to enable batch processing, adding special tokens (such as start-of-sequence and end-of-sequence markers) as needed.

3.4. Feature Extraction Experts

In this section, we elaborate on the design and mathematical formulation of the modality-specific feature extraction experts. For each input modality $X^{\left(m\right)}$ with $m\in \{1,2,\dots ,M\}$, we deploy $K_m$ transformer encoder-based sub-experts. These sub-experts are designed to capture intricate temporal and contextual patterns inherent in the modality data. Below, we detail the processing pipeline for a given modality and the structure of each sub-expert.

3.4.1. Embedding and Preprocessing

Before entering the transformer encoder, the raw input $X^{\left(m\right)}$ is first projected into a latent space using a modality-specific embedding function. For modalities that are inherently continuous (physiological signals and audio), this step involves a linear transformation, while for discrete data (text), it involves a lookup into an embedding matrix. Formally, we define the embedding as follows:

$$E^{\left(m\right)}={\varphi }^{\left(m\right)}\left(X^{\left(m\right)}\right),\hspace{1em}{\varphi }^{\left(m\right)}:{\mathbb{R}}^{T_m\times d_m}\to {\mathbb{R}}^{T_m\times d},$$

(3)

where $T_m$ is the number of time steps or tokens in modality m, $d_m$ is the input feature dimension, and d is the common embedding dimension for the transformer encoder.

3.4.2. Transformer Encoder Architecture for Sub-Experts

Each sub-expert $f_{{\theta }^{(m,k)}}$ for modality m is implemented as a stack of L transformer encoder layers. The k-th sub-expert for modality m computes its output feature representation as follows:

$$H^{(m,k)}=f_{{\theta }^{(m,k)}}\left(X^{\left(m\right)}\right)={\mathrm{TransformerEncoder}}_L\left({\varphi }^{\left(m\right)}\left(X^{\left(m\right)}\right)\right),$$

(4)

where ${\theta }^{(m,k)}$ collectively denotes the parameters of the k-th sub-expert, including the weights and biases of each transformer layer.

In our implementation, each transformer encoder layer within a sub-expert is composed of the following components:

• Multi-Head Self-Attention (MHSA): Each layer employs multi-head self-attention to capture long-range dependencies. For a given head i in sub-expert k for modality m, we compute:

  $$\begin{array}{cc}\hfill Q_i^{(m,k)}& =E^{\left(m\right)}{W}_i^{Q,(m,k)},\hfill \\ \hfill K_i^{(m,k)}& =E^{\left(m\right)}{W}_i^{K,(m,k)},\hfill \\ \hfill V_i^{(m,k)}& =E^{\left(m\right)}{W}_i^{V,(m,k)},\hfill \end{array}$$

  (5)

  where $W_i^{Q,(m,k)},W_i^{K,(m,k)},W_i^{V,(m,k)}\in {\mathbb{R}}^{d\times d_h}$ are learnable projection matrices, and $d_h=d/h$ with h denoting the number of heads. The outputs from each head are concatenated and then projected via a matrix $W^{O,(m,k)}\in {\mathbb{R}}^{d\times d}$.
• Feed-Forward Network (FFN): Following the MHSA, a position-wise FFN is applied to further transform the output. The FFN consists of two linear transformations with a ReLU activation function in between:

  $${\mathrm{FFN}}^{(m,k)}\left(x\right)=\mathrm{ReLU}\left(x{W}_1^{(m,k)}+b_1^{(m,k)}\right)W_2^{(m,k)}+b_2^{(m,k)},$$

  (6)

  where $W_1^{(m,k)}\in {\mathbb{R}}^{d\times d_{\mathrm{ff}}}$, $W_2^{(m,k)}\in {\mathbb{R}}^{d_{\mathrm{ff}}\times d}$, and $b_1^{(m,k)}$, $b_2^{(m,k)}$ are bias terms.
• Residual Connections and Layer Normalization: To facilitate training and stabilize gradients, residual connections are employed around both the MHSA and the FFN blocks, followed by layer normalization.
• Additional Regularization and Positional Encoding: To better capture temporal dependencies and prevent overfitting, we incorporate dropout layers and positional encodings within each sub-expert.

The utilization of $K_m$ sub-experts for each modality serves multiple purposes: it fosters diversity in the feature representation, encourages each sub-expert to capture distinct aspects of the modality-specific signal, and facilitates expert specialization. The Mixture of Experts (MoE) framework then employs a dynamic gating mechanism to aggregate the contributions from the various sub-experts. This hybrid expert mechanism highlights the effectiveness of employing multiple specialized sub-networks to enhance overall model performance.

3.4.3. Feature Aggregation via Dynamic Gating

After obtaining the feature representations $H^{(m,k)}$ from all sub-experts, we aggregate them into a modality-specific feature $H^{\left(m\right)}$ using a dynamic gating mechanism. The gating network assigns weights to each sub-expert, ensuring that more relevant experts contribute more significantly to the final representation. Formally, this aggregation is defined as follows:

$$H^{\left(m\right)}=\sum _{k=1}^{K_m}{w}_k^{\left(m\right)}·H^{(m,k)},$$

(7)

where the weights ${\mathbf{w}}^{\left(m\right)}=[w_1^{\left(m\right)},w_2^{\left(m\right)},\dots ,w_{K_m}^{\left(m\right)}]$ are computed by a gating function applied to a pooled version of the sub-experts’ outputs.

The combination of multiple transformer encoder-based sub-experts and a dynamic gating mechanism forms the hybrid expert (MoE) framework. This architecture not only improves scalability and specialization but also enhances the overall performance by allowing the model to adaptively select and fuse the most informative features from each modality.

3.5. Dynamic Gating Mechanism

The dynamic gating mechanism is a central component of our MoE framework; it enables the model to selectively leverage the most informative sub-experts for each modality. In this section, we provide an extensive explanation of the dynamic gating mechanism, including the computation of gating weights, the application of sparse activation via Top-k selection, and the introduction of diversity regularization to promote expert specialization.

3.5.1. Gating Network Formulation

For each modality m with corresponding input $X^{\left(m\right)}$ and $K_m$ sub-experts, the gating network computes a weight vector ${\mathbf{w}}^{\left(m\right)}\in {\mathbb{R}}^{K_m}$ that determines the contribution of each sub-expert. To achieve this, we first extract a condensed representation of the input using a pooling function. Let

$${\mathbf{c}}^{\left(m\right)}=Pool\left(X^{\left(m\right)}\right)\in {\mathbb{R}}^d,$$

(8)

where $Pool(·)$ is typically instantiated as mean or max pooling over the temporal (or token) dimension, and d is the dimensionality of the pooled representation.

Next, this pooled representation is linearly transformed to produce raw gating scores:

$${\mathbf{z}}^{\left(m\right)}=W_g^{\left(m\right)}{\mathbf{c}}^{\left(m\right)}+{\mathbf{b}}_g^{\left(m\right)}\in {\mathbb{R}}^{K_m},$$

(9)

where $W_g^{\left(m\right)}\in {\mathbb{R}}^{K_m\times d}$ and ${\mathbf{b}}_g^{\left(m\right)}\in {\mathbb{R}}^{K_m}$ are learnable parameters. These scores capture the relevance of each sub-expert for the given input instance.

The raw scores are then normalized using the softmax function to obtain a probability distribution over the $K_m$ experts:

$$w_k^{\left(m\right)}={\displaystyle \frac{exp\left(z_k^{\left(m\right)}\right)}{{\sum }_{j=1}^{K_m}exp\left(z_j^{\left(m\right)}\right)}}\mathrm{for}k=1,\dots ,K_m.$$

(10)

Thus, we have the following:

$${\mathbf{w}}^{\left(m\right)}=Softmax\left(W_g^{\left(m\right)}{\mathbf{c}}^{\left(m\right)}+{\mathbf{b}}_g^{\left(m\right)}\right).$$

(11)

3.5.2. Sparse Activation via Top-k Selection

To enhance computational efficiency and interpretability, we impose a sparsity constraint on the gating weights through a Top-k selection mechanism. In our implementation, k is set as a fixed value ($k=3$) for each modality. This value was empirically determined via validation experiments that balanced the trade-off between retaining sufficient expert capacity and enforcing a sparse representation.

Specifically, we retain only the k highest weights in ${\mathbf{w}}^{\left(m\right)}$ and set the remaining $K_m-k$ entries to zero. Let $S^{\left(m\right)}\subset \{1,2,\dots ,K_m\}$ be the set of indices corresponding to the k largest elements of ${\mathbf{w}}^{\left(m\right)}$. The sparse gating vector ${\tilde{\mathbf{w}}}^{\left(m\right)}$ is then defined as follows:

$${\tilde{w}}_k^{\left(m\right)}=\left\{\begin{array}{cc}{w}_k^{\left(m\right)},\hfill & \mathrm{if}k\in S^{\left(m\right)},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(12)

To ensure that the sparse weights still form a valid probability distribution, we perform a renormalization step:

$${\tilde{w}}_k^{\left(m\right)}={\displaystyle \frac{w_k^{\left(m\right)}}{{\sum }_{j\in S^{\left(m\right)}}{w}_j^{\left(m\right)}}} \mathrm{for} k\in S^{\left(m\right)}.$$

(13)

Once the sparse gating weights are computed, they are used to aggregate the outputs of the corresponding sub-experts. We denote the output of the k-th sub-expert for modality m as $H^{(m,k)}$. The aggregated modality-specific feature $H^{\left(m\right)}$ is then given as follows:

$$H^{\left(m\right)}=\sum _{k=1}^{K_m}{\tilde{w}}_k^{\left(m\right)}·H^{(m,k)}.$$

(14)

To promote specialization among the sub-experts, we introduce an auxiliary diversity loss function that penalizes uniform distributions of gating weights. We define the diversity loss for modality m as follows:

$${\mathcal{L}}_{\mathrm{div}}^{\left(m\right)}=\sum _{k=1}^{K_m}{w}_k^{\left(m\right)}log\left(w_k^{\left(m\right)}\right).$$

(15)

Minimizing ${\mathcal{L}}_{\mathrm{div}}^{\left(m\right)}$ encourages the gating distribution to become more peaked, concentrating probability mass on a few experts, thereby enforcing diversity in expert activations.

This dynamic gating mechanism integrates seamlessly with the MoE architecture, ensuring that each modality’s features are refined by the most relevant sub-experts. By leveraging both sparse activation and diversity regularization, our model achieves computational efficiency and rich, specialized feature representations.

3.6. Cross-Modal Interaction Module

To facilitate the exchange of complementary information across modalities, we introduce a cross-modal attention mechanism that selectively integrates features from different modalities. This module augments the modality-specific features $H^{\left(m\right)}$ by leveraging context from all other modalities $H^{\left(n\right)}$ ($n\ne m$). Below, we provide explanations of the cross-attention procedure, including its multi-head extension, residual connections, and integration with the gating network.

3.6.1. Query–Key–Value Projections

For each modality m, we first obtain a query representation by projecting its current feature $H^{\left(m\right)}$ into a lower-dimensional subspace:

$${\mathbf{Q}}^{\left(m\right)}=H^{\left(m\right)}{W}_Q,$$

(16)

where $W_Q\in {\mathbb{R}}^{d\times d_k}$ is a learnable projection matrix, d is the dimensionality of $H^{\left(m\right)}$, and $d_k$ is the dimensionality of the projected space. Similarly, for every other modality $n\ne m$, we compute key and value matrices:

$${\mathbf{K}}^{\left(n\right)}=H^{\left(n\right)}{W}_K,{\mathbf{V}}^{\left(n\right)}=H^{\left(n\right)}{W}_V,$$

(17)

where $W_K,W_V\in {\mathbb{R}}^{d\times d_k}$. These key and value representations encapsulate the contextual information that modality m will attend to. Using the query, key, and value matrices, we apply the scaled dot-product attention mechanism:

$${CrossAttn}^{(m,n)}=Softmax\left({\displaystyle \frac{{\mathbf{Q}}^{\left(m\right)}{\mathbf{K}}^{\left(n\right)\top }}{\sqrt{d_k}}}\right){\mathbf{V}}^{\left(n\right)}.$$

(18)

This operation allows modality m to selectively focus on the most relevant parts of modality n’s feature representation.

3.6.2. Multi-Head Cross-Attention

To capture a richer set of dependencies, we extend the above formulation to multi-head attention:

$${head}_i^{(m,n)}=Softmax\left({\displaystyle \frac{{\mathbf{Q}}_i^{\left(m\right)}{\mathbf{K}}_i^{\left(n\right)\top }}{\sqrt{d_k/h}}}\right){\mathbf{V}}_i^{\left(n\right)}.$$

(19)

The individual heads are then concatenated and projected back to dimension $d_k$:

$${MHA}^{(m,n)}({\mathbf{Q}}^{\left(m\right)},{\mathbf{K}}^{\left(n\right)},{\mathbf{V}}^{\left(n\right)})=Concat\left({head}_1^{(m,n)},\dots ,{head}_h^{(m,n)}\right)W_O,$$

(20)

where $W_O\in {\mathbb{R}}^{(h·(d_k/h))\times d_k}$ is a learnable projection matrix.

Since each modality m may benefit from information in multiple other modalities, we aggregate the attention outputs from all $n\ne m$:

$${CrossAttn}^{\left(m\right)}=\sum _{n\ne m}{MHA}^{(m,n)}({\mathbf{Q}}^{\left(m\right)},{\mathbf{K}}^{\left(n\right)},{\mathbf{V}}^{\left(n\right)}).$$

(21)

Next, we update $H^{\left(m\right)}$ by combining it with the aggregated cross-modal attention via a residual connection:

$${\tilde{H}}^{\left(m\right)}=LayerNorm\left(H^{\left(m\right)}+{CrossAttn}^{\left(m\right)}\right),$$

(22)

where $LayerNorm(·)$ stabilizes training and enhances gradient flow.

The dynamic gating mechanism operates in tandem with the cross-modal interaction module. After each modality m is enhanced with cross-modal information, the gating network can re-evaluate or refine the weights assigned to sub-experts. In practice, we incorporate ${\tilde{H}}^{\left(m\right)}$ into the gating function to produce updated gating weights:

$${\mathbf{w}}^{\left(m\right)}\leftarrow Softmax\left(W_g^{\left(m\right)}·Pool\left({\tilde{H}}^{\left(m\right)}\right)+{\mathbf{b}}_g^{\left(m\right)}\right),$$

(23)

thus allowing the model to adaptively select experts based on cross-modal context.

3.6.3. Visualization Example of Our Cross-Modal Attention Mechanisms

For better explainability of our cross-modal attention mechanisms, we provide an illustrative example of attention-weight heat maps in Figure 2. In this example, we designate the textual modality as the query and compute multi-head attention toward the physiological, audio, and facial modalities. This visualization is crucial for understanding how the model fuses information across modalities in practice. Warmer (yellow) regions indicate higher attention scores, revealing which temporal segments or tokens the textual queries consider most relevant when integrating context from the other modalities. By highlighting these attention distributions, we demonstrate that the model is not merely concatenating features but is selectively focusing on salient aspects of each modality. Such interpretability is vital for emotion recognition tasks, where different modalities (e.g., facial expressions, vocal cues, physiological signals) contribute complementary signals that may vary in importance depending on the context. Analyzing these attention patterns thus offers insights into why certain tokens or timesteps drive the final fused representation, shedding light on both the model’s decision process and its ability to adapt to diverse and potentially noisy inputs.

3.7. Feature Fusion Strategy

Once each modality’s representation has been updated by the cross-modal interaction module, we aggregate these refined features into a single, unified embedding suitable for final classification. This feature fusion step serves two main purposes: (1) it consolidates the multi-modal information into a coherent representation, and (2) it provides a global mechanism for weighting each modality’s contribution. Below, we detail the fusion procedure and discuss its underlying motivations.

3.7.1. Concatenation of Updated Features

Let ${\left\{{\tilde{H}}^{\left(m\right)}\right\}}_{m=1}^M$ denote the updated modality-specific features after cross-modal interactions have been processed. Each ${\tilde{H}}^{\left(m\right)}\in {\mathbb{R}}^d$ (or ${\mathbb{R}}^{T_m\times d}$ if still retaining a temporal dimension). We first concatenate these embeddings along their feature dimension:

$$H_{\mathrm{concat}}={\tilde{H}}^{\left(1\right)}\oplus {\tilde{H}}^{\left(2\right)}\oplus \dots \oplus {\tilde{H}}^{\left(M\right)},$$

(24)

where ⊕ denotes the concatenation operation. The resulting $H_{\mathrm{concat}}$ is in ${\mathbb{R}}^{M·d}$ (or ${\mathbb{R}}^{T^{\prime }\times (M·d)}$ if temporal alignment is preserved). This straightforward concatenation ensures that the model retains each modality’s distinct contribution prior to any global weighting or gating. Although simple concatenation gathers the information in a single tensor, it does not inherently regulate the relative importance of each modality. To address this, we introduce a global gating network that dynamically weights the concatenated representation. Formally, we compute the following:

$${\mathbf{w}}_{\mathrm{global}}=Softmax\left(W_{\mathrm{global}}·H_{\mathrm{concat}}+{\mathbf{b}}_{\mathrm{global}}\right),$$

(25)

where $W_{\mathrm{global}}\in {\mathbb{R}}^{M\times (M·d)}$ (or an appropriately shaped matrix if the fusion is performed per time step) and ${\mathbf{b}}_{\mathrm{global}}\in {\mathbb{R}}^M$. The softmax function ensures that the resulting weight vector ${\mathbf{w}}_{\mathrm{global}}$ lies in the simplex ${\Delta }^M$, with each component corresponding to one of the M modalities.

Interpretability and Adaptivity:

• The learned weights ${\mathbf{w}}_{\mathrm{global}}$ indicate how much each modality contributes to the fused representation on a sample-by-sample basis.
• Unlike a static fusion scheme, this dynamic weighting mechanism can adapt to varying input conditions (e.g., noisy physiological signals or unreliable audio), thereby enhancing robustness.

3.7.2. Weighted Summation for Fusion

With ${\mathbf{w}}_{\mathrm{global}}$ computed, the fused feature is obtained via a weighted sum of the updated modality embeddings:

$$H_{\mathrm{fused}}=\sum _{m=1}^M{w}_{\mathrm{global},m}·{\tilde{H}}^{\left(m\right)}.$$

(26)

This linear combination effectively emphasizes modalities that are more informative for the current sample while down-weighting less reliable or redundant sources. As a result, $H_{\mathrm{fused}}$ encodes a balanced and context-sensitive multimodal representation.

3.8. Emotion Classification Network

After obtaining a fused representation $H_{\mathrm{fused}}$ that integrates the information from all modalities, we perform emotion classification using a Multi-Layer Perceptron (MLP). This section describes the architectural details of the classification network, the rationale behind its design, and the loss functions employed for end-to-end training.

3.8.1. MLP Architecture

• Input Layer: The input to the classifier is the fused feature vector $H_{\mathrm{fused}}\in {\mathbb{R}}^d$. This vector represents a compact summary of the multimodal data after gating, cross-modal interaction, and global fusion.
• Hidden Layers: Although a single hidden layer can suffice for simpler tasks, we employ more fully connected layers to increase the network’s representational capacity. Concretely, let the first hidden layer be:

  $${\mathbf{h}}_1=ReLU\left(W_h·H_{\mathrm{fused}}+{\mathbf{b}}_h\right),$$

  (27)

  where $W_h\in {\mathbb{R}}^{d^{\prime }\times d}$ and ${\mathbf{b}}_h\in {\mathbb{R}}^{d^{\prime }}$. Here, $d^{\prime }$ is the dimensionality of the hidden layer, chosen based on validation performance.
• Output Layer: The final classification layer projects the last hidden representation ${\mathbf{h}}_L\in {\mathbb{R}}^{d^{\prime }}$ to a C-dimensional vector, where C is the number of emotion classes:

  $$\mathbf{z}=W_c·{\mathbf{h}}_L+{\mathbf{b}}_c,$$

  (28)

  with $W_c\in {\mathbb{R}}^{C\times d^{\prime }}$ and ${\mathbf{b}}_c\in {\mathbb{R}}^C$. A softmax function is then applied to $\mathbf{z}$ to produce the final probability distribution:

  $$\mathbf{p}=Softmax\left(\mathbf{z}\right)\in {\mathbb{R}}^C.$$

  (29)
  Each entry $p_c$ corresponds to the predicted probability of the c-th emotion class.

3.8.2. Training Objective

The classifier is trained in conjunction with the entire multimodal framework using a composite loss that comprises a primary classification loss and an auxiliary diversity loss:

• Cross-Entropy Loss ${\mathcal{L}}_{\mathrm{CE}}$: This is the primary loss function for multi-class classification, defined for a single training instance with ground-truth label y as:

  $${\mathcal{L}}_{\mathrm{CE}}=-\sum _{c=1}^C{y}_{c}log{p}_c,$$

  (30)

  where $y_c\in \{0,1\}$ is the one-hot indicator for class c, and $p_c$ is the model’s predicted probability. Over a batch of N instances, we typically average or sum ${\mathcal{L}}_{\mathrm{CE}}$ across all samples.
• Diversity Loss ${\mathcal{L}}_{\mathrm{div}}$: To promote specialization among sub-experts in the earlier stages of the network, we add an auxiliary term:

  $${\mathcal{L}}_{\mathrm{div}}=\sum _{m=1}^M\sum _{k=1}^{K_m}\left(w_k^{\left(m\right)}log{w}_k^{\left(m\right)}\right),$$

  (31)

  which penalizes uniform gating distributions by encouraging the gating weights $w_k^{\left(m\right)}$ to be more peaked. This term indirectly influences the classification network by shaping the upstream feature representations.
• Total Loss ${\mathcal{L}}_{\mathrm{total}}$: The overall objective balances the cross-entropy and diversity terms:

  $${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{CE}}+\lambda {\mathcal{L}}_{\mathrm{div}},$$

  (32)

  where $\lambda$ is a hyperparameter controlling the impact of the diversity constraint.

4. Experiments

This section presents an experimental evaluation of the proposed Mixture of Experts (MoE) framework for multimodal emotion recognition. We outline the datasets, evaluation metrics, and baseline models used for comparison. We also detail the experimental setup used to rigorously assesses the performance and robustness of our approach.

4.1. Experiment Setup

This section describes the software environment and hardware used in the experiment. Keras, which is an open source deep learning library based on Tensorflow, was used to build the learning model. All experiments were conducted on a PC Server with an AMD Ryzen 7 2700x Eight-core processor 3.7 GHz processor, two GPUs (NVIDIA GeForce RTX 3090), and 32 GB of memory.

Evaluation Metric

In this article, the performance evaluations were carried out based on the following metrics:

• Accuracy: Accuracy is a metric used in attack detection that represents the correctly identified traffic samples as a proportion of all identified samples. It can be defined as follows:

  $$Accuracy={\displaystyle \frac{(TP+TN)}{(TP+TN+FP+FN)}}$$

  (33)
• Precision: Precision is a performance metric that measures the percentage of correctly identified samples in Class A out of all the samples that were identified as Class A. Mathematically, precision can be calculated as follows:

  $$Precision={\displaystyle \frac{TP}{(TP+FP)}}$$

  (34)
• Recall: Recall measures the proportion of actual positive instances that are correctly identified by a classifier or model. It is calculated as the ratio of true positive instances to the sum of true positive and false negative instances. It is used to evaluate the completeness or sensitivity of a model in detecting positive instances, defined as follows:

  $$Recall=TPR={\displaystyle \frac{TP}{(TP+FN)}}$$

  (35)
• F1-score: The F1-score considers both precision and recall. It is the harmonic mean of precision and recall and provides a single score that summarizes the model’s performance. A higher score indicates better performance. It is defined as follows:

  $$F-Measure={\displaystyle \frac{(1+{\beta }^2)\times Recall\times Precision)}{({\beta }^2\times Recall\times Precision)}}$$

  (36)
• G-mean: The G-mean metric measures the classification performance balance between the majority and minority class. A low G-mean value suggests poor prediction of positive examples, regardless of the correct classification of negative examples. Therefore, it is a crucial metric to avoid overfitting to the negative class and assess how well the positive class is represented. It is defined as follows:

  $$G-mean=\sqrt{{\displaystyle \frac{TP}{TP+FN}}\times {\displaystyle \frac{TN}{TN+FP}}}$$

  (37)

4.2. Dataset

In our experiments, we employed two multimodal emotion recognition datasets: the ASCERTAIN dataset and the Korean Emotion Multimodal Database (KEMDy20). These datasets provide complementary perspectives on emotional expression across different cultural and interaction contexts.

4.2.1. ASCERTAIN Dataset

The ASCERTAIN dataset comprises multimodal physiological and facial responses collected from 58 participants who viewed 36 carefully selected video clips, yielding approximately 2088 individual samples. What sets this dataset apart is its integration of personality assessments with a range of physiological and facial expression measurements. The dataset provides two main modalities: (1) Physiological signals, including ElectroCardioGram (ECG), ElectroEncephaloGram (EEG), and Galvanic Skin Response (GSR), along with (2) facial emotion (EMO) features as the facial modality. Each signal contributes uniquely to emotional state recognition: ECG reflects cardiovascular activity, EEG captures neural responses across 14 channels, and GSR measures arousal via changes in skin conductance. EMO features track dynamic changes in facial expressions. The physiological signals were preprocessed through the following steps: low-pass filtering to eliminate high-frequency noise, standardization to zero mean and unit variance to reduce inter-subject variability, and resampling using interpolation to align different sampling rates. For ECG, we specifically extracted the final 14 features known to carry relevant cardiac information based on domain knowledge. These signals were segmented into fixed-length windows and synchronized with the facial modality. The resulting inputs were normalized and fed into modality-specific transformer encoders. It is important to note that the ASCERTAIN dataset does not contain audio or text modalities. In our experiments, we partitioned the ASCERTAIN dataset into training, validation, and test sets using a 70%:10%:20% split. This division ensures robust training, proper hyperparameter tuning, and reliable model evaluation. The personality traits in ASCERTAIN follow the Big-Five model: Extraversion, Agreeableness, Conscientiousness, Neuroticism, and Openness.

Figure 3a,b illustrate the relative importance of different physiological features in predicting the emotional dimensions of arousal and valence. These visualizations show that ECG and GSR features contribute most significantly, particularly for arousal prediction. The class distribution analysis presented in Figure 4 shows a relatively balanced representation of personality traits across participants, with some natural variation typical to psychological datasets.

4.2.2. Korean Emotion Multimodal Database (KEMDy20)

The Korean Emotion Multimodal Database 2020 (KEMDy20) is a comprehensive dataset designed to capture emotional expressions across multiple synchronized channels. It was collected from 80 Korean-speaking adults aged 19–39 who participated in dyadic, naturalistic conversation sessions. Each session was recorded under ethical guidelines approved by the Korea National Institute for Bioethics Policy. In total, the KEMDy20 dataset comprises approximately 13,462 labeled utterance samples reflecting diverse emotional expressions. The dataset provides three key modalities: (1) speech data, including raw audio recordings, verbal content, paralinguistic features, and time-aligned annotations; (2) physiological data, consisting of ElectroDermal Activity (EDA), Inter-Beat Interval (IBI), and skin TEMPerature (TEMP) measurements synchronized with the speech segments; and (3) text, extracted from the transcribed speech data. Physiological signals were segmented into fixed-length windows synchronized with speech and text, then normalized and passed into dedicated transformer encoders. The textual data was processed using the KoElectra-base-v3-discriminator [59], a transformer-based model fine-tuned for Korean language understanding, which ensured rich semantic and syntactic representations. It is important to note that the KEMDy20 dataset does not include facial expression data. For our analyses, we partitioned the KEMDy20 dataset into training, validation, and test sets using a 70%:10%:20% split. This proportional division ensures model robustness during training and reliability during hyperparameter tuning and evaluation. Figure 5 illustrates the distribution of emotion labels in the dataset, where “neutral” dominates, followed by “happy”, and then relatively fewer samples of “surprise”, “angry”, “sad”, and “fear”. This imbalance reflects the natural occurrence of emotions in real-world conversations and emphasizes the challenge of categorical emotion classification. Additionally, the presence of continuous arousal ratings on a 1-to-5 scale allows for nuanced evaluation of emotional intensity beyond discrete categories.

4.3. Results Analysis

4.3.1. Results Analysis on the ASCERTAIN Dataset

Training Loss Evaluation

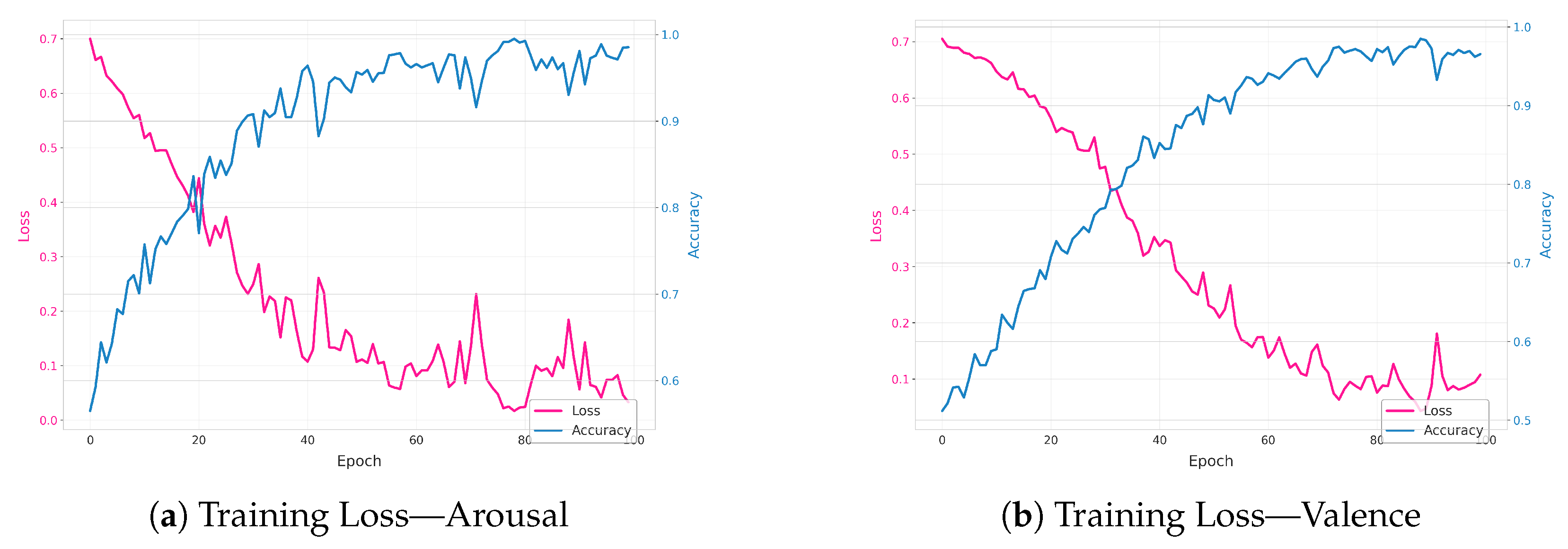
The plots in Figure 6 showcase the losses that we obtained after training the proposed approach on the ASCERTAIN dataset focusing on both arousal and valence. In the first plot (arousal), the training loss (pink) starts relatively high but steadily falls as the model learns, while the accuracy (blue) steadily rises toward near-perfect levels. This behavior indicates that the model effectively captures arousal-related features over the training epochs; however, such high accuracy warrants checking against a separate test or validation set to rule out potential overfitting.

The second plot (valence) exhibits a similar pattern—loss decreases while accuracy increases—yet the trajectory shows a bit more fluctuation, suggesting that valence prediction may be a slightly trickier or noisier target. Periodic spikes in the loss, especially later in training, can occur when the optimizer encounters challenging batches or takes more aggressive steps. Nevertheless, the overall downward trend of the loss and upward trend of accuracy confirm that the model successfully learns from the valence data.

Model Performance

In this section, we present a thorough analysis of our model’s classification performance on both arousal and valence tasks. As summarized in

Table 1. Classification results for arousal and valence prediction on ASCERTAIN dataset.

Metrics	Arousal Prediction (%)	Valence Prediction (%)
Accuracy	99.71	99.71
Precision	100.00	99.92
Recall	99.65	99.60
F1 Score	99.83	99.76
G-Mean	99.38	99.73
AUC-ROC	99.99	100.00

, we evaluated the model for accuracy, precision, recall, F1-score, G-mean, and AUC-ROC (Area Under the Receiver Operating Characteristic curve). It achieved consistently high values across both prediction setups. In particular, arousal prediction achieved an accuracy of 99.71%, precision of 100%, recall of 99.65%, F1 of 99.83%, G-mean of 99.38%, and an AUC-ROC of 99.99%. Meanwhile, valence prediction demonstrates an accuracy of 99.71%, precision of 99.92%, recall of 99.60%, F1 of 99.76%, G-mean of 99.73%, and a perfect AUC-ROC of 100%. These metrics collectively illustrate the model’s robust performance and high discriminative power in differentiating the emotional states within the ASCERTAIN dataset.

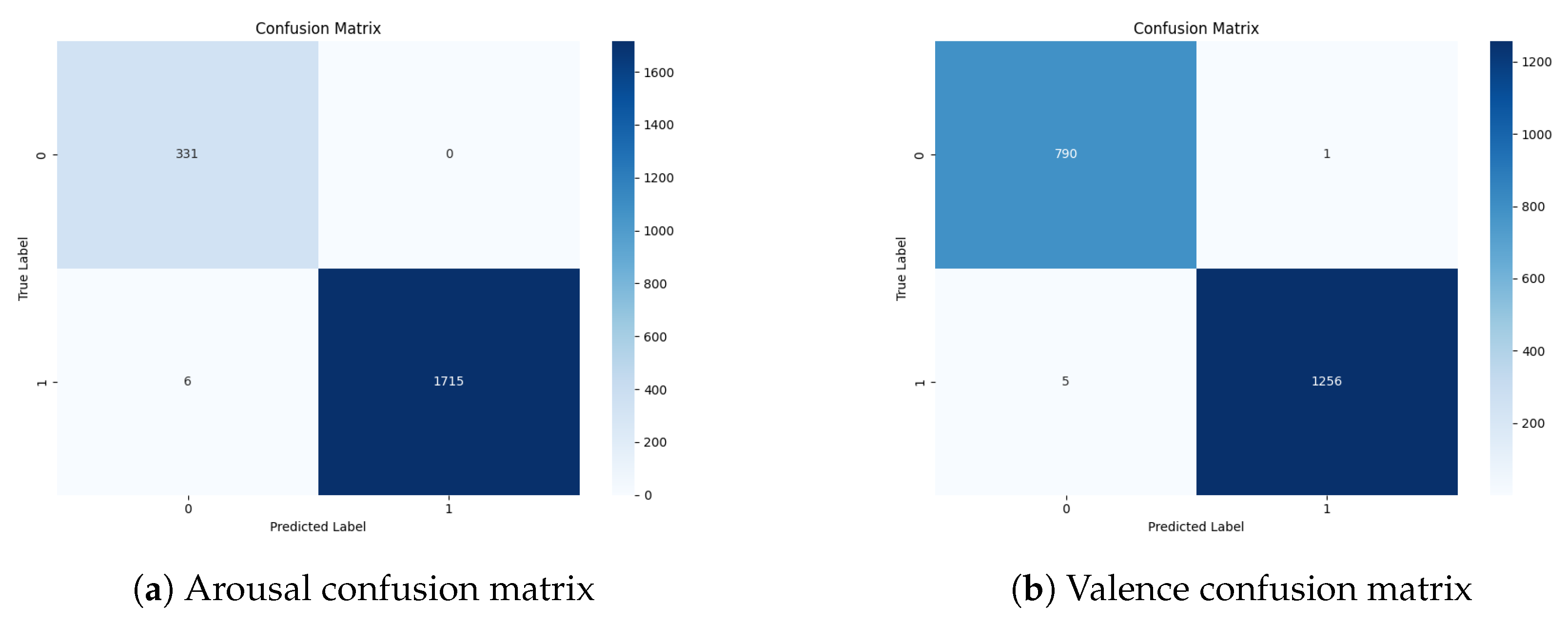
In Figure 7, we present the confusion matrix for both prediction types. Focusing on the arousal confusion matrix, the model correctly identified 331 “low” arousal samples (true negatives) with zero false positives while accurately classifying 1715 “high” arousal samples (true positives) at the cost of only 6 misclassifications (false negatives). This near-perfect balance between precision (100%) and recall (99.65%) directly leads to a high F1-score of 99.83%, reflecting the model’s ability to consistently make correct predictions for both classes. The G-mean of 99.38% confirms that performance is not skewed toward any one class, while an AUC-ROC of 99.99% highlights the model’s excellent capacity to separate “low” and “high” arousal instances under various decision thresholds.

Turning to the valence confusion matrix, the model demonstrates similarly high fidelity: 790 “low” valence samples are correctly classified and only 1 is misclassified (false positive), while 1256 “high” valence samples are correctly identified with merely 5 false negatives. This yields a high precision of 99.92% and recall of 99.60%, contributing to an F1-score of 99.76%. Notably, the G-mean of 99.73% points to well-balanced performance across the two valence levels, and the flawless 100% AUC-ROC indicates the model’s ability to discriminate “low” vs. “high” valence over the full spectrum of potential classification thresholds. Overall, these results attest to the robustness and generalizability of our transformer-based approach for emotion classification with the ASCERTAIN dataset.

Visualization of Learned Feature Representations

To gain deeper insights into the feature representations learned by our model, we employ t-distributed Stochastic Neighbor Embedding (t-SNE), a popular dimensionality reduction technique that visualizes high-dimensional data in a two-dimensional space. The goal of this experiment is to assess the quality of the learned feature representations for both arousal and valence prediction by examining how well the feature embeddings separate different emotional states.

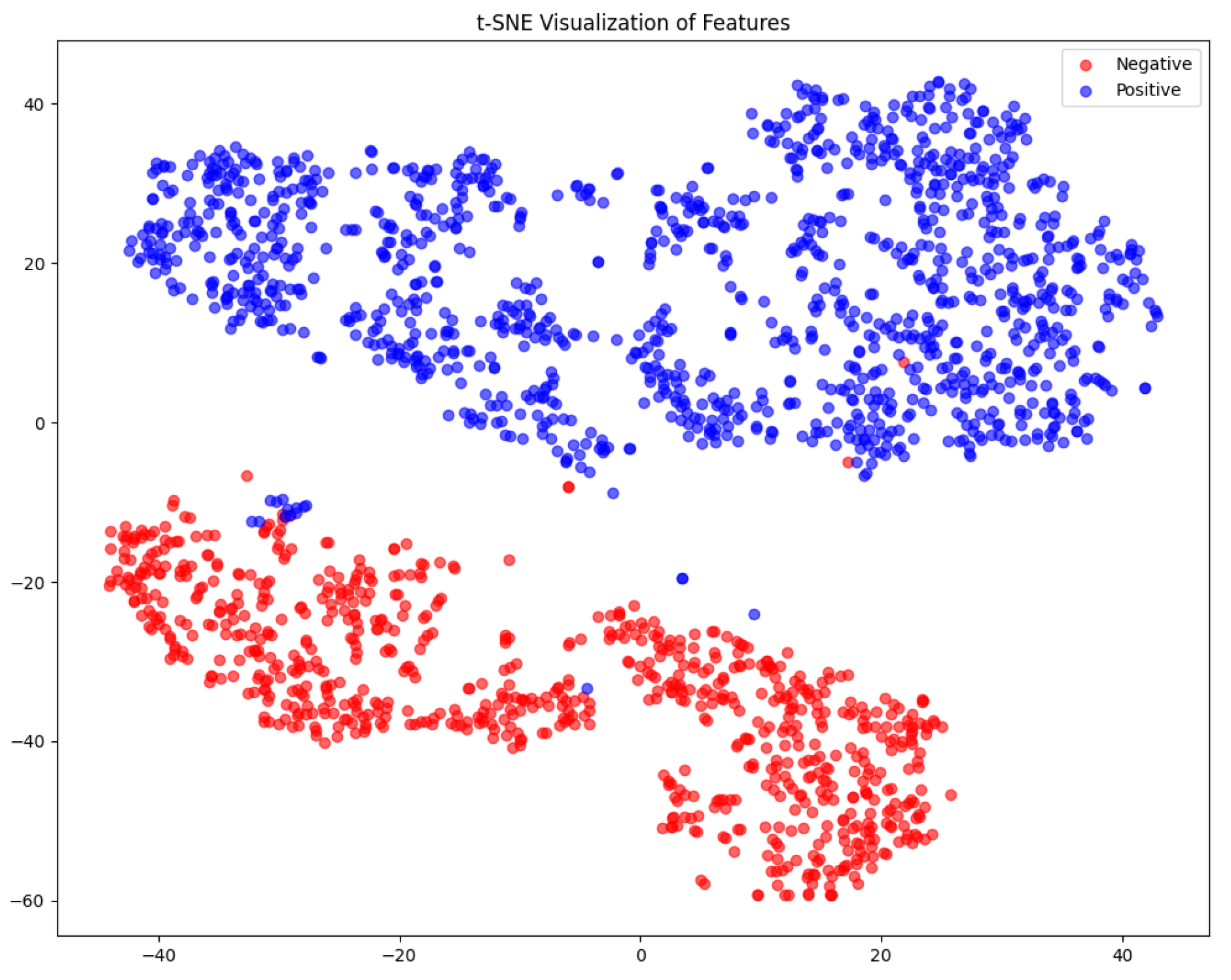
As presented in Figure 8, the t-SNE visualization for arousal prediction reveals two well-separated clusters, indicating that the model effectively distinguishes between positive and negative arousal states. The strong separation suggests that the learned feature representations capture variations in arousal accurately, minimizing ambiguity. The low degree of overlap between clusters highlights the model’s discriminative power, reinforcing its ability to classify arousal states with high confidence. However, a few scattered points near the boundary suggest the presence of ambiguous cases, where arousal levels may not be strictly high or low, potentially leading to minor misclassifications.

For the valence prediction depicted in Figure 9, we can see that the two clusters remain distinct from each other. However, the separation margin appears slightly smaller than it is for arousal. The increase in overlapping points suggests that distinguishing between positive and negative valence is relatively more challenging. Despite this, the tight clustering indicates that the model learns compact and well-structured feature representations for valence classification. The inter-cluster separation remains evident, which is encouraging, though a few scattered points near the boundary may reflect instances of mixed emotional valence, where emotions are not clearly polarized.

These findings validate the effectiveness of our approach and suggest that further fine-tuning could focus on reducing any overlap in valence representations to improve classification accuracy further.

Impact Analysis of Different Expert Combinations

In this section, we review our extensive evaluation of how different modality–expert combinations impact arousal prediction performance. This experiment is crucial because it clarifies how each physiological or contextual signal—from ECG to EEG to GSR to EMO— contributes unique information. It also shows how combining these signals in various ways either enhances or diminishes the model’s ability to accurately classify arousal states.

Focusing first on the single-modality expert performance in

Table 2. Single-modality expert performance evaluation for arousal prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG	75.97	93.86	76.35	84.20	82.37	85.85
EEG	99.17	99.59	99.42	99.51	99.29	99.94
GSR	85.38	87.10	96.92	91.75	90.83	71.80
EMO	86.55	91.40	92.68	92.04	92.53	87.33

, we see that EEG stands out with an accuracy of 99.17%, an F1-score of 99.51%, and an almost perfect AUC-ROC of 99.94%. This suggests that brain activity signals alone carry substantial information for arousal detection. GSR (Galvanic Skin Response) and EMO (presumably emotion-related contextual cues) achieve moderate yet solid performances, each exceeding 85% in accuracy and surpassing 90% in G-mean, indicating a decent balance across both classes. However, ECG (electrocardiogram) yields the lowest accuracy at 75.97%, despite having relatively high precision. The lower recall of 76.35% for ECG suggests that while it rarely mislabels non-arousal samples, it is not as adept at capturing all positive (high-arousal) instances, which lowers the overall F1-score to 84.20%.

Table 3. Two-modality expert performance evaluation for arousal prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG	99.71	100.00	99.65	99.83	99.78	100.00
ECG + GSR	95.96	99.88	95.29	97.53	96.84	99.76
ECG + EMO	88.11	99.86	85.94	92.38	90.73	98.53
EEG + EMO	99.17	99.71	99.30	99.51	99.62	99.97
GSR + EEG	98.88	100.00	98.66	99.33	99.69	99.96
GSR + EMO	93.57	99.44	92.85	96.03	94.86	99.27

depicts the results of combining two modalities; the synergy from using two signals emerges clearly. ECG + EEG achieves a near-flawless accuracy of 99.71% and a perfect 100% AUC-ROC, signifying the strong complementarity nature of using heart-rate and brain wave data together for emotion recognition. Similarly, EEG + EMO and GSR + EEG both exceed 98.8% accuracy, reinforcing the value of EEG as a critical modality. In the three-modality experts results represented in

Table 4. Three-modality expert performance evaluation for arousal prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG + EMO	98.73	100.00	98.49	99.24	99.15	100.00
ECG + GSR + EEG	99.95	100.00	99.94	99.97	99.93	100.00
ECG + GSR + EMO	95.13	99.94	94.25	97.01	96.89	99.80
GSR + EEG + EMO	99.12	99.88	99.07	99.47	99.19	99.98

, ECG + GSR + EEG stands out with a remarkable accuracy of 99.95%, an F1-score of 99.97%, and a 100% AUC-ROC—making it arguably the best performing combination overall. Interestingly, adding all four modalities (ECG + EEG + GSR + EMO), as presented in

Table 5. All-modality expert performance evaluation for arousal prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG + GSR + EMO	99.71	100.00	99.65	99.83	99.38	99.99

maintains an impressive accuracy of 99.71% with a 99.99% AUC-ROC, though it does not surpass the top three-modality expert. This slight dip indicates that introducing additional signals does not always guarantee higher accuracy, highlighting the importance of judicious modality selection and fusion strategies for optimal arousal classification.

Furthermore, we also analyzed the valence-prediction performance across various modality--expert combinations. By systematically comparing single-modality experts against multi-modal configurations, we identified which signals—and how many—most effectively captured the underlying valence patterns.

Looking first at the single-modality experts in

Table 6. Single-modality expert performance evaluation for valence prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG	62.62	62.39	98.65	76.44	72.38	52.10
EEG	98.78	98.66	99.37	99.01	99.18	99.96
GSR	53.90	85.55	30.06	44.48	42.89	67.76
EMO	80.12	99.08	68.28	80.85	79.89	94.32

, EEG achieves the highest accuracy (98.78%) and nearly perfect AUC-ROC (99.96%), suggesting that brain wave features alone offer a strong basis for valence discrimination. EMO also delivers respectable performance (80.12% accuracy, 80.85% F1-score), while ECG shows a moderate 62.62% accuracy but surprisingly high recall (98.65%), indicating a tendency to over-predict the positive class. In contrast, GSR registers the lowest accuracy (53.90%) and recall (30.06%), illustrating that skin-conductance data by itself may not be sufficient for accurately capturing valence variations.

Turning to Two-modality experts (

Table 7. Two-modality expert performance evaluation for valence prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG	99.76	99.84	99.76	99.80	99.72	99.99
ECG + GSR	88.84	94.56	86.84	90.53	89.96	96.72
ECG + EMO	84.60	96.01	78.19	86.19	80.96	95.86
EEG + EMO	99.37	98.98	100.00	99.49	98.99	99.98
GSR + EEG	99.66	99.68	99.76	99.72	99.87	99.99
GSR + EMO	94.40	96.66	94.13	95.38	93.99	99.23

), combining ECG + EEG yields an impressive 99.76% accuracy and a near-perfect 99.99% AUC-ROC, highlighting the complementary nature of heart-rate and brain wave cues. Likewise, GSR + EEG attains 99.66% accuracy and a 99.99% AUC-ROC, demonstrating that GSR’s limitations are significantly mitigated when coupled with EEG’s robust signal features. Notably, EEG + EMO also excels, with 99.37% accuracy and 99.98% AUC-ROC, indicating the added benefit of contextual or behavioral signals alongside neural activity.

Examining the three-modality experts in

Table 8. Three-modality expert performance evaluation for valence prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG + EMO	99.03	99.76	98.65	99.20	98.72	99.97
ECG + GSR + EEG	99.85	99.92	99.84	99.88	99.06	100.00
ECG + GSR + EMO	90.59	94.87	89.53	92.13	90.39	98.11
GSR + EEG + EMO	98.78	99.52	98.49	99.00	98.77	99.97

, ECG + GSR + EEG stands out with a near-perfect 99.85% accuracy and 100% AUC-ROC, showcasing exceptional synergy among these signals. Meanwhile, ECG + EEG + EMO achieves 99.03% accuracy and 99.97% AUC-ROC, and GSR + EEG + EMO is only slightly behind at 98.78% accuracy. Finally, fusing all four modalities (ECG + EEG + GSR + EMO) in

Table 9. All-modality expert performance evaluation for valence prediction on ASCERTAIN dataset.

Modalities Expert	Accuracy	Precision	Recall	F1-Score	G-Mean	AUC-ROC
ECG + EEG + GSR + EMO	99.71	99.92	99.60	99.76	99.73	100.00

produces a 99.71% accuracy with a flawless 100% AUC-ROC, surpassing most three-expert combinations. This outcome underscores the value of multimodal integration for capturing nuanced valence patterns while also showing that EEG is a critical contributor to high-fidelity valence classification.

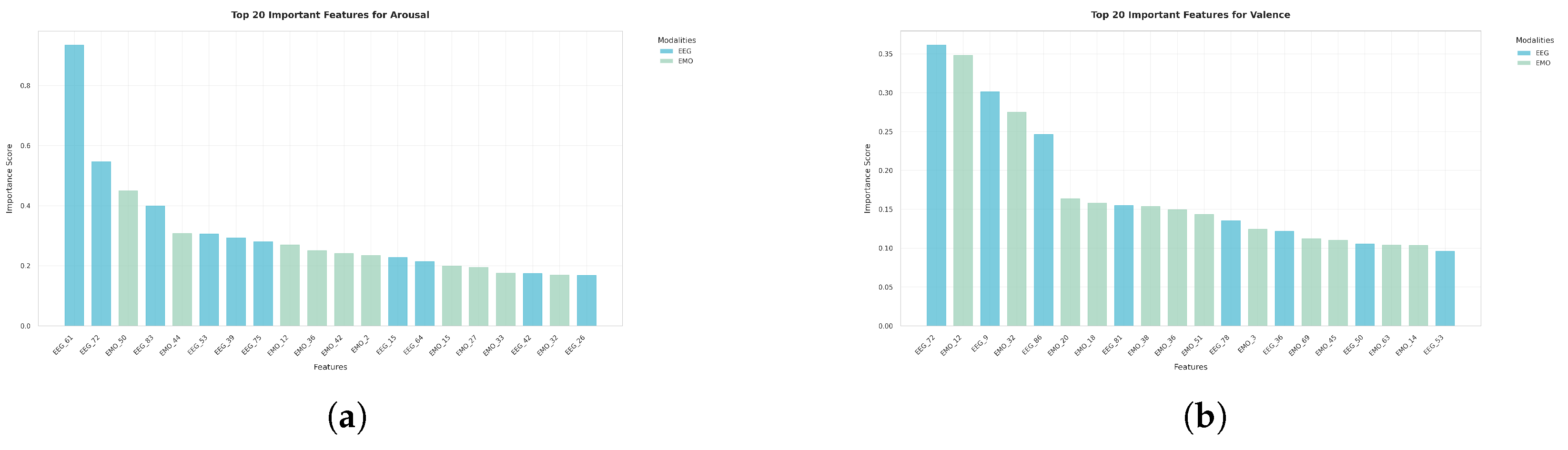
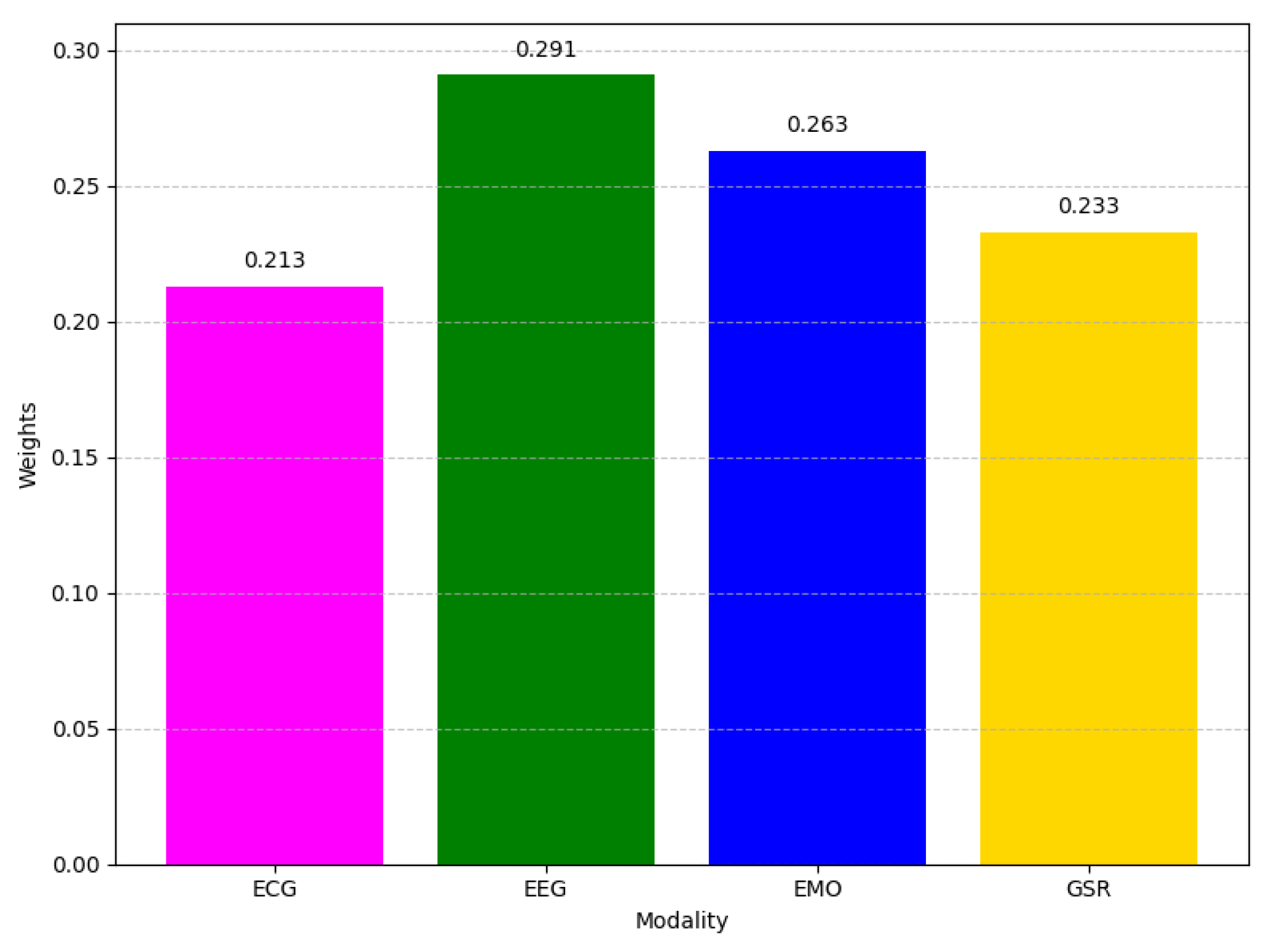
In Figure 10, which gives the importance weighting of each input modality for arousal prediction, EEG exhibits the highest normalized fidelity score at 0.291, reinforcing earlier observations that neural activity signals contain rich information for accurately distinguishing different arousal levels. EMO ranks second (0.263), implying that emotional or behavioral contextual cues also play a substantial role in the arousal inference. GSR (0.233) is slightly less important but still makes a non-trivial contribution, while ECG (0.213) shows the smallest weight in the ensemble. This pattern generally aligns with our single-modality and multi-modality experiments, suggesting that EEG remains the leading modality for capturing arousal, though other signals reinforce the final decision.

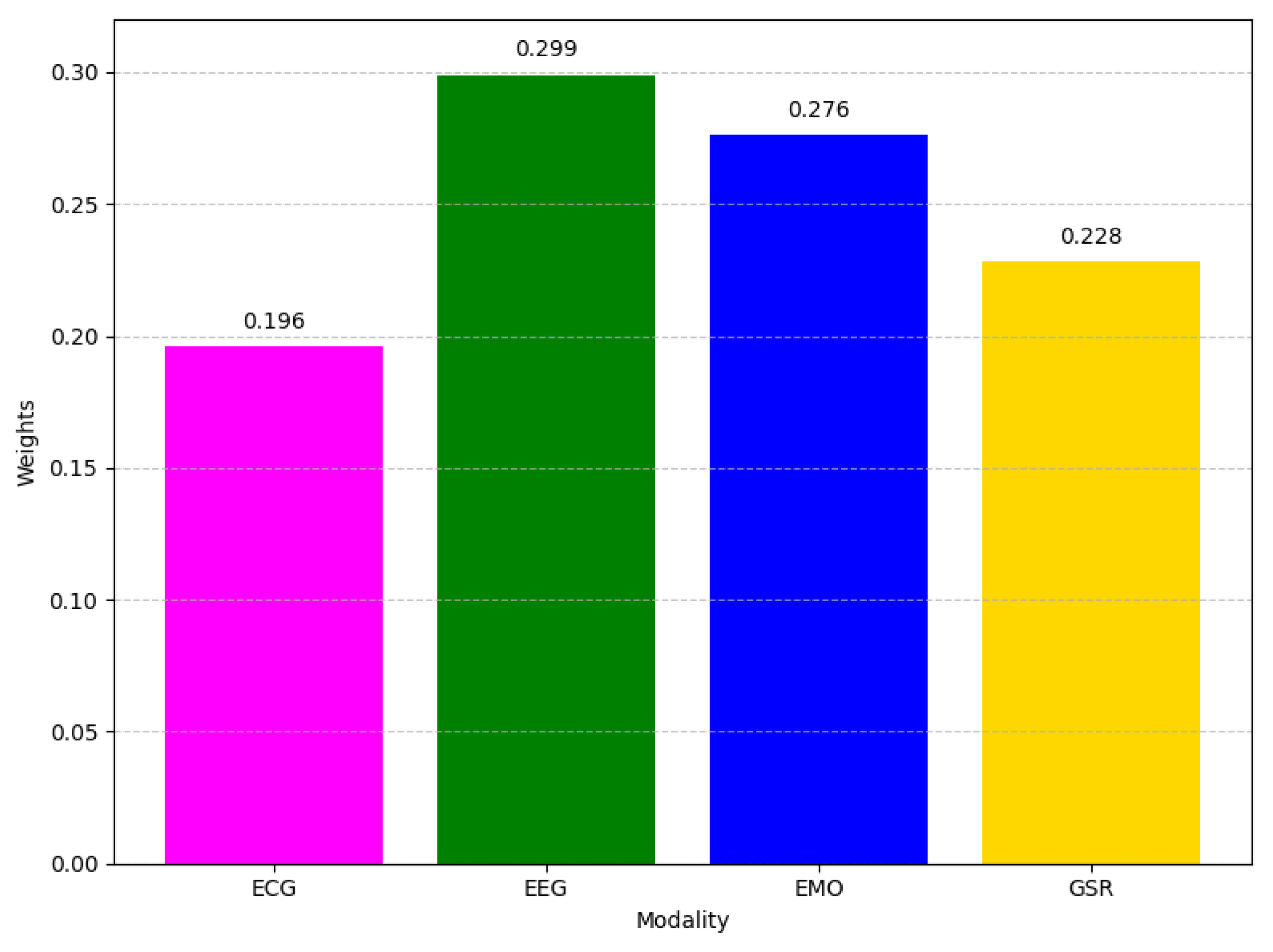
A similar trend is depicted in Figure 11, which gives the relative importance of each modality in valence prediction, where EEG (0.299) maintains the largest impact by a comfortable margin. EMO (0.276) again closely follows, confirming that capturing emotional or contextual signals continues to be highly valuable for distinguishing positive and negative valence. Meanwhile, GSR (0.228) and ECG (0.196) show comparatively lower importance, mirroring the relative contributions observed in the arousal task. Hence, across both experiments, EEG consistently emerges as the most valuable source of information, with EMO often reinforcing classification performance. GSR and ECG make smaller yet still meaningful contributions to the model’s predictive power.

Comparative Study with State-of-the-Art Approaches

In this section, as presented in

Table 10. Comparison of different approaches for arousal and valence prediction.

Approach	Arousal Prediction (%)	Valence Prediction (%)
LSTM [60]	81.60	79.18
Deep CNN [61]	78.70	75.60
Deep CNN-CBAM [61]	78.70	75.60
Ensemble approach [62]	95.00	93.00
LSTMP [60]	89.17	86.49
Our Approach	99.71	99.71

, we provide a comprehensive comparison of our method against several highly regarded works in the literature, illustrating how our approach advances the state of the art for both arousal and valence prediction. Examining the table, we see that traditional deep learning architectures like LSTM [60] achieve 81.60% for arousal and 79.18% for valence, while Deep CNN and Deep CNN-CBAM [61] both score around 78.7% and 75.6% for valence and arousal predictions, respectively. Although the ensemble approach [62] improves these metrics to 95% for arousal and 93% for valence, and LSTMP [60] achieves scores of 89.17% and 86.49%, respectively, our proposed technique exceeds all previous methods with an exceptional 99.71% for both arousal and valence.

These results indicate that our transformer-based architecture, combined with its effective fusion strategy, substantially enhances emotional state classification performance. The improvements are particularly pronounced when compared to methods that rely solely on recurrent or convolutional layers. Overall, this comparison underscores the value of our design choices in capturing nuanced features from multimodal signals, thus advancing the benchmark for emotion recognition in terms of both predictive accuracy and robustness.

4.3.2. Results Analysis on the KEMDy20 Dataset

Training Loss Evaluation

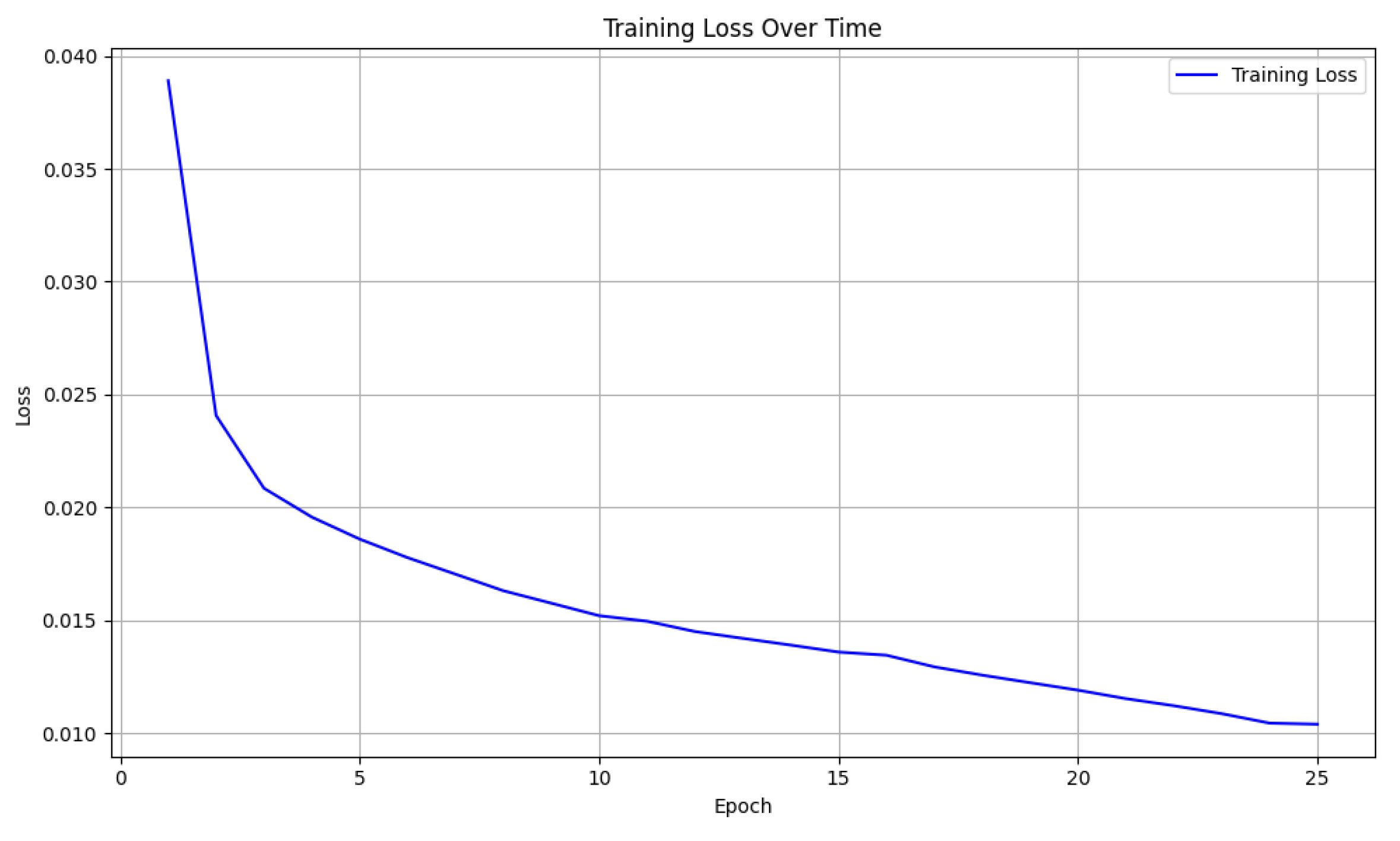
Looking the training–loss curve in Figure 12, we see a rapid drop during the initial few epochs from just under 0.040 down to approximately 0.020, indicating the model is able to quickly learn fundamental patterns in the data. As training progresses beyond epoch five, the loss continues to decrease but at a more gradual pace, suggesting a smooth fine-tuning phase in which the network refines its internal representations. By epoch 25, the loss settles at around 0.009, a reflection that the model has effectively converged without obvious signs of plateauing too early or overfitting in the training phase. Overall, this trajectory aligns well with standard deep learning behavior, illustrating stable learning progress and reinforcing that the model is successfully capturing relevant signals in the KEMDy20 dataset.

Model Performance

The following results in

Table 11. Model classification performance summary on KEMDy20 dataset.

Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	G-Mean (%)	AUC (%)
94.49	90.14	94.49	92.25	91.77	94.82

highlight our model’s classification performance on the KEMDy20 dataset across seven emotional categories. By examining both the standard metrics and the confusion matrix, we can assess how effectively our approach distinguishes among fine-grained emotional states: neutrality, happiness, surprise, anger, sadness, disgust, and fear. Overall, the accuracy reaches 94.49%, with a recall of 94.49% and a precision of 90.14%, yielding an F1-score of 92.25% and a G-mean of 91.77%. These results suggest the model not only classifies most instances correctly but also balances minority classes reasonably well.

Furthermore, the 94.82% AUC value indicates the model’s strong discriminative power over various decision thresholds. In the confusion matrix presented in the Figure 13, “Neutral” obtains a correct classification rate of 0.911, “Happy” 0.921, “Surprise” 0.913, “Angry” 0.939, “Sad” 0.922, “Disgust” 0.910, and “Fear” 0.945. These high scores underline the model’s robust performance across all categories.

Moving to misclassifications, “Disgust” is confused with “Neutral” 4.8% of the time, while “Happy” can be misclassified as “Sad” (3.6%) or “Angry” (2.9%). Similarly, “Fear” occasionally overlaps with “Neutral” (4.3%), though the model still correctly labels 94.5% of “Fear” instances. These small but not insignificant overlaps suggest that certain emotional states exhibit subtle common features. Overall, the strong diagonal entries confirm the model’s effectiveness in capturing distinguishing patterns for each emotion, while the relatively small off-diagonal values mark areas where further fine-tuning or context-aware features could help reduce confusion between closely related emotions.

Visualization of Learned Feature Representations

This experiment offers an intuitive way to inspect how well the model’s learned representations separate different emotional classes in a reduced two-dimensional space. By compressing high-dimensional feature vectors into just two components, we can visually ascertain whether similar emotion categories cluster together and whether distinct emotions form clearly separated regions.

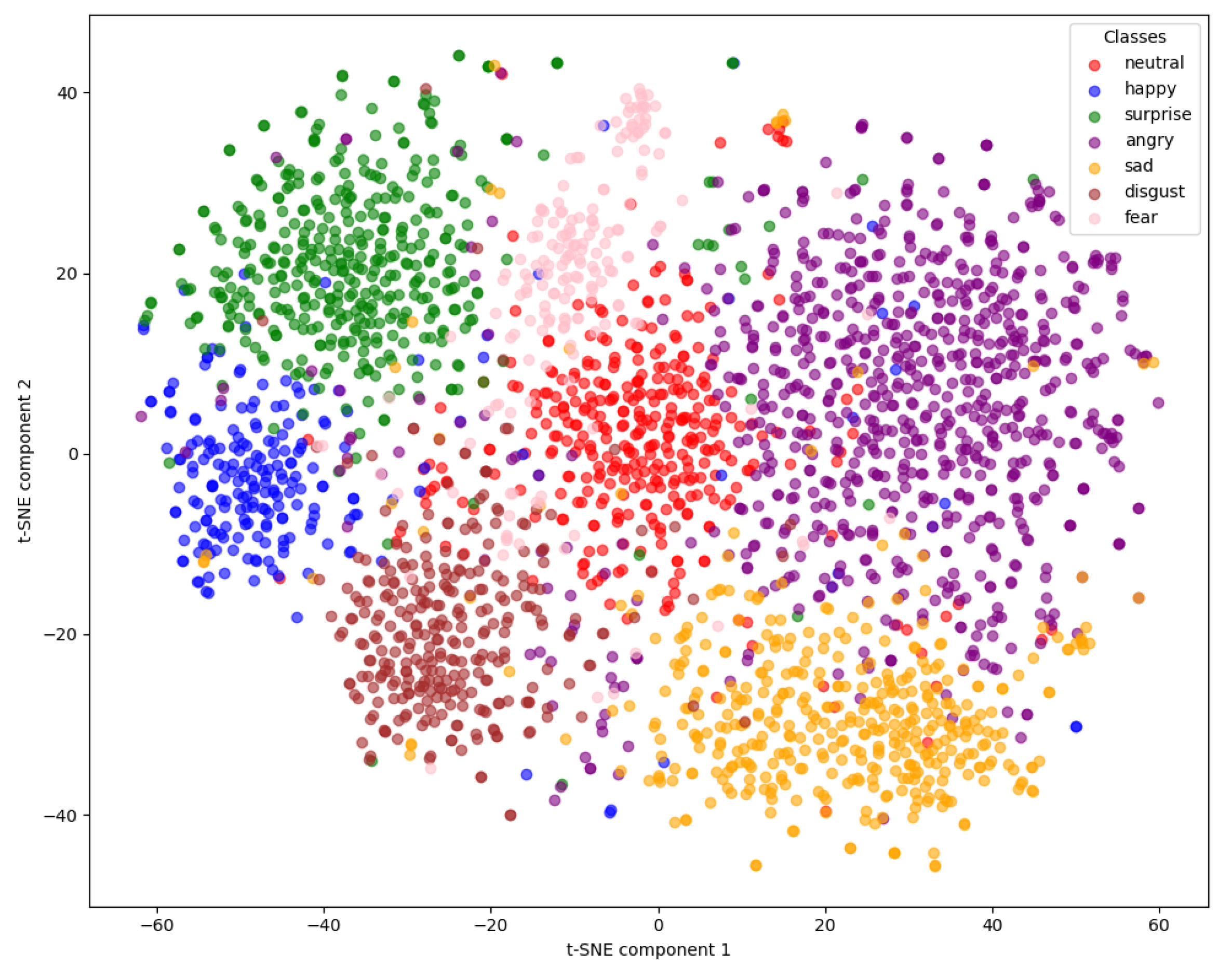
In Figure 14, we can observe coherent clusters for each emotion category. “Neutral” (red) is grouped centrally, surrounded by a relatively uniform boundary as it transitions into other states. “Happy” (blue) appears more isolated on the left, reflecting its distinctiveness from neighboring classes, while “Sad” (orange) and “Angry” (brown) form well-defined groups closer to one another. A subtle overlap between “Surprise” (green), “Disgust” (purple), and certain fringe points of “Fear” (pink) suggests that these expressions share some overlapping features or transition states. Overall, the tight grouping within each emotional class and minimal spread into other regions reveal that our model’s internal feature representations effectively capture the distinguishing characteristics of the seven emotion categories in the KEMDy20 dataset.

Impact Analysis of Different Expert Combinations

In the following, we analyze the model’s performance results when using different combinations of text, audio, and Physiological Signal (PS) experts to clarify which expert, or combination of experts, contributes most toward robust predictions. By comparing single-modality experts (text, audio, PS) with two-modality fusions (text + audio, text + PS, audio + PS), we gain insight into whether certain modalities complement each other or largely overlap in the features they capture.

As presented in

Table 12. Performance of single-modality and two-modality experts on KEMDy20 dataset.

Modalities Expert	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	G-Mean (%)	AUC (%)
Text	87.75	83.29	87.75	85.44	83.99	86.73
Audio	87.63	83.06	87.63	85.25	86.82	80.36
Physiological Signals (PS)	87.30	76.21	87.30	81.38	79.96	73.87
Text + Audio	88.41	83.81	88.41	86.00	84.87	80.51
Text + PS	88.01	83.25	88.01	85.49	85.08	78.96
Audio + PS	88.45	83.72	88.45	85.94	84.79	89.99

, we see that text alone achieves 87.75% accuracy and an F1-score of 85.44%. Audio (87.63% accuracy, 85.25% F1) and PS (87.30% accuracy, 81.38% F1) perform at roughly similar levels, although it should be noted that PS lags slightly in terms of precision (76.21%). When combining two modalities, all configurations exceed 88% accuracy, with audio + PS yielding the highest accuracy (88.45%) and a notably superior AUC (89.99%). Meanwhile, text + audio attains 88.41% accuracy, and text + PS delivers 88.01% accuracy along with balanced scores across other metrics. These findings suggest that while individual modalities capture core emotional cues, combining them often enhances performance, particularly when leveraging audio and physiological signals together.

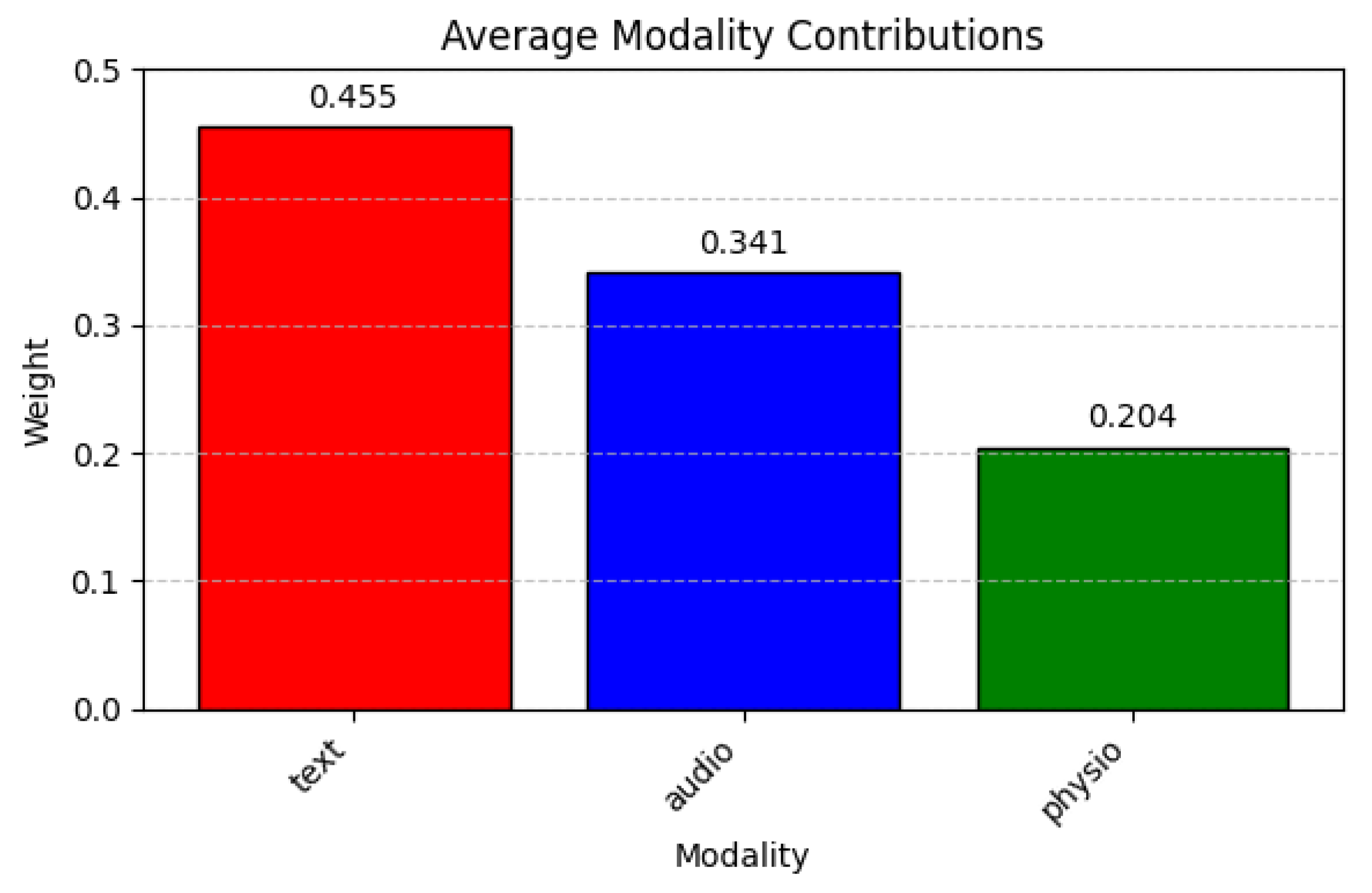
We were also interested in evaluating the importance weighting of each modality because it reveals how the final classification is influenced by each expert contribution to the overall system. Figure 15 shows that text provides the largest contribution (0.455), followed by audio (0.341), then physiological signals (0.204).

This distribution indicates that textual cues are particularly influential for the model, with vocal features also supplying meaningful information, while physiological data act as a more modest but still valuable source of confirmation.

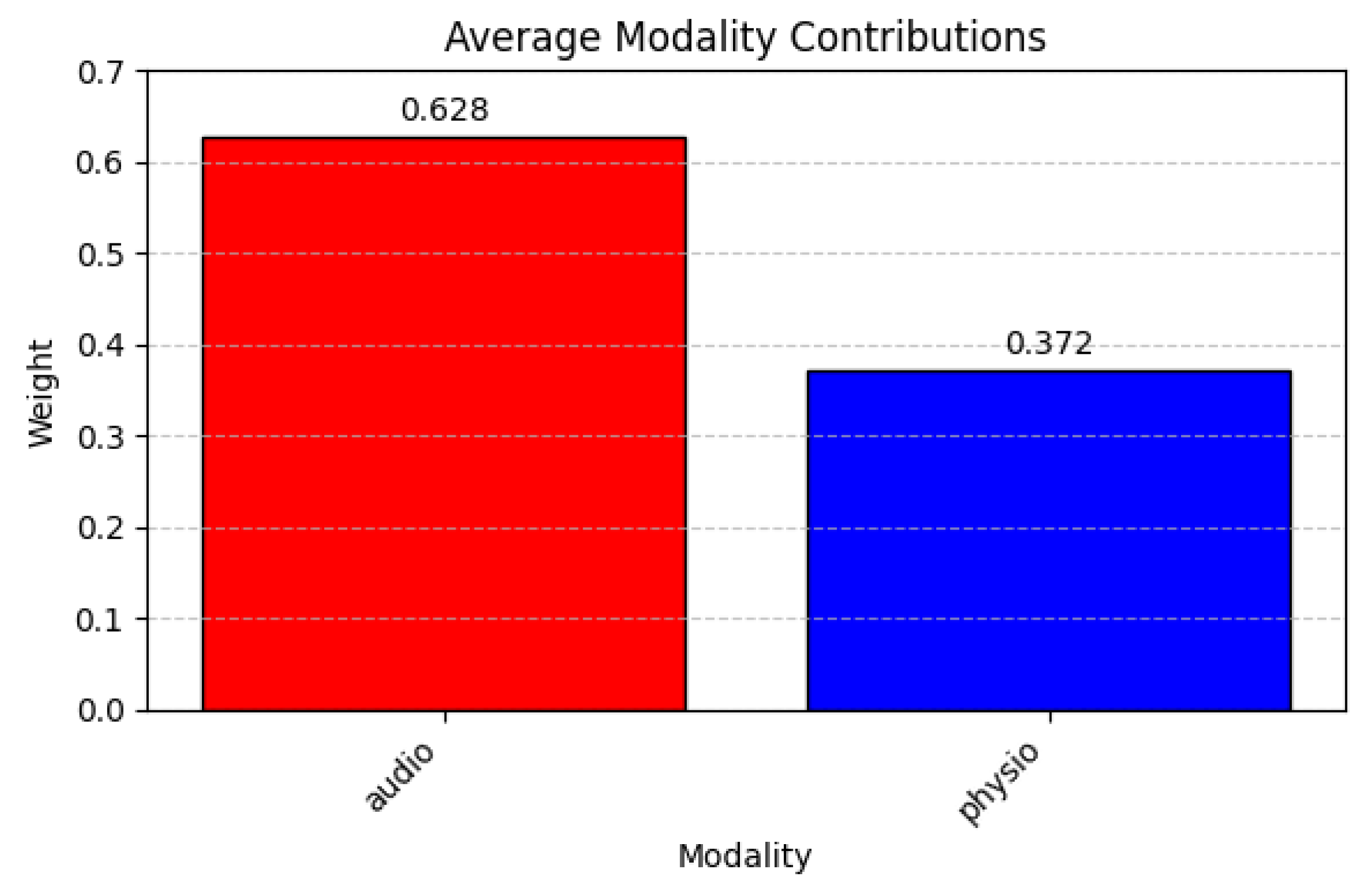
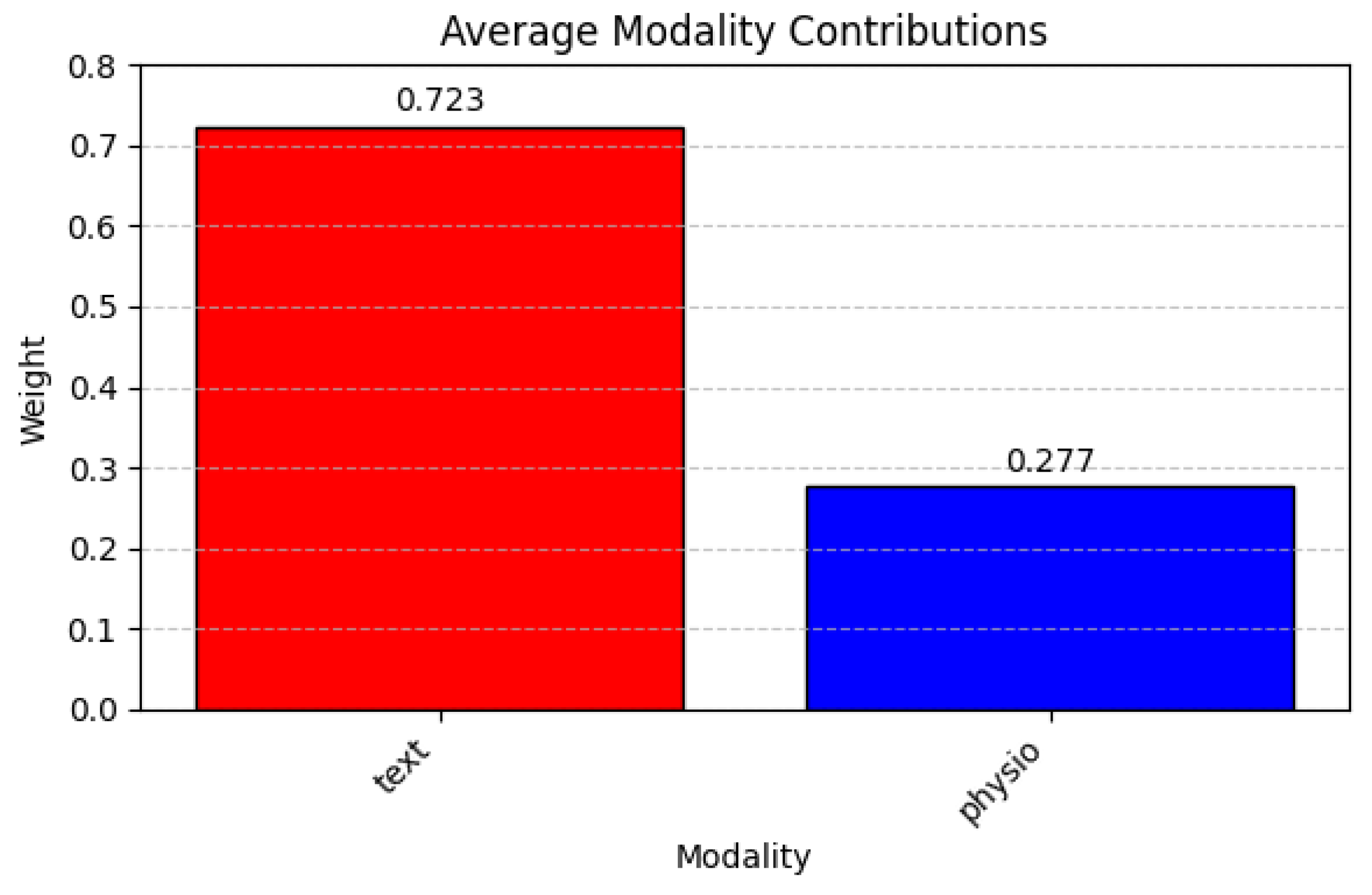
Turning to the pairwise setups, Figure 16 similarly underscores text’s dominance (0.577) compared with audio (0.423). Figure 17 shows audio commanding a weight of 0.628, considerably overshadowing physiological signals at 0.372. Finally, Figure 18 (text + physio) magnifies text’s influence (0.723) even further against physiological signals (0.277). In all these settings, text or audio consistently emerges as the more decisive expert, whereas physiological signals provide secondary support, suggesting that linguistic and acoustic features capture the brunt of emotional or affective cues in this dataset.

Comparative Study with State-of-the-Art Approaches

We present a thorough comparison of the proposed method against several previously reported approaches on the ETRI dataset. As shown in

Table 13. Comparison of different approaches.

Approaches	Accuracy (%)	F1-Score (%)
Transfer Learning [63]	84.80	N/A
KoELECTRA [59]	92.39	89.02
Multi-modal Cross Attention [64]	92.08	89.89
Bidirectional Cross Modal Attention [65]	77.63	77.70
KoHMT [66]	77.45	77.44
HyFusER [65]	79.77	79.75
Our Approach	94.49	92.25

, transfer learning [63] achieves an accuracy of 84.8% (no F1-score is provided), while KoELECTRA [59] and multi-modal cross attention [64] both surpass 92% accuracy, accompanied by F1-scores of around 89%. Furthermore, we have expanded our comparison to include additional recent approaches, bidirectional cross-modal attention [65], KoHMT [66], and HyFusER [65], which achieve accuracies of 77.63%, 77.45%, and 79.77% with corresponding F1-scores of 77.70%, 77.44%, and 79.75%, respectively. Despite the strong performances of several baselines, our approach outperforms all existing methods with an accuracy of 94.49% and an F1-score of 92.25%, thereby providing quantitative evidence of its superiority over both conventional static fusion methods and other recent multimodal approaches.

These results underscore the technical novelty of our method. Unlike conventional static fusion methods, our model integrates multiple modules including dynamic gating with sparse activation and cross-modal attention whose synergistic interplay provides substantial quantitative advantages in terms of accuracy, robustness, and overall discriminative power. The quantitative superiority of our approach clearly demonstrates that the proposed architecture not only captures the nuances within individual modalities but also effectively fuses complementary information across modalities.

4.3.3. Robustness Testing with Incomplete/Inaccurate Data

To further evaluate the resilience of our model under real-world conditions where data may be incomplete or inaccurate, we conducted additional experiments on both the ASCERTAIN and KEMDy20 datasets. In these experiments, we simulate two types of perturbations:

• Incomplete Data: We randomly remove 20% of the samples from the dataset.
• Inaccurate Data: We inject Gaussian noise into the feature values, with a noise level corresponding to 10% of the typical feature magnitude.

These perturbations mimic common issues such as sensor dropout or measurement errors.

Robustness on the ASCERTAIN Dataset

Table 14. Performance metrics for arousal and valence prediction on perturbed ASCERTAIN data.

Metrics	Arousal Prediction (%)	Valence Prediction (%)
Accuracy	97.58	97.41
Precision	98.83	98.65
Recall	97.29	97.14
F1-Score	97.93	97.75
G-Mean	97.45	97.35
AUC-ROC	98.54	98.63

reports the performance metrics for arousal and valence prediction under these perturbed conditions. In comparison to the baseline results on clean data (accuracy: 99.71%, precision: 100%/99.92%, recall: 99.65%/99.60%, F1-score: 99.83%/99.76%, G-mean: 99.38%/99.73%, AUC-ROC: 99.99%/100%), we observe a slight degradation. Specifically, the accuracy drops to approximately 97.58% for arousal and 97.41% for valence. Similarly, other metrics (precision, recall, F1-score, G-mean, and AUC-ROC) decrease by about 1.5–2.5% on average. These results suggest that, even in the presence of data incompleteness and noise, our model maintains a high level of performance, demonstrating its robustness.

The model’s performance on the ASCERTAIN dataset experiences a modest reduction in all metrics (approximately 1.5–2.5%), yet remains high (accuracy above 97% and AUC above 98%). This slight decline indicates that our model is highly resilient to both sample removal and noise injection, preserving its ability to accurately differentiate between low and high-arousal/valence states.

Robustness on the KEMDy20 Dataset

Table 15. Performance metrics for KEMDy20 dataset on perturbed data.

Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	G-Mean (%)	AUC (%)
90.37	87.58	90.33	88.89	88.26	90.75

shows the performance metrics for the KEMDy20 dataset after similar perturbations. The baseline performance on the clean dataset was an accuracy of 94.49%, precision of 90.14%, recall of 94.49%, F1-score of 92.25%, G-mean of 91.77%, and AUC of 94.82%. Under the perturbed conditions, accuracy decreases to 90.37%, and precision, recall, F1-score, and G-mean decline by roughly 3.5–4.5%, with the AUC slightly lower at 90.75%. While the degradation is more pronounced in the KEMDy20 dataset than in the ASCERTAIN dataset, the results still indicate that our model retains strong discriminative power and generalization capability, even with incomplete or noisy data.

In contrast, the performance on the KEMDy20 dataset shows a more noticeable reduction (around 3.5–4.5% drop in key metrics), with the overall accuracy falling to 90.37% and the AUC to 90.75%. Although the performance degrades more in this scenario, the model still exhibits robust classification capabilities across the seven emotional categories. The higher sensitivity of the KEMDy20 dataset to data perturbations may be attributed to its fine-grained emotional labels and inherent class imbalances.

Overall, these experiments validate the robustness and generalizability of our transformer-based approach. Even under conditions of incomplete or inaccurate data, our model maintains strong discriminative power and balanced performance across tasks, which is critical for real-world applications where data imperfections are common.

4.3.4. Ablation Study: Evaluating the Contributions of Key Modules

To thoroughly evaluate how each part of our model contributes to its overall performance, we conducted a detailed ablation study. We systematically removed three important components, one at a time: (1) the Mixture of Experts (MoE) processing block with its dynamic gating mechanism, (2) the cross-modal attention mechanism, and (3) the diversity loss term. For each configuration, we measured performance using accuracy, precision, recall, F1-score, G-mean, and AUC.

Table 16. Ablation study on the ASCERTAIN dataset: module-wise contribution analysis.

Configuration	Acc (%)	Pre (%)	Rec (%)	F1-Score (%)	G-Mean (%)	AUC (%)
Full Model	99.71	100.00	99.65	99.83	99.38	99.99
Without Diversity Loss	97.32	98.88	93.78	93.78	94.69	98.97
Without Cross-Modal Attention	95.99	95.42	96.88	96.18	95.69	94.85
Without MoE and Dynamic Gating	91.98	89.77	91.82	90.82	89.98	90.87

and

Table 17. Ablation study on the KEMDy20 dataset: module-wise contribution analysis.

Configuration	Acc (%)	Pre (%)	Rec (%)	F1-Score (%)	G-Mean (%)	AUC (%)
Full Model	94.49	90.14	94.49	92.25	91.77	94.82
Without Diversity Loss	91.99	89.26	87.98	88.58	90.82	91.79
Without Cross-Modal Attention	88.86	88.09	85.99	87.04	87.99	87.58
Without MoE and Dynamic Gating	85.78	85.99	84.39	85.14	83.93	84.99

summarize the quantitative results.

Results on the ASCERTAIN Dataset

For the ASCERTAIN dataset, we focused on arousal prediction as the representative task since we observed similar patterns for both valence and arousal. The complete model performed exceptionally well, achieving an F1-score of 99.83% and an AUC of 99.99%. These near-perfect scores demonstrate the model’s strong ability to distinguish between different classes and its excellent generalization capability.

When we removed the diversity loss component, we observed a significant drop in performance, with the F1-score decreasing by 6.05% and the AUC dropping by 1.02%. This decline highlights how important it is to encourage different experts in the model to learn distinct patterns. The diversity loss prevents redundancy by pushing each expert to specialize in different aspects of the input features. The removal of the cross-modal attention mechanism caused even greater performance drops across all metrics. This component allows the model to identify important relationships between different modalities (such as visual, audio, and text inputs). Without it, the model struggles to determine which parts of one modality are relevant to parts of another modality. This suggests that capturing relationships between modalities is crucial for understanding emotional states. The most dramatic performance decrease occurred when we removed both the MoE block and its dynamic gating mechanism. This configuration resulted in a 7.73% drop in accuracy and a 9.12% reduction in AUC. These substantial decreases confirm that having specialized experts for different aspects of the input, along with a mechanism to selectively activate the most relevant experts for each input, is fundamental to the model’s effectiveness. The dynamic gating allows the model to focus on the most informative modalities while reducing the influence of noisy or irrelevant inputs.

Results on the KEMDy20 Dataset

Our experiments on the KEMDy20 dataset showed similar patterns to those observed with ASCERTAIN. The complete model consistently outperformed all modified versions, achieving the highest AUC (94.82%) and F1-score (92.25%). Removing the diversity loss caused a moderate decrease in performance (F1-score dropped by 3.67%), once again demonstrating its role in helping experts specialize and improve generalization. This decrease was less dramatic than in the ASCERTAIN dataset, suggesting that expert specialization may be more critical for certain types of emotional recognition tasks or data structures. The absence of cross-modal attention resulted in a more significant performance drop, with the F1-score decreasing by 5.21% and AUC by 7.24%. This component seems particularly important for integrating the different types of information in the KEMDy20 dataset, which includes speech patterns and text semantics. The temporal dynamics in speech and the meaning in text need to be properly aligned and integrated for accurate emotion recognition. As with the ASCERTAIN dataset, removing the MoE block and dynamic gating caused the largest performance drop, with a reduction of 7.11% in F1-score and 9.83% in AUC. This consistent finding across both datasets strongly validates our architectural design choice of using adaptive expert selection to process multimodal inputs.

In summary, across both datasets, each architectural component contributes uniquely and synergistically to the final performance. The Mixture of Experts (MoE) module with dynamic gating serves as the core mechanism for adaptive modality selection, the cross-modal attention aligns complementary signals across modalities, and the diversity loss regularizes expert behavior to maximize specialization. Their combined effect results in substantial improvements in classification robustness, discrimination, and generalization across different emotional states and datasets.

4.3.5. Resource and Computational Efficiency Analysis

In this section, we present the computational cost and time of the proposed approach. This experiment is important because it demonstrates the feasibility of deploying our method in real-world settings, where resource constraints often dictate which algorithms can be used effectively. By quantifying both memory requirements and execution speed, we establish a practical benchmark that helps researchers and practitioners gauge whether the model’s performance justifies the underlying computational burden.

From the summarized results, we note that the number of trainable parameters typically follows $\mathcal{O}(dh+h^2)$, where d is the input or embedding dimension and h is the hidden dimension. This leads to a medium memory usage profile. Moreover, the overall time per epoch is reported to be fast, aided by a mostly linear or near-linear computational scaling relative to the dataset size. Specifically, while the self-attention mechanism in our transformer-based architecture has a theoretical $\mathcal{O}(N^2\ast d)$ complexity for sequence length N and embedding dimension d, our results indicate that optimized implementations and hardware acceleration keep per-epoch execution times within practical limits. Consequently, the approach balances strong predictive performance with resource requirements that are manageable on standard GPU-based systems, reinforcing its utility for emotion-recognition tasks.

5. Conclusions

In this paper, we introduced a dynamically gated Mixture of Experts (MoE) framework for multimodal emotion recognition, integrating specialized transformer-based sub-expert networks, a sparse Top-k gating mechanism, and a cross-modal attention module to fuse data from physiological signals, audio features, and textual input. Our experimental results on both the ASCERTAIN and KEMDy20 datasets confirm that the proposed approach consistently outperforms state-of-the-art methods, achieving near-perfect classification metrics in arousal/valence tasks on ASCERTAIN and substantially improving accuracy and F1-scores relative to previous models on KEMDy20. Additional analysis further revealed the relative importance of each modality in capturing emotional cues, with EEG and text often emerging as dominant experts depending on the dataset’s characteristics. It was also demonstrated that carefully chosen multi-expert combinations can significantly boost performance over single-modality models. From a practical standpoint, the training curves, confusion matrices, and t-SNE visualizations indicate that our model learns well-separated feature representations, even though multiple emotional states share subtle overlaps. The auxiliary diversity loss not only encourages specialized experts but also avoids redundancy among them, enhancing our approach’s overall discriminative power. Importantly, our analyses of the computational resources required by the proposed framework show that it remains tractable on conventional GPU setups, making it a viable choice for real-world applications. In summary, by effectively exploiting heterogeneous signals and leveraging sparse dynamic gating, our MoE framework advances multimodal emotion recognition, setting new performance baselines and opening avenues for future research in affective computing.