Sine Unit Exponentiated Half-Logistic Distribution: Theory, Estimation, and Applications in Reliability Modeling
Abstract
1. Introduction
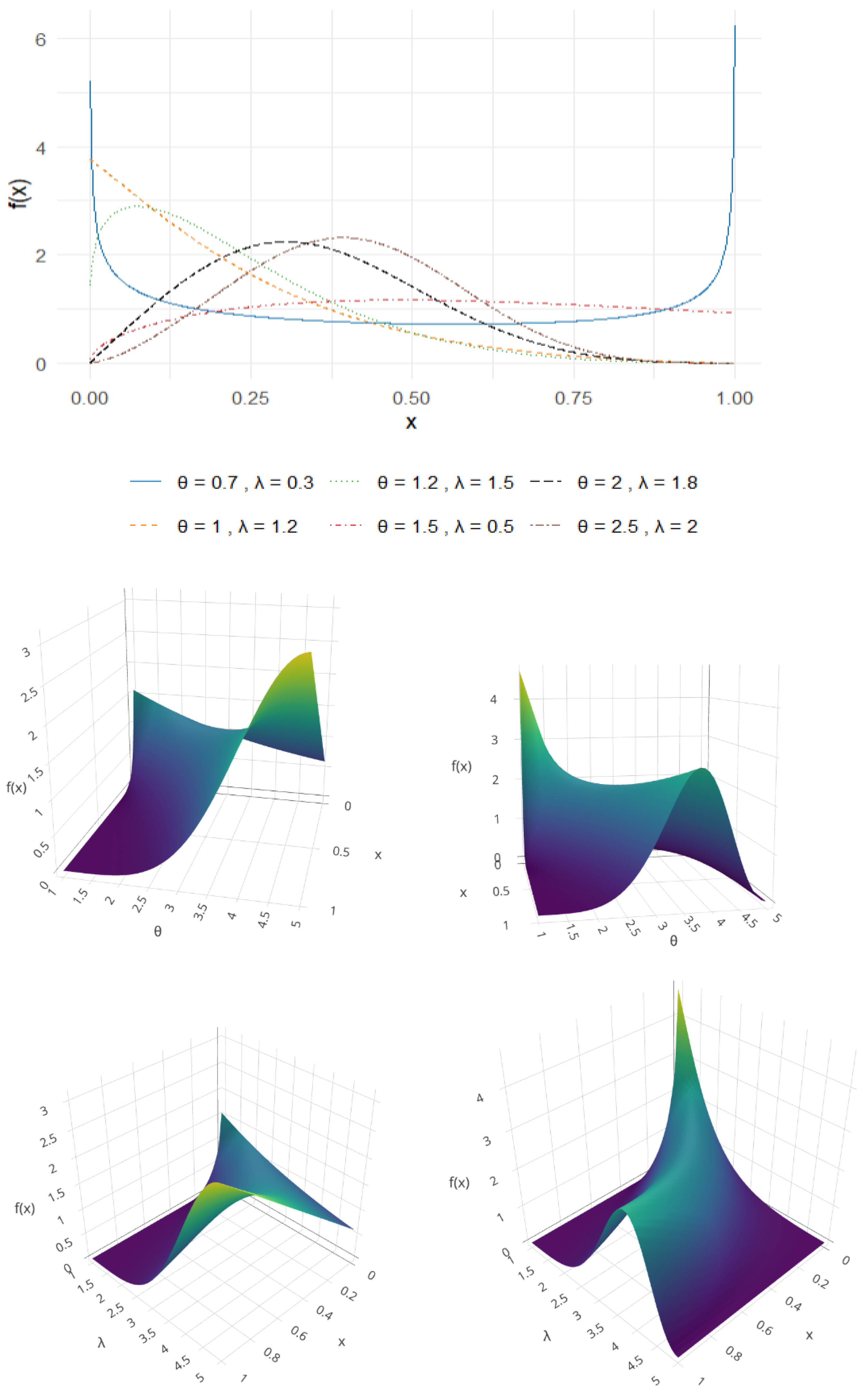
2. Description of the Model
3. Some Statistical Characteristics
3.1. Quantile Function
3.2. Moments
3.3. Reliability Analysis
3.3.1. Stress–Strength Reliability
3.3.2. Inverse Hazard Rate and Mean Residual Life
3.4. Information Measures
4. Estimation Methods
4.1. Maximum Likelihood Estimation
4.2. Anderson–Darling Methods
4.3. Ordinary and Weighted Least-Squares
4.4. Cramér–Von Mises
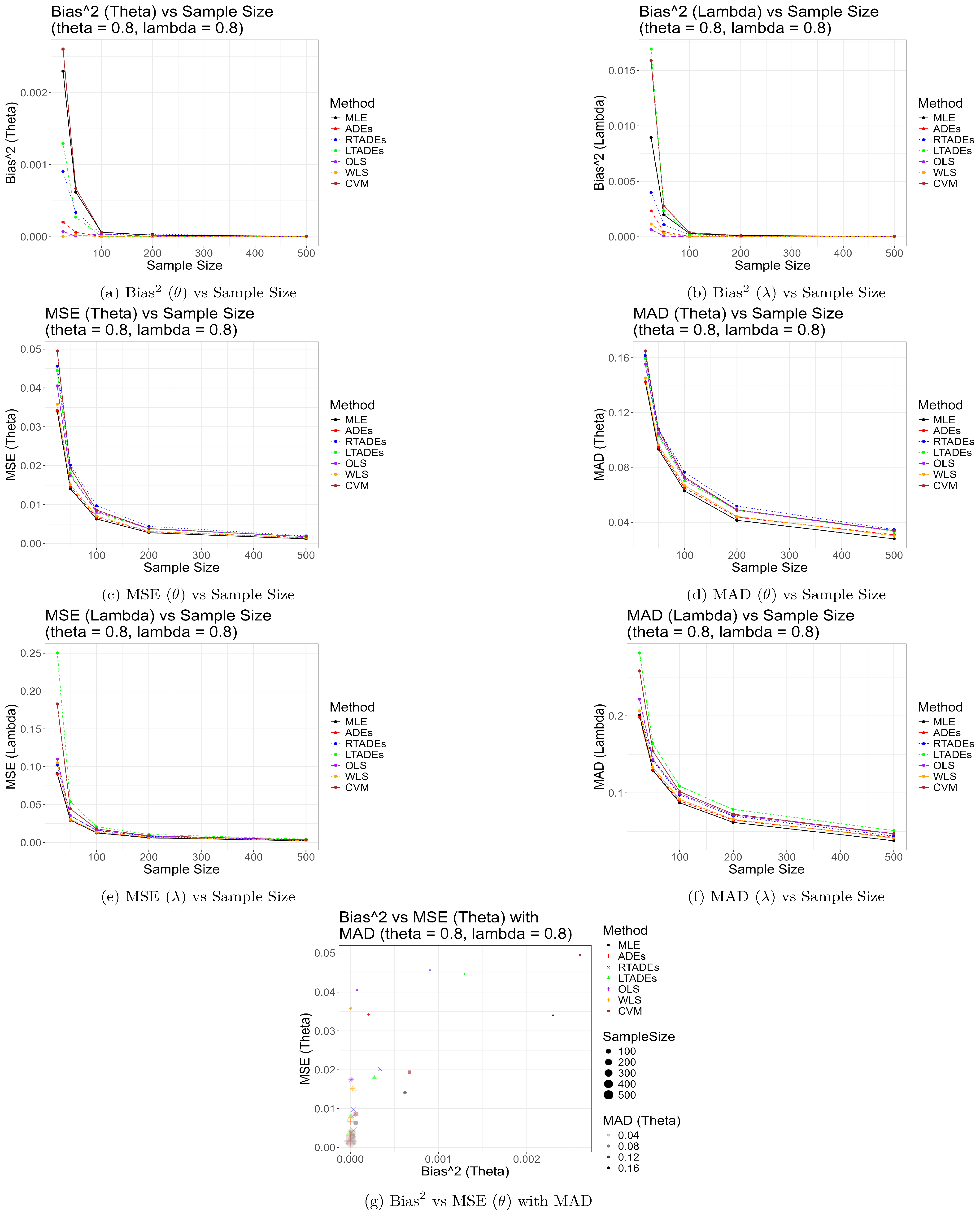
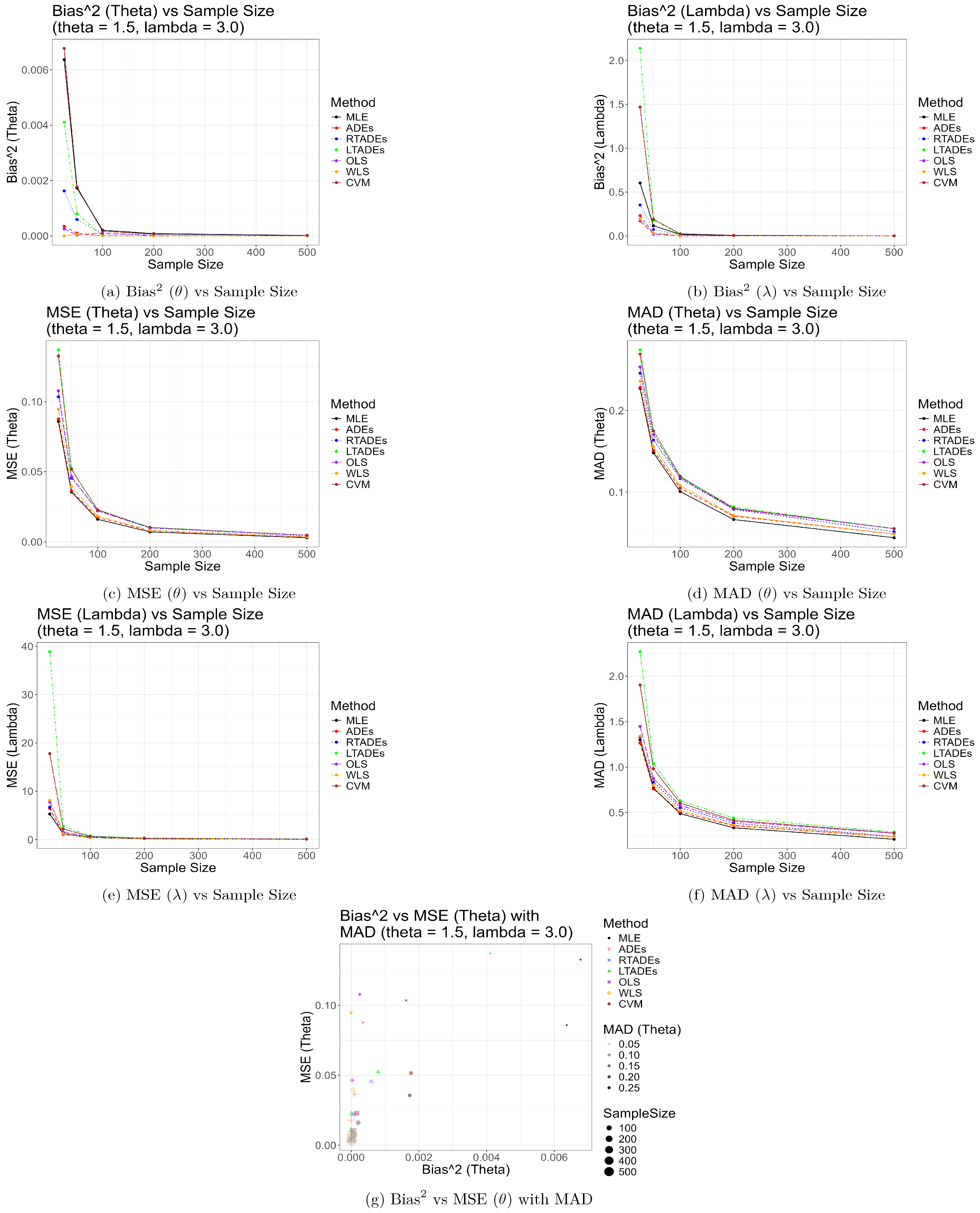
5. Numerical Simulation
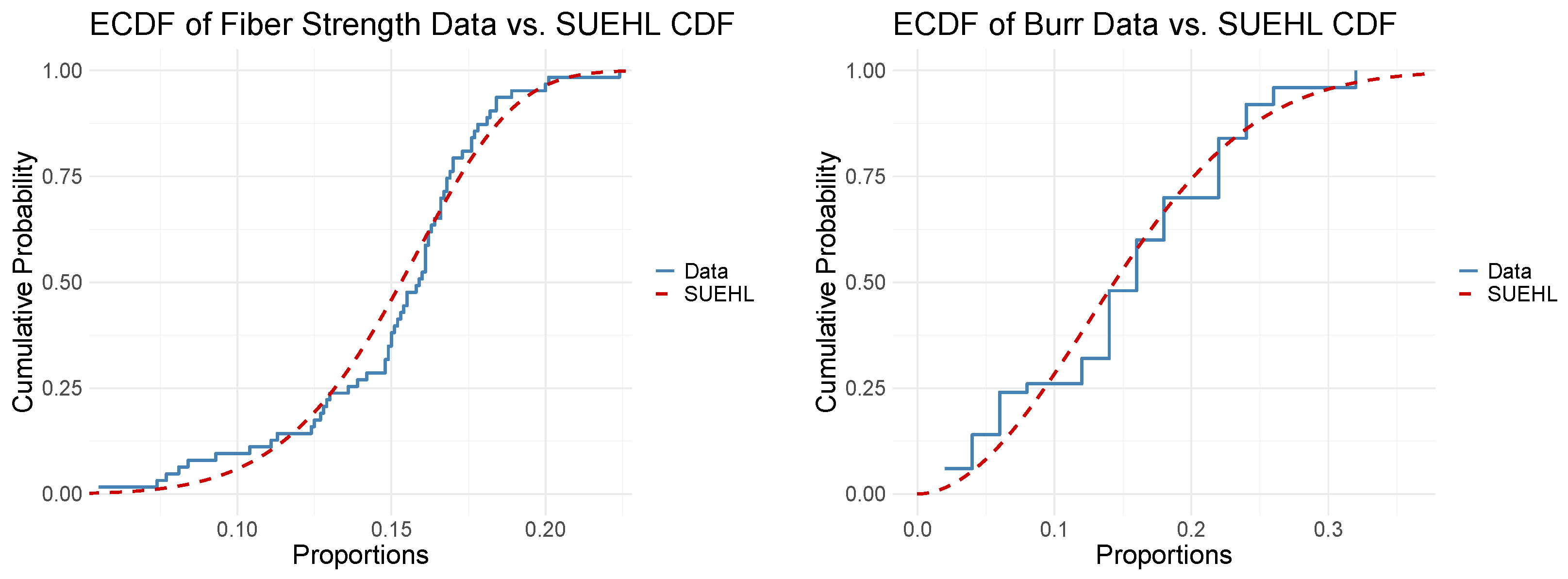
6. Illustration with Real Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDF | Cumulative Distribution Function |
| CVM | Cramér–von Mises |
| ECDF | Empirical Cumulative Distribution Function |
| MAD | Mean Absolute Deviation |
| MLE | Maximum Likelihood Estimation |
| MSE | Mean Squared Error |
| Probability Density Function | |
| SD | Standard Deviation |
| SUEHL | Sine Unit Exponentiated Half-Logistic |
| UEHL | Unit Exponentiated Half-Logistic |
| ADE | Anderson–Darling Estimator |
| OLS | Ordinary Least-Squares |
| RTADE | Right-Tail Anderson–Darling Estimator |
| LTADE | Left-Tail Anderson–Darling Estimator |
| WLS | Weighted Least-Squares |
References
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Famoye, F.; Lee, C. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Marshall, A.; Olkin, I. A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Yegen, D.; Ozel, G. Marshall-Olkin half logistic distribution with theory and applications. Alphanumeric J. 2018, 6, 408–416. [Google Scholar] [CrossRef]
- Elgarhy, M.; Hassan, A.S.; Fayomi, S. Maximum likelihood and Bayesian estimation for two-parameter type I half logistic Lindley distribution. J. Comput. Theor. Nanosci. 2018, 15, 1–9. [Google Scholar] [CrossRef]
- Al-Shomrani, A.; Arif, O.; Shawky, A.; Hanif, S.; Shahbaz, M.Q. Topp-Leone family of distributions: Some properties and application. Pak. J. Stat. Oper. Res. 2016, 12, 443–451. [Google Scholar] [CrossRef]
- Hassan, A.S.; El-Sherpieny, E.A.; El-Taweel, S.A. New Topp Leone-G family with mathematical properties and applications. J. Phys. Conf. Ser. 2021, 1860, 012011. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elgarhy, M.; Haq, M.A.; Alrajhi, S. On type II half logistic Weibull distribution with applications. Math. Theory Model. 2019, 19, 49–63. [Google Scholar] [CrossRef]
- Mohammad, G.S. A new two-parameter modified half-logistic distribution: Properties and Applications. Stat. Optim. Inf. Comput. 2022, 10, 589–605. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, U.; Singh, S.K. A new distribution using sine function-its application to bladder cancer patients data. J. Stat. Appl. Prob. 2015, 4, 417–427. [Google Scholar]
- Cordeiro, G.M.; Alizadeh, M.; Ortega, E.M.M. The exponentiated half logistic family of distributions: Properties and applications. J. Probab. Stat. 2014, 2014, 864396. [Google Scholar] [CrossRef]
- Mahmood, Z.; Chesneau, C.; Tahir, M.H. A new sine-G family of distributions: Properties and applications. Bull. Comput. Appl. Math. 2019, 7, 53–81. [Google Scholar]
- Hassan, A.S.; Alsadat, N.; Elgarhy, M.; Sapkota, L.P.; Balogun, O.S.; Gemeay, A.M. A novel asymmetric form of the power half-logistic distribution with statistical inference and real data analysis. Electron. Res. Arch. 2025, 33, 791–825. [Google Scholar] [CrossRef]
- Muhammad, M.; Alshanbari, H.M.; Alanzi, A.R.A.; Liu, L.; Sami, W.; Chesneau, C.; Jamal, F. A new generator of probability models: The exponentiated sine-G family for lifetime studies. Entropy 2021, 23, 1394. [Google Scholar] [CrossRef]
- Jose, J.K.; Manoharan, M. Beta half logistic distribution: A new probability model for lifetime data. J. Stat. Manag. Syst. 2016, 19, 587–604. [Google Scholar] [CrossRef]
- Bantan, R.; Hassan, A.S.; Elsehetry, M.; Kibria, B.M. Half-logistic xgamma distribution: Properties and estimation under censored samples. Discrete Dyn. Nat. Soc. 2020, 2020, 9136513. [Google Scholar] [CrossRef]
- Hassan, A.S.; Fayomi, A.; Algarni, A.; Almetwally, E.M. Bayesian and non-Bayesian inference for unit-exponentiated half-logistic distribution with data analysis. Appl. Sci. 2022, 12, 11253. [Google Scholar] [CrossRef]
- Özbilen, Ö.; Genç, A.I. A bivariate extension of the omega distribution for two-dimensional proportional data. Math. Slovaca 2022, 72, 1605–1622. [Google Scholar] [CrossRef]
- Usman, R.M.; Haq, A.M.; Talib, J. Kumaraswamy half-logistic distribution: Properties and applications. J. Stat. Appl. Prob. 2017, 6, 597–609. [Google Scholar] [CrossRef]
- Anwar, M.; Bibi, A. The half-logistic generalized Weibull distribution. J. Probab. Stat. 2018, 2018, 8767826. [Google Scholar] [CrossRef]
- Algarni, A.; Almarashi, A.M.; Elbatal, I.; Hassan, A.S.; Almetwally, E.M.; Daghistani, A.M.; Elgarhy, M. Type I half logistic Burr X-G family: Properties, Bayesian, and non-Bayesian estimation under censored samples and applications to COVID-19 data. Math. Probl. Eng. 2021, 2021, 5461130. [Google Scholar] [CrossRef]
- Hashempour, M. An extended type I half-logistic family of distributions: Properties, applications and different method of estimations. Math. Slovaca 2022, 72, 745–764. [Google Scholar] [CrossRef]
- Arshad, R.M.I.; Tahir, M.H.; Chesneau, C.; Khan, S.; Jamal, F. The gamma power half-logistic distribution: Theory and applications. Sao Paulo J. Math. Sci. 2023, 17, 1142–1169. [Google Scholar] [CrossRef]
- Alghamdi, S.M.; Shrahili, M.; Hassan, A.S.; Gemeay, A.M.; Elbatal, I.; Elgarhy, M. Statistical inference of the half logistic modified Kies exponential model with modeling to engineering data. Symmetry 2023, 15, 586. [Google Scholar] [CrossRef]
- Alizadeh, M.; MirMostafee, S.; Ortega, E.; Ramires, T.; Cordeiro, G. The odd log-logistic logarithmic generated family of distributions with applications in different areas. J. Stat. Distrib. App. 2017, 4, 1–25. [Google Scholar] [CrossRef][Green Version]
- Nadarajah, S.; Kotz, S. The exponentiated Fréchet distribution. Interstat 2003, 14, 1–7. [Google Scholar]
- Oliveira, J.; Santos, C.; Xavier, D.; Trindade, D.; Cordeiro, G.M. The McDonald half-logistic distribution: Theory and practice. Commun. Stat. Theory Methods 2016, 45, 2005–2022. [Google Scholar] [CrossRef]
- Xavier, T.; Jose, J.K. A study of stress-strength reliability using a generalization of power transformed half-logistic distribution. Commun. Stat. Theory Methods 2020, 50, 4335–4351. [Google Scholar] [CrossRef]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M.M. General results for the Kumaraswamy-G distribution. J. Stat. Comput. Simul. 2013, 83, 951–979. [Google Scholar] [CrossRef]
- Xavier, T.; Jose, J.K.; Nadarajah, S. An additive power-transformed half-logistic model and its applications in reliability. Qual. Reliab. Eng. Int. 2022, 38, 3179–3196. [Google Scholar] [CrossRef]
- Hjorth, U. A reliability distribution with increasing, decreasing, constant and bathtub-shaped failure rates. Technometrics 1980, 22, 99–107. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Cordeiro, G.M.; Ortega, M.M.E. On the additive Weibull distribution. Commun. Stat. Theory Methods 2014, 43, 2066–2080. [Google Scholar] [CrossRef]
- Xie, M.; Lai, C.D. Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 1995, 52, 87–93. [Google Scholar] [CrossRef]
- Wang, F.K. A new model with bathtub-shaped failure rate using an additive Burr XII distribution. Reliab. Eng. Syst. Saf. 2000, 70, 305–312. [Google Scholar] [CrossRef]
- Hassan, A.H.; Elgarhy, M.; Shakil, M. Type II half logistic family of distributions with applications. Pak. J. Stat. Oper. Res. 2017, 13, 245–264. [Google Scholar] [CrossRef]
- Smith, R.L.; Naylor, J.C. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Appl. Stat. 2002, 36, 358–369. [Google Scholar] [CrossRef]
- Cheng, R.C.H.; Amin, N.A.K. Maximum product-of-spacings estimation with applications to the log-normal distribution. Univ. Wales IST Math Rep. 1979, 79, 103. [Google Scholar]
- Cheng, R.C.H.; Amin, N.A.K. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. Ser. B Methodol. 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Ranneby, B. The maximum spacing method: An estimation method related to the maximum likelihood method. Scand. J. Stat. 1984, 11, 93–112. [Google Scholar]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Krishnarani, S.D. On a power transformation of half-logistic distribution. J. Probab. Stat. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Dasgupta, R. On the distribution of burr with applications. Sankhya B 2011, 73, 1–19. [Google Scholar] [CrossRef]

| 0.5 | 0.5 | 0.00105 | 0.00433 | 0.01859 | 0.04510 | 0.14793 | 0.35028 | 0.71854 | 0.96804 |
| 1 | 0.00026 | 0.00108 | 0.00469 | 0.01154 | 0.04000 | 0.10739 | 0.30674 | 0.69669 | |
| 2 | 0.00006 | 0.00027 | 0.00118 | 0.00290 | 0.01021 | 0.02839 | 0.09133 | 0.28971 | |
| 4 | 0.00002 | 0.00007 | 0.00029 | 0.00073 | 0.00256 | 0.00720 | 0.02394 | 0.08531 | |
| 6 | 0.00001 | 0.00003 | 0.00013 | 0.00032 | 0.00114 | 0.00321 | 0.01073 | 0.03917 | |
| 8 | 0.00000 | 0.00002 | 0.00007 | 0.00018 | 0.00064 | 0.00181 | 0.00606 | 0.02229 | |
| 1 | 0.5 | 0.03235 | 0.06580 | 0.13633 | 0.21236 | 0.38461 | 0.59184 | 0.84767 | 0.98389 |
| 1 | 0.01618 | 0.03293 | 0.06848 | 0.10740 | 0.20000 | 0.32770 | 0.55384 | 0.83468 | |
| 2 | 0.00809 | 0.01647 | 0.03428 | 0.05386 | 0.10102 | 0.16850 | 0.30221 | 0.53825 | |
| 4 | 0.00404 | 0.00824 | 0.01715 | 0.02695 | 0.05064 | 0.08486 | 0.15472 | 0.29209 | |
| 6 | 0.00270 | 0.00549 | 0.01143 | 0.01797 | 0.03378 | 0.05665 | 0.10361 | 0.19792 | |
| 8 | 0.00202 | 0.00412 | 0.00857 | 0.01348 | 0.02534 | 0.04251 | 0.07783 | 0.14930 | |
| 2 | 0.5 | 0.17986 | 0.25651 | 0.36923 | 0.46082 | 0.62017 | 0.76931 | 0.92069 | 0.99191 |
| 1 | 0.12720 | 0.18148 | 0.26169 | 0.32772 | 0.44721 | 0.57245 | 0.74421 | 0.91361 | |
| 2 | 0.08995 | 0.12834 | 0.18515 | 0.23207 | 0.31784 | 0.41049 | 0.54974 | 0.73366 | |
| 4 | 0.06360 | 0.09076 | 0.13094 | 0.16416 | 0.22503 | 0.29130 | 0.39335 | 0.54045 | |
| 6 | 0.05193 | 0.07410 | 0.10692 | 0.13404 | 0.18378 | 0.23801 | 0.32189 | 0.44488 | |
| 8 | 0.04497 | 0.06417 | 0.09259 | 0.11609 | 0.15917 | 0.20617 | 0.27898 | 0.38639 | |
| 3 | 0.5 | 0.31864 | 0.40371 | 0.51467 | 0.59661 | 0.72724 | 0.83959 | 0.94640 | 0.99460 |
| 1 | 0.25292 | 0.32054 | 0.40913 | 0.47534 | 0.58480 | 0.68943 | 0.82122 | 0.94154 | |
| 2 | 0.20075 | 0.25444 | 0.32486 | 0.37764 | 0.46573 | 0.55233 | 0.67107 | 0.81344 | |
| 4 | 0.15934 | 0.20195 | 0.25786 | 0.29981 | 0.36997 | 0.43944 | 0.53685 | 0.66349 | |
| 6 | 0.13919 | 0.17642 | 0.22527 | 0.26192 | 0.32325 | 0.38405 | 0.46968 | 0.58277 | |
| 8 | 0.12647 | 0.16029 | 0.20467 | 0.23797 | 0.29371 | 0.34899 | 0.42696 | 0.53050 | |
| 5 | 0.5 | 0.50348 | 0.58029 | 0.67130 | 0.73352 | 0.82605 | 0.90041 | 0.96749 | 0.99676 |
| 1 | 0.43832 | 0.50528 | 0.58495 | 0.64004 | 0.72478 | 0.80001 | 0.88854 | 0.96450 | |
| 2 | 0.38159 | 0.43989 | 0.50935 | 0.55751 | 0.63224 | 0.70036 | 0.78716 | 0.88348 | |
| 4 | 0.33219 | 0.38295 | 0.44344 | 0.48541 | 0.55068 | 0.61057 | 0.68851 | 0.78181 | |
| 6 | 0.30632 | 0.35313 | 0.40890 | 0.44761 | 0.50783 | 0.56317 | 0.63545 | 0.72326 | |
| 8 | 0.28919 | 0.33338 | 0.38604 | 0.42259 | 0.47946 | 0.53173 | 0.60011 | 0.68361 | |
| 10 | 0.5 | 0.70956 | 0.76177 | 0.81933 | 0.85646 | 0.90887 | 0.94890 | 0.98361 | 0.99838 |
| 1 | 0.66206 | 0.71083 | 0.76482 | 0.80002 | 0.85134 | 0.89443 | 0.94262 | 0.98209 | |
| 2 | 0.61773 | 0.66324 | 0.71369 | 0.74666 | 0.79514 | 0.83687 | 0.88722 | 0.93994 | |
| 4 | 0.57636 | 0.61883 | 0.66591 | 0.69671 | 0.74208 | 0.78139 | 0.82977 | 0.88420 | |
| 6 | 0.55346 | 0.59424 | 0.63945 | 0.66904 | 0.71262 | 0.75044 | 0.79715 | 0.85045 | |
| 8 | 0.53776 | 0.57739 | 0.62132 | 0.65007 | 0.69243 | 0.72920 | 0.77467 | 0.82681 |
| n | Method | Bias () | Bias () | MSE () | MSE () | MAD () | MAD () | SD () | SD () |
|---|---|---|---|---|---|---|---|---|---|
| 25 | MLE | 0.0479 | 0.0947 | 0.0340 | 0.0910 | 0.1424 | 0.2009 | 0.1782 | 0.2866 |
| ADEs | 0.0143 | 0.0483 | 0.0342 | 0.0904 | 0.1423 | 0.1980 | 0.1845 | 0.2969 | |
| RTADEs | 0.0301 | 0.0631 | 0.0456 | 0.1020 | 0.1617 | 0.2063 | 0.2115 | 0.3133 | |
| LTADEs | 0.0360 | 0.1301 | 0.0445 | 0.2502 | 0.1596 | 0.2817 | 0.2080 | 0.4832 | |
| OLS | −0.0086 | 0.0255 | 0.0405 | 0.1102 | 0.1554 | 0.2215 | 0.2012 | 0.3312 | |
| WLS | 0.0018 | 0.0340 | 0.0358 | 0.1051 | 0.1452 | 0.2062 | 0.1894 | 0.3226 | |
| CVM | 0.0510 | 0.1261 | 0.0495 | 0.1830 | 0.1650 | 0.2585 | 0.2167 | 0.4090 | |
| 50 | MLE | 0.0249 | 0.0445 | 0.0141 | 0.0299 | 0.0932 | 0.1293 | 0.1163 | 0.1671 |
| ADEs | 0.0079 | 0.0210 | 0.0146 | 0.0291 | 0.0946 | 0.1299 | 0.1205 | 0.1695 | |
| RTADEs | 0.0184 | 0.0331 | 0.0201 | 0.0357 | 0.1079 | 0.1420 | 0.1408 | 0.1862 | |
| LTADEs | 0.0165 | 0.0484 | 0.0180 | 0.0537 | 0.1031 | 0.1639 | 0.1331 | 0.2268 | |
| OLS | −0.0031 | 0.0086 | 0.0175 | 0.0354 | 0.1047 | 0.1435 | 0.1322 | 0.1880 | |
| WLS | 0.0052 | 0.0178 | 0.0152 | 0.0305 | 0.0965 | 0.1331 | 0.1233 | 0.1739 | |
| CVM | 0.0259 | 0.0527 | 0.0194 | 0.0445 | 0.1074 | 0.1543 | 0.1369 | 0.2043 | |
| 100 | MLE | 0.0079 | 0.0173 | 0.0063 | 0.0125 | 0.0629 | 0.0872 | 0.0792 | 0.1107 |
| ADEs | −0.0007 | 0.0053 | 0.0067 | 0.0130 | 0.0651 | 0.0895 | 0.0822 | 0.1139 | |
| RTADEs | 0.0061 | 0.0130 | 0.0097 | 0.0159 | 0.0764 | 0.0971 | 0.0986 | 0.1256 | |
| LTADEs | 0.0026 | 0.0161 | 0.0080 | 0.0207 | 0.0704 | 0.1088 | 0.0892 | 0.1431 | |
| OLS | −0.0063 | −0.0013 | 0.0083 | 0.0162 | 0.0722 | 0.0990 | 0.0910 | 0.1272 | |
| WLS | −0.0010 | 0.0049 | 0.0071 | 0.0137 | 0.0668 | 0.0917 | 0.0843 | 0.1172 | |
| CVM | 0.0080 | 0.0195 | 0.0086 | 0.0179 | 0.0730 | 0.1016 | 0.0926 | 0.1323 | |
| 200 | MLE | 0.0048 | 0.0106 | 0.0028 | 0.0061 | 0.0414 | 0.0618 | 0.0528 | 0.0773 |
| ADEs | 0.0005 | 0.0043 | 0.0031 | 0.0067 | 0.0438 | 0.0647 | 0.0554 | 0.0819 | |
| RTADEs | 0.0062 | 0.0105 | 0.0044 | 0.0079 | 0.0518 | 0.0698 | 0.0662 | 0.0881 | |
| LTADEs | 0.0013 | 0.0081 | 0.0038 | 0.0106 | 0.0490 | 0.0786 | 0.0620 | 0.1025 | |
| OLS | −0.0023 | 0.0005 | 0.0038 | 0.0083 | 0.0487 | 0.0713 | 0.0615 | 0.0914 | |
| WLS | 0.0009 | 0.0049 | 0.0032 | 0.0070 | 0.0443 | 0.0657 | 0.0562 | 0.0833 | |
| CVM | 0.0048 | 0.0108 | 0.0039 | 0.0088 | 0.0491 | 0.0726 | 0.0621 | 0.0932 | |
| 500 | MLE | 0.0022 | 0.0049 | 0.0012 | 0.0023 | 0.0279 | 0.0379 | 0.0346 | 0.0473 |
| ADEs | −0.0002 | 0.0046 | 0.0015 | 0.0029 | 0.0309 | 0.0423 | 0.0393 | 0.0535 | |
| RTADEs | 0.0009 | 0.0063 | 0.0020 | 0.0031 | 0.0347 | 0.0439 | 0.0444 | 0.0553 | |
| LTADEs | 0.0028 | 0.0071 | 0.0018 | 0.0044 | 0.0334 | 0.0511 | 0.0421 | 0.0657 | |
| OLS | −0.0000 | 0.0021 | 0.0018 | 0.0034 | 0.0337 | 0.0467 | 0.0423 | 0.0579 | |
| WLS | 0.0013 | 0.0037 | 0.0014 | 0.0027 | 0.0301 | 0.0413 | 0.0377 | 0.0515 | |
| CVM | 0.0028 | 0.0062 | 0.0018 | 0.0034 | 0.0339 | 0.0471 | 0.0424 | 0.0584 |
| n | Method | Bias () | Bias () | MSE () | MSE () | MAD () | MAD () | SD () | SD () |
|---|---|---|---|---|---|---|---|---|---|
| 25 | MLE | 0.0798 | 0.7768 | 0.0859 | 5.2885 | 0.2272 | 1.2992 | 0.2821 | 2.1656 |
| ADEs | 0.0186 | 0.4815 | 0.0877 | 6.4589 | 0.2284 | 1.2639 | 0.2957 | 2.4967 | |
| RTADEs | 0.0403 | 0.5933 | 0.1035 | 6.7127 | 0.2460 | 1.3293 | 0.3194 | 2.5233 | |
| LTADEs | 0.0641 | 1.4618 | 0.1371 | 38.8830 | 0.2746 | 2.2710 | 0.3648 | 6.0649 | |
| OLS | −0.0159 | 0.4130 | 0.1078 | 7.7753 | 0.2537 | 1.4474 | 0.3281 | 2.7590 | |
| WLS | 0.0010 | 0.4375 | 0.0946 | 8.1206 | 0.2362 | 1.3409 | 0.3078 | 2.8173 | |
| CVM | 0.0823 | 1.2118 | 0.1327 | 17.7807 | 0.2695 | 1.9049 | 0.3550 | 4.0409 | |
| 50 | MLE | 0.0416 | 0.3418 | 0.0356 | 1.1962 | 0.1480 | 0.7695 | 0.1842 | 1.0395 |
| ADEs | 0.0100 | 0.1794 | 0.0365 | 1.0783 | 0.1508 | 0.7591 | 0.1909 | 1.0233 | |
| RTADEs | 0.0244 | 0.2711 | 0.0456 | 1.4647 | 0.1638 | 0.8351 | 0.2123 | 1.1801 | |
| LTADEs | 0.0283 | 0.4210 | 0.0523 | 2.7439 | 0.1752 | 1.0410 | 0.2271 | 1.6029 | |
| OLS | −0.0055 | 0.1443 | 0.0464 | 1.5464 | 0.1705 | 0.8736 | 0.2154 | 1.2358 | |
| WLS | 0.0078 | 0.1818 | 0.0397 | 1.2499 | 0.1557 | 0.7988 | 0.1992 | 1.1036 | |
| CVM | 0.0421 | 0.4366 | 0.0516 | 2.1923 | 0.1751 | 0.9819 | 0.2233 | 1.4155 | |
| 100 | MLE | 0.0143 | 0.1332 | 0.0161 | 0.4234 | 0.1006 | 0.4870 | 0.1262 | 0.6372 |
| ADEs | −0.0017 | 0.0554 | 0.0175 | 0.4381 | 0.1050 | 0.5055 | 0.1324 | 0.6599 | |
| RTADEs | 0.0076 | 0.1089 | 0.0224 | 0.5736 | 0.1165 | 0.5536 | 0.1496 | 0.7499 | |
| LTADEs | 0.0035 | 0.1267 | 0.0224 | 0.7390 | 0.1185 | 0.6311 | 0.1496 | 0.8507 | |
| OLS | −0.0103 | 0.0285 | 0.0221 | 0.5874 | 0.1178 | 0.5772 | 0.1484 | 0.7663 | |
| WLS | −0.0018 | 0.0577 | 0.0185 | 0.4754 | 0.1079 | 0.5252 | 0.1360 | 0.6874 | |
| CVM | 0.0130 | 0.1590 | 0.0230 | 0.6893 | 0.1193 | 0.6044 | 0.1511 | 0.8153 | |
| 200 | MLE | 0.0091 | 0.0760 | 0.0071 | 0.1828 | 0.0662 | 0.3320 | 0.0838 | 0.4209 |
| ADEs | 0.0009 | 0.0372 | 0.0079 | 0.2051 | 0.0704 | 0.3544 | 0.0891 | 0.4516 | |
| RTADEs | 0.0081 | 0.0728 | 0.0099 | 0.2419 | 0.0787 | 0.3817 | 0.0994 | 0.4867 | |
| LTADEs | 0.0009 | 0.0574 | 0.0105 | 0.3380 | 0.0816 | 0.4400 | 0.1025 | 0.5788 | |
| OLS | −0.0035 | 0.0216 | 0.0100 | 0.2712 | 0.0793 | 0.4025 | 0.1002 | 0.5206 | |
| WLS | 0.0019 | 0.0426 | 0.0082 | 0.2167 | 0.0713 | 0.3615 | 0.0905 | 0.4638 | |
| CVM | 0.0082 | 0.0849 | 0.0103 | 0.2946 | 0.0800 | 0.4148 | 0.1011 | 0.5364 | |
| 500 | MLE | 0.0036 | 0.0315 | 0.0030 | 0.0669 | 0.0438 | 0.2052 | 0.0544 | 0.2568 |
| ADEs | 0.0013 | 0.0226 | 0.0036 | 0.0836 | 0.0482 | 0.2308 | 0.0602 | 0.2885 | |
| RTADEs | 0.0032 | 0.0312 | 0.0041 | 0.0885 | 0.0510 | 0.2364 | 0.0643 | 0.2960 | |
| LTADEs | 0.0020 | 0.0349 | 0.0047 | 0.1298 | 0.0549 | 0.2856 | 0.0684 | 0.3588 | |
| OLS | −0.0000 | 0.0197 | 0.0047 | 0.1137 | 0.0548 | 0.2708 | 0.0687 | 0.3368 | |
| WLS | 0.0021 | 0.0264 | 0.0037 | 0.0850 | 0.0483 | 0.2323 | 0.0604 | 0.2905 | |
| CVM | 0.0046 | 0.0446 | 0.0048 | 0.1180 | 0.0551 | 0.2736 | 0.0690 | 0.3408 |
| n | Method | Bias () | Bias () | MSE () | MSE () | MAD () | MAD () | SD () | SD () |
|---|---|---|---|---|---|---|---|---|---|
| 25 | MLE | 0.1610 | 4.3959 | 0.3259 | 179.9965 | 0.4414 | 6.4115 | 0.5480 | 12.6820 |
| ADEs | 0.0403 | 3.5144 | 0.3460 | 336.1982 | 0.4485 | 6.5414 | 0.5871 | 18.0048 | |
| RTADEs | 0.0896 | 5.0821 | 0.4297 | 577.9565 | 0.4854 | 7.9407 | 0.6497 | 23.5092 | |
| LTADEs | 0.1628 | 18.0926 | 0.6699 | 6997.1987 | 0.5761 | 21.1877 | 0.8026 | 81.7100 | |
| OLS | −0.0290 | 3.3116 | 0.4146 | 338.3528 | 0.4967 | 7.2326 | 0.6436 | 18.1029 | |
| WLS | 0.0040 | 3.2366 | 0.3634 | 366.4664 | 0.4619 | 6.6776 | 0.6032 | 18.8772 | |
| CVM | 0.1639 | 8.1126 | 0.5140 | 1021.1021 | 0.5286 | 10.7883 | 0.6983 | 30.9232 | |
| 50 | MLE | 0.0839 | 1.7705 | 0.1344 | 27.4259 | 0.2869 | 3.4186 | 0.3571 | 4.9311 |
| ADEs | 0.0206 | 1.0701 | 0.1407 | 24.6804 | 0.2945 | 3.3359 | 0.3747 | 4.8538 | |
| RTADEs | 0.0483 | 1.5950 | 0.1724 | 39.9968 | 0.3168 | 3.7832 | 0.4126 | 6.1229 | |
| LTADEs | 0.0619 | 2.6264 | 0.2155 | 101.8249 | 0.3504 | 5.0231 | 0.4603 | 9.7479 | |
| OLS | −0.0097 | 1.0384 | 0.1780 | 37.3259 | 0.3337 | 3.8781 | 0.4220 | 6.0236 | |
| WLS | 0.0163 | 1.1176 | 0.1516 | 28.5001 | 0.3039 | 3.5211 | 0.3893 | 5.2229 | |
| CVM | 0.0837 | 2.3997 | 0.1988 | 58.1630 | 0.3431 | 4.5343 | 0.4382 | 7.2427 | |
| 100 | MLE | 0.0299 | 0.6823 | 0.0606 | 8.1764 | 0.1949 | 2.0659 | 0.2444 | 2.7782 |
| ADEs | −0.0031 | 0.3508 | 0.0666 | 8.3615 | 0.2045 | 2.1320 | 0.2581 | 2.8717 | |
| RTADEs | 0.0155 | 0.6430 | 0.0847 | 12.5950 | 0.2255 | 2.4058 | 0.2908 | 3.4920 | |
| LTADEs | 0.0091 | 0.7654 | 0.0895 | 17.0043 | 0.2350 | 2.7483 | 0.2992 | 4.0540 | |
| OLS | −0.0196 | 0.2874 | 0.0847 | 11.6059 | 0.2305 | 2.4526 | 0.2906 | 3.3963 | |
| WLS | −0.0030 | 0.3765 | 0.0704 | 9.2215 | 0.2106 | 2.2255 | 0.2654 | 3.0148 | |
| CVM | 0.0262 | 0.8530 | 0.0882 | 14.2915 | 0.2336 | 2.6129 | 0.2960 | 3.6848 | |
| 200 | MLE | 0.0188 | 0.3677 | 0.0266 | 3.2305 | 0.1283 | 1.3691 | 0.1622 | 1.7602 |
| ADEs | 0.0021 | 0.2064 | 0.0301 | 3.5843 | 0.1372 | 1.4591 | 0.1735 | 1.8829 | |
| RTADEs | 0.0160 | 0.3737 | 0.0371 | 4.4829 | 0.1520 | 1.5975 | 0.1919 | 2.0851 | |
| LTADEs | 0.0026 | 0.3224 | 0.0414 | 6.1336 | 0.1612 | 1.8285 | 0.2036 | 2.4568 | |
| OLS | −0.0064 | 0.1642 | 0.0384 | 4.8240 | 0.1552 | 1.6654 | 0.1960 | 2.1913 | |
| WLS | 0.0041 | 0.2343 | 0.0311 | 3.8233 | 0.1389 | 1.4911 | 0.1764 | 1.9422 | |
| CVM | 0.0164 | 0.4322 | 0.0394 | 5.3719 | 0.1566 | 1.7356 | 0.1978 | 2.2782 | |
| 500 | MLE | 0.0072 | 0.1472 | 0.0110 | 1.1509 | 0.0845 | 0.8469 | 0.1049 | 1.0632 |
| ADEs | 0.0026 | 0.1140 | 0.0137 | 1.4687 | 0.0938 | 0.9601 | 0.1172 | 1.2071 | |
| RTADEs | 0.0061 | 0.1529 | 0.0154 | 1.5706 | 0.0984 | 0.9872 | 0.1238 | 1.2445 | |
| LTADEs | 0.0045 | 0.1802 | 0.0184 | 2.3186 | 0.1084 | 1.1922 | 0.1356 | 1.5128 | |
| OLS | 0.0001 | 0.1132 | 0.0181 | 2.0291 | 0.1072 | 1.1292 | 0.1345 | 1.4207 | |
| WLS | 0.0042 | 0.1318 | 0.0139 | 1.5004 | 0.0940 | 0.9685 | 0.1177 | 1.2184 | |
| CVM | 0.0092 | 0.2176 | 0.0183 | 2.1261 | 0.1078 | 1.1456 | 0.1350 | 1.4425 |
| Dataset | Mean | Median | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| Fiber Strength | 0.151 | 0.159 | 0.032 | 0.055 | 0.224 |
| Burr | 0.152 | 0.160 | 0.078 | 0.020 | 0.320 |
| Distribution | Parameters | AIC | BIC | KS Stat | p (KS) | AD Stat | p (AD) | CVM Stat | p (CVM) | |
|---|---|---|---|---|---|---|---|---|---|---|
| SUEHL | −260.72 | −256.72 | −252.44 | 0.15 | 0.13 | 1.14 | 0.29 | 0.20 | 0.27 | |
| Beta | −244.43 | −240.43 | −236.14 | 0.21 | 0.01 | 2.89 | 0.03 | 0.53 | 0.03 | |
| UEHL | −259.71 | −255.71 | −251.43 | 0.15 | 0.11 | 1.24 | 0.25 | 0.21 | 0.24 | |
| Topp–Leone | −76.76 | −74.76 | −72.61 | 0.48 | 0.00 | 18.42 | 0.00 | 3.86 | 0.00 | |
| Sine-G | −52.42 | −50.42 | −48.27 | 0.68 | 0.00 | 37.40 | 0.00 | 8.26 | 0.00 |
| Distribution | Parameters | AIC | BIC | KS Stat | p (KS) | AD Stat | p (AD) | CVM Stat | p (CVM) | |
|---|---|---|---|---|---|---|---|---|---|---|
| SUEHL | −115.23 | −111.23 | −107.41 | 0.16 | 0.15 | 1.23 | 0.26 | 0.19 | 0.28 | |
| Beta | −111.86 | −107.86 | −104.04 | 0.20 | 0.04 | 1.56 | 0.16 | 0.29 | 0.15 | |
| UEHL | −114.64 | −110.64 | −106.82 | 0.17 | 0.11 | 1.32 | 0.23 | 0.21 | 0.24 | |
| Topp–Leone | −65.29 | −63.29 | −61.38 | 0.33 | 0.00 | 6.73 | 0.00 | 1.25 | 0.00 | |
| Sine-G | −40.90 | −38.90 | −36.99 | 0.56 | 0.00 | 23.19 | 0.00 | 5.10 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Genç, M.; Özbilen, Ö. Sine Unit Exponentiated Half-Logistic Distribution: Theory, Estimation, and Applications in Reliability Modeling. Mathematics 2025, 13, 1871. https://doi.org/10.3390/math13111871
Genç M, Özbilen Ö. Sine Unit Exponentiated Half-Logistic Distribution: Theory, Estimation, and Applications in Reliability Modeling. Mathematics. 2025; 13(11):1871. https://doi.org/10.3390/math13111871
Chicago/Turabian StyleGenç, Murat, and Ömer Özbilen. 2025. "Sine Unit Exponentiated Half-Logistic Distribution: Theory, Estimation, and Applications in Reliability Modeling" Mathematics 13, no. 11: 1871. https://doi.org/10.3390/math13111871
APA StyleGenç, M., & Özbilen, Ö. (2025). Sine Unit Exponentiated Half-Logistic Distribution: Theory, Estimation, and Applications in Reliability Modeling. Mathematics, 13(11), 1871. https://doi.org/10.3390/math13111871





