Model Validation and Strategy Analysis in Retrial Queues with Delayed Vacations and Feedback Based on Monte Carlo Simulation

Abstract

Inspired by call centers, this paper models them as a constant retrial queue, with feedback and delayed vacations to balance high efficiency and low cost for service agents. After completing the service, the server randomly waits for an idle period. If customers arrive during this period, the service is provided immediately, otherwise, the server will take a vacation. We first derive steady-state probabilities and key performance measures. Then, the system cost is modeled. Particle Swarm Optimization (PSO), Ant Colony Algorithm (ACA) and Sparrow Search Algorithm (SSA) are applied to obtain the minimum system cost, respectively. To verify the correctness of the theoretical results of the system model, we simulate the model using Monte Carlo simulation to obtain the probabilities of different server states and the expected number of customers in the system, and then compare them with the theoretical values. At the same time, the sensitivity of the performance measures obtained by Monte Carlo simulation to the system parameters is also analyzed. Finally, customer behavior is analyzed, and equilibrium and socially optimal arrival rates are derived. In addition, the efficiency of the system is evaluated by examining efficiency indicators such as throughput and price of anarchy.

1. Introduction

Since the retrial phenomenon is common in real life, retrial queueing systems have been widely used in computer systems, call centers, production management, traffic management, and other fields. For the purpose of energy saving and cost control, when there is no customer or a small number of customers in the system, the system will pause the work to take a vacation. Li and Yang [1] explored the M/G/1 retrial model with a finite number of customers and vacations, and the limiting probability distribution and some key performance measures were obtained using the complementary variables approach. In terms of multi-server queues, Ke et al. [2] dealt with an M/M/c balking retrial queue with vacation, and they optimized the cost function to obtain the optimal number of servers as well as the mean service rate. Sztrik et al. [3] investigated a retrial queue for a particular mechanism, namely two-way communication, where the server can fail at any time. Due to the unreliability of equipment, Shanmugam and Saravanarajan [4] proceeded with an M/G/1 unreliable retrial queue with a working vacation and two-phase service.

Recently, providing feedback has become highly demanded for service quality. Similarly to Ke et al. [2], Chang et al. [5] further analyzed the unreliable retrial queue with feedback and impatience using Quasi-Newton, Pattern Search, and Nelder–Mead Simplex Direct Search Methods for cost optimization. Later, a retrial queue with working vacation and impatient customers was studied by including the feature of imperfect service during a working vacation in Jain et al. [6], and customers got additional service if they were not satisfied with the primary work. Sundarapandiyan and Nandhini [7] proposed an M/G/1 retrial queue with feedback and delayed repair, where an application of a computerized processing system was presented.

In queueing systems, it is a natural tendency for customers to decide whether to join the system based on their personal utility. In contrast to the traditional analysis of queueing systems, customers can decide whether or not to join the system based on the information they receive upon arrival, i.e., to maximize their individual utility under the reward–cost structure. These systems can be modeled as a game between customers, and the fundamental problem is to determine the Nash equilibrium. Fundamental results in this area, with an extensive literature review, can be found in the monograph by Hassin and Haviv [8] and Hassin [9].

For the study of queues with vacations from an economic perspective, Economou et al. [10] considered the queue with vacations or failures and quantified the value of reneging for customers. Zhang and Xu [11] studied equilibrium strategies in observable queues with variable vacation and vacation interruptions, and the model had potential applications in CRNs and cloud computing. However, in real life, the number of customers may be hidden to attract more customers, so it is more realistic to study the unobservable level of information. Zhang et al. [12] further studied the socially optimal strategies in the almost unobservable and completely unobservable cases. As an extension of the vacation policy, a working vacation is not a complete halt to work, but work is done at a lower rate during a vacation. A model with multiple working vacations was proposed by Sun and Li [13], which analyzed customers’ behavior from an economic perspective. A large number of recent papers have explored working vacations, and interested readers can refer to [14,15,16].

Nowadays, a growing number of papers have studied retrial queues from an economic perspective. Economou and Kanta [17] considered equilibrium strategies and maximized social welfare with a constant retrial rate. With a classical retrial queue, Wang and Zhang [18] presented the equilibrium joining probability and equilibrium social welfare under two levels of information. Zhang [19] examined the joining strategy in a constant retrial queue with a single vacation. Sun and Wang [20] considered an equilibrium strategy in a constant retrial queue with Bernoulli vacation, where there is no buffer ahead of the server. In recent years, the economic analysis of delayed vacations was presented by Wang and Zhang [21], which focused on the delayed vacation under classical retrial queue, and the pricing strategy was obtained from the exploration of individual and social benefits. Then, Zhang and Wang [22] made a trade-off between power consumption and delay performance, and they studied the optimal pricing strategy for the M/G/1 retrial queue with setup time and delayed vacations. Gao et al. [23] studied an unreliable retrial queue with delayed vacations to derive the equilibrium strategies for customers in non-cooperative and cooperative cases. However, all of the above papers study classical retrial queues with delayed vacations. Based on Zhang and Wang [22], Wang et al. [24] investigated the constant retrial queue with reserved time and vacation, and the equilibrium strategies of customers and the socially optimal strategy were derived. Then, Shi and Liu [25] analyzed the same problem under the retrial queue, with delayed vacations and two types of customers.

In the call center of an insurance company, the server can not only handle some requests from external calls, such as a basic understanding of car insurance products, consulting the claims process, making insurance appointments, etc., but also make calls to potential customers to advertise or sell new products. The primary incoming call arrives according to the Poisson process. Incoming calls that find the server idle receive their services immediately, or either register in the waiting queue and retry to seek service independently of others after a period of time, or leave forever. There will be a chance that the caller will be dissatisfied with the service after completion, and the caller will continue to be queued for the next service. When the server is idle, free time is generated in which to wait for the next incoming call. If there are no incoming calls during the idle period, the server can make outgoing calls for some time. In this scenario, queueing, retrial-seeking service policies, idle cycles, calls corresponding to orbit, retrial policies, limited idle periods, and customers are the queueing terms.

The main contributions of this paper are as follows. (1) Using the generating function method, the steady-state probability and the important performance measures are obtained. The system cost model is developed to investigate the effect of different system parameters on the decision variables and minimum cost through three optimization algorithms (PSO, ACA, and SSA). (2) Due to the complexity of the model, Monte Carlo simulation is used to simulate and analyze the system, and important system parameters are compared with theoretical values to verify the correctness of the theory. (3) Based on the performance measures and reward–cost structure, the optimal arrival rates of customers are analyzed and efficiency indicators such as system throughput and the price of anarchy are calculated to evaluate the efficiency of the system. The decision-maker can detect these two indicators to optimize system performance while reducing losses to find the optimal balance between system performance and individual interests.

The rest of the paper is organized as follows. In Section 2, we focus on a detailed description of the model. Section 3 analyzes the steady-state probabilities and some important performance measures through the generating functions. Section 4 optimizes the cost function based on three optimization algorithms. Monte Carlo simulations verify the accuracy of the theoretical part of the model in Section 5. Individual equilibrium and socially optimal strategies are studied in Section 6. Then, in Section 7, we focus on understanding the effects of the price of anarchy (PoA) and throughput. Finally, we explore the equilibrium arrival rate and the maximum social welfare under different system parameters through numerical analysis in Section 8.

2. Model Description

Consider a retrial queue with delayed vacations and feedback, where arriving customers can get neither the state of the server nor the number of customers in the system. Potential customers arrive individually, according to a Poisson process, with rate $\Lambda$. Upon arrival, the customers join the system with a probability q, and balk with the probability $1-q$. Then, the effective arrival rate is $\lambda =\Lambda q$. When a customer enters the system, if the server is idle, the customer immediately accepts the service, and the service time follows an exponential distribution with rate $\mu$. Otherwise, the customer enters a retrial space with infinite capacity to retry, and the retrial process follows a Poisson process with parameter $\theta$.

After completing the service, the server randomly keeps a period of idle time, which is exponentially distributed with rate $\alpha$. If a customer arrives during this idle period, the server immediately provides service. Otherwise, the server will have a vacation, which is exponentially distributed with rate $\beta$. Upon completion of a vacation period, the server re-enters an idle period, waiting for potential arrivals. After the service, customers will leave the system with a probability b, and will return to the orbit with probability $1-b$ due to dissatisfaction with the service. It is assumed that inter-arrival times, service times, retrial times, and vacation times are independent of each other.

Suppose that each customer gains a reward of R units after completing the service while having to pay a waiting cost of C per unit time to remain in the system. All customers are indistinguishable and rational to pursue their own profit maximization, and they have the right to decide whether or not to enter the system at the time of their arrival. Explicitly, customers tend to enter if they gain more from the service than they pay for the cost, otherwise, they prefer to balk. On the other hand, if the reward is equal to the cost, customers do not care whether they enter or not.

Let $\left(I\right(t),N(t\left)\right)$ represent the system state at time t, where $I\left(t\right)$ is the status of the server and $N\left(t\right)$ is the number of customers in the orbit, and 

$$I\left(t\right)=\left\{\begin{array}{cc}\hfill 0,& \mathrm{the} \mathrm{server} \mathrm{is} \mathrm{idle} \mathrm{at} \mathrm{time} t,\hfill \\ \hfill 1,& \mathrm{the} \mathrm{server} \mathrm{is} \mathrm{busy} \mathrm{at} \mathrm{time} t,\hfill \\ \hfill 2,& \mathrm{the} \mathrm{server} \mathrm{is} \mathrm{on} \mathrm{vacation} \mathrm{at} \mathrm{time} t.\hfill \end{array}\right.$$

We obtain the state space as $\Omega =\left\{(i,n):i=0,1,2,n⩾0\right\}$, and the state transition diagram is shown in Figure 1. The stationary queue length distribution is denoted by ${\displaystyle \left\{{\pi }_{i,n}:(i,n)\in \Omega \right\}.}$

Based on the method of matrix analysis, the stability condition of the system is given by ${\displaystyle \frac{\lambda \beta (\lambda +\theta )+\lambda \mu (\alpha +\beta \overline{b})}{\theta \mu b\beta }<1}$.

The proof can be found in Appendix A.

3. Steady-State Analysis of the System

Here, we consider the completely unobservable case. Assume that the system is stable; then, we can easily get the balance equations:

$$(\lambda +\mu b+\mu \overline{b}){\pi }_{1,0}=\lambda {\pi }_{0,0}+\theta {\pi }_{0,1},$$

(1)

$$(\lambda +\mu b+\mu \overline{b}){\pi }_{1,n}=\lambda {\pi }_{0,n}+\theta {\pi }_{0,n+1}+\lambda {\pi }_{1,n-1},n⩾1,$$

(2)

$$(\lambda +\alpha ){\pi }_{0,0}=\mu b{\pi }_{1,0}+\beta {\pi }_{2,0},$$

(3)

$$(\lambda +\alpha +\theta ){\pi }_{0,n}=\mu b{\pi }_{1,n}+\beta {\pi }_{2,n}+\mu \overline{b}{\pi }_{1,n-1},n⩾1,$$

(4)

$$(\lambda +\beta ){\pi }_{2,0}=\alpha {\pi }_{0,0},$$

(5)

$$(\lambda +\beta ){\pi }_{2,n}=\alpha {\pi }_{0,n}+\lambda {\pi }_{2,n-1},n⩾1.$$

(6)

Define the probability-generating functions of each state i:

$$Q_i\left(z\right)=\sum _{n=0}^{\infty }{\pi }_{i,n}{z}^n,i=0,1,2.$$

Theorem 1.

Consider the retrial queue with delayed vacations and feedback.

(i) The probabilities that the server is idle, busy, on vacation, and ${\pi }_{0,0}$ are as follows:

$$Q_0\left(1\right)={\displaystyle \frac{\beta (\mu b-\lambda )}{\mu b(\alpha +\beta )}},$$

$$Q_1\left(1\right)={\displaystyle \frac{\lambda }{\mu b}},$$

$$Q_2\left(1\right)={\displaystyle \frac{\alpha (\mu b-\lambda )}{\mu b(\alpha +\beta )}},$$

$${\pi }_{0,0}={\displaystyle \frac{F}{\mu \theta b(\alpha +\beta )}},$$

where $F=-\beta {\lambda }^2-\lambda (\mu \overline{b}\beta +\alpha \mu +\theta \beta )+\theta \mu b\beta$.

(ii) The expected sojourn time in the system of a tagged customer who decides to enter the system is given by

$$W\left(\lambda \right)={\displaystyle \frac{(\beta (\alpha +\beta )-\alpha \mu b){\lambda }^2+M\lambda +{\mu }^{2}b((\alpha +\beta )(\alpha +\beta \overline{b})+\alpha \theta b)}{\mu b(\alpha +\beta )F}},$$

where $M=(\alpha +\beta )(\beta \mu +\beta \theta +\alpha \mu \overline{b})+\alpha \mu b(\mu b-\theta )$.

Proof. 

From the balance equations above, we multiply Equations (2), (4), and (6) with $z^n$ and sum over n, then adding (1), (3), and (5), respectively, gives

$$\left\{\begin{array}{c}{\displaystyle (\lambda +\mu -\lambda z)Q_1\left(z\right)=\left(\lambda +\frac{\theta }{z}\right)Q_0\left(z\right)-\frac{\theta }{z}{\pi }_{0,0},}\hfill \\ {\displaystyle (\lambda +\alpha +\theta )Q_0\left(z\right)=(\mu b+\mu \overline{b}z)Q_1\left(z\right)+\beta Q_2\left(z\right)+\theta {\pi }_{0,0},}\hfill \\ {\displaystyle (\lambda +\beta -\lambda z)Q_2\left(z\right)=\alpha Q_0\left(z\right).}\hfill \end{array}\right.$$

Then, we simplify the above equations and obtain the generating functions as follows:

$$\left\{\begin{array}{c}{\displaystyle Q_0\left(z\right)=\frac{t\theta -\frac{\theta }{z}y}{\left(\lambda +\alpha +\theta -\frac{\alpha \beta }{m}\right)t-\lambda y-\frac{\theta y}{z}}{\pi }_{0,0},}\hfill \\ {\displaystyle Q_1\left(z\right)=\frac{(\theta -\frac{\theta }{zt}y)(\lambda +\frac{\theta }{z})}{\left(\lambda +\alpha +\theta -\frac{\alpha \beta }{m}\right)t-\lambda y-\frac{\theta y}{z}}{\pi }_{0,0}-\frac{\theta }{zt}{\pi }_{0,0},}\hfill \\ {\displaystyle Q_2\left(z\right)=\frac{\alpha }{m}\frac{t\theta -\frac{\theta }{z}y}{\left(\lambda +\alpha +\theta -\frac{\alpha \beta }{m}\right)t-\lambda y-\frac{\theta y}{z}}{\pi }_{0,0},}\hfill \end{array}\right.$$

(7)

where $m=\lambda +\beta -\lambda z$, $t=\lambda +\mu -\lambda z$ and $y=\mu b+\mu \overline{b}z$. Bringing $z=1$ into (7), we have

$$Q_0\left(1\right)={\displaystyle \frac{\lambda \theta -\mu \theta b}{\lambda (\lambda +\theta )+\frac{\lambda \alpha \mu }{\beta }-\theta \mu b+\lambda \mu \overline{b}}}{\pi }_{0,0},$$

(8)

$$Q_1\left(1\right)={\displaystyle \frac{\lambda +\theta }{\mu }}{\displaystyle \frac{\lambda \theta -\mu \theta b}{\lambda (\lambda +\theta )+\frac{\lambda \alpha \mu }{\beta }-\theta \mu b+\lambda \mu \overline{b}}}{\pi }_{0,0}-{\displaystyle \frac{\theta }{\mu }}{\pi }_{0,0},$$

(9)

$$Q_2\left(1\right)={\displaystyle \frac{\alpha }{\beta }}{\displaystyle \frac{\lambda \theta -\mu \theta b}{\lambda q(\lambda +\theta )+\frac{\lambda q\alpha \mu }{\beta }-\theta \mu b+\lambda \mu \overline{b}}}{\pi }_{0,0}.$$

(10)

According to the normalization condition $Q_0\left(1\right)+Q_1\left(1\right)+Q_2\left(1\right)=1$, we obtain the probabilities in each state and ${\pi }_{0,0}$.

Next, we will calculate customers’ expected sojourn time. The generating functions in each state are obtained in (7). By taking the derivative of z, we derive $Q_i^{\prime }\left(z\right)$ (i = 0, 1, 2). Then, we put $z=1$ into $Q_i^{\prime }\left(z\right)$, as follows:

$$\left\{\begin{array}{c}{\displaystyle Q_0^{\prime }\left(1\right)=\frac{-\theta \mu bF+\theta (\lambda q-\mu b)\left(\frac{\alpha }{\beta }{\left(\lambda q\right)}^2(1-\frac{\mu }{\beta })-\theta \mu b\right)}{\mu \theta bF(\alpha +\beta )},}\hfill \\ {\displaystyle Q_1^{\prime }\left(1\right)=\frac{\lambda +\theta }{\mu }{Q}_0^{\prime }\left(1\right)+\frac{\lambda q(\lambda +\theta )-\theta \mu }{{\mu }^2}{Q}_0\left(1\right)-\frac{\lambda q\theta -\theta \mu }{{\mu }^2}{\pi }_{0,0},}\hfill \\ {\displaystyle Q_2^{\prime }\left(1\right)=\frac{\lambda q\alpha }{{\beta }^2}{Q}_0\left(1\right)+\frac{\alpha }{\beta }{Q}_0^{\prime }\left(1\right).}\hfill \end{array}\right.$$

(11)

By simplifying (11), the expected number of customers in the system is

$$\begin{array}{cc}\hfill N& =Q_1\left(1\right)+Q_0^{\prime }\left(1\right)+Q_1^{\prime }\left(1\right)+Q_2^{\prime }\left(1\right)\hfill \\ \hfill & ={\displaystyle \frac{(\beta (\alpha +\beta )-\alpha \mu b){\lambda }^3+M{\lambda }^2+\lambda {\mu }^{2}b((\alpha +\beta )(\alpha +\beta \overline{b})+\alpha \theta b)}{\mu b(\alpha +\beta )F}}.\hfill \end{array}$$

According to Little’s formula, ${\displaystyle W\left(\lambda \right)=\frac{N}{\lambda }}$.    □

4. Cost Analysis

A cost function plays an essential role in the queueing model as it represents the total cost incurred by the system. The prime goal of the queueing analysis is to increase revenue, but providing customers with high-quality service and less waiting time will increase the cost of the system. Therefore, we need to optimize the cost function. The different cost notations involved in the cost function are illustrated as follows:

$C_i$: cost per unit time the server is idle,

$C_b$: cost per unit time the server is busy,

$C_v$: cost per unit time the server is on vacation,

$C_o$: holding cost per unit time of a customer staying in the orbit,

$C_s$: cost per unit time of providing a service rate $\mu$.

The cost function is defined as follows:

$$Cost(\mu ,\beta )=C_i{Q}_0\left(1\right)+C_b{Q}_1\left(1\right)+C_{o}N+C_v{Q}_2\left(1\right)+\mu C_s.$$

(12)

The cost function given by (12) is nonlinear with respect to $(\mu ,\beta )$. Therefore, using classical optimization techniques to evaluate the exact analysis results of $({\mu }^{\ast },{\beta }^{\ast })$ is a difficult task. We use PSO, ACA, and SSA to obtain the optimal decision variables $({\mu }^{\ast },{\beta }^{\ast })$. Since the results obtained are randomized, we average the results over 20 runs. Meanwhile, for the settings in PSO, population size = 500; maximum number of iterations = 40; and the learning factors are 0.4 and 0.3, respectively. SSA: sparrow count = 40; maximum iteration count = 40; Safety threshold = 0.6. For ACA, ant count = 500; maximum iteration count = 40; pheromone evaporation coefficient = 0.9; and transfer probability constant = 0.2.

With both $\mu$ and $\beta$ in the interval range of $[4,10]$ and $\Lambda =1.5,\lambda =1,b=0.9,\alpha =1,$ $\theta =5$, we perform the cost optimization with three different cost notations. Cost set I: $C_i$ = 10; $C_b$ = 20; $C_v$ = 3; $C_o$ = 5; $C_s$ = 10. Cost set II: $C_i$ = 20; $C_b$ = 30; $C_v$ = 4; $C_o$ = 6; $C_s$ = 12. Cost set III: $C_i$ = 30; $C_b$ = 40; $C_v$ = 5; $C_o$ = 9; $C_s$ = 15.

In the following, we present three optimization algorithms and some important parameters, respectively, and the effect of different system parameters on the decision variables and the minimum system cost is investigated.

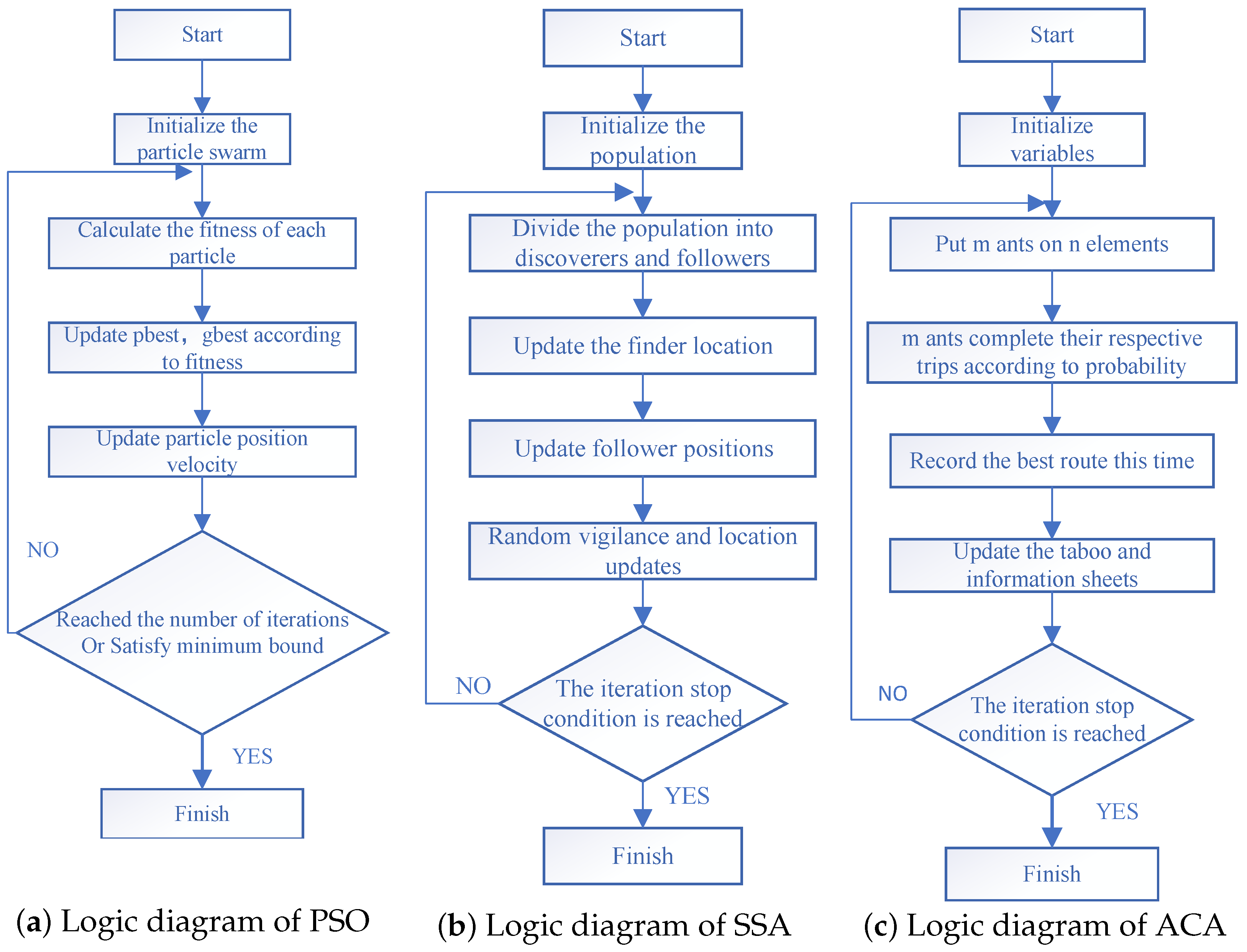
4.1. Implementation of PSO

PSO is a type of evolutionary algorithm and was proposed by Kennedy and Eberhart [26]. The algorithm was originally inspired by the regularity of the activity of clusters of flying birds and seeks to find an optimal solution through collaboration and information sharing between individuals in the group. This algorithm has attracted academic attention for its easy implementation, high accuracy, and fast convergence, and has demonstrated its superiority in solving practical problems.

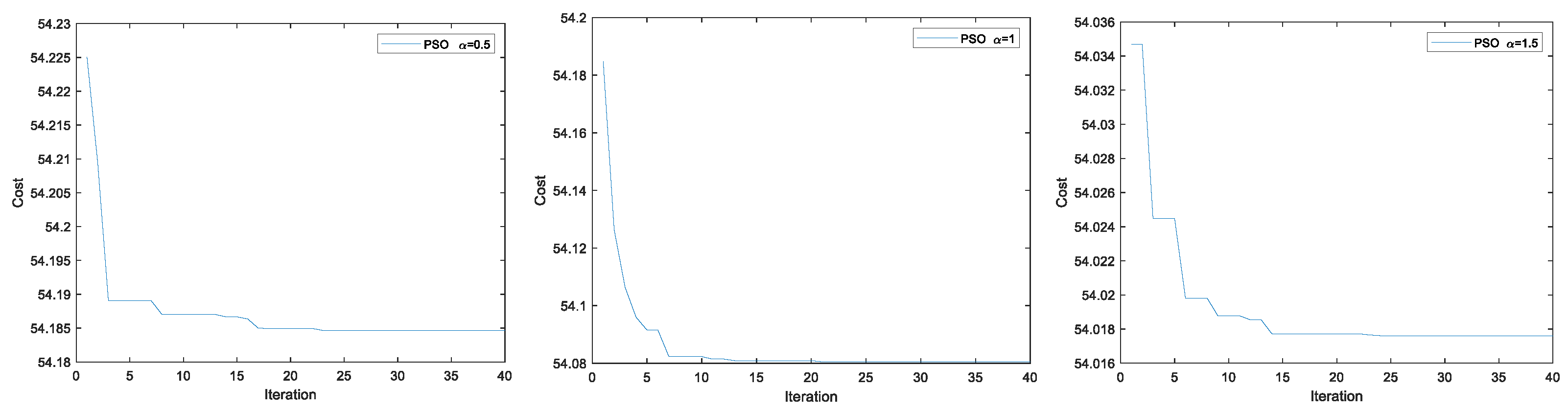
We optimize $\mu$ and $\beta$ to obtain the corresponding minimum value of the cost function. Figure 2a shows the logic diagram of the PSO algorithm. The cost convergence graphs for the three cases are shown in Figure 3, based on Cost set I, which demonstrates the change in the optimization results of the cost function as the number of iterations increases when $\alpha =0.5,1,1.5$, respectively. The fitness value usually decreases rapidly during the initial iterations as the particles explore the solution space, gradually approaching the optimal region. As the number of iterations increases, the rate of convergence may slow down and the curve flattens out, indicating that the algorithm may have found a local or global optimum.

4.2. Implementation of SSA

The SSA is an emerging meta-heuristic algorithm, which is a swarm intelligence algorithm optimized based on the social characteristics of a group. The algorithm simulates the foraging and anti-predator behavior of sparrows by constantly updating individual positions. Compared with the traditional algorithms, the SSA has a simple structure, few control parameters, and strong local search capability.

The SSA mainly achieves positional optimization by mimicking sparrows’ foraging and anti-predation behaviors to find the local optimum. In the preset of this algorithm, the sparrow population is internally categorized into two roles: discoverer and follower, while mimicking real predation scenarios and adding a danger warning mechanism for sparrows. The safety threshold is empirically determined to avoid premature convergence. Based on the logic diagram in Figure 2b, we perform an optimization analysis of the decision variables $\mu$, $\beta$, and $Cost({\mu }^{\ast },{\beta }^{\ast })$. 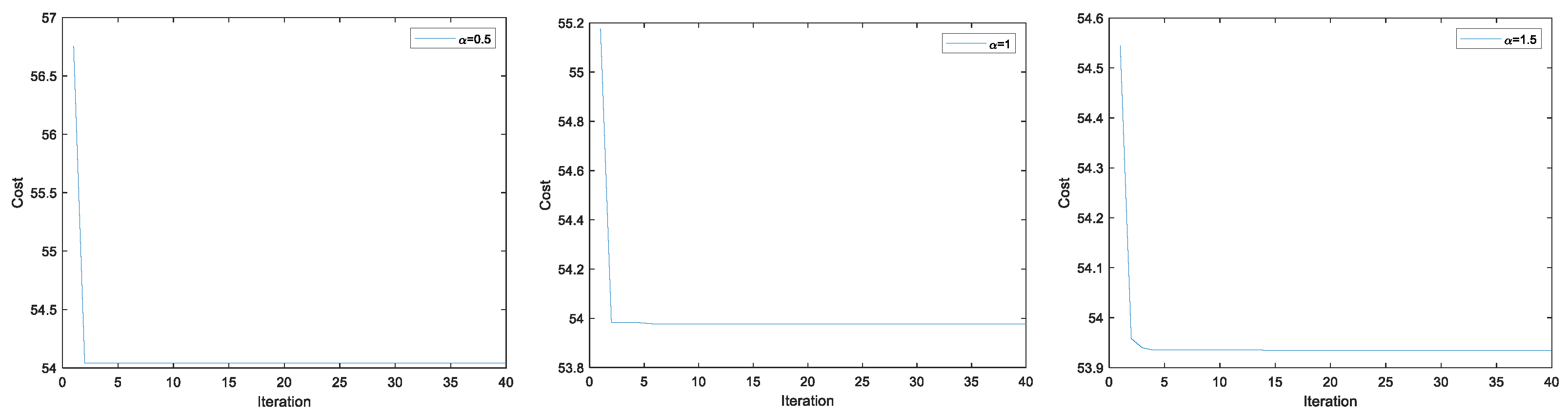The number of iterations is set to 40, in line with the PSO. The convergence plots of the cost function and the number of iterations in the three scenarios are shown in Figure 4.

In Figure 4, we find that the initial period of convergence decreases rapidly, which is because the discoverers will quickly disperse to different regions of the search space to actively explore the potential optimal solutions, and the followers will directly gather to the better positions among the discoverers to quickly reduce the search scope, forming a ‘centralized’ local development and avoiding ineffective random searches.

4.3. Implementation of ACA

The ACA is a heuristic algorithm that simulates the foraging behavior of ants in nature, and it is widely used in the solution of optimization problems. The basic idea of ACA is to place a group of ants in the solution space of the problem and let them gradually find the optimal solution by transferring and volatilizing pheromones.

Figure 2c shows the exact steps of the ACA algorithm. The cost convergence graphs for the three cases are shown in Figure 5. At the beginning of the iteration, pheromone distribution is uniform, ants randomly choose paths, and convergence is slow. As the pheromone concentration of the high-quality path increases significantly, the ants are guided to concentrate their search, accelerating the convergence and subsequently finding the locally optimal solution. So, the cost convergence graphs show a trend of very slow iterations followed by a rapid decline until a locally or globally optimal solution is sought.

4.4. The Effect of Parameters on the Decision Variables and Cost

As $\alpha$ and $\theta$ varies, decision variables $({\mu }^{\ast },{\beta }^{\ast })$ and $Cost({\mu }^{\ast },{\beta }^{\ast })$ are shown in

Table 1. Effect of $\alpha$ on $({\mu }^{\ast },{\beta }^{\ast },Cost({\mu }^{\ast },{\beta }^{\ast }))$.

$\mathit{\alpha }$	Algorithm	Cost Set I	Cost Set II	Cost Set III
	PSO	(4, 6.71, 54.24)	( 4, 4.38, 63.32)	(4, 4.52, 94.19)
0.5	SSA	(4, 6.346, 54.04)	(4, 4, 63.27)	(4, 4, 94.12)
	ACA	(4, 6.48, 54.12)	(4, 5.20, 63.42)	(4, 5.48, 94.33)
	PSO	(4, 7.86, 53.98)	(4, 4.28, 62.72)	(4, 4.44, 93.46)
1	SSA	(4, 7.88, 53.98)	(4, 4, 62.67)	(4, 4, 93.40)
	ACA	(4, 7.75, 54.02)	(4, 5.29, 62.88)	(4, 5.34, 93.67)
	PSO	(4, 8.68, 53.94)	(4, 4.27, 62.3)	(4, 4.58, 93.02)
1.5	SSA	(4, 9.42, 53.94)	(4, 4, 62.29)	(4, 4.20, 93.00)
	ACA	(4, 8.66, 53.94)	(4, 5.14, 62.45)	(4, 5.87, 93.20)

and 

Table 2. Effect of $\theta$ on $({\mu }^{\ast },{\beta }^{\ast },Cost({\mu }^{\ast },{\beta }^{\ast }))$.

$\mathit{\theta }$	Algorithm	Cost Set I	Cost Set II	Cost Set III
	PSO	(4, 9.36, 54.94)	(4, 5.33, 64.12)	(4, 6.99, 95.76)
3	SSA	(4, 10, 54.93)	(4, 5.28, 64.11)	(4, 6.90, 95.76)
	ACA	(4, 8.76, 54.97)	(4, 6.14, 64.14)	(4, 7.27, 95.77)
	PSO	(4, 9.08, 54.32)	(4, 4.46, 63.22)	(4, 4.67, 94.32)
4	SSA	(4, 10, 54.31)	(4, 4, 63.18)	(4, 4.34, 94.31)
	ACA	(4, 8.30, 54.34 )	(4, 5.09, 63.29)	(4, 5.16, 94.39)
	PSO	(4, 7.86, 53.98)	(4, 4.28, 62.72)	(4, 4.44, 93.46)
5	SSA	(4, 7.897, 53.98)	(4, 4, 62.67)	(4, 4, 93.40)
	ACA	(4, 7.75, 54.02)	(4, 5.29, 62.88)	(4, 5.34, 93.67)

. The data show that there is little difference between the results of the three optimization algorithms, but the results for SSA are slightly lower and the results for 20 optimizations are more stable. The convergence plot of cost versus number of iterations shows that PSO is slightly slower to optimize than the other two algorithms, while SSA has the fastest iterations. The SSA algorithm has a short run time, while the PSO algorithm has a relatively long run time. The SSA algorithm is relatively slightly better than the other two algorithms.

From these tables, it is evident that as $\alpha$ decreases, ${\beta }^{\ast }$ decreases and $Cost({\mu }^{\ast },{\beta }^{\ast })$ increases. Additionally, with an increase in $\theta$, both $Cost({\mu }^{\ast },{\beta }^{\ast })$ and ${\beta }^{\ast }$ decrease. However, ${\mu }^{\ast }$ remains relatively stable throughout these changes. As $\alpha$ decreases, $Cost({\mu }^{\ast },{\beta }^{\ast })$ increases, while ${\beta }^{\ast }$ decreases. As $\alpha$ increases, the reserved idle time decreases. The expected number of customers in the system and the probability of the server being busy decreases, so the optimal cost value decreases. As $\theta$ varies, the minimum value of the cost function decreases with the decrease of the $\mu$, so the optimal service rate remains unchanged under the change in $\theta$ and $\mu$. Moreover, $Cost({\mu }^{\ast },{\beta }^{\ast })$ shows a significant increase as cost notations rise.

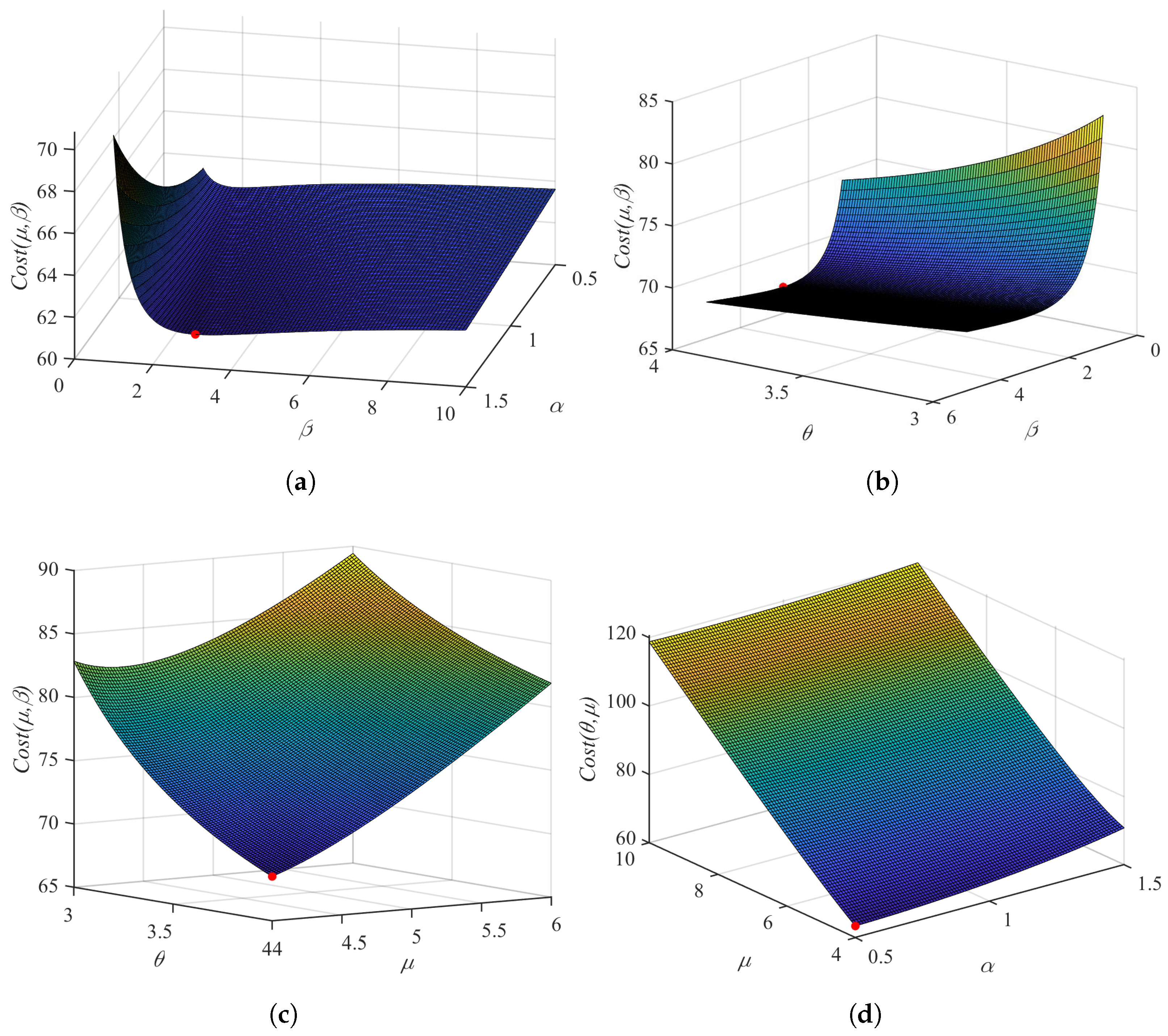
Figure 6 demonstrates the effect of different system parameters on the cost function. These graphs also confirm our analysis of the optimization results. The red dots indicate the points corresponding to the minimum cost values. In Figure 6a, the cost function shows an increasing trend as $\alpha$ decreases, and $Cost({\mu }^{\ast },{\beta }^{\ast })$ also increases. Because as $\alpha$ increases, the reserved idle time decreases. The average number of customers in the orbit and the probability that the server is busy decrease, so the optimal cost value decreases, which is consistent with the changes in the data in Table 1, suggesting that shorter idle periods reduce both orbit congestion and operational costs. From Figure 6b, it can be seen that as $\theta$ increases, the cost function shows a decreasing trend. Because as $\theta$ increases, the retrial interval for customers in the orbit decreases, consequently leading to a downward trend in the cost function. As the other parameters vary, the point of the minimum cost value is always shifted on the curve with $\mu =4$ in Figure 6c,d. The minimum value of the cost function decreases with the decrease of the $\mu$. As the service rate increases, the number of customers in the orbit and the probability that the service desk is busy decrease, but the partial increase in the cost of providing service dominates.

These findings of cost optimization are highly beneficial for the systems as they facilitate efficient resource allocation, reduction of wastage, and improved performance. By carefully managing costs, managers can enhance their competitiveness, profitability, and overall effectiveness. This not only supports sustainable operations but also enables better resource utilization, ultimately contributing to long-term success and growth in a competitive landscape.

5. Monte Carlo Simulation

Monte Carlo simulation is a mathematical technique based on random numbers that is used to simulate complex systems and computational problems, especially those that involve a large number of variables and a large amount of uncertainty. Details can be found in [27]. In the field of queueing theory, customers’ arrival times and service times are uncertain. The majority of queueing systems operate in a stochastic state, and the complexity of the study of queueing systems lies in the randomness of the system, which fits with the Monte Carlo simulation. Monte Carlo simulations have begun to appear in the papers of many researchers in the areas of queueing theory and so on (see Liu [28] and Fitzgerald et al. [29]). Now, let us run a Monte Carlo simulation of this model. The steps of the simulation are described as follows:

Step 1: Input: number of simulations (n), the cost notations, system parameters, simulation time (t).

Step 2: Define the simulation variables: current server status (S), the time of the next transition (T), number of customers in system (N), service variable ($VS$), the arrival time of customers in orbit ($tim{e}_{orbit}$), time of commencement of vacation ($tim{e}_{break}$), current time, the arrival time of the source customer ($tim{e}_{main}$), the service completion time ($tim{e}_{finish}$), vacation end time ($tim{e}_{breakend}$).

Step 3: Initialization variables: set $S=0$, $T=0$, $N=0$, $VS=0$, $tim{e}_{orbit}=inf$, and $tim{e}_{break}=inf.$

Step 4: Simulation: by simulating and analyzing the model, the specific algorithm is shown in Algorithm 1.

Algorithm 1 Monte Carlo Simulation

1: for i in 1: n do   2:    Service the first customer. Update $tim{e}_{finish}$ and $tim{e}_{main}$. We set $T=min(tim{e}_{finish},tim{e}_{main})$ and t = T;   3:    while current time $<t$ do   4:      if $T=tim{e}_{main}$ then   5:         Update $S=1$ and $VS=1$;   6:      end if   7:      if $T=tim{e}_{orbit}$ then   8:         Set $N=N-1$ and update $S=1,VS=1$;   9:      end if 10:      if $VS=1$ then 11:         Update $tim{e}_{finish}$ and $tim{e}_{main}$. Set $T=min(tim{e}_{finish},tim{e}_{main})$, current time = T + current time and $N=N+1$; 12:         Keep performing the above steps until the service ends; 13:      end if 14:      Set $VS=0$, if the customer is unsatisfied with the service, then $N=N+1$; 15:      if $T=tim{e}_{break}$ then 16:         Set $S=2$, update $tim{e}_{breakend}$ and $tim{e}_{main}$, set $N=N+1$ and $T=min(tim{e}_{berakend},tim{e}_{main})$ until vacation ends; 17:      end if 18:      initialize state $S=0$, update $tim{e}_{orbit},tim{e}_{main},tim{e}_{break}$ according to exponential distribution, and $T=min(tim{e}_{orbit},tim{e}_{main},tim{e}_{break})$; 19:    end while 20: end for

Step 5: Count the number of customers in each state and calculate 95% confidence intervals for n simulations.

First, some important performance measures are obtained, which illustrate the accuracy of the model. The details are shown in

Table 3. Simulation results and theoretical values with $\mu$.

System Parameter	$\mathit{\mu }=3$		$\mathit{\mu }=4$		$\mathit{\mu }=5$		$\mathit{\mu }=6$
	Exact	Sim	Exact	Sim	Exact	Sim	Exact	Sim
$P_0$	0.315	0.314	0.361	0.357	0.389	0.386	0.407	0.395
$P_1$	0.370	0.363	0.278	0.274	0.222	0.226	0.185	0.183
$P_2$	0.315	0.323	0.361	0.369	0.389	0.388	0.407	0.422
N	4.250	4.271	2.702	2.722	2.211	2.250	1.975	1.968

and

Table 4. Simulation results and theoretical values with $\beta$.

System Parameter	$\mathit{\beta }=1$		$\mathit{\beta }=2$		$\mathit{\beta }=3$		$\mathit{\beta }=4$
	Exact	Sim	Exact	Sim	Exact	Sim	Exact	Sim
$P_0$	0.361	0.380	0.482	0.469	0.542	0.529	0.578	0.586
$P_1$	0.278	0.260	0.278	0.280	0.278	0.264	0.278	0.258
$P_2$	0.361	0.361	0.241	0.251	0.181	0.177	0.144	0.141
N	2.702	2.700	1.018	1.029	0.698	0.686	0.572	0.620

. The system parameters are $\Lambda =1.5;\lambda$ = 1; $\mu$ = 5; $\theta$ = 4; $\beta$ = 1; and b = 0.9. The model is further validated by comparison with theoretical values. All data are within 95% confidence intervals.

Next, we analyze the costs through Monte Carlo simulation. In Figure 7, the theoretical values of the expected number of customers in the system follow the same trend as the simulated experimental values. We can also observe that the difference between the exact number of customers and the simulation results is small and follows the same trend. Therefore, in cases where the system is complex or no expression is shown, we can consider using the simulation to model cost minimization.

6. Customer Strategy Analysis

In this section, we derive customers’ equilibrium behaviors and the socially optimal arrival rates of customers, respectively.

In the following analysis, we assume that the system is stable, i.e., $F>0$; then, $\lambda$ ranges in $[0,{\lambda }_{max})$, where ${\lambda }_{max}$ is the only non-negative solution for $F=0$. We discuss customers’ equilibrium strategies. The equilibrium arrival rate of customers is analyzed based on the reward–cost function and game theory. Next, in order to obtain the optimal arrival rate, we need to derive the monotonicity of the expected sojourn time. The following lemma provides the result of the monotonicity of the expected sojourn time.

Lemma 1.

The monotonicity of $W\left(\lambda \right)$ is discussed in the classification:

(i) When $A⩾0$, $W\left(\lambda \right)$ is monotonically increasing with $\lambda \in [0,{\lambda }_{max})$;

(ii) When $A<0$ and $\overline{\lambda }⩾{\lambda }_{max}$, $W\left(\lambda \right)$ is monotonically growing with $\lambda \in [0,{\lambda }_{max}),$ where $\overline{\lambda }$ is the only positive solution which satisfies $W^{\prime }\left(\lambda \right)=0;$

(iii) When $A<0$ and $\overline{\lambda }\in [0,{\lambda }_{max})$, $W\left(\lambda \right)$ will initially increase and then decrease,where $A={\beta }^2-\alpha \beta +\alpha \mu$.

Proof. 

The derivative of $W\left(\lambda \right)$ with respect to $\lambda$ is given by

$${\displaystyle \frac{\mathrm{d}W\left(\lambda \right)}{\mathrm{d}\lambda }}={\displaystyle \frac{A{\lambda }^2+B\lambda +D}{F^2}},$$

where

$$A={\beta }^2-\alpha \beta +\alpha \mu ,$$

$$B=2\beta (\beta \theta +\alpha \mu +\beta \mu \overline{b}),$$

$$\begin{array}{cc}\hfill D=& {\displaystyle \beta \mu \theta (1+\overline{b})(\alpha +\beta )+\alpha {\mu }^2(2\beta \overline{b}+\alpha +\theta b)+{\beta }^2({\mu }^2{\overline{b}}^2+{\theta }^2).}\hfill \end{array}$$

We know that $B,D>0$, so $W\left(0\right)⩾0$.

In case (i), when $A⩾0$, $W\left(\lambda \right)$ is increasing, since $W^{\prime }\left(\lambda \right)⩾0$ with $\lambda \in [0,{\lambda }_{max})$.

In case (ii), when $A<0$ and $\overline{\lambda }$∉ [0, ${\lambda }_{max}$), $W^{\prime }\left(\lambda \right)>0$ with $\lambda \in [0,{\lambda }_{max})$, where $\overline{\lambda }$ is the only solution satisfying $W^{\prime }\left(\lambda \right)=0$. So, $W\left(\lambda \right)$ grows monotonically with $\lambda \in [0,{\lambda }_{max}$).

In case (iii), when $A<0$ and $\overline{\lambda }\in [0,{\lambda }_{max})$, $W^{\prime }\left(\lambda \right)$ is first greater than 0 in $[0,\overline{\lambda }]$ and then less than 0 in $[\overline{\lambda },{\lambda }_{max})$, where $\overline{\lambda }$ is the only solution satisfying $W^{\prime }\left(\lambda \right)=0$. So, $W\left(\lambda \right)$ first increases and then decreases. □

Under the reward–cost structure, the expected net benefit of an arriving tagged customer who finds the server unavailable and decides to enter the system is

$$U\left(\lambda \right)=R-CW\left(\lambda \right).$$

Next, we derive customers’ equilibrium behaviors based on the reward–cost function in the following Theorem.

Theorem 2.

Consider the M/M/1 retrial queue with delayed vacations and feedback.

• Case I. When $A⩾0$ or When $A<0$ and $\overline{\lambda }⩾{\lambda }_{max}$,

  $${\lambda }_e=\left\{\begin{array}{c}{\displaystyle 0,\frac{R}{C}⩽\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )},}\hfill \\ {\displaystyle min\left\{{\lambda }_1,\Lambda \right\},\frac{R}{C}>\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )},}\hfill \end{array}\right.$$

  where ${\lambda }_1$ satisfies $R-CW\left(\lambda \right)=0$ and ${\lambda }_1\in [0,{\lambda }_{max})$.
• Case II. When $A>0$, $\overline{\lambda }\in [0,{\lambda }_{max})$.

1. 

If ${\displaystyle \frac{R}{C}⩽\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$,

$${\lambda }_e=\left\{\begin{array}{c}{\displaystyle 0,{\lambda }_2>\Lambda ,}\hfill \\ {\displaystyle \left\{0,{\lambda }_2,\Lambda \right\},{\lambda }_2⩽\Lambda ,}\hfill \end{array}\right.$$

where ${\lambda }_2$ is the nonnegative solution of $R-CW\left(\lambda \right)=0$.

2. 

If ${\displaystyle \frac{R}{C}>\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$, there are two cases.

If $U\left(\overline{\lambda }\right)>0$, ${\lambda }_e=\Lambda$. If $U\left(\overline{\lambda }\right)<0$, then

$${\lambda }_e=\left\{\begin{array}{c}{\displaystyle \Lambda ,{\lambda }_3>\Lambda ,}\hfill \\ {\displaystyle {\lambda }_3,{\lambda }_3⩽\Lambda <{\lambda }_4,}\hfill \\ {\displaystyle \left\{{\lambda }_3,{\lambda }_4,\Lambda \right\},{\lambda }_4⩽\Lambda ,}\hfill \end{array}\right.$$

where ${\lambda }_3$ and ${\lambda }_4({\lambda }_4⩾{\lambda }_3)$ are the solutions of $R-CW\left(\lambda \right)=0$.

Proof. 

In case I, according to the monotonicity of $W\left(\lambda \right)$, when $A>0$ or $A<0$ and $\overline{\lambda }⩾{\lambda }_{max}$, $W\left(\lambda \right)$ increases with $\lambda \in [0,{\lambda }_{max})$; thus, $U\left(\lambda \right)$ decreases in $\lambda$. $U\left(\lambda \right)$ reaches its maximum at $\lambda =0$, so we have

$${\displaystyle \underset{\lambda \to 0}{lim}W\left(\lambda \right)=\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}.}$$

When ${\displaystyle \frac{R}{C}⩽\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$, $U\left(\lambda \right)⩽0$ for $\lambda \in [0,{\lambda }_{max})$. The customer’s best response is to balk, so ${\lambda }_e=0$.

When ${\displaystyle \frac{R}{C}>\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$, there is a unique root ${\lambda }_1\in [0,{\lambda }_{max})$ of $R-CW\left(\lambda \right)=0$. If ${\lambda }_1>\Lambda$, $U\left(\lambda \right)⩾0$ for every $\lambda \in [0,{\lambda }_{max})$. If ${\lambda }_1⩽\Lambda$, ${\lambda }_1$ will be the mix strategy. Therefore, ${\lambda }_e=min\left\{{\lambda }_1,\Lambda \right\}.$

In case II, when $A>0$ and $\overline{\lambda }\in [0,{\lambda }_{max})$, $U\left(\lambda \right)$ first decreases and then grows based on the monotonicity of $W\left(\lambda \right)$.

When ${\displaystyle \frac{R}{C}⩽\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$, ${\lambda }_e=0$ is always the equilibrium arrival rate, since nobody can obtain any profits by entering the system when others choose to balk, and ${\lambda }_2\in [0,{\lambda }_{max})$ is the root of $U\left(\lambda \right)=0$. If ${\lambda }_2>\Lambda$, $U\left(\lambda \right)⩽0$, so the best response is balk and ${\lambda }_e=0$. If ${\lambda }_2⩽\Lambda$, ${\lambda }_e=\left\{0,{\lambda }_2,\Lambda \right\}$, because customers are always willing to join if ${\displaystyle \frac{R}{C}⩾W\left(\lambda \right)}$.

When ${\displaystyle \frac{R}{C}>\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$, if $U\left(\overline{\lambda }\right)>0$, the minimum value of the individual utility function is greater than 0 and the best response is joining, so ${\displaystyle {\lambda }_e=\Lambda }$. If $U\left(\overline{\lambda }\right)<0$, we know ${\displaystyle \frac{R}{C}>\frac{\alpha +\beta \overline{b}}{\beta \theta b}+\frac{\alpha }{\beta (\alpha +\beta )}}$; thus, the individual utility function has two points of intersection with the x-axis. There are two roots (${\lambda }_3$ and ${\lambda }_4$) of $U\left(\lambda \right)=0$, then the analysis is as above. □

Now, we investigate social welfare, which is the sum of all the customers’ expected net benefits. The goal of the social planner is to maximize social welfare, and the expression of the social welfare is given by

$$S\left(\lambda \right)=\lambda (R-CW(\lambda \left)\right).$$

Due to the complexity of social welfare, we solve the socially optimal arrival rate by the PSO in Section 8.

7. Efficiency Measures: PoA and Throughput

In this section, we focus on understanding the price of anarchy (PoA) and throughput. The goal is to find an optimal balance between system performance and individual benefit. This information holds significance for aiding social planners in making well-informed decisions.

Throughput denotes the number of customers that can be served within a given time. Higher throughput means better system performance and more efficient service to customers within the system. We get the throughput as follows:

$$TH\left(\lambda \right)=\lambda \left(\sum _{n=0}^{\infty }{\pi }_{0,n}+\sum _{n=0}^{\infty }{\pi }_{1,n}+\sum _{n=0}^{\infty }{\pi }_{2,n}\right)$$

A common measure of this availability is the price of anarchy (PoA), which is the ratio of socially optimal welfare to equilibrium social welfare. The PoA is usually calculated as the ratio between a worst-case scenario, reflecting non-cooperative behavior, and a best-case scenario, representing the outcome of full cooperation. For more details, see [30]. The PoA is defined as follows:

$$PoA={\displaystyle \frac{S\left({\lambda }^e\right)}{S\left({\lambda }^{\ast }\right)}}$$

A price of anarchy (PoA) of 1 indicates that there is no loss of efficiency due to selfish or uncoordinated behavior, which means that the system is operating at optimal efficiency. In contrast, a PoA less than 1 indicates that selfish behavior or lack of coordination between individuals leads to suboptimal performance, resulting in a loss of efficiency.

8. Numerical Results

In this section, we first analyze the relationship between the equilibrium and the socially optimal arrival rates under different parameters and analyze the influence of system parameters on the maximum social welfare. Then, we analyze the variation of throughput and PoA under different parameters.

8.1. Equilibrium Strategy and Social Welfare Analysis

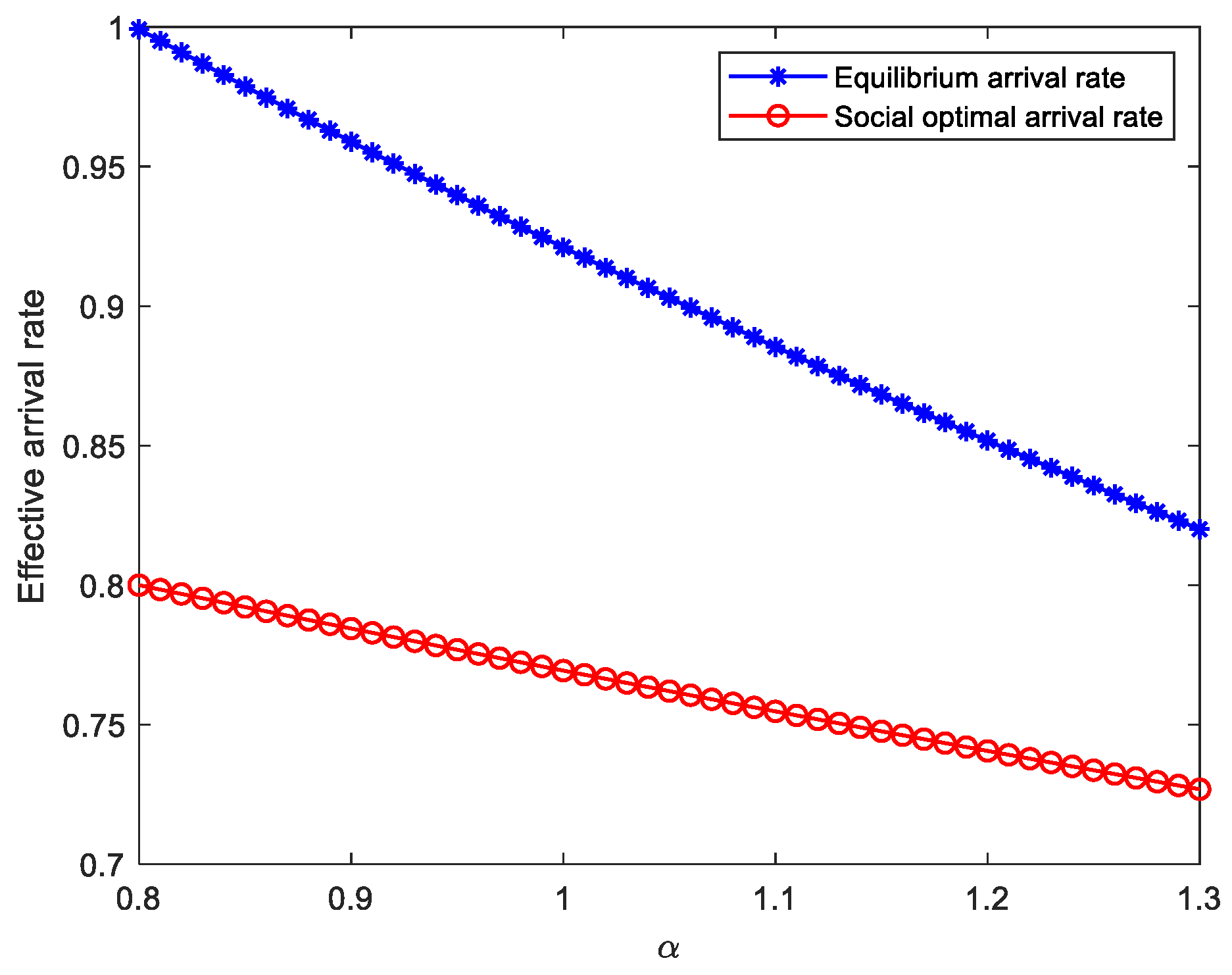
Figure 8, Figure 9 and Figure 10 show the trend of the equilibrium and socially optimal arrival rates as the parameters $\mu$, $\alpha$, and $\beta$ vary. First, in Figure 8, the equilibrium arrival rate declines as $\alpha$ rises. This is because customers are less likely to accept service with less reserved time and more waiting time, so customers are more inclined to balk. Thus, the arrival rate is reduced in both cooperative and uncooperative states.

Figure 9 and Figure 10 similarly demonstrate that both equilibrium and socially optimal arrival rates increase with higher values of $\mu$ and $\beta$. The $\mu$ represents the service rate and $\beta$ represents the vacation rate. It is easy to understand that by reducing the service time and the vacation time, the waiting time for customers will decrease. Therefore, they are more willing to join the system. At this point, there will be a phenomenon of following the crowd, thinking that there will be excessive customers in the system. For an FCFS queueing system, impose more waiting time will be imposed on any other customer who arrives after this initial one once a customer decides to join it. This is called a negative externality, and because of it, the upward arrival rate of the equilibrium arrival rate will gradually slow down.

From the above analysis, we find that the equilibrium arrival rate is not smaller than the socially optimal arrival rate. This can be explained from an economic point of view. Selfish customers always ignore the negative externalizes they bring to the system. As a result, public resources are over-utilized and the system is more crowded than the social planner expects. The classical approach for this is to charge customers for joining the system to make the equilibrium arrival rate consistent with the socially optimal arrival.

Then, we show the effect of the system parameters on the maximum social welfare in Figure 11, Figure 12 and Figure 13. As $\mu$ and $\theta$ increase, customers’ sojourn time is reduced and customers become more willing to join the system in Figure 11, which will contribute to increasing the maximum social welfare. It is clear that as R increases, the socially optimal welfare increases, which is in line with our intuition. Similarly, as C increases, it leads to higher costs per unit of time and is not favorable for socially optimal welfare. In Figure 13, as $\alpha$ increases, the reserved idle time and sojourn time increase, so social welfare decreases. As $\theta$ increases, the customer’s sojourn time decreases, which is favorable to increasing social welfare.

8.2. Throughput and PoA

To evaluate the performance of the throughput and PoA with respect to socially optimal and individual equilibrium strategies, we analyze the throughput and PoA vs. the system parameters. The results are presented in

Table 5. Comparison of the throughput and the PoA with individual and social equilibrium vs. some system parameters.

System Parameter	Parameter Values	$\mathit{TH}\left({\mathit{\lambda }}^{\mathit{e}}\right)$	$\mathit{TH}\left({\mathit{\lambda }}^{\ast }\right)$	PoA
	4	0.8194	0.6105	0.9093
$\mu$	5	0.8056	0.6690	0.9928
	6	0.6944	0.6944	1
	7	0.6845	0.6845	1
	1	0.8194	0.8194	1
$\alpha$	2	0.7292	0.6680	0.9797
	3	0.6750	0.4700	0.3065
	4	0.6708	0.4549	0.1291
	3	0.7593	0.5562	0.4734
$\theta$	4	0.7292	0.6680	0.9797
	5	0.7111	0.7111	1
	6	0.6991	0.6991	1
	1	0.6790	0.5841	0
$\beta$	2	0.7593	0.5562	0.4734
	3	0.8074	0.7600	0.9893
	4	0.8395	0.8395	1

.

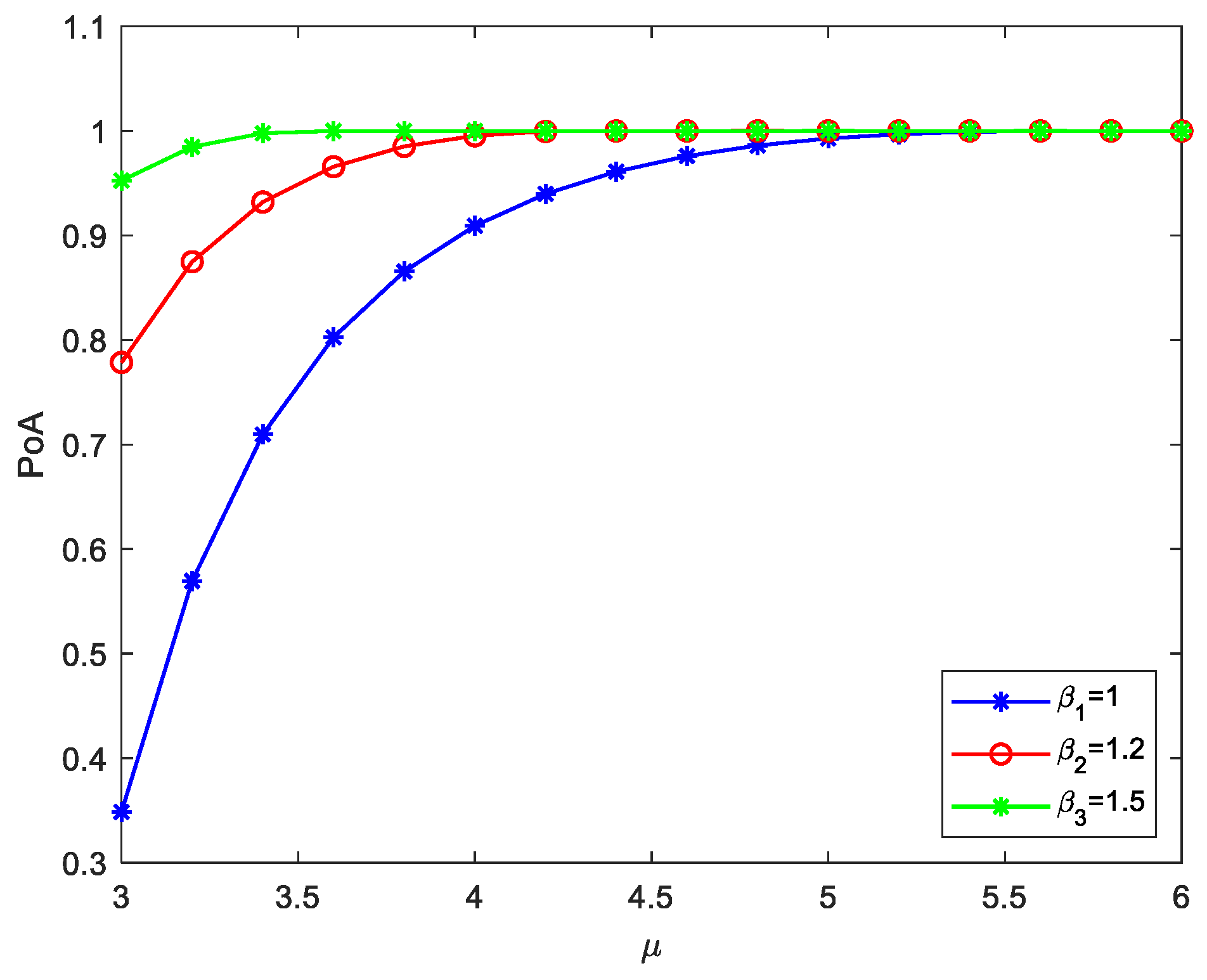
Firstly, it can be demonstrated that $TH\left({\lambda }^e\right)$ is greater than or equal to $TH\left({\lambda }^{\ast }\right)$ under identical parameters. As $\alpha$ increases, $TH\left({\lambda }^e\right)$ and $TH\left({\lambda }^{\ast }\right)$ decrease. It can be observed that as the value of $\beta$ increases, $TH\left({\lambda }^e\right)$ and $TH\left({\lambda }^{\ast }\right)$ increase. An increase in both $\mu$ and $\theta$ results in a reduction in $TH\left({\lambda }^e\right)$, while $TH\left({\lambda }^{\ast }\right)$ initially rises and then decreases after reaching a certain level.

It can be shown that when PoA is equal to 1, $TH\left({\lambda }^e\right)$ and $TH\left({\lambda }^{\ast }\right)$ are identical. In the case of minimal $\alpha$ values, the PoA stabilizes at a value of 1 and then decreases as the value of $\alpha$ increases. As illustrated by Figure 14 and Figure 15, PoA rises in conjunction with the value of $\mu$ and $\theta$, reaching a maximum value of 1.

9. Conclusions

This paper focuses on the socially optimal and equilibrium arrival rates of the M/M/1 constant retrial queue with delayed vacations and feedback. Firstly, we obtain the key performance measures of the system according to the probability-generating functions. Subsequently, the cost function is optimized to provide suggestions for decision-makers through three optimization algorithms. Due to the complexity of the calculation, we use the Monte Carlo method to simulate customers’ behavior. Some important performance measures are obtained and we then compare them with the theoretical values, which further verify the accuracy of the model. The expected net benefit is derived from the reward–cost function to further analyze the equilibrium and the socially optimal arrival rates. Then, we focus on understanding the effects of the price of anarchy (PoA) and throughput. Finally, we analyze the customers’ strategy, the throughput, and PoA with the system parameters. Future research can investigate systems with general service rates. The model can be further extended by combining the N-policy and the customer’s hesitation behavior.