Abstract
With the rapid development of e-commerce, Return Freight Insurance (RFI) has emerged as a vital tool for retailers and customers to mitigate the financial burden posed by high return rates in online shopping. This paper investigates the strategic decision-making of RFI providers (insurers), examining whether they should offer fixed-compensation insurance at a lower price or full-coverage insurance at a higher price under varying market conditions. Specifically, we develop game-theoretic models to analyze insurers’ strategic decisions in both monopoly and duopoly markets, accounting for customer return cost and product mismatch probability heterogeneity. Our findings reveal that in a monopoly market, when customer return costs are relatively low and concentrated, insurers benefit from offering fixed compensation insurance (i.e., pre-set reimbursement amounts) at a lower price to attract a broader customer base. By contrast, when return costs are more dispersed and higher, full-coverage insurance (which reimburses actual freight costs) becomes more profitable, as the insurer can utilize its flexible pricing power to attract higher-paying customer segments. In a duopoly market, customer return cost heterogeneity significantly influences market equilibrium. When heterogeneity is high, full-coverage insurance dominates, as insurers can leverage precise market segmentation to justify higher premiums. Conversely, when return costs are more uniform, fixed compensation insurance is preferred for its affordability, appealing to a wider range of customers.
MSC:
90B50; 91A35
1. Introduction
The rapid advancement of internet technology and the ongoing digital transformation have created a significant growth market for internet insurance, an innovative product of financial technology (Fintech), and the insurance industry [1,2,3]. The procedure for entering this type of insurance contract generally involves customers purchasing coverage for a particular product or service offered online, either by searching for or collaborating with designated online insurers, and paying the premium directly through digital platforms [4]. In China, internet insurance premiums increased from 29 billion CNY (Chinese Yuan) in 2013 to 494.9 billion CNY in 2023, with an impressive average annual growth rate of 32% [5]. Analysis suggests this growth will continue, with a projected annual growth rate between 15% and 20% over the next five years [6].
E-commerce platforms, as the core carriers of the internet economy, offer diverse application scenarios for insurance products. This demonstrates the significant potential for innovative insurance products to address critical challenges within the e-commerce ecosystem. One prominent example is Return Freight Insurance (RFI), which has gained significant growth in recent years. RFI provides financial protection by covering the cost of return shipping when purchased products are sent back to the seller. It can be purchased either by customers, who voluntarily add it during the checkout process, or by retailers, who offer it as a value-added service to enhance customer satisfaction and streamline return logistics [7].
Based on insurance theory and risk-sharing theory [8], RFI aims to alleviate the financial burden of product return shipping costs. It significantly shares the potential financial risks and costs faced by customers and retailers during the return process, and is an innovative application in the field of insurance. China’s e-commerce platforms experience average return rates ranging from 5% to 20% [9,10,11], with product return costs accounting for approximately 9% of the total value of the electronic sales [10]. In response to these challenges, RFI plays an important role in enhancing the customer experience while mitigating financial risks for businesses. By covering return shipping expenses, RFI improves customer satisfaction, fosters customer confidence in online purchases, and contributes to the overall efficiency of e-commerce operations. The growing demand for RFI is evident from its market growth, with premium sales in China reaching CNY 8.27 billion in the first half of 2022 [12].
Similar to traditional insurance sectors such as auto and health insurance, the return freight insurance market is evolving toward greater diversification and customization. As customer demand for seamless and flexible return options grows, e-commerce platforms, retailers, and insurers are introducing RFI products with varying levels of coverage to cater to different shopping behaviors and risk preferences (see Figure 1). Specifically, some policies—such as those illustrated in Figure 1a—offer low compensation for a lower premium. In contrast, others—such as those shown in Figure 1b—provide greater compensation for a higher price. Furthermore, an increasing number of insurers are partnering with logistics providers to offer full-coverage RFI, which reimburses the entire return shipping cost when returns are processed through designated logistics services. Therefore, as the RFI market continues to expand and mature, insurers must strategically design their RFI offerings—whether to provide lower-cost fixed-compensation insurance or higher-priced full-coverage insurance.

Figure 1.
Diversified return freight insurance (RFI) options available on Taobao.com. (a) Low-priced RFI on Taobao.com. (b) High-priced RFI on Taobao.com.
Previous studies on RFI have primarily focused on the decision-makings of online retailers (e.g., [12,13,14,15,16,17]), while largely overlooking the role of insurers—let alone the competitive dynamics among RFI providers. Consequently, there remains a significant gap in understanding how RFI providers, i.e., insurers, strategically design and price their RFI products in response to changing market conditions, such as customer behavior and competitive dynamics.
To address this gap, this study investigates the strategic decision-making of RFI providers under varying market conditions. Specifically, it examines how insurers should tailor their RFI offerings in response to customer return behavior, associated return costs, and competitive dynamics. Using mathematical modeling and analytical comparison, this study examined insurers’ optimal RFI strategies in monopolistic as well as duopolistic markets, aiming to address the following research questions:
- (1)
- What impact does the return behavior of online shopping customers on the optimal choice of insurers between fixed-compensation insurance and full-coverage insurance?
- (2)
- How do different market structures (monopoly vs. duopoly) affect insurers’ optimal RFI strategies?
To address these research questions, we develop an analytical framework to examine customer purchase decisions and insurers’ strategic choices. Our findings suggest that RFI providers should tailor their offerings based on customer return behavior and market structures.
In a monopolistic market, when the monopolistic insurer only offers one type of RFI service, a fixed-compensation RFI strategy is more effective when return costs are relatively uniform and low, appealing to cost-sensitive customers. In contrast, a full-coverage strategy becomes optimal when return costs are highly variable or elevated, as it allows insurers to target segments purchasing high-value or bulky items, which typically incur higher return costs. This distinction reflects the differing market focus of each approach: fixed-compensation RFI attracts low-cost returners, while full-coverage RFI appeals to customers with greater risk exposure. By aligning insurance offerings with customer return cost profiles, insurers can enhance both market efficiency and profitability.
In a competitive market where both fixed-compensation and full-coverage return freight insurance options coexist, insurers must carefully consider the fixed compensation amount. When the distribution of return shipping costs is relatively concentrated and falls near the fixed compensation level, offering fixed-compensation insurance is more advantageous. Conversely, when return shipping costs are highly dispersed and frequently exceed the fixed compensation amount, insurers can profitably offer full-coverage insurance at a higher price, as it becomes more attractive to customers facing greater return cost uncertainty. In such cases, full-coverage insurance captures a larger share of the market and yields higher profitability.
This study contributes to both the literature and practice in two key aspects. First, we extend the research on return freight insurance for e-commerce by analyzing the insurer as a primary decision-maker and introducing it into a competitive market setting. To the best of our knowledge, this is the first study examining the simultaneous deployment of multiple RFI types—fixed-compensation and full-coverage—within such a setting. Second, the study relaxes the prevailing assumption of constant return costs and return probabilities found in prior work (e.g., [7,13,18,19,20]). By incorporating heterogeneous customer return costs and product misfit probabilities, the model presents a more realistic representation of the market, which allows for a deeper exploration of how variations in customer return behavior influence insurers’ optimal choice of RFI offerings.
The structure of this paper is organized as follows. Section 2 provides a review of the relevant literature. Section 3 delineates the problem being studied. Section 4 analyzes the optimal RFI strategy for an insurer in a monopolistic context. Section 5 extends the analysis to a duopolistic environment. Concluding remarks are presented in Section 6, and proofs of all propositions are included in the Appendix A.
2. Literature Review
As business activities increasingly shift to digital platforms, internet insurance—an integral component of fintech innovation—has been reshaping the traditional insurance landscape. This transformation has catalyzed a growing body of scholarly research examining innovative internet insurance and their market penetration (e.g., [1,2,3,9]).
Researchers have highlighted how insurtech is innovating insurance processes, enhancing both service efficiency and user experience [1]. Digital transformation, in particular, has been identified as a key factor in improving insurers’ competitiveness [2]. This technological evolution extends beyond basic digitization, as the integration of blockchain and Fintech has transformed investment management and financial solutions, offering enhanced security and transparency for insurance products. Complementing these advances, digital identity verification technologies, such as biometric authentication, have significantly improved the safety and convenience of insurance services [21]. Simultaneously, the rise of RegTech has delivered innovative solutions for regulatory compliance in the insurance sector [22]. Together, these technological advances drive the evolution of internet insurance, creating a more efficient, inclusive, and customer-centric ecosystem. As a result, internet insurance offerings have diversified substantially, extending beyond traditional property and health insurance to include emerging products such as return freight insurance and sharing economy insurance—tailored to address the evolving demands of digitalized business environments [3].
In the e-commerce sector, internet insurance develops innovative products in response to emerging business scenarios, thereby extending market coverage [9,10]. Among all these innovations, RFI—a typical internet insurance product in the e-commerce sector—has gained significant growth by mitigating financial concern for both buyers and sellers during return transactions [23]. The current literature on RFI is gorwing, yet remains limited in both scope and depth.
Early studies on RFI primarily examined monetary leniency, focusing on money-back guarantees ranging from no refund to partial and full refund policies (e.g., [24,25,26]). Fan and Chen [16] reported that etailers offer free RFI mainly when the insurance premiums they face are low and the return shipping compensation is substantial. In contrast, those manufacturers less inclined to provide such insurance at no cost typically do so only if they bear high premiums. Lin et al. [17] highlighted that retailers often vary RFI offerings with product values, tailoring return pricing and policies to reflect customer heterogeneity and the proportion of value customers place on the products. These studies also suggest that RFI could yield additional benefits for retailers, contingent upon the balance between insurance cost and return fees.
Building on these foundational insights, platform-based research has explored how e-commerce ecosystems influence RFI design and implementation. For example, Feldman et al. [27] showed that Alibaba leverages historical data from Taobao sellers to refine its recommendation algorithms, while also initiating proprietary data-sharing arrangements with retailers. Liu et al. [28] examined how platforms may strategically manipulate information sharing to reinforce their market position—potentially at the expense of other stakeholders. Meanwhile, Yang et al. [20] argued that limiting customers’ RFI purchase options could protect retailers from adverse effects of high return rates, although such a strategy might disadvantage less-informed customers by exposing them to higher premiums.
From the retailer and manufacturer perspective, several studies have investigated how RFI affects pricing strategies and profit optimization. Chen et al. [14] examined how retailer profits vary when product quality differs and RFI decisions must be made under uncertainty. Their findings suggest that when RFI premiums are high, retailers of higher-quality products are more likely to include RFI in the sale, while those with lower-quality items may pass the decision to customers. Similarly, Bian and Xiao [29] analyzed manufacturers’ RFI strategies and pricing decisions within multi-stakeholder ecosystems. Their results indicate that free RFI offerings can reduce the “showrooming effect”—shifting customer preferences from offline to online—while benefiting all players: retailers, manufacturers, and insurers.
More recently, scholars have focused on how retail strategies and customer behavior intersect with RFI. This includes the adoption of dynamic pricing models, the impact of insurance terms on customer decisions, and broader effects on profitability across the supply chain [13,14,16]. In addition, Li et al. [13] examine insurance pricing strategies in an monopolistic market, comparing scenarios where RFI is provided by retailers or purchased directly by customers.lXiong and Liu [12] explore the returns strategy choices among retailers of different qualities in a duopoly market based on the uncertain satisfaction of customers. They find that when the RFI premium is low, low-quality retailers will not provide RFI, and high-quality retailers will only offer free RFI to customers when the premium is relatively low. Li et al. [30] analyzed a supply chain competition model with two return services named RFI and return pickup service (RPS) in both in monopoly and duopoly markets. They showed that highly similar or differentiated products favor RFI, as intense price competition or reduced service - based competition drives this preference. In contrast, moderately differentiated products encourage RPS adoption, where service quality is a key competitive factor. Geng et al. [7] noted a significant research gap in understanding how insurers align product design with actual customer needs, arguing that most studies overly emphasize the insurer’s risk perception. In this context, Li et al. [19] explored optimal RFI policies by analyzing restocking fees and return costs in a monopolistic market. Their findings suggest that when return processing costs are high and customer return shipping fees are moderate, offering Customer Return Shipping Insurance (CRSI) as a separate product may be more effective. This also increases the likelihood that customers will opt for Retailer Return Shipping Insurance (RRSI) when restocking fees are imposed.
The preceding discussion reveals a fragmented yet evolving body of literature on return freight insurance, underscoring a notable gap concerning the role and competitive behavior of insurers. In particular, existing research offers limited insight into insurers’ participation within the e-commerce supply chain, especially their function as independent decision-makers. Furthermore, there are few studies on insurers’ adaptive strategies in changing market conditions. This study aims to address these gaps by examining insurance firms’ perspectives on the dynamics of offering RFIs in the e-commerce supply chain.
3. Problem Description
We consider the decision-making process of an RFI provider, i.e., an insurer, who offers RFI for an online retailer on an e-commerce platform. The insurer operates in either a monopolistic market (as the sole RFI provider) or a competitive environment (where two RFI providers compete) to maximum his profit.
Specifically, the retailer (she) invites the insurer (he) to offer Customer Return Freight Insurance (CRFI) for her online sales of a product priced at p. Under the CRFI mode [15,19,31], customers decide whether to purchase the RFI when buying the product and directly pay the associated premium. As RFI provider, the insurer needs to determine which type of RFI to offer—either a lower-cost fixed-compensation insurance or a higher-priced full-coverage insurance, and then decide the corresponding premium rates accordingly. Note that in the monopoly case, only one type of service and a single price are provided. In contrast, in the duopoly case, two insurers compete by offering two different types of services at distinct prices.
For analytical convenience, the customer base is normalized to have unit mass. Customers have heterogeneous valuations for the product, denoted by . Additionally, customer return behavior varies along two relevant dimensions: the probability of misfit and the return freight cost . The probability of product misfit represents the likelihood that a purchased item does not meet the expectations of customer i, and therefore resulting in a return. Following the work of [14,19], we assume follows a uniform distribution over the interval , where and denote the minimum and maximum probabilities of product misfit, respectively. Similar to [30], the return freight cost refers to the cost incurred by the customer i when returning an item, which is uniformly distributed over the interval , with is simply the maximum possible return freight cost.
When fixed-compensation insurance is provided, the insurer reimburses customers a pre-specified compensation amount that is independent of the actual return freight cost. We assume that the compensation amount is exogenously determined, as “in practice, the insurance compensation is a pre-specified amount calculated based on the route from a customer’s home to a retailer’s return-handling facility, subject to a maximum amount per transaction” [19]. This limitation “reflects the insurer’s general lack of flexibility in adjusting compensation levels” [18]. Moreover, following the literature [13], we posit that to exclude scenarios where the fixed compensation insurer would invariably operate at a loss. In contrast, when full-coverage insurance is provided, the insurer reimburses customers for their exact incurred return freight costs . Our model employs a sequential Stackelberg game, and the equilibrium outcomes are derived via backward induction. Table 1 lists the symbols and notations used throughout this paper. The sequence of events of the game is shown in Figure 2.

Table 1.
List of Notations.

Figure 2.
Sequence of Events.
4. Choosing RFI Strategies in a Monopolistic Setting
In this section, we examine the insurer’s strategic choice of CRFI offering—between fixed compensation and full coverage—for an RFI provider in a monopolistic market.
4.1. Fixed-Compensation CRFI in a Monopolistic Setting
We begin by analyzing the optimal premium rate and corresponding profit for the insurer when implementing a low-cost, fixed-compensation RFI strategy in a monopolistic market (denoted by superscript F).
Under this setting, the decision-making process unfolds in two stages. In the first stage, the insurer—who commits to providing fixed compensation in the event of a return—sets the insurance premium, denoted by . In the second stage, the retailer offers customers the option to purchase the RFI directly from the insurer at the point of product sale. If a customer returns a product, the insurer compensates the customer with a fixed amount . The market structure of this scenario is further illustrated by Figure 3a.
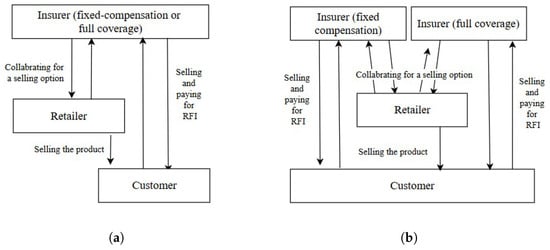
Figure 3.
Market structures under monopoly and duopoly settings. (a) Monopoly market structure: the retailer collaborates with a single insurer (offering either fixed-compensation or full-coverage RFI), who provides coverage for customer return shipping costs. (b) Duopoly market structure: the retailer concurrently collaborates with two insurers—one offering fixed-compensation RFI and the other full-coverage RFI—allowing customers to choose between competing insurance options when purchasing the product.
Decision-Making of customers. Under the CRFI, customers can choose either to purchase the product alone or to purchase it together with the RFI. Reflecting common patterns in online shopping behavior, customers typically decide whether to add CRFI after first choosing to purchase the product. A customer i will purchase the RFI only if the utility of purchasing the product with RFI is greater than the utility of purchasing the product without RFI.
Given the product price p, the utility of customer i when purchasing the product alone is determined by his valuation of the product (), the probability of product misfit (), and the incurred shipping costs () associated with returning the product. This utility is given by:
When purchasing the product with RFI coverage, customer i’s utility is further influenced by the RFI premium and the compensation provided in the case of a return. This utility is formulated as:
Customers will consider purchasing RFI from insurers only if . In this situation, their probability of product misfit satisfies the condition: . Under these conditions, the demand for the CRFI sold by the insurer is given by:
Pricing of the RFI. Based on the previously derived sales quantity, we now calculate the insurer’s profit under the fixed-compensation RFI strategy, denoted by :
Note that the insurer makes a profit of when no return occurs; while it needs to pay the RFI compensation in the case of a product return. The optimal RFI price, sales quantity, and resulting profit under this fixed-compensation strategy are summarized in Lemma 1.
Lemma 1.
For a monopolistic RFI provider offering fixed-compensation CRFI, the optimal RFI price is , the corresponding sales quantity is , and the insurer’s resulting profit is .
Proposition 1.
In a monopolistic setting, when an insurer offers fixed-compensation CRFI,
(1) The optimal RFI rate , the corresponding sales quantity , and the profit are irrelevant to the upper bound of customer return costs ;
(2) The optimal RFI rate increases in the RFI pre-specified compensation , while the resulting sales quantity remains unaffected by . However, the profit increases as rises.
Proposition 1 illustrates how key parameters—such as customer return costs and compensation levels—affect the insurer’s pricing, sales quantity, and profitability when offering fixed-compensation CRFI in a monopolistic market.
First, Proposition 1 states that the optimal RFI premium, the corresponding sales quantity, and the insurer’s profit are irrelevant to the maximum level of customer return costs. This indicates that even if customers face different return shipping costs, the insurer’s pricing strategy and financial outcomes remain unchanged under this scenario. The reason behind this is that the compensation provided through RFI is fixed, meaning it does not vary based on the actual cost incurred by the customer when returning a product.
Second, the proposition highlights the effect of the pre-specified compensation amount on the insurer’s decision-making. It states that as the compensation amount increases, the optimal RFI rate also increases, indicating the insurer charges a higher premium commensurate with the increased compensation offered. Interestingly, the sales quantity remains constant despite changes in , suggesting that customer demand for RFI is inelastic with respect to the compensation level. This inelasticity arises because, as long as the insurer adjusts the RFI premium proportionally to , the customer’s net utility from purchasing the RFI remains unchanged. As a result, the insurer’s profit increases with , creating a favorable scenario where higher compensation levels translate directly to enhanced profitability without affecting market penetration. However, it is important to remember that the insurer’s limited ability to adjust the compensation levels, as well as the exogenous nature of the fixed compensation amount, limit how this enhanced profitability is achieved in practice.
Economically, this suggests that under fixed-compensation CRFI, the insurer does not consider actual customer return costs when setting RFI prices because the compensation amount is predetermined, which limits both the insurer’s financial risk and potential profitability.
4.2. Full-Coverage CRFI in a Monopolistic Setting
We then analyze the optimal premium rate and corresponding profit for the insurer when implementing a high-cost, full-coverage CRFI strategy in a monopolistic market (denoted by superscript L).
In this setting, the insurer commits to fully reimbursing the actual return shipping cost in the event of a customer return. The insurer sets the RFI premium, denoted by , in the first stage. In the second stage, the retailer offers customers the opportunity to purchase the RFI directly from the insurer when purchasing the product. If a customer returns the product, the insurer compensates the full return shipping cost, denoted by . If there is no return, no compensation is provided. The market structure associated with this scenario is illustrated in Figure 3a.
Decision-making of customers. The behavior of customers in this scenario is analogous to that in Section 4.1. When customer i purchases only the product without RFI, the utility is defined as:
When purchasing the product with the offered RFI, customer i’s utility is influenced by his valuation of the product () and the probability of product misfit (), while the return cost is fully covered by the RFI. The resulting utility is:
Customers will choose to purchase the RFI from the insurer if , in this situation, their return shipping cost satisfies the condition: . Under these conditions, the demand for the RFI sold by the insurer is given by:
Pricing of the insurer. Based on the sales quantity derived above, we now calculate the insurer’s profit, denoted as , under the full-coverage RFI strategy:
Note that the revenue of the insurer is and the total expected cost incurred by the insurer to cover return claims is . The corresponding optimal premium, sales quantity, and profit under this scenario are summarized in Lemma 2.
Lemma 2.
For a monopolistic RFI provider offering full-coverage CRFI, the optimal RFI price is , the resulting sales quantities of RFI is , and the corresponding insurer profit is .
From Lemma 2, we further derive Proposition 2.
Proposition 2.
In a monopolistic setting where an insurer offers full-coverage CRFI, the optimal RFI price increases with the maximum level of customer return costs , the resulting sales quantity remains unaffected by , and the insurer’s profit increases with .
Proposition 2 examines the impact of customer return costs on optimal pricing strategies and profitability for a monopolistic insurer offering full-coverage RFI. It demonstrates that as the maximum customer return cost () increases, the optimal premium () also rises. This relationship implies that the perceived value of RFI is directly linked to customers’ actual return costs: the higher the return cost, the more valuable the insurance coverage becomes. Consequently, insurers can justify higher premiums in response to increasing return costs.
Notably, the equilibrium quantity of RFI sold, , remains constant despite changes in return costs. This invariance reveals an important strategic insight: the full-coverage RFI purchase are primarily impacted by uncertainty regarding product fit, rather than by the magnitude of potential return costs. This is because the insurer adjusts premiums to reflect expected return costs. Consequently, as long as product-fit uncertainty persists, demand remains stable.
4.3. Comparison of Fixed-Compensation and Full-Coverage CRFI in a Monopolistic Setting
This subsection proceeds by comparing the performance of two CRFI strategies—fixed-compensation and full-coverage–—of an insurer under a monopolistic market structure.
Proposition 3.
The equilibrium premiums, market shares, and profits of an insurer offering either fixed compensation RFI or full-coverage RFI are related as follows:
(1) When , ; when , , where ;
(2) ;
(3) When , ; when , , where .
The threshold relationship identified in Proposition 3 demonstrates how heterogeneity in customer return shipping costs fundamentally shapes the optimal insurance strategy in a monopolistic market. Specifically, when return costs are low (), fixed-compensation RFI outperforms full-coverage RFI; conversely, when return costs are high (), full-coverage RFI yields superior outcomes.
When is low, the full-coverage insurer can pool low and moderate return costs effectively, thereby reducing risk and offering a lower premium relative to the fixed-compensation alternative. In contrast, the fixed-compensation insurer, offering a a pre-defined amount, charges a higher premium due to its fixed cost structure and broader customer appeal. As increases, the full-coverage insurer faces greater risk from high-cost customers and responds by raising . Figure 4a captures this crossover, highlighting the sensitivity of full-coverage premiums to return cost heterogeneity.
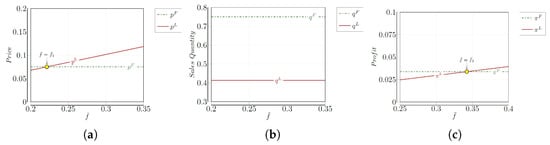
Figure 4.
The equilibrium premiums, sales quantities, and profits for the full-coverage insurer and the fixed-compensation insurer in monopolistic setting ( vs , vs , vs ) (, , and ). (a) and . (b) and . (c) and .
This premium dynamic interacts with quantity sold, shaping overall profitability. As shown in Figure 4b, fixed-compensation RFI consistently secures higher demand () across all values . When is low, this demand advantage, combined with a favorable premium, allows fixed-compensation RFI to generate higher profits. However, as rises and full-coverage premium increases, the insurer begins to extract greater surplus from high-cost customers. Once exceeds the threshold , the higher per-customer premium under full coverage offsets its smaller market share, resulting in higher profits (). Figure 4c illustrates this transition, showing how the balance between pricing and volume ultimately determines the superior RFI strategy under different market conditions.
5. Choosing RFI Strategies in a Competitive Setting
Building on the monopolistic case discussed in Section 4, we now turn to a competitive setting where two insurance providers operate in parallel. Specifically, we consider a scenario where both providers simultaneously offer distinct CRFI options—namely, fixed-compensation and full-coverage—through a retailer’s purchasing platform, allowing customers to choose between competing contract designs when making product purchases.
5.1. Competition Between Fixed-Compensation and Full-Coverage CRFIs
In this setting, customers purchasing a product can choose between two types of RFI by selecting one option and paying the corresponding premium. The chosen insurer then provides coverage in the event of a product return—either by paying a pre-specified compensation amount or by covering the actual return shipping costs. The competitive market structure is illustrated in Figure 3b.
With competitive RFI offering, when purchasing a product, customers evaluate the utilities associated with three options: purchasing RFI from the fixed-compensation insurer, denoted by F, purchasing RFI from the full-coverage insurer, denoted by L, or buying the product without any insurance coverage. The utility for customers who purchase the product without any RFI is given by:
When purchasing the product with RFI of the insurer F, the resulting utility of customer i’ is further influenced by the RFI premium and the compensation provided in the case of a return. This utility is xpressed as:
Similarly, we derive the utility of customers who purchasing RFI from insurer L as:
Clearly, when and (i.e., ), the customer will choose the RFI offered by insurer F; when and (i.e., ), the customer will pay for the services provided by insurer L. Otherwise, the customer will purchase the product without any RFI coverage. The resulting RFI sales for the two insurers can be formulated as:
Based on these sales quantities, the profits of the two insurers can be derived as follows:
The Insurer makes a profit of in the case of no return; while it loses the RFI compensation (insurer F) or (insurer L) in the case of product returns. We then summarize the optimal pricing, market shares, and total profits of the two insurers under this competitive setting in Lemma 3.
Lemma 3.
When two insurance providers offer different types of RFI in a competitive setting, the resulting equilibrium is characterized as follows:
(1) The optimal RFI rate for insurer F is ;
(2) The optimal RFI rate for insurer L is .
The resulting sales quantities ( and ) and profits ( and ) are presented in Table A1 of the Appendix A.
5.2. Comparison of Fixed-Compensation and Full-Coverage RFI in a Competitive Setting
To assess the relative performance of different RFI strategies in a competitive setting, this subsection contiune to compares the performance of the two strategies established in the Section 5.1.
Proposition 4.
In a competitive setting, the equilibrium premiums, sales quantities, and profits of the insurer offering fixed-compensation RFI and the insurer offering full-coverage RFI are related as follows:
(1) When , the premium charged by insurer F is lower than that of insurer L, i.e., ; conversely, when , then .
(2) When , the market share of insurer F is smaller than that of insurer L, i.e., ; conversely, when , then .
(3) When , the profit of insurer F is lower than that of insurer L, i.e., ; conversely, when , then .
Proposition 4 suggests that a full-coverage RFI policy becomes increasingly attractive in markets with significant heterogeneity in customers’ return shipping costs. When there is minimal heterogeneity in return shipping costs, fixed-compensation RFI policies gain a competitive advantage. In such cases, shipping costs are relatively predictable and consistent across customers, making the simplicity and predictability offered by fixed-compensation schemes more appealing.
Conversely, when there is substantial variation in return shipping costs, competition induces market segmentation. Specifically, customers with lower return costs tend to prefer the fixed-compensation RFI, while those facing higher return costs are more inclined to choose full-coverage RFI, which offers complete reimbursement. Therefore, as the dispersion in return shipping costs widens, full-coverage policies become increasingly valuable by customers seeking protection against high potential losses. Therefore, as the spread in return shipping costs increases, full-coverage RFI policies gain a competitive advantage.
Figure 5 further provides a graphical illustration of these findings. It shows how equilibrium premiums, sales quantities, and profits for both insurers vary with changes in customer return costs.
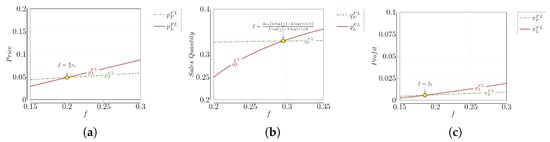
Figure 5.
The equilibrium premiums, sales quantities, and profits for the full-coverage insurer and the fixed-compensation insurer in competitive setting ( vs , vs , vs ) (, , and ). (a) and . (b) and . (c) and .
6. Conclusions
This study examines the strategic choice between two alternative CRFI offering—fixed-compendsoin or full-coverage—across both monopolistic and duopolistic settings. By modeling insurers as key decision-makers within the e-commerce supply chain, we derive several key insights.
In monopolistic markets, fixed-compensation RFI is optimal when customer return costs are low and relatively uniform. This strategy appeals to cost-sensitive customers and supports insurer profitability through stable, predictable pricing. As return costs become more variable or exceed a certain threshold, full-coverage RFI becomes more advantageous, catering to customers with higher return costs and enabling insurers to charge premium prices and generate greater profits.
In duopolistic markets, full-coverage RFI provides a competitive advantage when customer return costs are highly heterogeneous. Market segmentation under such conditions allows insurers to target diverse customer needs and justify higher premiums. Conversely, when return costs are relatively homogeneous, fixed-compensation RFI proves more effective due to its simplicity and predictability, which drive broader adoption despite lower per-policy margins.
Theoretically, this study contributes to the literature on reverse logistics and e-commerce insurance by shifting the analytical focus from retailers to insurers as primary decision-makers. Our model incorporates heterogeneity in return costs and misfit probabilities, offering a more realistic depiction of customer behavior than conventional uniform-assumption models. Furthermore, we introduce the concept of RFI competition among insurers with differentiated service structures, illustrating how variations in service quality and cost parameters shape market dynamics.
Practically, the findings highlight the importance of aligning RFI offerings with product characteristics and customer return profiles. In monopolistic settings, insurers should assess the distribution of return costs to determine the suitability of fixed-compensation versus full-coverage strategies. In competitive markets, differentiation through superior service design and strategic pricing can help insurers expand market share. For example, insurers may offer full-coverage RFI for high-value or bulky items—such as household appliances or electronics—where return shipping costs are significant. These products justify higher premiums while offering meaningful financial protection to customers. In contrast, for low-cost, frequently returned items like clothing or accessories, insurers can offer fixed-compensation RFI at lower premiums, helping customers control insurance costs without overpaying for coverage. These strategies are already visible in practice. For instance, Taobao and other major Chinese e-commerce platforms have launched RFI services tailored to product categories, offering full coverage for electronics and simplified, fixed-compensation schemes for fast fashion. These differentiated offerings not only reduce return-related friction but also serve as a competitive advantage in enhancing customer loyalty and satisfaction.
From the consumer’s wallet perspective, these tailored RFI options allow buyers to make more informed, value-conscious decisions. When return costs are high, choosing full-coverage RFI helps avoid large, unexpected expenses—effectively reducing sunk costs. On the other hand, for lower-value purchases, fixed-compensation insurance keeps the total cost of ownership low, offering basic protection at a fraction of the cost.
This study has several limitations that suggest directions for future research. It assumes static customer return behavior, whereas in practice, customers may adapt based on return experiences. Incorporating dynamic behavioral responses could offer deeper insights. The model also treats compensation levels as exogenous, although insurers are likely to adjust them in response to competitive pressures; future work could examine endogenous compensation design and dynamic pricing strategies, as well as use real corporate data to simulate potential strategic choice scenarios. Additionally, the interactions between insurers, retailers, and platforms—such as through contractual arrangements or co-developed services—remain underexplored and warrant further investigation.
Author Contributions
Conceptualization, L.H. and J.Q.; methodology, L.H.; software, J.Q.; validation, L.H., J.Q. and Y.C.; formal analysis, L.H.; investigation, L.H.; resources, L.H.; data curation, L.H.; writing—original draft preparation, L.H.; writing—review and editing, J.Q.; visualization, L.H. and J.Q.; supervision, Y.C.; project administration, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Faculty Research Grant (FRG-24-077-MSB) of Macau University of Science and Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof
Proof of Lemma 1.
Based on Equation (4), taking the first and second order derivative of with respect to , we obtain
To determine the maximum profit of the insurer with respect to , we need to evaluate the endpoint values for . In this case, the feasible range for is . The first-order derivative , and the first-order derivative . So, the optimal price of the insurer can be determined by the first-order derivative condition. Solving the first-order derivative condition for p, we obtain
By substituting into Equations (3) and (4), we obtain the associated optimal sales quantity and insurer’s profit as stated in Lemma 1: and . □
Proof of Lemma 2.
To determine the maximum profit of the insurer with respect to p, we need to evaluate the endpoint values for . In this case, the feasible range for p is . The first derivative and the first derivative . Therefore, the optimal price of the insurer can be determined by the first-order derivative condition. Solving the first-order derivative condition for p, we obtain
The associated optimal sales quantities of RFI are , and the insurer’s profit is . □
Proof of Proposition 1.
Based on the result in Lemma 1, we have , and of insurer F. By taking the first order derivative of , and with respect to , we obtain
Therefore, we have the results in Proposition 1. □
Proof of Proposition 2.
Based on the result in Lemma 2, we have , and of insurer L. By taking the first order derivative of , and with respect to , we obtain
Therefore, we have the results in Proposition 2. □
Proof of Proposition 3.
The optimal outcomes for each insurer in monopoly scenarios have been derived in Lemmas 1 and 2. Based on these results, we begin by comparing and , and we obtain
Setting this expression to zero, we solve for :
Thus, when , ; when , .
Next, we compare the optimal sales quantities and .
Therefore, .
Finally, we compare the optimal profits. We calculate
Setting this expression to zero, we solve for :
Since , we conclude that when , , and when , . □

Table A1.
Symbols and expressions.
Table A1.
Symbols and expressions.
| Symbol | Expression |
|---|---|
Proof of Lemma 3.
In the duopoly competition model, we first need to derive the profit maximization conditions for the two insurers. We begin by considering the profit maximization problem for insurer F, taking the first and second derivatives of with respect to , we obtain:
Because the second derivative is less than 0, which proves that the original function increases first and then decreases with respect to . Then we examine whether the optimal price is the point where the first derivative equals 0. In this case, the feasible range for is . The first-order derivative , and the first-order derivative . Therefore, the point where the first derivative equals zero represents the optimal decision for insurer F.
Next, we consider the optimal solution of the insurer L’ by deciding the insurance premium . Note that is a cubic function, and its optimization requires consideration of the second-order derivative condition. We take the first, second, and third derivatives of with respect to as follows:
The second derivative is greater than 0, which proves that original function increases first and then decreases with respect to . Then we examine whether the optimal price is the point where the first derivative equals 0. In this case, the feasible range for is . The first-order derivative , and the first-order derivative .
By solving the simultaneous equations of the first-order conditions of and , we obtain optimal values for and :
By substituting the optimal premiums into Equations (12) and (13), we obtain the corresponding sales quantities and profits for both insurers in Lemma 3 with details in Table A1.
□
Proof of Proposition 4.
Based on the results in Lemma 3, we have . Setting this formula to zero, we have . And because , then we derive result (1) in Proposition 4.
As for sales quantities, . Setting this formula to zero, we have . Then we derive result (2) in Proposition 4.
As for profits, . Setting this formula to zero, we have
Then we substitute the two solutions into the numerical values and find that solution 1 does not meet our model assumption of . Therefore, solution 2 is the optimal solution we are looking for.
Finally, we have the results in Proposition 4. □
References
- Wilamowicz, A. The great FinTech disruption: InsurTech. Bank. Financ. Law Rev. 2019, 34, 215–238. [Google Scholar]
- Liu, J.; Ye, S.; Zhang, Y.; Zhang, L. Research on InsurTech and the technology innovation level of insurance enterprises. Sustainability 2023, 15, 8617. [Google Scholar] [CrossRef]
- Chen, D. Chinese Commercial Banks and Fintech-Competition and Collaboration. In Commercial Banking in Transition: A Cross-Country Analysis; Springer: Cham, Switzerland, 2024; pp. 333–353. [Google Scholar]
- Park, W.Y.; Lee, S.J.; Park, C.; Jung, S.; Kim, H.K.; Student, D. The effect of service quality of internet insurance on intention to purchase online. Int. J. Smart Bus. Technol. 2021, 9, 63–70. [Google Scholar] [CrossRef]
- CCTVNews. The “2024 Report on the Development of Internet Insurance in China” Was Released with Significant Attention, and CCTV Provided an In-Depth Analysis of the Opportunities and Challenges Facing the Industry. Available online: https://news.qq.com/rain/a/20250321A029XG00?web_channel=wap&openApp=false&suid=&media_id= (accessed on 21 March 2025).
- Keju, W. China’s Internet Insurance Sector to See Nearly 20% Annual Growth. Available online: https://www.chinadaily.com.cn/a/202501/14/WS678649bca310f1265a1dacc2.html (accessed on 14 January 2025).
- Geng, S.; Li, W.; Qu, X.; Chen, L. Design for the pricing strategy of return-freight insurance based on online product reviews. Electron. Commer. Res. Appl. 2017, 25, 16–28. [Google Scholar] [CrossRef]
- Berg, E.; Blake, M.; Morsink, K. Risk sharing and the demand for insurance: Theory and experimental evidence from Ethiopia. J. Econ. Behav. Organ. 2022, 195, 236–256. [Google Scholar] [CrossRef]
- Arora, S.; Chu, F.; Melnikov, S.; Zhang, L. E-Commerce Is Entering a New Phase in Southeast Asia. Are Logistics Players Prepared; McKinsey & Company: Chicago, IL, USA, 2022. [Google Scholar]
- Wang, X.; Xie, J.; Fan, Z.P. B2C cross-border E-commerce logistics mode selection considering product returns. Int. J. Prod. Res. 2021, 59, 3841–3860. [Google Scholar] [CrossRef]
- Orendorff, A. The Plague of Ecommerce Return Rates and How to Maintain Profitability. Shopify Plus. 2019. Available online: https://www.shopify.com/enterprise/ecommerce-returns (accessed on 7 December 2019).
- Xiong, H.; Liu, J. Return insurance in a competitive market: Benefiting the high-quality or low-quality retailer? Int. J. Prod. Econ. 2023, 255, 108719. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Tayi, G.K.; Cheng, T. Return shipping insurance: Free versus for-a-fee? Int. J. Prod. Econ. 2021, 235, 108110. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Z.P.; Zhu, S.X. Extracting values from consumer returns: The role of return-freight insurance for competing e-sellers. Eur. J. Oper. Res. 2023, 306, 141–155. [Google Scholar] [CrossRef]
- Ren, M.; Liu, J.; Feng, S.; Yang, A. Pricing and return strategy of online retailers based on return insurance. J. Retail. Consum. Serv. 2021, 59, 102350. [Google Scholar] [CrossRef]
- Fan, Z.P.; Chen, Z. When should the e-tailer offer complimentary return-freight insurance? Int. J. Prod. Econ. 2020, 230, 107890. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, J.; Cheng, T.C.E. Optimal pricing and return policy and the value of freight insurance for a retailer facing heterogeneous consumers with uncertain product values. Int. J. Prod. Econ. 2020, 229, 107767. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, M.; Chen, J. Signaling quality with return insurance: Theory and empirical evidence. Manag. Sci. 2022, 68, 5847–5867. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Pan, X.A. Optimal return shipping insurance policy with consumers’ anticipated regret. Prod. Oper. Manag. 2023, 32, 3209–3226. [Google Scholar] [CrossRef]
- Yang, X.; Dai, X.; Liu, Z. The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 706–724. [Google Scholar] [CrossRef]
- Vacca, J.R. Biometric Technologies and Verification Systems; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Anagnostopoulos, I. Fintech and regtech: Impact on regulators and banks. J. Econ. Bus. 2018, 100, 7–25. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Song, W.; Dang, X. Welfare promoter or profit obstructor? The role of return-freight insurance in online retailing. Electron. Commer. Res. Appl. 2023, 57, 101230. [Google Scholar] [CrossRef]
- Akçay, Y.; Boyacı, T.; Zhang, D. Selling with money-back guarantees: The impact on prices, quantities, and retail profitability. Prod. Oper. Manag. 2013, 22, 777–791. [Google Scholar] [CrossRef]
- McWilliams, B. Money-back guarantees: Helping the low-quality retailer. Manag. Sci. 2012, 58, 1521–1524. [Google Scholar] [CrossRef]
- Su, X. Consumer returns policies and supply chain performance. Manuf. Serv. Oper. Manag. 2009, 11, 595–612. [Google Scholar] [CrossRef]
- Feldman, P.; Papanastasiou, Y.; Segev, E. Social learning and the design of new experience goods. Manag. Sci. 2019, 65, 1502–1519. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, D.J.; Zhang, F. Information sharing on retail platforms. Manuf. Serv. Oper. Manag. 2021, 23, 606–619. [Google Scholar] [CrossRef]
- Bian, Y.; Xiao, T. Return Freight Insurance Strategy and Price Decisions for a Dual-Channel Supply Chain in the Presence of Showrooming. IEEE Trans. Eng. Manag. 2024, 71, 3741–3754. [Google Scholar] [CrossRef]
- Li, Q.; Fang, Y.; Chen, Y. Return Strategies of Competing E-Sellers: Return Freight Insurance vs. Return Pickup Services. Mathematics 2025, 13, 296. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.; Choi, T.M.; Zhou, Q. Who should pay for the return freight in e-commerce? Platforms, retailers or consumers. Int. J. Prod. Econ. 2024, 277, 109375. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).