An Iterative Approximate Method for Solving 2D Weakly Singular Fredholm Integral Equations of the Second Kind
Abstract
1. Introduction
2. Basic Results About the Existence and Uniqueness of the 2D-WSFIE
- (i)
- , such that .
- (ii)
- the weakly singular kernel is a real-valued function satisfying
- (iia)
- (iib)
- .
- (iii)
- .
3. Numerical Results and Discussion
- Step 1: Weakly Singular Kernel Decomposition
- (IV)
- The weakly singular kernel, , of Equation (13) can be decomposed into the product of two functions namely and . That is, we assume that
- (V)
- .
- (VI)
- All singular characteristics of the weakly singular kernel are contained in the part such that
- Step 2: Reformulation of the Integral Equation
- Step 3: Cubature Approximation
- Step 4: Using Properties of Definite Integration
- Step 5: Polynomial Interpolation of
- Step 6: Evaluating and Estimating an Upper Bound for
- When , we haveThus, the error satisfies , indicating a decrease in convergence order caused by the weak singularity , which affects both spatial dimensions.
- When , then the term can be considered insignificant compared to the leading term . Therefore, the error is again estimated as . Thus, it is advisable to select to balance the error contributions from both spatial dimensions.
- The error upper bound indicates that there is interdependence between step sizes h and k because it involves terms and . Therefore, balancing between h and k is required to avoid an increase in errors.
- When , we can assume that where . Therefore,Also, from the MacLaurin expansion near , we have:ThusTherefore, refining the mesh in the k-direction alone does not lead to a significant improvement in the error unless the mesh size h is also decreased. This highlights the importance of maintaining a balanced mesh size in both dimensions. A similar arguments hold for .
- Step 7: Iterative Solution via the Fixed Point Algorithm
4. Accuracy and Convergence Rate of the Approximate Solution
- The effect of iterating number M appears in the term . Since , increasing M leads to exponential decay in the error and thus enhances accuracy. The smaller is (i.e., ), the fewer iterations we need to obtain good accuracy.
- As the parameter σ gets close to 1, the denominator becomes small, causing the second term in the error upper bound to increase. This increase slows the convergence rate of the algorithm. Hence, it is crucial to maintain to guarantee the stability, robustness, and accuracy of the approximate solution, and to obtain rapid convergence.
- As the parameter ν approaches 1, the weak singularity in the kernel becomes stronger. This causes the denominators and to decrease, raising the overall error upper bound and leading to increased numerical errors with the same discretization parameters and iteration count.
- The impact of the scaling factor on the interaction between the discretization parameters h and k, and how to minimize numerical errors, is addressed in Remark 1.
5. Application
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khachatryan, K.; Petrosyan, H. Solvability of Two-Dimensional Integral Equations with Concave Nonlinearity in the Plane. J. Math Sci. 2023, 269, 239–255. [Google Scholar] [CrossRef]
- Jian, M.; Jin, H. Collocation method for solving two-dimensional nonlinear Volterra–Fredholm integral equations with convergence analysis. J. Comput. Appl. Math. 2023, 428, 115188. [Google Scholar]
- Solhi, E.; Mirzaee, F.; Naserifar, S. Approximate solution of two dimensional linear and nonlinear stochastic Itô–Volterra integral equations via meshless scheme. Math. Comput. Simul. 2023, 207, 369–387. [Google Scholar] [CrossRef]
- Öztürk, H.; Anlı, F. Exponential approximation to Chandrasekhar’s H-function for isotropic scattering. Indian J. Phys. 2023, 97, 2289–2296. [Google Scholar] [CrossRef]
- Yethiraj, A.; Sung, B.; Lado, F. Integral equation theory for two-dimensional polymer melts. J. Chem. Phys. 2005, 122, 094910. [Google Scholar] [CrossRef] [PubMed]
- Crucinio, F.R.; Johansen, A.M. Solving Fredholm Integral Equations of the Second Kind via Wasserstein Gradient Flows. 2024. Available online: http://arxiv.org/abs/2409.19642 (accessed on 20 February 2025).
- George, C.H.; Wolfgang, L.W. Boundary Integral Equations, 2nd ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Strelnikova, E.; Choudhary, N.; Degtyariov, K.; Kriutchenko, D.; Vierushkin, I. Boundary element method for hypersingular integral equations: Implementation and applications in potential theory. Eng. Anal. Bound. Elem. 2024, 169, 105999. [Google Scholar] [CrossRef]
- Foltran, A.; Marchi, C.; Moura, L. Verification of numerical solutions of thermal radiation problems in participating and nonparticipating media. Numer. Heat Transf. Part Fundam. 2023, 84, 143–165. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Yang, C.; Yuan, Z. A New Fast Monte Carlo Code for Solving Radiative Transfer Equations Based on the Neumann Solution. Astrophys. J. Suppl. Ser. 2021, 254, 38. [Google Scholar]
- Abdou, M.; Soliman, A.; Abdel–Aty, M. On a discussion of Volterra–Fredholm integral equation with discontinuous kernel. J. Egypt. Math. Soc. 2020, 28, 11. [Google Scholar] [CrossRef]
- Katani, R.; McKee, S. Numerical solution of two-dimensional weakly singular Volterra integral equations with non-smooth solutions. J. Comput. Appl. Math. 2022, 402, 113779. [Google Scholar] [CrossRef]
- Iyikal, O. Numerical Investigation of the Two-Dimensional Fredholm Integral Equations of the Second Kind by Bernstein Operators. Symmetry 2022, 14, 625. [Google Scholar] [CrossRef]
- Laguardia, A.; Russo, M. A Nyström Method for 2D Linear Fredholm Integral Equations on Curvilinear Domains. Mathematics 2023, 11, 4859. [Google Scholar] [CrossRef]
- Mezzanotte, D.; Occorsio, D.; Russo, M.G. Combining Nyström Methods for a Fast Solution of Fredholm Integral Equations of the Second Kind. Mathematics 2021, 9, 2652. [Google Scholar] [CrossRef]
- Micula, S. An iterative numerical method for fractional integral equations of the second kind. J. Comput. Appl. Math. 2018, 339, 124–133. [Google Scholar] [CrossRef]
- Agarwal, R.; Meehan, M.; O’Regan, D. Fixed Point Theory and Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
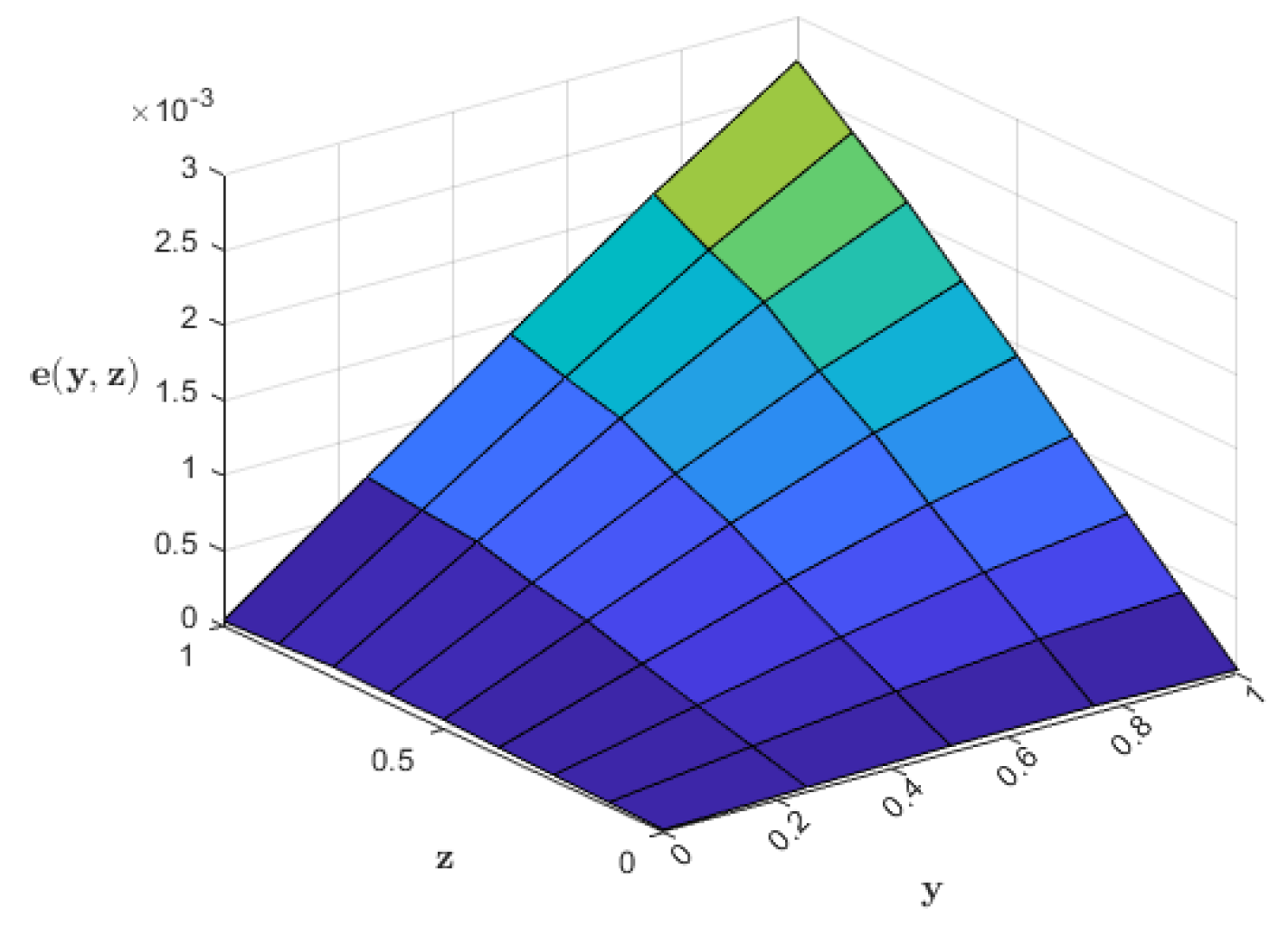
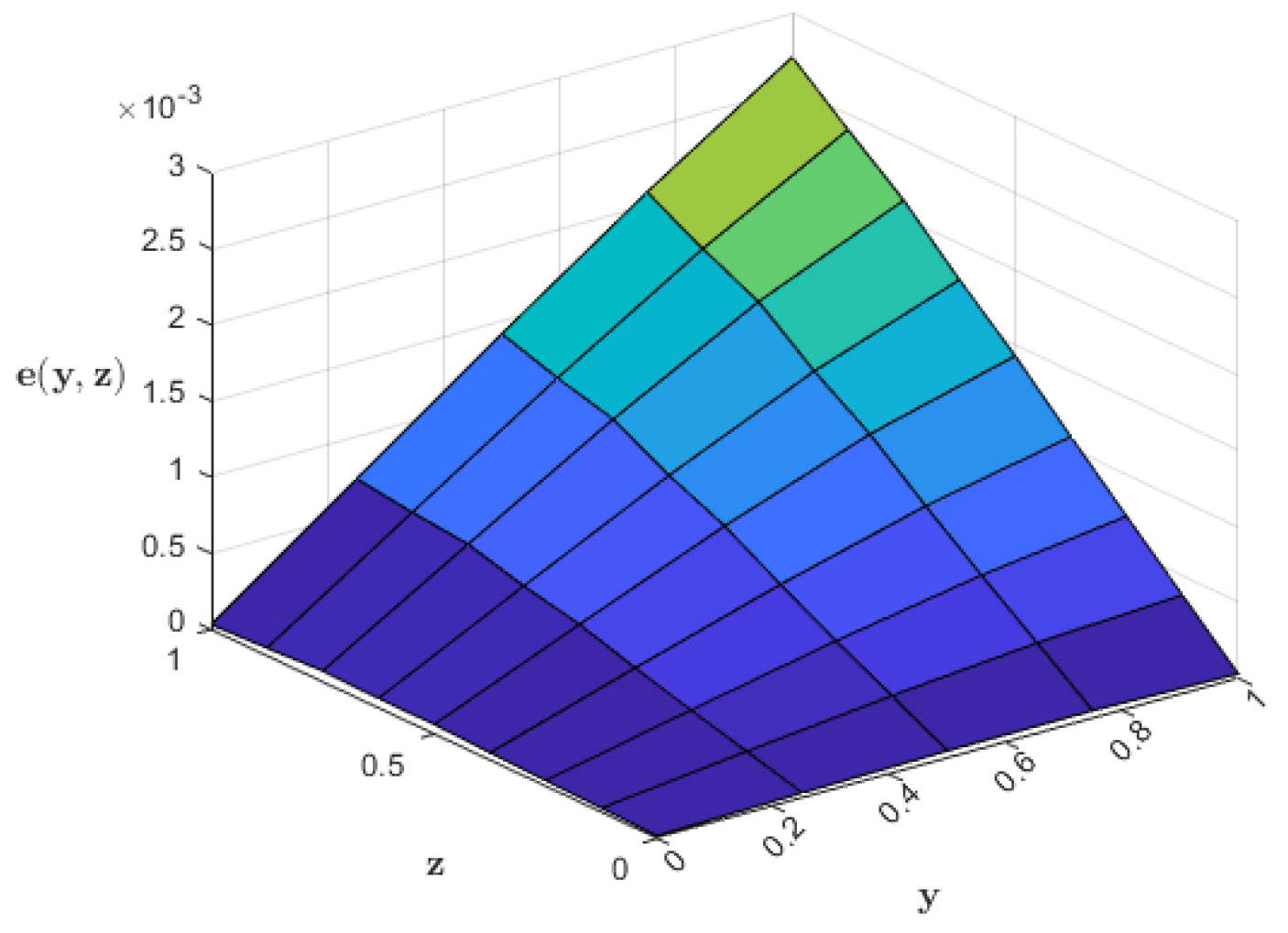
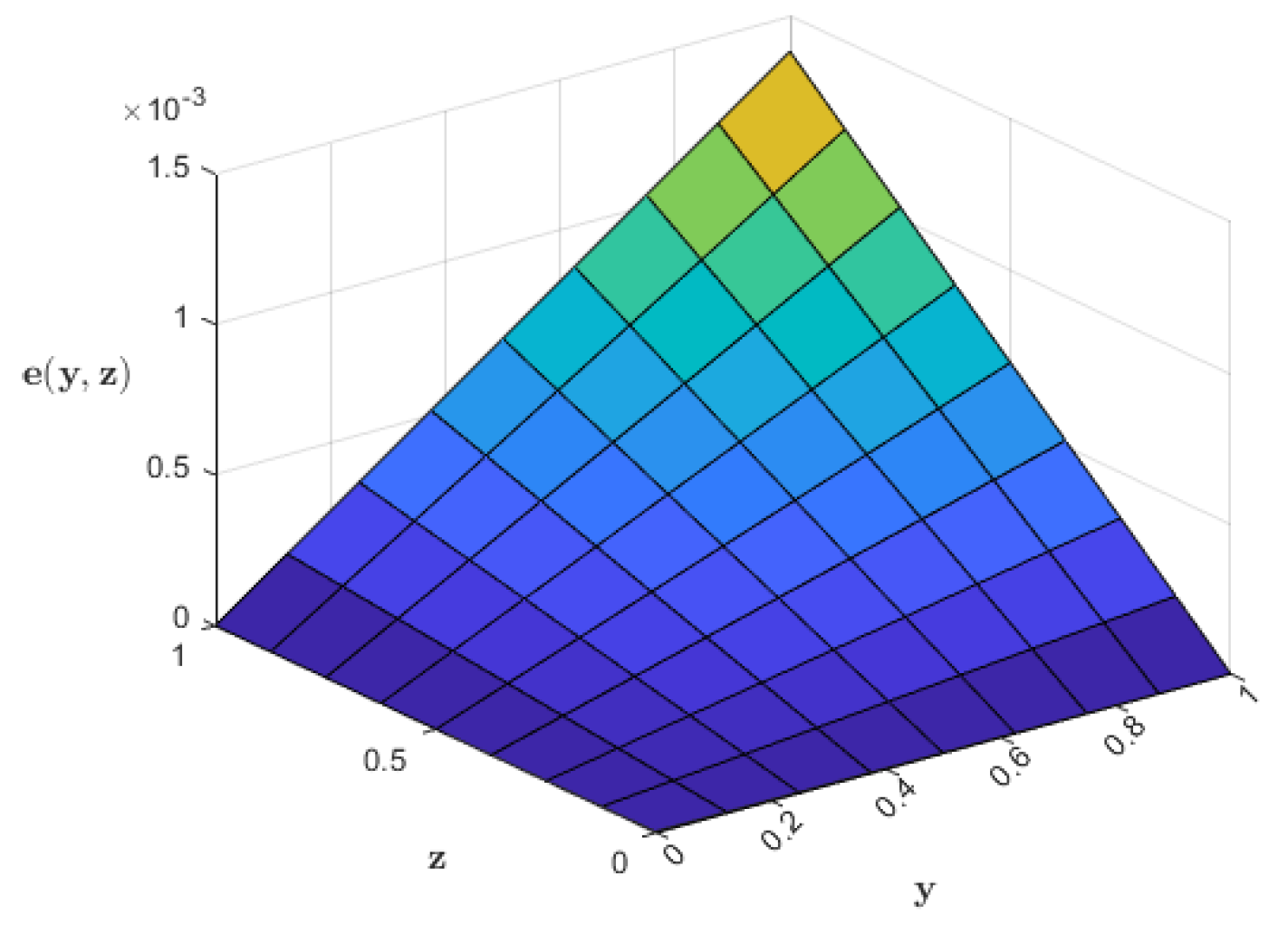

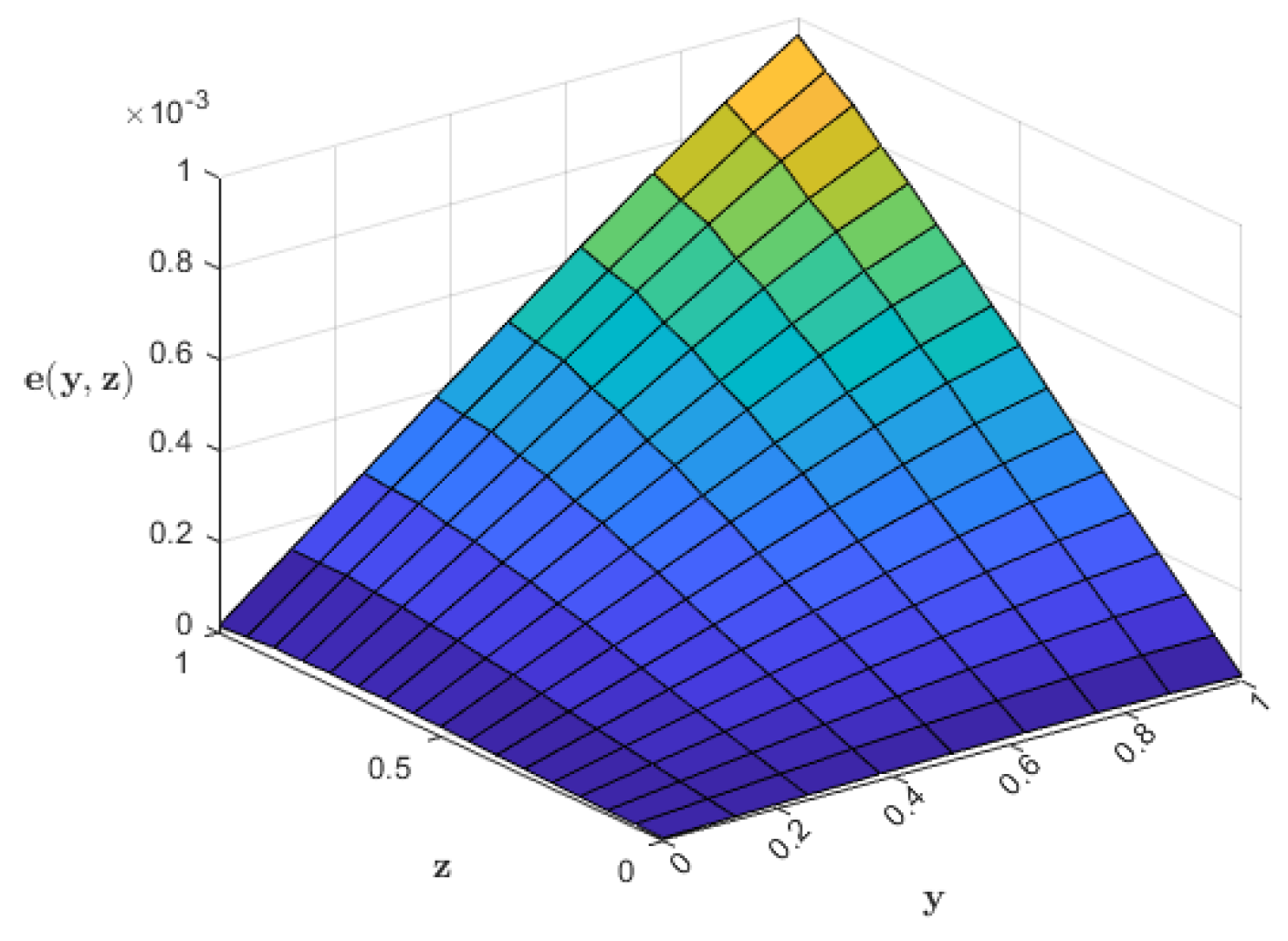
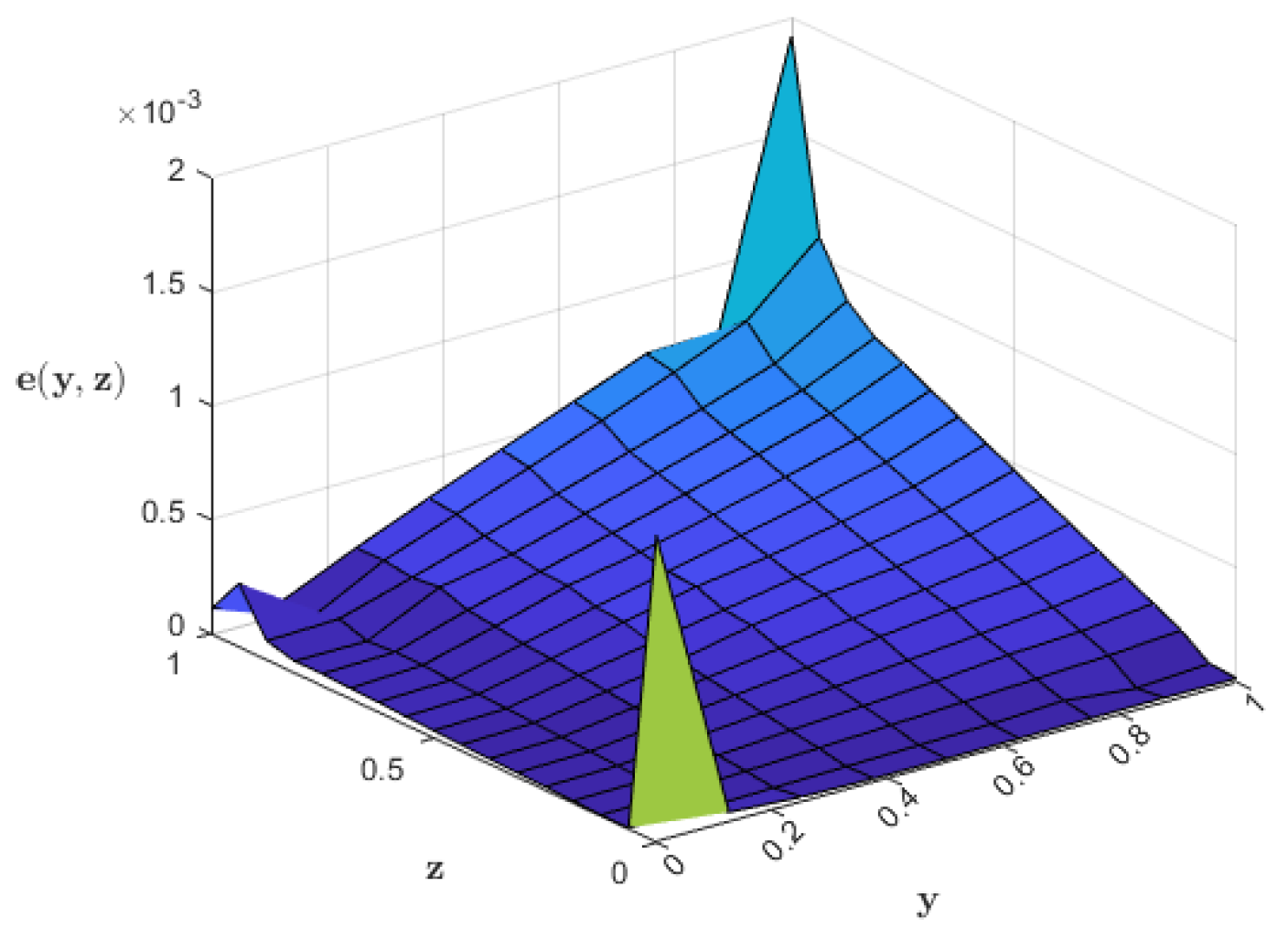
| Points | Exact Sol. | Approx. Sol. (6th Iter.) | Approx. Sol. (Nyström) | |||||
|---|---|---|---|---|---|---|---|---|
| y | z | Value | Prop. Alg. | Abs. Err. | CPU | Value | Abs. Err. | CPU |
| 0.0 | 0.0 | 0.0000 | ||||||
| 0.2 | 0.2 | |||||||
| 0.4 | 0.4 | |||||||
| 0.6 | 0.6 | |||||||
| 0.8 | 0.8 | |||||||
| 1.0 | 1.0 | |||||||
| Points | Exact Sol. | Approx. Sol. (6th Iter.) | Approx. Sol. (Nyström) | |||||
|---|---|---|---|---|---|---|---|---|
| y | z | Value | Prop. Alg. | Abs. Err. | CPU | Value | Abs. Err. | CPU |
| 0.0 | 0.0 | 0.0000 | ||||||
| 0.2 | 0.2 | |||||||
| 0.4 | 0.4 | |||||||
| 0.6 | 0.6 | |||||||
| 0.8 | 0.8 | |||||||
| 1.0 | 1.0 | |||||||
| Points | Exact Sol. | Approx. Sol. (6th Iter.) | Approx. Sol. (Nyström) | |||||
|---|---|---|---|---|---|---|---|---|
| y | z | Value | Prop. Alg. | Abs. Err. | CPU | Value | Abs. Err. | CPU |
| 0.0 | 0.0 | 0.0000 | ||||||
| 0.2 | 0.2 | |||||||
| 0.4 | 0.4 | |||||||
| 0.6 | 0.6 | |||||||
| 0.8 | 0.8 | |||||||
| 1.0 | 1.0 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssef, M.I.; Abdou, M.A.; Gharbi, A. An Iterative Approximate Method for Solving 2D Weakly Singular Fredholm Integral Equations of the Second Kind. Mathematics 2025, 13, 1854. https://doi.org/10.3390/math13111854
Youssef MI, Abdou MA, Gharbi A. An Iterative Approximate Method for Solving 2D Weakly Singular Fredholm Integral Equations of the Second Kind. Mathematics. 2025; 13(11):1854. https://doi.org/10.3390/math13111854
Chicago/Turabian StyleYoussef, Mohamed I., Mohamed A. Abdou, and Abdulmalik Gharbi. 2025. "An Iterative Approximate Method for Solving 2D Weakly Singular Fredholm Integral Equations of the Second Kind" Mathematics 13, no. 11: 1854. https://doi.org/10.3390/math13111854
APA StyleYoussef, M. I., Abdou, M. A., & Gharbi, A. (2025). An Iterative Approximate Method for Solving 2D Weakly Singular Fredholm Integral Equations of the Second Kind. Mathematics, 13(11), 1854. https://doi.org/10.3390/math13111854






