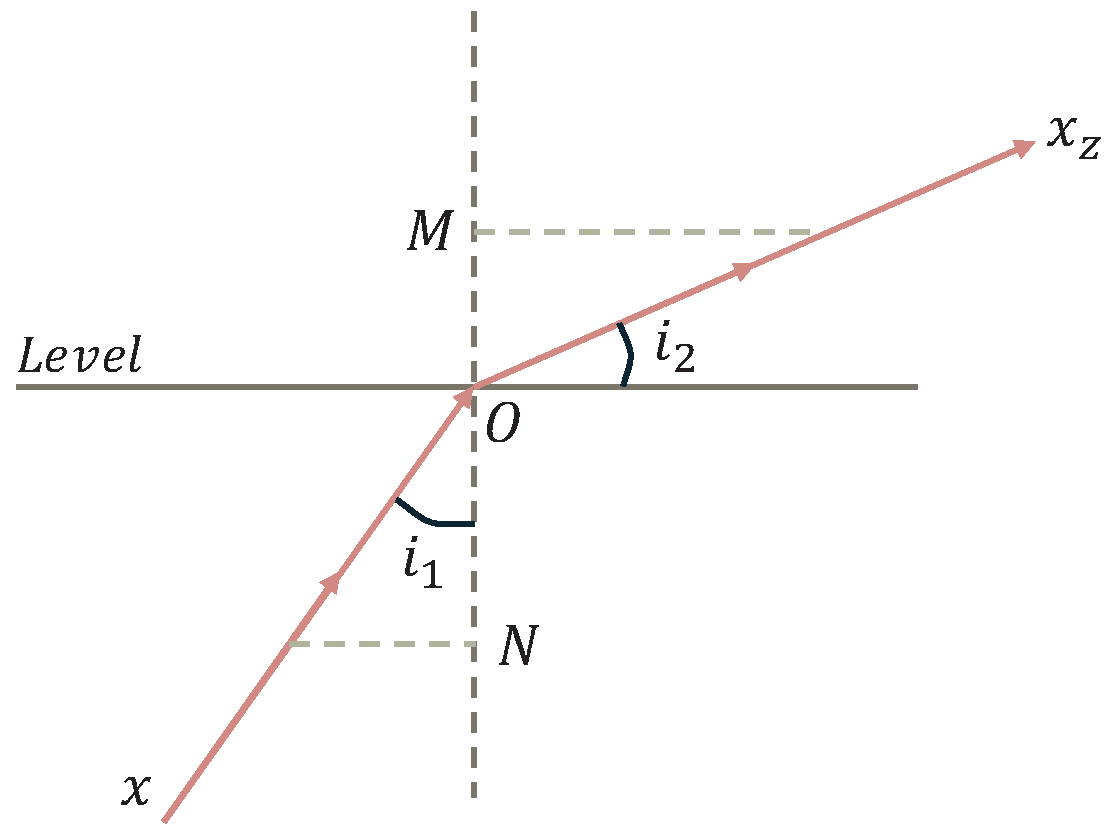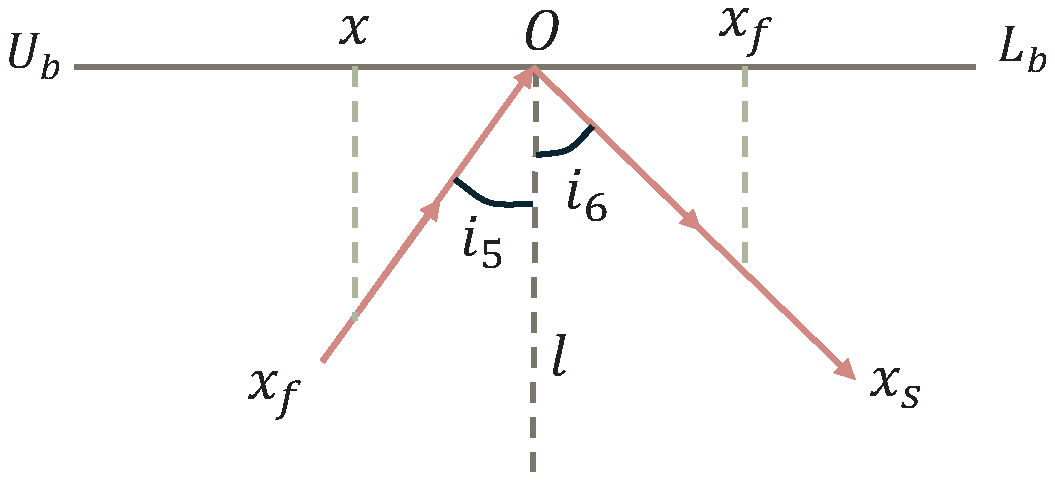3.3.1. Fata Morgana Algorithm (FATA)
The Fata Morgana Algorithm (FATA) [
28] is adopted as the core optimization engine in the SOE framework. The FATA algorithm is a heuristic optimization algorithm inspired by the physical phenomenon of Fata Morgana mirages. It employs a two-tiered search strategy based on the behavior of light propagation, combining population-level and individual-level searches to enhance global exploration and local convergence efficiency. The algorithm operates in two phases. In the first phase, inspired by definite integral principles, it simulates the propagation of multiple light beams through a non-uniform medium to perform global guidance over the entire population. A dynamic light-filtering mechanism is introduced at this stage to evaluate the fitness of beam paths within the objective space, thereby strengthening the algorithm’s population-wide exploratory capability. In the second phase, trigonometric principles are employed to simulate light refraction and reflection at boundary interfaces, guiding individuals to adjust their positions along new directions and thereby improving the precision and convergence speed of local search. Through this physical analogy mechanism, the FATA algorithm achieves an effective synergy between global exploration and local exploitation during the search process, offering efficient solution-space navigation for complex multi-objective scheduling problems.
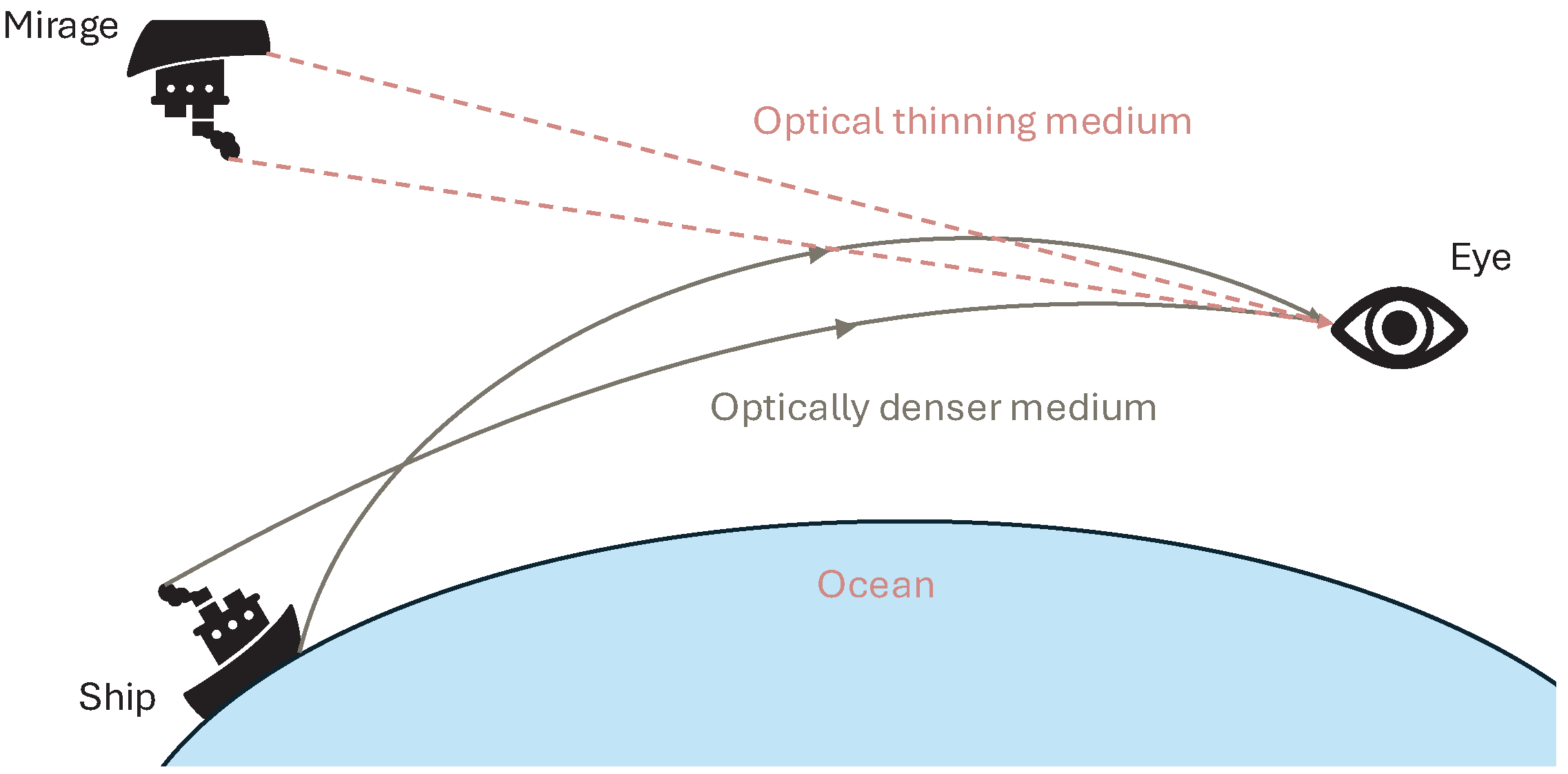
The FATA algorithm simulates the formation process of Fata Morgana mirages to construct its population-based search mechanism, as shown in
Figure 2. As illustrated in
Figure 2, a ship emits two types of light in such a phenomenon. Most light (“other light” in
Figure 2) does not undergo significant refraction during propagation and, thus, fails to produce visible mirages. In contrast, a distinct class of light becomes strongly refracted when passing through air layers with density gradients, ultimately forming observable mirage images. This light is referred to as mirage light in this study. Effective discrimination between these two light types is essential for identifying the global optimum (
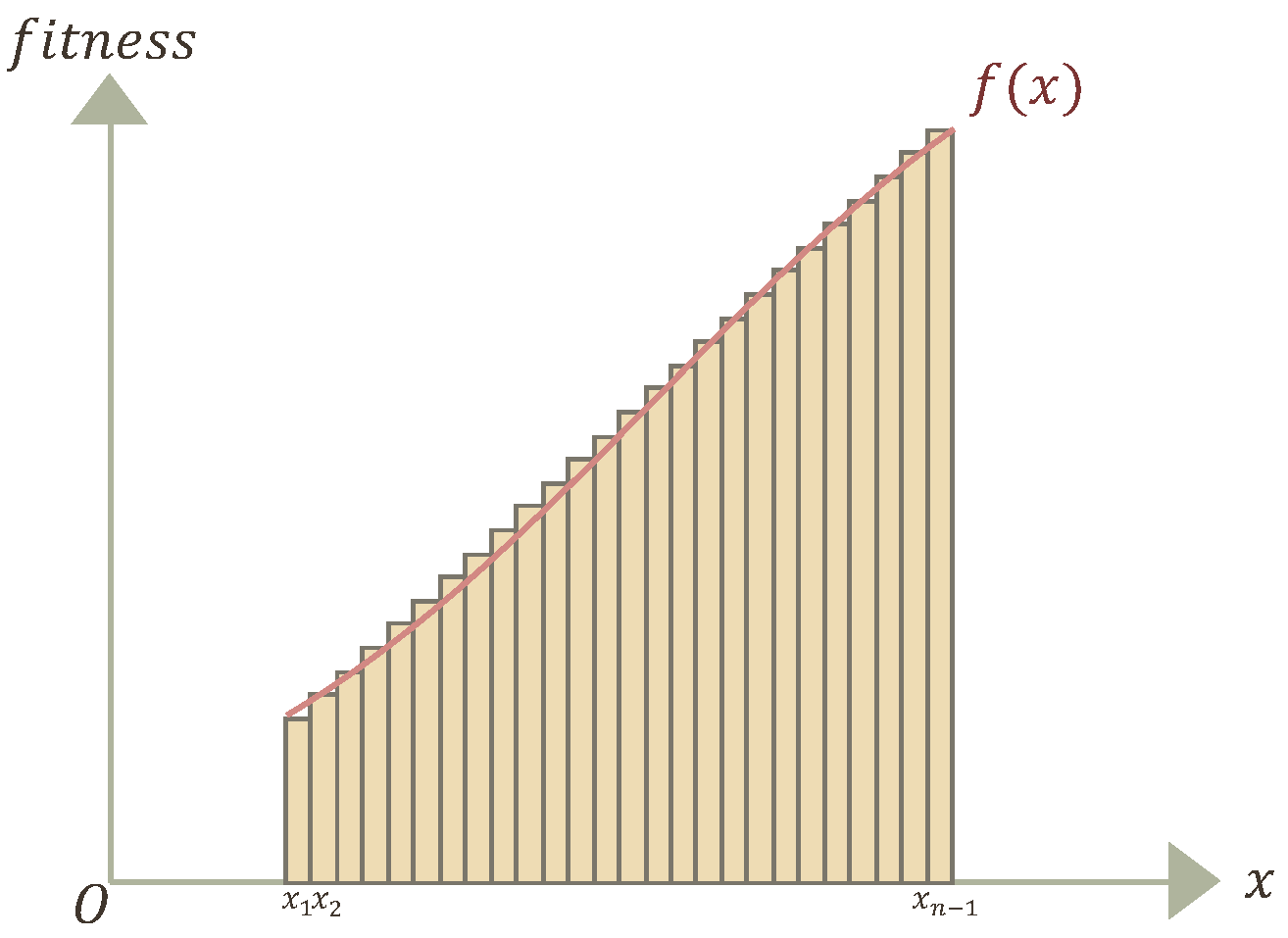
) during the optimization process. To this end, the FATA algorithm introduces a light-beam quality evaluation mechanism based on definite integral theory to assess the overall adaptability of the population. First, the FATA algorithm calculates the fitness of each individual according to the defined fitness function and ranks the population accordingly, as shown in
Figure 3. Then, following the principles of definite integration (see Equations (
12) and (
13)), the FATA algorithm performs integration over the individual fitness curve (
) to compute the population’s adaptive area (
S) and uses Equation (
14) to select high-quality individuals for the subsequent evolutionary process. As shown in
Figure 2 and
Figure 4, the FATA algorithm applies differentiated strategies to distinct light populations: For a random number (
), the light group is considered to have traversed a non-uniform medium and, thus, possesses guiding capability. In this case, the population is re-initialized using Equation (
15) to enhance search diversity. Otherwise, the light is assumed to have followed non-refracted paths, and the algorithm invokes the individual search strategy derived from light propagation principles to update positions and guide the population toward locally optimal regions.
where
and
are parameters.
This is the population quality fitting function (
), with points on the curve expressed as
and
.
where
P is the quality factor of the light population,
represents the quality of the worst population, and
represents the quality of the best population.
where
x is the light individual,
is the new individual,
represents the upper limit of the individual position, and
represents the lower limit of the individual position.
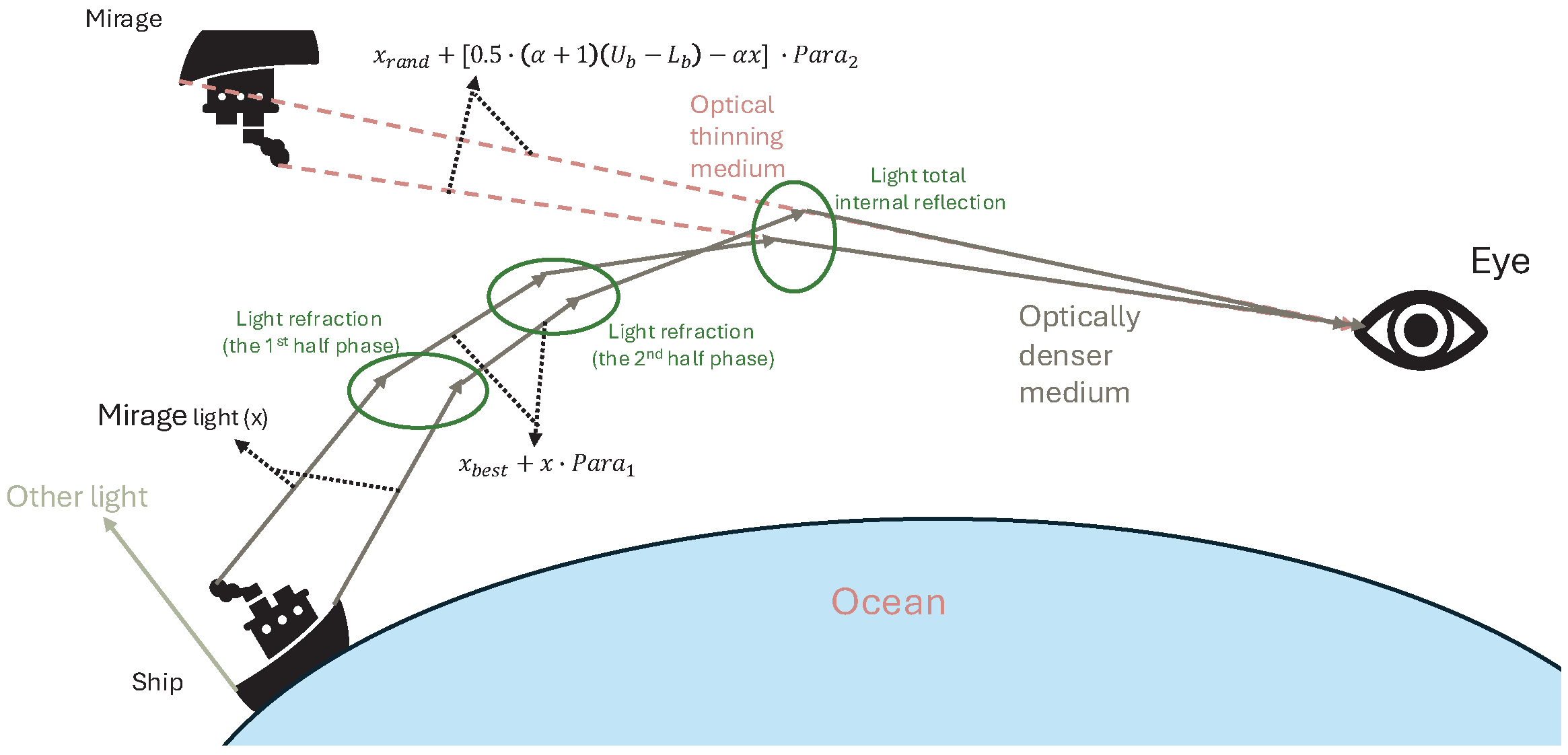
In the FATA algorithm, the light propagation principle is executed after the mirage light-filtering phase and serves as the core strategy for individual-level search. It is designed to facilitate local exploitation within the search space and uncover potential local optima. As illustrated in
Figure 4, light selected from the filtering stage is emitted from the source point and undergoes a sequence of refraction and reflection behaviors. This process defines three core local search mechanisms in the FATA algorithm: Refraction Phase I, Refraction Phase II, and Total Internal Reflection. These behaviors collectively enable the algorithm to coordinate exploration and convergence within local neighborhoods.
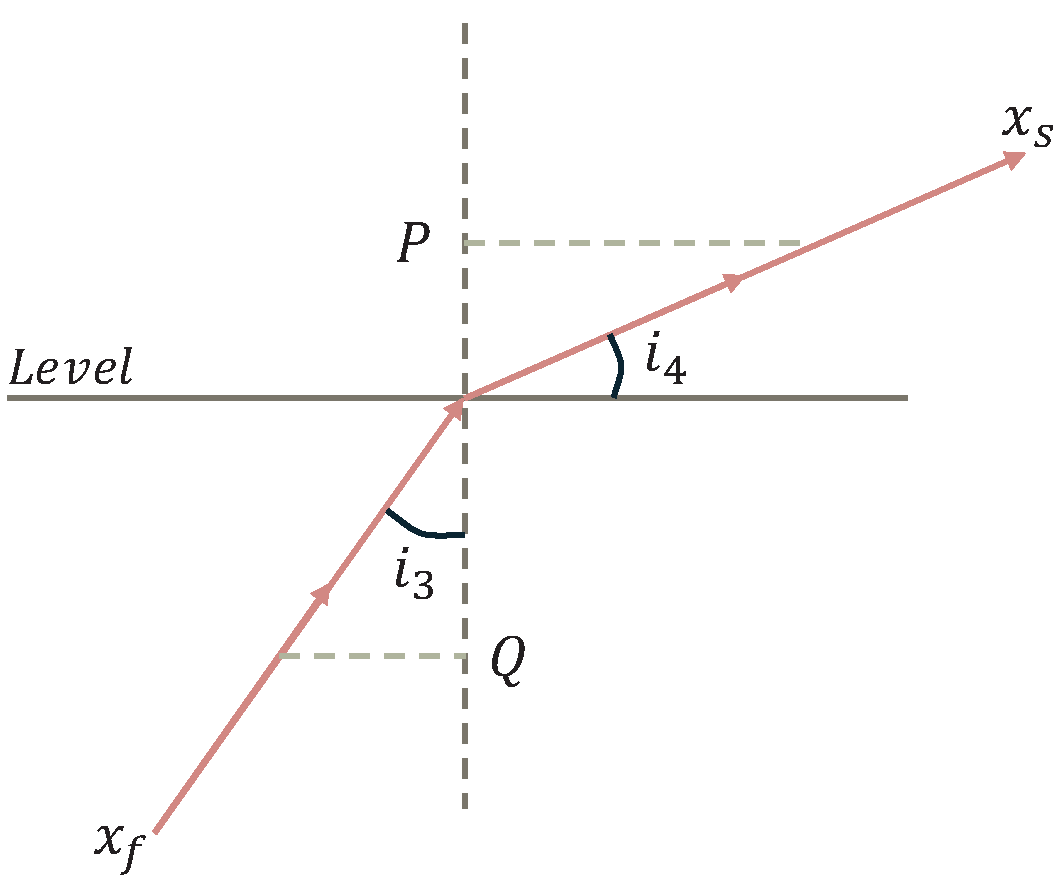
Refraction Phase I. In the initial phase, the individual light (
x) propagates from an optically dense medium into a less dense medium, undergoing its first refraction due to the non-uniform refractive index of the environment. This process alters the light’s direction vector and propagation intensity, which corresponds to the generation of a new candidate solution within the search space. As illustrated in
Figure 5, the incidence angle (
) is smaller than the refraction angle (
), indicating an outward expansion in the search direction. In this phase, the FATA algorithm updates the individual’s position based on Equations (
16), (
17) and (
20) and applies a partial reflection strategy to modulate the search range.
where
is the current best individual.
where
is the incidence angle and
is the refraction angle.
Refraction Phase II. After the initial refraction phase, the light undergoes a second refraction at a randomly selected position to further adjust its propagation direction. As illustrated in
Figure 6, the incidence angle (
) remains smaller than the refraction angle (
), and the refraction index parameter (Para2) is dynamically adjusted in response to the continuous change in medium density. In this strategy, the FATA algorithm generates a new individual (
) based on the current light (
) and a randomly selected individual (
) from the search space, with the aim of enhancing local perturbation and search diversity. This process is described by Equations (
18)–(
20).
where
denotesrandom individuals and
is the reflectance of the reflection strategy, which controls the pattern of change in the light individual.
where
is the incidence angle and
is the reflection angle.
where
q is the individual quality factor,
represents the fitness of the current individual (
x),
represents the fitness of the worst individual, and
represents the fitness of the best individual.
Total Internal Reflection. When the refraction angle gradually increases beyond the critical angle, the light undergoes total internal reflection within the non-uniform medium and is redirected in the opposite direction. This mechanism constitutes the third-phase search strategy in the FATA algorithm, encouraging the population to migrate toward unexplored regions, thereby enhancing the algorithm’s global search capability. As shown in
Figure 7, the incidence angle (
) equals the reflection angle (
), demonstrating the directional symmetry of the reversal. In the figure, point
denotes the center of the search interval
, and points
E and
F represent the horizontal projections of the incidence and reflection points, respectively. Under this strategy, individual
x is transformed into
and redirected in the opposite direction to ensure escape from local optima. This process is defined by Equations (
21)–(
24).
where
is the individual reflected by the total internal reflection strategy.
where
E and
F are the distances of the incident and refracted light to the horizontal plane, respectively.
3.3.2. MOFATA
As the FATA algorithm was originally designed as a single-objective optimization algorithm, it lacks the capacity to simultaneously address multiple critical goals in complex network defense tasks—such as preserving benign traffic, intercepting malicious flows, and balancing resource loads. To overcome this limitation, we extend its original loss formulation to a four-dimensional objective vector, which shown in Equation (
25), representing distinct dimensions of system performance. Specifically,
measures the effectiveness of benign traffic servicing,
quantifies the degree of load imbalance across servers,
and
capture the proportion of benign traffic and malicious traffic that is allowed to pass through, and
assesses the system’s ability to isolate malicious traffic. This vectorized formulation unifies multiple performance metrics into a dimensionless mathematical representation, allowing the problem to be rigorously addressed under a multi-objective optimization framework.
In SOE, each candidate solution is initially represented as a discrete
N-dimensional vector (
), as shown in Equation (
26), indicating the assignment of traffic source
i to one of
M servers. This discrete representation faithfully reflects the inherently discrete nature of real-world resource allocation decisions. However, to leverage the efficient global search capabilities of the FATA algorithm in continuous domains, we relax the discrete decision variables by mapping each
to a continuous variable defined over the interval of
. The search and update processes are performed in this relaxed continuous domain, after which the solution is discretized via rounding to generate executable scheduling schemes.
To achieve effective trade-offs among multiple conflicting objectives, the concept of Pareto optimality is introduced. A multi-objective solution set is constructed through a non-dominated sorting mechanism. Specifically, in the continuous search domain, each candidate solution (
x) corresponds to an objective vector as defined in Equation (
27).
where each objective function (
) represents performance dimensions such as benign traffic assurance, malicious traffic interception, load balancing, and attack isolation.
According to the classical Pareto dominance rule, for any two solutions (
x and
y),
x is said to dominate
y (denoted by
) if Equations (
28) and (
29) hold.
To enhance the algorithm’s ability to discriminate fine-grained performance differences and avoid premature convergence or policy degeneration, we incorporate the concept of
-dominance. Under this strategy, a solution
x -dominates solution
y only if Equation (
30) holds:
Based on these principles, non-dominated sorting is applied to partition the population into multiple Pareto fronts. Tournament selection and crowding distance mechanisms are subsequently used to maintain solution diversity and promote a well-distributed set of high-quality solutions across all objectives. This hybrid approach effectively combines the discrete characteristics of the scheduling decision with the powerful search capability of continuous optimization. The integration of
-dominance further enhances the global exploration capacity and fine-resolution performance discrimination of the proposed MOFATA algorithm. The pseudocode of MOFATA is presented as Algorithm 1:
| Algorithm 1 MOFATA: Multi-objective Extension Based on FATA |
- Require:
: population size; : maximum generations; : multi-objective fitness function; : -dominance threshold; M: number of servers; FATA() function (baseline optimizer) - Ensure:
Final Pareto front of discrete scheduling vectors - 1:
Initialize population via FATA() - 2:
for all in population do - 3:
Evaluate fitness vector - 4:
end for - 5:
Perform non-dominated sorting → obtain initial Pareto front - 6:
for to do - 7:
Execute one FATA generation to update population - 8:
for all in population do - 9:
Discretize by rounding to nearest integer in - 10:
Evaluate multi-objective fitness - 11:
end for - 12:
Apply -dominance filtering and non-dominated sorting - 13:
Use crowding distance to maintain diversity - 14:
Update Pareto front with current non-dominated individuals - 15:
end for - 16:
return Final Pareto front
|