Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions
Abstract
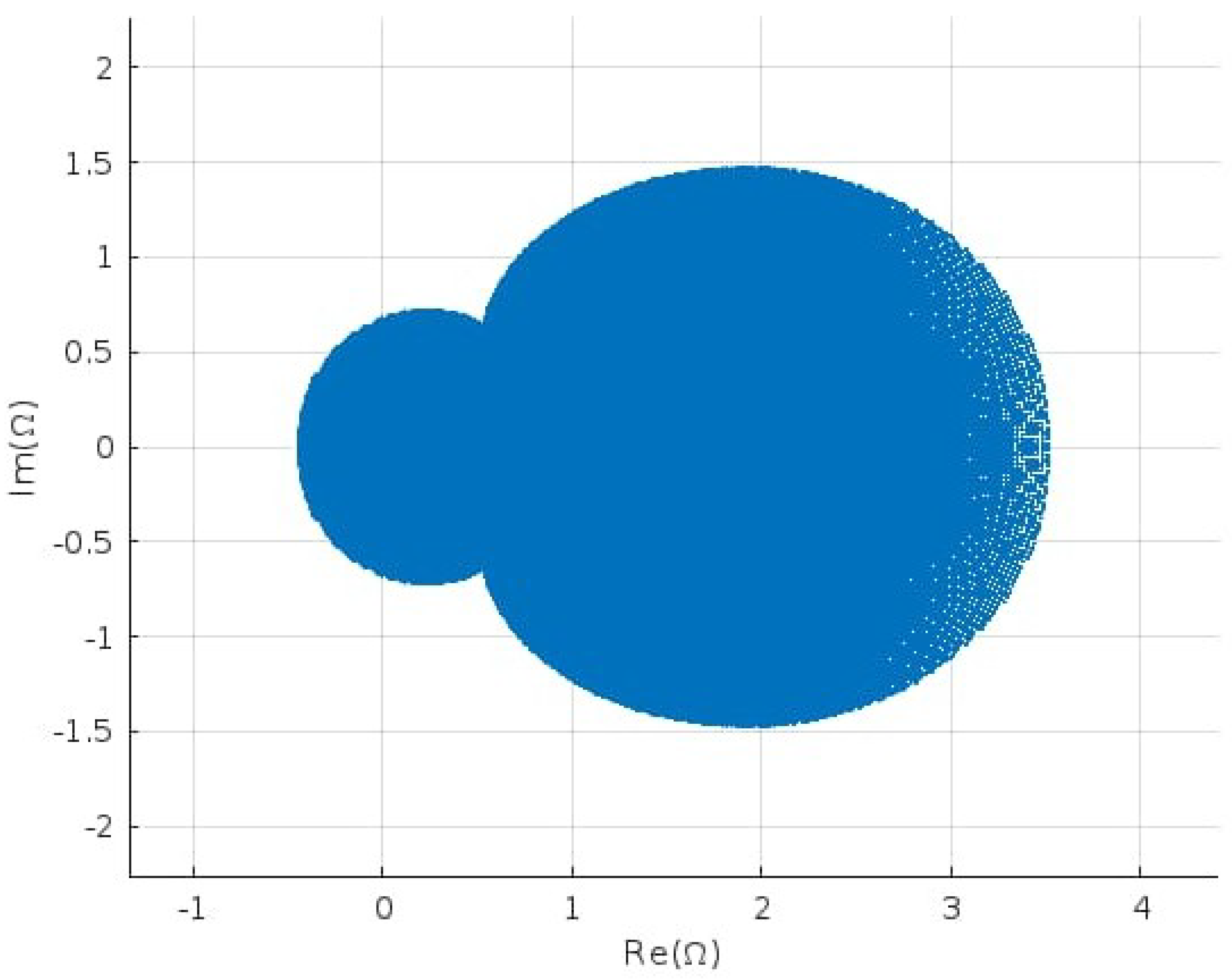
1. Introduction and Preliminaries
- ;
- ;
- (see [13]).
- is univalent with ;
- is starlike with respect to ;
- is symmetric about the real axis;
- .
2. Coefficient Bounds, Fekete–Szegö Inequality and Hankel Determinants
- If that is, , then by using Lemma 5, we get
- If that is, then by using Lemma 5, we get
- If that is, then by using Lemma 5, we get
- For we have
- 2.
- For we obtain
3. Logarithmic Coefficient Inequalities
- For we have
- 2.
- For we get
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, S.S.; Mocanu, P.T. Differential Subordination. Theory and Applications, Series on Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker Inc.: New York, NY, USA; Basel, Switzerland, 2000; Volume 225. [Google Scholar]
- Ma, W.C.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis; International Press: Cambridge, UK, 1994; pp. 157–169. [Google Scholar]
- Sokól, J.; Stankiewicz, J. Radius of convexity of some subclasses of strongly starlike functions. Zesz. Nauk. Politech. Rzesz. Mat. 1996, 19, 101–105. [Google Scholar]
- Janowski, W. Extremal problems for a family of functions with positive real part and for some related families. Ann. Polon. Math. 1971, 23, 159–177. [Google Scholar] [CrossRef]
- Sharma, K.; Jain, N.K.; Ravichandran, V. Starlike functions associated with a cardioid. Afr. Mat. 2016, 27, 923–939. [Google Scholar] [CrossRef]
- Wani, L.A.; Swaminathan, A. Starlike and convex functions associated with a nephroid domain. Bull. Malays. Math. Sci. Soc. 2021, 44, 79–104. [Google Scholar] [CrossRef]
- Sivaprasad Kumar, S.; Kamaljeet, G. A cardioid domain and starlike functions. Anal. Math. Phys. 2021, 11, 54. [Google Scholar]
- Mendiratta, R.; Nagpal, S.; Ravichandran, V. A subclass of starlike functions associated with left-half of the lemniscate of Bernoulli. Int. J. Math. 2014, 25, 1450090. [Google Scholar] [CrossRef]
- Mendiratta, R.; Nagpal, S.; Ravichandran, V. On a subclass of strongly starlike functions associated with exponential function. Bull. Malays. Math. Sci. Soc. 2015, 38, 365–386. [Google Scholar] [CrossRef]
- Janowski, W. Some extremal problems for certain families of analytic functions. I. Ann. Polon. Math. 1973, 28, 297–326. [Google Scholar] [CrossRef]
- Owa, S.; Srivastava, H.M. Some generalized convolution properties associated with certain subclasses of analytic functions. J. Inequal. Pure Appl. Math. 2002, 3, 42. [Google Scholar]
- Uralegaddi, B.A.; Ganigi, M.D.; Sarangi, S.M. Univalent functions with positive coefficients. Tamkang J. Math. 1994, 25, 225–230. [Google Scholar] [CrossRef]
- Ravichandran, V.; Verma, S. Bound for the fifth coefficient of certain starlike functions. C. R. Math. Acad. Sci. Paris 2015, 353, 505–510. [Google Scholar] [CrossRef]
- Palei, S.; Soren, M.M.; Cotîrlǎ, L.-I. Coefficient Bounds for Alpha-Convex Functions Involving the Linear q-Derivative Operator Connected with the Cardioid Domain. Fractal Fract. 2025, 9, 172. [Google Scholar] [CrossRef]
- Krushkal, S.L. Proof of the Zalcman conjecture for initial coefficients. Georgian Math. J. 2010, 17, 663–681. [Google Scholar] [CrossRef]
- Lecko, A.; Sim, Y.J. Coefficient Problems in the Subclasses of Close-to-Star Functions. Results Math. 2019, 74, 104. [Google Scholar] [CrossRef]
- Ravichandran, V.; Verma, S. Generalized Zalcman conjecture for some classes of analytic functions. J. Math. Anal. Appl. 2017, 450(1), 592–605. [Google Scholar] [CrossRef]
- Pommerenke, C. On the coefficients and Hankel determinants of univalent functions. J. Lond. Math. Soc. 1966, 1, 111–122. [Google Scholar] [CrossRef]
- Pommerenke, C. On the Hankel determinants of univalent functions. Mathematika 1967, 14, 108–112. [Google Scholar] [CrossRef]
- Ye, K.; Lim, L.H. Every matrix is a product of Toeplitz matrices. Found. Comput. Math. 2016, 16, 577–598. [Google Scholar] [CrossRef]
- Kowalczyk, B.; Lecko, A. Second Hankel determinant of logarithmic coefficients of convex and starlike functions. Bull. Aust. Math. Soc. 2022, 105, 458–467. [Google Scholar] [CrossRef]
- Kowalczyk, B.; Lecko, A. The second Hankel determinant of the logarithmic coefficients of strongly starlike and strongly convex functions. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 2023, 117, 91. [Google Scholar] [CrossRef]
- Murugusundaramoorthy, G.; Bulboacǎ, T. Hankel Determinants for New Subclasses of Analytic Functions Related to a Shell Shaped Region. Mathematics 2020, 8, 1041. [Google Scholar] [CrossRef]
- Saliu, A.; Noor, K.I. On Coefficients Problems for Certain Classes of Analytic Functions. J. Math. Anal. 2021, 12, 13–22. [Google Scholar]
- Zhang, H.-Y.; Huo, T. A study of fourth-order Hankel determinants for starlike functions connected with the sine function. J. Funct. Spaces 2021, 2021, 9991460. [Google Scholar] [CrossRef]
- Shafiq, M.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Darus, M.; Kiran, S. An upper bound of the third Hankel determinant for a subclass of q-starlike functions associated with k-Fibonacci numbers. Symmetry 2020, 12, 1043. [Google Scholar] [CrossRef]
- Güney, H.Ö.; Murugusundaramoorthy, G.; Srivastava, H.M. The second hankel determinant for a certain class of bi-close-to-convex function. Results Math. 2019, 74, 13. [Google Scholar] [CrossRef]
- Mahmood, S.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Khan, B.; Ali, I. Upper bound of the third Hankel determinant for a subclass of q-starlike functions. Symmetry 2019, 11, 347. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ahmad, Q.Z.; Khan, N.; Khan, N.; Khan, B. Hankel and Toeplitz determinants for a subclass of q-starlike functions associated with a general conic domain. Mathematics 2019, 7, 181. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Khan, B.; Khan, N.; Tahir, M.; Ahmad, S.; Khan, N. Upper bound of the third Hankel determinant for a subclass of q-starlike functions associated with the q-exponential function. Bull. Sci. Math. 2021, 167, 16. [Google Scholar] [CrossRef]
- Hayman, W.K. On the second Hankel determinant of mean univalent functions. Proc. Lond. Math. Soc. 1968, 18, 77–94. [Google Scholar] [CrossRef]
- Noonan, J.W.; Thomas, D.K. On the second Hankel determinant of areally mean p-valent functions. Trans. Am. Math. Soc. 1976, 223, 337–346. [Google Scholar] [CrossRef]
- Jangteng, A.; Halim, S.A.; Darus, M. Coefficient inequality for a function whose derivative has a positive real part. J. Inequal. Pure Appl. Math. 2006, 7, 1–5. [Google Scholar]
- Orhan, H.; Magesh, N.; Yamini, J. Bounds for the second Hankel determinant of certain bi-univalent functions. Turk. J. Math. 2016, 40, 679–687. [Google Scholar] [CrossRef]
- Babalola, K.O. On H3(1) Hankel determinant for some classes of univalent functions. Inequal. Theory Appl. 2007, 6, 1–7. [Google Scholar]
- Zaprawa, P. Third Hankel determinants for subclasses of univalent functions. Mediterr. J. Math. 2017, 14, 10. [Google Scholar] [CrossRef]
- Raza, M.; Malik, S.N. Upper bound of third Hankel determinant for a class of analytic functions related with lemniscate of Bernoulli. J. Inequal. Appl. 2013, 2013, 8. [Google Scholar] [CrossRef]
- Cho, N.E.; Kowalczyk, B.; Kwon, O.S.; Lecko, A.; Sim, J. Some coefficient inequalities related to the Hankel determinant for strongly starlike functions of order alpha. J. Math. Inequal. 2017, 11, 429–439. [Google Scholar] [CrossRef]
- Lecko, A.; Sim, Y.J.; Śmiarowska, B. The sharp bound of the Hankel determinant of the third kind for starlike functions of order 1/2. Complex Anal. Oper. Theory 2019, 13, 2231–2238. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Ahmad, Q.Z.; Darus, M.; Khan, N.; Khan, B.; Zaman, N.; Shah, H.H. Upper bound of the third Hankel determinant for a subclass of close-to-convex functions associated with the lemniscate of Bernoulli. Mathematics 2019, 7, 848. [Google Scholar] [CrossRef]
- Duren, P.T. Univalent Functions; Springer: New York, NY, USA, 1983. [Google Scholar]
- Keogh, F.R.; Merkes, E.P. A coefficient inequality for certain classes of analytic functions. Proc. Am. Math. Soc. 1969, 20, 8–12. [Google Scholar] [CrossRef]
- Pommerenke, C. Univalent Functions; Vandenhoeck and Ruprecht: Gottingen, Germany, 1975; Volume 1, p. 1. [Google Scholar]
- Kwon, O.S.; Lecko, A.; Sim, Y.J. On the fourth coefficient of functions in the Carathéodory class. Comput. Methods Funct. Theory 2018, 18, 307–314. [Google Scholar] [CrossRef]
- Efraimidis, I. A generalization of Livingston’s coefficient inequalities for functions with positive real part. J. Math. Anal. Appl. 2016, 435, 369–379. [Google Scholar] [CrossRef]
- Libera, R.J.; Zlotkiewicz, E.J. Coefficient bounds for the inverse of a function with derivatives in P. Proc. Am. Math. Soc. 1983, 87, 251–257. [Google Scholar] [CrossRef]
- Krushkal, S.L. Univalent functions and holomorphic motions. J. Anal. Math. 1995, 66, 253–275. [Google Scholar] [CrossRef]
- Ali, M.F.; Allu, V. On logarithmic coefficients of some close-to-convex functions. Proc. Am. Math. Soc. 2018, 146, 1131–1142. [Google Scholar] [CrossRef]
- Ali, M.F.; Vasudevarao, A.; Thomas, D.K.; Lecko, A. On the third logarithmic coefficients of close-to- convex functions. In Current Research in Mathematical and Computer Sciences II; Publisher UWM: Olsztyn, Poland, 2018; pp. 271–278. [Google Scholar]
- Girela, D. Logarithmic coefficients of univalent functions. Ann. Acad. Sci. Fenn. 2000, 25, 337–350. [Google Scholar]
- Roth, O. A sharp inequality for the logarithmic coefficients of univalent functions. Proc. Am. Math. Soc. 2007, 135, 2051–2054. [Google Scholar] [CrossRef]
- Thomas, D.K. On logarithmic coefficients of close to convex functions. Proc. Am. Math. Soc. 2016, 144, 1681–1687. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palei, S.; Soren, M.M.; Cotîrlǎ, L.-I.; Breaz, D. Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions. Mathematics 2025, 13, 1845. https://doi.org/10.3390/math13111845
Palei S, Soren MM, Cotîrlǎ L-I, Breaz D. Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions. Mathematics. 2025; 13(11):1845. https://doi.org/10.3390/math13111845
Chicago/Turabian StylePalei, Sudhansu, Madan Mohan Soren, Luminiţa-Ioana Cotîrlǎ, and Daniel Breaz. 2025. "Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions" Mathematics 13, no. 11: 1845. https://doi.org/10.3390/math13111845
APA StylePalei, S., Soren, M. M., Cotîrlǎ, L.-I., & Breaz, D. (2025). Sharp Coefficient Bounds for Analytic Functions Related to Bounded Turning Functions. Mathematics, 13(11), 1845. https://doi.org/10.3390/math13111845







