Abstract
In the increasingly competitive manufacturing industry, optimizing production decision making and quality control is crucial for the strategic development of companies. To maximize cost effectiveness and enhance market competitiveness, scientific decision-making and effective quality inspection are particularly important. Among the various types of decision models for production processes, extensive research has been conducted in different fields to address diverse decision problems for production processes, resulting in the establishment of multiple models that aid in the analysis of factors that influence processes at various stages. In this paper, we propose a production decision optimization method based on a multi-agent mixed-integer programming model, which integrates multistage decision analysis and quality inspection. By incorporating Monte Carlo simulation, we can simulate the fluctuations in defect rates during actual production processes and optimize decision-making under multiple confidence levels. This model effectively balances production costs and product quality, achieving maximum cost-effectiveness through the optimization of decision pathways during the production stages. Experimental results show that our model can provide robust and efficient decision support in dynamic manufacturing environments.
Keywords:
multi-agent mixed-integer programming; production process decision-making; quality inspection; multistage decision-making; Monte Carlo simulation MSC:
90C11; 93C43; 90C29; 62P05; 68Q70
1. Introduction
In recent years, the optimization of production decision making has attracted widespread attention in both academia and industry [1]. Production decisions lie at the heart of operational management in manufacturing enterprises, directly affecting how resources are allocated, as well as impacting production costs and product quality. As manufacturing environments become more complex, the number of factors that influence these decisions continues to grow [2]. This is especially true in electronics manufacturing, where component quality [3] plays a key role. To maintain product quality, companies must perform rigorous inspections upon component arrival and make appropriate decisions regarding non-conforming finished products, for instance, scrapping or disassembling for component reuse. Although disassembly helps preserve the value of the component, it also comes at an extra cost. In such a competitive market, reducing production costs while ensuring quality has become a critical issue.
Although many studies have explored decision making in production systems, most rely on traditional models such as dynamic programming or decision trees. Dynamic programming is suitable for multistage decision problems, but often leads to local optima in complex scenarios [4,5,6]. Decision tree methods are computationally efficient and easy to interpret, but deep trees risk overfitting and reduced generalizability [7,8,9]. More recently, mixed-integer programming (MIP) has shown strong capabilities in finding globally optimal solutions for complex decision problems. In parallel, multi-agent systems (MAS) [10,11,12] have been applied in domains requiring decentralized decision making, especially under uncertainty.
In terms of specific model development, Casanova et al. proposed the MaSTNU framework—a combination of multi-agent simple temporal networks (MaSTN) and simple temporal networks with uncertainty (STNU)—to handle dynamic controllability [13] in limited communication settings. Hu et al. applied multi-agent models in game-theoretic contexts using Hamilton–Jacobi Reachability [14] to support optimal decision making when agents face opposing goals. Pendharkar proposed the cTAEMS framework(Collaborative Task Analysis, Execution, and Modeling Specification) [15], incorporating constraint programming and problem decomposition to address complex scheduling problems involving time windows and non-linear objectives. These studies demonstrate the flexibility of MAS in dynamic environments, but relatively few directly focus on real-world production systems.
Therefore, this paper focuses on production decision-making problems with uncertainty in component quality and varying cost trade-offs. We propose a model that combines multi-agent systems and mixed-integer programming to support more effective decision-making across different stages of the production process. Compared with centralized or rule-based approaches, the multi-agent model allows each agent, representing a process unit, resource, or decision node, to make decisions independently while collaborating through global constraints.
The main contributions of this paper are as follows:
- We develop a multi-agent mixed-integer programming model tailored for production systems with uncertain component quality and recycling decisions.
- We define agent roles and interactions in the production decision process, clarifying how they coordinate under cost-benefit trade-offs.
- We incorporate trial-based dynamic programming and a branch-and-bound mechanism to optimize decision paths with delayed evaluation.
- We compare the proposed method with traditional approaches to show its effectiveness in improving cost efficiency.
The model aims to provide robust and practical decision support, especially in manufacturing environments where quality fluctuations and cost control are critical.
To address the pressing challenges of cost control and quality assurance in modern manufacturing, this paper develops a decision optimization model that combines multi-agent systems with mixed-integer programming. The following section introduces the structure and rationale of the proposed model, including its core components—quality inspection and decision-making modules—along with the interactions between agents to achieve global coordination.
2. Multi-Agent Hybrid Integer Programming Decision Model for Production Processes
This paper explores the optimization problem of production decision making faced by enterprises when dealing with precise data on the defect rates of spare parts and finished products. The multi-agent mixed-integer programming model consists of two main components: quality inspection and decision-making. The quality inspection component determines whether to accept a batch of spare parts for the production process. If the requirements are met, the batch proceeds to the decision-making component, which is the primary decision-making body represented by an integer programming model. The flow chart of the model decision-making process is shown in Figure 1.
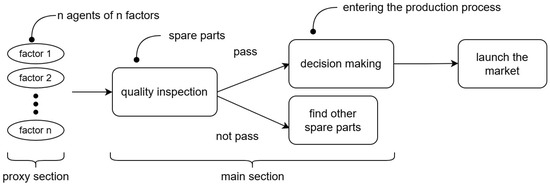
Figure 1.
Flowchart of the decision-making process in the proposed multi-agent mixed-integer programming model, highlighting key steps, such as component inspection, decision node interaction, and cost-based path evaluation.
To clearly articulate the multi-agent component of the proposed approach, we summarize its structure, functionality, and advantages as follows. In the system, each agent represents a unique decision factor, such as cost estimation, component availability, supplier reliability, or production scheduling, and encapsulates domain-specific logic and preferences. Although these agents operate autonomously, they exchange information through a shared communication protocol, allowing them to dynamically adapt to environmental changes and updates from other agents.
Through this collaborative mechanism, agents negotiate and coordinate their actions to resolve potential conflicts (for instance, between cost minimization and timely delivery), thus collectively optimizing global system performance. This decentralized and modular design improves system flexibility and scalability: agents can be added or modified without requiring a complete redesign. Moreover, the parallel nature of multi-agent decision-making facilitates faster convergence when solving complex problems, while also enhancing robustness, since localized disruptions can be isolated and managed without affecting the overall system.
Importantly, this architecture reflects the realities of modern manufacturing and supply chain environments, where multiple stakeholders interact concurrently with partially overlapping objectives. As such, the proposed multi-agent structure not only strengthens the methodological contribution of the work but also reinforces its practical relevance.
To establish a comprehensive and efficient production decision-making system, this paper will formulate a foundational decision-making process and refine it into several key nodes, each involving decision-making based on integer programming. The goal is to ultimately identify a decision scheme that satisfies all constraints while optimizing the objective function, thus maximizing production efficiency. The flow chart of the production process is shown in Figure 2.
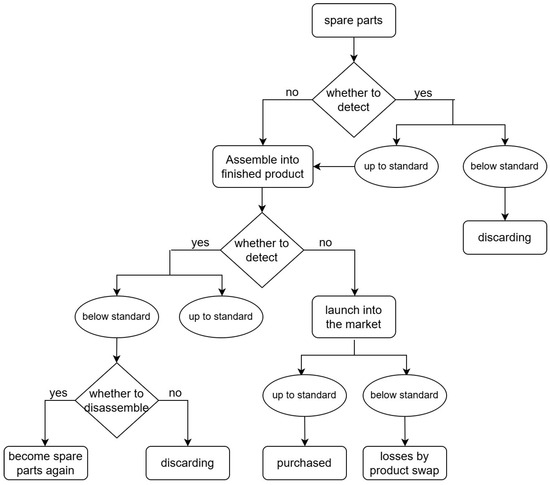
Figure 2.
Schematic overview of the production process, including spare part procurement, quality inspection, assembly, and the disassembly of defective products.
2.1. Quality Inspection
The model focuses on the inspection of statistical sampling by building a hypothesis testing model for defect rates. Using the approximation of normal distribution in large samples, a formula is drawn to calculate the minimum sample size to determine whether the defect rate of spare parts meets the nominal value. The sample size refers to the number of sampling inspections, which directly affects detection efficiency and cost. In practical applications, key variables, such as the nominal defect rate, the actual defect rate, and the number of inspections must be defined, followed by the formulation of different inspection schemes. Finally, the normal distribution approximation method is used to estimate the minimum sample size required and analyze the variation in the sample size under different actual defect rates.
2.1.1. Scheme Establishing
We explore the trend of variation in sample size under two different schemes, relying on the principles of hypothesis testing and the normal distribution approximation method. A sample size calculation model is constructed to achieve a precise quantitative analysis of the number of sampling inspections. In practice, the schemes formulated may vary due to environmental influences. Under the condition that the supplier guarantees, the defect rate of a batch of spare parts does not exceed 10% (the nominal value):
- Scheme 1: If the defect rate is detected to exceed 10% at a 95% confidence level, the company will reject the spare parts batch.
- Scheme 2: If it is confirmed at a 90% confidence level that the defect rate does not exceed 10%, the company will accept the batch of spare parts.
This model examines how a company can determine whether the defect rate of spare parts meets the nominal value through a simple random sampling inspection to decide whether to accept the batch. The defect rate P of the spare parts purchased from the supplier does not exceed the nominal value . However, the actual defect rate can fluctuate due to various factors, such as variability in the production process, changes in environmental conditions, instability in the supply chain, and changes in market demand and consumer preferences. To enhance the robustness of the model, a comprehensive consideration of the range of values is necessary, allowing the calculation of inspection numbers in different scenarios and ensuring the effectiveness of the sampling plan in various contexts.
2.1.2. Sample Detection Model of Defective Rate
Assuming that the number of defective items X follows a binomial distribution based on the properties of the defect rate P:
where n is the total number of products and P is the defect rate.
To analyze the proportion of defective items, we define the sample proportion as . Since the expectation and variance of a binomially distributed variable X are and , the expectation and variance of can be obtained as
Since suppliers typically provide a large quantity of products and we are concerned with the scenario of large sample sizes, by the central limit Theorem (CLT), the binomial distribution can be approximated by a normal distribution. Therefore, we use the normal distribution model to simplify the calculations.
To determine the sample size, this study employs the following hypothesis testing framework to design a simple random sampling scheme.
- Null hypothesis : The actual defect rate of spare parts does not exceed the nominal value .
- Alternative Hypothesis : The actual defect rate exceeds the nominal value .
This framework assesses whether to accept or reject products at confidence levels of 95% and 90%. At the 95% confidence level, the critical value for rejecting is ; at the 90% confidence level, it is . In order to account for potential uncertainties in the production process, a safety margin Z is introduced. This parameter helps buffer against variations in demand or supply conditions, ensuring that production plans remain feasible under minor disruptions. The value of Z is typically determined based on historical data or predefined service level requirements. The null hypothesis is rejected when the test statistic Z satisfies the condition:
The number of defects X in the sample is less than or equal to the critical value k, expressed as follows:
where is the significance level; n is the total number of products; is the nominal defect rate; the critical value k is calculated using a normal approximation:
If the number of defects detected X is less than or equal to k, the null hypothesis is accepted; otherwise it is rejected.
Although quality inspection forms the first barrier to ensuring component integrity, it is insufficient alone to determine the most cost-effective production strategy. Therefore, in the subsequent section, we integrate the inspection results into a comprehensive decision-making process modeled through integer programming. This enables dynamic responses to quality variations while minimizing overall costs through optimized decisions at each production stage.
2.2. Decision Making
The decision-making process encompasses multiple layers, including the inspection of spare parts and finished products, the disassembly of non-conforming finished goods, and the management of customer returns. An integer programming model is used to compare the costs associated with each decision path, with the objective of maximizing cost-effectiveness and identifying the optimal route. Taking into account the complexity of the decision paths and the variability in costs, this study uses the branch-and-bound method for path optimization. The branch-and-bound technique is adept at addressing problems that involve multiple decision stages by systematically decomposing the problem and employing pruning strategies [16] to explore all potential decision paths, ultimately leading to the identification of the optimal solution and the maximization of cost effectiveness. In this model, the method operates by first branching the entire decision space into smaller sub-problems, each representing a partial solution. For each branch, a cost bound is computed. If this bound is worse than the best known feasible solution, the branch is discarded early; this is the bounding and pruning step. By continuously comparing and eliminating unpromising branches, the algorithm efficiently identifies the globally optimal decision path without exhaustively evaluating all possibilities. This greatly reduces the computational time while maintaining the accuracy of the solutions [17].
2.2.1. Integer Programming Decision Model
To begin with, let us consider a single production stage where we define two types of spare parts, as illustrated in the following diagram (Figure 3).
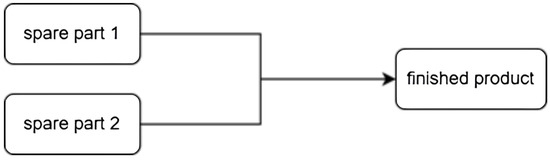
Figure 3.
Diagram of the single-stage production decision model. Each decision variable (inspection, disassembly) corresponds to binary options used in the optimization.
- Step 1: Define the decision variables.
- Step 2: Set the constraints.
Based on the decision variables and the production flow diagram (Figure 2), since the decision variables are independent of the quantities of spare parts, and each cost element (purchase cost, inspection cost, assembly cost, disassembly cost, and replacement loss cost) is treated as an independent cost per product, the total cost of producing all products can be obtained by multiplying the quantity of products.
This approach is common in batch production and cost analysis. Therefore, we set the constraints: the quantities of both types of spare parts purchased are equal to 1.
- Step 3: Set the objective function.
The total cost of the entire process can be expressed as the objective function C:
where and represent the purchasing cost, inspection cost, assembly cost, disassembly cost, and replacement loss, respectively; and denote the unit purchase prices of parts 1 and 2; and are inspection costs for parts 1, 2, and the finished product; A is the assembly cost; and are the defect rates for parts 1 and 2; p represents the defect rate for the finished product; is the disassembly cost; is the loss incurred from replacing nonconforming products.
The maximum profit selections for parts 1 through 6 are determined using integer programming.
2.2.2. Multistage Decision-Making Model
This model builds on the aforementioned single-layer decision model by incorporating additional production stages and decision points. Decision points and production processes can be added as needed based on actual circumstances. In this model, the number of production stages is increased to two, and the initial parameters are expanded to 13, as illustrated in the figure below (Figure 4).
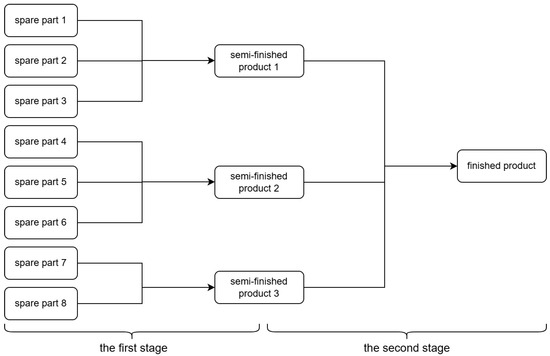
Figure 4.
Multistage production model structure involving sequential decision points for semi-finished and finished products, allowing analysis of cumulative cost and inspection strategies.
- 1. Production stage 1: the process of producing semi-finished products from components.
Define new decision variables:
The remaining variables are the same as those in the previous model.
The cost objective function for the production of semi-finished products from components is defined as follows:
where h represents the first stage; is the unit purchase price of component 3 (which is 0 when composing the semi-finished product 3); is the inspection cost for component 3; is the defect rate for component 3. The meanings of the other parameters remain the same as in the previous model.
- 2. Production stage 2: the process of producing finished products from semi-finished products.
New decision variables are introduced on the basis of the first stage.
The cost objective function for producing finished products from semi-finished products is as follows:
where the subscript ℓ denotes the second stage; the meanings of the parameter variables are the same as in the first stage.
- 3. Presentation of the integrated optimization model.
The objective function for the total production cost is derived from the following considerations.
Since three semi-finished products need to be composed, and one of the semi-finished products is made up of two components, is the sum of three different values.
The multi-stage decision model builds on single-stage optimization by incorporating additional complexity from real-world production processes. To assess the feasibility and effectiveness of the proposed model under varied scenarios, the next section presents numerical experiments and analytical evaluations across both quality inspection and decision-making modules.
3. Results and Analyses
This section will provide the data necessary for the calculation results, resulting in the decision results for the two phases of the main model, quality inspection and decision-making, and will analyze the possible reasons for such decisions.
3.1. Results and Analyses of Quality Inspection
According to the derivation in Section 2.1, the following formula is obtained to estimate the minimum sample size, that is, the minimum number of inspections n:
where is the critical value of the standard normal distribution; is the nominal defect rate; E is the allowable error:
where is the actual defect rate.
To enhance flexibility, the variation in the sample size n with respect to different values is examined. Specifically, the sample sizes corresponding to the confidence levels of 95% and 90% are calculated for various values . In practical scenarios, when approaches or equals , the required sample size can become excessively large. Consequently, a constraint is introduced to ensure that the sample size n does not exceed the production batch size, thus maintaining the model’s operability.
The solution of the aforementioned model yields the calculated sample sizes n at different confidence levels and varying values.
Figure 5 and Figure 6 illustrate the relationship between the defect rate and the required sample size. As shown in Figure 5, the required sample size increases sharply as approaches the defect threshold (), reflecting the increasing difficulty in distinguishing conforming from non-conforming batches. Figure 6, which magnifies the range , reveals that the required sample size can equal or exceed the batch size, at which point it plateaus due to sampling saturation.
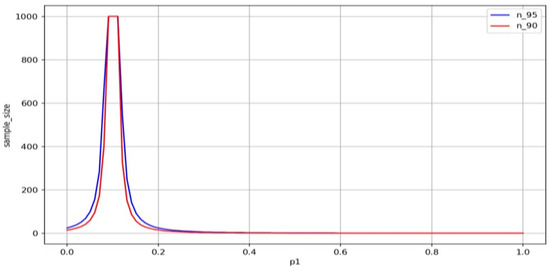
Figure 5.
Variation in the required sample size n with respect to different actual defect rates at a 95% confidence level, based on normal approximation for binomial distribution.
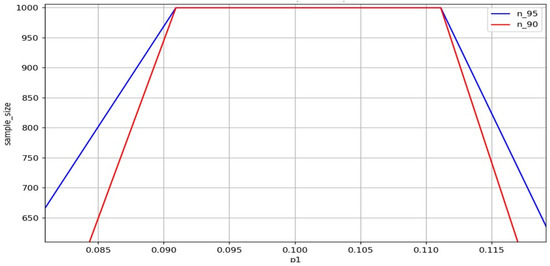
Figure 6.
Detailed view of sample size n behavior within the critical range , where values plateau due to exceeding batch size.
Figure 7 and Figure 8 compare the sampling requirements to reject non-conforming batches with confidence 95% (Figure 7) and accept conforming batches with confidence 90% (Figure 8). The former requires 98 samples when , whereas the latter requires only 60. This highlights that stricter rejection confidence requires larger sample sizes. Moreover, increasing allows for smaller sample sizes while maintaining decision reliability due to the clearer distinction between conforming batches and defective batches.
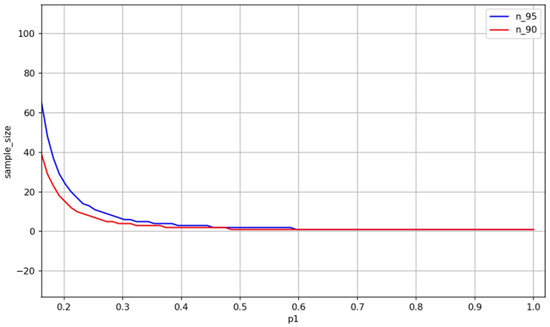
Figure 7.
Required sample size n at a 95% confidence level when the actual defect rate exceeds the nominal rate.
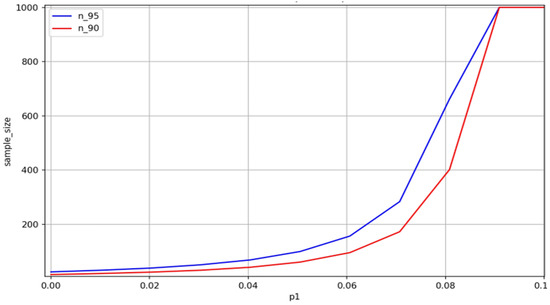
Figure 8.
Required sample size n at a 90% confidence level when the actual defect rate does not exceed the nominal rate.
- 1.
- Relationship between sample size and :
- Initial stage: When is below the nominal defect rate (approximately 0), the sample size is small, and both curves remain at lower levels.
- Approaching nominal defect rate: As approaches the nominal defect rate , the sample size increases rapidly, peaking near .
- Exceeding nominal defect rate: Once exceeds the nominal defect rate, the sample size gradually decreases with increasing , tending toward zero.
- 2.
- Comparison of sample sizes at different confidence levels:
- Sample size requirements: At a confidence level 95%, the required sample size is larger than at a confidence level 90%, which is consistent with the principle that higher confidence levels require more samples to reduce the likelihood of erroneous judgments.
- Variation in differences: The difference in sample sizes between confidence levels 95% and 90% varies with different values. When is small, the difference is significant; however, as increases, the difference gradually decreases.
3.2. Results and Analyses of Decision Making
In this section, for the convenience of calculating results, this paper presents the defect rates, purchase unit prices, inspection costs, and disassembly costs associated with the relevant components.
The following data pertain to a single-stage decision-making framework that provides six possible scenarios. The subsequent analysis will identify the optimal scenario and the decision-making approach (Table 1).

Table 1.
Input parameters for single-stage decision model under six scenarios. This table lists the defect rates, purchase prices, detection costs, assembly costs, market prices, and replacement losses for spare parts and finished products in six single-stage production scenarios. These inputs are used to evaluate inspection and disassembly strategies.
The following data pertain to the multistage decision-making framework (Table 2).

Table 2.
Input data for multistage decision model: components, semi-finished products, and final assembly. Provides parameter values including defect rates, purchase prices, and process costs for components and semi-finished products used in multistage production simulations.
- 1. Results and analysis of the single-stage decision-making framework.
Substituting the data into the aforementioned model to solve for each group yields the optimal decision results under the six different scenarios as follows:
Table 1 and Table 3 and Figure 3 summarize the optimal decisions under six parameter settings in the single-stage decision framework, revealing that

Table 3.
Optimal decision strategies and performance metrics in single-stage scenarios. Shows the resulting inspection and disassembly decisions, total cost, and expected profit for each of the six single-stage cases based on integer programming.
- Scenarios without inspection and disassembly: Situations 1, 2, 3, and 6 yield low minimum costs; however, they are characterized by considerable profit variability due to market losses.
- Full inspection and disassembly: In Situation 4, stable profit margins are achieved while minimizing market losses through effective control of defective product influx, albeit at a higher cost.
- Balanced approach: Scenario 5, which involves inspecting finished products and disassembling non-conforming units, strikes a favorable balance between cost and profit, thus making it a highly recommended option.
- Impact of purchase volume: Profit differentials remain negligible when purchasing a single set of components, but they become pronounced with larger acquisitions, such as one million components.Compared to static decision trees or rule-based logic, the proposed model consistently delivers superior cost efficiency. For example, using identical parameter settings reduces the total cost by up to 40% and increases the profit by more than 160%. This significant improvement highlights the potential of the model for real-world applications where minimizing operational overhead while maintaining quality is crucial to competitiveness.
- Practical application: The establishment of a company cost budget, along with the inclusion of additional constraints, can enhance the model’s applicability and improve alignment with real-world conditions.
These findings suggest that a more intensive inspection does not necessarily yield better results. Optimal decision making is biased on the interaction between inspection costs, defect rates, and the economic consequences of undetected defects.
- 2. Results and analysis of the multistage decision-making framework.
In the first stage, after comparing costs, the decision results are as follows:
In the second stage, after comparing costs, the decision results are as follows:
The results of the multi-stage decision model, detailed in Table 2, Table 4 and Table 5 and Figure 4, surprisingly suggest the foregoing inspection and disassembly at all stages. This seemingly risky strategy proves to be rational upon closer examination. The model opts to accept a small risk of defective units entering the market due to a low defect rate (10%), coupled with high inspection and disassembly costs. Furthermore, the lower cost of customer compensation for defective products compared to the product’s market value supports this cost-benefit trade-off.

Table 4.
First stage decision outcomes and metrics for multistage framework presents inspection/disassembly decisions, costs, and profits for spare part processing in the first stage of a multistage production path.

Table 5.
Second stage optimization results: from semi-finished to final products. Summarizes decisions regarding finished product inspection and disassembly, along with resulting costs.
Under these assumptions, the model achieves a total cost of 128 and a net profit of 72, outperforming alternative strategies under comparable conditions.
The model’s findings can be summarized as follows: no inspection and no disassembly. Analyzing the defect rates presented in Table 2, along with known parameters, such as purchase price and inspection costs, the rationale for the decision of ’no inspection and no disassembly’ can be outlined.
- Low overall defect rate: The defect rates for spare parts, semi-finished products, and finished products are all 10%. Given the low defect rates across all three production stages, the need for inspection can be deemed unnecessary in most scenarios, allowing for the avoidance of inspection costs.
- High costs of inspection and disassembly of finished products: The purchase price for spare parts is generally high, ranging between 8 and 12 units, along with significant assembly costs. In light of the relatively low defect rates, it is optimal to eliminate the high costs associated with inspection and disassembly.
- Significant discrepancy between market price and replacement loss: The market price of finished products substantially exceeds the replacement loss of non-conforming products by 160 units. Given that the defect rate for finished products is only 10%, non-conformity can be considered a low-probability event, thereby reducing the need for inspection of finished products.
In conclusion, the decision to forgo inspection and disassembly is supported by low defect rates, high inspection costs, and favorable market conditions for finished products.
Having demonstrated how the proposed decision framework responds to different production settings, it is crucial to further validate its robustness and superiority. Therefore, the following section conducts comprehensive evaluations, including Monte Carlo simulations and comparative analysis against baseline models, to assess accuracy, stability, and practical advantages.
4. Model Evaluations
This section includes three key evaluations:
- 1.
- Quality inspection validation: A Monte Carlo simulation is used to verify the accuracy of the sampling process.
- 2.
- Stability analysis of decision making: A stability test is conducted to identify the factors that most significantly impact the results in a simplified environment.
- 3.
- Accuracy assessment of decision outcomes: The decision tree is used to make decisions in the production process. The results obtained from this simulation are compared with those derived from the proposed model to demonstrate its superiority.
Using these evaluations, we aim to ensure the robustness and reliability of the proposed model in optimizing production decisions.
4.1. Evaluation with Monte Carlo Simulation
In the sampling inspection process for spare part defect rates, the effectiveness and reliability of the model are paramount. To validate the precision of our defect rate sampling inspection model at various confidence levels [18], we employ the Monte Carlo simulation method. This approach uses extensive random sampling to effectively assess sample sizes and inspection criteria in real-world production environments.
This paper conducts the following validations:
- 1.
- Rejection rule accuracy: At a confidence level 95%, we assess the accuracy of the rejection rule when the defect rate exceeds the nominal value.
- 2.
- Reliability of the acceptance rule: At a confidence level 90%, we evaluate the reliability of the acceptance rule when the defect rate does not exceed the nominal value.
- 3.
- Detection effectiveness assessment: We analyze the performance of the selected sample size under varying defect rate conditions to ensure the sensitivity and stability of the inspection.
Through these validations, our aim is to confirm the robustness of our sampling inspection model in determining the quality status of spare parts. In the Monte Carlo simulation, we first define the parameters by setting the nominal defect rate and hypothesizing multiple values for the defect rate ranging from 0.11 to 0.20. Next, we determine the sample sizes and corresponding to different confidence levels (95% and 90%) and calculate their specific values using Equation (5).
Subsequently, we compute the critical value k, which represents the threshold for the number of defects, using the cumulative distribution function of the binomial distribution. The expression for the cumulative distribution function is given by the following:
where n is the sample size; p is the defect rate; k is the threshold for the number of defective items.
For each hypothesized defect rate , we perform 10,000 random samples, recording whether the model correctly determines the acceptance or rejection of the components in each sample. We then calculate the proportion of correct judgments in all simulations to evaluate the applicability of the sample size and the testing rules.
With a fixed sample size, we assess whether the actual defect rate exceeds 0.1, taking into account the variability of the actual defect rate. We plot the possible values in the interval , corresponding to the rejection probabilities at a 95% confidence level for defect rates exceeding the nominal value, and the rejection probabilities at a 90% confidence level for defect rates not exceeding the nominal value.
Monte Carlo simulations () evaluated the robustness of the sampling schemes (Figure 9, Figure 10, Figure 11 and Figure 12). For , Figure 9 shows a rejection rate of 40.5% with , increasing to 47.1% in Figure 10 with . Under , the acceptance rates are 41.6% and 99.4% in Figure 11 and Figure 12, respectively, which vary with sample size.
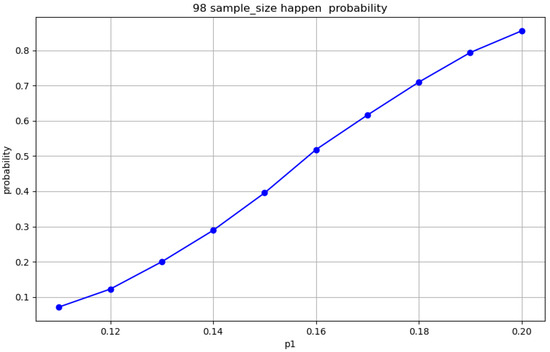
Figure 9.
The Monte Carlo simulation of rejection rate for , at 95% confidence.
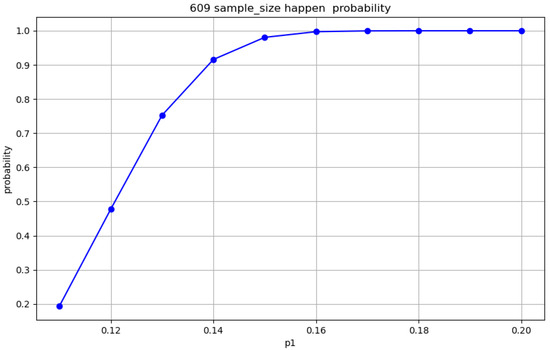
Figure 10.
The Monte Carlo simulation of rejection accuracy at , , 95% confidence.
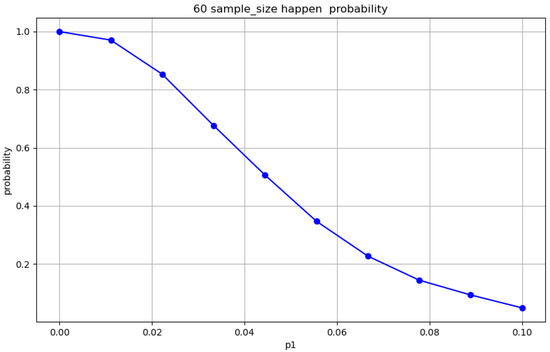
Figure 11.
Acceptance Monte Carlo simulation at , , 90% confidence.
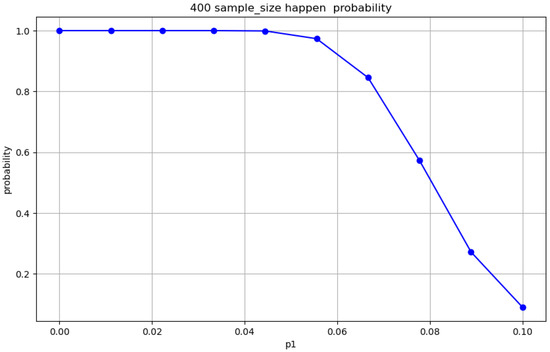
Figure 12.
Acceptance Monte Carlo simulation at , , 90% confidence.
As predicted, the rejection/acceptance rates converged to the target confidence levels with increasing sample size. This consistency between simulation and analytical results validates the sampling strategies. This validation is crucial to ensure the reliability of sampling plans in practical applications, particularly when the true defect rate is unknown.
The Monte Carlo simulation allows for a visual assessment of the model’s performance under varying defect rates. For each defect rate , the simulation results include the following:
- 1.
- Results at 95% confidence level: When the defect rate approaches the nominal value , the execution rate of the rejection rule is relatively low. However, as the defect rate increases, the rejection rate increases significantly. The simulation results indicate that, with the selected sample size , when the defect rate exceeds , the model effectively rejects non-conforming batches, demonstrating a high level of sensitivity and reliability.
- 2.
- Results at 90% confidence level: When the defect rate is close to or below the nominal value , the execution rate of the acceptance rule is high, effectively identifying conforming batches and reducing the risk of erroneous rejection. As the defect rate exceeds , the acceptance rate decreases, further validating the accuracy of the model under different conditions.
- 3.
- Applicability of the sample size: The simulation demonstrates that the selected sample size effectively achieves the desired quality control objectives across various defect rates. For components with low defect rates, the model can accept batches in a timely manner, while under high defect rate conditions, it can effectively reject batches, ensuring the production quality of the enterprise.
4.2. Stability Testing of Integer Programming Model
Through comparative research, we conclude that in simpler environments, the defect rate of the integer programming model is the primary factor that influences decision making. As the complexity of the environment increases, the number of significant influencing factors also increases. In practical applications, the defect rate exhibits variability. In case analysis, we introduced random fluctuations into the sampling model to more accurately reflect the actual defect rate [19], which is mainly analyzed and calculated based on the nominal value. Therefore, our approach to verification is to perform stability testing of the integer programming model by varying the nominal value.
Adjust the nominal value to 20% and recalculate the defective rate of the components (Table 6):

Table 6.
Estimated Defect Rates and Confidence Intervals for Spare Parts . Lists empirical defect rate estimates and corresponding confidence intervals for individual components under increased nominal defect assumptions.
The defective rate of the semi-finished products and finished products (Table 7):

Table 7.
Estimated Defect Rates and Confidence Intervals for Semi-Finished and Finished Products. Provides statistical summaries of quality inspection results at later stages in production under nominal defect rate .
The decision-making situation for the first and second stages is obtained accordingly (Table 8 and Table 9):

Table 8.
First stage decision results under elevated nominal defect rate . Summarizes inspection and disassembly choices, as well as costs, for spare parts in the first stage under revised defect rate assumptions.

Table 9.
Second stage decision outcomes for final assembly under elevated defect rate . Details whether to inspect or disassemble final products, along with associated costs, under updated quality conditions.
In summary, under the complete production path, the total cost of a single finished product entering the market is 124.171972, and the total profit is 75.828028.
Compared to the results of the multistage model, the changes in total cost and total profit are minimal. However, decision-making has undergone significant alterations. After the increase in defect rates, the decision-making model was significantly adjusted, with the results of the trial run indicating no detection and no splitting. However, as the defect rate varied, the detection value increased, leading to the incorporation of part inspections in the final decision, specifically selecting the lowest-cost inspection option. Therefore, this model demonstrates good stability and is capable of maximizing profit based on changing conditions.
4.3. Advantage Assessment
For the single-stage production process, this article uses a decision tree for decision making and compares its results with those obtained from the proposed model.
The results of the decisions of the decision tree [20] are shown in Table 10.

Table 10.
Comparison of decision tree outcomes for single-stage production. Compares final decisions, profits, and costs under a traditional decision tree approach to highlight differences from the proposed model.
Based on the analysis of the decision results, final costs, and profits, it is evident that decision costs range from 50 to 101, and profits are often single-digit or even negative. In contrast, the model proposed in this paper achieves decision costs between 35 and 40, with profits reaching approximately 20.
For the multistage production process, based on the data presented in Table 2, the decision results have been obtained from the decision tree (Table 11, Table 12 and Table 13).

Table 11.
Comparison of decision tree outcomes for single-stage production. Compares final decisions, profits, and costs under a traditional decision tree approach to highlight differences from the proposed model.

Table 12.
Decision tree-based actions for semi-finished product processing. Summarizes inspection and disassembly strategies applied to semi-finished products and associated costs.

Table 13.
Decision tree-based final product processing and performance indicators. Presents outcomes for finished product inspection and disassembly, along with cost and profit results, under a decision tree framework.
The results of the table indicate that the total production cost is 218, with a final profit of −18. In contrast, the total cost obtained from the model presented in this paper is 128, resulting in a final profit of 72. This shows that the total cost of the proposed model is significantly lower than the result obtained from the decision tree, while the profit is considerably higher.
This indicates that the model presented in this paper has significant advantages over traditional decision models.
- 1.
- Broader adaptability: The six scenarios analyzed in this paper demonstrate significant differences in production environments. The results of traditional model decisions exhibit substantial cost fluctuations and noticeable profit variability. In contrast, the results of the decisions of the proposed model indicate a smaller range of cost fluctuations and stable profits. This shows that the proposed model can produce superior decision outcomes in various environments.
- 2.
- Superior decision results: The results obtained from the proposed model show that profits in all six scenarios are significantly higher than those from traditional decision models, thereby demonstrating the model’s effectiveness in enhancing corporate profits.
- 3.
- Proficiency in multi-stage decision-making: Traditional models have proven inadequate in ensuring profitability in multistage decision-making. In contrast, the model presented in this paper is capable of making better decisions in more complex production processes.
In summary, the proposed model not only yields superior profit margins under the same constraints but also maintains cost stability across varied scenarios, a key strength over conventional approaches that exhibit significant variability and inefficiency. The results consistently show that our method offers the following:
- 1.
- Up to 90 fewer units in total cost in multistage settings.
- 2.
- Up to 160% higher profitability in single-stage decisions, based on the comparison between the traditional model and the proposed multi-agent model.
- 3.
- Robust adaptability in the presence of fluctuating defect rates and parameter uncertainties.
To further explore the potential for the application of the model, we conducted a focused case study that simulates realistic conditions [21] in component manufacturing. This allowed us to investigate the effects of fluctuating defect rates in more detail and validate the flexibility of the model to adapt to real world variability.
5. Case Study
This model primarily performs a decision analysis on the manufacturing process of components. In the absence of other detailed contextual information, the defect rate is identified as the most significant factor that influences the outcomes of the decision. However, there may be additional key factors that influence practical applications. This case only considers fluctuations in the actual defect rate, introducing a proxy point for defect rate variability. Therefore, it is necessary to reassess the defect rates of components, semi-finished products, and finished products.
To achieve this, a batch sampling method can be employed, in which samples are taken from each batch of produced components, semi-finished products, or finished products for inspection. Hypothesis testing can then be applied to confirm whether these defect rates meet expectations. Finally, the results will be incorporated into a multistage model to derive the final results of the decision.
5.1. Sample Inspection to Assess Defect Rate
Let the nominal value of the defect rate be , and let the parameter be estimated by the actual defect rate . In the sampling inspection, the sample size for each sampling is set as n, and the number of defective items is denoted as X.
Assuming that the inspection result X follows a binomial distribution, it can be expressed as follows:
The point estimate of the actual defect rate can be calculated from the number of defects detected X using the formula
This is the maximum likelihood estimate of the defect rate used to represent the proportion of defects in the sample.
To assess the acceptability of the actual calculated defect rate , a hypothesis test is performed. The following hypotheses are established:
- Null hypothesis: (the defect rate does not exceed the nominal value);
- Alternative hypothesis: (the defect rate exceeds the nominal value).
This study evaluates whether the company should accept or reject products at confidence levels of 95% and 90%.
When using the normal approximation method for testing, the estimated defect rate can be approximated as a normal distribution due to the large sample size. This allows us to apply the properties of the normal distribution for hypothesis testing, simplifying calculations and enhancing the efficiency of the test:
The test statistic is the following:
Given a significance level and the corresponding critical value for a two-sided test, the following rules can be applied to decide whether to reject the null hypothesis :
- If , reject and conclude that the defect rate exceeds the nominal value.
- If , do not reject and conclude that the defect rate does not exceed the nominal value.
From the above steps, we obtain the following:
where is the critical value of the standard normal distribution corresponding to the confidence level.
Through the above steps, we calculated the estimated defect rates for different components, semi-finished products, and finished products at each stage, applying these estimates to both single-segment and multistage production decisions. Based on the newly estimated defect rates, we reevaluated, using the aforementioned integer programming model, whether to inspect components or finished products and under what circumstances to dismantle defective products, to optimize the overall production costs.
Considering that defect rates can vary in real-life scenarios under the same parameter conditions, this paper employs the following two methods for differentiation.
- 1.
- Introducing random errors: We introduce random errors during the calculations to simulate random fluctuations in the production process. Specifically, we assume that the error terms follow a normal distribution with a mean of 0 and a standard deviation of 0.01. This approach reflects the fluctuations in defect rates caused by uncontrollable factors in production.
- 2.
- Manual setting of variations in : Within the acceptable parameter range, the sample size typically remains unchanged; therefore, we manually adjust the initial defect rate to take any value among 10%, 8%, and 6%. This error simulates systematic deviations caused by insufficient stability in production equipment or processes.
5.2. Results and Analyses
This paper uses a method that introduces random errors and manually adjusts the parameter to differentiate the defect rates of various products (including different components and semi-finished products) within the same stage. This approach more accurately reflects the variations in defect rates present in real production environments. Under the same theoretical conditions, the resulting defect rates for components, semi-finished products, and finished products exhibit significant variability, thereby enhancing the robustness and accuracy of the model in practical applications.
5.2.1. Result of Sample Inspection
The table above shows that, at the confidence level 95%, the actual detected defect rate is 0.115604 when the sample size is 1,000,000, ensuring that the defect rate does not exceed .
Figure 13 and Figure 14 compare the behavior of the estimated defect rate under different conditions, examining how the sample size and estimation noise influence the accuracy and stability of the parameter estimate.
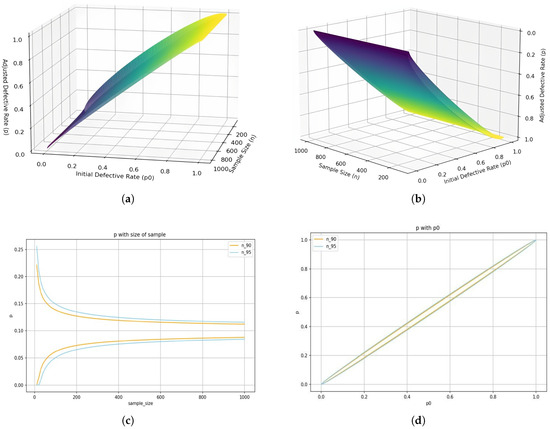
Figure 13.
Surface plots illustrating the impact of nominal defect rate and sample size on estimated defect probability under different settings: (a,b) Surface plot of as a function of and . (c,d) Surface plot of as a function of .
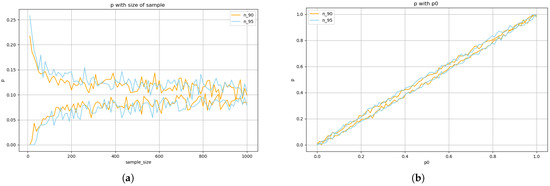
Figure 14.
Graphical representation of how the average estimated defect rate varies with sample size and initial value , with random fluctuations added: (a) Plot of versus the average sample size considering random errors. (b) Plot of versus the initial probability considering random errors.
Figure 13 illustrates that, ideally, noise-free estimates converge to the true defect rate as the average sample size increases. A small leads to a high variability in estimates due to statistical uncertainty. Increasing significantly reduces the variance of , enhancing precision. However, this improvement diminishes with larger , indicating a saturation point where further increases offer marginal gains.
Figure 14 simulates realistic measurement conditions by introducing normally distributed random error. The results show that the minor estimation error () has a minimal impact on the accuracy of the estimation, especially when the nominal parameter closely reflects the actual defect rate. However, misalignment between and the true quality of the process, arising from outdated assumptions or uncalibrated priors, can amplify the effects of sampling variability and estimation error, leading to inaccurate quality assessments and suboptimal decisions. This highlights the critical need for accurate baseline process characterization in practical applications.
The new defect rate estimates may require the rejection of inspections or the disassembly of non-conforming products in certain cases to reduce overall costs and increase profits. In complex decision-making involving multiple processes, the new defect rates add complexity, but optimization models yield more refined optimal path selections.
5.2.2. Result of Multistage Model
In summary, the total cost of a single finished product entering the market along the entire production path is 128.0, with a total profit of 72.0.
The results of the case study confirm that the proposed decision model maintains optimality even under varying quality conditions. In the next and final section, we summarize the key findings, highlight the contributions of the model, and outline future directions to extend its practical applicability (Table 14, Table 15, Table 16 and Table 17).

Table 14.
Estimated defect rates of eight components from batch sampling . Lists point estimates of defect rates for all components used in the case study based on empirical inspection.

Table 15.
Estimated Defect Rates for Semi-Finished and Finished Products in Case Study. Reports updated defect rate estimates for higher-level products based on batch inspection under nominal quality thresholds.

Table 16.
Decision results for Stage 1 component processing based on sampled defect Rates. Indicates optimized inspection and disassembly decisions and related costs for each component set in the first process stage.

Table 17.
Optimized Stage 2 decisions for semi-finished to final product conversion. Shows whether inspection and disassembly are selected for finished products, and total cost incurred during final assembly.
6. Conclusions
This study investigates a fundamental production process using the core of a multi-agent integer programming model, without considering external influencing factors (i.e., agent points). In practical applications, other models can be integrated to assess the impact of external factors on decision-making, ultimately forming a comprehensive multi-agent integer programming model, where each agent operates independently and converges into the main decision model, enhancing the model’s completeness and the clarity of decisions. To address decision-making issues in the production process, this paper considers the defect rates of products at each stage, employing a multi-agent integer programming model for final decisions. This model incorporates a sampling inspection model and introduces random fluctuations in defect rates, making the defect rates at various stages more representative of actual conditions, thus refining resource allocation and ensuring product quality. From this perspective, sampling inspection and hypothesis testing jointly complete the quality assessment process, supported by Monte Carlo simulation to ensure the accuracy of sample sizes, allowing for defect rate estimation at minimal sampling costs. The proposed multi-agent integer programming model effectively addresses most decision problems involving discrete decision variables. There remains a potential for optimization, such as using ant colony algorithms to explore the solution space and find approximate optimal solutions for integer programming problems to ensure solution accuracy. However, in practical environments, an excessive number of agent points may lead to high time complexity, necessitating further research to identify methods for complexity simplification. Thus, while the model has limitations in certain extreme conditions, it can still effectively resolve the majority of decision-making issues in production processes. Overall, the proposed model stands out as a cost-effective and scalable decision-making solution for modern manufacturing systems. Through a combination of intelligent sampling design and multi-agent optimization, it consistently outperforms traditional strategies in both single- and multi-stage scenarios [22]. Comparative analyses strongly validate their role in achieving substantial cost savings without compromising quality, positioning them as a valuable tool for enterprises seeking to optimize operational efficiency under uncertainty.
Author Contributions
Conceptualization, S.W. and Y.L.; methodology, S.W. and Y.L.; software, J.W.; validation, S.W., Y.L. and J.W.; formal analysis, S.W.; investigation, Y.L.; resources, S.W.; data curation, J.W.; writing—original draft preparation, S.W.; writing—review and editing, S.W.; visualization, J.W.; supervision, S.W. and Y.L.; project administration, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nagy, M.; Figura, M.; Valaskova, K.; Lăzăroiu, G. Predictive maintenance algorithms, artificial intelligence digital twin technologies, and internet of robotic things in big data-driven Industry 4.0 manufacturing systems. Mathematics 2025, 13, 981. [Google Scholar] [CrossRef]
- Lee, H.-H.; Chen, C.-H.; Kao, L.-Y.; Wu, W.-T.; Liu, C.-H. New perspectives on the causes of stagnation and decline in the sharing economy: Application of the hybrid multi-attribute decision-making method. Mathematics 2025, 13, 1051. [Google Scholar] [CrossRef]
- Urosevic, K.; Gligoric, Z.; Jankovic, I.; Gluscevic, B.; Beljic, C. Simulation of MCDM process—Stope and fan pattern selection in an underground mine with uncertainty. Mathematics 2025, 13, 786. [Google Scholar] [CrossRef]
- Eddy, S.R. What is dynamic programming? Nat. Biotechnol. 2004, 22, 909–910. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- De Ville, B. Decision trees. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 448–455. [Google Scholar] [CrossRef]
- Kingsford, C.; Salzberg, S.L. What are decision trees? Nat. Biotechnol. 2008, 26, 1011–1013. [Google Scholar] [CrossRef] [PubMed]
- Rokach, L.; Maimon, O. Decision trees. In Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, L.; Zhao, J.; Wang, W. A mixed integer programming optimization method based on multi-agent model. Control Decis. 2019, 34, 362–368. [Google Scholar] [CrossRef]
- Caridi, M.; Sianesi, A. Multi-agent systems in production planning and control: An application to the scheduling of mixed-model assembly lines. Int. J. Prod. Econ. 2000, 68, 29–42. [Google Scholar] [CrossRef]
- Jing, Y.; Liang, B.; Li, S.; Liu, F.; Zhao, W.; Liu, P. A multi-agent learning framework for mixed-integer linear programming. INFOR 2024, 62, 588–598. [Google Scholar] [CrossRef]
- Casanova, G.; Pralet, C.; Lesire, C.; Vidal, T. Solving dynamic controllability problem of multi-agent plans with uncertainty using mixed integer linear programming. In Proceedings of the 22nd European Conference on Artificial Intelligence (ECAI 2016), The Hague, The Netherlands, 29 August–2 September 2016; pp. 930–938. [Google Scholar] [CrossRef]
- Hu, H.; Bui, M.; Chen, M. Multi-agent reach-avoid games: Two attackers versus one defender and mixed integer programming. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, 13–15 December 2023; IEEE: New York, NY, USA, 2023; pp. 7227–7233. [Google Scholar] [CrossRef]
- Pendharkar, P.C. Game theoretical applications for multi-agent systems. Expert Syst. Appl. 2012, 39, 273–279. [Google Scholar] [CrossRef]
- Beale, E.M.L. Branch and bound methods for mathematical programming systems. Ann. Discret. Math. 1979, 5, 201–219. [Google Scholar] [CrossRef]
- Boyd, S.; Mattingley, J. Branch and Bound Methods; Notes for EE364b; Stanford University: Stanford, CA, USA, 2006; p. 7. Available online: https://stanford.edu/class/ee364b/lectures/bb_notes.pdf (accessed on 26 May 2025).
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, MA, USA, 1997; Available online: https://dl.acm.org/doi/book/10.5555/548834 (accessed on 26 May 2025).
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Mateo, CA, USA, 1993. [Google Scholar] [CrossRef]
- Floudas, C.A. Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications; Oxford University Press: Oxford, UK, 1995; Available online: https://global.oup.com/academic/product/nonlinear-and-mixed-integer-optimization-9780195100563 (accessed on 26 May 2025).
- Shen, W.; Hao, Q.; Yoon, H.-J.; Norrie, D.H. Applications of agent-based systems in intelligent manufacturing. Expert Syst. Appl. 2006, 31, 735–745. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).