3. The Power of the n-Cycle
As a special case, now we consider for and obtain the exact values of as follows. For convenience, without loss of generality, we may assume that for a c-partition of a graph G. By Proposition 5, as we have the following result.
Corollary 2. Let be a c-partition of and , where . For a set with vertices, if , then can form a coalition with at most one singleton set in π; if , then can form a coalition with at most singleton sets in π.
Proof. It is easy to see that, for , and . Suppose that is a positive integer. By Proposition 1, we have for . By Proposition 2, we have for . By Proposition 4, we have for or . By Proposition 3, we have for . By Corollary 1, we have for . In the following, we only need to show that for , for , and .
Claim A. for .
Proof of Claim A. By Lemma 2, for any . Now we show that for by contradiction. Now we consider the following four cases.
Case 1. .
Suppose that and is a c-partition of . Then we just need to consider the case: and . By Corollary 2, can form a coalition with each of, at most, 3 singleton sets in . Then, in , there are at least eight singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction. Therefore, we have .
Suppose that and is a c-partition of . Then, we need to consider the two cases as follows.
Subcase 1.1. and .
By Lemma 1, can form a coalition with each of, at most, five singleton sets in . Then, in , there are at least five singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 1.2. and .
By Corollary 2, (, resp.) can form a coalition with each of, at most, three singleton sets in . Then, in , there are at least three singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Combining Subcases 1.1 and 1.2, we have .
Case 2. .
Suppose that , and is a c-partition of . Then, we need to consider the two cases as follows.
Subcase 2.1. and .
The proof is similar to the proof of Subcase 1.1.
Subcase 2.2. , and .
The proof is similar to the proof of Subcase 1.2.
Combining Subcases 2.1 and 2.2, we have .
Suppose that , and is a c-partition of . Then, we need to consider the three cases as follows.
Subcase 2.3. , and .
The proof is similar to the proof of Subcase 1.1.
Subcase 2.4. , and .
By Lemma 1, can form a coalition with each of, at most, five singleton sets in . By Corollary 2, can form a coalition with each of, at most, two singleton sets in . Then, in , there are at least two singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 2.5. , and .
The proof is similar to the proof of Subcase 1.2.
Combining Subcases 2.3–2.5, we have .
Case 3. .
Suppose that , and is a c-partition of . Then, we need to consider the three cases as follows.
Subcase 3.1. , and .
The proof is similar to the proof of Subcase 1.1.
Subcase 3.2. , and .
The proof is similar to the proof of Subcase 2.4.
Subcase 3.3. , and .
The proof is similar to the proof of Subcase 1.2.
Combining Subcases 3.1–3.3, we have .
Suppose that , and is a c-partition of . Then, we need to consider the five cases as follows.
Subcase 3.4. , and .
The proof is similar to the proof of Subcase 1.1.
Subcase 3.5. , and .
The proof is similar to the proof of Subcase 2.4.
Subcase 3.6. , and .
If and form a coalition, then by Lemma 1, (, resp.) can form a coalition with each of, at most, four singleton sets in . Therefore, in , there exist at least one singleton set which cannot form a coalition with any other set in , which is a contradiction.
If and do not form a coalition, then there exists a vertex . Thus, each set in forms a coalition with or must dominate . Since , then the number of the sets in that each can form a coalition with or is, at most, five, and there are at least five singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 3.7. , and .
The proof is similar to the proof of Subcase 2.4.
Subcase 3.8. , and .
The proof is similar to the proof of Subcase 1.2.
Combining Subcases 3.4–3.8, we have .
Case 4. .
Suppose that , and is a c-partition of . Then, we need to consider the five cases as follows.
Subcase 4.1. , and .
The proof is similar to the proof of Subcase 1.1.
Subcase 4.2. , and .
By Lemma 1, can form a coalition, with each of, at most, five singleton sets in . cannot form a coalition with any singleton set in . Then, in , there are, at least, five singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 4.3. , and .
The proof is similar to the proof of Subcase 3.6.
Subcase 4.4. , and .
The proof is similar to the proof of Subcase 4.2.
Subcase 4.5. , and .
It is not difficult to see that, in this case, each singleton set in cannot form a coalition with any other set in , a contradiction.
Combining Subcases 4.1–4.5, we have .
Suppose that , and is a c-partition of . Then, we need to consider the seven cases as follows.
Subcase 4.6. , and .
The proof is similar to the proof of Subcase 1.1.
Subcase 4.7. , and .
The proof is similar to the proof of Subcase 4.2.
Subcase 4.8. , and .
The proof is similar to the proof of Subcase 3.6.
Subcase 4.9. , and .
The proof is similar to the proof of Subcase 4.2.
Subcase 4.10. , and .
If and form a coalition, then by Lemma 1, (, resp.) can form a coalition with each of, at most, four sets in . Then, in , there exists at least one set that cannot form a coalition with any other set in , which is a contradiction.
If and do not form a coalition, then there exists a vertex . Then, each set in forming a coalition with or must dominate . Since , the number of sets in —each of which can form a coalition with or —is at most five, and at least three singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 4.11. , and .
The proof is similar to the proof of Subcase 4.2.
Subcase 4.12. , and .
The proof is similar to the proof of Subcase 4.5.
Combining Subcases 4.6–4.12, we have .
Combining Cases 1–4, we have for .
The proof of Claim A is complete. □
Claim B. for .
Proof of Claim B. We consider the two cases as follows.
Case 1. .
Suppose that , and is a c-partition of . Then, we need to consider the seven subcases as follows.
Subcase 1.1. , and .
The proof is similar to the proof of Subcase 1.1 in Claim A.
Subcase 1.2. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 1.3. , and .
The proof is similar to the proof of Subcase 2.4 in Claim A.
Subcase 1.4. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 1.5. , and .
By Corollary 2, (, resp.) can form a coalition with each of, at most, four singleton sets in . cannot form a coalition with any singleton set in . Then, in , there is, at least, one singleton set which cannot form a coalition with any other set in , which is a contradiction.
Subcase 1.6. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Subcase 1.7. , and .
The proof is similar to the proof of Subcase 4.5 in Claim A.
Combining Subcases 1.1–1.7, we have .
Case 2. .
Suppose that , and is a c-partition of . Then, we need to consider the 22 subcases as follows.
Subcase 2.1. , and .
The proof is similar to the proof of Subcase 1.1 in Claim A.
Subcase 2.2. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 2.3. , and .
The proof is similar to the proof of Subcase 2.4 in Claim A.
Subcase 2.4. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 2.5. and .
The proof is similar to the proof of Subcase 3.6 in Claim A.
Subcase 2.6. , and .
By Lemma 1, can form a coalition with each of, at most, five singleton sets in . By Corollary 2, can form a coalition with, at most, one singleton set in . Since cannot form a coalition with any singleton set in . Then, in , there are, at least, three singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 2.7. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 2.8. , and .
The proof is similar to the proof of Subcase 3.6 in Claim A.
Subcase 2.9. , and .
The proof is similar to the proof of Subcase 4.10 in Claim A.
Subcase 2.10. , and .
The proof is similar to the proof of Subcase 2.4 in Claim A.
Subcase 2.11. , and .
The proof is similar to the proof of Subcase 2.6 in Claim B.
Subcase 2.12. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 2.13. , and .
If any two of the three sets , and can form a coalition; then, by Lemma 1, (, resp.) in can form a coalition with each of, at most, three singleton sets in . By Corollary 2, can form a coalition with, at most, one singleton set in . Then, in , there are at least two singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
If and form a coalition, and (or and ) do not form a coalition. Then, there exists a vertex . Thus, each set in forming a coalition with or must dominate . Since , the number of sets in —each of which can form a coalition with or —is at most five. Since and form a coalition, then . Then, the number of singleton sets in that each of them can form a coalition with or is, at most, four. By Lemma 1, can form a coalition with each of, at most, four singleton sets in . Then, in , there exists, at least, one set which cannot form a coalition with any other set in , which is a contradiction.
If and do not form a coalition, then there exists a vertex . Then, each set in forming a coalition with or must dominate . Since . By Corollary 2, can form a coalition with, at most, one singleton set in . Then, in , there are at least three singleton sets in which each of them cannot form a coalition with any other set in , a contradiction.
Subcase 2.14. , and .
If and form a coalition, and there exist and , such that and form a coalition. Without loss of generality, we may assume that and form a coalition. Then, by Lemma 1, can form a coalition with each of, at most, three singleton sets in , and can form a coalition with each of, at most, four singleton sets in . Since (, resp.) cannot form a coalition with any singleton set in . Then, in , there exists at least one set which cannot form a coalition with any other set in , which is a contradiction.
If and form a coalition, and for each and , and cannot form a coalition. Since (, resp.) cannot form a coalition with any singleton set in , then and must form a coalition. Note that and do not form a coalition. Then there exists a vertex . Thus, each set in forming a coalition with or must dominate . Since , the number of sets in , each of which can form a coalition with or , is at most five. Since and form a coalition, then . Since and form a coalition, then . Then, the number of singleton sets in that each can form a coalition with or is, at most, three. By Lemma 1, can form a coalition with each of, at most, four singleton sets in . Then, in , there exists at least one set which cannot form a coalition with any other set in , which is a contradiction.
If and do not form a coalition, then there exists a vertex . Then, each set in forming a coalition with or must dominate . Since , the number of singleton sets in that each of them can form a coalition with or is, at most, five, and at least three singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Subcase 2.15. , and .
The proof is similar to the proof of Subcase 2.6 in Claim B.
Subcase 2.16. , and .
The proof is similar to the proof of Subcase 2.6 in Claim B.
Subcase 2.17. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Subcase 2.18. , and .
The proof is similar to the proof of Subcase 1.2 in Claim A.
Subcase 2.19. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Subcase 2.20. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Subcase 2.21. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Subcase 2.22. , and .
The proof is similar to the proof of Subcase 4.5 in Claim A.
Combining Subcases 2.1–2.22, we have .
Combining Cases 1–2, we have for .
The proof of Claim B is complete. □
Claim C. .
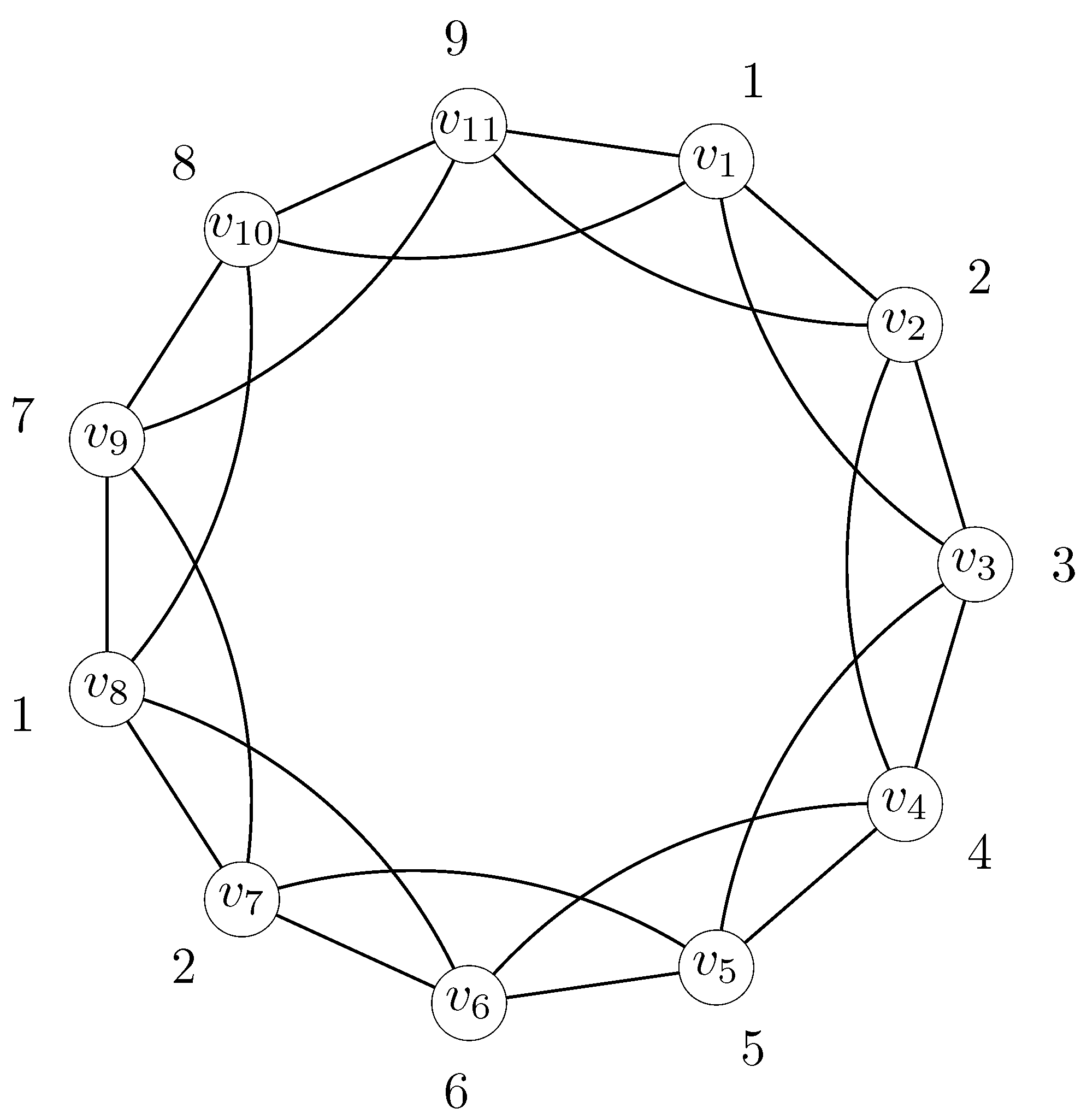
Proof of Claim C. Let , in which , , , , , , , , , , . It is easy to check that can form a coalition with , , and ; can form a coalition with , , and ; and can form a coalition with and . Now we have .
Now we show that by contradiction. Suppose that , and is a c-partition of . Then, we need to consider the 15 cases as follows.
Case 1. , and .
The proof is similar to the proof of Subcase 1.1 in Claim A.
Case 2. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Case 3. , and .
The proof is similar to the proof of Subcase 2.4 in Claim A.
Case 4. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Case 5. , and .
The proof is similar to the proof of Subcase 3.6 in Claim A.
Case 6. , and .
The proof is similar to the proof of Subcase 2.6 in Claim B.
Case 7. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Case 8. , and .
The proof is similar to the proof of Subcase 4.10 in Claim A.
Case 9. , and .
If and form a coalition, then by Lemma 1, can form a coalition with each of, at most, four singleton sets in . By Corollary 2, (, resp.) can form a coalition with each of, at most, two singleton sets in . Then, in , there exists at least one set which cannot form a coalition with any other set in , which is a contradiction.
If and do not form a coalition, then there exists a vertex . So each set in forming a coalition with or must dominate . Since . By Corollary 2, can form a coalition with, at most, two singleton sets in . Then, in , there are at least two singleton sets in which each of them cannot form a coalition with any other set in , which is a contradiction.
Case 10. , and .
The proof is similar to the proof of Subcase 2.6 in Claim B.
Case 11. , and .
The proof is similar to the proof of Subcase 4.2 in Claim A.
Case 12. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Case 13. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Case 14. , and .
The proof is similar to the proof of Subcase 1.5 in Claim B.
Case 15. , and .
The proof is similar to the proof of Subcase 4.5 in Claim A.
Combining Cases 1–15, we have .
The proof of Claim C is complete. □
Combining Claims A, B, and C, the proof of the main result is complete. □