A Two-Step Sequential Hyper-Reduction Method for Efficient Concurrent Nonlinear FE2 Analyses
Abstract
1. Introduction
2. Mathematical Formulation
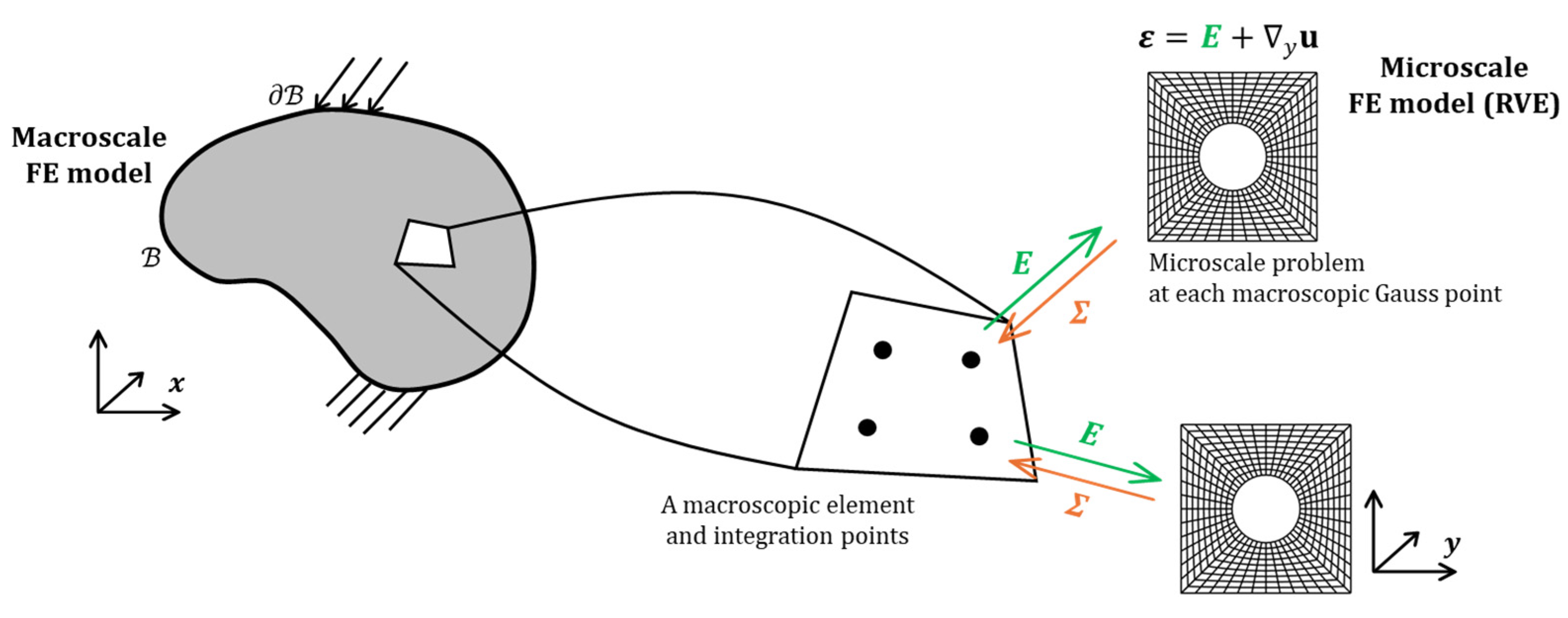
2.1. Brief Review of Nonlinear Multiscale Finite Element Method (FE2 Method)
2.2. Proper Orthogonal Decomposition-Based Discrete Empirical Interpolation Method (POD-DEIM)
| Algorithm 1. Sampling point selection of the DEIM [35] |
|
2.3. A Two-Step, Sequential Hyper-Reduction Method for Nonlinear FE2 Analysis
| Algorithm 2. Microscopic problem applying the DEIM based on displacement control |
|
| Algorithm 3. Macroscopic problem applying the DEIM |
|
3. Numerical Examples
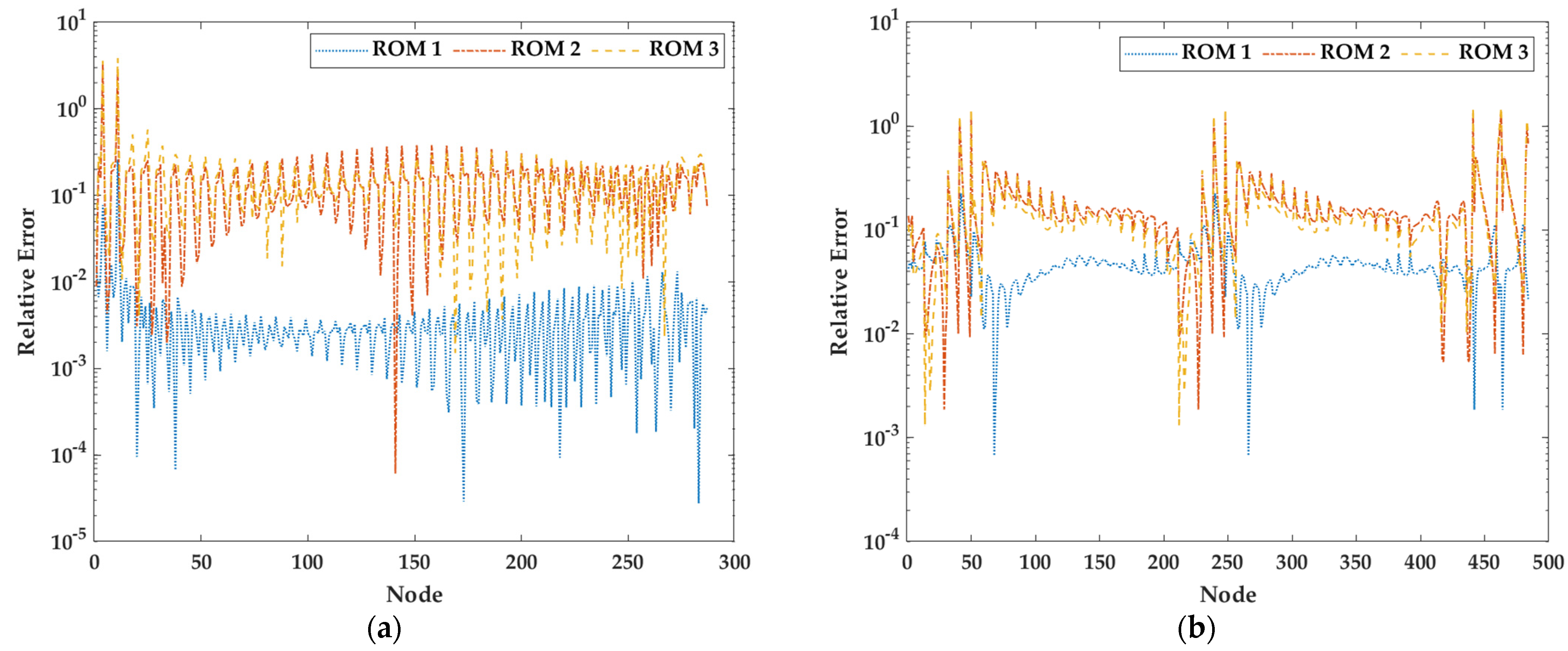
- ROM 1: ROM of Algorithm 2 applied in the microscopic domain;
- ROM 2: ROM of Algorithm 3 applied in the macroscopic domain;
- ROM 3: combination of ROM 1 and ROM 2 (proposed).
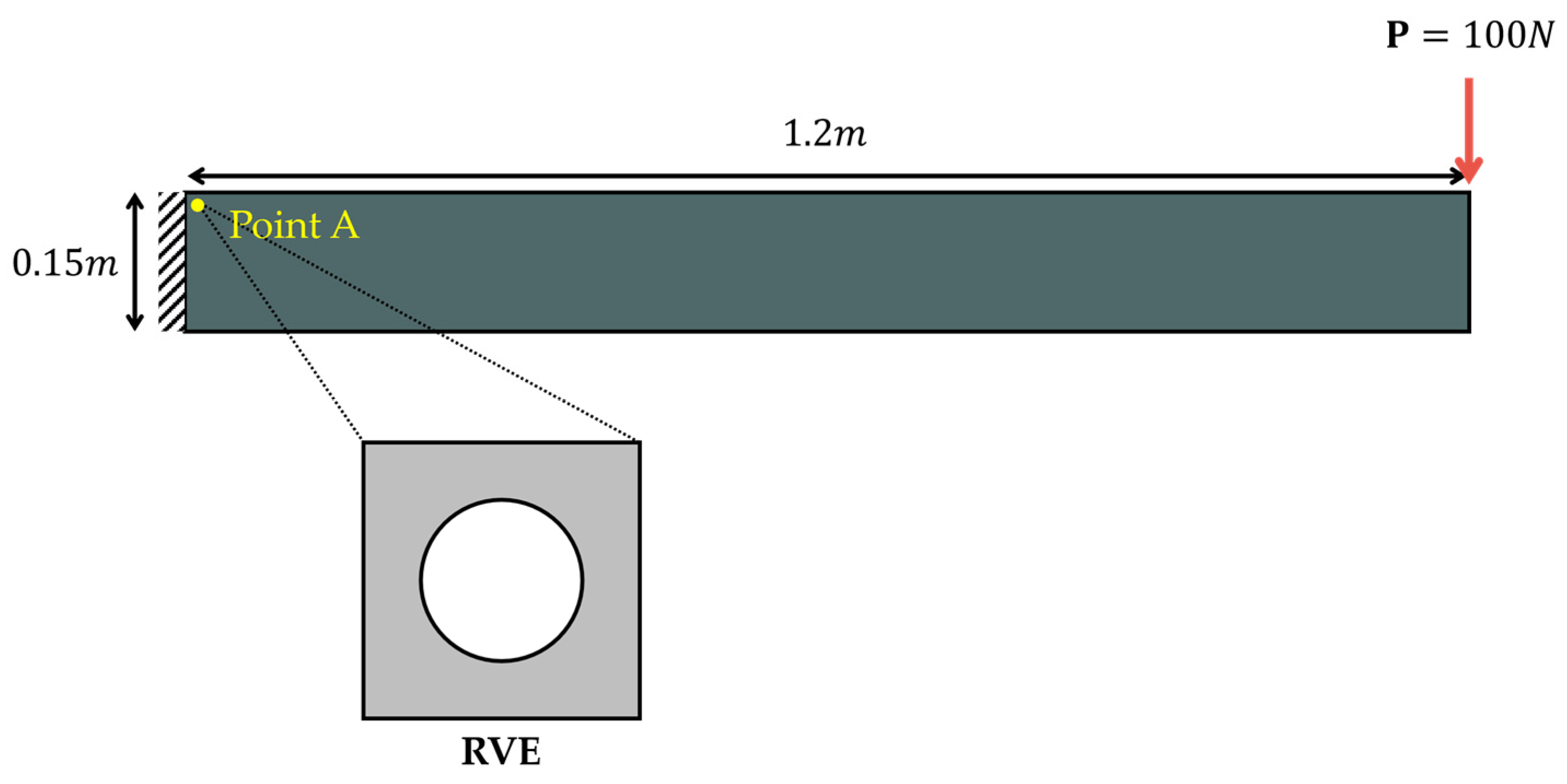
3.1. Example 1: Beam Model
3.1.1. Construction of a Microscopic ROM (ROM1)
3.1.2. Construction of a Macroscopic ROM (ROM 2)
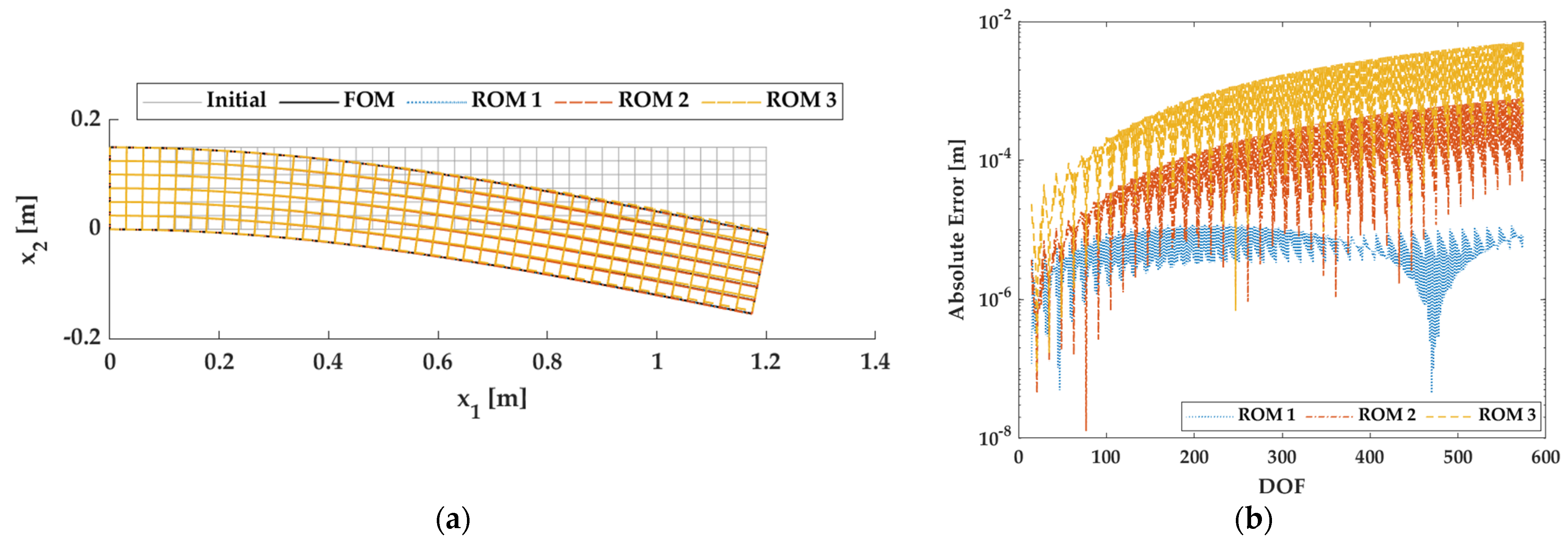
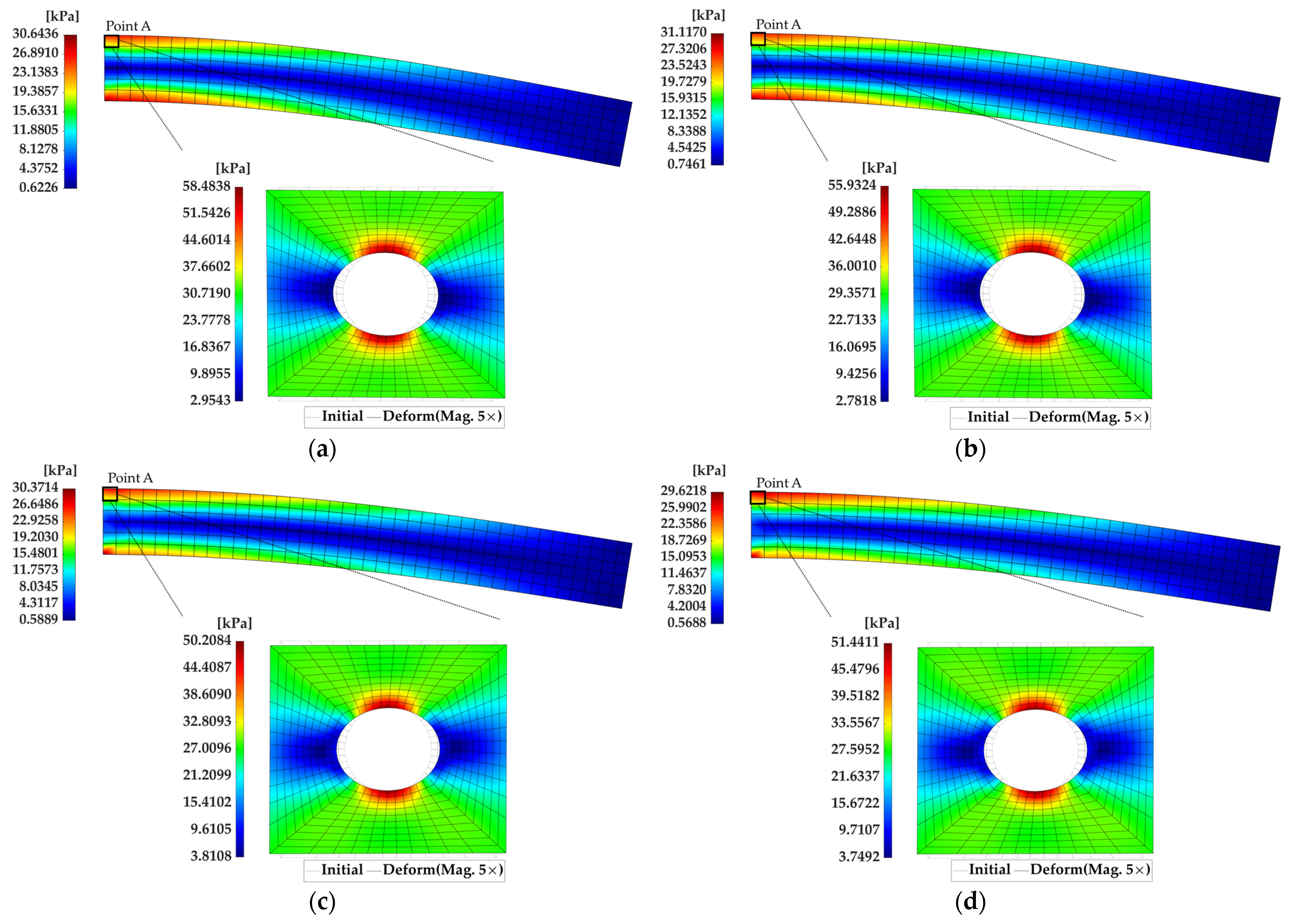
3.1.3. Results of FE2 Analysis Using ROMs
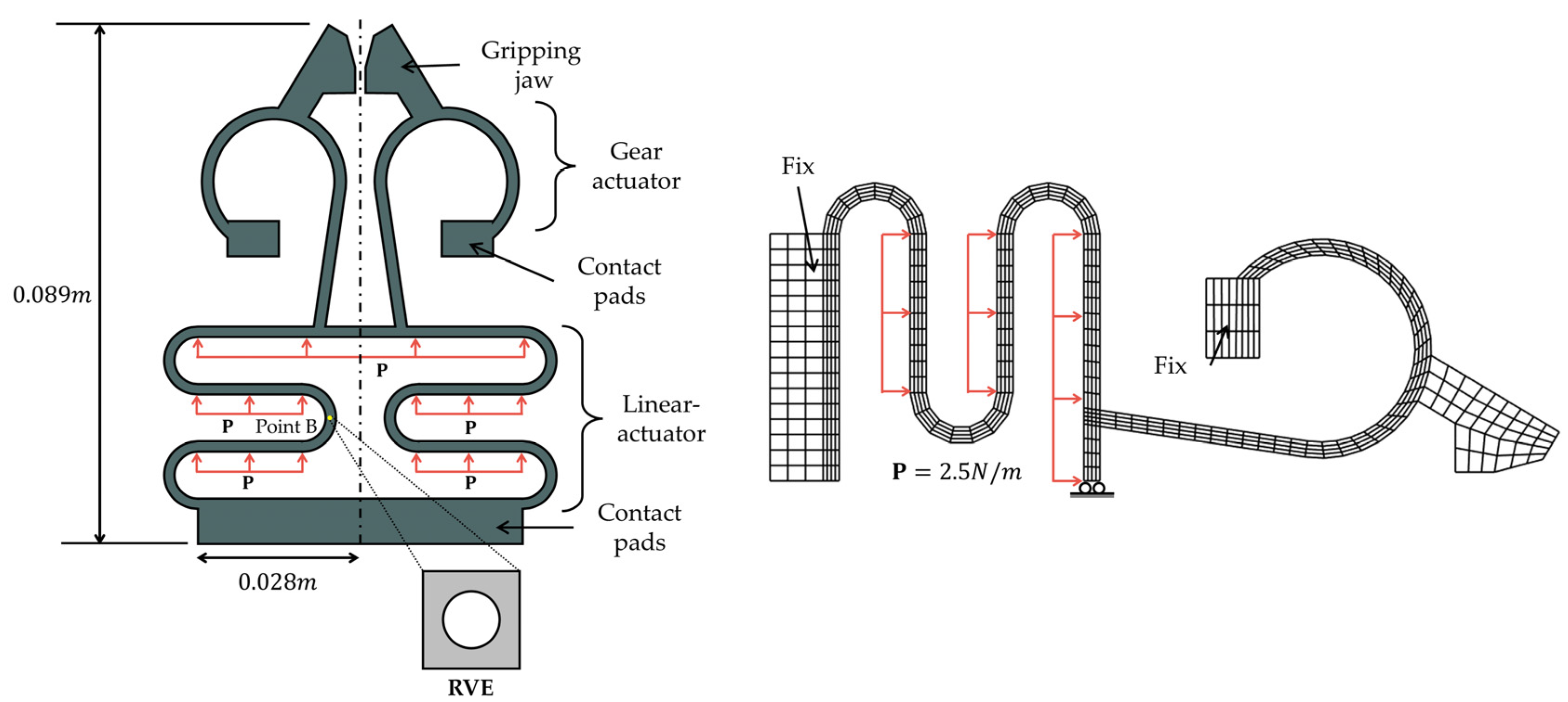
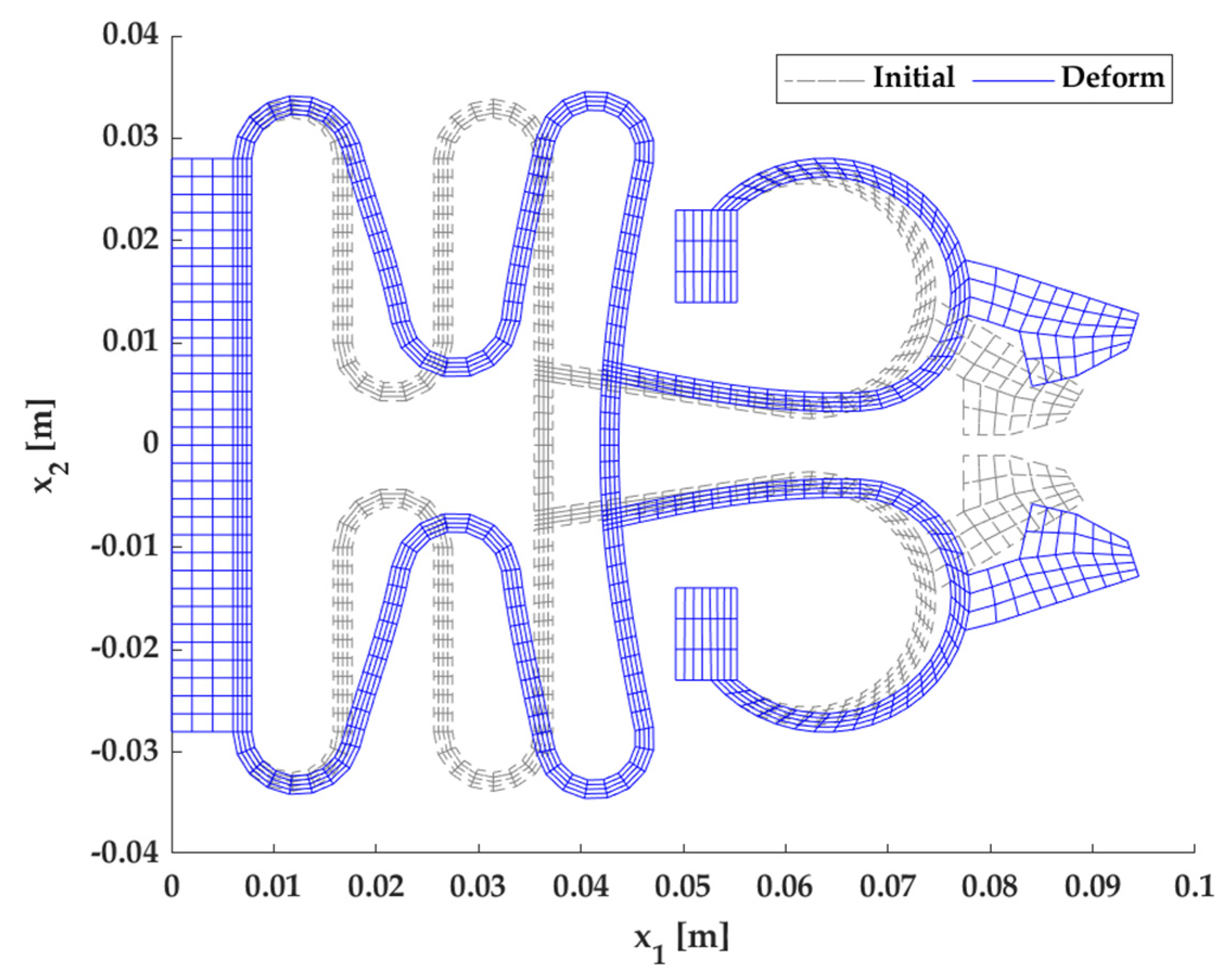
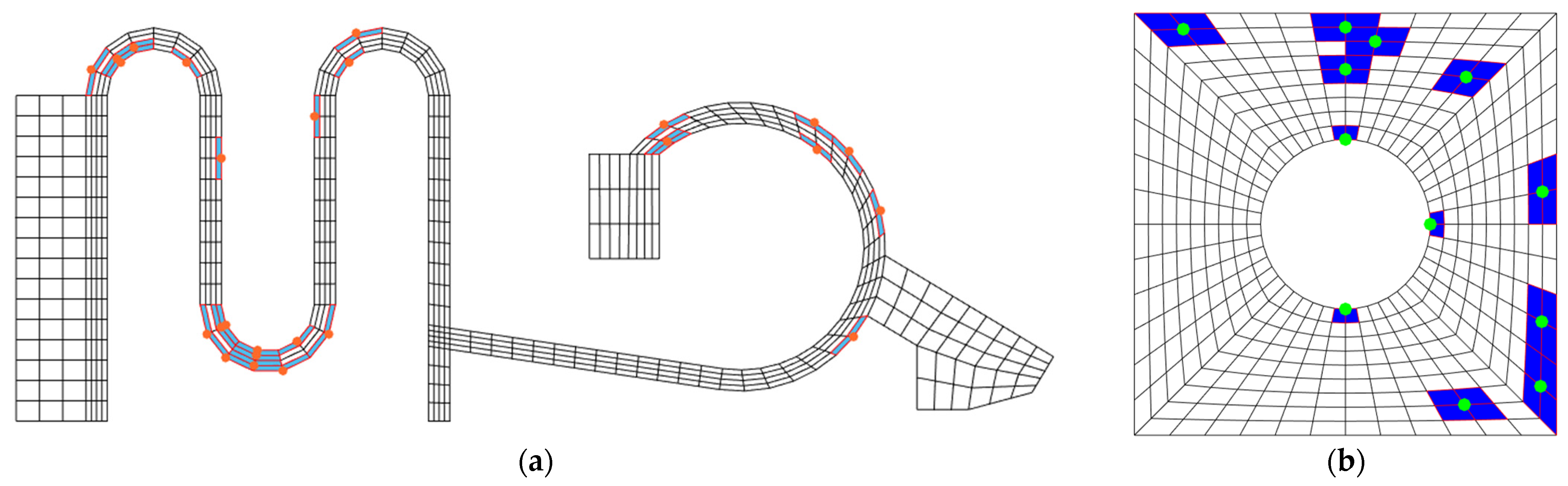
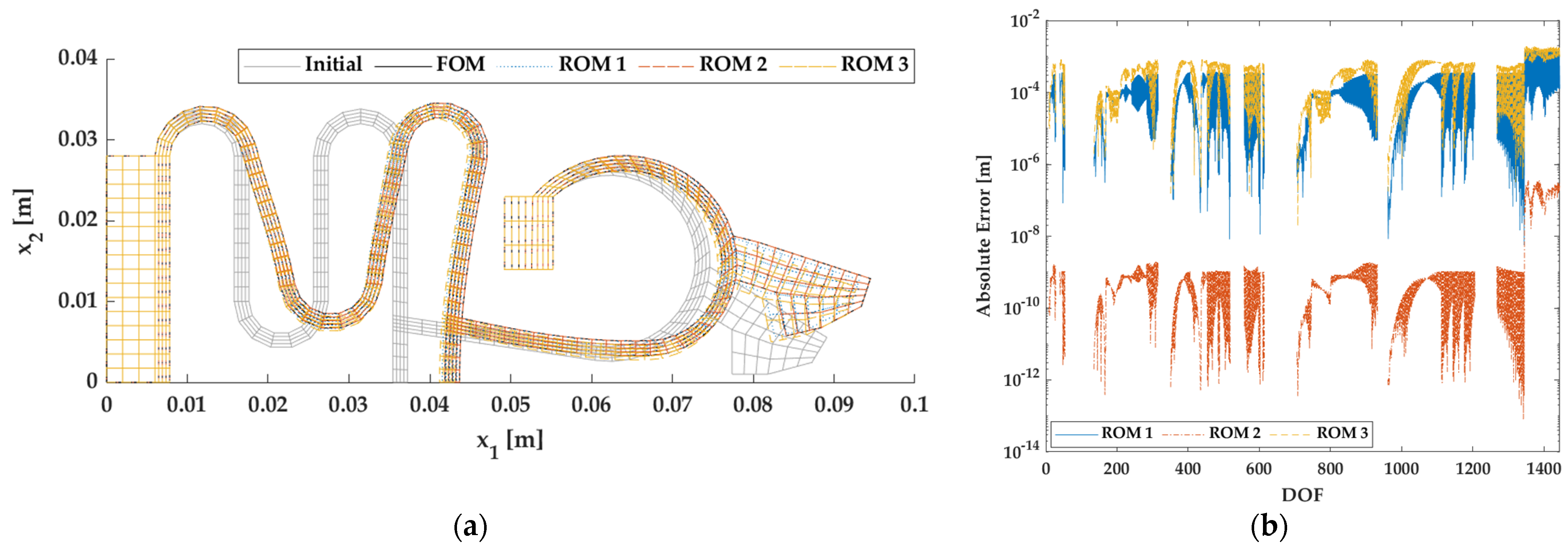
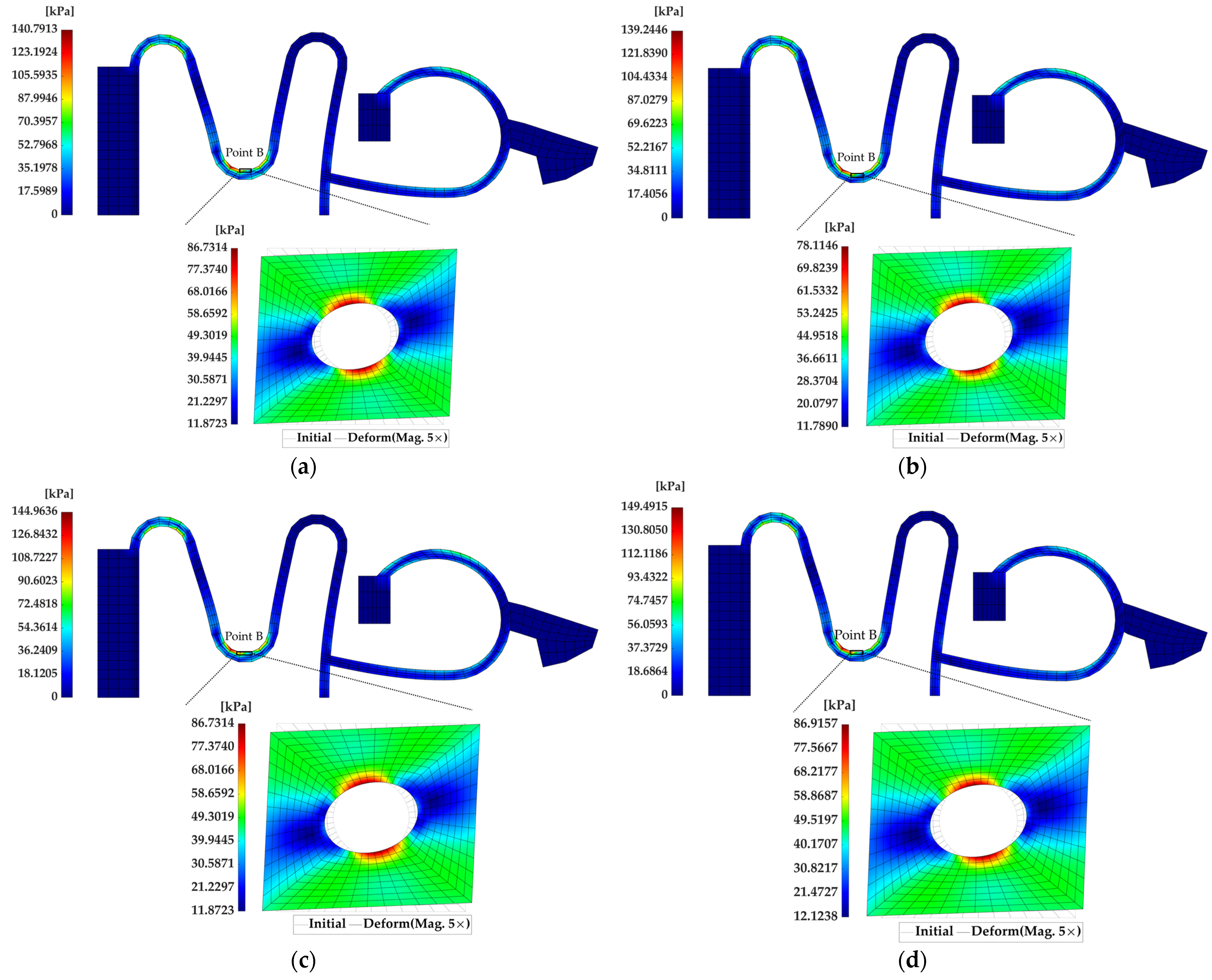
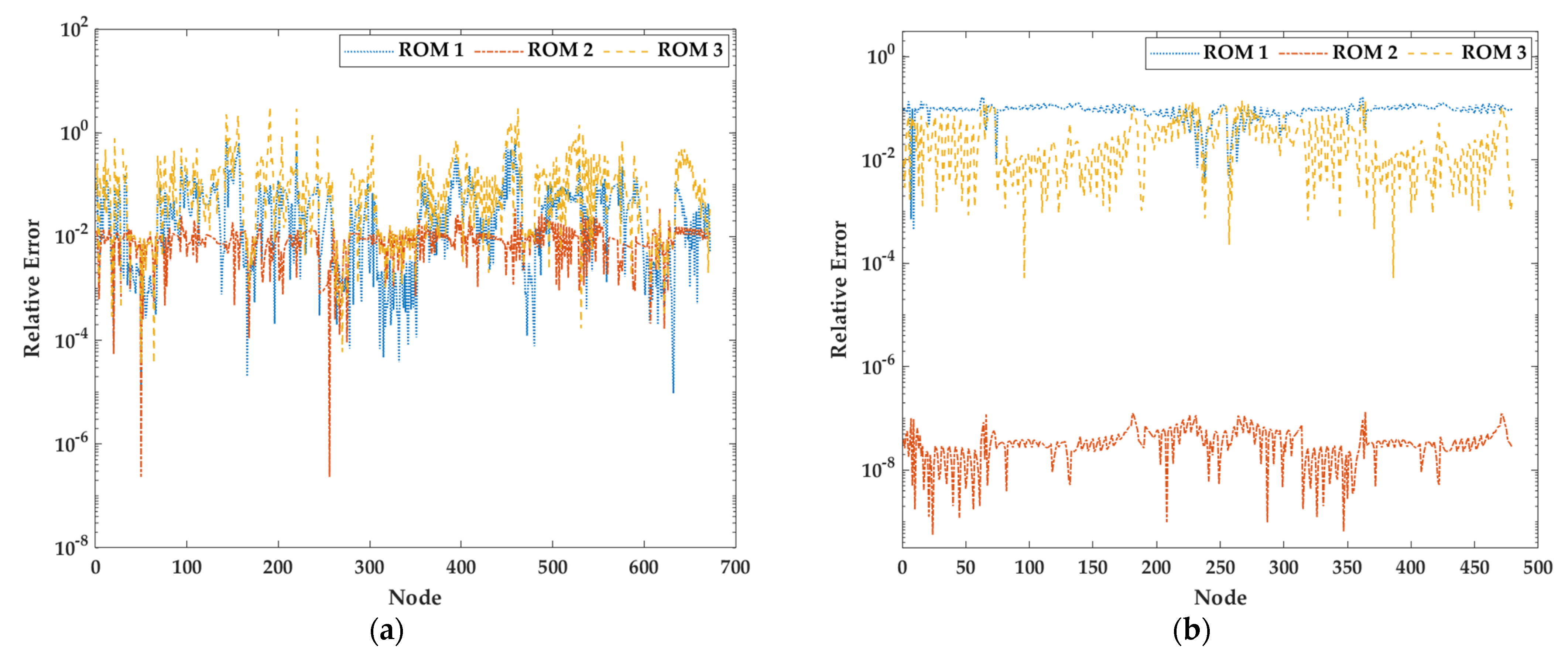
3.2. Example 2: Microgripper Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uchida, M.; Kaneko, Y. Nonlocal multiscale modeling of deformation behavior of polycrystalline copper by second-order homogenization method. Eur. Phys. J. B 2019, 92, 189. [Google Scholar] [CrossRef]
- Bleiler, C.; Castañeda, P.P.; Röhrle, O. Tangent second-order homogenisation estimates for incompressible hyperelastic composites with fibrous microstructures and anisotropic phases. J. Mech. Phys. Solids 2021, 147, 104251. [Google Scholar] [CrossRef]
- Kouznetsova, V.G.; Geers, M.G.; Brekelmans, W. Multi-scale second-order computational homogenization of multi-phase materials: A nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 2004, 193, 5525–5550. [Google Scholar] [CrossRef]
- Matsui, K.; Terada, K.; Yuge, K. Two-scale finite element analysis of heterogeneous solids with periodic microstructures. Comput. Struct. 2004, 82, 593–606. [Google Scholar] [CrossRef]
- Xu, R.; Yang, J.; Yan, W.; Huang, Q.; Giunta, G.; Belouettar, S.; Hu, H. Data-driven multiscale finite element method: From concurrence to separation. Comput. Methods Appl. Mech. Eng. 2020, 363, 112893. [Google Scholar] [CrossRef]
- Feng, N.; Zhang, G.; Khandelwal, K. Finite strain FE2 analysis with data-driven homogenization using deep neural networks. Comput. Struct. 2022, 263, 106742. [Google Scholar] [CrossRef]
- Kim, S.; Shin, H. Deep learning framework for multiscale finite element analysis based on data-driven mechanics and data augmentation. Comput. Methods Appl. Mech. Eng. 2023, 414, 116131. [Google Scholar] [CrossRef]
- Kim, S.; Shin, H. Data-driven multiscale finite-element method using deep neural network combined with proper orthogonal decomposition. Eng. Comput. 2024, 40, 661–675. [Google Scholar] [CrossRef]
- Tan, V.B.C.; Raju, K.; Lee, H.P. Direct FE2 for concurrent multilevel modelling of heterogeneous structures. Comput. Methods Appl. Mech. Eng. 2020, 360, 112694. [Google Scholar] [CrossRef]
- Xu, J.; Li, P.; Poh, L.H.; Zhang, Y.; Tan, V.B.C. Direct FE2 for concurrent multilevel modeling of heterogeneous thin plate structures. Comput. Methods Appl. Mech. Eng. 2022, 392, 114658. [Google Scholar] [CrossRef]
- Liu, K.; Meng, L.; Zhao, A.; Wang, Z.; Chen, L.; Li, P. A hybrid direct FE2 method for modeling of multiscale materials and structures with strain localization. Comput. Methods Appl. Mech. Eng. 2023, 412, 116080. [Google Scholar] [CrossRef]
- Liu, K.; Tian, L.; Gao, T.; Wang, Z.; Li, P. An explicit D-FE2 method for transient multiscale analysis. Int. J. Mech. Sci. 2025, 285, 109808. [Google Scholar] [CrossRef]
- Cremonesi, M.; Néron, D.; Guidault, P.A.; Ladevèze, P. A PGD-based homogenization technique for the resolution of nonlinear multiscale problems. Comput. Methods Appl. Mech. Eng. 2013, 267, 275–292. [Google Scholar] [CrossRef]
- El Halabi, F.; González, D.; Chico, A.; Doblaré, M. FE2 multiscale in linear elasticity based on parametrized microscale models using proper generalized decomposition. Comput. Methods Appl. Mech. Eng. 2013, 257, 183–202. [Google Scholar] [CrossRef]
- Yvonnet, J.; Zahrouni, H.; Potier-Ferry, M. A model reduction method for the post-buckling analysis of cellular microstructures. Comput. Methods Appl. Mech. Eng. 2007, 197, 265–280. [Google Scholar] [CrossRef]
- Oliver, J.; Caicedo, M.; Huespe, A.E.; Hernández, J.A.; Roubin, E. Reduced order modeling strategies for computational multiscale fracture. Comput. Methods Appl. Mech. Eng. 2017, 313, 560–595. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Kerfriden, P.; Goury, O.; Rabczuk, T.; Bordas, S.P.A. A partitioned model order reduction approach to rationalise computational expenses in nonlinear fracture mechanics. Comput. Methods Appl. Mech. Eng. 2013, 256, 169–188. [Google Scholar] [CrossRef]
- Raschi, M.; Lloberas-Valls, O.; Huespe, A.; Oliver, J. High performance reduction technique for multiscale finite element modeling (HPR-FE2): Towards industrial multiscale FE software. Comput. Methods Appl. Mech. Eng. 2021, 375, 113580. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y.; Lee, J.; Cho, M. Non-intrusive reduced-order modeling for nonlinear structural systems via radial basis function-based stiffness evaluation procedure. Comput. Struct. 2024, 304, 107500. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Cho, H.; Kim, E.; Cho, M. Reduced-order modeling of nonlinear structural dynamical systems via element-wise stiffness evaluation procedure combined with hyper-reduction. Comput. Mech. 2021, 67, 523–540. [Google Scholar] [CrossRef]
- Van Tuijl, R.A.; Remmers, J.J.; Geers, M.G. Integration efficiency for model reduction in micro-mechanical analyses. Comput. Mech. 2018, 62, 151–169. [Google Scholar] [CrossRef] [PubMed]
- An, S.S.; Kim, T.; James, D.L. Optimizing cubature for efficient integration of subspace deformations. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Hernández, J.A.; Caicedo, M.A.; Ferrer, A. Dimensional hyper-reduction of nonlinear finite element models via empirical cubature. Comput. Methods Appl. Mech. Eng. 2017, 313, 687–722. [Google Scholar] [CrossRef]
- Lange, N.; Hütter, G.; Kiefer, B. A monolithic hyper ROM FE2 method with clustered training at finite deformations. Comput. Methods Appl. Mech. Eng. 2024, 418, 116522. [Google Scholar] [CrossRef]
- Giuliodori, A.; Hernández, J.A.; Soudah, E. Multiscale modeling of prismatic heterogeneous structures based on a localized hyperreduced-order method. Comput. Methods Appl. Mech. Eng. 2023, 407, 115913. [Google Scholar] [CrossRef]
- Hernández, J.A. A multiscale method for periodic structures using domain decomposition and ECM-hyperreduction. Comput. Methods Appl. Mech. Eng. 2020, 368, 113192. [Google Scholar] [CrossRef]
- Guo, T.; Rokoš, O.; Veroy, K. A reduced order model for geometrically parameterized two-scale simulations of elasto-plastic microstructures under large deformations. Comput. Methods Appl. Mech. Eng. 2024, 418, 116467. [Google Scholar] [CrossRef]
- Rocha, I.B.; Kerfriden, P.; van der Meer, F.P. Micromechanics-based surrogate models for the response of composites: A critical comparison between a classical mesoscale constitutive model, hyper-reduction and neural networks. Eur. J. Mech. A/Solids 2020, 82, 103995. [Google Scholar] [CrossRef]
- Ghavamian, F.; Tiso, P.; Simone, A. POD-DEIM model order reduction for strain-softening viscoplasticity. Comput. Methods Appl. Mech. Eng. 2017, 317, 458–479. [Google Scholar] [CrossRef]
- Tiso, P.; Rixen, D.J. Discrete Empirical Interpolation Method for Finite Element Structural Dynamics. In Proceedings of the 31st IMAC A Conference on Structural Dynamics, Garden Grove, CA, USA, 11–14 February 2013. [Google Scholar] [CrossRef]
- Carlberg, K.; Tuminaro, R.; Boggs, P. Preserving Lagrangian structure in nonlinear model reduction with application to structural dynamics. SIAM J. Sci. Comput. 2015, 37, B153–B184. [Google Scholar] [CrossRef]
- Carlberg, K.; Tuminaro, R.; Boggs, P. Efficient structure-preserving model reduction for nonlinear mechanical systems with application to structural dynamics. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Bonomi, D.; Manzoni, A.; Quarteroni, A. A Matrix DEIM Technique for Model Reduction of Nonlinear Parametrized Problems in Cardiac Mechanics. Comput. Methods Appl. Mech. Eng. 2017, 324, 300–326. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Soldner, D.; Brands, B.; Zabihyan, R.; Steinmann, P.; Mergheim, J. Computational Homogenisation using Reduced-Order Modelling applied to Hyperelasticity. In Proceedings of the Applied Mathematics and Mechanics, Braunschweig, Germany, 7–11 March 2016. [Google Scholar] [CrossRef]
- Soldner, D.; Brands, B.; Zabihyan, R.; Steinmann, P.; Mergheim, J. A numerical study of different projection-based model reduction techniques applied to computational homogenisation. Comput. Mech. 2017, 60, 613–625. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hill, R. On constitutive macro-variables for heterogeneous solids at finite strain. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 1972. [Google Scholar] [CrossRef]
- Hill, R. On macroscopic effects of heterogeneity in elastoplastic media at finite strain. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar] [CrossRef]
- Matouš, K.; Geers, M.G.; Kouznetsova, V.G.; Gillman, A. A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials. J. Comput. Phys. 2017, 330, 192–220. [Google Scholar] [CrossRef]
- Terada, K.; Kikuchi, N. A class of general algorithms for multi-scale analyses of heterogeneous media. Comput. Methods Appl. Mech. Eng. 2001, 190, 5427–5464. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. Comp. Rendus Math. 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Radermacher, A.; Reese, S. POD-based model reduction with empirical interpolation applied to nonlinear elasticity. Int. J. Numer. Meth. Engng. 2015, 107, 407–495. [Google Scholar] [CrossRef]
- Kim, N.H. Introduction to Nonlinear Finite Element Analysis; Springer: Berlin/Heidelberg, Germany, 2015; pp. 183–199. [Google Scholar] [CrossRef]
- Amsallem, D.; Haasdonk, B. PEBL-ROM: Projection-error based local reduced-order models. Adv. Model. Simul. Eng. Sci. 2016, 3, 6. [Google Scholar] [CrossRef]
- Cho, H.; Shin, S.; Kim, H.; Cho, M. Enhanced model-order reduction approach via online adaptation for parametrized nonlinear structural problems. Comput. Mech. 2020, 65, 331–353. [Google Scholar] [CrossRef]
- Kohl, M.; Krevet, B.; Just, E. SMA microgripper system. Sens. Actuators A Phys. 2002, 97, 646–652. [Google Scholar] [CrossRef]
- Cheon, S.; Lee, J. An enhanced hybrid-level interface-reduction method combined with an interface discrimination algorithm. Mathematics 2023, 11, 4867. [Google Scholar] [CrossRef]
- Cheon, S.; Lee, S.; Lee, J. A system-level interface sampling and reduction method for component mode synthesis with varying parameters. Appl. Math. Comput. 2024, 476, 128778. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Hosseini, B.; Kovachki, N.B.; Stuart, A.M. Model reduction and neural networks for parametric PDEs. SMAI J. Comput. Math. 2021, 7, 121–157. [Google Scholar] [CrossRef]
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Kast, M.; Guo, M.; Hesthaven, J.S. A non-intrusive multifidelity method for the reduced order modeling of nonlinear problems. Comput. Methods Appl. Mech. Eng. 2020, 364, 112947. [Google Scholar] [CrossRef]
- Conti, P.; Guo, M.; Manzoni, A.; Frangi, A.; Brunton, S.L.; Nathan Kutz, J. Multi-fidelity reduced-order surrogate modelling. Proc. R. Soc. A 2024, 480, 20230655. [Google Scholar] [CrossRef]


| 1 | −0.025 | −0.025 | −0.025 |
| 2 | 0.025 | −0.025 | −0.025 |
| 3 | −0.025 | 0.025 | −0.025 |
| 4 | 0.025 | 0.025 | −0.025 |
| 5 | −0.025 | −0.025 | 0.025 |
| 6 | 0.025 | −0.025 | 0.025 |
| 7 | −0.025 | 0.025 | 0.025 |
| 8 | 0.025 | 0.025 | 0.025 |
| FOM | ROM 1 | |
|---|---|---|
| # of DOFs | 968 | - |
| # of elements | 440 | 87 |
| # of bases | - | 32 |
| # of sample points | - | 32 |
| FOM | ROM 2 | |
|---|---|---|
| # of DOFs | 574 | - |
| # of elements | 240 | 16 |
| # of bases | - | 6 |
| # of sample points | - | 6 |
| FOM | ROM 1 | ROM 2 | ROM 3 | |
|---|---|---|---|---|
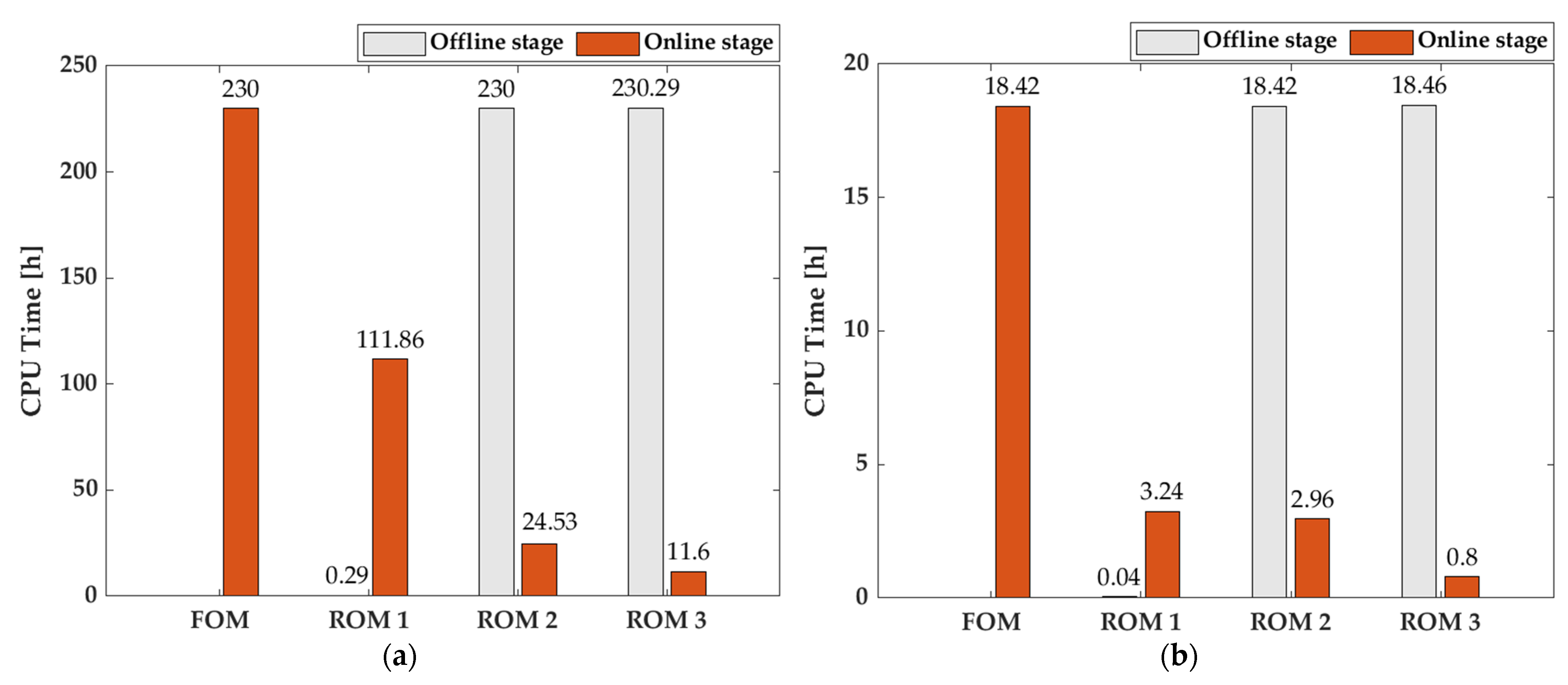
| Offline stage [h] | - | 0.29 | 230 | 230.29 |
| Online stage [h] | 230 | 111.86 | 24.53 | 11.6 |
| ROM 1 | ROM 2 | |
|---|---|---|
| # of elements | 41 | 53 |
| # of bases | 13 | 27 |
| # of sample points | 13 | 27 |
| FOM | ROM 1 | ROM 2 | ROM 3 | |
|---|---|---|---|---|
| Offline stage [h] | - | 0.04 | 18.42 | 18.46 |
| Online stage [h] | 18.42 | 3.24 | 2.96 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
So, Y.; Lee, J. A Two-Step Sequential Hyper-Reduction Method for Efficient Concurrent Nonlinear FE2 Analyses. Mathematics 2025, 13, 1790. https://doi.org/10.3390/math13111790
So Y, Lee J. A Two-Step Sequential Hyper-Reduction Method for Efficient Concurrent Nonlinear FE2 Analyses. Mathematics. 2025; 13(11):1790. https://doi.org/10.3390/math13111790
Chicago/Turabian StyleSo, Yujin, and Jaehun Lee. 2025. "A Two-Step Sequential Hyper-Reduction Method for Efficient Concurrent Nonlinear FE2 Analyses" Mathematics 13, no. 11: 1790. https://doi.org/10.3390/math13111790
APA StyleSo, Y., & Lee, J. (2025). A Two-Step Sequential Hyper-Reduction Method for Efficient Concurrent Nonlinear FE2 Analyses. Mathematics, 13(11), 1790. https://doi.org/10.3390/math13111790






