Square-Based Division Scheme for Image Encryption Using Generalized Fibonacci Matrices

Abstract

This paper proposes a novel image encryption and decryption scheme, called Square Block Division-Fibonacci (SBD-Fibonacci), which dynamically partitions any input image into optimally sized square blocks to enable efficient encryption without resizing or distortion. The proposed encryption scheme can dynamically adapt to the image dimensions and ensure compatibility with images of varying and high resolutions, while it serves as a yardstick for any symmetric-key image encryption algorithm. An optimization model, combined with the Lagrange Four-Square theorem, minimizes trivial block sizes, strengthening the encryption structure. Encryption keys are generated using the direct sum of generalized Fibonacci matrices, ensuring key matrix invertibility and strong diffusion properties and security levels. Experimental results on widely-used benchmark images and a comparative analysis against State-of-the-Art encryption algorithms demonstrate that SBD-Fibonacci achieves high entropy, strong resistance to differential and statistical attacks, and efficient runtime performance—even for large images.

1. Introduction

Cryptography is of significant importance in many aspects of our society. It serves as a fundamental pillar in the security of mobile phone communications, e-commerce platforms, email exchanges, financial transmissions, ATM card protection, and computer passwords. Cryptography, rooted in mathematics, has expanded its scope to tackle the ever-increasing demands of our digital world, particularly in the realm of image and video transmission [1,2]. Therefore, the integration of cryptography with modern computer science has become a necessity [3]. Images are vulnerable to unauthorized access and manipulation and may pose significant risks to individuals and organizations. Consequently, image encryption ensures the integrity and trustworthiness of digital visual data. Although image encryption is not a new concept, recent years have witnessed a growing interest in the development of efficient and secure image encryption algorithms [4,5] capable of real-time encryption and decryption. This is particularly vital in environments such as cloud or fog and edge computing, where the need for fast and reliable encryption mechanisms is paramount [6,7,8].

A common approach for image encryption is to apply a symmetric-key encryption algorithm, i.e., a cryptographic technique that uses a single key for both the encryption and decryption processes. The key is presented in the form of a matrix and is used by both the sender and the receiver to secure the images’ pixels. Algorithms in this category are widely used for image encryption due to their simplicity and low processing power requirements, which makes them preferred for encrypting big data. They apply simple mathematical operations, such as permutation and transformation, to image pixels or blocks of pixels. However, the key must be an invertible matrix for reversible encryption and decryption processes. The application of symmetric key encryption for images poses several challenges related to key size, key management, and image handling, especially in cases of non-square images. Therefore, an approach that will facilitate key management by reducing the volume of data needed for key extraction is necessary. In addition, a way of applying the primitive cryptographic operation is required for images that are oddly sized or too large. Given the current requirements concerning the volume of data exchanged and the accepted communication speeds, any proposed approach should be fast enough and not induce any significant overhead.

Most of the prior research has concentrated on encryption algorithms for square images, with little attention paid to non-square ones. In [9], the authors develop an encryption–decryption approach studying $m\times n$ images for special values of m, n and using two different types of key matrices, the generalized Fibonacci matrix and the Pascal matrix. They use the Lagrange Four-Square theorem for the encryption process along with two different types of key matrices, the generalized Fibonacci matrix and the Pascal matrix. However, their approach is time-consuming and has significant computational costs, especially in high-quality images. In this study, a fast and novel encryption approach is presented, tailored to non-square images by introducing a square block division scheme.

The proposed scheme uses an optimization process to divide the entire non-square image into square blocks of different sizes; thus ensuring that the algorithm can be applied to diverse image dimensions while enhancing the encryption strength and dispersing the effects of encryption throughout the entire image. Each image block is encrypted by a different key matrix resulting from the direct sum of powers of generalized Fibonacci matrices, whose rightmost element of the first row is one. The encryption scheme, called Square Block Division-Fibonacci (SBD-Fibonacci), tackles the invertibility constraint imposed by the cipher algorithm since the determinant of the key matrix always equals +1 or −1. This design allows the cipher algorithm to be applied efficiently and robustly to any type of image. The following list summarizes our contributions:

• A novel and efficient square block division scheme based on an optimization model is proposed for fast processing of non-square images.
• A key generation approach based on generalized Fibonacci matrices ensures invertibility and simplifies key management (SBD-Fibonacci algorithm).
• The Lagrange Four-Square theorem is used to minimize the percentage of small encryption blocks and to increase encryption security images of any size/dimension.
• A statistical analysis of our approach is conducted, using various widely used benchmark images, to confirm that it performs well and is effective.

The remainder of the paper is organized as follows. Section 2 refers to some recent progress in the field of image encryption and Section 3 provides a concise overview of the fundamental matrix theory utilized in the encryption and decryption processes. Section 4 is devoted to a detailed description of the proposed image encryption and decryption algorithms based on a novel square block division technique. Section 5 illustrates the optimization process used to minimize the number of multiple single pixels generated within the preceding scheme. An extended experimental evaluation using various widely used benchmark images that showcases the performance of the proposed regime in resisting various statistical attacks is provided in Section 6, followed by a comprehensive discussion, in Section 7 where we compare our findings with the existing literature. Finally, Section 8 concludes the paper.

2. Related Work

During the past decade, numerous researchers have explored encryption methods that leverage chaos theory with several cryptographic techniques, see [10,11,12,13,14,15,16,17] and the references therein. In [18], the authors proposed a technique based on improved chaotic maps and a secure variant of Hill Cipher. Their method provided pixel-by-pixel encryption, unlike the conventional Hill Cipher, encrypting pairs of adjacent pixels two by two. The authors in [19] introduced a hyperchaotic map and a pixel fusion strategy to encrypt images more effectively and speed up calculations. They performed encryption by grouping multiple pixels into one, thus reducing computational cost, and produced a common keystream, simplifying key management. True random number generators can contribute to the development of high-security cryptographic schemes [20,21,22]. In [23], the researchers proposed a random number generator combining a deep learning model with chaotic systems for the image encryption key to exhibit strong randomness and preserve the statistical properties of the original data without revealing sensitive information. A scheme of color image encryption based on an improvement of the Hill Cipher algorithm was proposed in [24,25]. The algorithm was based on an affine transformation provided by a three-order invertible matrix and a chaotic translation vector.

Generalized Fibonacci matrices, which have an important place in the field of mathematics, have been utilized in several encryption and decryption techniques because of their connection to the interesting behavior of the Fibonacci sequence [26,27]. The algorithms designed in [28] were based on Fibonacci polynomials and combinations of Hill Cipher encryption alongside the sigmoid logistic map and Kronecker product matrix techniques. The encryption schemes in [29,30,31] benefited from the mathematical robustness of the generalized Fibonacci matrices in modifying the pixel values to enhance the diffusion effect on neighboring pixels and make it harder for attackers to decipher the image. The presented image encryption technique in [32] utilized a Fibonacci matrix for image scrambling and a Fibonacci matrix for the diffusion phase. Chaotic maps were also employed to generate key sequences and introduce further confusion in the image pixels.

As encryption scheme continues to evolve, researchers have begun exploring the integration of optical technologies, biological-inspired coding methods or a combination of two or more techniques. To this effect, image encryption strategies now dictate more robust and computationally efficient approaches. Recent advances have leveraged the combination of optical imaging, chaos encryption and DNA coding. For instance, a dual-channel image encryption and authentication technique has been proposed in [33]. In this scheme, a 4D chaotic system and DNA operations have been employed for image encryption in the digital channel, while Computational Ghost Imaging and the Logistic map have been used for the authentication in the optical channel. The utilization of optical technologies in image encryption offers high parallelism and complexity to the encryption process [34].

Chaos-based methods and DNA manipulation maintain a high level of security for image encryption while ensuring the minimum hardware resources [35,36,37,38]. Nevertheless, certain security flaws can be detected upon being subjected to cryptanalysis, a pivotal process in ensuring the rationality, practicality, and security of image encryption algorithms or schemes. Based on the cryptanalysis of the Quantum Chaotic Map and DNA Coding scheme in [39], security weaknesses were revealed due to the existence of an equivalent key and the absence of both confusion and diffusion in the DNA domain encryption. In addition to integrating modalities such as optics, hybrid approaches combining encryption with watermarking have emerged to tackle persistent security challenges. The authors in [40] developed a new model for the embedding of digital watermarks using a frequency domain transformation and a channel attention mechanism. Their model improved the adaptability and robustness of the watermark across different types of content.

3. Materials and Methods

Generalized Fibonacci Matrix: For a positive integer $k\ge 2$ and nonnegative real numbers $c_1,c_2,\dots ,c_k$, the n-th term of the k-generalized Fibonacci number is defined recursively as

$$f_n=c_1{f}_{n-1}+c_2{f}_{n-2}+\cdots +c_k{f}_{n-k},n\ge k+1,$$

(1)

with initial values $f_1=\cdots =f_k=1$. Let $Q(c_1,\dots ,c_k)$ be the $k\times k$ generalized Fibonacci matrix associated with the sequence ${\left(f_n\right)}_{n\ge k+1}$, namely

$$Q(c_1,\dots ,c_k)=\left[\begin{array}{cc}\mathsf{q}& c_k\\ I_{k-1}& \mathbf{0}\end{array}\right],$$

(2)

where $\mathsf{q}=\left[\begin{array}{ccc}{c}_1& \cdots & c_{k-1}\end{array}\right]$ is an $1\times (k-1)$ matrix, $I_{k-1}$ is the $(k-1)\times (k-1)$ identity matrix and 0 is the $(k-1)\times 1$ zero matrix. Then, the linear recurrence relation (1) can be represented in the matrix form

$$\left[\begin{array}{c}{f}_n\\ f_{n-1}\\ ⋮\\ f_{n-k+1}\end{array}\right]=Q(c_1,\dots ,c_k)\left[\begin{array}{c}{f}_{n-1}\\ f_{n-2}\\ ⋮\\ f_{n-k}\end{array}\right]$$

for every $n\ge k+1$. Note that $Q^n(1,1)$ derives the Fibonacci sequence while $Q^n(1,1,1)$ produces the Tribonacci sequence. The powers of $Q(c_1,\dots ,c_k)$ play a crucial role in the design of image encryption schemes as they provide closed forms for higher-order terms in generalized Fibonacci sequences [26]. This property is employed in efficient confusion and diffusion processes of image pixel values and leads to faster implementations, reducing the time as well as the space complexity of the security process. Furthermore, the determinants of these powers extend known identities such as Cassini’s and Sharpe’s identities, and their spectral analysis leads to sharp spectral radius bounds [26,41]. A simple calculation gives that $det\left(Q(c_1,\dots ,c_k)\right)={(-1)}^{k+1}{c}_k$.

For the implementation of our proposed algorithm, we consider the entries $c_1,\dots ,c_{k-1}$ in Equation (2) to be randomly generated nonnegative integers, $c_k=1$, and take the generalized Fibonacci matrix

$$Q(c_1,\dots ,c_{k-1},1)=\left[\begin{array}{ccccc}{c}_1& c_2& \cdots & c_{k-1}& 1\\ 1& 0& \cdots & 0& 0\\ 0& 1& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 1& 0\end{array}\right]:=Q,$$

(3)

with determinant

$$det\left(Q\right)={(-1)}^{k+1}=\pm 1\ne 0.$$

(4)

The latter equality guarantees that the matrix Q is invertible within modular arithmetic, that is, $gcd\left(det\right(Q),\nu )=1$ for any $\nu \in \mathbb{N}$ with $\nu \ge 2$, allowing reversible image data transformations. The randomly selected parameters $c_1,\dots ,c_{k-1}$ lead to complex diffusion patterns across the image that can form a large and sensitive key space, thus enhancing the security level of our scheme against unauthorized decryption attempts.

Direct sum of matrices: Let $A_1,\dots ,A_p$ be $n\times n$ matrices whose entries are nonnegative integers; their direct sum, which is denoted by “⊕”, is defined by the $np\times np$ matrix

$$A_1\oplus A_2\oplus \cdots \oplus A_p=diag(A_1,A_2,\dots ,A_p)=\left[\begin{array}{cccc}{A}_1& \mathbb{O}& \cdots & \mathbb{O}\\ \mathbb{O}& A_2& & ⋮\\ ⋮& & \ddots & \mathbb{O}\\ \mathbb{O}& \cdots & \mathbb{O}& A_p\end{array}\right],$$

(5)

where $\mathbb{O}$ denotes the $n\times n$ zero matrix. Recall that $det(A_1\oplus A_2\oplus \cdots \oplus A_p)=det\left(A_1\right)\times det\left(A_2\right)\times \cdots \times det\left(A_p\right)$.

Encryption and Decryption: Let P be an $m\times n$ matrix and K be an $m\times m$ matrix with nonnegative integers as entries. The encryption process is performed by

$$E=\left(KP\right)mod\omega ,$$

(6)

where $\omega \in \mathbb{N}$ is the cardinality of the set of numbers in P and K is called key matrix. An essential feature of the key matrix K in Equation (6) is that it must be invertible, which means $det\left(K\right)\ne 0$. Then, the decryption process is defined by the reverse operation of the encryption algorithm and it is formulated by

$$P=\left(K^{-1}E\right)mod\omega ,$$

(7)

where $K^{-1}$ denotes the inverse matrix of K. The modulo operation applied on each element of the resulting matrices $KP$ and $K^{-1}E$ in Equations (6) and (7), respectively, ensures that the values lie within the required range $[0,\omega -1]$.

Additionally, notice that the determinant of the key matrix and the modular base $\omega$ used in the encryption must be coprime, that is $gcd\left(det\right(K),\omega )=1$. It is worthwhile to note that for $K={(Q_1\oplus \cdots \oplus Q_p)}^r$, where $Q_i$, $i=1,\dots ,p$ are $k\times k$ generalized Fibonacci matrices as in Equation (3) and $r\in \mathbb{N}$, we obtain

$$\begin{array}{cc}\hfill det\left(K\right)& ={\left(det\left(Q_1\right)\right)}^r\times \cdots \times {\left(det\left(Q_p\right)\right)}^r={(-1)}^{(k+1)pr}=\pm 1,\hfill \end{array}$$

(8)

due to Equation (4). Hence, the key matrix K constructed in this way is always an invertible matrix and also

$$gcd\left(det\right(K),\omega )=1.$$

(9)

For the encryption and decryption of images, an identical mechanism may be employed, which initially involves converting the image into a matrix whose entries correspond to its pixel values. According to the aforementioned setting, P, E and K represent the original image, the encrypted image and the encryption key, respectively. We note that in a grayscale image $\omega =256$, because each pixel element has an assigned intensity in the range [0, 255].

Table 1. Nomenclature.

Symbol	Meaning
P	original image (plaintext) of size $m\times n$
E	encrypted image (or ciphertext)
D	decrypted image
K	encryption key (key-matrix)
$K^{-1}$	the inverse matrix of K
Q	generalized Fibonacci matrix
$A\oplus B$	the direct sum of the matrices $A,B$
$b^p$	largest block size divisions
$SB$	list of Square Blocks
s	s-th block in $SB$ of size $b^z\times b^z$, where $z\in [0,p]$
$s.r$	row position in P
$s.c$	column position in P
$s.\ell$	length of s
$s.sP$	sub-image of P associated to s-th block
L	master key (list of random values $[0,255]$)
$sL$	size of master key L
$index$	current position in L
d	the smallest divisor of $b^z$ that is $\ge 2$

summarizes the notation adopted in this paper.

4. SBD-Fibonacci Algorithm

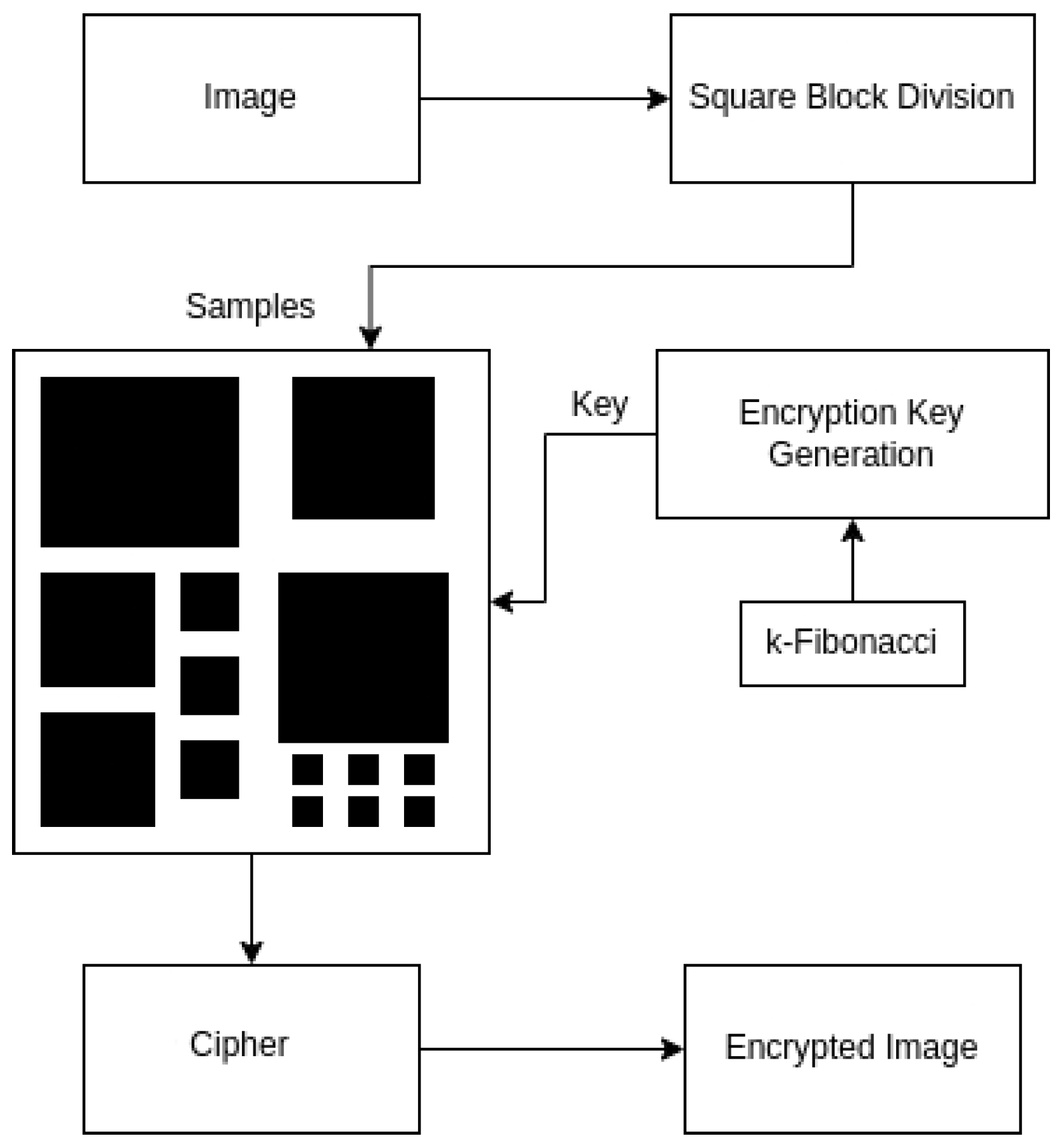
The basic steps of the proposed SBD-Fibonacci algorithm for image encryption are the following: (1) Square Block Division (SBD). The input image is divided into non-overlapping square blocks of varying sizes (Section 4.1). (2) Optimization using Lagrange Four-Square Theorem. To minimize the number of vulnerable small blocks ($1\times 1$ or $2\times 2$), the Lagrange Four-Square theorem is applied. This technique merges multiple small blocks into larger, more secure blocks (Section 4.2). (3) Master Key Generation: A master key consisting of a list of randomly generated integer values is created providing the basis for the construction of encryption keys for all individual blocks (Section 4.3). (4) Encryption Key Construction. This step is applied to each square block. Specifically, if the block size is greater than 2 × 2, a generalized Fibonacci matrix is generated and modified using the master key. Otherwise, a simple multiplication with a master key element is applied (Section 4.3). (5) Block-wise Encryption. Each block is encrypted individually using its corresponding key matrix (Section 4.3). (6) Cipher Image Assembly. The encrypted blocks are recombined to form the final encrypted image (Section 4.3).

The execution flow of the SBD-Fibonacci algorithm is presented in Figure 1. Based on that, initially, the image will be segmented into a collection of blocks via our SBD scheme. After that, using a generalized Fibonacci matrix as our key basis, an encryption key will be generated and finally, each block will be encrypted using the basic steps of the cipher algorithm described in the previous section.

4.1. Square Block Division (SBD)

In this subsection, we present a novel division scheme that divides the entire image into square blocks of different sizes, which will also be called samples. To the best of our knowledge, this is the first time such an approach has been presented and also applied in image cryptography. Algorithm 1 demonstrates the division process of the SBD-Fibonacci algorithm in a top-down approach.

Algorithm 1 Square Block Division Algorithm

Input:  $m,n,b,p$

Output: list of square blocks, $SB$

1: $R_{max}\leftarrow 0$, $C_{max}\leftarrow 0$ 2: $SB\leftarrow \varnothing$ 3: for $z\leftarrow p$ to 1 do 4:     $R_{max}^{\prime }\leftarrow R_{max}$, $C_{max}^{\prime }\leftarrow C_{max}$ 5:     $x\leftarrow b^z$ 6:     for $i\leftarrow R_{max}^{\prime }$ to m step x do 7:         for $j\leftarrow C_{max}^{\prime }$ to n step x do 8:             createBlock(i,j,x) 9:         end for 10:   end for 11:   if $z\ne p$ then 12:       for $i\leftarrow 0$ to $R_{max}^{\prime }$ step x do 13:           for $j\leftarrow C_{max}^{\prime }$ to n step x do 14:               createBlock(i,j,x) 15:           end for 16:       end for 17:       for $i\leftarrow R_{max}^{\prime }$ to m step x do 18:          for $j\leftarrow 0$ to $C_{max}^{\prime }$ step x do 19:               createBlock(i,j,x) 20:           end for 21:       end for 22:    end if 23: end for 24: return $SB$

The algorithm requires four inputs. The variables m and n represent the total number of rows and columns of the image, respectively. The division is performed iteratively (lines 3–23), starting with large sample sizes and gradually reducing the sample sizes based on the next two input parameters: the base size b and the number of divisions p. At each iteration, the algorithm attempts to fit as many square blocks of size $b^p,b^{p-1},\dots ,b^0$ as possible within the remaining undivided areas. This ensures the efficient handling of large images with varying dimensions. To select the optimal values of b and p for a given image, an optimization process is employed and presented in Section 5. The goal is to minimize the number of single-pixel or very small blocks, as they may pose vulnerabilities in the encryption strength. The optimization is based on a heuristic that analyzes how different choices of b and p impact the fragmentation of the image, seeking combinations that reduce the number of isolated pixels. The outer for loop (line 3) is executed p times and in each iteration, one or more square blocks of size $b^z\times b^z$ are generated with $z\in \mathbb{N}$, $z\in [0,p]$, starting with $b^p\times b^p$ blocks and gradually reducing to $b^0\times b^0$. After the division process, the maximum size of the blocks will be $b^p\times b^p$, while the minimum size will be $1\times 1$ (if any). Note that not all iterations will result in square blocks, as the current block size, $b^z$, may exceed the remaining dimensions of the undivided image.

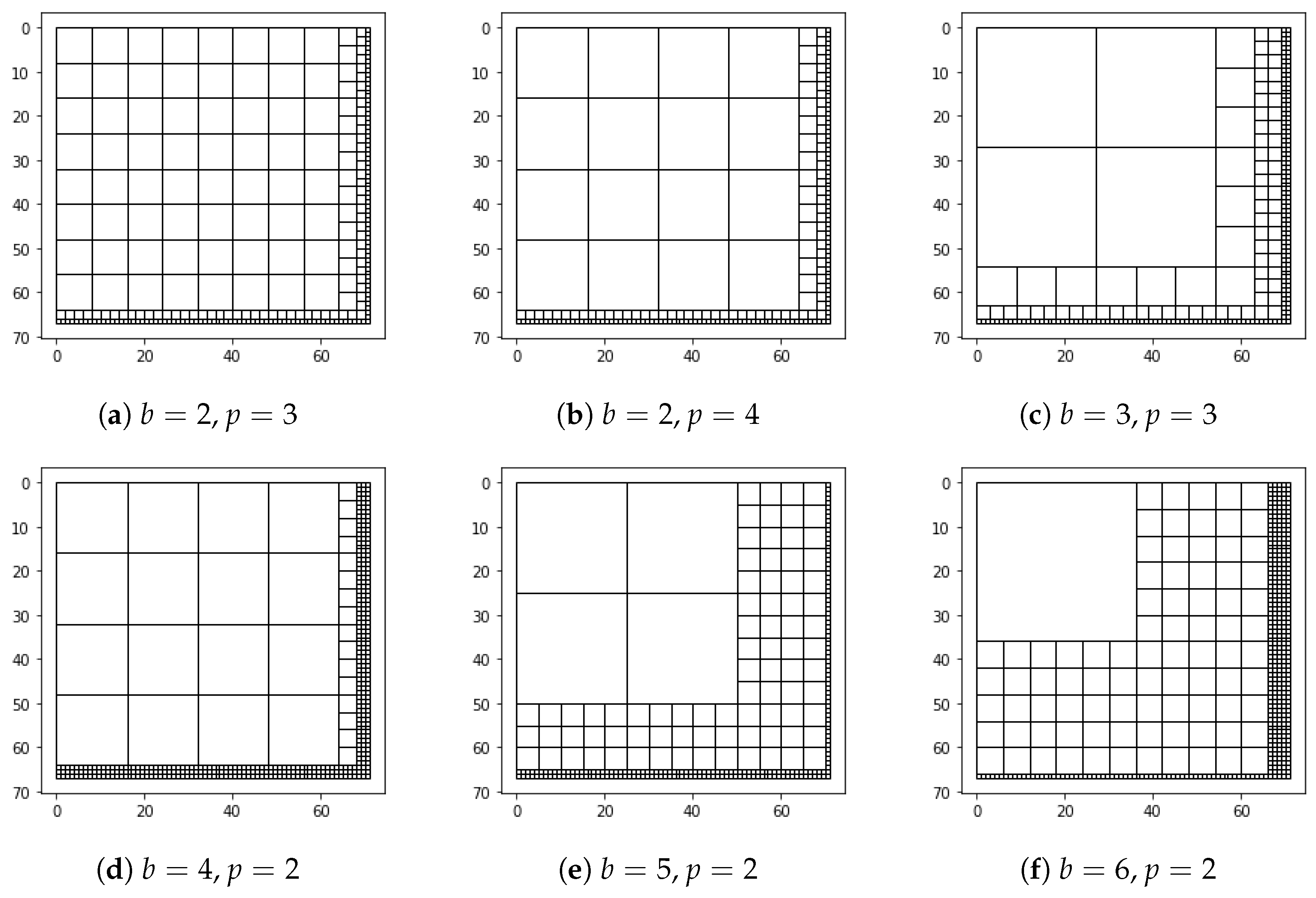
In Figure 2, we use a $67\times 71$ sample image to illustrate different scenarios of square block division when varying b and p values.

Table 2. Square blocks characteristics.

	Figure 2a	Figure 2b	Figure 2c	Figure 2d	Figure 2e	Figure 2f
$1\times 1$	137	137	203	405	207	401
$2\times 2$	67	67
$3\times 3$			65
$4\times 4$	16	16		16
$5\times 5$					82
$6\times 6$						65
$8\times 8$	64
$9\times 9$			13
$16\times 16$		16		16
$25\times 25$					4
$27\times 27$			4
$36\times 36$						1

displays the total number and size of the square blocks generated for each combination. Note that these small image dimensions of prime numbers are employed solely for demonstration purposes. In more practical scenarios, image dimensions are larger and more efficient, and b and p values need to be selected in a way that prevents the formulation of numerous instances of $1\times 1$ blocks. Therefore, the optimization process described in Section 5 is initially performed to determine the best combination of b and p. These optimized values are then used as inputs in SBD.

Variables $R_{max}^{\prime }$ and $C_{max}^{\prime }$ represent the maximum row and column value encountered during each division step, respectively. They are updated within the algorithm when a new division iteration is initiated (line 4). These variables play an important role in the proposed algorithm as they are used to keep track of the current maximum row and column offsets from the previous square block division. As a result, the subsequent iterations of the algorithm will only focus on the remaining undivided parts of the image, eliminating redundant checks on the previously divided sections. This optimization leads to significant gains in the overall execution runtime of the algorithm.

The purpose of the inner loops is to perform the necessary divisions in the image (lines 6–10, 12–16, and 17–21). Their operation is similar, however by varying their ranges and step sizes, different parts of the same image are considered for division. In the first iteration of the outer loop both $R_{max}^{\prime }$ and $C_{max}^{\prime }$ are set to zero and the inner nested loop (lines 6–10) iterates over the entire image with a step size of x. In this way, the image is divided into $b^p\times b^p$ blocks, with $b^p$ being the maximum accepted size. In the subsequent iterations, when the if condition of line 11 is true, all three nested for loops are executed and examine different undivided portions of the image. The third inner loop (lines 17, 18) iterates over the bottom-left part of the image, the second inner loop (line 12, 13) iterates over the top-right part, while the first inner loop (line 6, 7) iterates over the remaining image.

Algorithm 2 Function createBlock

Input:  $r,c,\ell$

1: if $r+\ell -1<m$ && $c+\ell -1<n$ then 2:     $s=\langle r,c,\ell ,sP\rangle$ 3:     push s into $SB$ 4:     if $r+\ell >R_{max}$ then 5:         $R_{max}\leftarrow r+\ell$ 6:     end if 7:     if $c+\ell >C_{max}$ then 8:         $C_{max}\leftarrow c+\ell$ 9:     end if 10: end if 11: Update  $SB,R_{max},C_{max}$

The createBlock function is an essential component of the SBD algorithm, being called within a nested loop structure to execute specific tasks during each iteration of the division process. This function serves three main purposes: block creation, list appending and updating maximum cut dimensions. We consider each square block as a tuple of four elements: $s=\langle r,c,\ell ,sP\rangle$, where r and c represent the row and column position (index) of the block within the image, ℓ describes the length of the block and $sP$ is an $\ell \times \ell$ sub-image of P that contains a sample from the plaintext from $r:r+\ell$ row and $c:c+\ell$ column. The algorithm starts with an empty list $SB$ (Algorithm 1, line 2) and progressively appends square blocks (Algorithm 2, line 3) into $SB$. Line 1 in Algorithm 2 guarantees that block dimensions do not exceed image boundaries. Through lines 4–9 in Algorithm 2, variables $R_{max}$ and $C_{max}$ keep track of the maximum row and column value encountered during the creation of a new square block.

4.2. Lagrange Four-Square

The SBD algorithm can generate multiple $2\times 2$ and $1\times 1$ square blocks depending on the size of the image. This could be considered a weak point in our encryption approach, making the block structure uniform and easy to predict. To address this issue and introduce more variability in the division scheme, we apply the Lagrange Four-Square theorem, which asserts that a positive integer can be expressed as the sum of at most four squares of positive integers. In this context, all pixel values of the above blocks are concatenated into a single vector of size $vl$ and then the theorem is applied to $vl$, i.e., $vl=i^2+j^2+k^2+l^2$, where $i,j,k,l\in \mathbb{N}\cup \left\{0\right\}$. To find the list $fsd:=[i,j,k,l]$, we use brute-force search in Algorithm 3 by testing all possible combinations of $i\le j\le k\le \sqrt{vl}$ and we calculate l by the formula $l=\sqrt{vl-i^2-j^2-k^2}$ (lines 2–5). If the resulting l is an integer, the required 4-tuple of integers is returned (lines 6–13). The if statement in line 10 ensures that the output list will contain the fewest possible zeros and ones. Afterwards, the vector containing the pixel values is reshaped in SBD-Fibonacci algorithm (lines 11–12) to form new square blocks with dimensions determined by the positive integers from the output list. This technique limits the maximum number of vulnerable $2\times 2$ and $1\times 1$ square blocks to four, thus reinforcing our encryption scheme and enhancing its security.

Algorithm 3 Lagrange Four-Square

Input: Vector Length, $vl$

Output: Four-Square Dimensions, $fsd$

1: initialize empty list $squares$ 2: for i∈$[0,\sqrt{vl}]$ do 3:     for j∈$[i,\sqrt{vl}]$ do 4:         for k∈$[j,\sqrt{vl}]$ do 5:             l←$\sqrt{vl-i^2-j^2-k^2}$ 6:             if l∈$\mathbb{R}$$l=\lfloor l\rfloor$ then 7:                 $tmp\_squares$←$[i,j,k,l]$ 8:                 $num\_ones$←$sum(temp\_squares=1)$ 9:                 $num\_zeros$←$sum(temp\_squares=0)$ 10:               if $isempty\left(squares\right)$$(num\_ones+num\_zeros)<\left(sum\right(squares=1)+sum(squares=0\left)\right)$ then 11:                   $squares$←$tmp\_squares$ 12:                 end if 13:             end if 14:         end for 15:      end for 16: end for 17: return $squares$ as $fsd$

4.3. Key Generation and Encryption

The proposed SBD-Fibonacci algorithm illustrates the encryption process and generates the required key matrix. Its input is the list $SB$, which consists of the square blocks, s, produced by SBD and represents the plaintext P.

Algorithm 4 Key_Generation function

Input: $kq,kd,d,index,L$

Output: Encryption key, K

1: for $i\leftarrow 0$ to $kd$ step d do 2:     for $j\leftarrow i$ to $i+d-1$ do 3:         $k{q}_{i,j}\leftarrow L_{index}$ 4:         $index\leftarrow index+d-1$ 5:     end for 6: end for 7: return $kq$ as K

In order to encrypt and decrypt the divided image, a simple solution could be to create and store a different key, K, for each block s. However, this would require an undefined number of unique keys and would create significant implications for key management. Instead, to avoid that, the algorithm starts by generating a master key L, which is a list of randomly selected integers within the range $[0,255]$ with length $sL=256$. Algorithm 4 is implemented to incorporate L into each K corresponding to a block s with $s.\ell >=2$.

Algorithm 5 SBD-Fibonacci Algorithm

Input: $SB$

Output: Encrypted image, E

1: $ls\leftarrow \varnothing ,l{s}^{\prime }\leftarrow \varnothing$ 2: generate list L 3: $index\leftarrow 0$ 4: for each s∈$SB$ do 5: if  $s.\ell \le 2$ then 6:      $l{s}^{\prime }.append\left(s\right)$ 7:      $SB.remove\left(s\right)$ 8: end if 9: end for 10: Convert square blocks of $l{s}^{\prime }$ into a vector, $ls$ 11: $sd\leftarrow LFS\left(len\right(ls\left)\right)$ 12: Generate Square Blocks from $sd$ 13: Append new Square Blocks into $SB$ 14: for each $s\in SB$ do 15:     if  $index=256$ then 16:          $index\leftarrow 0$ Reuse elements if $sL$ is exceeded 17:     end if 18:     if  $s.\ell =1$ then 19:          $K\leftarrow L_{index}$ 20:          $index\leftarrow index+1$ 21:          $e\leftarrow (K\times s.sP)mod256$ 22:     else 23:          if $s.\ell \ne 2$ then $d\leftarrow$ SD($s.\ell$) s.t $d\ge 3$ else $d=2$ 24:          $kd\leftarrow s.\ell /d$ 25:          $kq\leftarrow \underset{kd\mathrm{times}}{\underbrace{Q\oplus \cdots \oplus Q}}$ 26:          $K\leftarrow Key\_Generation(kq,index)$ 27:          $K\leftarrow K^d$ 28:          $e\leftarrow (K\times s.sP)mod256$ 29:     end if 30:     place e into E 31: each for 32: return  E

The master key L serves as the foundation for constructing the encryption keys for each block. For blocks with $s.\ell \ge 2$, the key generation process involves several steps to ensure the security and uniqueness of each block’s key matrix. Initially, a generalized Fibonacci matrix Q is generated based on randomly selected parameters. This matrix is then expanded using the direct sum operation to match the size of the block. Specifically, the direct sum $kq=Q\oplus Q\oplus \cdots \oplus Q$ is created, where $kd$ is the ratio of the block size to the smallest divisor d of the block size. The elements in the first row of each Q in the direct sum are replaced with the values from the master key L, except for the rightmost element, which remains fixed at one. This ensures that the resulting key matrix K is always invertible. The key matrix K is then raised to the power of d to construct the final encryption key for the block.

A detailed description of the key generation process and encryption scheme is provided in the following paragraphs.

Algorithm 5 examines each block s contained in $SB$ in an iterative fashion. As previously mentioned, the SBD process generates square blocks of various sizes $s.\ell \times s.\ell$, with a minimum of $s.\ell =1$ pixel. However, multiple blocks with $s.\ell \le 2$ can lead to security breaches and put the encryption process at risk. To address this issue and strengthen the encryption, we employ the Lagrange Four-Square theorem, as explained in the relevant subsection. Hence, the $2\times 2$ and single-pixel blocks are excluded from the main list $SB$ and stored separately in a vector, called $ls$ (lines 4–9). Then, Algorithm 3 is applied to the length of the vector $ls$ to return a list, $sd$, of four nonnegative integers (line 11). The positive integers in $sd$ will determine the size of at most four new square image blocks that will be added to $SB$ (lines 12–13). Note that this process can still create $2\times 2$ and $1\times 1$ blocks, but now their number is reduced to a maximum of four, thus making the encryption process more robust.

The key generation and encryption processes are carried out between lines 14 and 31. Lines 18–21 involve multiplying a single pixel s with an element from the master key L, which represents the encryption key K. Once the multiplication is completed, the encrypted block, e, is created using the modulo-256 operation ensuring its value remains within the permissible pixel range. Alternatively, when the block s has $s.\ell \ne 2$ we proceed as outlined in lines 23–28. The following steps are conducted for key generation. Initially, we calculate the smallest divisor $d=\mathrm{SD}(s.\ell )$ of $s.\ell$ that is greater than or equal to 3, otherwise, we set $d=2$ (line 23). Then, a random $d\times d$ generalized Fibonacci matrix Q is considered as defined in Equation (3). This matrix is later enlarged to define the direct sum $kq=Q\oplus Q\oplus \cdots \oplus Q$ as in Equation (5) of $kd$ generalized Fibonacci matrices, where $kd$ is the ratio of $s.\ell$ to d (lines 24–25). This operation ensures that the size of the key matrix will be compatible with the dimensions of the sample to be encrypted. Afterwards, Algorithm 4 is executed to replace the $d-1$ elements in the first row of every matrix Q in $kq$ with entries from the list L and return the direct sum $Q_1\oplus \cdots \oplus Q_{kd}$ (line 26). The resulting direct sum consisting now of $kd$ different Fibonacci matrices is raised to the power of d to construct the encryption key $K={(Q_1\oplus \cdots \oplus Q_{kd})}^d$ (line 27). Throughout the procedure, it should be noted that all elements within the first row of $Q_j$, $j=1,\dots ,kd$, have changed, except for the rightmost element, which is fixed at a value of one. This fact, combined with the discussion presented in Section 3 and Equation (8), guarantees that the matrix K is always invertible and satisfies Equation (9). Then, the key matrix K is multiplied by the sample and the modulo 256 operation is performed (line 28).

It is important to note that if the number of elements of L, which are used in the key generating process, exceeds 256, then those elements are reused according to lines 15–17 of Algorithm 5. The algorithm then combines all the encrypted blocks into an image that has the same dimensions as the original image P. This process leads to the encrypted image E and occurs between lines 30 and 32.

4.4. Decryption

The decryption scheme follows the process described in Section 3 to decrypt each block e of the encrypted image E and return the decrypted version D. Note that, when decrypting single pixels, the randomly generated integer key of the list L divides the encrypted sample and modulo 256 is applied to retrieve the original sample values. For square blocks of larger size, decryption is performed by applying Equation (7) to each square block e. Then, the intermediate results are combined and the plaintext is reconstructed. It should be noted that, as a means to decrypt an image, the receiver must be aware of the optimized values b and p to generate the image’s blocks, as well as the list L to be able to generate the keys for each block and finally decrypt.

5. Optimizing SBD-Fibonacci

The SBD-Fibonacci algorithm partitions the plaintext into multiple square blocks of sizes ranging from $b^p\times b^p$ down to $b^0\times b^0$. Depending on the chosen values of variables b and p, various solutions can be generated. However, it is uncertain whether each of these solutions is suitable for image cryptography, as it is possible to generate multiple instances of single pixels. Encrypting numerous single blocks with the same key could potentially reveal meaningful information to an adversary. For example, as illustrated in Table 2, if we apply the division procedure, when $b=2$ and $p=3$, 137 single pixels will be generated. Similarly, setting $b=4$ and $p=2$ generates 405 single pixels. Motivated by all the above, in this section, we present:

(a)

the mathematical equations determining the total number of single pixels generated for any given values of b and p,

(b)

an optimization model that minimizes the total number of single pixels, and a straightforward and efficient heuristic method for calculating the optimal b and p values.

The total number of single pixels is determined by applying two recursive formulas. To calculate the number of rows that are located at the bottom part of the image and contain entirely single pixels, we set $x_{k+1}=x_{k}mod{b}^{p-k}$ and $x_1=mmod{b}^p$. In the same fashion, setting $y_{k+1}=y_{k}mod{b}^{p-k}$ and $y_1=nmod{b}^p$ will result in the number of total columns that contain entirely single pixels (right part of the image). The total number of rows and columns with single pixels are saved to the variables $x_p$ and $y_p$, respectively. The overall number of single pixels after the block division procedure is formulated by

$$Z(b,p)=n·x_p+m·y_p-x_p·y_p.$$

(10)

Notice that in Equation (10) the term $x_p·y_p$ is subtracted to avoid the duplication of single pixels in the count.

As a demonstration example, we consider Figure 2f, where we set $b=6$ and $p=2$ and obtain 401 single pixels, as seen in Table 2. Using the following recursive calls: $x_1=67mod{6}^2=31$, $x_2=31mod{6}^1=1$; therefore $x_p=x_2=1$. Similarly, $y_1=71mod{6}^2$, $y_2=35mod{6}^1=5$; therefore $y_p=y_2=5$. Substituting into Equation (10) the above quantities, we take $Z(6,2)=71·1+67·5-1·5=401$ verifying the total number of single pixels.

The objective of SBD-Fibonacci can be formally stated as follows: given an image of size $m\times n$, find b and p values that minimize Equation (10) under the constrained minimization problem expressed by Equations (11) and (12) as follows:

$$\underset{b,p}{min}Z(b,p)$$

(11)

$$\begin{array}{ccc}\hfill \mathrm{subject} \mathrm{to}:& & x_{k+1}=x_{k}mod{b}^{p-k},y_{k+1}=y_{k}mod{b}^{p-k}\hfill \\ & & x_1=mmod{b}^p,y_1=nmod{b}^p\hfill \\ & & b,p>1\hfill \\ & & b^p>2\hfill \\ & & b,p\in \mathbb{N}.\hfill \end{array}$$

(12)

Block size affects both security and performance. Larger blocks enhance diffusion and security but increase computation and memory needs, while smaller blocks speed up processing but may degrade the resistance to common attacks. Therefore, the block size must be carefully balanced to optimize both security and performance. In particular, minimizing the number of $1\times 1$ blocks is crucial and this balance is the primary motivation behind the proposed optimization strategy.

To solve the above optimization problem, we propose a fast heuristic algorithm presented in Algorithm 6. Overall, the heuristic aims to provide a combination of b and p, used in SBD, that minimizes the instances of singular pixels forming as blocks. This value is represented in variable $z_{best}$, which is initiated as $+\infty$, (line 1). The combination of b and p should also generate a $b^p\times b^p$ block with $b^p\le min\{m,n\}$. In lines 3–14, we examine different b values starting from a predefined threshold $b_{max}$ up to 2, $b_{max}$ can be set from [10, 20] according to image dimensions. The iteration is performed in descending order as the powers $b^p$ will always produce the same modulo value when divided by x, where $x:=min\{m,n\}$. Also, since the powers $b^p$ provide the same modulo, we do not need to iterate through all permutations of $b,p$; thus, we calculate its logarithm (line 4). In lines 4–7, we exclude the possibility of $p=1$ whilst being a feasible solution as it would force SBD to create $b\times b$ blocks. In line 8, we calculate the number of singular pixels using Equation (10) and keep the best $b,p$ combination in variables $b_{best},p_{best}$. The overall time complexity of this algorithm is $\mathcal{O}\left(b_{max}\right)$.

Algorithm 6 SBD-Fibonacci optimizer

Input: $m,n$

Output: $b_{best},p_{best}$ values

1: $z_{best}\leftarrow +\infty$ 2: $x\leftarrow min(m,n)$ 3: for $b\leftarrow b_{max}$ to 2 step $-1$ do 4:     $p\leftarrow \lfloor lo{g}_{b}x\rfloor$ 5:     if $p\le 1$ then 6:         continue 7:     end if 8:     $z^{\prime }\leftarrow Z(b,p)$ 9:     if $z^{\prime }<z_{best}\wedge (b^p\ne m\wedge b^p\ne n)$ then 10:       $z_{best}\leftarrow z^{\prime }$ 11:       $b_{best}\leftarrow b$ 12:       $p_{best}\leftarrow p$ 13:   end if 14: end for 14: return  $b_{best},p_{best}$

6. Experimental Evaluation

Image datasets: We report on the experimental evaluation of the SBD-Fibonacci algorithm relying on six images from [42,43] as depicted in

Table 3. Images characteristics and selected $b,p$ values.

	Lena	Barbara	Street	House	Staircase	Josue
Size	$512\times 512$	$472\times 694$	$2880\times 1920$	$1600\times 2400$	$4032\times 3024$	$6000\times 4000$
b	16	2	20	20	18	10
p	2	8	2	2	2	3

, where $b_{max}$ is equal to 20.

The adopted images are extensively used in the relevant literature (e.g., Lena and Barbara) and also cover a wide range of different image properties e.g., resolution, dimensions, and low-high luminance. Each color image is transformed to grayscale by decomposing the color channels (R, G, and B) into a single channel representing the grayscale intensity. The transformation is performed using the average method ($Gray=(R+G+B)/3$). We should note that the SBD-Fibonacci algorithm can be applied in both grayscale and color images. When dealing with color images, the encryption process involves a two-step approach. First, the color image is decomposed into its respective (R, G, B) components. Each component is then encrypted separately using SBD-Fibonacci. Finally, the encrypted components are concatenated together to obtain the encrypted color image.

Figure 3 describes the process based on which the SBD algorithm produces the blocks illustrated by the red grids.

Performance evaluation: In the following sections, we present simulation results and performance analysis of the SBD-Fibonacci algorithm. Since a robust cryptosystem should demonstrate resistance against various known attacks, our evaluation of the SBD-Fibonacci includes key space analysis, statistical analysis and differential analysis. To ensure statistical reliability, the algorithm has been executed 50 times under identical conditions, i.e., the image dimensions and parameters b and p remain invariant per each experiment. This method of averaging over multiple runs has been employed to compensate for the impact of random variability leading to a more stable and reliable assessment of the algorithm’s capabilities. The results obtained from these 50 runs have been averaged and then discussed in Section 6.1, Section 6.2, Section 6.3, Section 6.4, Section 6.5 and Section 7.

6.1. Histogram Analysis

Histogram analysis provides information on the frequency distribution of gray levels within an image. To ensure the security of an encryption algorithm, it is essential that the histogram of the cipher image exhibits an evenly distributed pattern and is significantly different from the plaintext. From the histograms presented in Figure 4, Figure 5 and Figure 6 it is obvious that the encrypted images are random images and their histograms are distributed uniformly. This shows that there is no connection between the information in the encrypted image and the information in the plaintext one, so a potential attacker does not gain insight into the actual information by checking the encrypted image.

6.2. Key Space Analysis

A secure encryption scheme necessitates a key space that is sufficiently large so as to resist brute-force attacks [12,19]. The proposed encryption algorithm is a symmetric encryption algorithm with a master key L. This is a list of 256 integer values in the range of $[0,255]$. The elements of the list are used to populate the matrices that will be used to encrypt partial blocks of the image. The actual order according to which the elements of L will be used and the minimum number of elements required are defined by the dimensions of the matrix to be encrypted and the choice of parameters b and p. In order for encryption or decryption operations to proceed, both the master key L and the $b,p$ parameters must be known. The key space comprises all possible combinations of master keys with parameters $b,p$. The length of the master key list is $sL=256$; thus, the number of possible keys is calculated as ${256}^{sL}={\left(2^8\right)}^{sL}=2^{8sL}=2^{2024}$.

Therefore, the key space provides a level of security of 2048 bits. Taking into account that different combinations of parameters $b,p$ trigger different combinations of master key (L) elements, the actual level of security is even higher than 2048 bits. The selected value for $sL$, in addition to providing the required level of security, provides the required number of values to minimize reuse of identical K matrices as partial keys. Even for large images (e.g., $8K$ image with high resolution $7680·4320$), the reuse of elements is bearable. The described findings prove that the proposed algorithm is robust against key brute force attacks because of the key space and against key reuse attacks because the probability of having the same key multiple times is negligible.

6.3. Key Sensitivity Analysis

Key sensitivity analysis assesses the level of security provided by an encryption algorithm. It measures how small changes in the encryption key impact the confidentiality of the encrypted image, helping to identify vulnerabilities and enhance the algorithm’s robustness against attacks. Higher values of key sensitivity indicate the robustness of the encryption algorithm [12,19].

Toward the evaluation of the key sensitivity of the proposed algorithm, each image has been encrypted twice using two keys that slightly vary. Once the image is encrypted with the first encryption key generated by Algorithm 4, the second key is created similarly by slightly altering the elements of L, increasing them by 1. Following the generation of the second key, the encryption process is applied to the same image employing the modified key. Finally, the two encrypted images are compared to assess the key sensitivity of the SBD-Fibonacci algorithm.

The key sensitivity value for each image is Lena: 99.549; Barbara: 99.560; Street: 99.551; House: 99.514; Staircase: 99.527; Josue: 99.498. We observe that every image has a key sensitivity value of at least 99%. This verifies that SBD-Fibonacci is key-sensitive; thus, minor changes in the encryption key lead to significant differences in the corresponding encrypted images. The fact that the proposed algorithm is key sensitive makes it robust against any attacks trying to manipulate its operation and retrieve part of or the full encryption key by an iterative similarity-based search in the key space.

6.4. Correlation Analysis

Correlation analysis is a crucial assessment of the quality of the encryption provided by an algorithm, as well as its resistance against attacks and the level of probable information leakage, by evaluating the correlation patterns between the elements of an image, in its original and encrypted form. The similarity or dissimilarity between the corresponding image elements will provide a clear depiction of the algorithm’s security. An image contains adjacent pixels with high correlation (high similarity). When encrypted by a good encryption algorithm, these pixels should not correlate in any way (high dissimilarity). To evaluate our algorithm, we calculate the correlation coefficients in a horizontal, vertical, and diagonal direction, which is given by

$$CC={\displaystyle \frac{{\sum }_{i=1}^n(x_i-\frac{1}{n}{\sum }_{j=1}^n{x}_j)(y_i-\frac{1}{n}{\sum }_{j=1}^n{y}_j)}{\sqrt{{\sum }_{i=1}^n{(x_i-\frac{1}{n}{\sum }_{j=1}^n{x}_j)}^2}\sqrt{{\sum }_{i=1}^n{(y_i-\frac{1}{n}{\sum }_{j=1}^n{y}_j)}^2}}}$$

(13)

In Equation (13), $x_i$ and $y_i$ consist of a pair of adjacent pixels in any of the aforementioned directions, while n is the total number of pairs of adjacent pixels.

The correlation analysis is presented in

Table 4. Correlation between pairs of plaintext and encrypted images.

Image (Size)	CC(P)-H	CC(E)-H	CC(P)-V	CC(E)-V	CC(P)-D	CC(E)-D
Lena ($512\times 512$)	0.9719	0.0580	0.9850	0.0059	0.9593	0.0044
Barbara ($472\times 694$)	0.9107	0.0560	0.9596	0.0003	0.8930	−0.0003
Street ($2880\times 1920$)	0.9751	0.0327	0.9851	−0.0001	0.9661	−0.0003
House ($1600\times 2400$)	0.9677	0.0551	0.9619	−0.0027	0.9400	0.0004
Staircase ($4032\times 3024$)	0.9875	0.1572	0.9949	−0.0081	0.9848	−0.0030
Josue ($6000\times 4000$)	0.9955	0.1472	0.9933	−0.0018	0.9896	0.0012

, Figure 7 and Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5 of the Appendix A, where CC(P), CC(E) denote the correlation coefficient of the plaintext and encrypted image, respectively, and the terms H, V, and D denote the horizontal, vertical, and diagonal directions, respectively. From the results, it can be seen that the correlation for the plaintext image is close to 1, while the encrypted image’s results are close to 0. The above further verifies that the encrypted images by SBD-Fibonacci have an extremely low correlation. This proves that there are no artifacts in the encrypted images that can be attributed to elements of the plaintext images. The encryption process removes any information that may be related to the content of the plaintext image and in practice, hinders potential attackers from easily retrieving such information.

6.5. Information Entropy Analysis

In the context of image encryption, information entropy analysis is a technique used in image encryption to measure the level of uncertainty presented in an encrypted image. It quantifies the diversion among pixel values, thus providing useful insights about the complexity of the encrypted image. The entropy of an image X is given by

$$H\left(X\right)=-\sum _{i=1}^{mn}P\left(x_i\right){log}_{2}P\left(x_i\right),$$

(14)

where $P\left(x_i\right)$ represents the probability of pixel $x_i$ and $m·n$ is the total number of pixels in an encrypted image. To find the probability distribution $P\left(x\right)$, we analyze the frequency of occurrence of each pixel value in the image by (a) counting pixel occurrences, (b) calculating the respective probabilities for each pixel and (c) normalizing probabilities if they do not sum up to one. A grayscale image that achieves an entropy close to 8 confirms the effectiveness of the proposed encryption scheme. Recall that each pixel data has $2^8=256$ possible values; thus the theoretical entropy value is equal to 8 when pixels appear with the same probability.

Interpreting the results in

Table 5. Results for entropy in Equation (14) of the encrypted images in Table 3 by SBD-Fibonacci.

Image	Lena	Barbara	Street	House	Staircase	Josue
(Size)	($\mathbf{512}\times \mathbf{512}$)	($\mathbf{472}\times \mathbf{694}$)	($\mathbf{2880}\times \mathbf{1920}$)	($\mathbf{1600}\times \mathbf{2400}$)	($\mathbf{4032}\times \mathbf{3024}$)	($\mathbf{6000}\times \mathbf{4000}$)
SBD-Fibonacci	7.9995	7.9993	7.9999	7.9998	7.9993	7.9994

, we can state that the average entropy value is greater than 99.99% for all images, which suggests that the proposed algorithm is resistant to statistical analysis and cryptographic attacks.

The current test corroborates previous studies by demonstrating that once the encryption algorithm is deployed, the output images are completely random and reveal no discernible information about the initial plaintext images.

6.6. Differential Attack

In image cryptography, an adversary can potentially exploit the following vulnerability: modify a single pixel or a group of pixels in plaintext and observe the encrypted results. By carefully observing these changes, the adversary can attempt to uncover meaningful relationships between the encrypted images and the plaintext. In this section, we measure the sensitivity of the SBD-Fibonacci algorithm employing two quantitative metrics, the Number of Pixel Change Rate (NPCR), which is given by

$$\mathrm{NPCR}={\displaystyle \frac{{\sum }_{i=1}^m{\sum }_{j=1}^n{D}_{ij}}{mn}}\times 100$$

(15)

and the Unified Average Changing Intensity (UACI), which is given by

$$\mathrm{UACI}={\displaystyle \frac{1}{mn}}\sum _{i=1}^m\sum _{j=1}^n\left|{\displaystyle \frac{C_1(i,j)-C_2(i,j)}{255}}\right|\times 100,$$

(16)

where $C_1$ is the $m\times n$ encrypted image and $C_2$ is the encrypted image after changing a pixel of the plaintext image. Also, $D_{ij}$ equals 1, when the ($i,j$)-th pixels of $C_1$ and $C_2$ are different [12,19]. For an 8-bit grayscale image, the ideal average values of NPCR and UACI are 99.6094% and 33.4635%, respectively [44].

The results shown in

Table 6. Results of NPCR in Equation (15) and UACI in Equation (16) for the images in Table 3 by SBD-Fibonacci.

Image	Lena	Barbara	Street	House	Staircase	Josue
(Size)	($\mathbf{512}\times \mathbf{512}$)	($\mathbf{472}\times \mathbf{694}$)	($\mathbf{2880}\times \mathbf{1920}$)	($\mathbf{1600}\times \mathbf{2400}$)	($\mathbf{4032}\times \mathbf{3024}$)	($\mathbf{6000}\times \mathbf{4000}$)
NPCR (%)	99.6452	99.5405	99.5021	99.4690	98.9307	99.6090
UACI (%)	33.6144	33.7707	32.9965	33.5718	33.2928	33.3734

demonstrate that our proposed algorithm is very sensitive to changes in the plaintext image by one pixel and sufficiently secure to resist differential attack.

Differential attacks aim at extracting information about the encryption key through an iterative process of encrypting plaintext images that are slightly changed. The proposed algorithm is robust against such attacks and does not exhibit relevant vulnerabilities.

6.7. Robustness Analysis

To further validate the robustness of the proposed SBD-Fibonacci encryption scheme, we evaluate its performance under noise and cropping attacks, following the methodology in [19]. For noise attacks, salt-and-pepper noise, with a density of 0.01, 0.02, and 0.05, was added to the encrypted images, and the corrupted ciphertexts were then decrypted. We selected the House image of dimensions 1600 × 2400 for experimentation, and Figure 8 demonstrates the overall results. Even when the noise intensity is high (5%) the proposed algorithm can effectively retrieve the original image despite noise corruption, indicating strong robustness.

6.8. Time Complexity

All experiments were carried out on a Linux machine with an 8-core AMD Radeon 7 5825U CPU running at 4.5 GHz, using hyper-threading (16 logical cores). In

Table 7. Execution Runtime.

Image	Lena	Barbara	Street	House	Staircase	Josue
(Size)	($\mathbf{512}\times \mathbf{512}$)	($\mathbf{472}\times \mathbf{694}$)	($\mathbf{2880}\times \mathbf{1920}$)	($\mathbf{1600}\times \mathbf{2400}$)	($\mathbf{4032}\times \mathbf{3024}$)	($\mathbf{6000}\times \mathbf{4000}$)
SBD (s)	0.00005	0.00045	0.00156	0.00014	0.00176	0.00068
Encryption (s)	0.31577	0.31361	4.66453	4.02217	9.25244	18.87192
SBD-Fibonacci (s)	0.32447	0.37068	5.16071	4.10639	9.76481	19.20553
(Total)

, we present the execution time for (a) the SBD scheme, (b) the encryption process, and (c) the entire (total) execution of the SBD-Fibonacci algorithm. We note that our square block division scheme has the minimum time overhead upon the total execution of our program, while the execution of the encryption algorithm process is the most time-consuming part. In cases of images with large dimensions (e.g., Staircase and Josue), a surge in the runtime of the encryption procedure is observed. However, this increase can be compensated by using coarse-grained parallelism, where each thread is tasked with encrypting and decrypting a different group of pixels. Our encryption scheme benefits from this approach, showcasing a runtime reduction of up to 65%. It should be noted that in the total runtime of our scheme, there are parts of the program that cannot be excluded from the calculation due to their functionality, e.g., RGB to grayscale conversion and image reconstruction from the existing blocks.

7. Discussion

In this section, we compare our proposed algorithm with several recently published State-of-the-Art methods found in [9,10,11,13,14,15,18,20,21,24,28,29,30,36,45,46,47]. Using the Lena image from [42], we encrypted it using SBD-Fibonacci at three different sizes: $128\times 128$, $256\times 256$ and $512\times 512$. Carrying out 50 repetitions of our algorithm for each image size, we measure the quality and the performance of our encryption process by calculating the Entropy, NPCR, and UACI metrics as defined in Equations (14), (15) and (16), respectively. Taking the mean value for each metric corresponding to Lena’s image size, we present the resulting values in “SBD-Fibonacci” row of

Table 8. Comparison of Entropy, NPCR, and UACI values between SBD-Fibonacci algorithm and other encryption methods for “Lena” image across different sizes.

Size	Algorithm Ref	Entropy	NPCR	UACI
$128\times 128$	[45]	7.9882	-	-
	[28]	-	99.6190	33.5000
	[15]	7.9981	99.6073	33.4477
	Average	7.9932	99.6132	33.4739
	SBD-Fibonacci	7.9905	99.6459	33.5420
$256\times 256$	[45]	7.9972	99.6100	31.5400
	[36]	7.5954	99.6302	33.4277
	[30]	7.9974	99.6109	33.4347
	[46]	7.9801	99.3600	32.7200
	[47]	7.9970	99.5800	33.2533
	[10]	7.9973	99.6100	33.4900
	[11]	7.9974	99.6259	33.4718
	[29]	7.9972	99.6246	33.4226
	[13]	7.9974	99.5941	33.4719
	[20]	7.9972	99.6231	30.9135
	[21]	7.9977	99.6000	33.4500
	[15]	7.8993	99.6891	33.3272
	[9]	7.9970	99.5362	31.3218
	Average	7.9624	99.5838	32.8264
	SBD-Fibonacci	7.9975	99.6796	33.3978
$512\times 512$	[45]	7.9992	-	-
	[11]	7.9994	99.6273	33.4691
	[29]	7.9993	99.6174	33.4322
	[14]	7.9998	99.6200	33.4700
	[18]	7.9998	99.6453	33.4733
	[24]	7.9996	99.7453	33.5232
	Average	7.9995	99.6510	33.4735
	SBD-Fibonacci	7.9995	99.6452	33.6144

. In addition, Table 8 displays the respective scores obtained by the above references. In addition to that and for the sake of comparison, the “Average” row in the same table contains the mean value calculated from the associated works outlined. Notice that in each category of size and metric, the greater value between the “Average” and “SBD-Fibonacci” rows is highlighted in bold.

As observed in Table 8, the Entropy, NPCR, and UACI values of our method for Lena $256\times 256$ are superior compared to the average among the related methods. It is also notable that the SBD-Fibonacci algorithm, by operating the direct sum of different generalized Fibonacci matrices, is more powerful against differential attacks than the one proposed in [9], based on the Kronecker product of the identity matrix with a generalized Fibonacci matrix. The above can be justified by the larger variability of encryption keys produced by the direct sum. For Lena $128\times 128$, we have achieved the highest NPCR score of 99.6459% and the highest UACI score of 33.5420%. Even though in this case the Entropy is not the maximum, it is still effective as it is very close to the ideal theoretical value. Finally, for Lena $512\times 512$ our Entropy value coincides with the average of the related works maintaining its effectiveness, while UACI reaches the highest value. On the other hand, NPCR is close to the ideal value. It is worth mentioning that in terms of the Entropy metric, it is evident that the performance of the SBD-Fibonacci algorithm improves as the image size increases, a remarkable attribute that renders SBD-Fibonacci algorithm an appropriate candidate for the encryption of high-resolution images used in modern applications.

8. Conclusions

In this paper, we introduce a novel encryption-decryption approach, termed SBD-Fibonacci, suitable for the encryption of non-square and high-resolution images used in modern applications. This is achieved by a square block division scheme combined with an optimization process that dynamically partitions any input image into optimally sized square blocks to enable efficient encryption without resizing or distortion. The security of this scheme is further enhanced by the Lagrange Four-Square algorithm to eliminate all the small-sized square sub-blocks produced by the block division. The encryption key is generated using the direct sum of powers of generalized Fibonacci matrices, ensuring key matrix invertibility, strong diffusion properties, and security levels. Extensive experiments conducted on a range of commonly used benchmark images indicate that SBD-Fibonacci exhibits high resistance to differential and cryptographic attacks, as well as noise corruption and cropping attacks. Moreover, a comparative analysis of the proposed techniques with some recently published State-of-the-Art algorithms on several metrics demonstrates that SBD-Fibonacci achieves a high level of security. Most notably, its performance improves in terms of the entropy metric as the image size increases, rendering it well-suited for the encryption of high-resolution images. Although SBD-Fibonacci offers significant efficiency in handling non-square images and simplifies key management, there is still room for further improvements. The first next step is to extensively test the proposed algorithm against State-of-the-Art cryptanalysis techniques. In the future, we plan to exploit hybrid methods found in the literature to ameliorate our proposed SBD-Fibonacci image encryption scheme in terms of the encryption complexity of large-scale images and encryption key management. A future goal will also involve the application of parallel computing techniques to optimize computational speed and performance on color image encryption of medical images, multimedia, and real-time image streams.