An Optimization Framework for Allocating and Scheduling Multiple Tasks of Multiple Logistics Robots
Abstract
1. Introduction
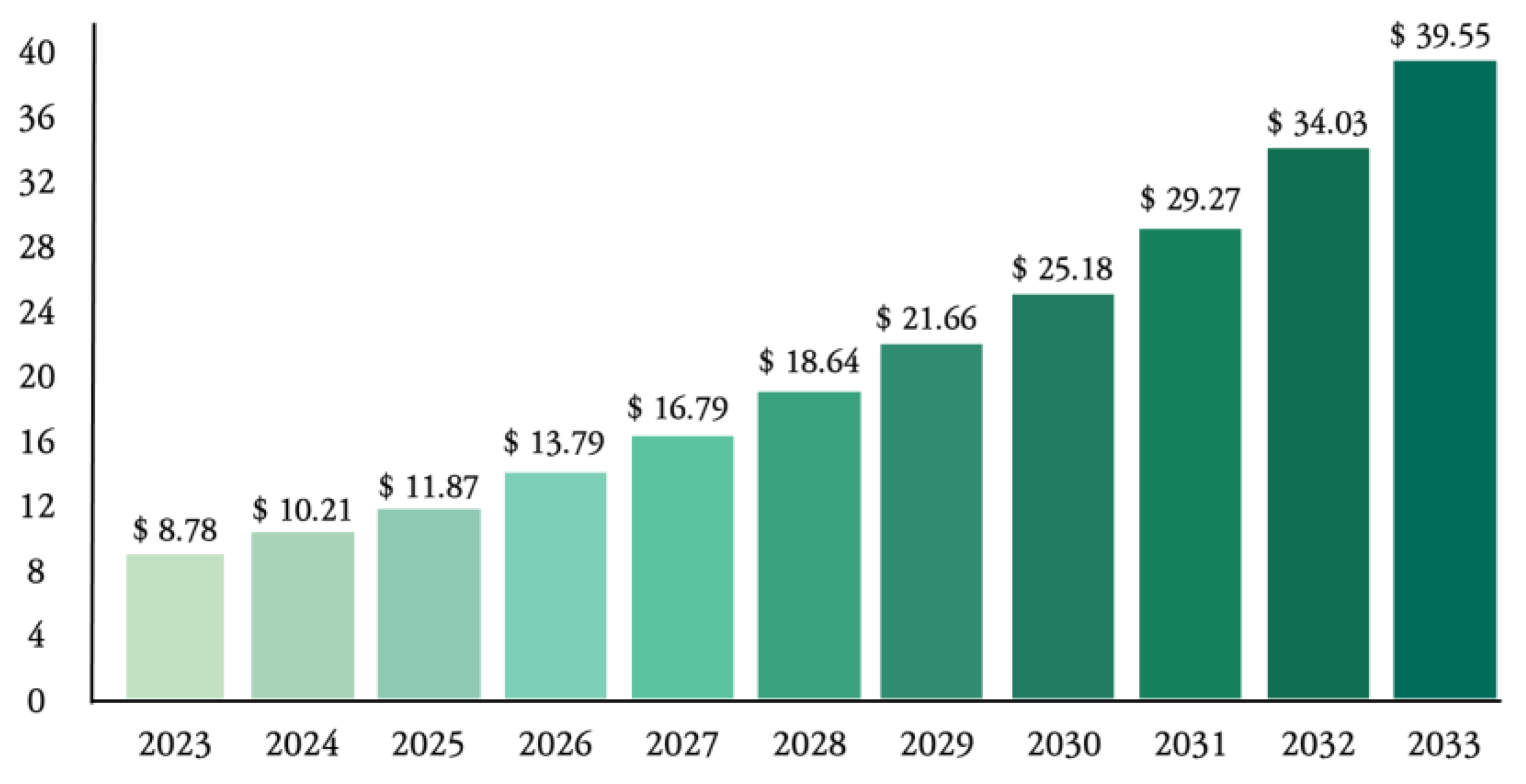
1.1. Logistics Robot Trends
1.2. Introduction to Logistics Robots and Control Systems
- Path planning: Computing efficient travel routes between a robot’s current location and its destination.
- Task allocation: Assigning tasks from upper-level systems to individual robots based on their current state.
- Traffic control: Predicting potential collisions or congested zones and preventing jams or bottlenecks to minimize robot downtime.
- Charging management: Issuing charging commands based on the robot’s battery status and operational schedule.
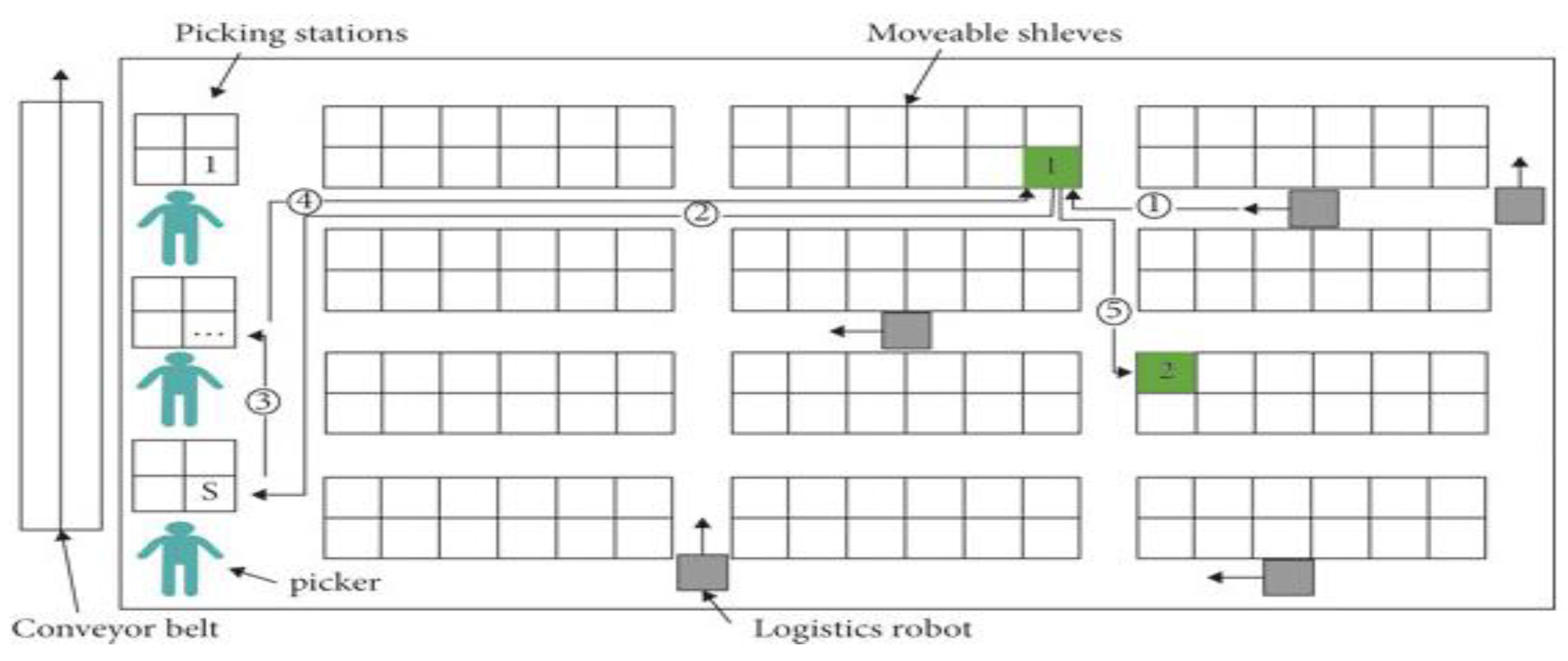
1.3. Introduction to Order Picking and Its Methods
- Individual picking: Picking one order at a time; simple but inefficient due to high travel time. Used in industries with specialized items.
- Batch picking: Grouping multiple orders to collect shared items together, often used in the RMFS.
- Cluster picking: Grouping orders with overlapping item locations to improve efficiency; one worker processes multiple orders at once.
- Wave picking: Grouping and processing orders in scheduled time intervals, useful for handling real-time e-commerce orders.
1.4. Research Distinctiveness and Purpose
- Single-task robot (ST): Robots perform only one task at a time.
- Multi-task robot (MT): Robot performs multiple tasks at a time.
- Single-robot task (SR): One robot is required to perform a task.
- Multi-robot task (MR): Two or more robots are required to perform a task.
2. Literature Review
2.1. Multi-Robot Task Allocation in Distribution Centers
2.2. Multi-Robot Task Allocation in Various Environments
3. Task Scheduling Framework
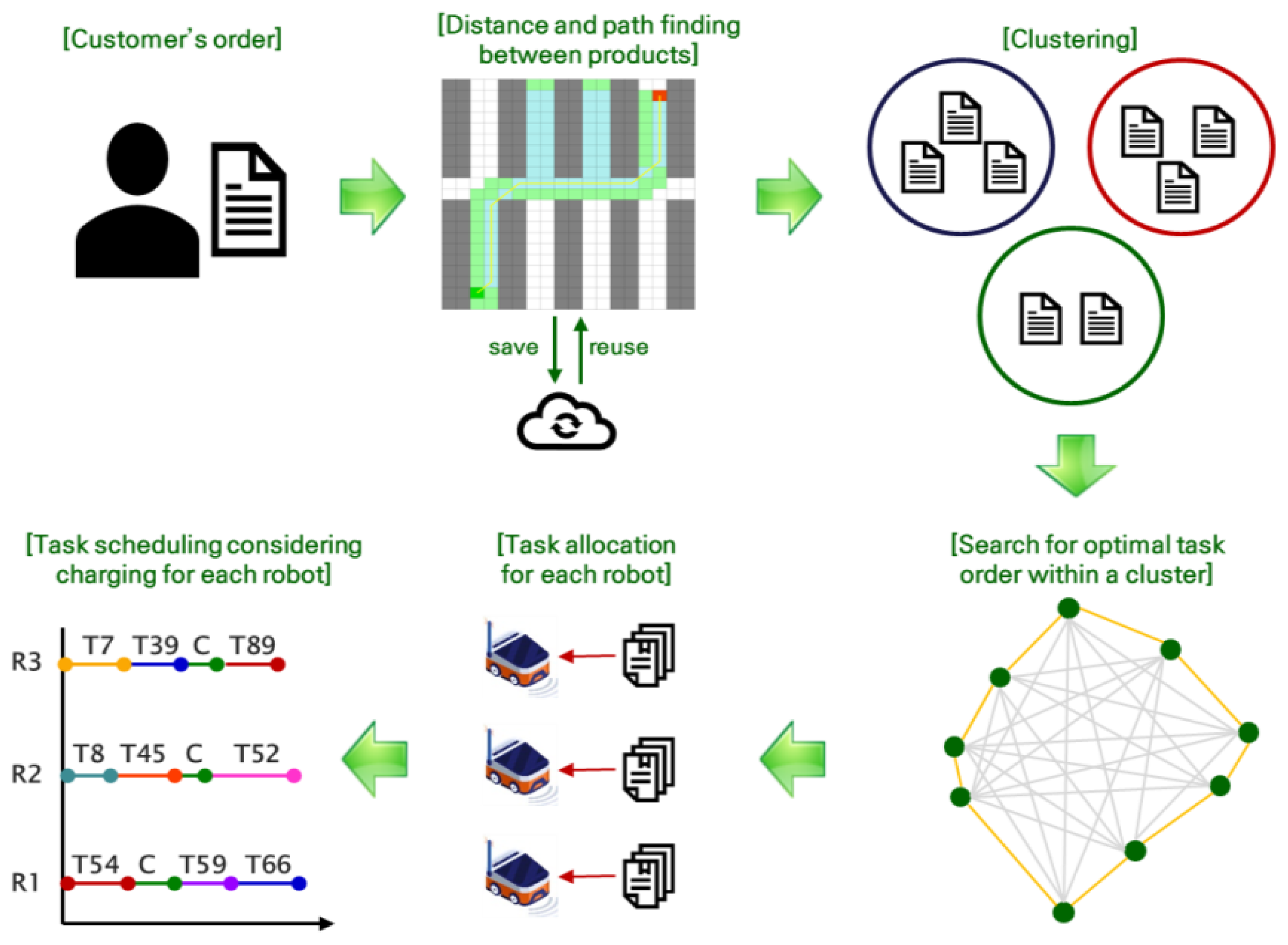
3.1. Problem Definition and Framework
- Step 1: Distance and path calculation
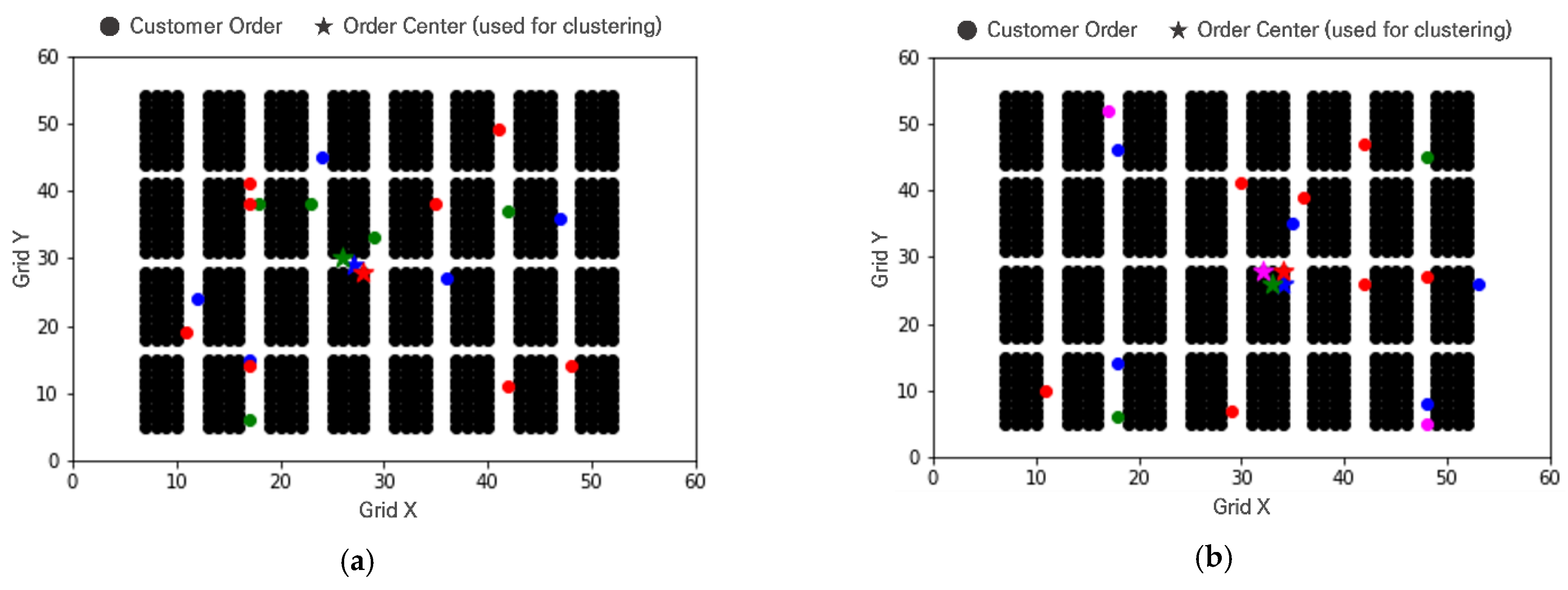
- Step 2: Order clustering
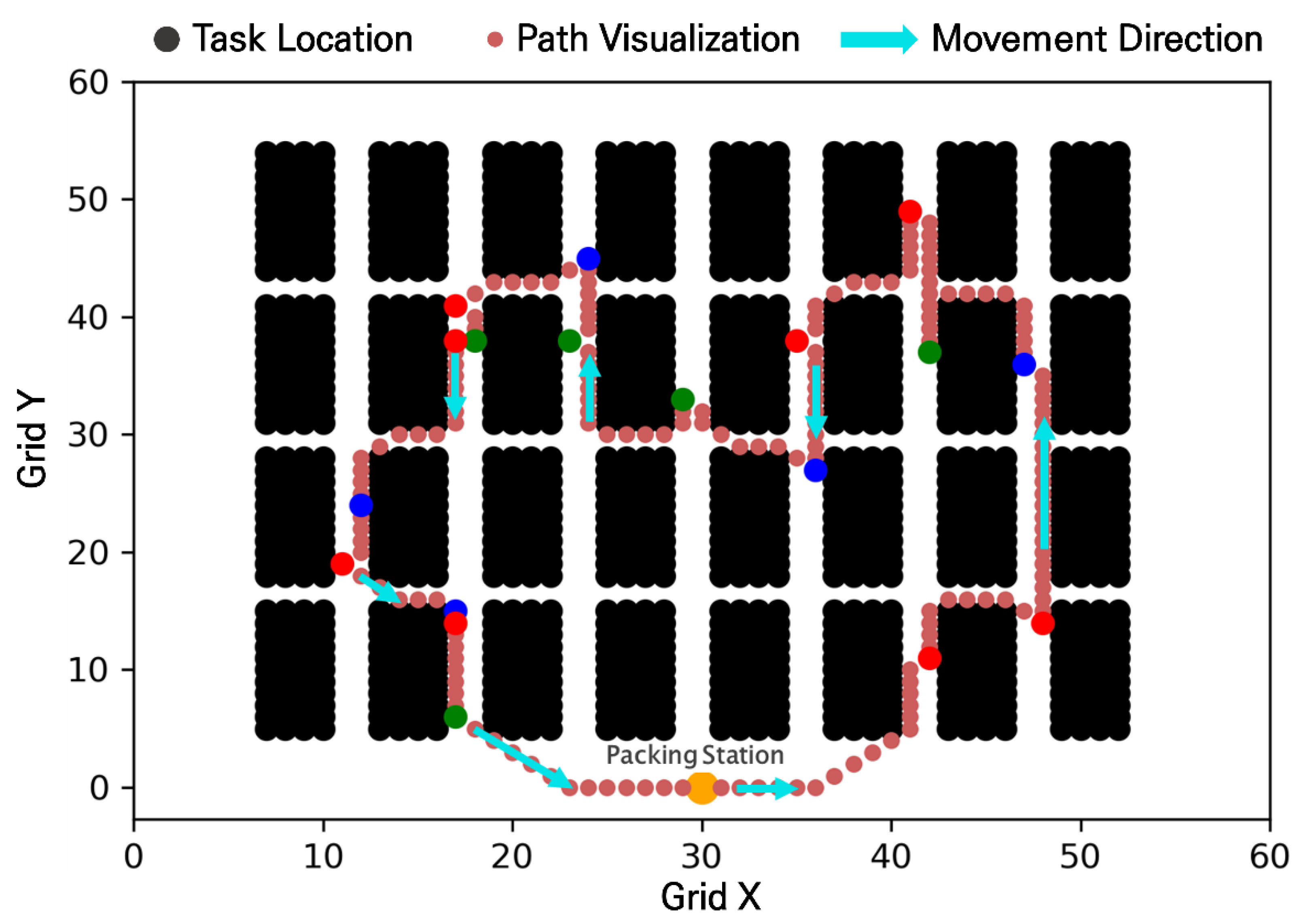
- Step 3: Intra-cluster task sequencing
- Step 4: Robot-level task allocation
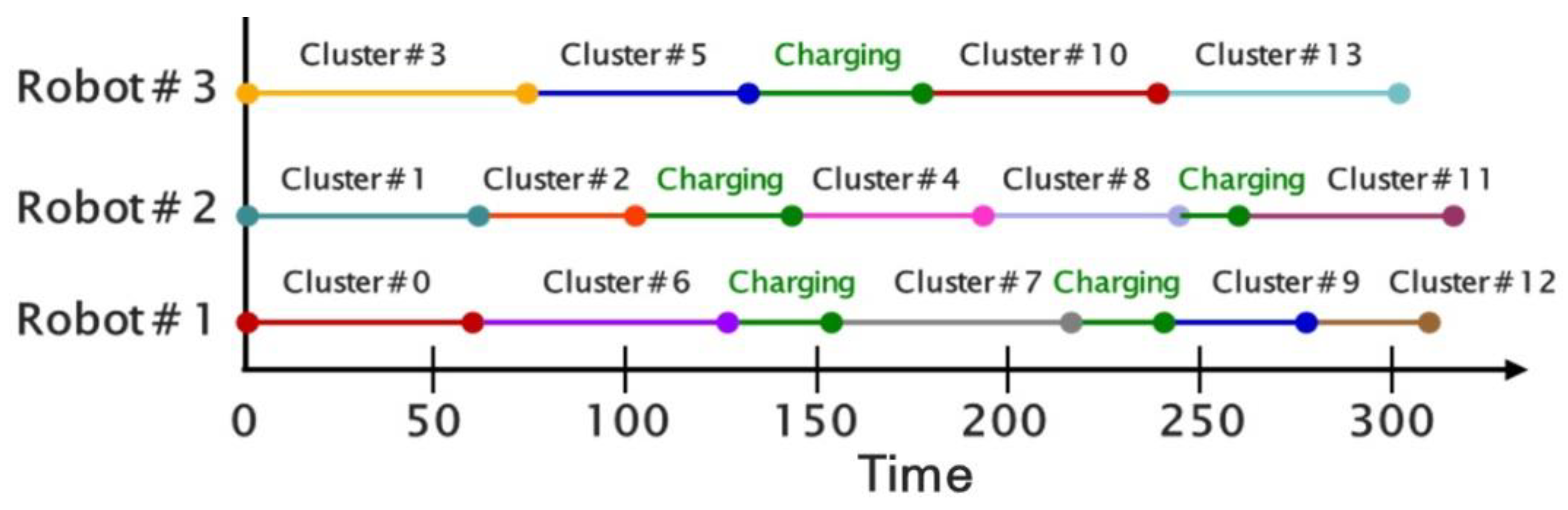
- Step 5: Charging-aware task scheduling
3.2. Path Planning Algorithm
| Algorithm 1 A* algorithm flowchart. | |
| 1. | Define the start node and target node . |
| 2. | Add to the open list and compute its . |
| 3. | Select the node with the smallest from the open list as the current node and move it to the closed list. |
| 4. | For each neighboring node not in the closed list, update its , set the current node as its parent, and add it to the open list. |
| 5. | Repeat steps 3–4 until the goal node is selected as the current node. |
3.3. Clustering
| Algorithm 2 Capacity-Constrained Hierarchical Clustering | |
| 1. | Input: |
| 2. | WorksetNum: Order |
| 3. | Time: Working time |
| 4. | Capacity: Order Capacity |
| 5. | Distance: Distance between |
| 6. | Output: Clusters |
| 7. | While min(Capacity) + nextMin(Capacity) ≤ 1 do |
| 8. | P ← pairs with combined capacity ≤ 1 |
| 9. | minDistance ← ∞ |
| 10. | For all pairs (a, b) in P do |
| 11. | If Distance[a][b] < minDistance then |
| 12. | minDistance ← Distance[a][b] |
| 13. | A, B ← a, b |
| 14. | End if |
| 15. | End for |
| 16. | Merge clusters A and B |
| 17. | Update cluster list, delete merged entries |
| 18. | Recalculate distances using single linkage |
| 19. | End while |
3.4. Search for Optimal Work Order Within a Cluster
3.5. Task Allocation for Each Robot
3.6. Scheduling for Each Robot
4. Numerical Experiment and Results
4.1. Experimental Configuration
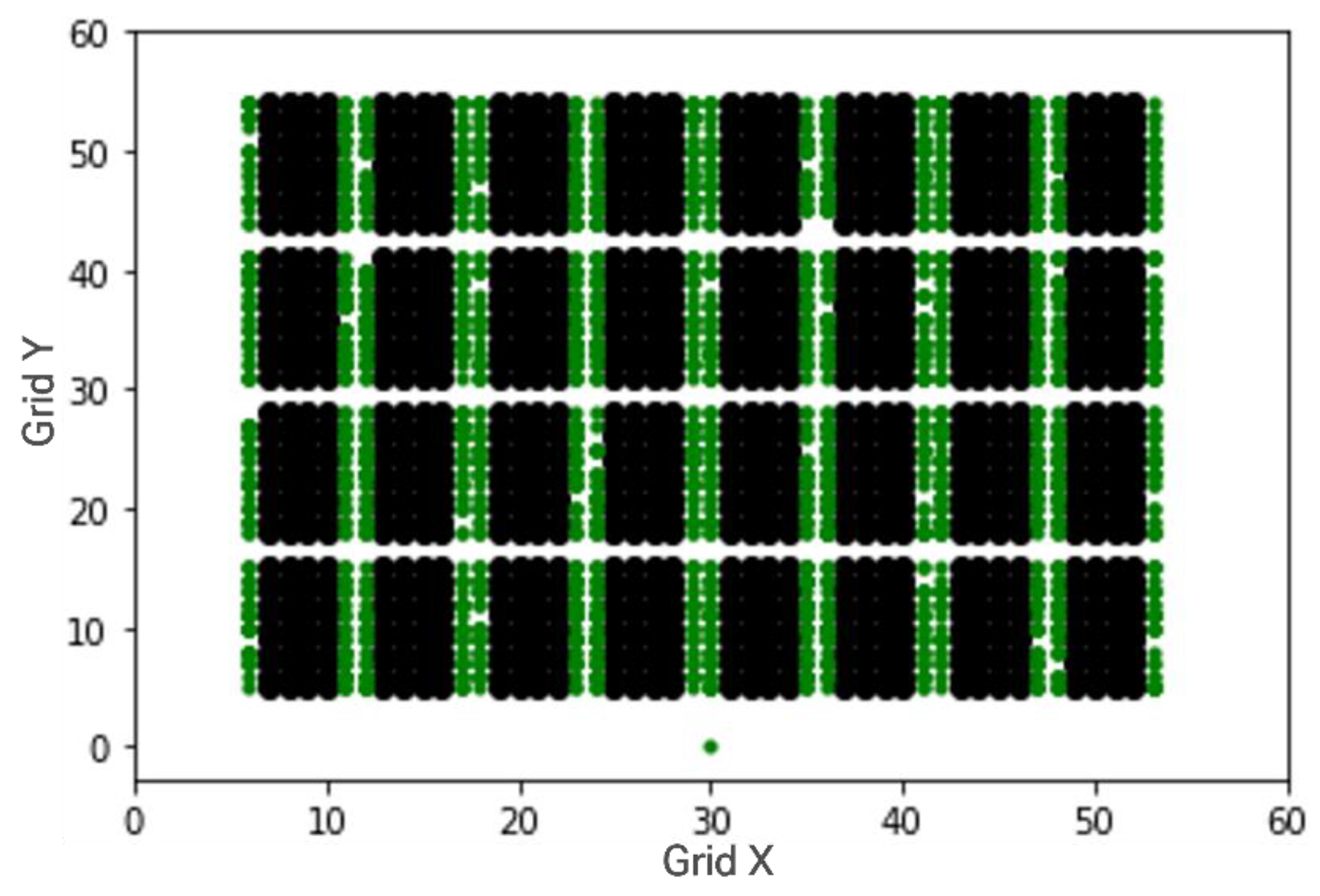
4.2. Numerical Experiment 1—Distance and Path Search Time
4.3. Numerical Experiment 2—Framework Execution Time and Scalability
5. Conclusions and Future Studies
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.-Y. A Study on Implement of QRcode Recognition System for Localization and Work Efficiency of Logistics Robot. Master’s Thesis, Hankyong National University, Anseong, Republic of Korea, 2019. [Google Scholar]
- Seo, J.-H. Multi-Robot Path Planning for Dynamic Environments Including Multiple Waypoints Based on Genetic Algorithms and Reinforcement Learning. Master’s Thesis, Kyungpook National University, Daegu, Republic of Korea, 2023. [Google Scholar]
- Hana Securities Co., Ltd. Logistics Robots (AMR) Overweight: Why Invest in Logistics Robots Now? Available online: https://www.hanaw.com/download/research/FileServer/WEB/industry/industry/2023/05/12/230512_AMR_industry.pdf (accessed on 26 May 2024).
- Precedence Research. Logistics Robotics Market Size, Share, and Trends 2024 to 2033. Available online: https://www.precedenceresearch.com/logistics-robotics-market (accessed on 2 July 2024).
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order-picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Yuan, R.; Li, J.; Wang, X.; He, L. Multirobot Task Allocation in e-Commerce Robotic Mobile Fulfillment Systems. Math. Probl. Eng. 2021, 2021, 6308950. [Google Scholar] [CrossRef]
- Azadeh, K.; Roy, D.; de Koster, R.; Khalilabadi, S.M.G. Zoning strategies for human–robot collaborative picking. Decis. Sci. 2023, 56, 50–70. [Google Scholar] [CrossRef]
- Azadeh, K.; De Koster, R.; Roy, D. Robotized Warehouse Systems: Developments and Research Opportunities; ERIM report series research in management, ERS-2017-009-LIS; Erasmus Research Institute of Management: Rotterdam, The Netherlands, 2017. [Google Scholar]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Agrawal, A.; Bedi, A.S.; Manocha, D. Rtaw: An attention inspired reinforcement learning method for multi-robot task allocation in warehouse environments. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1393–1399. [Google Scholar]
- Sarkar, C.; Paul, H.S.; Pal, A. A scalable multi-robot task allocation algorithm. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 5022–5027. [Google Scholar]
- Yuan, R.; Dou, J.; Li, J.; Wang, W.; Jiang, Y. Multi-robot task allocation in e-commerce RMFS based on deep reinforcement learning. Math. Biosci. Eng. MBE 2022, 20, 1903–1918. [Google Scholar] [CrossRef] [PubMed]
- Oh, S. Multi-Agent Route Optimization for Robotic Mobile Fulfillment Systems. Master’s Thesis, Seoul National University, Seoul, Republic of Korea, 2020. [Google Scholar]
- Chen, X.; Li, Y.; Liu, L. A coordinated path planning algorithm for multi-robot in intelligent warehouse. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2945–2950. [Google Scholar]
- Yang, S.; Zhang, Y.; Ma, L.; Song, Y.; Zhou, P.; Shi, G.; Chen, H. A novel maximin-based multi-objective evolutionary algorithm using one-by-one update scheme for multi-robot scheduling optimization. IEEE Access 2021, 9, 121316–121328. [Google Scholar] [CrossRef]
- Shetty, N.; Sah, B.; Chung, S.H. Route optimization for warehouse order-picking operations via vehicle routing and simulation. SN Appl. Sci. 2020, 2, 311. [Google Scholar] [CrossRef]
- Žulj, I.; Salewski, H.; Goeke, D.; Schneider, M. Order batching and batch sequencing in an AMR-assisted picker-to-parts system. Eur. J. Oper. Res. 2022, 298, 182–201. [Google Scholar] [CrossRef]
- Martin, J.G.; Muros, F.J.; Maestre, J.M.; Camacho, E.F. Multi-robot task allocation clustering based on game theory. Robot. Auton. Syst. 2023, 161, 104314. [Google Scholar] [CrossRef]
- Tihanyi, D.; Lu, Y.; Karaca, O.; Kamgarpour, M. Multi-robot task allocation for safe planning against stochastic hazard dynamics. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar]
- Paul, S.; Ghassemi, P.; Chowdhury, S. Learning scalable policies over graphs for multi-robot task allocation using capsule attention networks. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 8815–8822. [Google Scholar]
- Shibata, K.; Jimbo, T.; Odashima, T.; Takeshita, K.; Matsubara, T. Learning locally, communicating globally: Reinforcement learning of multi-robot task allocation for cooperative transport. IFAC-PapersOnLine 2023, 56, 11436–11443. [Google Scholar] [CrossRef]
- Park, B.; Kang, C.; Choi, J. Cooperative multi-robot task allocation with reinforcement learning. Appl. Sci. 2021, 12, 272. [Google Scholar] [CrossRef]
- Cai, Y. Online Scheduling of Operator Assistance for Multi-Robot Teams with Uncertain Robot Capabilities and Environments. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2023. [Google Scholar]
- Hussein, A.; Khamis, A. Market-based approach to multi-robot task allocation. In Proceedings of the 2013 International Conference on Individual and Collective Behaviors in Robotics (ICBR), Sousse, Tunisia, 15–17 December 2013; pp. 69–74. [Google Scholar]
- Choi, H.L.; Brunet, L.; How, J.P. Consensus-based decentralized auctions for robust task allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- Dimmig, C.A.; Wolfe, K.C.; Moore, J. Multi-robot planning on dynamic topological graphs using mixed-integer programming. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 5394–5401. [Google Scholar]
- Hong, S.; Hwang, I.; Jang, Y.J. Practical q-learning-based route-guidance and vehicle assignment for oht systems in semiconductor fabs. IEEE Trans. Semicond. Manuf. 2022, 35, 385–396. [Google Scholar] [CrossRef]
- Chung, S.Y.; Hwang, M.J.; Yoon, H.J. Task Allocation Method for Multiple Manipulators to Insert Pem Nuts in Press Forming Process; Institute of Control, Robotics and Systems (ICROS): Seoul, Republic of Korea, 2016; pp. 102–103. [Google Scholar]
- Ghassemi, P.; Chowdhury, S. Multi-robot task allocation in disaster response: Addressing dynamic tasks with deadlines and robots with range and payload constraints. Robot. Auton. Syst. 2022, 147, 103905. [Google Scholar] [CrossRef]
- Shelkamy, M.; Elias, C.M.; Mahfouz, D.M.; Shehata, O.M. Comparative analysis of various optimization techniques for solving multi-robot task allocation problem. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 538–543. [Google Scholar]
- Liu, X.F.; Lin, B.C.; Zhan, Z.H.; Jeon, S.W.; Zhang, J. An efficient ant colony system for multi-robot task allocation with large-scale cooperative tasks and precedence constraints. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–8. [Google Scholar]
- Kong, X.; Gao, Y.; Wang, T.; Liu, J.; Xu, W. Multi-robot task allocation strategy based on particle swarm optimization and greedy algorithm. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 1643–1646. [Google Scholar]
- Patle, B.K.; Babu, G.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of autonomous path planning algorithms for mobile robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]

| Higher System Interface | Interfaces with upper systems (e.g., ERP, MES, WMS) to receive work orders, report results, and transmit status of ACS and logistics robots. |
| Path finding | Calculates optimal routes based on departure/arrival nodes to ensure efficient task execution. |
| Task allocation | Assigns and adjusts work orders based on robot status and workload. |
| Traffic control | Prevents congestion by predicting interference zones and rerouting robots to avoid delays. |
| Charging | Issues charging commands based on battery level and robot activity state (e.g., moving, standby) to maintain continuous operation. |
| Logistics robot control system operation concept | 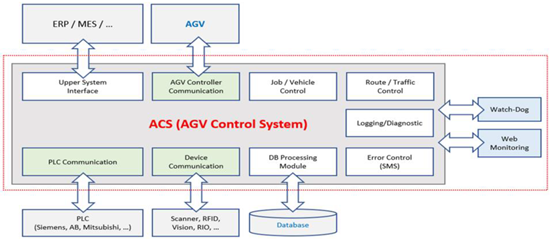 |
| Ref. | Method | Approach | Techniques | MRTA Type |
|---|---|---|---|---|
| [2] | GTP | Task allocation and path planning | Meta-heuristic, Reinforcement learning | ST-SR |
| [6] | GTP | Task scheduling | Meta-heuristic | |
| [10] | GTP | Task allocation | Reinforcement learning | |
| [11] | GTP | Task clustering | Clustering | |
| [12] | GTP | Task allocation | Reinforcement learning | |
| [13] | GTP | Path planning | MILP | |
| [14] | GTP | Path planning | Path planning | |
| [15] | GTP | Multi-robot scheduling | Meta-heuristic | |
| [16] | PTP | Route optimization | MILP | |
| [17] | PTP | Batching and sequencing | Heuristic |
| Ref. | Environment | Approach | Techniques | MRTA Type |
|---|---|---|---|---|
| [18] | Thermal power plant | Task clustering and assignment | Game theory | ST-SR |
| [19] | Dynamic risky environment | Risk-aware task allocation | MDP | ST-SR |
| [20] | Fixed deadline tasks | Reinforcement learning | Graph RL, CapAM | ST-SR |
| [21] | Multi-robot coordination | Task selection | MDP + RL | ST-SR |
| [22] | Scalable robot/task space | Cross-attention RL | Deep RL | ST-SR |
| [23] | Human-robot system | Assisted task scheduling | Operator support model | MT-SR |
| [24] | Heterogeneous robot system | Auction-based allocation | Utility function | ST-SR |
| [25] | Multi-tasking system | Multi-allocation auction | Consensus bundle algorithm | MT-SR |
| [26] | Cooperative group planning | Task planning | Dynamic topology graph | ST-SR |
| [27] | Semiconductor transport | Vehicle-path assignment | Q-learning | ST-SR |
| [28] | Robotized assembly | Task sequencing | Collision-aware scheduling | ST-SR |
| [29] | Task-range-payload constraints | Multi-tour scheduling | Bipartite graph matching | ST-SR |
| [30] | General MRTA | Solver comparison | GA, ACO | ST-SR |
| [31] | Time-extended cooperation | MRTA with constraints | ACO | ST-SR |
| [32] | Large-scale MRTA | Task-robot pairing | PSO + Greedy | ST-SR |
| Order ID | Subtask IDs | Center Point (x, y) | Capacity |
|---|---|---|---|
| 0 | 1034, 2827 | (32, 10) | 0.09 |
| 1 | 1387, 1764, 1112, 1029 | (22, 18) | 0.21 |
| 2 | 2187, 1485, 2856, 1035, 744 | (27, 29) | 0.32 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 47 | 670, 2199, 1747, 2567, 2546, 2907, 1841 | (34, 28) | 0.40 |
| 48 | 755, 1064, 2144 | (21, 41) | 0.19 |
| 49 | 1395, 2917 | (36, 26) | 0.17 |
| Cluster ID | Order IDs | Total Capacity |
|---|---|---|
| 0 | 2, 32, 40 | 0.91 |
| 1 | 4, 18, 47, 20 | 0.96 |
| 2 | 5, 14 | 0.62 |
| 3 | 6, 41, 48, 38 | 0.98 |
| 10 | 17, 45, 46, 28, 3 | 0.97 |
| 11 | 19, 21, 1, 37, 27 | 0.82 |
| 12 | 24 | 0.54 |
| 13 | 25, 43, 31, 22 | 0.89 |
| Parameters and Decision Variable | ||
|---|---|---|
| Set of sub-task nodes | ||
| Number of sub-task nodes | ||
| { | 0, Otherwise | |
| Artificial variables to prevent subtours | ||
| Cluster ID | Order IDs | Subtask IDs |
|---|---|---|
| 0 | 2, 32, 40 | 2187, 1485, 2856, 1035, 744, 2557, 1773, 1118, 1026, 1418, 2894, 2138, 679, 2509, 1058, 1061, 1034, 2531 |
| 1 | 4, 18, 47, 20 | 2888, 1126, 3206, 1094, 2135, 1086, 2925, 670, 2199, 1747, 2567, 2546, 2907, 1841, 2885, 1072 |
| 2 | 5, 14 | 3217, 2123, 1114, 1852, 2895, 2905, 2488, 2212, 2574, 1752 |
| ⋮ | ⋮ | ⋮ |
| 11 | 19, 21, 1, 37, 27 | 378, 745, 733, 1387, 1764, 1112, 1029, 1452, 1774, 725, 2857, 370, 1029, 1462, 1819 |
| 12 | 24 | 738, 1065, 2512, 1059, 2481, 2846, 2830, 2493 |
| 13 | 25, 43, 31, 22 | 3218, 1043, 379, 1814, 2183, 1085, 1477, 1777, 2474, 1752, 2472, 2893, 1386, 1425, 705, 1760 |
| Cluster ID | Subtask ID Sequence | Total Time |
|---|---|---|
| 0 | 2531 → 2894 → 2856 → 2557 → 2509 → 2138 → 2187 → 1773 → 1418 → 1485 → 1061 → 1118 → 1058 → 744 → 679 → 1035 → 1034 → 1026 | 63 m |
| 1 | 2885 → 2888 → 3206 → 2907 → 2546 → 2135 → 2199 → 2925 → 2567 → 1841 → 1072 → 1126 → 1094 → 670 → 1086 → 1747 | 64 m |
| 2 | 1752 → 1114 → 1852 → 2212 → 2574 → 3217 → 2905 → 2895 → 2488 → 2123 | 37 m |
| ⋮ | ⋮ | ⋮ |
| 11 | 1029 → 1029 → 725 → 370 → 378 → 733 → 745 → 1112 → 1774 → 2857 → 1764 → 1819 → 1462 → 1452 → 1387 | 53 m |
| 12 | 738 → 1059 → 1065 → 2512 → 2493 → 2846 → 2481 → 2830 | 34 |
| 13 | 1752 → 1814 → 1760 → 2183 → 2474 → 2472 → 2893 → 3218 → 1777 → 1477 → 1425 → 705 → 379 → 1043 → 1085 → 1386 | 59 |
| Parameters and Decision Variable | ||
|---|---|---|
| Set of robots | ||
| Set of clusters | ||
| Time limit when all robots have finished their work | ||
| { | 0, Otherwise | |
| Parameters and Decision Variable | |
|---|---|
| Set of clusters assigned to a robot | |
| F | Maximum battery capacity of the robot |
| Robot | Cluster Execution Order (Execution Time) | End Time |
|---|---|---|
| 1 | 0(63) → 6(70) → Charging (19) → 7(59) → Charging (32) → 9(31) → 12(34) | 308 |
| 2 | 1(64) → 2(37) → Charging (43) → 4(49) → 8(54) → Charging (15) → 11(53) | 315 |
| 3 | 3(73) → 5(61) → Charging (44) → 10(63) → 13(59) | 300 |
| Iteration | 1 | 2 | 3 | 4 | 5 | Full Work |
|---|---|---|---|---|---|---|
| Time required | 8 m 57 s | 6 m 56 s | 5 m 15 s | 4 m 3 s | 2 m 37 s | About 35 m |
| Number of Orders (Subtasks) | Number of Robots | Clustering | TSP | Task Allocation | Scheduling | Total |
|---|---|---|---|---|---|---|
| 50 (203) | 3 | 0.02 s | 5 s | 0.1 s | 0.1 s | 5.22 s |
| 5 | 0.1 s | 0.2 s | 5.32 s | |||
| 100 (409) | 3 | 0.14 s | 8 s | 0.1 s | 0.2 s | 8.44 s |
| 5 | 0.1 s | 0.3 s | 8.54 s | |||
| 10 | 0.2 s | 0.5 s | 8.84 s | |||
| 300 (1213) | 5 | 4 s | 65 s (5 s) | 0.3 s | 0.6 s | 69.9 s (9.9 s) |
| 10 | 1.2 s | 1.0 s | 71.2 s (11.2 s) | |||
| 30 | 4.2 s | 2.5 s | 75.7 s (15.7 s) | |||
| 1000 (4007) | 30 | 142 s | 397 s (7 s) | 19 s | 2.4 s | 560.4 s (170.4 s) |
| 50 | 40 s | 3.0 s | 582.0 s (192 s) | |||
| 100 | 156 s | 4.2 s | 699.2 s (309.2 s) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, B.; Kim, M.; Kim, H. An Optimization Framework for Allocating and Scheduling Multiple Tasks of Multiple Logistics Robots. Mathematics 2025, 13, 1770. https://doi.org/10.3390/math13111770
Choi B, Kim M, Kim H. An Optimization Framework for Allocating and Scheduling Multiple Tasks of Multiple Logistics Robots. Mathematics. 2025; 13(11):1770. https://doi.org/10.3390/math13111770
Chicago/Turabian StyleChoi, Byoungho, Minkyu Kim, and Heungseob Kim. 2025. "An Optimization Framework for Allocating and Scheduling Multiple Tasks of Multiple Logistics Robots" Mathematics 13, no. 11: 1770. https://doi.org/10.3390/math13111770
APA StyleChoi, B., Kim, M., & Kim, H. (2025). An Optimization Framework for Allocating and Scheduling Multiple Tasks of Multiple Logistics Robots. Mathematics, 13(11), 1770. https://doi.org/10.3390/math13111770







