(2, 4)-Colorability of Planar Graphs Excluding Cycles with 3, 4, and 6 Vertices

Abstract

A defectivek-coloring is a coloring on the vertices of a graph with colors $1,2,\dots ,k$ where adjacent vertices may have the same color. A $(d_1,d_2)$-coloring of a graph G is a defective two-coloring such that each vertex colored by i has at most $d_i$ adjacent vertices of the same color, where $i=1,2$. A graph G is $(d_1,d_2)$-colorable if it admits $(d_1,d_2)$-coloring. For planar graphs excluding cycles with three, four, and six vertices, Dross and Ochem, and additionally Sittitrai and Pimpasalee, have studied their defective 2-coloring. They showed that such graphs are $(0,6)$- and $(3,3)$-colorable, respectively. We show in this work that these graphs are also $(2,4)$-colorable.

1. Introduction

Independently, Andrews and Jacobson [1], Cowen et al. [2], and Harary and Jones [3] initiated the idea of defective coloring (or improper coloring). Let $d_1,d_2,\dots ,d_k$ be non-negative integers. A $(d_1,d_2,\dots ,d_k)$-coloring of a graph G is a coloring on the vertices of G using colors $1,2,\dots ,k$ so that every vertex with color i has at most $d_i$ adjacent vertices of the same color $(i\in \{1,2,\dots ,k\left\}\right)$. A graph G is $(d_1,d_2,\dots ,d_k)$-colorable if it admits $(d_1,d_2,\dots ,d_k)$-coloring.

Due to the fact that any k-colorable graph is a $(d_1,d_2,\dots ,d_k)$-colorable graph where $d_i=0$ for $i=1,2,3,\dots ,k$, defective coloring generalizes the notion of proper coloring. For example, one way to rephrase the Four Color Theorem, which was established by Appel and Haken [4,5], is that all planar graphs are $(0,0,0,0)$-colorable.

There are several sufficient conditions for a planar graph to be three-colorable, or equivalently $(0,0,0)$-colorable. All planar graphs, for example, that exclude cycles with three vertices are three-colorable (Grötzsch [6]). Every planar graph excluding cycles with four and five cycles was speculated to be three-colorable, known as Steinberg’s conjecture (appearing in open problem 2.9 of Jensen and Toft [7]). Although Cohen-Addad et al. [8] later disproved this conjecture, several researchers have persisted in investigating results related with Steinberg’s conjecture by using defective coloring [9,10]. Several studies investigate $(d_1,d_2,d_3)$-colorable planar graphs that exclude cycles with specific numbers of vertices (e.g., [2,11,12,13]).

A $(d_1,d_2)$-coloring on planar graphs excluding cycles with four and five vertices was first studied by Sittitrai and Nakprasit [14], who were motivated by Steinberg’s conjecture. These graphs were shown to be $(2,9)$-, $(3,5)$-, and $(4,4)$-colorable. Later, Liu and Lv [15] showed that these graphs are $(2,6)$-colorable, while Liu and Xiao [16], and independently Li et al. [17] proved that these graphs are $(3,3)$-colorable.

In addition, planar graphs excluding cycles with four and six vertices were shown to be $(2,9)$-colorable by Ma et al. [18], and $(3,4)$-colorable by Nakprasit et al. [19].

Havet and Sereni [20] showed that planar graphs excluding three particular short cycles are $(2,2)$-colorable, whereas Borodin and Kostochka [21] proved that planar graphs excluding cycles with three, four, and five vertices (i.e., planar graphs with girth at least six) are $(1,4)$-colorable.

Dross and Ochem [22] showed that planar graphs excluding cycles with three, four, and six vertices are $(0,6)$-colorable. Sittitrai and Pimpasalee [23] also showed that these graphs are also $(3,3)$-colorable. These prompted the following conjecture.

Conjecture 1. 

Every planar graph excluding cycles with three, four, and six vertices is $(d_1,d_2)$-colorable if $d_1+d_2\ge 6$.

In this work, we partially verify the conjecture via the following theorem.

Theorem 1. 

Every planar graph excluding cycles with three, four, and six vertices is $(2,4)$-colorable.

We present here the notation and terminology used in this work. An h-vertex is a vertex with degree h, whereas $h^{+}$-vertex and $h^{-}$-vertex are vertices with a degree not less than h and not more than h, respectively. These definitions extend similarly to faces.

Let f be a face. The boundary walk corresponding to f is denoted by $b\left(f\right)$. A vertex v located on the boundary walk $b\left(f\right)$ is said to be incident to f. We let $N_h\left(f\right)$ denote the number of incident h-vertices of f.

To prove the main result, we suppose to the contrary that a minimal counterexample to the main result exists. We proceed to accumulate structures of any minimal counterexample in Section 2. The discharging method is used in Section 3 to show that a minimal counterexample does not exist, and the main result is thus verified. Finally, Section 4 gives a conclusion and some remarks related to the result.

2. Structures of Minimal Counterexamples

Suppose to the contrary that a graph G, which is a minimal counterexample to Theorem 1, exists. That is, G has no cycles with three, four, and six vertices and is not $(2,4)$-colorable, but any proper subgraph of G is $(2,4)$-colorable.

To reach the main result, this section provides certain properties of G. The next section uses these properties to show this minimal counterexample does not exist.

Two observations about a minimal counterexample G that have been generally used for the proof of two-defective coloring are as follows. First, G is connected, otherwise each component is $(2,4)$-colorable which results on G is $(2,4)$-colorable. Second, G has minimum degree of at least two; otherwise, we have a $(2,4)$-coloring for $G-v$ where v has a degree of at most one, and we can extend $(2,4)$-coloring to v easily. From now on, these facts are assumed on G throughout the paper.

For each of the three figures in this section, a solid vertex has a degree equal to the number of edges incident to it in the figure, while a hollow vertex has a degree of at least the number of edges incident to it in the figure.

Lemma 1 

(Lemmas 2.1 and 2.2 in [24]). Suppose that G is a minimal non-$(d_1,d_2)$-colorable graph with $d_1\le d_2$. At least two ${(d_1+2)}^{+}$-vertices, including a ${(d_2+2)}^{+}$-vertex, are adjacent to v if v is a $3^{-}$-vertex in G.

Lemma 2. 

Let v be a vertex of G.

(i)

There are two $4^{+}$-vertices, where one is a $6^{+}$-vertex, that are adjacent to v if v is a $3^{-}$-vertex. (See Figure 1)

(ii)

A $6^{+}$-vertex is adjacent to v if v is a 4-vertex. (See Figure 2)

Proof. 

(i) It follows from Lemma 1 immediately.

(ii) Consider a four-vertex v of G. A $(2,4)$-coloring of the graph $G-v$ exists due to the minimality of G.

Suppose to the contrary that v is adjacent to four $5^{-}$-vertices, namely $v_1,v_2,v_3$, and $v_4$. We recolor $v_i$ to color one if it is colored with color two and all of its adjacent vertices in $G-v$ are likewise colored with color two.

On the other hand, we give a color two to $v_i$ if at most three of its adjacent vertices are colored with color two. Finally, by giving a color two to v, we have a $(2,4)$-coloring of G. The proof is complete by this contradiction. □

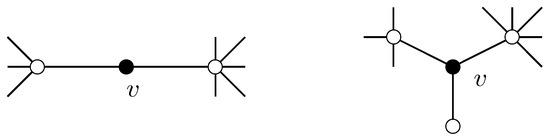
Figure 1. Adjacent vertices of a $3^{-}$-vertex v in Lemma 2(i).

Figure 1. Adjacent vertices of a $3^{-}$-vertex v in Lemma 2(i).

Figure 2. Adjacent vertices of a 4-vertex v in Lemma 2(ii).

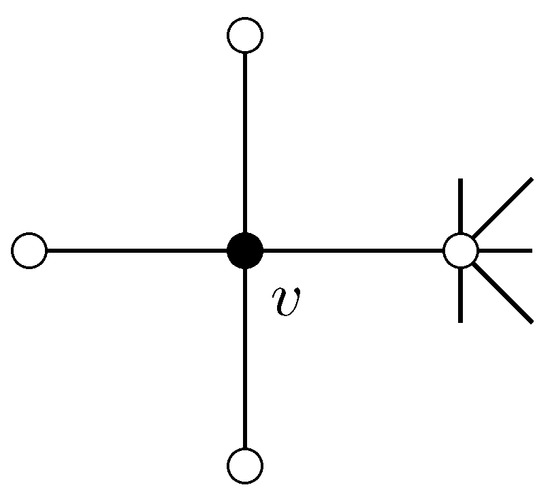
Figure 2. Adjacent vertices of a 4-vertex v in Lemma 2(ii).

Lemma 3. 

The graph G has the following properties.

(i)

If f is an h-face with $3\le h\le 9$, then $b\left(f\right)$ is an h-cycle.

(ii)

There are no h-faces in G where $h\in \{3,4,6\}$.

(iii)

At most, one five-face can be incident to a two-vertex v.

Proof. 

The fact that G has neither one-vertices nor cycles with three, four, or six vertices immediately leads to (i) and (ii).

Using (i) and (ii) with Lemma 2(i) yields Lemma 3(iii). See Figure 3 for all cases considered. □

Lemma 4. 

Each h-face f in G has the following properties.

(i)

$N_2\left(f\right)\le \lfloor {\displaystyle \frac{h}{2}}\rfloor$.

(ii)

If $N_2\left(f\right)<\lfloor {\displaystyle \frac{h}{2}}\rfloor$, then $N_3\left(f\right)\le h-2N_2\left(f\right)-1$.

(iii)

If $N_2\left(f\right)=\lfloor {\displaystyle \frac{h}{2}}\rfloor$, then $N_3\left(f\right)=0$.

Proof. 

Consider f to be an h-face of G such that $b\left(f\right)=v_1{v}_2\dots v_h$.

Each subscript takes modulo h for the definition of the following sets:

The set $v_i$, where $v_i$ is a two-vertex, is represented by A.

The set $v_i$, where $v_i$ is a three-vertex, is represented by B.

The set $v_i$, where $v_{i+1}$ is a two-vertex, is represented by C.

According to the definitions and Lemma 2(i), the pairwise disjointness of the sets $A,B,$ and C is established. Moreover, it is not possible that $A\cup B\cup C$ is the set of all adjacent vertices of v. Note that $\left|A\right|=\left|C\right|=N_2\left(f\right)$ and $\left|B\right|=N_3\left(f\right).$ Thus, we have $h\ge |A\cup B\cup C|+1=2\left|A\right|+\left|C\right|+1=2N_2\left(f\right)+N_3\left(f\right)+1.$ This inequality leads to Lemma 4 immediately. □

3. Proof of the Main Result by Discharging Method

Recall that G is a minimal counterexample of Theorem 1. We will use a discharging method in combination with structures of G obtained from the previous section to show that G does not exist.

A discharging method is a technique that assigns an initial charge to objects in a graph. The discharging rule is regulated to move a charge from one object to another while maintaining the sum of charge. Usually, the proof by discharging method is complete when we show that the sum of the initial charge is different from the sum of the new charge, which results in the impossibility of a counterexample.

The following is the charging process: The initial charge for each vertex v in G is $\mu \left(v\right)=d\left(v\right)-4$, where $d\left(v\right)$ represents the degree of the vertex v. Similarly, each face f in G has an initial charge $\mu \left(f\right)=d\left(f\right)-4$, where $d\left(f\right)$ represents the degree of the face f.

The following equation is obtained by using the Handshaking lemma and Euler’s formula, which establishes that $\left|V\right(G\left)\right|-\left|E\right(G\left)\right|+\left|F\right(G\left)\right|=2$:

$${\displaystyle \sum _{v\in V\left(G\right)}\mu \left(v\right)+\sum _{f\in F\left(G\right)}\mu \left(f\right)=-8.}$$

Next, we redistribute the charge across vertices and faces to establish a new charge ${\mu }^{*}\left(x\right)$ for all $x\in V\left(G\right)\cup F\left(G\right)$. The following are the discharging rules:

(R1)

Each of the adjacent two-vertices of a four-vertex v receives a charge t from v, where $t={\displaystyle \frac{1}{9}}$ if v is adjacent to exactly one $4^{+}$-vertex, and $t={\displaystyle \frac{1}{6}}$ otherwise.

(R2)

Each of the adjacent $3^{-}$-vertices of a five-vertex v receives charge ${\displaystyle \frac{1}{5}}$ from v.

(R3)

Each of the adjacent $4^{-}$-vertices of a $6^{+}$-vertex v receives a charge t from v, where $t={\displaystyle \frac{1}{3}}$ if v is not adjacent to a $5^{+}$-vertex, and $t={\displaystyle \frac{2}{5}}$ otherwise.

(R4)

Each of the incident two-vertices of a five-face f receives a charge t from f, where $t={\displaystyle \frac{5}{9}}$ if f is incident to one two-vertex, and $t={\displaystyle \frac{1}{2}}$ otherwise.

(R5)

Each of the incident two-vertices of a $7^{+}$-face f receives a charge 1 from f.

(R6)

After the application of rules (R1) through (R5), redistribute the charges so that each of the two two-vertices incident to the same five-face has an equal charge.

(R7)

Each of the incident three-vertices of a $5^{+}$-face f receives a charge ${\displaystyle \frac{2}{9}}$ from f.

The sum of all the new charges ${\mu }^{*}\left(x\right)$ after discharging process remains $-8$. For any $x\in V\left(G\right)\cup F\left(G\right)$, we aim to show that the final charge ${\mu }^{*}\left(x\right)\ge 0$, which results in a contradiction, to complete the proof. When x is a four-vertex, it is obvious that ${\mu }^{*}\left(x\right)\ge 0$ holds, while an h-face where $h\in \{3,4,6\}$ does not exist.

Let us now examine an h-vertex v.

(1) We consider v to be a two-vertex that is not incident to a five-face. Lemma 3 indicates that v is incident to two $7^{+}$-faces. Consequently, ${\mu }^{*}\left(v\right)\ge -2+2\times 1=0$ via (R5).

(2) We consider v to be a two-vertex incident to a five-face f, and f is incident to exactly one two-vertex. According to Lemma 3, the other incident face of v is a $7^{+}$-face. Then, ${\mu }^{*}\left(v\right)\ge -2+{\displaystyle \frac{1}{9}}+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{5}{9}}+1=0$ via (R1)–(R5).

(3) We consider v to be a two-vertex incident to a five-face f, and f is incident to two two-vertices. Let $b\left(f\right)=v{v}_1{v}_{2}u{v}_3$. We can assume that u is a two-vertex and each of $v_1,v_2$, and $v_3$ is a $4^{+}$-vertex according to Lemma 1. According to Lemma 3, the other face incident to both u and v is a $7^{+}$-face.

In the next three subcases, we consider ${\mu }^{*}\left(v\right)+{\mu }^{*}\left(u\right)$ by (R6) instead of ${\mu }^{*}\left(v\right)$.

(i) Both $v_1$ and $v_2$ are $6^{+}$-vertices according to Lemma 2(i) if $v_3$ is a four- or five-vertex. Since $v_1$ and $v_2$ are both adjacent to a $6^{+}$-vertex, ${\mu }^{*}\left(v\right)+{\mu }^{*}\left(u\right)\ge 2\times (-2+{\displaystyle \frac{1}{9}}+{\displaystyle \frac{2}{5}}+{\displaystyle \frac{1}{2}}+1)>0$ via (R1)–(R5).

(ii) Since both $v_1$ and $v_2$ are four- or five-vertices and $v_3$ is a $6^{+}$-vertex, it follows that each of $v_1$ and $v_2$ is a five-vertex or is adjacent to at least two $4^{+}$-vertices according to Lemma 2(ii). Thus, ${\mu }^{*}\left(v\right)+{\mu }^{*}\left(u\right)\ge 2\times (-2+{\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{2}}+1)=0$ via (R1)–(R5).

(iii) According to (R3)–(R5), ${\mu }^{*}\left(v\right)+{\mu }^{*}\left(u\right)>-4+3\times {\displaystyle \frac{1}{3}}+2\times {\displaystyle \frac{1}{2}}+2\times 1=0$ if $v_3$ is a $6^{+}$-vertex and $v_1$ or $v_2$ is a $6^{+}$-vertex.

Using (R6), we have ${\mu }^{*}\left(v\right)\ge 0$ for all subcases.

(4) We consider v to be a three-vertex. According to Lemma 2(i), a $6^{+}$-vertex is adjacent to the vertex v. Consequently, ${\mu }^{*}\left(v\right)\ge -1+{\displaystyle \frac{1}{3}}+3\times {\displaystyle \frac{2}{9}}=0$ via (R2), (R5), and (R7).

(5) We consider v to be a four-vertex. According to Lemma 2(ii), a $6^{+}$-vertex is adjacent to the vertex v. Then, ${\mu }^{*}\left(v\right)\ge 0-3\times {\displaystyle \frac{1}{9}}+{\displaystyle \frac{1}{3}}=0$ if v is adjacent to exactly one $4^{+}$-vertex. Otherwise, ${\mu }^{*}\left(v\right)\ge 0-2\times {\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{3}}=0$ via (R1) and (R3).

(6) We consider v to be a five-vertex. Then, ${\mu }^{*}\left(v\right)\ge 1-5\times {\displaystyle \frac{1}{5}}=0$ via (R2).

(7) We consider v to be an h-vertex where $h\ge 6$. If a $5^{+}$-vertex is adjacent to v, then ${\mu }^{*}\left(v\right)\ge (k-4)-(k-1)\times {\displaystyle \frac{2}{5}}\ge 0$, otherwise, ${\mu }^{*}\left(v\right)\ge (k-4)-k\times {\displaystyle \frac{1}{3}}>0$ via (R3).

Next, we consider f to be an h-face. Recall that the number of incident t-vertices of f is indicated by $N_t\left(f\right)$.

(8) We consider f to be a five-face. According to Lemma 4(i), we have $N_2\left(f\right)\le 2$.

If $N_2\left(f\right)=0$, then $N_3\left(f\right)\le 4$ according to Lemma 4(ii), and hence, ${\mu }^{*}\left(f\right)\ge 1-4\times {\displaystyle \frac{2}{9}}>0$ via (R7).

If $N_2\left(f\right)=1$, then $N_3\left(f\right)\le 2$ according to Lemma 4(ii), and hence, ${\mu }^{*}\left(f\right)\ge 1-{\displaystyle \frac{5}{9}}-2\times {\displaystyle \frac{2}{9}}=0$ via (R4) and (R7).

If $N_2\left(f\right)=2$, then $N_3\left(f\right)=0$ according to Lemma 4(iii), and hence, ${\mu }^{*}\left(f\right)=1-2\times {\displaystyle \frac{1}{2}}=0$ via (R4).

(9) We consider f to be an h-face where $h\ge 7$ and $N_2\left(f\right)=\lfloor {\displaystyle \frac{h}{2}}\rfloor$. According to Lemma 4(iii), $N_3\left(f\right)=0$. We have ${\mu }^{*}\left(f\right)=(h-4)-\lfloor {\displaystyle \frac{h}{2}}\rfloor \times 1\ge 0$ via (R5).

(10) We consider f to be an h-face where $h\ge 7$ and $N_2\left(f\right)\ne \lfloor {\displaystyle \frac{h}{2}}\rfloor$.

Lemma 4(i) implies that $N_2\left(f\right)<\lfloor {\displaystyle \frac{h}{2}}\rfloor$. Applying Lemma 4(ii), we have $N_3\left(f\right)\le h-2N_2\left(f\right)-1$.

From (R5) and (R7), we have

$$\begin{array}{cc}\hfill {\mu }^{*}\left(f\right)& =(h-4)-N_2\left(f\right)\times 1-N_3\left(f\right)\times {\displaystyle \frac{2}{9}}\hfill \\ \hfill & \ge (h-4)-N_2\left(f\right)\times 1-(h-2\times N_2\left(f\right)-1)\times {\displaystyle \frac{2}{9}}\hfill \\ \hfill & ={\displaystyle \frac{7}{9}}h-{\displaystyle \frac{34}{9}}-{\displaystyle \frac{5}{9}}{N}_2\left(f\right).\hfill \end{array}$$

If $h=7,$ then ${\mu }^{*}\left(f\right)\ge {\displaystyle \frac{49}{9}}-{\displaystyle \frac{34}{9}}-{\displaystyle \frac{10}{9}}>0.$

If $h\ge 8,$ then ${\mu }^{*}\left(f\right)\ge {\displaystyle \frac{7}{9}}h-{\displaystyle \frac{34}{9}}-{\displaystyle \frac{5}{9}}\times {\displaystyle \frac{h}{2}}={\displaystyle \frac{1}{2}}h-{\displaystyle \frac{34}{9}}>0.$

From (1) to (10) we can infer that for any $x\in V\left(G\right)\cup F\left(G\right)$, ${\mu }^{*}\left(x\right)\ge 0$. The proof is complete by this contradiction.

4. Conclusions and Remarks

In this work, we partially verify Conjecture 1 that planar graphs without cycles of length $3,4,$ and 6 are $(d_1,d_2)$-colorable when $d_1+d_2\ge 6$ by showing that such graphs are $(2,4)$-colorable.

Considering the results of Dross and Ochem [22]) and Sittitrai and Pimpasalee [23], such graphs are $(0,6)$- and $(3,3)$-colorable, respectively. The remaining open case is the problem whether such graphs are $(1,5)$-colorable.

Another direction for further study is finding a more restricted coloring. For example, an affirmative result for a $(2,3)$-coloring on planar graphs without cycles of length three, four, and six, if true, will improve both results on $(2,4)$- and $(3,3)$-coloring. Furthermore, it is interesting to see whether we can achieve a similar coloring if the constraint of forbidden cycles is relaxed.

Recently, we have been advised about exploring the intersection between defective colorings and graph labeling problems. For example, Alkasasbeh et al. [25] applied a Skolem sequence to gracefully label new families of triangular windmills. The aforementioned work and this work focus on constrained graph structures and properties related to structural decomposition. Another interesting research direction could be investigating whether techniques or results from graceful labeling theory can inform defective coloring strategies in specialized graph families such as cacti or windmills.