Abstract
Guided-wave structural health monitoring offers exceptional sensitivity to localized defects but relies on high-fidelity simulations that are prohibitively expensive for real-time use. Reduced-order models can alleviate this cost but hinge on affine parameterization of system operators. This assumption breaks down for complex, non-affine damage behavior. To overcome these limitations, we introduce a novel, non-intrusive space–time empirical interpolation method that is applied directly to the full wavefield. By greedily selecting key spatial, temporal, and parametric points, our approach builds an affine-like reduced model without modifying the underlying operators. We then train a Gaussian-process surrogate to map damage parameters straight to interpolation coefficients, enabling true real-time digital-twin predictions. Validation on both analytic and finite-element benchmarks confirms the method’s accuracy and speed-ups. All MATLAB 2024b. scripts for EIM, DEIM, Kriging, and wave propagation are available in the GitHub (version 3.4.20) repository referenced in the Data Availability statement, ensuring full reproducibility.
Keywords:
structural health monitoring; digital twins; surrogate models; model order reduction; wave propagation MSC:
65
1. Introduction
As the stakes of unexpected failures in modern infrastructures grow ever higher, real-time structural health monitoring (SHM) has emerged as a linchpin of safety and sustainability. SHM systems aim to detect, localize, and quantify damage, including fatigue cracks in bridges, composite delamination, or stiffness losses in beams, by continuously analyzing data from sensor networks [1,2]. Traditionally, purely physics-based approaches have leveraged high-fidelity finite element (FE) models grounded in first principles [3], while data-driven methods have applied machine learning algorithms to large vibration or wave-propagation datasets [4,5]. Recently, these once-separate paradigms have converged under the digital-twin umbrella [6,7], in which physics-based “full-order” simulations generate synthetic training data for statistical or deep learning classifiers [8], and measured signals continually update an evolving numerical replica through Bayesian model [9,10] and Kalman filter [11,12] updating. Among SHM modalities, guided-wave techniques stand out for their sensitivity to localized defects and long-range coverage, though modeling Lamb--wave interactions requires very fine FE meshes and small time steps, making real-time inversion via naïve FE solves infeasible [13,14,15]. Real-time predictions are necessary as delayed fault detection can lead to catastrophic failure, especially in the case of aerospace structures, where impact events produce guided-wave signatures that traverse a wing panel in microseconds, requiring an immediate structural integrity assessment to deploy countermeasures. Hence, to realize digital twins that are both accurate and computationally tractable, it is imperative to develop reduced representations that retain essential wave-based dynamics while enabling near-instantaneous predictions [16,17].
Model-order reduction (MOR) strategies address the computational bottleneck of high-fidelity simulations by projecting large FE systems onto low-dimensional subspaces [18,19] or by condensing out unobserved degrees of freedom via substructuring [20,21]. Static-condensation methods such as Guyan reduction [22,23] and its dynamic extensions (SEREP, IRS, IIRS) [24,25] eliminate inaccessible DOFs using Schur complements of mass and stiffness matrices [26,27], while projection-based methods employ Proper Orthogonal Decomposition (POD) [28], balanced truncation [29], or Krylov subspace-based approaches [30] to extract the most energetic modes from snapshot ensembles. These ROMs can be evaluated orders of magnitude faster than their parent FE models [31], but their reliance on explicit affine decompositions of parameter-dependent operators limits their applicability to the complex, non-discrete damage scenarios encountered in SHM [32]. To overcome this, researchers have fused MOR with machine learning—training neural networks to map from damage and environmental parameters directly to ROM coefficients; thereby accelerating both the offline model reduction and the online inference phases [33]. Deep architectures such as fully convolutional networks (FCNs) [34] and recurrent long short-term memory (LSTM) networks [35,36] have been successfully employed to classify damage states from time-series vibration data, using ROM-generated training libraries to keep the computational cost during deployment minimal [17,37].
In many-query applications such as uncertainty quantification, Bayesian inversion, and parametric sweeps, the need to propagate parameter uncertainty through dynamical systems further strains computational resources [38,39]. Monte Carlo sampling over high-fidelity models can become prohibitive, driving the adoption of surrogate-assisted MOR techniques [40,41,42]. Polynomial chaos expansions (PCEs) decouple randomness from time evolution but suffer from non-optimal basis functions at each time step, prompting asynchronous or adaptive-basis variants [43,44]. Nonlinear autoregressive with exogenous input (NARX) models have been combined with PCEs [45] or Kriging [46] to separately capture temporal dynamics and parameter dependence. However, constructing universally accurate NARX models remains challenging [47]. An alternative is the POD–surrogate framework wherein POD compresses the time-dependent solution manifold into a handful of spatial modes, and a Gaussian process (Kriging) emulator then maps input parameters to the corresponding modal coefficients. These POD–Kriging ROMs achieve substantial speed-ups, often two to three orders of magnitude, while preserving accuracy across wide parameter ranges [48]. Multi-fidelity surrogates further leverage cheap low-fidelity ROM samples [49,49] to enrich high-fidelity data, using deep neural networks or hierarchical co-Kriging [50,51] to learn nonlinear correlations adaptively, thus reducing the offline data-generation burden without sacrificing predictive quality [34].
Despite these advances, most surrogate-assisted ROMs assume that operators or solution fields vary affinely with parameters—an assumption violated by the localized, nonlinear damage laws prevalent in SHM [52]. The Empirical Interpolation Method (EIM) and its discrete counterpart (DEIM) remedy this by enforcing an affine-like expansion of either the parametric operators or the solution itself, without requiring analytical separability [53]. DEIM begins with a truncated POD basis and greedily identifies the degrees of freedom with maximal residuals, assembling an interpolation set that ensures accurate recovery of the full solution from a small subset of entries [54,55]. Continuous EIM extends this idea to the space–time domain, directly locating the global maxima of the interpolation residual to construct basis functions from previously unidentified solution features [56]. By decoupling parameter dependence from spatial–temporal variation, (D)EIM produces compact, yet highly expressive, ROMs capable of handling arbitrarily complex damage models [57]. However, to date, (D)EIM has seen little application in wave-based SHM, and its integration with probabilistic surrogates for coefficient prediction remains an open frontier—one that promises to unlock truly real-time digital twins for damage localization and quantification.
In this paper, we introduce a novel framework that brings together greedy empirical interpolation and Gaussian process surrogates to deliver truly affine-like reduced-order models for wave-based SHM, as illustrated in Figure 1. Departing from classical operator-based (D)EIM, we apply both discrete and continuous EIM directly to the time–space wavefield, enabling accurate interpolation even when damage laws induce highly localized, non-affine behavior. To support real-time inference, we then employ Kriging to learn the mapping from the damage parameter to the interpolation weights , completely eliminating the need for additional full-order simulations. The method is validated against both an analytical double-Gaussian pulse and a full finite-difference time-domain beam with a localized stiffness defect, carefully characterizing the trade-offs among basis dimensionality and worst-case error. All MATLAB scripts for snapshot assembly, interpolation, and surrogate training are provided via the GitHub repository linked in the Data Availability statement, ensuring full reproducibility and facilitating rapid adoption by the SHM community.
The remainder of this paper is organized as follows. Section 2.1 reviews the governing elastodynamic equations and formulates the numerical model for wave propagation in a heterogeneous medium with spatially varying damage. Section 2.2 presents the discrete and continuous empirical interpolation methods applied directly to the wavefield, detailing the greedy algorithms for basis construction and interpolation-point selection. Section 2.3 introduces the Kriging surrogate for mapping damage parameters to interpolation coefficients, including hyperparameter estimation and the offline–online computational decomposition. Section 3 reports two numerical studies, i.e., a parametrized double-Gaussian pulse and a numerically driven prismatic beam with a localized stiffness defect; comparing DEIM and EIM in terms of error convergence and basis dimensionality. Finally, Section 4 provides concluding remarks, discusses potential extensions, and outlines prospects for practical SHM integration.
2. Methodology
2.1. Governing Equations
Considering an arbitary domain with dimensionality d; wave propagation in time within a corresponding heterogeneous material layout is described in Figure 1 using the linear elastodynamics equations over
subject to appropriate initial and boundary conditions, where contains mass density and denotes the divergence operator. The term represents a spatially varying damage parameter, encoding damage location, width, and severity; for example, local stiffness reductions, cracks, delaminations, or inclusions at each point [58]. The displacement u’s dependence on is always implied, even if occasionally omitted in writing for brevity. The stress is defined through a constitutive law where the infinitesimal strain tensor is kinematically described , with representing the gradient operator. The fourth-order Cauchy isotropic material tensor incorporates the spatial variability due to damage. Each new damage law, potentially accommodating attenuative layers, discontinuities, etc. [59], alters and subsequently the stiffness matrix, making its direct analytic factorization or reduced-order modeling difficult. A finite element (FE) semi-discretization in space, incorporating the desired initial and boundary conditions produces
where is the vector of displacements comprising degrees-of-freedom. The quantities , , and denote mass, Rayleigh damping, and stiffness matrices, respectively; and the operator represents a time derivative . Dissipation is incorporated into through a linear combination of and . The classical structural dynamics formalism in Equation (2) denotes a second-order system of Ordinary Differential Equations (ODEs) in time and may be solved at time steps using classical time-stepping algorithms [60]. For wave-based SHM, executing a parametric sweep, i.e., repeatedly solving large systems for different , is expensive. Affine parameterization is a common strategy to mitigate this cost [61], but the presence of nonlinear or complex damage models often prevents a standard closed-form decomposition of [62]. Section 2.2 describes how an empirical interpolation approach can instead produce an affine-type approximation of the solution , independent of whether is readily factorizable.
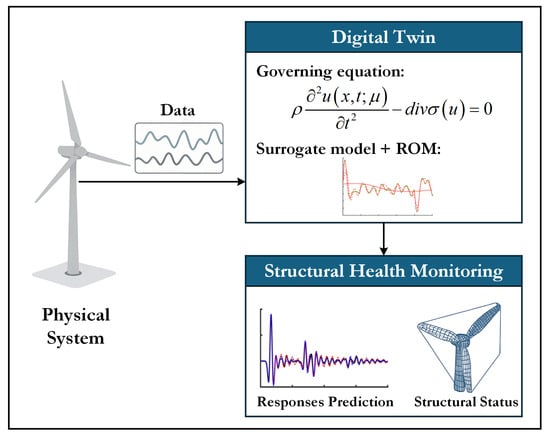
Figure 1.
Workflow of the surrogate-accelerated digital twin: sensor data drive a reduced-order model (DEIM/EIM + GP surrogate) to predict wave responses and enable real-time damage detection; inspired by [63].
2.2. Affine Parametrization of the Solution
Standard approaches in model-order reduction often attempt to decompose parameter-dependent system matrices using a separation of variables, i.e., into sums of parameter-independent components multiplied by scalar functions of the parameters. Such decompositions can become extremely cumbersome when the parameter encodes complex or localized damage phenomena. In many wave-based SHM applications, it is more direct to approximate the solution field as itself. By imposing a decomposition of the form
one circumvents the need for a factorization of each operator in Equation (2). The collection of scalar-valued coefficients depend only on the parameter and not on , so evaluating the solution for a new damage configuration simply entails solving a small interpolation or projection system. This strategy makes it possible to handle evolving or complicated damage models without re-deriving the entire parametric structure of the stiffness or damping operators.
The (Discrete) Empirical Interpolation Method [53] enforces this decomposition by selecting a finite number of interpolation conditions for the wave solution. These conditions are enforced either through a Proper Orthogonal Decomposition (POD)—in the discrete EIM procedure, or DEIM; or through greedy error-based indicators—in the continuous variant of EIM. In either case, the method constructs a reduced set of basis functions such that and . This array represents the main solution behaviors observed in a snapshot library.
2.2.1. Discrete Empirical Interpolation Method (DEIM)
DEIM constructs an interpolatory reduced-order model by selecting a small set of discrete DOFs at which to enforce exact matching of the dominant POD modes. Starting from the matrix comprising snapshots, its truncated Singular Valued Decomposition [64] reads
where , , denote singular values, right and left singular vectors, respectively. One seeks indices and basis vectors such that any can be reconstructed from its entries at . At enrichment iteration m, the residual of the mth mode is
where the Boolean matrix satisfies and selects previously chosen indices. The next interpolation index is chosen as the coordinate of maximal residual magnitude:
Append to , augment , and repeat until the relative Frobenius norm of the reconstruction error or , where denotes the snapshot matrix reconstructed with the current basis and interpolation indices . The quantities and denote a maximum error tolerance and iteration limit, respectively. Alternatively, the stopping criterion may also be enforced by a selected number of bases . Thereafter, any vector can be reconstructed by solving the small linear system
requiring only the entries filtered by . The DEIM procedure is summarized in Algorithm 1.
| Algorithm 1: Discrete Empirical Interpolation (DEIM) |
 |
2.2.2. Continuous Empirical Interpolation Method (EIM)
Continuous EIM extends the interpolation-point selection to the full space–time–parameter domain . After enrichment steps, one has basis functions and interpolation points where each point j corresponds to the triplet . The residual surface for each training parameter is accordingly defined
where solve the interpolation conditions in Equation (3) at . The next worst-case triplet is found by
and the new basis function is normalized so that
The affine coefficients at any are then computed by collocating Equation (3) at the interpolation points
involving only the values of u at the m selected points to yield the desired final affine-like expansion in Equation (3). The EIM method is summarized in Algorithm 2.
The continuous and discrete approaches thereby differ in how they identify new interpolation locations. DEIM confines its search to the discrete degrees of freedom employed by the numerical scheme, which is simpler for large-scale problems but potentially less refined if local maxima occur at different parameter points. The continuous method is conceptually more general, though it may be expensive to implement if and and admit no straightforward mechanism for locating or approximating the global maximum of the residual.
In both cases, the objective remains to represent in an affine-like form with respect to , circumventing the need for an explicit factorization of parameter-dependent operators. Orthogonality is not essential, since the interpolation step is enforced by point-wise or coordinate-wise matching. Although standard DEIM algorithms often begin with POD modes (which are orthonormal), continuous EIM commonly constructs each basis function directly from residuals of previously interpolated solutions. Both variants ultimately provide a set of functions and a small system of size that one solves to determine for new parameter instances. This representation is a cornerstone in forming a digital twin for wave-based SHM, because it enables rapid evaluation of under different damage scenarios, without requiring repeated full-scale finite element simulations.
| Algorithm 2: Continuous Empirical Interpolation (EIM) |
 |
2.3. Kriging Surrogate for the Coefficients
Although the systems of equations in Equations (7) and (11) are of size and can be solved rapidly for a single parameter value, many-query settings (e.g., uncertainty quantification, Bayesian inversion, or real-time deployment of a digital twin) require evaluating these coefficients at hundreds or even thousands of new parameter samples. Even small per-solve costs can accumulate, and repeated factorization of the collocation matrix impedes sub-millisecond response. To eliminate any online linear solves, the coefficient map is learned via Kriging regression [65]. To this end, each is described by a Gaussian-process surrogate
where denotes a vector of p user-selected regression functions, is constant, and is a zero-mean Gaussian process with covariance
An anisotropic squared-exponential kernel is adopted
with hyperparameters and identified, together with , by maximizing the log-likelihood of the training set . Denote
For any admissible parameter value the best linear unbiased predictor is
where
and has entries . Insertion of the predictors (15) into Equation (3) yields the surrogate solution
This surrogate thus provides a closed-form predictor for each that is evaluated in per query (apart from a fixed inversion of the training-size covariance), preserves smoothness across the parameter domain, and delivers an estimate of predictive uncertainty. Equation (16) thereby becomes fully real-time, without further recourse to any high-fidelity or interpolation solves. The Kriging algorithm and the overall workflow of the method are summarily presented in Algorithm 3 and Figure 2, respectively.
| Algorithm 3: Offline–online Kriging surrogate for a coefficient |
Input: Training set ; snapshots ; regression basis Output: Predictor for any query Offline calibration; ; ; for ; Online prediction;
; ; return |
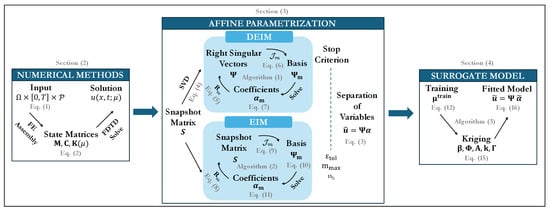
Figure 2.
Workflow of the proposed surrogate-accelerated empirical interpolation framework. High-fidelity wavefields are first generated via numerical simulations (Section 2.1), then reduced to an affine parametrization using either DEIM or continuous EIM (Section 2.2), and finally accelerated by training a Kriging surrogate for the interpolation coefficients (Section 2.3).
In the following section, the accuracy and efficiency of the surrogate (D)EIM will be evaluated through two relevant numerical examples. Subsequently, MATLAB implementations of the method with both examples are provided [66].
3. Numerical Results and Discussion
In this section, the performance of the surrogate-accelerated empirical interpolation framework is assessed through two case studies. First, an analytical double-Gaussian pulse highlights convergence behavior and basis efficiency in a controlled setting. Second, a high-fidelity finite element model of a prismatic beam with a localized stiffness defect demonstrates real-world applicability in structural health monitoring. The DEIM and EIM are compared in terms of interpolation accuracy and evaluation efficiency.
3.1. Analytical Case Study: Convergence on a Parameterized Double-Gaussian Pulse
To provide a controlled environment for analyzing the behavior of the DEIM and EIM, the first study employs the closed-form field inspired by [67]
where two Gaussian pulses, whose centers, widths, and amplitudes vary smoothly yet non-linearly with the scalar parameter , are superimposed. The expressions associated with each pulse, i.e., , , and , are provided in Appendix A. The field exhibits localization in both space and time while maintaining an analytic reference against which interpolation errors can be evaluated exactly. The spatial coordinate is restricted to and the temporal coordinate to . Uniform grids containing points in space and points in time generate degrees of freedom per snapshot. The parameter domain is uniformly divided up into points and the corresponding snapshots are stored column-wise in the matrix . The authors choose in this study, although this is not a necessary requirement. An enrichment termination limit of and is chosen.
This configuration allows the investigation of three aspects that are central to subsequent applications: the number of basis functions required to achieve the prescribed tolerance for strongly parameter-dependent and localized features, the spatial distribution of interpolation points selected by the two algorithms, and the resulting error convergence rates. Because the reference solution is exact, all reported errors are attributable solely to the approximation mechanisms introduced by empirical interpolation, unaffected by artifacts introduced by discretization. The progressive construction of interpolation bases through DEIM and EIM are illustrated in the form of residuals (see Equations (5) and (8)) in Figure 3 and Figure 4, respectively. Each figure depicts the evaluated interpolation modes at selected iterations (vertical direction) across a sampled parameter space (horizontal direction). These representations demonstrate how empirical interpolation progressively captures parameter-dependent behaviors by systematically enriching the solution bases.
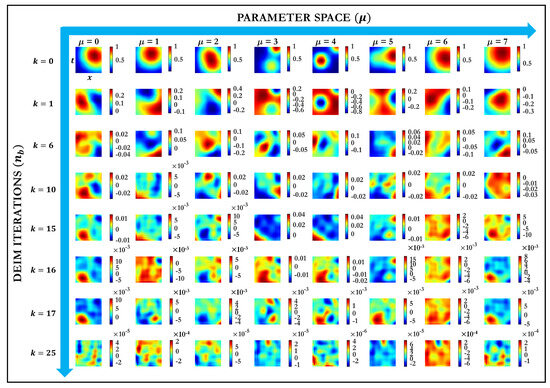
Figure 3.
DEIM residual modes at selected enrichment iterations () for each training parameter .
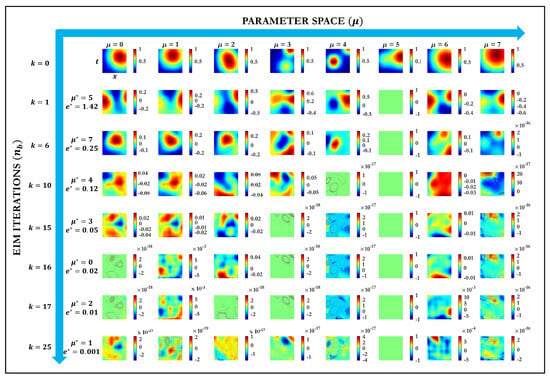
Figure 4.
EIM residual modes at selected enrichment iterations () for each training parameter .
In Figure 3, the DEIM basis modes evolve with successive iterations, highlighting the sequential reduction in the approximation residual across the parameter domain. Initial DEIM iterations () generate basis functions exhibiting prominent, smoothly varying Gaussian-like profiles. These initial basis modes clearly reflect dominant solution characteristics and spatial–temporal localization associated with lower-order approximations. As the DEIM iteration progresses (), the basis functions become increasingly complex and less coherent in their spatial–temporal structures, indicating that the main global features have been adequately captured, and the algorithm begins to target subtle local details for further improvement in accuracy. At advanced DEIM iterations (), the magnitudes of the residual modes notably decrease (observe the scale factors and ), suggesting that the incremental improvements offered by each additional basis mode become minor. At these iterations, the modes capture fine-grained nuances of the parameter-dependent solution behavior.
In comparison, Figure 4 shows the continuous EIM, which locates interpolation points by scanning the full space–time domain for the largest residuals, rather than restricting itself to a fixed set of POD coordinates. At the very first iterations (), EIM and DEIM both produce smooth, Gaussian-shaped modes, reflecting their common capture of the dominant solution structure. As the enrichment proceeds to intermediate and advanced steps (), however, the two methods diverge sharply. EIM basis functions begin to concentrate around precisely identified continuous maxima of the residual, revealing sub-grid features with high fidelity. These modes grow progressively more localized, irregular, and parameter-dependent—demonstrating EIM’s power to resolve sharply confined phenomena. In contrast, DEIM continues to distribute its point selections so as to minimize the global reconstruction error, yielding corrections that remain more spatially diffuse.
The convergence of the reconstruction error is plotted in Figure 5a as a function of the basis size . Both DEIM (blue) and continuous EIM (red) curves decrease monotonically, confirming that each additional basis vector reduces the worst-case error. For , DEIM yields a slightly faster error decay, reflecting its direct targeting of the global residual; for larger , the two methods converge to comparable accuracies around .
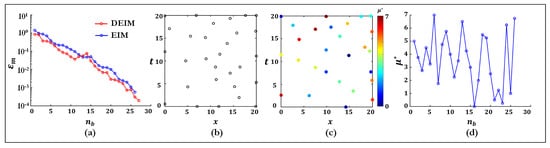
Figure 5.
Comparison of DEIM and continuous EIM: (a) reconstruction error versus basis size , (b) DEIM-selected discrete interpolation points, (c) continuous EIM points colored by selected parameter , and (d) EIM parameter selection trajectory over iterations.
Figure 5b shows the spatial–temporal coordinates selected by DEIM at each enrichment iteration (see Equation (6)). Since DEIM operates on the fixed discrete grid of size , each iteration picks the single degree of freedom (an node) with the largest residual; these appear as unfilled black circles. The spread of these points over the entire domain illustrates DEIM’s tendency to refine globally once the dominant POD modes have been accounted for. By contrast, Figure 5c depicts the continuous EIM interpolation points. Each filled marker denotes the continuous location at which the residual attains its maximum over the domain (see Equation (9)), and its color indicates the corresponding “worst-case” parameter value at that iteration (color bar on the right). The use of color in Figure 5c emphasizes that EIM not only chooses spatial–temporal points but simultaneously identifies which parameter yields the largest interpolation error. Early iterations concentrate on parameter regions where the solution’s non-affinity is strongest (e.g., –5), then gradually sample boundary values as the basis becomes more expressive. The parameter trajectory ( versus iteration index m) for EIM is extracted in Figure 5d. This confirms that the algorithm adaptively visits a non-uniform sequence of parameter samples—something not defined for DEIM, which relies instead on the pre-assembled snapshot matrix over all training parameters. The jagged oscillation of highlights EIM’s focus on the most challenging parameter configurations at each step. A paired t-test on the errors in panel (a) supply a p-value of , indicating that the DEIM-based surrogate offers a small but statistically meaningful accuracy advantage.
In summary, Figure 5 demonstrates that DEIM achieves marginally lower worst-case errors for a given basis size, reflecting its global minimization of the reconstruction error across a pre-assembled snapshot matrix. However, this advantage depends on an offline phase—collecting all snapshots and performing a truncated SVD—which can be computationally demanding. Continuous EIM, by contrast, constructs its basis sequentially and entirely online by greedily selecting the maximal-residual points, without any separate offline snapshot assembly. As a result, EIM may exhibit slightly higher errors at fixed yet offers immediate deployability and reduced pre-processing overhead. The subsequent section applies both DEIM and continuous EIM to a numerical model of guided-wave propagation in a beam with a localized stiffness defect, thereby illustrating how the balance between offline preparation and online flexibility manifests in a structural health monitoring context.
3.2. Guided-Wave Digital Twin for a Prismatic Beam with Localized Stiffness Defect
A uniform beam of length has a Young’s modulus , density , and a damping coefficient depicted in Figure 6. A localized defect is introduced by scaling the stiffness via
with degradation level over a width m centered at . Although the full methodology in Section 2.2 and Section 2.3 can accommodate all three parameters , only the defect location is chosen as a design variable in this study, for ease of presentation. Accordingly, is hereafter treated interchangeably with . Material degradation D profoundly alters impedance mismatches, so every interpolatory expansion must be recomputed from scratch for each new D.
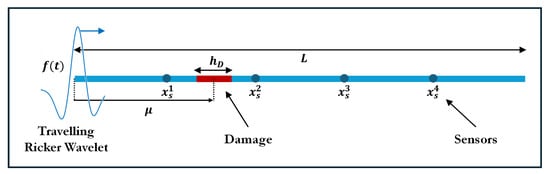
Figure 6.
Schematic of a beam with a localized stiffness defect.
The parametric space is partitioned into equally spaced points. Four displacement sensors at record the wavefield on a uniform time grid of points over , chosen to satisfy the CFL stability criterion. The spatial discretization employs degrees of freedom. The left boundary is driven by a Ricker wavelet , with central frequency kHz. The waveform’s spatial extent is chosen to match the order of the damage size, ensuring significant scattering and dispersion effects. All structural and method parameters are summarized in Table 1.

Table 1.
Structural and method parameters.
The reconstruction error at each sensor is plotted versus the number of basis functions in Figure 7. As recalled in Section 2.2.1, since the termination condition is driven by , the other convergence criterion and are not specified. Each curve corresponds to a training set of or 100 uniformly spaced parameter samples, and since both DEIM and EIM select at most one interpolation point per parameter. With very coarse sampling ( small), the parameter grid fails to resolve the error landscape, producing a steep initial drop in . As increases, the decay rate becomes more uniform, reflecting an increasingly accurate capture of the dominant parametric variations. In general, DEIM yields marginally faster convergence because it minimizes the global reconstruction error across the entire snapshot matrix, whereas continuous EIM greedily targets the largest local residuals.
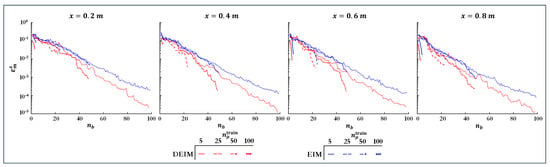
Figure 7.
Sensor−wise maximum interpolation error versus basis size at m for DEIM (blue) and continuous EIM (red) under varying training sample sizes .
To visualize the structure of the reduced basis under a deliberately coarse approximation, Figure 8 displays the first five modes obtained with and . Modes resemble the fundamental guided-wave pulse, spanning the entire beam length and the full time interval. Higher modes introduce localized corrections: spatial ripples near the damaged segment and temporal shifts that adjust the arrival times. These patterns illustrate how empirical interpolation augments a global propagating template with localized features to accommodate parameter-dependent distortions.
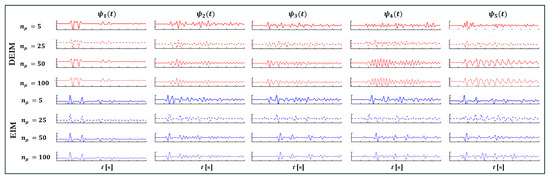
Figure 8.
First five basis functions obtained by DEIM (top four rows, red) and continuous EIM (bottom four rows, blue) for training set sizes .
Figure 9 compares the true expansion coefficients (green circles) with their Kriging-based predictions (solid curves) for training sets of size and 100. The DEIM coefficients exhibit pronounced, global oscillations across the parameter range, reflecting the method’s minimization of the overall reconstruction error. In contrast, the EIM coefficients show highly localized peaks in the first two modes and only develop broader oscillatory structure in higher-order modes (). With , the surrogate underestimates sharp local variations in , whereas for the fitted curves interpolate nearly all training points. Intermediate sample sizes strike a balance, capturing the main nonlinear trends with only minor deviations in the most sensitive regions. These results indicate that on the order of 20–50 parameter samples are required to reduce coefficient-fit errors below approximately . The authors employ an open source MATLAB toolbox ooDACE-1.4 [68,69] for optimized implementations of the Kriging–Gaussian process surrogate model described in Section 2.3.
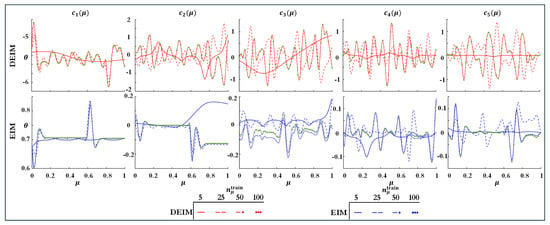
Figure 9.
True expansion coefficients (solid green) and Kriging surrogate predictions for the first five modes , computed with DEIM (top row) and continuous EIM (bottom row) using training set sizes .
The parameter (i.e., m) is omitted from training and used for validation. Figure 10 overlays the FE reference signal (solid black) with affine-interpolated reconstructions (dashed) at each sensor for . Both DEIM and continuous EIM reproduce the principal pulse arrival and amplitude, but subtle phase lags and amplitude errors remain. EIM’s residual-driven basis construction yields slightly smoother discrepancies, while DEIM’s globally optimized modes achieve marginally better amplitude matching at later times.
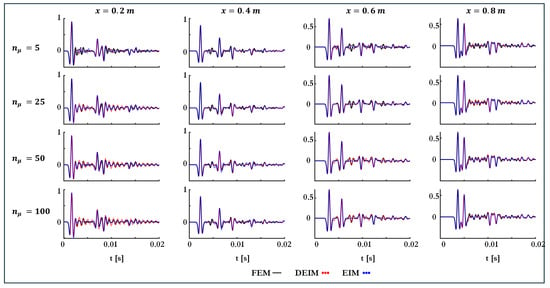
Figure 10.
Time-domain responses at sensors m (columns) for m, , with varying training set sizes (rows). Black solid lines: high-fidelity FEM reference; red dashed: DEIM reconstructions; blue dotted: continuous EIM reconstructions.
To assess overall predictive performance, Figure 11 plots the mean absolute error over unseen -values,
against . Both DEIM and EIM approach the same asymptotic error for , highlighting the inherent trade-off between offline sampling density and online basis dimension.
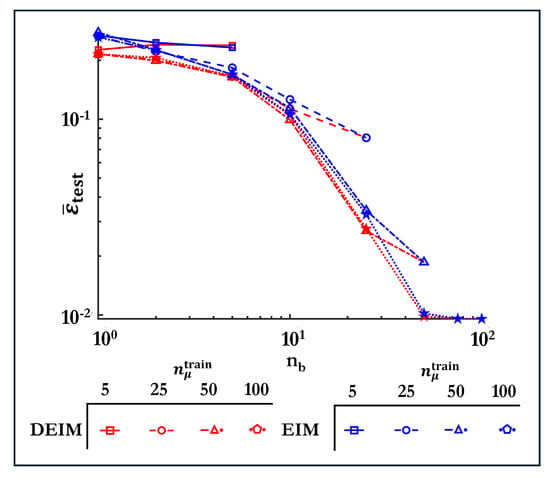
Figure 11.
Mean test error versus basis size on a log–log scale for DEIM (blue) and EIM (red) with training set sizes . Marker shapes denote different values as indicated in the legend.
The offline computational costs, shown in Figure 12a–c, reveal clear trade-offs between the number of training parameters and interpolation points . In panel (a), the time required to assemble high-fidelity snapshots rises roughly linearly from under 0.2 s at the smallest configuration to over 1 s when both dimensions reach 100. Panels (b) and (c) demonstrate that DEIM–Kriging and EIM–Kriging surrogate training exhibit virtually identical runtimes across all configurations, indicating no meaningful difference in offline cost between the two interpolation strategies for our problem sizes. This suggests that the choice between discrete and continuous empirical interpolation can be made based on accuracy or implementation convenience, without impacting the offline performance significantly.
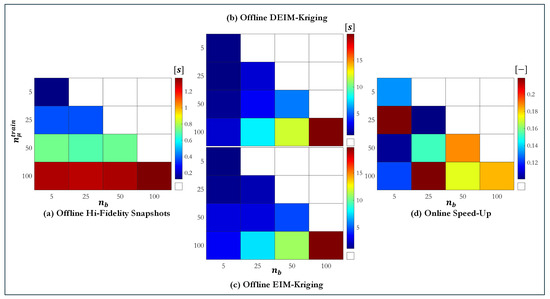
Figure 12.
Consolidated computational runtimes for varying and interpolation bases .
Panel (d) summarizes the online performance in terms of speed-up factors relative to full-order solutions. Across every tested design, the surrogate delivers a consistent acceleration, regardless of the offline sampling density. These results, averaged over three runs on a 64-bit machine with an Intel i7 2.3 GHz processor and 16 GB of RAM, highlight the robustness of the approach: increasing and enhances surrogate fidelity without compromising real-time feasibility. All reported times are mean values over three independent runs.
4. Conclusions and Future Perspectives
This work has introduced a unified framework for constructing efficient, real-time digital twins of wave-based structural health monitoring systems by combining greedy empirical interpolation with Gaussian-process surrogate modeling. Comprehensive numerical studies have demonstrated the efficacy of the proposed approach. In the analytical double-Gaussian pulse case, both DEIM and continuous EIM achieved rapid error decay as the basis size increased, with DEIM offering slightly faster convergence for small basis dimensions and EIM providing greater flexibility by constructing its basis entirely online. The second example, featuring a localized stiffness defect parameterized by its position, showed that, even with as few as 25–50 training samples, the Kriging surrogates predict interpolation coefficients to within 5% accuracy, and the resulting reduced-order models reproduce sensor time-series with peak errors below across a broad range of defect locations. Error versus basis-size and training-set density curves quantified the trade-offs between offline sampling cost, basis dimension, and online accuracy.
Several limitations of the current methodology merit discussion. First, the continuous EIM algorithm requires a global maximization of the interpolation residual over the entire space–time–parameter domain, which can become computationally expensive for high-dimensional or finely discretized problems. Second, the Kriging surrogate operates under the assumption of stationarity and Gaussianity, and its performance may degrade in the presence of strongly non-Gaussian coefficient behavior or when the parameter space has more than a few dimensions, owing to the curse of dimensionality in kernel interpolation. Third, the present framework assumes noise-free, deterministic high-fidelity snapshots; extending the approach to account for measurement noise or model discrepancy remains an open challenge. Finally, the offline cost of generating training snapshots and fitting hyperparameters, while modest compared to full-order parametric sweeps, may still be prohibitive for very complex three-dimensional structures or for problems requiring extremely fine time resolution.
Looking ahead, several avenues for future work emerge. On the algorithmic front, adaptive sampling strategies—such as active learning based on predictive uncertainty—could dramatically reduce the number of required training snapshots, particularly in regions of parameter space where the coefficient maps exhibit complex variation. Incorporating multi-fidelity data sources (e.g., combining coarse and fine discretizations or experimental measurements) via hierarchical co-Kriging could further accelerate surrogate construction while enhancing robustness. From an application standpoint, extending the framework to multi-parameter damage models (e.g., crack length and orientation) to nonlinear material behavior and to complex geometries will broaden its utility in practical SHM scenarios. Finally, experimental validation on physical test articles and integration with real sensor networks—complete with environmental variations and measurement uncertainty—will be critical steps toward deploying truly autonomous, real-time digital twins for structural health monitoring in the field.
Author Contributions
Conceptualization, A.S. and L.Z.; methodology, A.S.; formal analysis, A.S.; investigation, A.S. and L.Z.; resources, A.S., L.Z. and D.C.; data curation, A.S.; writing—original draft preparation, A.S. and L.Z.; writing—review and editing, A.S. and L.Z.; visualization, A.S. and L.Z.; supervision, D.C.; project administration, D.C.; funding acquisition, D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the HORIZON-MSCA-2022-PF-01 action under Marie Skłodowska-Curie project MULTIOpStruct (grant no. 101103218).
Data Availability Statement
The MATLAB code supporting the conclusions of this article is available in the GitHub repository “Wave-based SHM Empirical Interpolation MATLAB Code” [66] (accessed on 19 May 2025).
Acknowledgments
The authors would like to express their gratitude to their colleagues at LMSD, Gent for several fruitful discussions on damage localization and model order reduction.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Parametrized Double-Gaussian Pulse
Appendix B. Nomenclature

Table A1.
Nomenclature —list of primary symbols used.
Table A1.
Nomenclature —list of primary symbols used.
| General | Model-Order Reduction | ||
|---|---|---|---|
| Symbol | Meaning | Symbol | Meaning |
| x | Spatial position | Approximated solution | |
| Physical domain | Scalar-valued coefficients | ||
| Real number | Basis functions | ||
| t | Time | Singular values | |
| Damage parameter | Right singular vectors | ||
| Parameter space | Left singular vectors | ||
| u | Displacement | Interpolation indices | |
| Mass density | Residual | ||
| Stress | Boolean matrix | ||
| Strain tensor | Reconstruction error | ||
| ∇ | Gradient operator | Maximum error tolerance | |
| Tensor field | Maximum iteration limit | ||
| Mass | Regression functions | ||
| Rayleigh damping | Regression coefficient vector | ||
| Stiffness matrices | Local bias | ||
| — | — | Correlation function | |
| — | — | Process variance | |
| — | — | Roughness parameter | |
Appendix C. Abbreviations

Table A2.
List of abbreviations.
Table A2.
List of abbreviations.
| Abbreviation | Full Term |
|---|---|
| CFL | Courant–Friedrichs–Lewy condition |
| DEIM | Discrete Empirical Interpolation Method |
| DOF | Degrees of Freedom |
| EIM | Empirical Interpolation Method |
| FCN | Fully Convolutional Network |
| FEM | Finite-Element Method |
| GP | Gaussian Process |
| IIRS | Iterated Improved Reduced System |
| IRS | Improved Reduced System |
| LSTM | Long Short-Term Memory |
| MOR | Model Order Reduction |
| NARX | Nonlinear Autoregressive with Exogenous Input |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| PCE | Polynomial Chaos Expansion |
| POD | Proper Orthogonal Decomposition |
| ROM | Reduced-Order Model |
| SEREP | System Equivalent Reduction Expansion Process |
| SHM | Structural Health Monitoring |
| SVD | Singular Value Decomposition |
References
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Mardanshahi, A.; Sreekumar, A.; Yang, X.; Barman, S.K.; Chronopoulos, D. Sensing Techniques for Structural Health Monitoring: A State-of-the-Art Review on Performance Criteria and New-Generation Technologies. Sensors 2025, 25, 1424. [Google Scholar] [CrossRef] [PubMed]
- Marwala, T. Finite Element Model Updating Using Computational Intelligence Techniques: Applications to Structural Dynamics; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Chinesta, F.; Cueto, E.; Abisset-Chavanne, E.; Duval, J.L.; Khaldi, F.E. Virtual, digital and hybrid twins: A new paradigm in data-based engineering and engineered data. Arch. Comput. Methods Eng. 2020, 27, 105–134. [Google Scholar] [CrossRef]
- Fink, O.; Wang, Q.; Svensen, M.; Dersin, P.; Lee, W.J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Torzoni, M.; Manzoni, A.; Mariani, S. Structural health monitoring of civil structures: A diagnostic framework powered by deep metric learning. Comput. Struct. 2022, 271, 106858. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Big data analytics and structural health monitoring: A statistical pattern recognition-based approach. Sensors 2020, 20, 2328. [Google Scholar] [CrossRef]
- Kamariotis, A.; Chatzi, E.; Straub, D. Value of information from vibration-based structural health monitoring extracted via Bayesian model updating. Mech. Syst. Signal Process. 2022, 166, 108465. [Google Scholar] [CrossRef]
- Azam, S.E.; Mariani, S. Online damage detection in structural systems via dynamic inverse analysis: A recursive Bayesian approach. Eng. Struct. 2018, 159, 28–45. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S. Parameter identification in explicit structural dynamics: Performance of the extended Kalman filter. Comput. Methods Appl. Mech. Eng. 2004, 193, 3807–3835. [Google Scholar] [CrossRef]
- Azam, S.E.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60, 866–886. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Tian, T.; Deng, D.; Hu, M.; Ma, J.; Gao, D.; Zhang, J.; Ma, S.; Yang, L.; et al. A review on guided-ultrasonic-wave-based structural health monitoring: From fundamental theory to machine learning techniques. Ultrasonics 2023, 133, 107014. [Google Scholar] [CrossRef] [PubMed]
- Wierach, P. Lamb-Wave Based Structural Health Monitoring in Polymer Composites; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Taddei, T.; Penn, J.; Yano, M.; Patera, A.T. Simulation-based classification; a model-order-reduction approach for structural health monitoring. Arch. Comput. Methods Eng. 2018, 25, 23–45. [Google Scholar] [CrossRef]
- Rosafalco, L.; Corigliano, A.; Manzoni, A.; Mariani, S. A hybrid structural health monitoring approach based on reduced-order modelling and deep learning. Proceedings 2020, 42, 67. [Google Scholar] [CrossRef]
- Sreekumar, A.; Triantafyllou, S.P.; Chevillotte, F.; Bécot, F.X. Resolving vibro-acoustics in poroelastic media via a multiscale virtual element method. Int. J. Numer. Methods Eng. 2023, 124, 1510–1546. [Google Scholar] [CrossRef]
- Sreekumar, A.; Barman, S.K. Physics-informed model order reduction for laminated composites: A Grassmann manifold approach. Compos. Struct. 2025, 361, 119035. [Google Scholar] [CrossRef]
- Rixen, D.J. A dual Craig–Bampton method for dynamic substructuring. J. Comput. Appl. Math. 2004, 168, 383–391. [Google Scholar] [CrossRef]
- Arasan, U.; Sreekumar, A.; Chevillotte, F.; Triantafyllou, S.; Chronopoulos, D.; Gourdon, E. Condensed finite element scheme for symmetric multi-layer structures including dilatational motion. J. Sound Vib. 2022, 536, 117105. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Sreekumar, A. Multiscale Aeroelastic Modelling in Porous Composite Structures. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2022. [Google Scholar]
- O’Callahan, J.C. System equivalent reduction expansion process. In Proceedings of the 7th International Modal Analysis Conference 1989, Las Vegas, NV, USA, 30 January–2 February 1989. [Google Scholar]
- Gordis, J.H. An analysis of the improved reduced system (IRS) model reduction procedure. In Proceedings of the 10th International Modal Analysis Conference 1992, San Diego, CA, USA, 3–7 February 1992; Volume 1, pp. 471–479. [Google Scholar]
- Friswell, M.; Garvey, S.; Penny, J. Model reduction using dynamic and iterated IRS techniques. J. Sound Vib. 1995, 186, 311–323. [Google Scholar] [CrossRef]
- Sreekumar, A.; Chevillotte, F.; Gourdon, E. Numerical condensation for heterogeneous porous materials and metamaterials. In Proceedings of the 10e Convention de l’Association Européenne d’Acoustique, EAA 2023, Turin, Itlay, 11–15 September 2023. [Google Scholar]
- Besselink, B.; Tabak, U.; Lutowska, A.; Van de Wouw, N.; Nijmeijer, H.; Rixen, D.J.; Hochstenbach, M.; Schilders, W. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control. J. Sound Vib. 2013, 332, 4403–4422. [Google Scholar] [CrossRef]
- Flodén, O.; Persson, K.; Sandberg, G. Reduction methods for the dynamic analysis of substructure models of lightweight building structures. Comput. Struct. 2014, 138, 49–61. [Google Scholar] [CrossRef]
- Bai, Z. Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems. Appl. Numer. Math. 2002, 43, 9–44. [Google Scholar] [CrossRef]
- Rosafalco, L.; Torzoni, M.; Manzoni, A.; Mariani, S.; Corigliano, A. Online structural health monitoring by model order reduction and deep learning algorithms. Comput. Struct. 2021, 255, 106604. [Google Scholar] [CrossRef]
- Torzoni, M.; Rosafalco, L.; Manzoni, A. A combined model-order reduction and deep learning approach for structural health monitoring under varying operational and environmental conditions. Eng. Proc. 2020, 2, 94. [Google Scholar]
- Sepehry, N.; Shamshirsaz, M.; Bakhtiari Nejad, F. Low-cost simulation using model order reduction in structural health monitoring: Application of balanced proper orthogonal decomposition. Struct. Control. Health Monit. 2017, 24, e1994. [Google Scholar] [CrossRef]
- Torzoni, M.; Manzoni, A.; Mariani, S. A multi-fidelity surrogate model for structural health monitoring exploiting model order reduction and artificial neural networks. Mech. Syst. Signal Process. 2023, 197, 110376. [Google Scholar] [CrossRef]
- Du, J.; Zeng, J.; Wang, H.; Ding, H.; Wang, H.; Bi, Y. Using acoustic emission technique for structural health monitoring of laminate composite: A novel CNN-LSTM framework. Eng. Fract. Mech. 2024, 309, 110447. [Google Scholar] [CrossRef]
- Luo, H.; Huang, M.; Zhou, Z. A dual-tree complex wavelet enhanced convolutional LSTM neural network for structural health monitoring of automotive suspension. Measurement 2019, 137, 14–27. [Google Scholar] [CrossRef]
- Sengupta, P.; Chakraborty, S. An improved iterative model reduction technique to estimate the unknown responses using limited available responses. Mech. Syst. Signal Process. 2023, 182, 109586. [Google Scholar] [CrossRef]
- Kundu, A.; Adhikari, S. Transient response of structural dynamic systems with parametric uncertainty. J. Eng. Mech. 2014, 140, 315–331. [Google Scholar] [CrossRef]
- Sreekumar, A.; Kougioumtzoglou, I.A.; Triantafyllou, S.P. Filter approximations for random vibroacoustics of rigid porous media. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2024, 10, 031201. [Google Scholar] [CrossRef]
- Jacquelin, E.; Baldanzini, N.; Bhattacharyya, B.; Brizard, D.; Pierini, M. Random dynamical system in time domain: A POD-PC model. Mech. Syst. Signal Process. 2019, 133, 106251. [Google Scholar] [CrossRef]
- Gerritsma, M.; Van der Steen, J.B.; Vos, P.; Karniadakis, G. Time-dependent generalized polynomial chaos. J. Comput. Phys. 2010, 229, 8333–8363. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Jacquelin, E.; Adhikari, S.; Sinou, J.J.; Friswell, M.I. Polynomial chaos expansion and steady-state response of a class of random dynamical systems. J. Eng. Mech. 2015, 141, 04014145. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Mathelin, L.; Knio, O.M.; Hussaini, M.Y. Asynchronous time integration for polynomial chaos expansion of uncertain periodic dynamics. Discret. Contin. Dyn. Syst. 2010, 28, 199–226. [Google Scholar] [CrossRef]
- Spiridonakos, M.D.; Chatzi, E.N. Metamodeling of dynamic nonlinear structural systems through polynomial chaos NARX models. Comput. Struct. 2015, 157, 99–113. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Jacquelin, E.; Brizard, D. Uncertainty quantification of nonlinear stochastic dynamic problem using a Kriging-NARX surrogate model. In Proceedings of the 3rd International Conference on Uncertainty Quantification in Computational Sciences and Engineering, ECCOMAS, Crete, Greece, 24–16 June 2019; pp. 34–46. [Google Scholar]
- Bhattacharyya, B.; Jacquelin, E.; Brizard, D. A Kriging–NARX model for uncertainty quantification of nonlinear stochastic dynamical systems in time domain. J. Eng. Mech. 2020, 146, 04020070. [Google Scholar] [CrossRef]
- Bhattacharyya, B. Uncertainty quantification of dynamical systems by a POD–Kriging surrogate model. J. Comput. Sci. 2022, 60, 101602. [Google Scholar] [CrossRef]
- Zhong, L.; Chen, C.P.; Guo, J.; Zhang, T. Robust incremental broad learning system for data streams of uncertain scale. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 7580–7593. [Google Scholar] [CrossRef] [PubMed]
- Samadian, D.; Muhit, I.B.; Dawood, N. Application of data-driven surrogate models in structural engineering: A literature review. Arch. Comput. Methods Eng. 2024, 32, 735–784. [Google Scholar] [CrossRef]
- Hao, P.; Feng, S.; Li, Y.; Wang, B.; Chen, H. Adaptive infill sampling criterion for multi-fidelity gradient-enhanced kriging model. Struct. Multidiscip. Optim. 2020, 62, 353–373. [Google Scholar] [CrossRef]
- Brezzi, F.; Franzone, P.C.; Gianazza, U.; Gilardi, G. Analysis and Numerics of Partial Differential Equations; Springer: Cham, Switzerland, 2013. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Tiso, P.; Rixen, D.J. Discrete empirical interpolation method for finite element structural dynamics. In Proceedings of the Topics in Nonlinear Dynamics, Volume 1: Proceedings of the 31st IMAC, A Conference on Structural Dynamics, Garden Grove, CA, USA, 11–14 February 2013; Springer: New York, NY, USA, 2013; pp. 203–212. [Google Scholar]
- Nguyen, N.C.; Patera, A.T.; Peraire, J. A ‘best points’ interpolation method for efficient approximation of parametrized functions. Int. J. Numer. Methods Eng. 2008, 73, 521–543. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Development of reduced Preisach model using discrete empirical interpolation method. IEEE Trans. Ind. Electron. 2018, 65, 8072–8079. [Google Scholar] [CrossRef]
- Barrault, M.; Maday, Y.; Nguyen, N.C.; Patera, A.T. An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Math. 2004, 339, 667–672. [Google Scholar] [CrossRef]
- Dasgupta, A.; Pecht, M. Material failure mechanisms and damage models. IEEE Trans. Reliab. 1991, 40, 531–536. [Google Scholar] [CrossRef]
- Arefi, A.; van der Meer, F.P.; Forouzan, M.R.; Silani, M.; Salimi, M. Micromechanical evaluation of failure models for unidirectional fiber-reinforced composites. J. Compos. Mater. 2020, 54, 791–800. [Google Scholar] [CrossRef]
- Rossi, D.F.; Ferreira, W.G.; Mansur, W.J.; Calenzani, A.F.G. A review of automatic time-stepping strategies on numerical time integration for structural dynamics analysis. Eng. Struct. 2014, 80, 118–136. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Hosseini, B.; Kovachki, N.B.; Stuart, A.M. Model reduction and neural networks for parametric PDEs. SMAI J. Comput. Math. 2021, 7, 121–157. [Google Scholar] [CrossRef]
- Lassila, T.; Rozza, G. Parametric free-form shape design with PDE models and reduced basis method. Comput. Methods Appl. Mech. Eng. 2010, 199, 1583–1592. [Google Scholar] [CrossRef]
- Arefi, A.; Sreekumar, A.; Chronopoulos, D. A Programmable Hybrid Energy Harvester: Leveraging Buckling and Magnetic Multistability. Micromachines 2025, 16, 359. [Google Scholar] [CrossRef]
- Falini, A. A review on the selection criteria for the truncated SVD in Data Science applications. J. Comput. Math. Data Sci. 2022, 5, 100064. [Google Scholar] [CrossRef]
- Van Beers, W.C.; Kleijnen, J.P. Kriging interpolation in simulation: A survey. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1. [Google Scholar]
- Sreekumar, A. Wave-Based SHM Empirical Interpolation MATLAB Code. GitHub Repository. Available online: https://github.com/abhimuscat/wave-based-shm-empirical-interpolation-matlab.git (accessed on 25 April 2025).
- Stoter, S. 10–Model Order Reduction–(Discrete) Empirical Interpolation Method (DEIM). YouTube Video. 2023. Available online: https://www.youtube.com/watch?v=L70nwaBAjlQ (accessed on 24 April 2025).
- Gorissen, D.; Couckuyt, I.; Demeester, P.; Dhaene, T.; Crombecq, K. A surrogate modeling and adaptive sampling toolbox for computer based design. J. Mach. Learn. Res. Camb. Mass. 2010, 11, 2051–2055. [Google Scholar]
- Gorissen, D.; Couckuyt, S.; Demeester, Y.; Dhaene, J.; Riche, R.J.L. ooDACE Toolbox; Dual-Licensed Under GNU Affero GPL v3 and Commercial License; iMinds-SUMO Lab, Ghent University: Gent, Belgium, 2009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).