A Finite Element–Finite Volume Code Coupling for Optimal Control Problems in Fluid Heat Transfer for Incompressible Navier–Stokes Equations
Abstract
1. Introduction
2. Optimal Control Problems
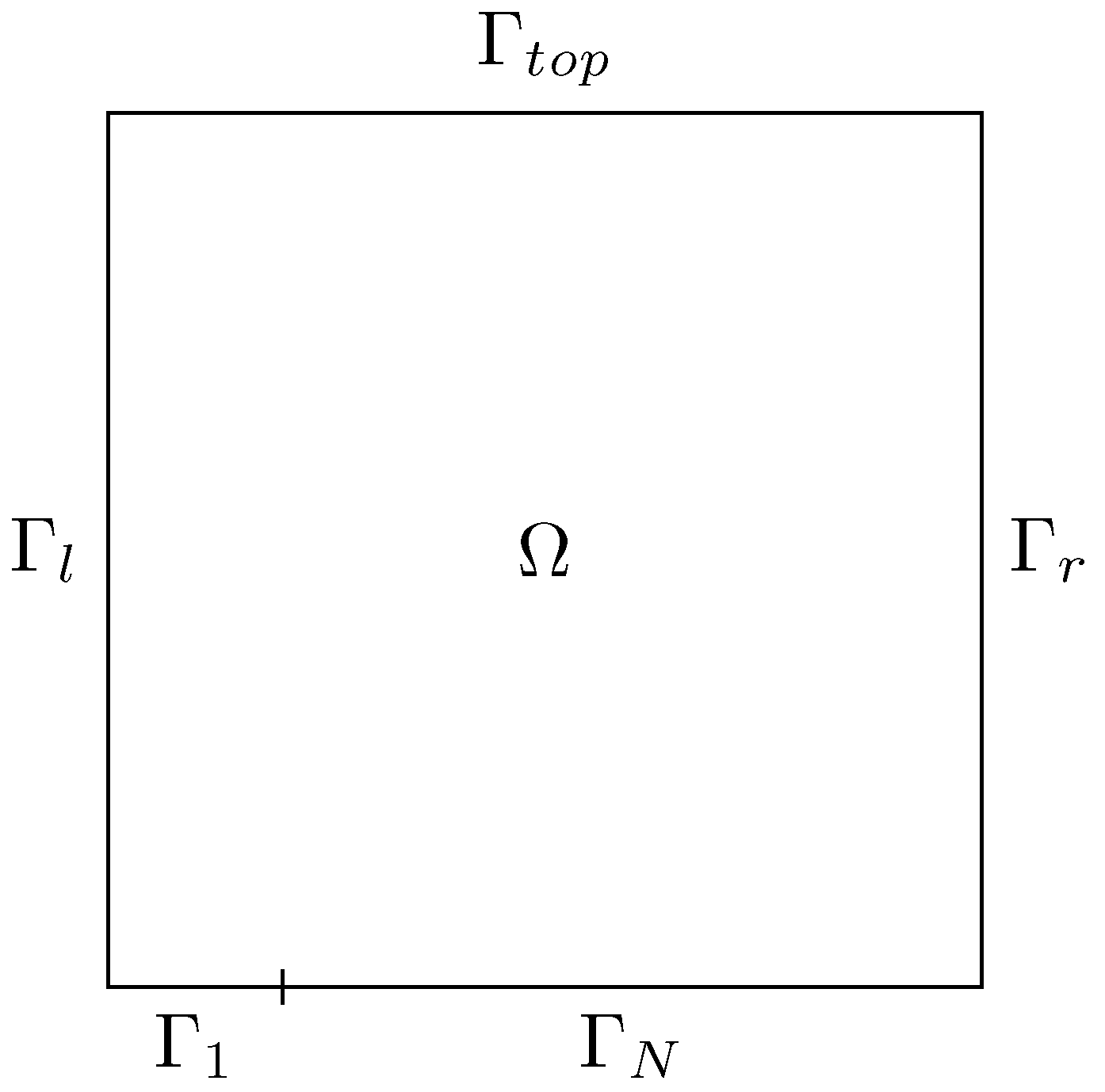
2.1. Rayleigh–Bénard Problem
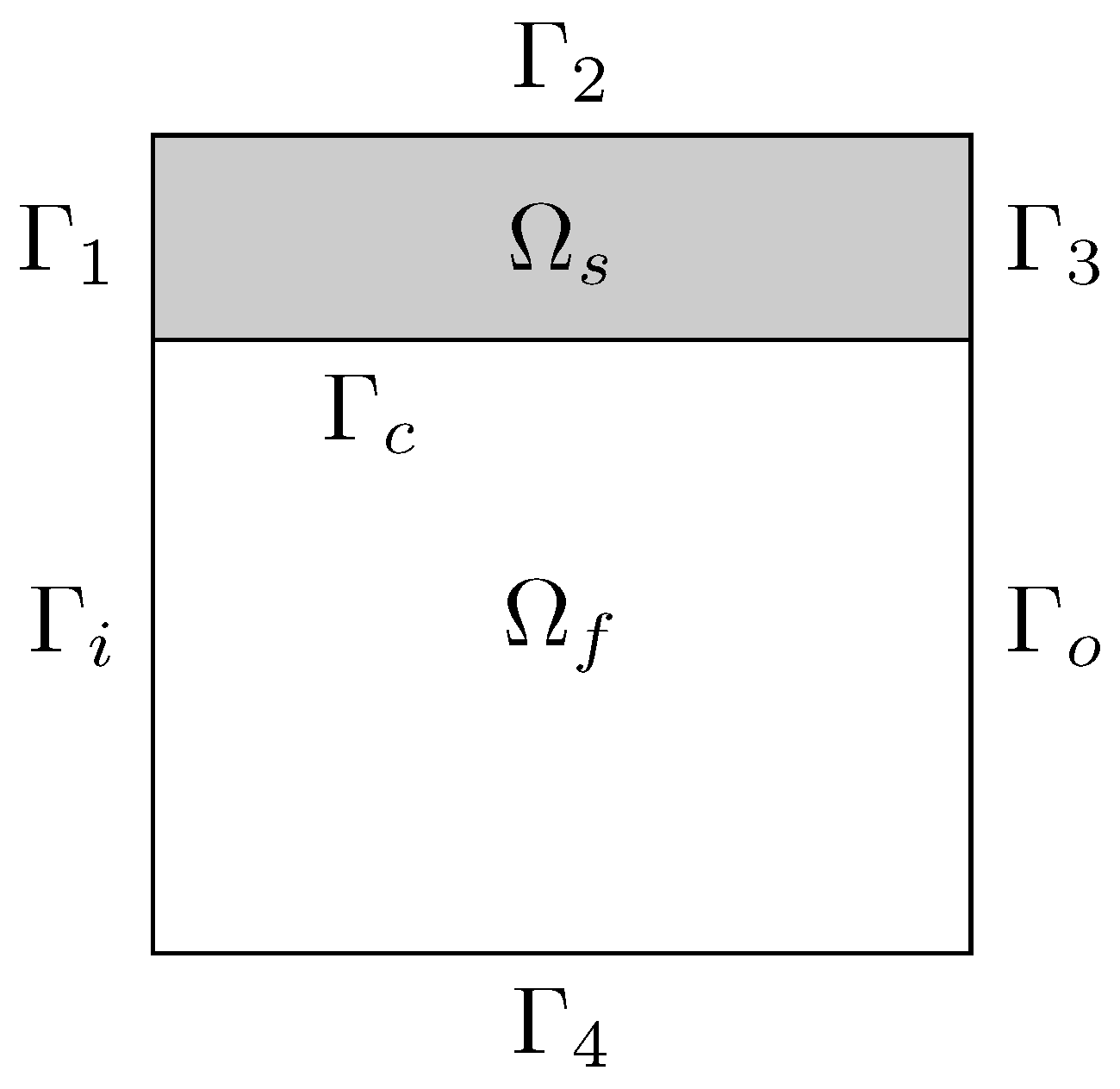
2.2. Solid/Fluid Heat Transfer Problem
2.3. Minimization Method
| Algorithm 1 Steepest gradient method |
|
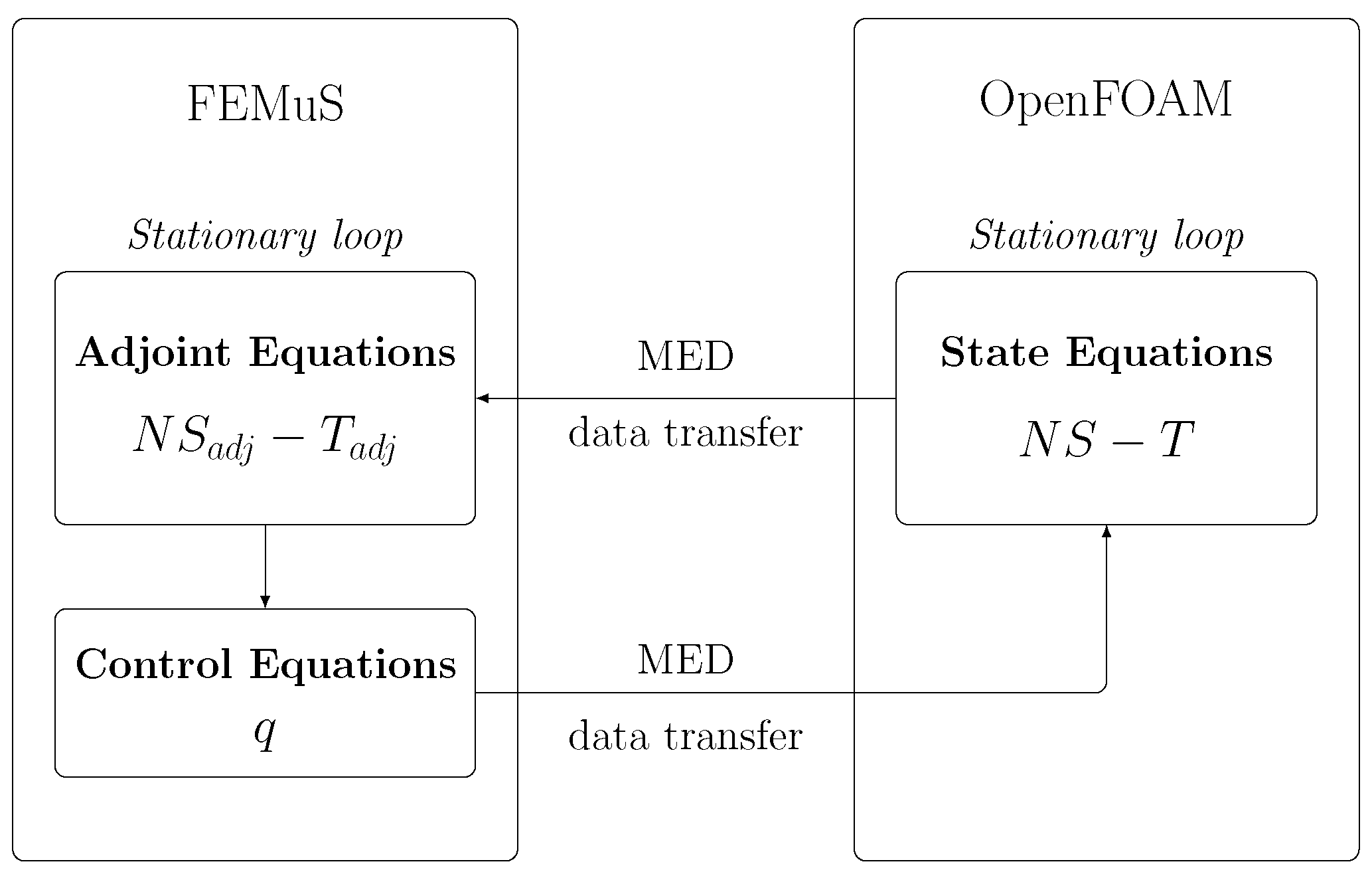
3. Coupling Algorithm
3.1. Rayleigh–Bénard Problem
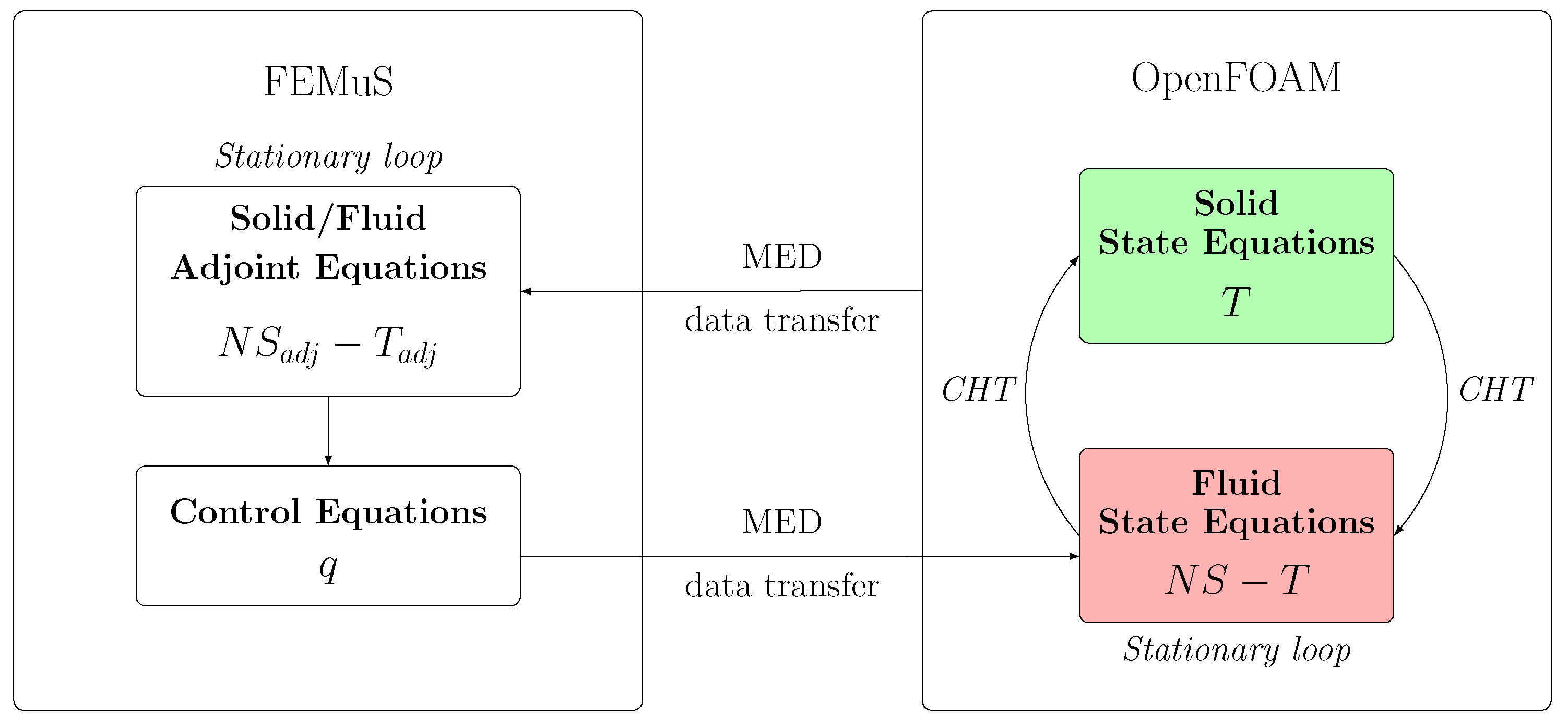
3.2. Solid/Fluid Heat Transfer Problem
3.3. Numerical Discretization
4. Numerical Results
4.1. Rayleigh–Bénard Problem
4.1.1. Uncontrolled Case
4.1.2. Distributed Control
4.1.3. Neumann Boundary Control
4.2. Solid/Fluid Heat Transfer Problem
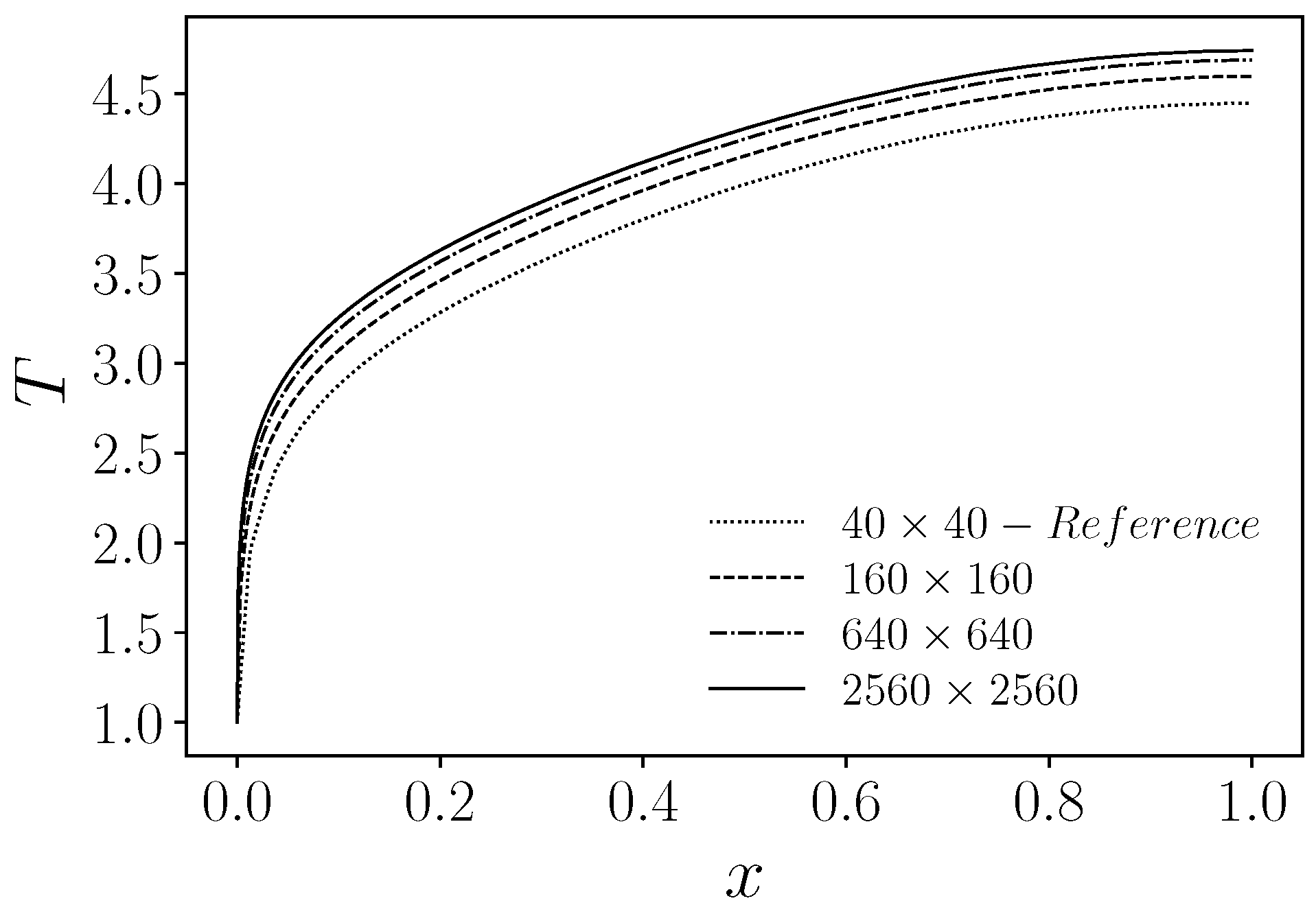
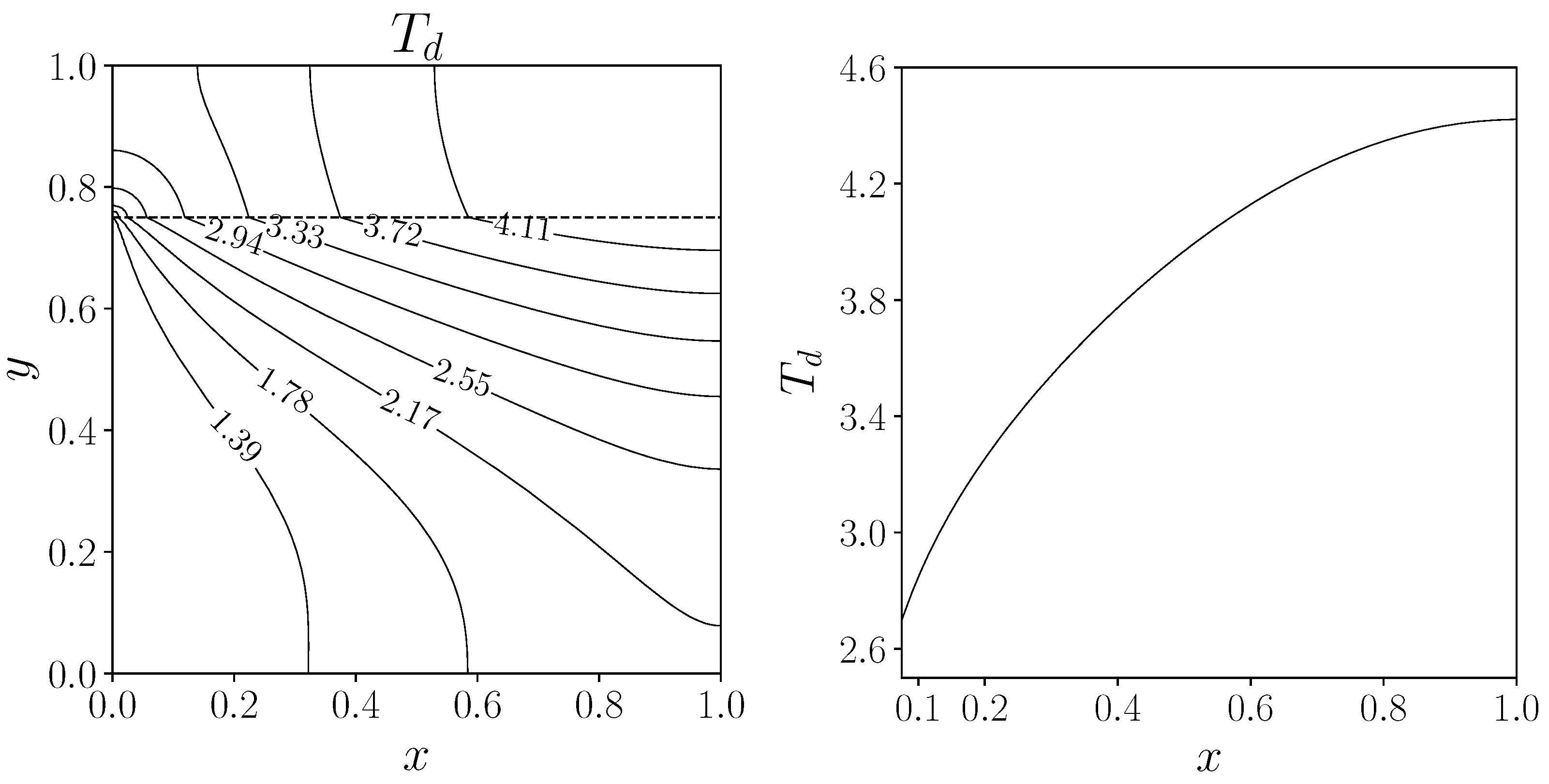
4.2.1. Definition of the Target Temperature
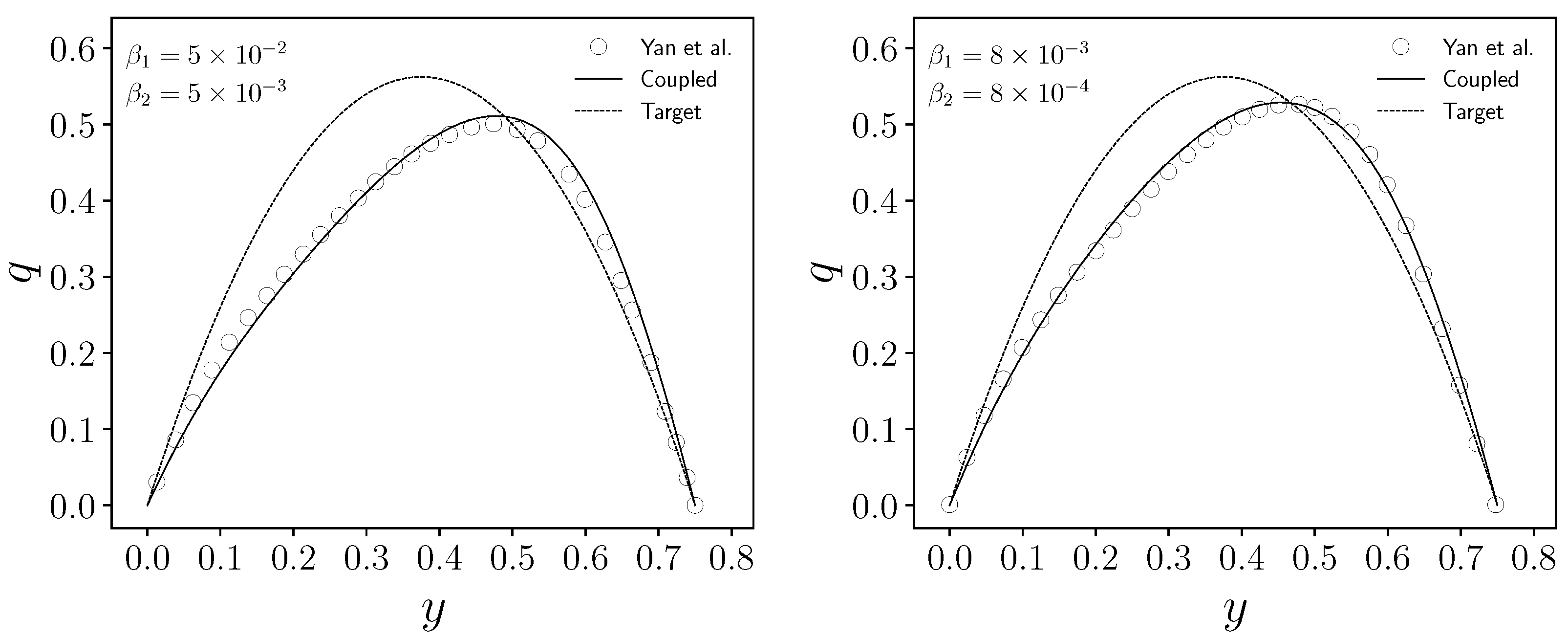
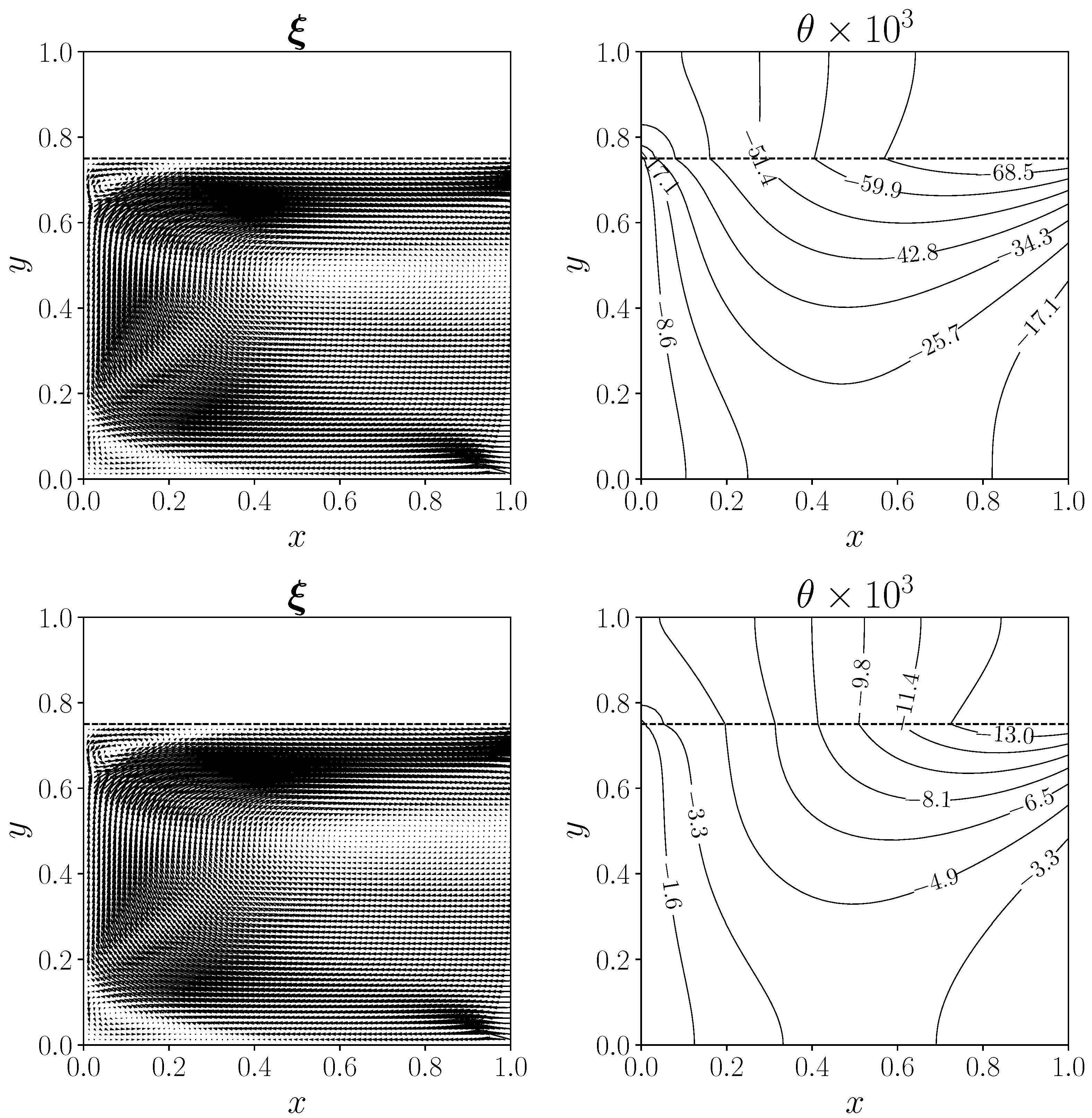
4.2.2. Dirichlet Boundary Control
4.3. Steepest Descent Convergence Order
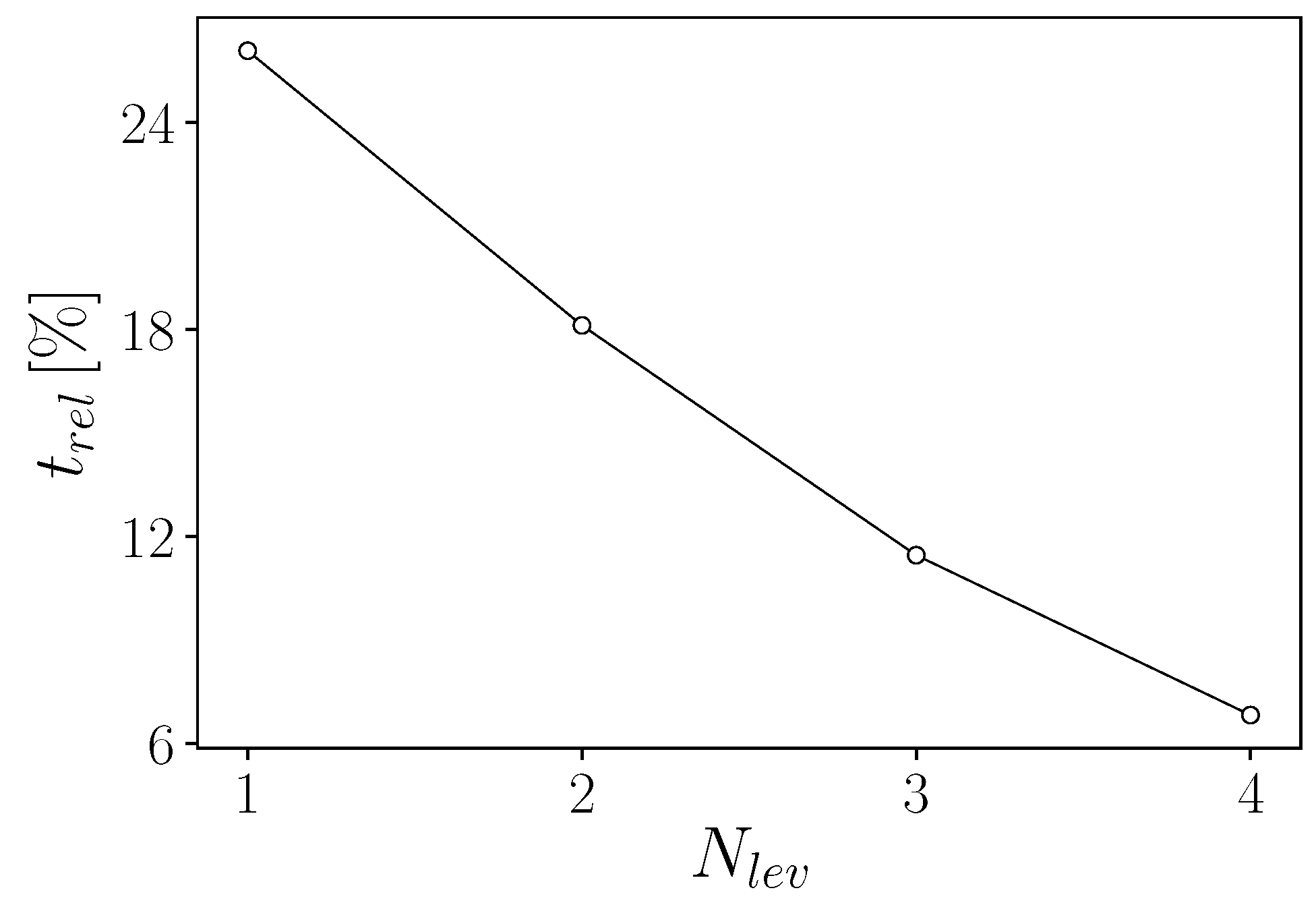
4.4. Data Transfer Overhead
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manzoni, A.; Quarteroni, A.; Salsa, S. Optimal Control of Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Jan, S.; Jean-Paul, Z. Introduction to Shape Optimization; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Chertovskih, R.; Ribeiro, V.M.; Gonçalves, R.; Aguiar, A.P. Sixty Years of the Maximum Principle in Optimal Control: Historical Roots and Content Classification. Symmetry 2024, 16, 1398. [Google Scholar] [CrossRef]
- Gunzburger, M.D. Perspectives in Flow Control and Optimization; SIAM: Bangkok, Thailand, 2002. [Google Scholar]
- Chierici, A.; Giovacchini, V.; Manservisi, S. Analysis and Computations of Optimal Control Problems for Boussinesq Equations. Fluids 2022, 7, 203. [Google Scholar] [CrossRef]
- Barbi, G.; Cervone, A.; Giangolini, F.; Manservisi, S.; Sirotti, L. Numerical Coupling between a FEM Code and the FVM Code OpenFOAM Using the MED Library. Appl. Sci. 2024, 14, 3744. [Google Scholar] [CrossRef]
- Baldini, S.; Barbi, G.; Cervone, A.; Giangolini, F.; Manservisi, S.; Sirotti, L. Optimal Control of Heat Equation by Coupling FVM and FEM Codes. Mathematics 2025, 13, 238. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007; Volume 1000, pp. 1–20. [Google Scholar]
- Barbi, G.; Bornia, G.; Cerroni, D.; Cervone, A.; Chierici, A.; Chirco, L.; Viá, R.; Giovacchini, V.; Manservisi, S.; Scardovelli, R.; et al. FEMuS-Platform: A numerical platform for multiscale and multiphysics code coupling. In Proceedings of the 9th International Conference on Computational Methods for Coupled Problems in Science and Engineering, COUPLED PROBLEMS, Chia Bay, Italy, 13–16 June 2021; International Center for Numerical Methods in Engineering: Barcelona, Spain, 2021; pp. 1–12. [Google Scholar]
- Ribes, A.; Caremoli, C. Salome platform component model for numerical simulation. In Proceedings of the 31st Annual International Computer Software and Applications Conference (COMPSAC 2007), Beijing, China, 23–37 July 2007; Volume 2, pp. 553–564. [Google Scholar]
- Lee, H.C. Optimal control problems for the two dimensional Rayleigh—Bénard type convection by a gradient method. Jpn. J. Ind. Appl. Math. 2009, 26, 93. [Google Scholar] [CrossRef]
- Yan, Y.; Keyes, D.E. Smooth and robust solutions for Dirichlet boundary control of fluid–solid conjugate heat transfer problems. J. Comput. Phys. 2015, 281, 759–786. [Google Scholar] [CrossRef]
- Cutelier, C. Optimal Control of a System Governed by the Navier-Stokes Equations Coupled with the Heat Equation. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 1976; Volume 21, pp. 81–98. [Google Scholar]
- Alekseev, G.; Tereshko, D. Stability of optimal controls for the stationary Boussinesq equations. Int. J. Differ. Equ. 2011, 2011, 535736. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Domnich, A.A.; Artemov, M.A. Optimal boundary control of non-isothermal viscous fluid flow. Fluids 2019, 4, 133. [Google Scholar] [CrossRef]
- Belmiloudi, A. Robin-type boundary control problems for the nonlinear Boussinesq type equations. J. Math. Anal. Appl. 2002, 273, 428–456. [Google Scholar] [CrossRef]
- Lee, H.C.; Imanuvilov, O.Y. Analysis of Neumann boundary optimal control problems for the stationary Boussinesq equations including solid media. SIAM J. Control Optim. 2000, 39, 457–477. [Google Scholar] [CrossRef]
- Lee, H.C.; Imanuvilov, O.Y. Analysis of optimal control problems for the 2-D stationary Boussinesq equations. J. Math. Anal. Appl. 2000, 242, 191–211. [Google Scholar] [CrossRef]
- Lee, H.C.; Shin, B.C. Piecewise optimal distributed controls for 2D Boussinesq equations. Math. Methods Appl. Sci. 2000, 23, 227–254. [Google Scholar] [CrossRef]
- Lee, H.C.; Shin, B.C. Dynamics for controlled 2-D Boussinesq systems with distributed controls. J. Math. Anal. Appl. 2002, 273, 457–479. [Google Scholar] [CrossRef]
- Lee, H.C. Analysis and computational methods of Dirichlet boundary optimal control problems for 2D Boussinesq equations. Adv. Comput. Math. 2003, 19, 255–275. [Google Scholar] [CrossRef]
- Li, S. Optimal controls of Boussinesq equations with state constraints. Nonlinear Anal. Theory Methods Appl. 2005, 60, 1485–1508. [Google Scholar] [CrossRef]
- Li, S.; Wang, G. The time optimal control of the Boussinesq equations. Numer. Funct. Anal. Optim. 2003, 24, 163–180. [Google Scholar] [CrossRef]
- Fursikov, A.V.; Imanuvilov, O.Y. Local exact boundary controllability of the Boussinesq equation. SIAM J. Control Optim. 1998, 36, 391–421. [Google Scholar] [CrossRef]
- Mallea-Zepeda, E.; Lenes, E.; Valero, E. Boundary control problem for heat convection equations with slip boundary condition. Math. Probl. Eng. 2018, 2018, 7959761. [Google Scholar] [CrossRef]
- Rueda-Gómez, D.A.; Villamizar-Roa, E.J. On the Rayleigh–Bénard–Marangoni system and a related optimal control problem. Comput. Math. Appl. 2017, 74, 2969–2991. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Lee, H.C. Analysis, approximation, and computation of a coupled solid/fluid temperature control problem. Comput. Methods Appl. Mech. Eng. 1994, 118, 133–152. [Google Scholar] [CrossRef]
- Gunzburger, M.D.; Hou, L.S.; Svobodny, T.P. The approximation of boundary control problems for fluid flows with an application to control by heating and cooling. Comput. Fluids 1993, 22, 239–251. [Google Scholar] [CrossRef]
- Adams, R.A.; Fournier, J.J. Sobolev Spaces; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Bornia, G.; Ratnavale, S. Different approaches for Dirichlet and Neumann boundary optimal control. AIP Conf. Proc. 2018, 1978, 270006. [Google Scholar]
- Bornia, G.; Chierici, A.; Ratnavale, S. A comparison of regularization methods for boundary optimal control problems. Int. J. Numer. Anal. Model. 2022, 19, 329–346. [Google Scholar]
- D’Elia, M.; Gunzburger, M. The fractional Laplacian operator on bounded domains as a special case of the nonlocal diffusion operator. Comput. Math. Appl. 2013, 66, 1245–1260. [Google Scholar] [CrossRef]
- Benzi, M.; Olshanskii, M.A. An Augmented Lagrangian-Based Approach to the Oseen Problem. SIAM J. Sci. Comput. 2006, 28, 2095–2113. [Google Scholar] [CrossRef]
- Furkisov, A.V.; Gunzburger, M.D.; Hou, L.S. Boundary Value Problems and Optimal Boundary Control for the Navier-Stokes systems: The two-dimensional case. SIAM J. Control Optim. 1998, 36, 852–894. [Google Scholar]
- Gunzburger, M.; Hou, L.; Svobodny, T.P. Analysis and finite element approximation of optimal control problems for the stationary Navier-Stokes equations with Dirichlet controls. ESAIM Math. Model. Numer. Anal. 1991, 25, 711–748. [Google Scholar] [CrossRef]
- David, G.L.; Yinyu, Y. Linear and Nonlinear Programming; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Ern, A.; Guermond, J.L. Theory and Practice of Finite Elements; Springer: Berlin/Heidelberg, Germany, 2004; Volume 159. [Google Scholar]
- Vivette, G.; Pierre-Arnaud, R. Finite Element Methods for Navier-Stokes Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Silva, G.H.; Le Riche, R.; Molimard, J.; Vautrin, A. Exact and efficient interpolation using finite elements shape functions. Eur. J. Comput. Mech. 2009, 18, 307–331. [Google Scholar] [CrossRef]
- Da Vià, R. Development of a Computational Platform for the Simulation of Low Prandtl Number Turbulent Flows. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2019. [Google Scholar]
- Pichi, F.; Strazzullo, M.; Ballarin, F.; Rozza, G. Driving bifurcating parametrized nonlinear PDEs by optimal control strategies: Application to Navier–Stokes equations with model order reduction. ESAIM Math. Model. Numer. Anal. 2022, 56, 1361–1400. [Google Scholar] [CrossRef]
- Meza, J.C. Steepest descent. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 719–722. [Google Scholar] [CrossRef]





| T | |||||
| Uncontrolled | |||
|---|---|---|---|
| [11] | [11] | [11] | |||||
|---|---|---|---|---|---|---|---|
| Uncontrolled | - | - | |||||
| Uncontrolled | |||
|---|---|---|---|
| [11] | [11] | [11] | |||||
|---|---|---|---|---|---|---|---|
| Uncontrolled | - | - | |||||
| - | - | - | |||||
| T | CHT | ||||||
| - | - | - | |||||
| CHT |
| Uncontrolled | - | ||||
| p | ||||
| Case 1 | Case 2 | |
|---|---|---|
| p |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldini, S.; Barbi, G.; Bornia, G.; Cervone, A.; Giangolini, F.; Manservisi, S.; Sirotti, L. A Finite Element–Finite Volume Code Coupling for Optimal Control Problems in Fluid Heat Transfer for Incompressible Navier–Stokes Equations. Mathematics 2025, 13, 1701. https://doi.org/10.3390/math13111701
Baldini S, Barbi G, Bornia G, Cervone A, Giangolini F, Manservisi S, Sirotti L. A Finite Element–Finite Volume Code Coupling for Optimal Control Problems in Fluid Heat Transfer for Incompressible Navier–Stokes Equations. Mathematics. 2025; 13(11):1701. https://doi.org/10.3390/math13111701
Chicago/Turabian StyleBaldini, Samuele, Giacomo Barbi, Giorgio Bornia, Antonio Cervone, Federico Giangolini, Sandro Manservisi, and Lucia Sirotti. 2025. "A Finite Element–Finite Volume Code Coupling for Optimal Control Problems in Fluid Heat Transfer for Incompressible Navier–Stokes Equations" Mathematics 13, no. 11: 1701. https://doi.org/10.3390/math13111701
APA StyleBaldini, S., Barbi, G., Bornia, G., Cervone, A., Giangolini, F., Manservisi, S., & Sirotti, L. (2025). A Finite Element–Finite Volume Code Coupling for Optimal Control Problems in Fluid Heat Transfer for Incompressible Navier–Stokes Equations. Mathematics, 13(11), 1701. https://doi.org/10.3390/math13111701


_Constantinou_Generalis.png)





