Robust Closed–Open Loop Iterative Learning Control for MIMO Discrete-Time Linear Systems with Dual-Varying Dynamics and Nonrepetitive Uncertainties
Abstract
1. Introduction
- The feedforward component ensures the convergence of tracking errors in the mathematical expectation, while the feedback controller compensates for missing tracking data from prior iterations using real-time tracking information.
- Comprehensive Handling of Multi-Source Non-Repetitive Uncertainties:
- Time-iteration dual-dimensional system dynamics variations.
- Iteration-varying trajectory lengths caused by stochastic task requirements.
- Non-repetitive external disturbances.
- Initial state deviations across iterations.
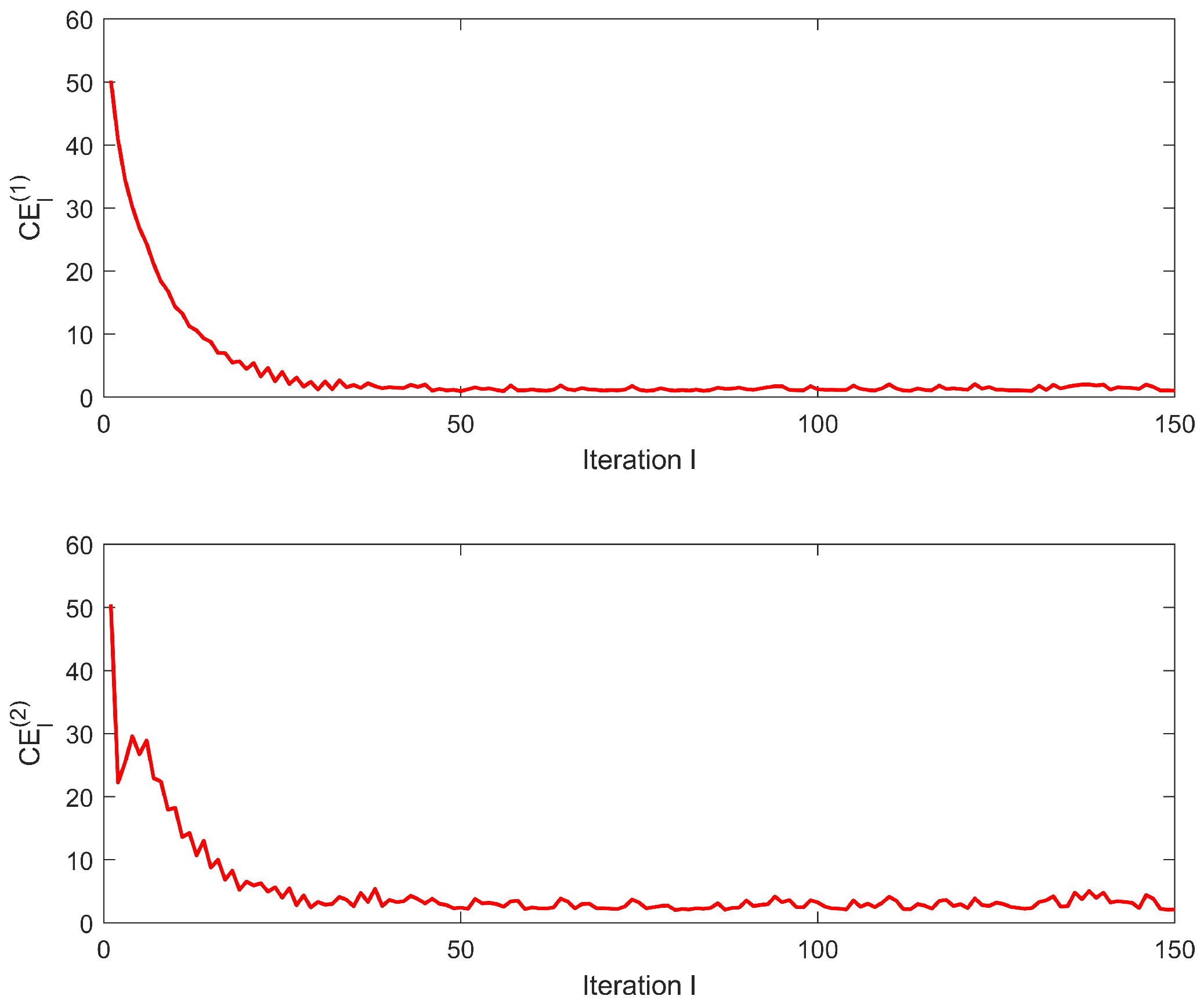
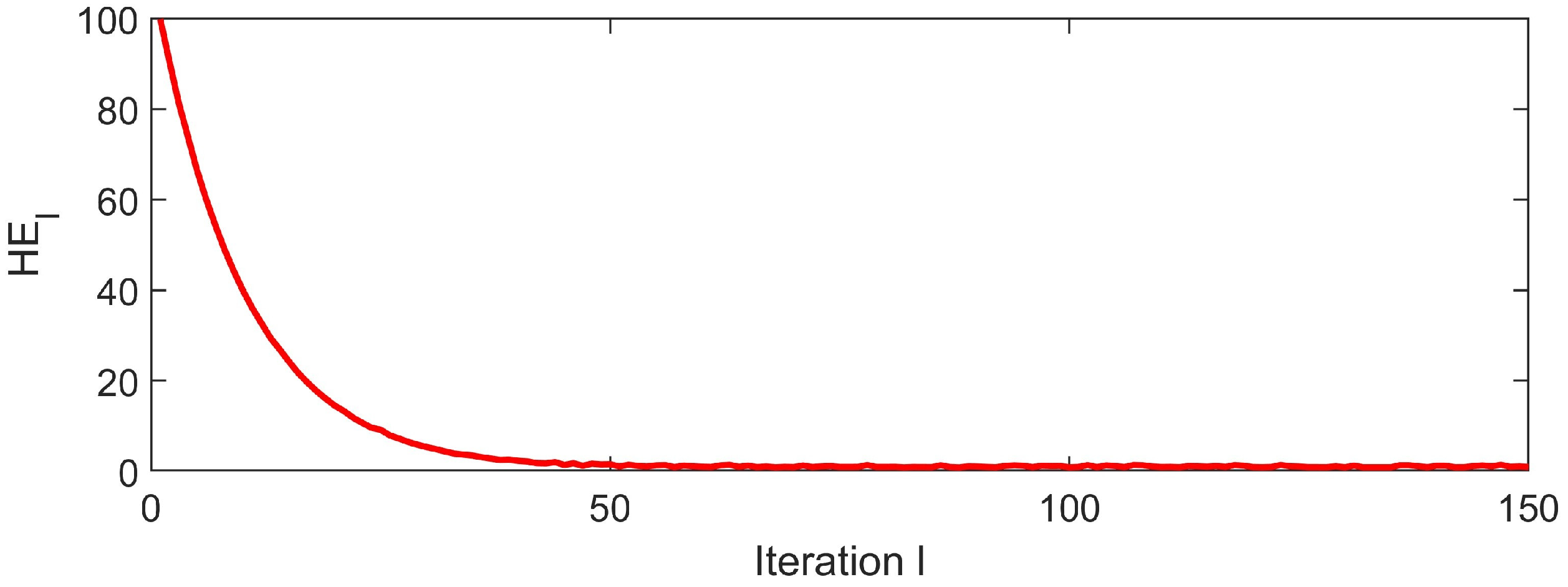
- Quantitative mappings between controller parameters and convergence rate/robustness metrics are established to guide algorithmic tuning. Experimental simulations on a piezoelectric motor system demonstrate ILC tracking error convergence to an ε-neighborhood in expectation. The feasibility of the proposed iterative learning control architecture was further confirmed through rigorous numerical simulation experiments, which provided quantitative performance validation for the transition of the open–closed loop iterative learning control law from theoretical formulation to practical operational environments.
2. Problem Formulation
2.1. Dynamics Description
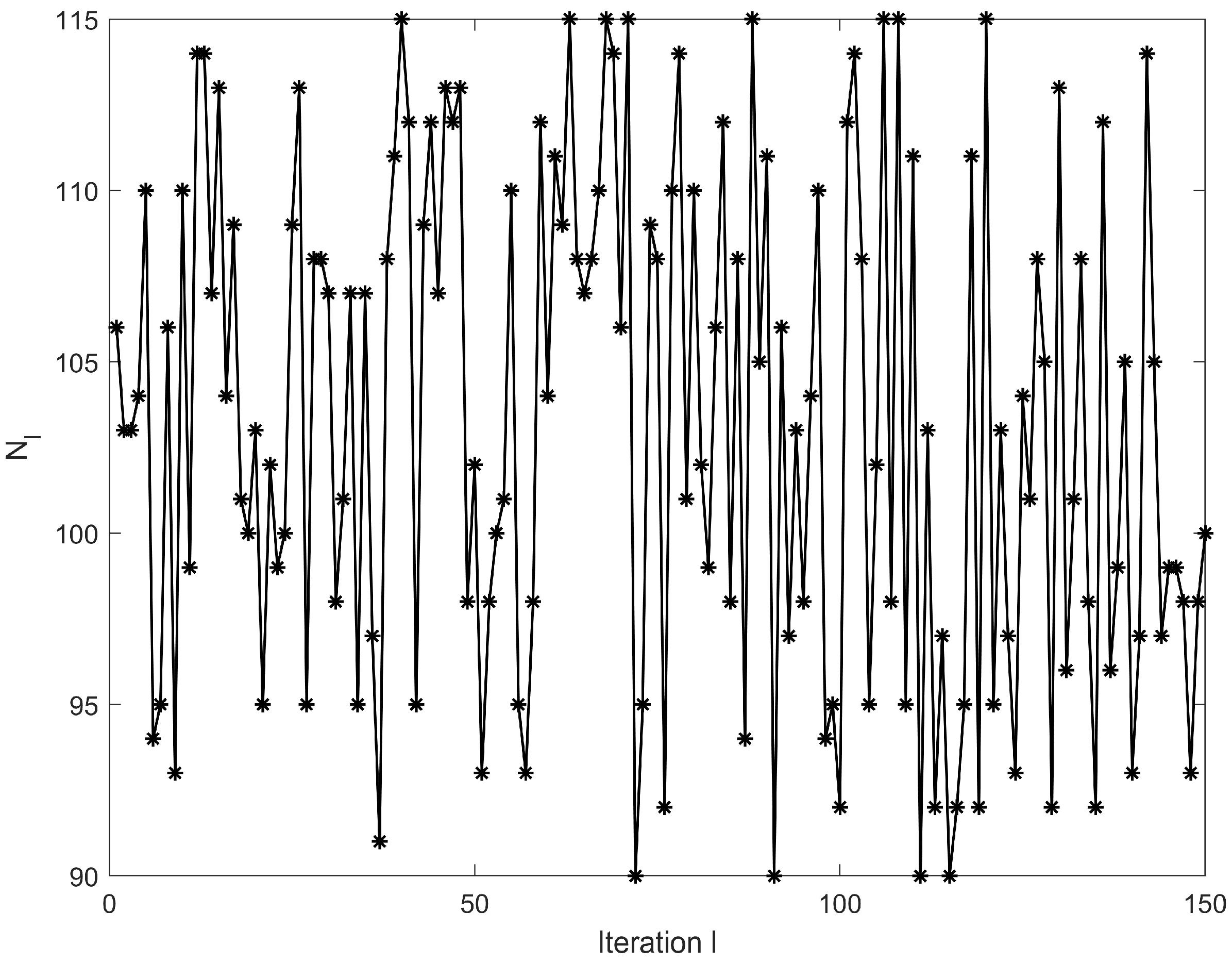
2.2. Varying Iteration Lengths
3. Open–Closed Loop Designs with Robustness and Convergence Analysis
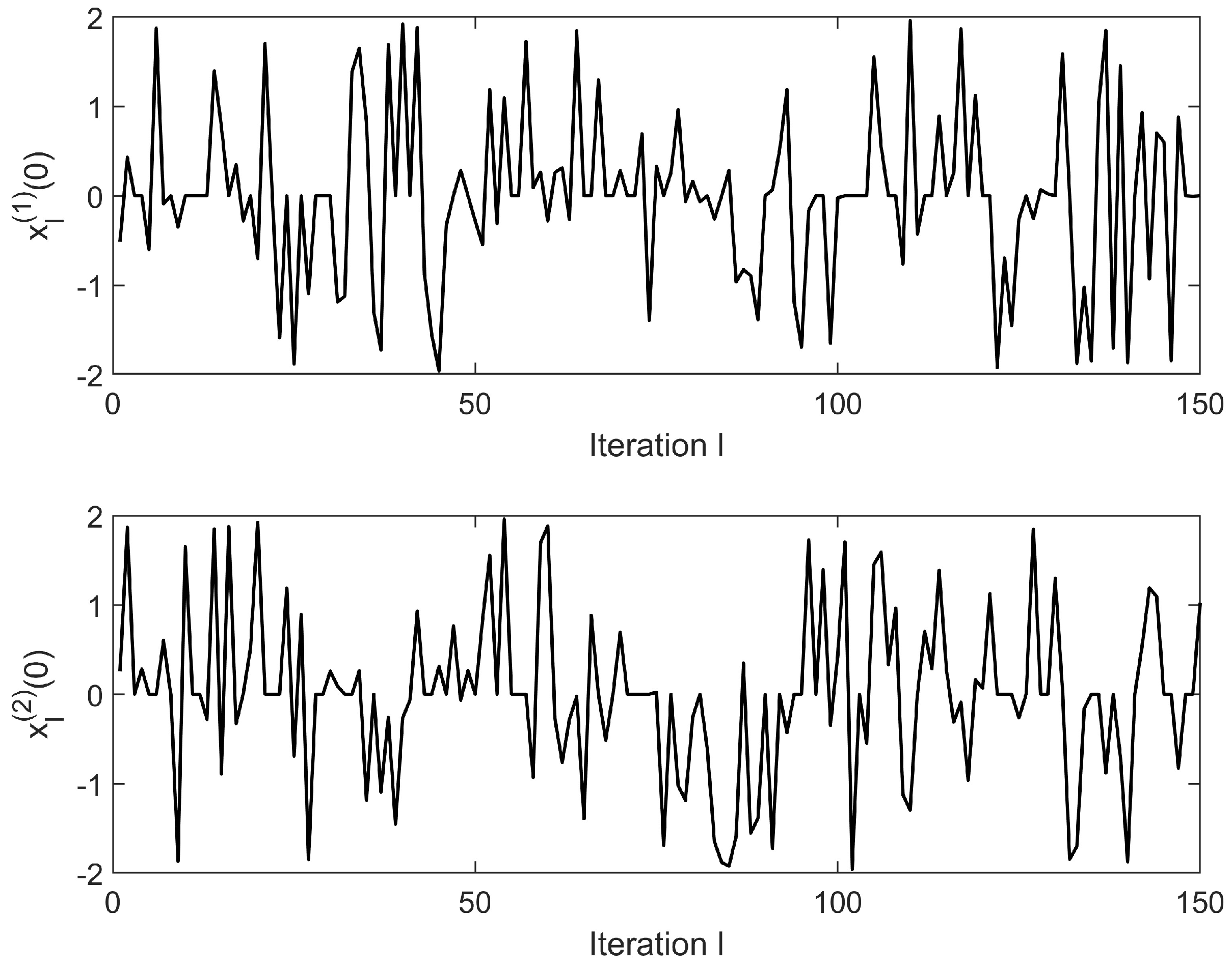
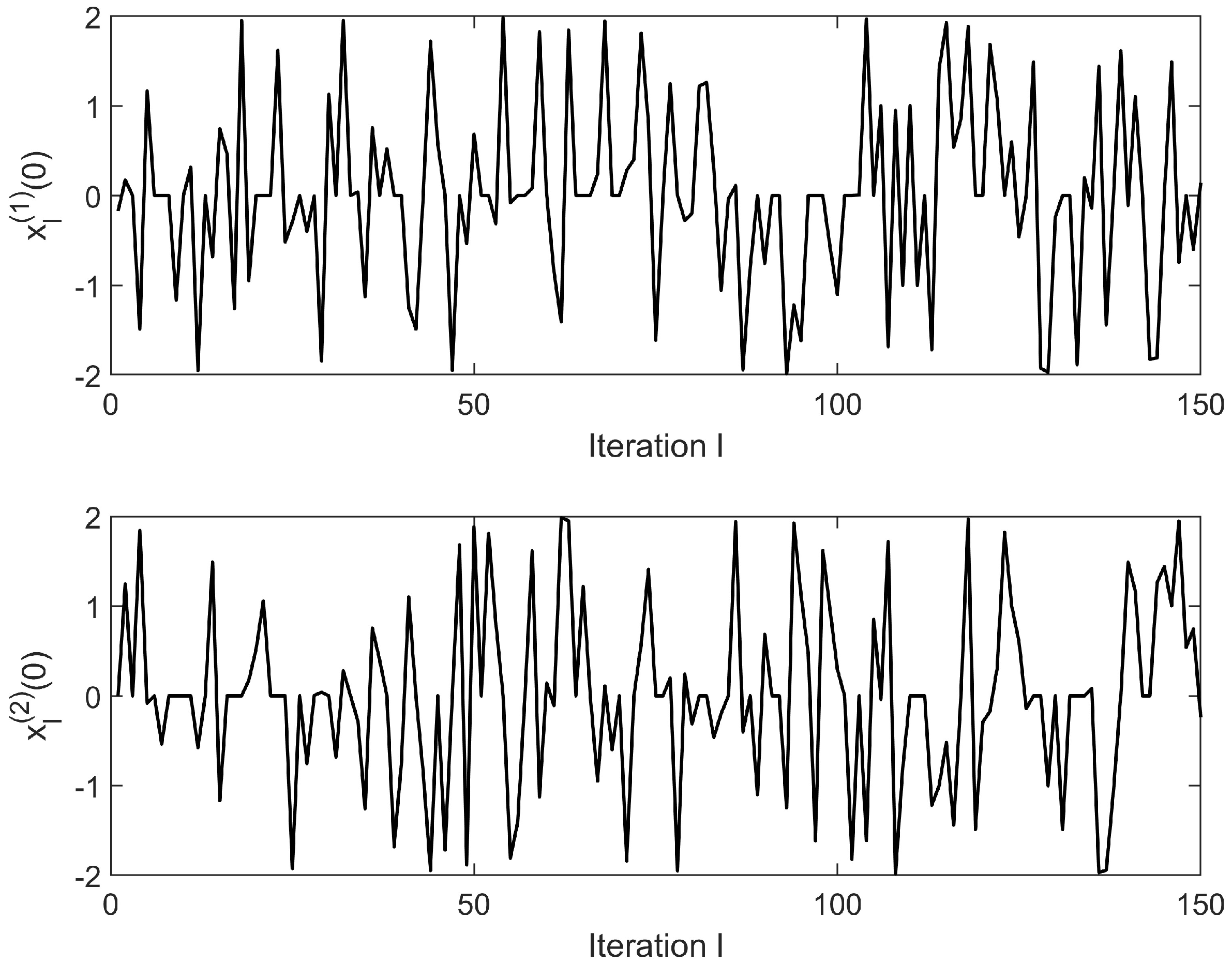
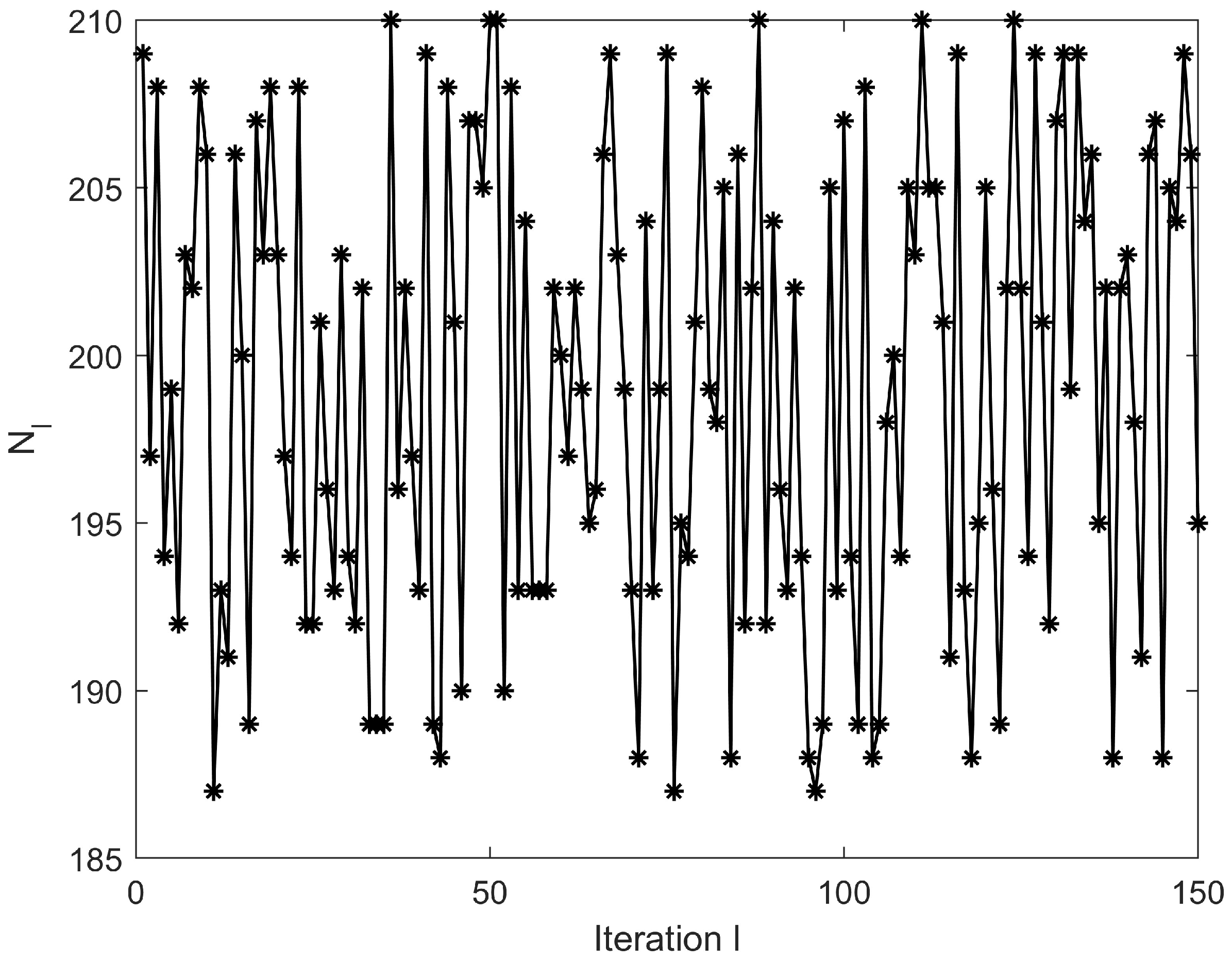
4. Illustrative Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| State of System | |
| Input of System | |
| Output of System | |
| State Transition Matrix | |
| Input Control Matrix | |
| Observation Output Matrix | |
| Target Trajectory | |
| Trail Length at the Iteration | |
| Desired Operation Length | |
| Tracking Error | |
| Feed-forward Control Gain Matrix | |
| Feedback Control Gain Matrix |
References
- Duran, O.; Garcia-Tabares, L.; Gonzalez, L.A.; Toral, F.; Arimoto, Y.; Yamada, T.; Yamamoto, A. Conceptual Design of a Conduction-Cooled Superconducting Quadrupole for ILC Main Linac With Large Temperature Margin. IEEE Trans. Appl. Supercond. 2025, 3, 4003605. [Google Scholar] [CrossRef]
- Yang, R.; Gong, Y.; Paszke, W. ILC-Based Tracking Control for Linear Systems With External Disturbances via an SMC Scheme. IEEE Trans. Autom. Sci. Eng. 2025, 22, 9698–9707. [Google Scholar] [CrossRef]
- Gao, K.; Zhou, Y.; Gao, F.; Lu, J. Optimally Selected Cycle-Based ILC for System With Randomly Varying Initial State. IEEE Trans. Autom. Control. 2025, 70, 2714–2721. [Google Scholar] [CrossRef]
- Liu, S.Y.; Meng, D.Y.; Cheng, L.; Chen, M. An Iterative Learning Controller for A Cable-Driven Hand Rehabilitation Robot. In Proceedings of the 43rd Annual Conference of the IEEE-Industrial-Electronics-Society (IECON), Beijing, China, 29 October–1 November 2017; pp. 5701–5706. [Google Scholar]
- He, W.; Meng, T.T.; Huang, D.Q.; Li, X.F. Adaptive Boundary Iterative Learning Control for an Euler-Bernoulli Beam System with Input Constraint. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1539–1549. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Wang, L.; Wang, H.H.; Xue, B. Consensus Control for Heterogeneous Multivehicle Systems: An Iterative Learning Approach. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5356–5368. [Google Scholar] [CrossRef]
- Huang, J.S.; Wang, W.; Su, X.J. Adaptive Iterative Learning Control of Multiple Autonomous Vehicles With a Time-Varying Reference Under Actuator Faults. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5512–5525. [Google Scholar] [CrossRef]
- Hui, Y.; Chi, R.H.; Huang, B.; Hou, Z.S. Extended State Observer-Based Data-Driven Iterative Learning Control for Permanent Magnet Linear Motor With Initial Shifts and Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1881–1891. [Google Scholar] [CrossRef]
- Meng, D.Y.; Zhang, J.Y. Convergence Analysis of Robust Iterative Learning Control Against Nonrepetitive Uncertainties: System Equivalence Transformation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3867–3879. [Google Scholar] [CrossRef]
- Guth, M.; Seel, T.; Raisch, J. Iterative Learning Control with Variable Pass Length Applied to Trajectory Tracking on a Crane with Output Constraints. In Proceedings of the 52nd IEEE Annual Conference on Decision and Control (CDC), Florence, Italy, 10–13 December 2013; pp. 6676–6681. [Google Scholar]
- Yu, Q.X.; Hou, Z.S. Adaptive Fuzzy Iterative Learning Control for High-Speed Trains With Both Randomly Varying Operation Lengths and System Constraints. IEEE Trans. Fuzzy Syst. 2021, 29, 2408–2418. [Google Scholar] [CrossRef]
- Nagy, Z.K. Model based robust control approach for batch crystallization product design. Comput. Chem. Eng. 2009, 33, 1685–1691. [Google Scholar] [CrossRef]
- Butcher, M.; Karimi, A. Linear Parameter-Varying Iterative Learning Control With Application to a Linear Motor System. IEEE-Asme Trans. Mechatron. 2010, 15, 412–420. [Google Scholar] [CrossRef]
- Liu, T.; Gao, F.R. Robust two-dimensional iterative learning control for batch processes with state delay and time-varying uncertainties. Chem. Eng. Sci. 2010, 65, 6134–6144. [Google Scholar] [CrossRef]
- Yu, M.; Chai, S. Iteration-dependent High-order Internal Model based Iterative Learning Control for Discrete-time Nonlinear Systems with Time-iteration-varying Parameter. In Proceedings of the 21st IFAC World Congress on Automatic Control—Meeting Societal Challenges, Berlin, Germany, 11–17 July 2020; pp. 1658–1663. [Google Scholar]
- Wang, L.; Huangfu, Z.W.; Li, R.W.; Wen, X.W.; Sun, Y.; Chen, Y.Y. Iterative learning control with parameter estimation for non-repetitive time-varying systems. J. Frankl. Inst. 2024, 361, 1455–1466. [Google Scholar] [CrossRef]
- He, C.; Li, J.M.; Liu, S.Y.; Wang, J.X. Robust model-based predictive iterative learning control for systems with non-repetitive disturbances. Nonlinear Anal. Hybrid Syst. 2024, 51, 101436. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Jiang, W.; Charalambous, T. Machine learning based iterative learning control for non-repetitive time-varying systems. Int. J. Robust Nonlinear Control 2023, 33, 4098–4411. [Google Scholar] [CrossRef]
- Liu, T.; Hao, S.L.; Wang, Y.Q.; Na, J. Predictive State Observer-Based Set-Point Learning Control for Batch Manufacturing Processes With Delay Response. IEEE Trans. Ind. Electron. 2024, 71, 788–797. [Google Scholar] [CrossRef]
- Fu, W.Y. Frequency-domain-based nonlinear normalized iterative learning control for three-dimensional ball screw drive systems. Isa Trans. 2025, 157, 224–232. [Google Scholar]
- Chai, S.; Yu, M.; Zhao, K. Robust adaptive event-triggered ILC scheme design for discrete-time non-repetitive nonlinear systems. Iet Control. Theory Appl. 2024, 18, 213–228. [Google Scholar] [CrossRef]
- Yu, Y.R.; Li, D.W.; Ma, A.Y.; Gao, F.R. Sliding Mode-Based Two-Dimensional Iterative Learning Control for Systems with Uncertainties and External Disturbances. In Proceedings of the IEEE 18th International Conference on Control and Automation (ICCA), Reykjavik, Iceland, 18–21 June 2024; pp. 641–646. [Google Scholar]
- Zhang, J.Y.; Meng, D.Y. Improving Tracking Accuracy for Repetitive Learning Systems by High-Order Extended State Observers. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10398–10407. [Google Scholar] [CrossRef]
- Wan, K.; Xie, H.; Xu, Q.Y. Robust Iterative Learning Control for 2-D Linear Nonrepetitive Discrete Systems With Iteration-Dependent Trajectory. IEEE Access 2022, 10, 125015–125026. [Google Scholar] [CrossRef]
- Barkhordar-pour, H.; Lim, J.G.; Ben Ayed, A.; Mitran, P.; Boumaiza, S. Linearizability Assessment of a 3.5 GHz 16-Chain Fully Digital MIMO Transmitter Under Wideband Modulated Signals. In Proceedings of the 103rd ARFTG Microwave Measurement Conference (ARFTG) on Advanced Measurement Techniques for Next-G Communication Systems, Washington, DC, USA, 21 June 2024. [Google Scholar]
- Kwon, G.; Liu, Z.; Conti, A.; Park, H.; Win, M.Z. Integrated Localization and Communication for Efficient Millimeter Wave Networks. IEEE J. Sel. Areas Commun. 2023, 41, 3925–3941. [Google Scholar] [CrossRef]
- Zhang, Z.; Zou, Q. Data-driven robust iterative learning control of linear systems. Automatica 2024, 164, 111646. [Google Scholar] [CrossRef]
- Aarnoudse, L.; Oomen, T. Random Learning Leads to Faster Convergence in ‘Model-Free’ ILC: With Application to MIMO Feedforward in Industrial Printing. Int. J. Adapt. Control. Signal Process. 2024. [Google Scholar] [CrossRef]
- Song, E.J.; Baek, S.G.; Oh, D.J.; Beak, J.M.; Koo, J.C. ILC-driven control enhancement for integrated MIMO soft robotic system. Intell. Serv. Robot. 2024, 17, 357–368. [Google Scholar] [CrossRef]
- Wei, Y.S.; Li, X.D. Robust higher-order ILC for non-linear discrete-time systems with varying trail lengths and random initial state shifts. Iet Control Theory Appl. 2017, 11, 2440–2447. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wei, Y.; Ye, Z.; Liu, S.; Chen, H.; Yan, Y.; Chen, J. Robust Closed–Open Loop Iterative Learning Control for MIMO Discrete-Time Linear Systems with Dual-Varying Dynamics and Nonrepetitive Uncertainties. Mathematics 2025, 13, 1675. https://doi.org/10.3390/math13101675
Zhang Y, Wei Y, Ye Z, Liu S, Chen H, Yan Y, Chen J. Robust Closed–Open Loop Iterative Learning Control for MIMO Discrete-Time Linear Systems with Dual-Varying Dynamics and Nonrepetitive Uncertainties. Mathematics. 2025; 13(10):1675. https://doi.org/10.3390/math13101675
Chicago/Turabian StyleZhang, Yawen, Yunshan Wei, Zuxin Ye, Shilin Liu, Hao Chen, Yuangao Yan, and Junhong Chen. 2025. "Robust Closed–Open Loop Iterative Learning Control for MIMO Discrete-Time Linear Systems with Dual-Varying Dynamics and Nonrepetitive Uncertainties" Mathematics 13, no. 10: 1675. https://doi.org/10.3390/math13101675
APA StyleZhang, Y., Wei, Y., Ye, Z., Liu, S., Chen, H., Yan, Y., & Chen, J. (2025). Robust Closed–Open Loop Iterative Learning Control for MIMO Discrete-Time Linear Systems with Dual-Varying Dynamics and Nonrepetitive Uncertainties. Mathematics, 13(10), 1675. https://doi.org/10.3390/math13101675





