1. Introduction
The study of probability distributions continues to be a vibrant area within statistical modeling. Recent years have seen growing interest in developing specialized distributions that effectively model data confined to the interval [0, 1]. These “unit distributions” are particularly valuable for analyzing probabilities, proportions, and percentages—quantities that frequently arise in medical research, actuarial science, and financial analysis. The literature has witnessed a proliferation of novel unit distributions. Notable examples include the unit-inverse Gaussian distribution in [
1], the unit-Gompertz distribution in [
2], the unit log-log distribution in [
3], the unit-Weibull distribution propsed in [
4], the unit Burr-XII distribution offered in [
5], the unit-Chen distribution in [
6], the unit generalized half normal distribution suggested in [
7], the unit-Muth distribution offered in [
8], and the unit Birnbaum–Saunders distribution in [
9]. Ref. [
10] suggests the unit two-parameter Mirra distribution, and Ref. [
11] proposes the unit power BurrX distribution.
Thus, Ref. [
12] introduces the U-LD through a transformation of the classic Lindley distribution. The U-LD has proven to be a powerful statistical tool for analyzing data within the
interval, distinguished by its mathematical properties and practical utility. As a member of the exponential family of distributions, it offers closed-form expressions for its moments, significantly simplifying statistical inference and analysis. The distribution’s theoretical framework has been enriched through various contributions, including the development of complete and incomplete moment expressions in [
13], an exponential variant that provides enhanced modeling flexibility [
14], and applications in reliability theory through stress-strength modeling where
is of interest [
15]. These mathematical properties, combined with successful implementations in fields such as public health research, demonstrate the distribution’s versatility in addressing real-world analytical challenges while maintaining computational tractability. Ref. [
16] advances the field by investigating parameter estimation in unit Lindley mixed effect models, specifically addressing the challenges posed by clustered and longitudinal proportional data. Bayesian inference of the three-component unit Lindley right censored mixture is presented in [
17]. The probability density function (PDF) of the U-LD [
12] is defined by
The cumulative distribution function (CDF) and hazard rate function (HRF) of the U-LD are given, respectively, by
and
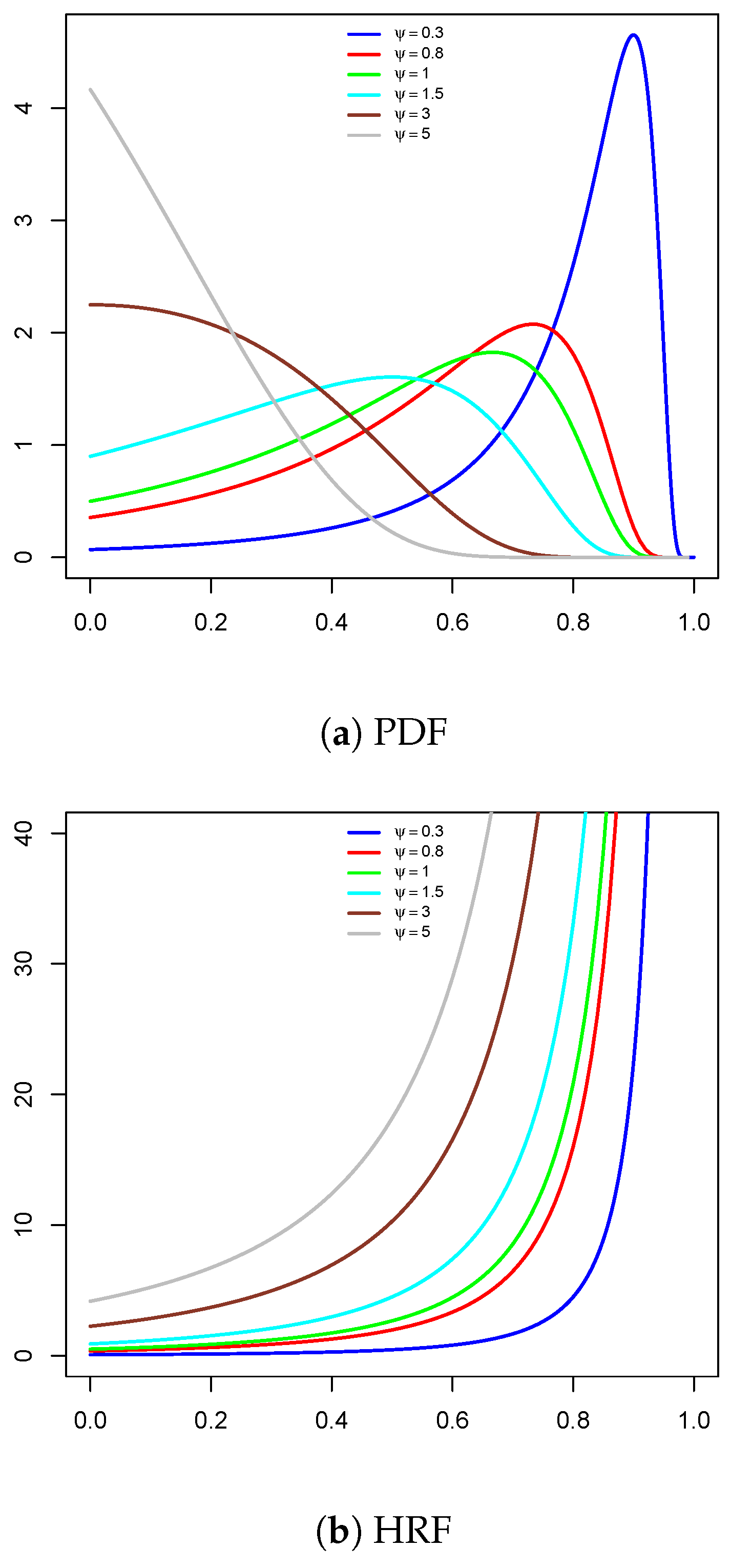
Figure 1 shows both the PDF and HRF for the U-LD distribution. The density function exhibits a unimodal shape, increasing–decreasing, and decreasing. Additionally, the hazard rate function demonstrates a monotonically increasing pattern.
The RSS emerged as an innovative approach to population mean estimation, improving upon traditional SRS methods. First introduced in [
18], RSS shines in its ability to capture more representative samples of target populations, delivering superior accuracy while saving both resources and time. The technique’s theoretical underpinnings were developed later in [
19], where mathematical proof was provided that RSS mean estimators maintain unbiasedness while achieving better precision compared to SRS estimates under perfect ranking conditions. Ref. [
20] further strengthens these findings by showing that RSS maintains its advantages even when ranking procedures are not perfect. The work demonstrates the method’s robustness and practical utility across various real-world scenarios where perfect ranking might not be feasible. Readers may consult references [
21,
22].
Over the past forty years, RSS has attracted considerable interest in statistical research, particularly in parameter estimation for various parametric families. Numerous studies have applied RSS to estimate unknown parameters. For example, Ref. [
23] estimates logistic model parameters using both SRS and RSS, demonstrating the efficiency gains of RSS in parameter estimation.
Ref. [
24] applies RSS to estimate the parameters of the Gumbel distribution, highlighting its advantages over traditional methods. Ref. [
25] investigates the estimation of
for the Weibull distribution using RSS, providing insights into improved estimation accuracy. Ref. [
26] employs both Bayesian and maximum likelihood estimation approaches to determine the parameters of the Kumaraswamy distribution under RSS. Ref. [
27] suggests best linear unbiased and invariant estimation in location-scale families based on double RSS, while Ref. [
28] further explores Bayesian inference for the same distribution. Ref. [
29] proposed generalizes robust-regression-type estimators under different RSS. Ref. [
30] focuses on efficient parameter estimation for the generalized quasi-Lindley distribution under RSS, demonstrating its practical applications. Ref. [
31] examines RSS-based estimation for the two-parameter Birnbaum–Saunders distribution, contributing to the broader literature on RSS efficiency. Additionally, Ref. [
32] provides an efficient stress–strength reliability estimate for the unit Gompertz distribution using RSS. Ref. [
33] considers the problem of estimating the parameter of Farlie–Gumbel–Morgenstern bivariate Bilal distribution by RSS. Ref. [
34] investigates the moving extreme RSS and MiniMax RSS for estimating the distribution function, and Ref. [
35] investigates parameter estimation for the exponential Pareto distribution under ranked and double-ranked set sampling designs, showcasing the effectiveness of these sampling strategies in reliability analysis.
Interested in the widespread applications of the RSS method across various fields, this study focuses on estimating the parameters of the U-LD. To achieve this, we employ several classical estimation approaches based on both RSS and SRS. The estimation techniques considered include maximum likelihood estimation (MLE), ordinary least squares (OLS), weighted least squares (WLS), maximum product of spacings (MPS), minimum spacing absolute distance (MSAD), minimum spacing absolute log-distance (MSALD), minimum spacing square distance (MSSD), minimum spacing square log-distance (MSSLD), linear-exponential (Linex), Anderson–Darling, right-tail AD (RAD), left-tail AD (LAD), left-tail second-order (LTS), Cramér–von Mises (CV), and Kolmogorov–Smirnov (KS).
To the best of our knowledge, this is the first study that considers the parameter estimation of the unit Lindley distribution using RSS. The proposed estimators under RSS are systematically compared with their SRS counterparts through simulation studies that assess their precision based on bias, mean squared error (MSE), and mean absolute relative error. Additionally, a real dataset is analyzed to demonstrate the practical effectiveness of the RSS-based estimators.
The structure of this paper is as follows: The RSS is defined in
Section 2,
Section 3 presents the estimation methods for the U-LD, while
Section 4 conducts a simulation study to evaluate and compare the performance of the proposed estimators.
Section 5 provides an analysis of a real dataset, and finally
Section 6 concludes with key remarks and insights.
2. Description of the RSS Scheme
We assume that the random variable of interest W has a PDF and CDF H(w). To illustrate the RSS procedure, we follow these steps:
Step 1: Select
m SRS each of size
m as
| , | , | ..., | |
| , | , | ..., | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| , | , | ..., | |
Step 2: Rank the unit within each set based on the variable of interest using visual inspection, expert judgment, or any inexpensive ranking method (without actual measurement) as
| , | , | ..., | |
| , | , | ..., | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| , | , | ..., | |
Step 3: Choose the
sth ranked unit from the
sth set as
| , | , | ..., | |
| , | , | ..., | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| , | , | ..., | |
Hence, the RSS units are , ,..., . Note that we identify units but only measure m of them. To increase the sample size, we extend Steps (1) through (3) to multiple cycles to construct a RSS sample of size . In this case, the RSS sample observations are denoted as The process of designing a RSS scheme involves selecting an optimal set size, typically limited to a maximum of five to reduce ranking errors.
For a fixed
u, the elements
are independent and follow the same distribution as the
sth order statistic from a sample of size
m. The PDF of
, assuming perfect ranking as described by Arnold et al. [
36], is given by
where
and
denote the PDF and CDF of
W, respectively.
4. Numerical Simulation
This section explores various estimation techniques for the U-LD parameter through simulation studies based on the RSS and SRS using set sizes of
with cycles
. For each combination of combination of
m and
r, we keep the sample sizes equivalent to
ensuring comparability between methods. For each generated sample, the parameter estimator
is computed based on the methods outlined in
Section 2. To assess estimation accuracy for each method and sampling design, four statistical metrics are computed, including the Average Estimator (AE), Absolute Bias (bias), Mean Squared Error (MSE), and Mean Absolute Relative Error (MRE) which assesses estimation accuracy relative to the true parameter value. These measures are given by, respectively,
and
Here,
N represents the number of simulations, and two values of parameter
are considered:
and
. For
, the results for SRS and RSS are presented in
Table 1 and
Table 2, respectively. For
, the results for SRS and RSS are presented in
Table 3 and
Table 4, respectively.
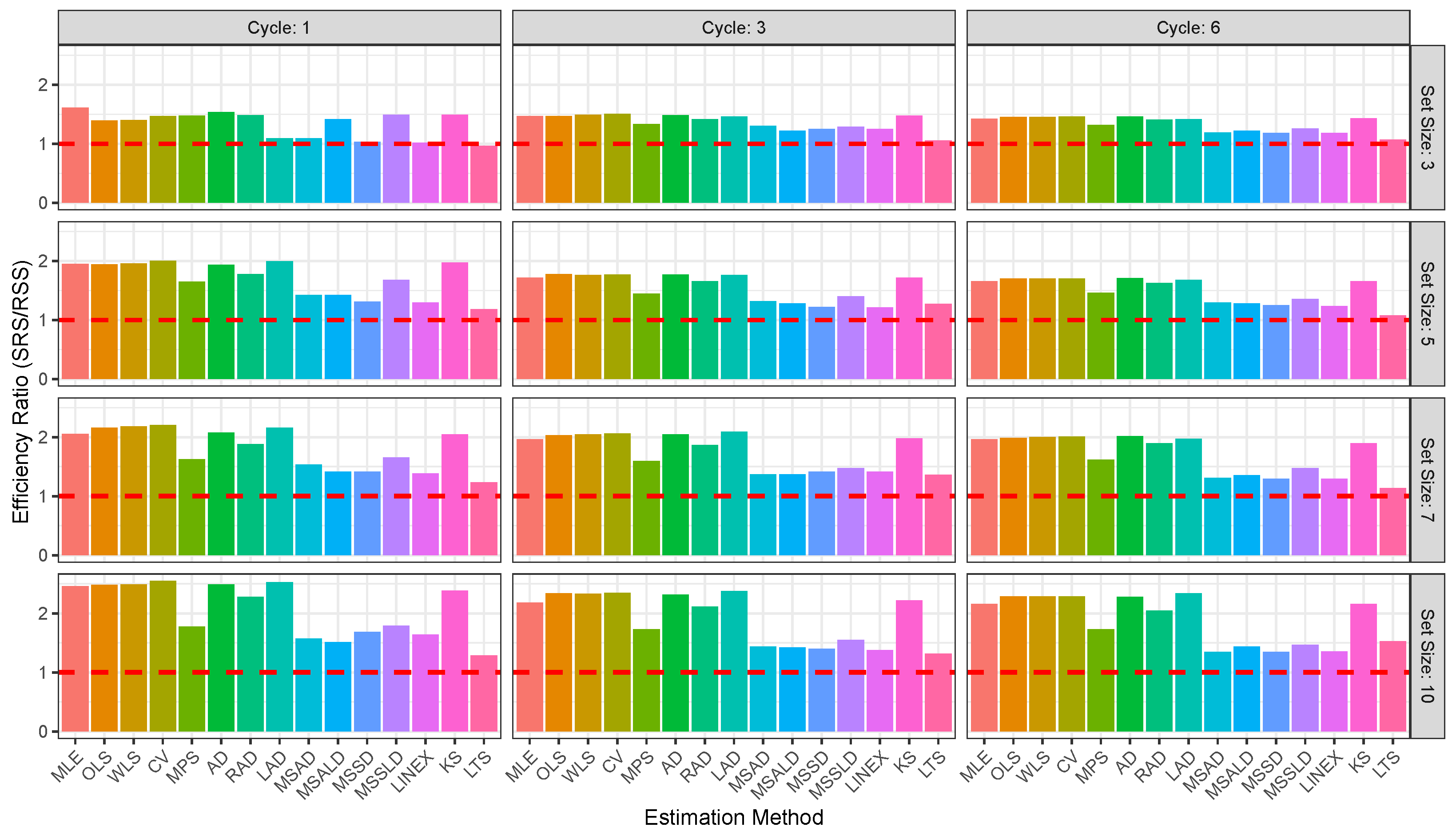
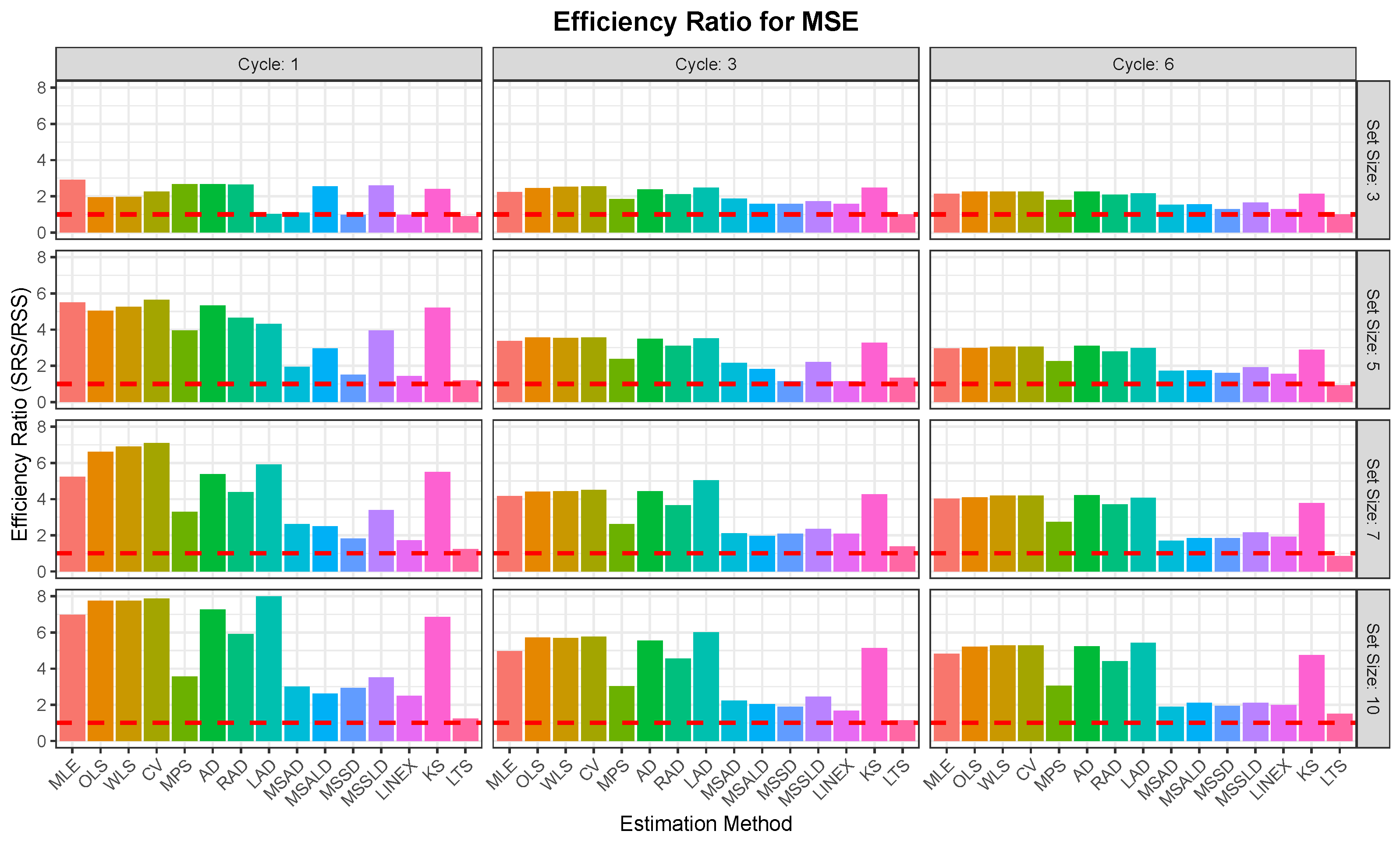
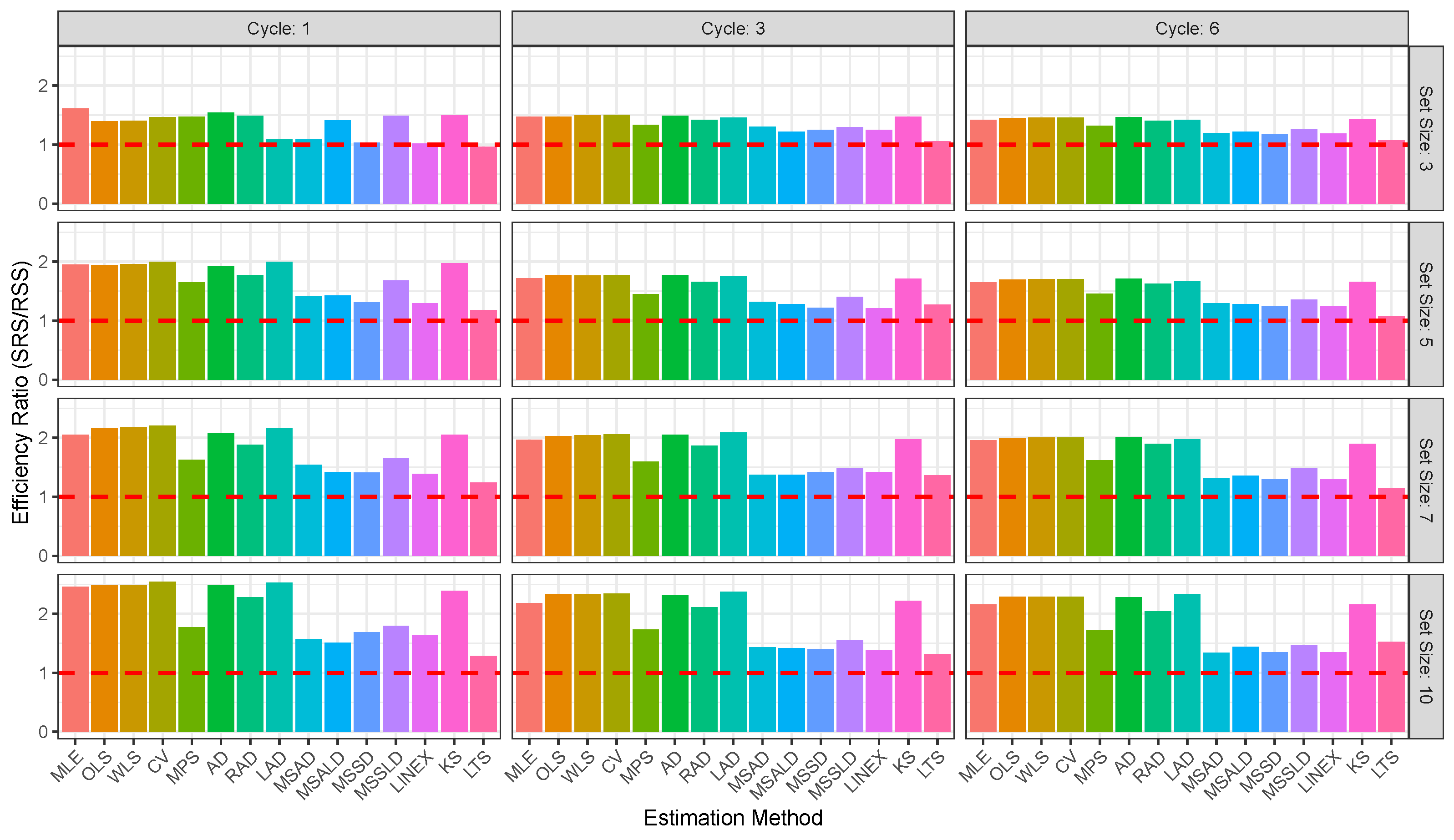
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7 enable direct comparison of estimation efficiency between SRS and RSS approaches. They display the efficiency ratios (ERs) between SRS and RSS which are calculated for the bias, MSE, and MRE as
For illustration of the reults given in
Table 1,
Table 2,
Table 3 and
Table 4, we consider three cases, namely the SRS with RSS, the parameter values based on SRS, and finally the effect of parameter values using RSS.
Table 1 and
Table 2 aim to compare the RSS and SRS based on a simulation study for
. The following observations can be concluded:
The RSS consistently outperforms SRS across the 15 estimation methods, MLE, OLS, WLS, CV, MPS, AD, RAD, LAD, MSAD, MSALD, MSSD, MSSLD, LINEX, KS, LTS, and various sample sizes, delivering mean estimates closer to the true value of , with lower bias, MSE, and MRE. For illustration:
- ⇒
The RSS produces estimators closest to parameter than SRS; for example, at , vs. , and at , vs. .
- ⇒
Also, RSS exhibits lower bias across all methods and sizes; e.g., at , vs. , and at , vs. .
- ⇒
Additionally, RSS achieves lower MSE, indicating better precision; e.g., at , vs. , and at , .
- ⇒
The RSS shows smaller relative errors; e.g., at , vs. , and at , vs. .
Based on different estimation methods:
- ⇒
MLE: RSS excels, e.g., , with MSE of 0.9807 vs. , with MSE value 2.8469; and for , vs. , with respective MSE values 0.0093 and 0.0450.
- ⇒
OLS: RSS outperforms, e.g., , with MSE of 0.0794 vs. , with MSE value 0.2823.
- ⇒
MPS: RSS shines, often closest to 2, e.g., , with MSE of 0.0827 vs. , with MSE value 0.1495.
- ⇒
LAD: RSS reduces larger errors, e.g., , with MSE of 0.0526 vs. , with MSE value 0.2650.
- ⇒
LTS: RSS mitigates poor performance, e.g., , MSE = 4.3108 vs. with MSE = 5.3731.
Based on the sample size impact, the RSS’s advantage is most notable in smaller samples. For example:
- ⇒
When , the MSE of the MLE is 0.9807 vs. SRS 2.8469, which narrows slightly in moderate sizes.
- ⇒
For , MSE of the MLE = 0.0353 vs. that based on the SRS 0.1468,
- ⇒
and it persists in larger sizes; for the MLE has MSE = 0.0093 vs. the 0.0450 MSE of SRS.
Based on
Table 1 and
Table 3 regarding parameter values,
(
Table 1) and
(
Table 3) under SRS design, one can see, in summary, that the results for
generally exhibit lower absolute bias and MSE, making them better in terms of raw accuracy and precision. However, we have the following specific comments:
The estimates in both tables tend to overestimate the true , with values consistently above 2 and 5, respectively. This overestimation is more pronounced in absolute terms for due to the larger true value.
Absolute bias is higher for than for across all methods and sample sizes. This is expected, as the same estimation error results in a larger deviation when the true value is 5 compared to 2. For instance, MPS has a bias of 0.8790 for vs. 1.9816 for at .
MSE is consistently higher for than for , reflecting the larger scale of errors when estimating a true value of 5. For example, MPS has an MSE of 1.8264 for vs. 5.9552 for at , and 0.0427 vs. 0.3321 at .
MRE provides a normalized measure of error and shows mixed results. For small sample sizes (e.g., ), MRE is lower for (e.g., 0.3963 vs. 0.4395 for MPS), indicating better relative accuracy. For larger sample sizes (e.g., ), MRE is slightly lower for (e.g., 0.0824 vs. 0.0926 for MPS), suggesting a slight advantage in relative terms as sample size increases.
As sample size n increases from to , both bias and MSE decrease significantly for and , indicating improved accuracy and precision with larger samples.
Utilizing the RSS method when
in
Table 1 and
in
Table 4, smaller
values lead to more stable and accurate estimation, and it is noted the following general trends:
As increases from 2 to 5, both bias and MSE increase for most estimators. This suggests that larger values of introduce more variability in estimation, making the estimation problem more challenging.
Increasing the sample size helps reduce the impact of larger , leading to lower bias and MSE. However, for , larger sample sizes are even more crucial to maintain estimation accuracy.
5. Real Data Analysis
To evaluate the effectiveness of the proposed estimation strategies, we chose two real-world datasets and performed a detailed analysis in this section. Our goal was to highlight potential applications and situations where these techniques can be successfully implemented. By carefully analyzing real-world data, this study highlights the practical significance of these estimation methods, demonstrating their relevance for applied research and data-driven decision-making. To compare the estimators, and to verify that our U-LD model provides a good fit for the dataset under study, we conduct a Kolmogorov–Smirnov (KSt) test, Anderson–Darling (ADt) test, and a Cramér–von Mises (CVt) test based on both SRS and RSS for all estimation methods considered in this study.
First Dataset: The first dataset under consideration consists of 20 items tested simultaneously, with their ordered failure times previously reported in [
44]. The observed ordered data are as follows (
Table 5).
A descriptive statistics to the data is given in
Table 6, which shows that the skewness of the dataset is approximately 1.44, indicating that the distribution is positively skewed. Since the median is 0.1328, it means that
of the data points fall below this value, and a standard deviation of 0.1573 suggests that most of the data points are fairly spread out from the mean, with a decent level of variability.
Also,
Figure 8 presents graphical representations of the dataset, including the total time on test (TTT) plot, box plot, and violin plot. The estimated PDF, CDF, and probability–probability (PP) plots for failure times data are presented in
Figure 9. These visualizations offer valuable insights into the dataset’s characteristics, facilitating a deeper understanding of its structure and trends.
Based on these data, we select a small RSS of size 4 while using the same sample size for the SRS. It is important to note that the SRS and RSS methods are compared using the same number of measured units. Using these methods, we estimate
for each design, assuming perfect ranking. The results are summarized in
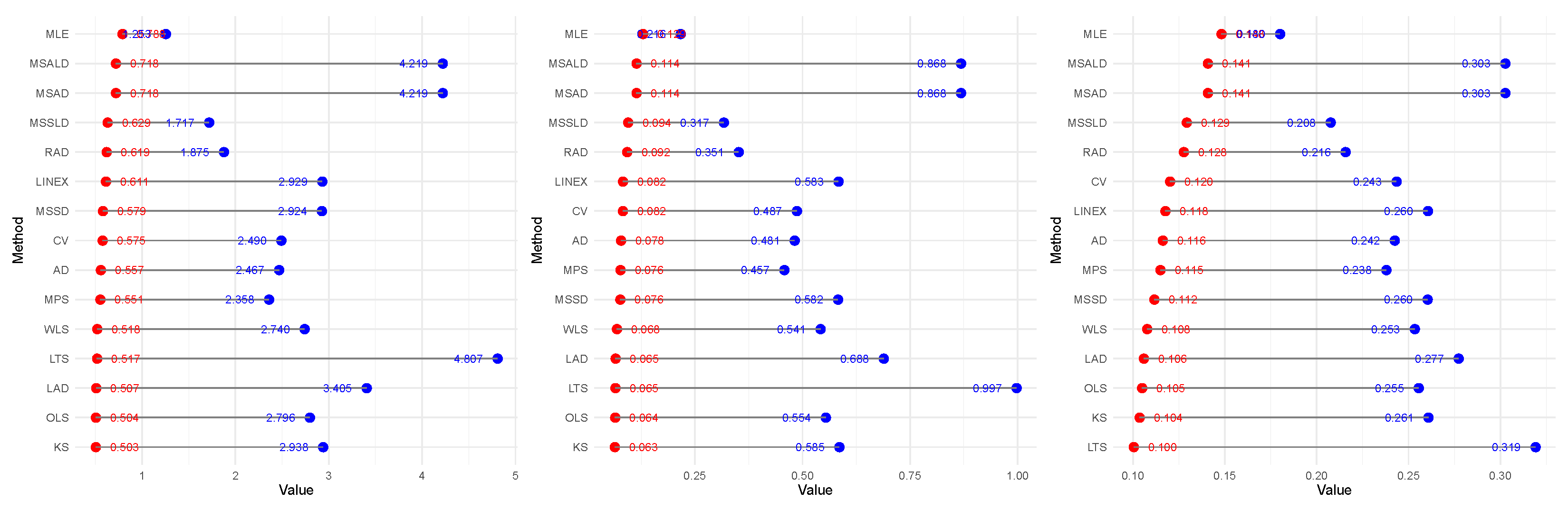
Table 7, indicating that the U-LD model fits the data well, as supported by various plots. For instance, for the OLS method based on RSS, the KS
t value is 0.1812 with a
p-value of 0.3756. The Anderson–Darling test yields a value of 2.2621 using SRS, while the Cramér–von Mises test result is 0.2151 in RSS. These findings collectively support the adequacy of our model in fitting the dataset.
Figure 10 further reinforces this conclusion, where blue dots represent SRS values, red dots red dots represent RSS values.
Table 7 highlights the superiority of RSS over SRS in estimating the distribution parameter. For illustration, based on the MSALD, the AD
t values are 4.2025 and 2.2891 using SRS and RSS, respectively.
Second Dataset: The second dataset pertains to Turkey, which documented its first COVID-19 patient recovery on 26 March 2020 according to the World Health Organization (WHO). This dataset contains 25 observations of g collected from 27 March through 20 April. It was subsequently analyzed in study [
45]. The chronologically ordered observations are as follows (
Table 8).
Descriptive statistics of the COVID-19 data are presented in
Table 9, revealing that the data are right-skewed with a skewness value of 0.91213. The COVID-19 data are illustrated using the TTT plot, box plot, and violin plot as shown in
Figure 11, and the estimated PDF, CDF, and PP plots are offered in
Figure 12.
Again, based on COVID-19 data, the estimators considered are compared and the U-LD model is fitted using the Kolmogorov–Smirnov test, the Anderson–Darling test, and the Cramér–von Mises test for both RSS and SRS across all estimation methods in this study. The results are summarized in
Table 10, while
Figure 13 presents the values of the AD
t, CV
t, and KS
t measures, where blue dots represent SRS and red dots represent RSS. The findings indicate that the U-LD model fits the data accurately, as supported by various plots. For clarification, in the LTS method based on RSS, the KS
t value is 0.1004 with a
p-value of 0.9410. The Anderson–Darling test value is 0.5166, while the Cramér–von Mises test result is 0.0648. Regarding the comparison between SRS and RSS,
Table 10 highlights the superiority of RSS over SRS in estimating the distribution parameter across all cases. For instance, based on the MSSD method, the KS values are 0.2603 and 0.1115, with corresponding
p-values of 0.0555 and 0.8812 for SRS and RSS, respectively.
However, in general, it is important to emphasize that the RSS design exhibits superior efficiency compared to the SRS design, as evidenced by its smaller goodness-of-fit values. This consistent advantage of RSS over SRS is observed across all estimates. These findings highlight the benefits of using the RSS approach over SRS for fitting the dataset to the model and obtaining more efficient estimates.
6. Conclusions
This paper thoroughly investigates various estimation methods for the parameter of the U-LD under both RSS and SRS designs. A wide range of estimation techniques is explored, including maximum likelihood estimation, ordinary least squares, weighted least squares, maximum product of spacings, minimum spacing absolute distance, minimum spacing absolute log-distance, minimum spacing square distance, minimum spacing square log-distance, linear-exponential, Anderson–Darling (AD), right-tail AD, left-tail AD, left-tail second order, Cramér–von Mises, and Kolmogorov–Smirnov. The simulation study performed as part of this research shows that the estimators derived from RSS consistently outperform those derived from SRS across all the criteria considered: mean squared error, bias, and efficiency. This suggests that RSS provides more reliable and efficient parameter estimates when applied to the U-LD distribution. Additionally, the analysis of two real-world datasets, failure times of items, and COVID-19 data demonstrates the practical applicability of the proposed estimation methods. The findings clearly highlight the advantages of using RSS over SRS for statistical inference, particularly in the context of U-LD parameter estimation. In conclusion, this study underscores the superiority of RSS-based estimators in parameter estimation for the U-LD distribution. The results emphasize the importance of considering the sampling design when choosing appropriate estimation methods and recommend RSS as a preferable choice for enhanced statistical inference in various practical applications. Further research could explore the robustness of these findings under different sampling schemes and distributional assumptions.