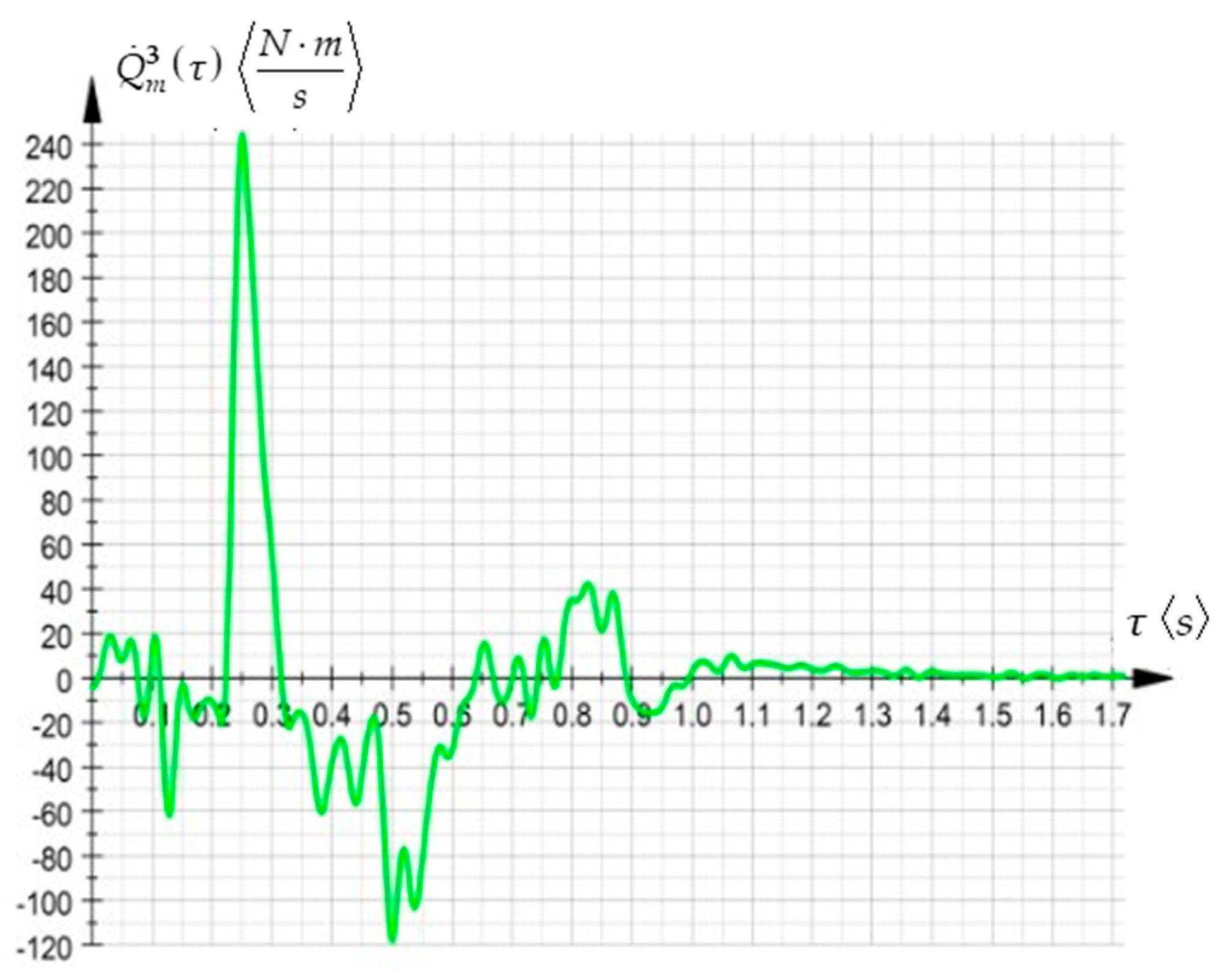
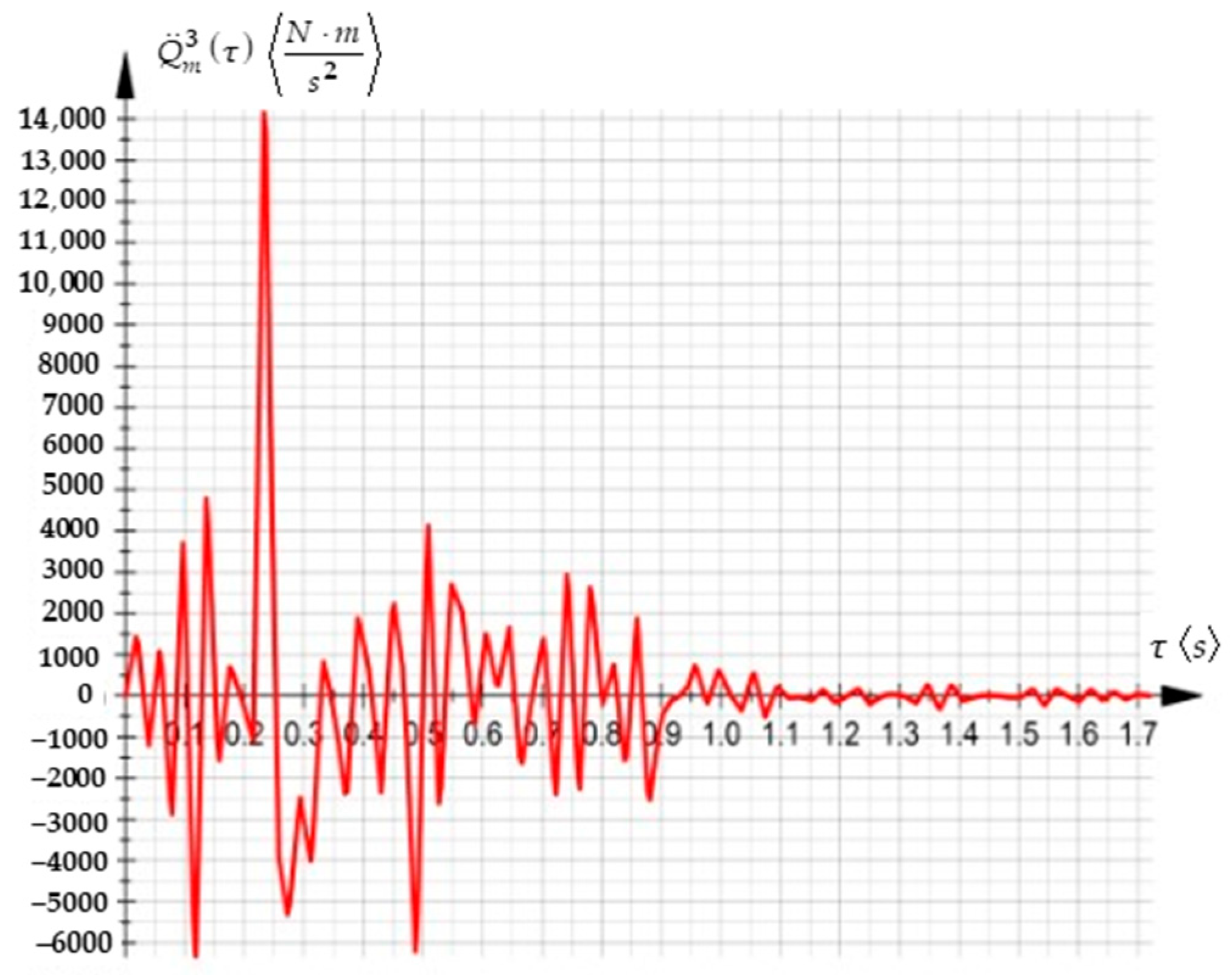
This theoretical study focuses on the advanced development of kinematic and dynamic principles in analytical mechanics, specifically concerning higher-order acceleration energies and their applications in complex mechanical systems.
2.1. Position and Orientation Parameters of Solid Body
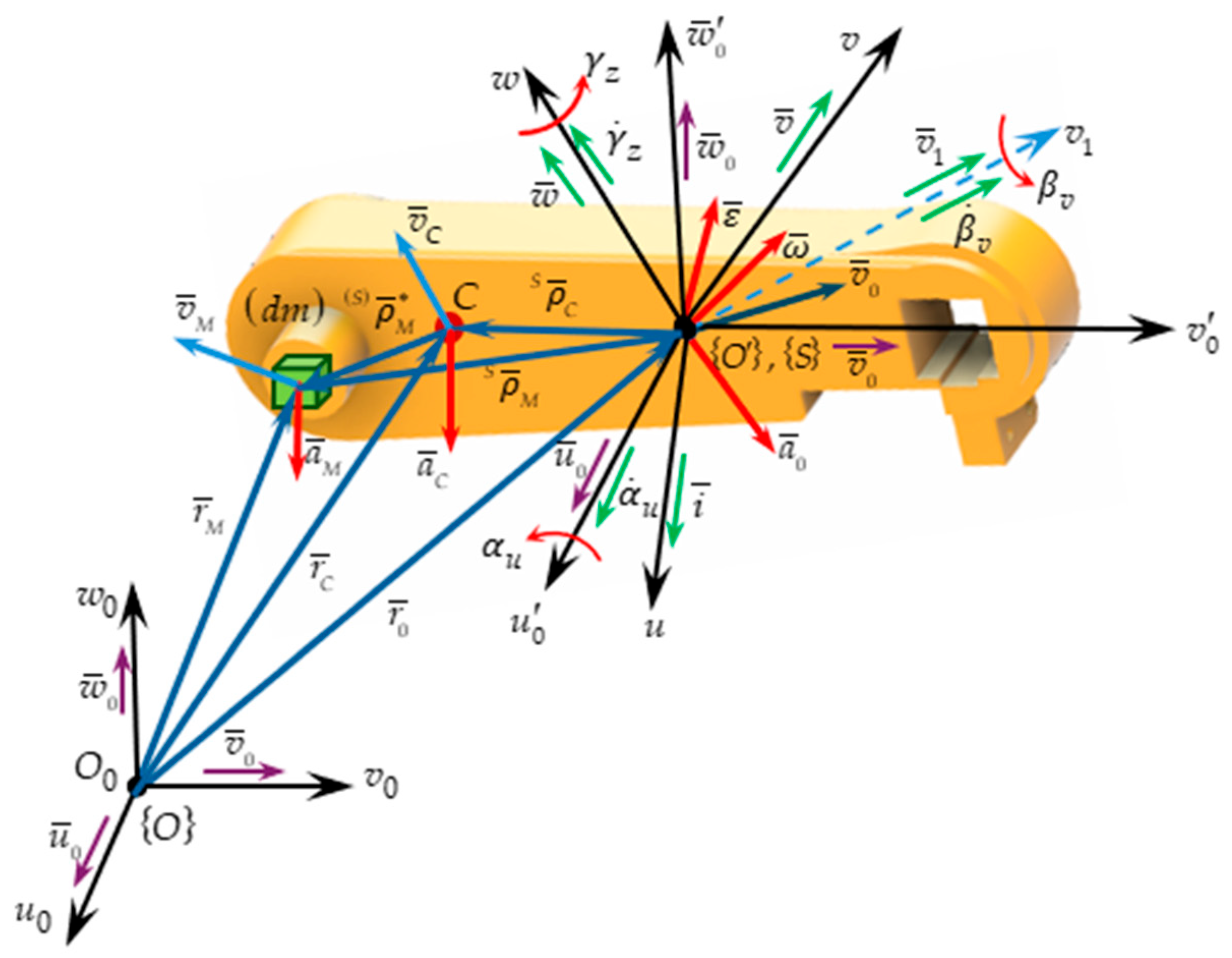
The solid body is a physical form of matter’s existence in the material universe. Consequently, the solid body is considered a material continuum. Based on this property to achieve an exact geometric solution, the solid body is decomposed into an infinite number of elementary particles, each with an infinitesimal mass and a continuous distribution throughout its geometric form. If the distances between the elementary particles are kept constant, the solid body will be characterized as a rigid solid (S). When density is consistently supported within the rigid structure, a homogeneous rigid solid is obtained. If the integration limits around the entire geometric contour are well defined, the homogeneous body will have a simple or regular geometric shape. In this case, geometric and mass integrals are applied. Before conducting the mechanical study (static, kinematic, and dynamic modeling), it is essential to show the geometric state of the rigid body at each moment of its movement in Cartesian space. To this end, the geometric state of the simplest mechanical model, the material point, is studied first (
Figure 1). Based on research from [
4,
5,
6], the following notations are introduced:
In Equation (1), the coordinates and axes of the Cartesian reference system are defined; in Equation (2), the unit vectors (versors) of the reference system axes are specified; and in Equation (3), the angles and direction cosines are defined.
Following
Figure 1, the rigid body is subject to geometric study. For this purpose, two reference systems are considered: the first system, denoted as
, is a fixed-reference system, and the second system,
, is a moving-reference system, permanently attached to the body, with its origin at point
, an arbitrary point on the rigid body. The reference system
, also represented in
Figure 1, is a system with its origin at point
, whose orientation remains constant throughout the motion and is identical to that of the fixed-reference system,
, meaning
. The geometric state of any point belonging to the rigid body (for example, an arbitrary point
) represents its
position, defined, according to
Figure 1, by the following position vector:
For a free material point, the three linear coordinates defined in Equation (5) are independent and represent the degrees of freedom (d.o.f.). The study then extends to a vector or an axis belonging to the Cartesian reference system (
Figure 1).
This geometric state is referred to as orientation (angular state). Orientation (angular state) is defined by using unit vectors. For any unit vector
, assumed to be known in relation to one of the reference systems
or
, the orientation will be defined by means of the direction cosines.
In accordance with linear algebra, the symbol
in Equation (6) defines the transpose of the matrix. Considering the second expression in Equation (6), it can be observed that the orientation of any vector or axis is defined by two independent angles. The geometric aspects presented earlier are examined in the context of an orthogonal, right-handed reference system (see
Figure 1,
) relative to the fixed-reference system
. In this case, the geometric state is represented by position and orientation. Position is defined by Equation (5) while orientation is defined by the rotation matrix [
4,
10,
11,
12,
13,
14]:
The resulting rotation matrix defined by Equation (7) contains the unit vectors of the reference system
relative to the fixed-reference system
. The rotation matrix, or direction cosine matrix, describes the orientation of each axis of the moving-reference system attached to the rigid body in relation to a fixed-reference system. Among the nine direction cosines in the rotation matrix, six mathematical relationships can be proved. Therefore, the orientation of a moving-reference system relative to a fixed-reference system can be defined by a maximum of three independent parameters, represented by the orientation angles. Consequently, the resulting orientation of a reference system
relative to another reference system,
or
, can be defined by three independent orientation angles (degrees of freedom), according to [
4,
6]:
The angles included in Equation (8) are components of the orientation column matrix
, which geometrically describe dihedral angles between two geometric planes:
Physically, the three angles defined by Equation (9) represent a simple rotation around one of the three axes of the Cartesian reference system: .
Based on the research in [
4,
6,
15], combining these three simple rotations results in twelve sets of orientation angles (8). Considering
, the expressions for the three simple rotation matrices are further developed as follows:
The following mathematical representation of the generalized rotation matrix is proposed:
Here,
and
By substituting Equations (13) and (14) into the generalized Equation (12), the simple rotation matrices defined in Equation (11) are obtained. The generalized matrix can thus be written as follows:
In Equation (15), the symbol
defines the antisymmetric matrix associated with vector (17) while
represents the diagonal matrix, determined as
The matrix (15) can also be defined by means of the following classical formulation:
According to the research [
4,
5], the three simple rotations defined by Equation (8) can be performed either around the fixed axes or the moving axes, belonging to the
and
/
reference systems. The resulting rotation matrix, denoted as
, which expresses the orientation of the
reference system relative to
fixed-reference system, is defined by expressions that also include matrix exponentials as follows:
Using the author’s research on matrix exponentials [
16], the resulting rotation matrix can be expressed in a new form as follows:
Equations (5) and (8), presented above, define the position and orientation of a right-handed reference system. These mathematical expressions will be generalized for the case of a rigid body. According to [
5,
11,
17], a rigid body is composed of an infinite number of material particles and an infinite number of geometric axes, parallel and perpendicular to each other, characterized by a continuous distribution throughout the entire volume of the rigid body. The rigid body also includes an infinite number of sets consisting of three orthogonal geometric planes, continuously distributed throughout its volume. Geometrically, to define a right-handed reference system with its origin at an arbitrary point
belonging to the rigid body, it is sufficient to select a single set composed of three orthogonal planes. According to Equation (4) and
Figure 2, this reference system is denoted as
. The reference system
is attached to the rigid body. Equations (5) and (8) define the position and orientation of this system.
Since the purpose of this paper is to study advanced dynamics, two material points belonging to the rigid body are considered, satisfying the conditions
and
. The expressions defining the absolute position become time-dependent vector functions [
4,
5] as follows:
Considering Equations (23) and (25), the absolute position equation can be written using matrix exponentials [
16] as follows:
The absolute position equation for any material point belonging to the rigid body can be determined when the position
and the orientation
of the moving system
are known. Analyzing Equations (23) and (24) reveals that the orientation is invariant for all points of the rigid body. Based on these geometric considerations, the body is represented by the reference system
. This system is geometrically defined by six independent parameters or degrees of freedom, included in the following symbol:
Here,
and
is the generalized coordinate;
is an operator that highlights the type of degrees of freedom:
The symbols presented in Equation (28) define higher-order generalized variables in the case of rapid motions, where is the order of the time derivative.
In advanced mechanics, instead of Equation (8), the following definition is used for the angular orientation vector:
Here,
is the angular transfer matrix, which is a
matrix defined as a function of the orientation angles, and specified according to the expression below:
The position and orientation of the
moving-reference system, relative to any other system, such as the
fixed-reference system, can be represented in matrix form using transformations based on matrix exponentials:
Equation (32) defines the position vector of the moving system relative to the fixed system while Equation (34) represents a vector defined as a function of screw parameters (homogeneous coordinates).
Matrix formulation is widely used in multibody system’s kinematics and dynamics. The application of matrix exponentials in kinematic and dynamic modeling of complex systems offers advantages over classical transformations, including a compact representation of components and the ability to use computer calculus. Also, in the matrix exponential calculus, reference frames are avoided; these, in robot structures, are typically assigned based on specific geometric constraints (which may introduce geometric errors). This property of matrix exponentials is due to the presence of screw parameters in the exponential functions. The conclusion and defining expressions presented in this introductory section will be applied further in the study of advanced kinematics and dynamics of mechanical systems.
2.2. Significance of Higher-Order Derivatives in Analytical Dynamics
In analytical mechanics, higher-order derivatives are essential for accurately describing and predicting the motion of complex mechanical systems. While velocity and acceleration (first- and second-order derivatives) are often sufficient for basic applications, more advanced systems require additional motion analysis. Higher-order derivatives allow for a more precise understanding of motion, especially in systems that involve rapid changes, complex interactions, and precise control requirements.
One important reason for using higher-order derivatives is to improve motion accuracy. In fields such as robotics, aerospace engineering, and biomechanics, acceleration alone is not always enough to describe how a system moves. Additional derivatives, such as jerk (third order) and snap (fourth order), help create smoother and more controlled motion paths. This is particularly useful in systems where sudden changes in speed or direction must be carefully managed to avoid mechanical stress or instability.
Higher-order derivatives also play a key role in modeling transient motion situations, where acceleration changes abruptly. Many mechanical systems, such as robotic arms, vehicles during sudden breaking, or flexible structures under load, experience these rapid transitions. Standard acceleration-based models often fail to capture these changes correctly, leading to inaccurate simulations or inefficient control. By including higher-order terms, models can better represent real-world movement and improve the design of mechanical systems. Another major advantage of higher-order derivatives is their application in vibration control and shock absorption. In areas such as structural mechanics and material science, engineers use these derivatives to design systems that reduce excessive vibrations and improve stability.
This is especially important in precision manufacturing, vehicle suspension design, and energy-efficient mechanical systems, where smooth transitions between different motion states help optimize performance and durability. Despite these benefits, using higher-order derivatives comes with challenges. One of the biggest difficulties is the increased complexity of calculations.
While these derivatives improve model accuracy, they also require more advanced numerical methods, which can make computations more expensive and time-consuming.
Higher-order derivatives are a valuable tool in analytical mechanics. They help improve motion accuracy, enhance control, and provide a better understanding of complex movements. While they introduce computational and measurement challenges, their advantages outweigh these limitations, making them an important part of modern engineering and mechanical system design.
2.3. The Parameters of Advanced Mechanics
Based on the authors’ research, this section will present a series of new formulations about advanced kinematic concepts. A rigid body (S) represented in
Figure 2 and undergoing general motion is considered. By applying the first-order absolute derivative to the parametric motion equations, we obtain the following:
According to [
12,
13,
14,
15,
16,
17], the antisymmetric matrix associated to angular vector is
Finally, expressions for linear velocities and accelerations are obtained in the form
The absolute position equation, expressed in terms of matrix exponential results, is
In advanced kinematics and dynamics, the higher-order derivatives applied to position vectors and rotation matrices are expressed as follows:
where
The defining expressions for angular velocities and accelerations can be proved based on matrix exponentials as follows:
Although the use of matrix exponentials may appear complex, it offers advantages, including the elimination of reference systems, which can impose certain restrictions.
This is evident in the previously presented equations by
, showing that the unit vectors correspond to the initial state of the reference system
. The position of the center of mass is found relative to the reference system
as
The position of the mass center relative to
reference system, at first in classical form and then in an exponential form, is presented:
If first- and second-order derivatives with respect to time are applied to Equation (44), the linear velocity and acceleration of the center of mass are ultimately obtained:
The absolute linear accelerations of higher orders, with respect to mass center, are as follows:
In dynamic modeling, the following expression is applied:
Using the author’s research [
18] on time functions for position and orientation, the following differential properties have been developed in the study of advanced kinematics and dynamics of the rigid body, according to the following expressions:
Based on Equations (52)–(54), the expressions for a rigid body are obtained:
Here,
.
Expressions (55) and (57) refer to the higher-order linear velocities and accelerations corresponding to the center of mass.
The other expressions, (56) and (58), define the higher-order angular velocities and accelerations specific to the rigid body in general motion.
The above expressions are also extended to multibody systems.
In case of rapid movements, higher-order operational and generalized accelerations develop within the mechanical structure (for example serial robot structures). Based on the research from [
18,
19], the following expressions are found:
Here,
represents the order of differentiation with respect to time, the symbol
is the column matrix of higher-order operational accelerations, and
is the column matrix of higher-order generalized accelerations, defined according to the following:
Based on the mathematical models presented in [
5], the Jacobian matrix can be found using matrix exponentials. Analyzing all input parameters in advanced kinematics reveals that they are functions of the generalized variables Equations (59) and (60) and their time derivatives.
Thus, following [
18], these can be developed using polynomial interpolation functions. It is important to mention that in the kinematic and dynamic study of robotic structures, the application of higher-order polynomial functions is recommended as their reunion defines the so-called motion trajectories.
Depending on the working process in which the structures are implemented and the imposed constraints, these polynomial functions become motion functions, known for each degree of freedom of the analyzed structure.
This paper proposes the following higher-order polynomial functions:
On each trajectory segment
, the number of unknowns is
, and the meaning of the terms contained in (61) is as follows
Determining the unknowns in Equation (63) requires, in accordance with [
8,
9,
10,
11,
12,
13,
14,
15,
16,
17], the application of geometric and kinematic constraints:
The results of the polynomial interpolation functions Equation (61) will be substituted into the expressions defining the concepts of advanced kinematics and dynamics. Expressions for input data and higher-order parameters are essential in defining the concepts of advanced dynamics. In this work, these are represented by kinetic energy and higher-order acceleration energies. These concepts will be integrated into dynamic equations characterizing the rapid motions of bodies.
The aspects presented above provide essential advantages in the inverse dynamic study of robots. The drawback of these functions lies in their mathematical nature as approximative functions, requiring many trajectory intervals to achieve an approximate solution. For standard motions (without the occurrence of higher-order accelerations), these polynomial functions transform into cubic spline polynomial functions.