Analytic Investigation of a Generalized Variable-Coefficient KdV Equation with External-Force Term
Abstract
1. Introduction
- When , and , Equation (1) becomeswhich describes radially ingoing acoustic waves in cylindrical plasma, interfacial waves in two-layer liquids, or Alfvén waves in non-interacting plasma. Its Lax pair, infinite conservation laws, and various exact solutions were obtained in [17].
- When and , Equation (1) is simplified toThis equation describes phenomena such as ISWs in the ocean, pressure pulses in fluid-filled tubes of special value in arterial dynamics, trapped quasi-one-dimensional Bose–Einstein condensates, and ion-acoustic solitary waves in plasmas. Its Lax pair, auto-Bäcklund transformation, nonlinear superposition formula, and an infinite number of conservation laws have been investigated in [18].
- In considering an artery as a prestressed, tapered, thin-walled, long, and circularly conical elastic tube, and blood as an incompressible inviscid fluid, the propagation of weakly nonlinear waves in such a fluid-filled elastic tube follows the following equation [19]:where coefficients and depend on the material of the tube and the initial deformation. When and , Equation (4) is a special case of Equation (1).
2. Painlevé Integrability
3. AKNS System and Soliton-like Solutions
3.1. Lax Pair
3.2. Riccati Form and Auto-Bäcklund Transformation
3.3. Nonlinear Superposition Formula
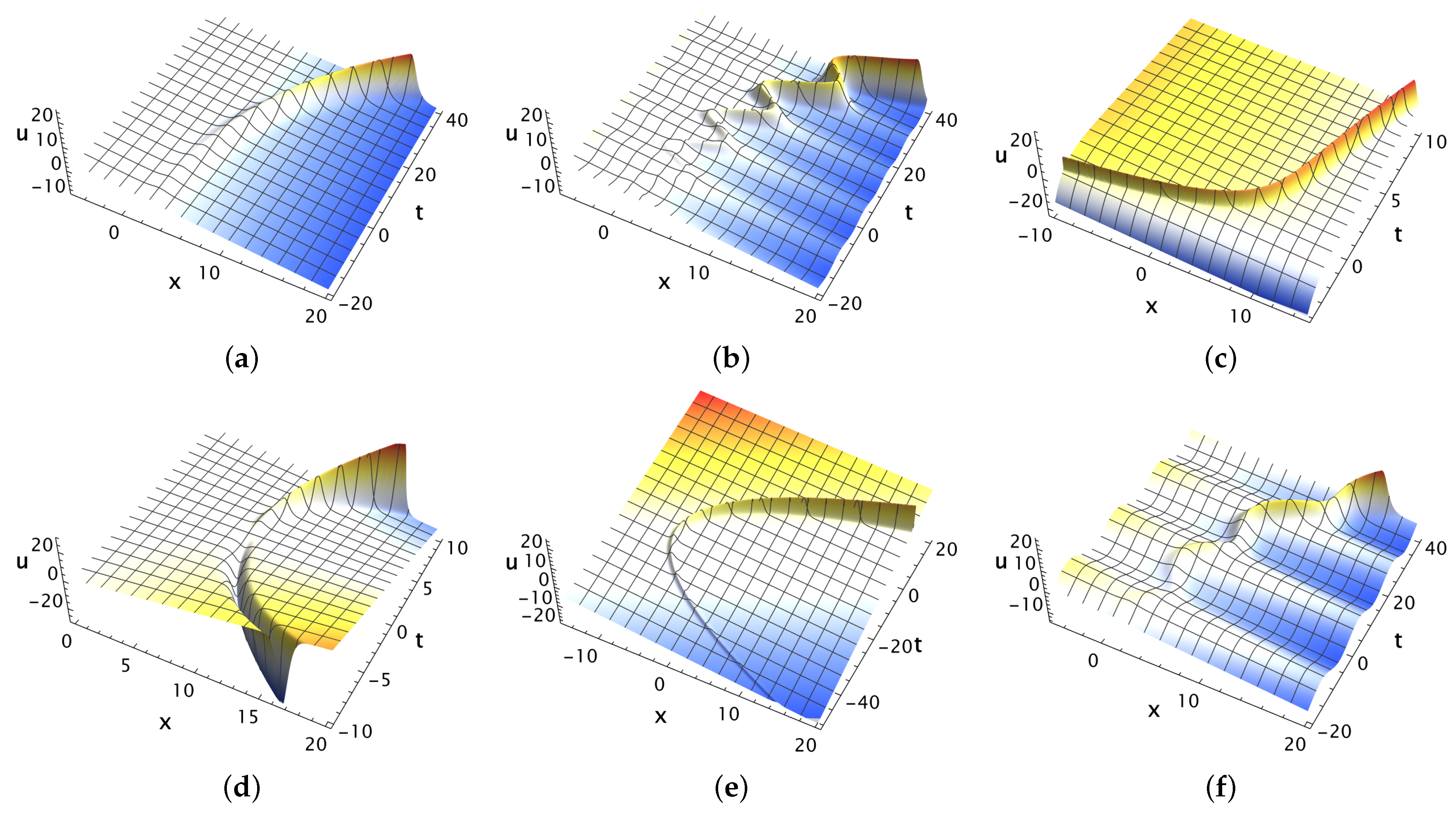
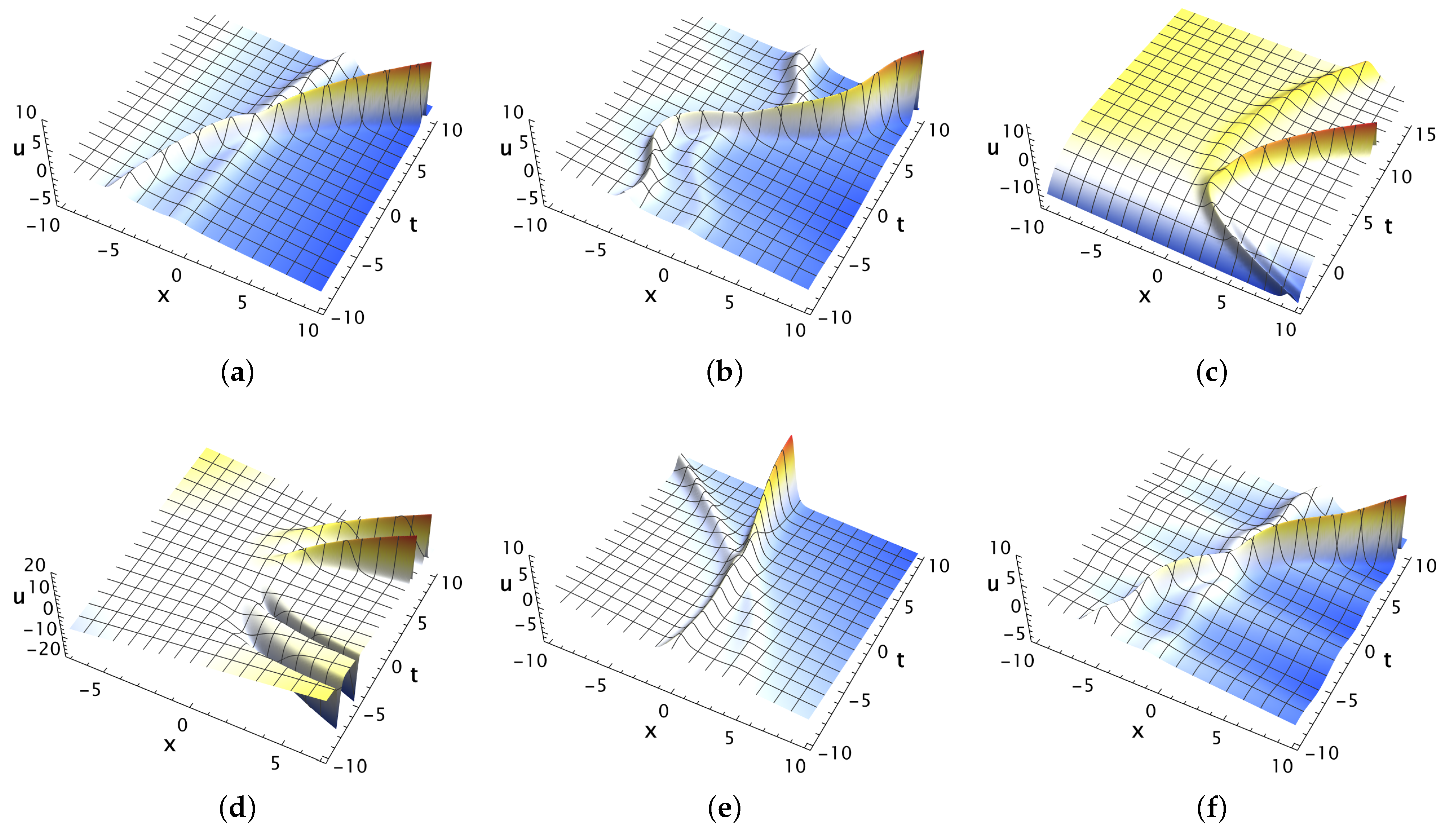
3.4. Soliton-like Solutions
4. Infinite Conservation Laws
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, T.; Li, J.; Zhang, H.Q.; Zhang, Y.X.; Hu, W.; Gao, Y.T.; Tian, B. Integrable aspects and applications of a generalized inhomogeneous N-coupled nonlinear Schrödinger system in plasmas and optical fibers via symbolic computation. Phys. Lett. A 2008, 372, 1990–2001. [Google Scholar] [CrossRef]
- Xu, T.; Tian, B.; Zhang, H.Q.; Li, J. Integrable decompositions for the (2+1)-dimensional Gardner equation. Z. Angew. Math. Phys. 2010, 61, 293–308. [Google Scholar] [CrossRef]
- Armesto, N.; Braun, M. Nuclear structure functions and heavy flavour leptoproduction off the nucleus at small x in perturbative QCD. Eur. Phys. J. C 2001, 22, 351–357. [Google Scholar] [CrossRef]
- Das, G.C.; Sarma, J. A new mathematical approach for finding the solitary waves in dusty plasma. Phys. Plasmas 1998, 5, 3918–3923. [Google Scholar] [CrossRef]
- Miao, S.; Yin, Z.Y.; Li, Z.R.; Pan, C.Y.; Wei, G.M. An Analysis of the Lie Symmetry and Conservation Law of a Variable-Coefficient Generalized Calogero–Bogoyavlenskii–Schiff Equation in Nonlinear Optics and Plasma Physics. Mathematics 2024, 12, 3619. [Google Scholar] [CrossRef]
- Gaik, T.K. Forced Korteweg–de Vries equation in an elastic tube filled with an inviscid fluid. Int. J. Eng. Sci. 2006, 44, 621–632. [Google Scholar] [CrossRef]
- Demiray, H. Forced KdV equation in a fluid-filled elastic tube with variable initial stretches. Chaos Solitons Fractals 2009, 42, 1388–1395. [Google Scholar] [CrossRef]
- Chudnovsky, D.V.; Chudnovsky, G.V. Solution of the pulse width modulation problem using orthogonal polynomials and Korteweg-de Vries equations. Proc. Natl. Acad. Sci. USA 1999, 96, 12263–12268. [Google Scholar] [CrossRef]
- Horii, Z. Formulation of the Korteweg–de Vries and the Burgers equations expressing mass transports from the generalized Kawasaki–Ohta equation. Phys. Lett. A 2002, 306, 45–51. [Google Scholar] [CrossRef]
- Zhang, L.P.; Xue, J.K. Effects of the dust charge variation and non-thermal ions on multi-dimensional dust acoustic solitary structures in magnetized dusty plasmas. Chaos Solitons Fractals 2005, 23, 543–550. [Google Scholar] [CrossRef]
- Chen, D.Y. Bäcklund Transformation and Multi-Soliton Solutions. In Introduction to Solitons; Science Press: Beijing, China, 2006. [Google Scholar]
- Zhao, Y.P.; Wang, J.Y.; Wei, G.M.; Liu, R.P. The Painlevé property, Bäcklund transformation, Lax pair and new analytic solutions of a generalized variable-coefficient KdV equation from fluids and plasmas. Phys. Scr. 2015, 90, 065203. [Google Scholar]
- Yu, X.; Gao, Y.T.; Sun, Z.Y.; Liu, Y. Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Phys. Rev. E 2011, 83, 056601. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Y.T.; Sun, Z.Y.; Yu, X. Multi-soliton solutions of the forced variable-coefficient extended Korteweg–de Vries equation arisen in fluid dynamics of internal solitary waves. Nonlinear Dyn. 2011, 66, 575–587. [Google Scholar] [CrossRef]
- Holloway, P.E.; Pelinovsky, E.; Talipova, T. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone. J. Geophys. Res. 1999, 104, 18333–18350. [Google Scholar] [CrossRef]
- Grimshaw, R.H.J. Long nonlinear internal waves in channels of arbitrary cross-section. J. Fluid Mech. 1978, 86, 415–431. [Google Scholar] [CrossRef]
- Wang, P.; Tian, B.; Liu, W.J.; Jiang, Y.; Xue, Y.S. Interactions of breathers and solitons of a generalized variable-coefficient Korteweg-de Vries-modified Korteweg-de Vries equation with symbolic computation. Eur. Phys. J. D 2012, 66, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Wei, G.M. Lax pair, auto-Bäcklund transformation and conservation law for a generalized variable-coefficient KdV equation with external-force term. Appl. Math. Lett. 2015, 45, 58–63. [Google Scholar] [CrossRef]
- Demiray, H. The effect of a bump on wave propagation in a fluid-filled elastic tube. Int. J. Eng. Sci. 2004, 42, 203–215. [Google Scholar] [CrossRef]
- Jimbo, M.; Kruskal, M.D.; Miwa, T. Painlevé test for the self-dual Yang–Mills equation. Phys. Lett. A 1982, 92, 59–60. [Google Scholar] [CrossRef]
- Wei, G.M.; Xu, X.G. Painlevé Analysis and auto-Bäcklund Transformation for a Variable-Coefficient KdV Equation. Math. Pract. Theory 2006, 36, 308–312. [Google Scholar]
- Weiss, J.; Tabor, M.; Carnevale, G. The Painlevé property for partial differential equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Weiss, J. The Painlevé property for partial differential equations. II: Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 1983, 24, 1405–1413. [Google Scholar] [CrossRef]
- Weiss, J. On classes of integrable systems and the Painlevé property. J. Math. Phys. 1984, 25, 13–24. [Google Scholar] [CrossRef]
- Weiss, J. The sine-Gordon equations: Complete and partial integrability. J. Math. Phys. 1984, 25, 2226–2235. [Google Scholar] [CrossRef]
- Wei, G.M.; Gao, Y.T.; Hu, W. Painlevé analysis, auto-Bäcklund transformation and new analytic solutions for a generalized variable-coefficient KdV equation. Eur. Phys. J. B 2006, 53, 343–350. [Google Scholar] [CrossRef]
- Gai, X.L.; Gao, Y.T.; Wang, L.; Meng, D.X.; Lü, X.; Sun, Z.Y.; Yu, X. Painlevé property, Lax pair and Darboux transformation of the variable-coefficient modified Kortweg-de Vries model in fluid-filled elastic tubes. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1776–1782. [Google Scholar] [CrossRef]
- Konno, K.; Wadati, M. Simple derivation of Bäcklund transformation from Riccati form of inverse method. Prog. Theor. Phys. 1975, 53, 1652–1656. [Google Scholar] [CrossRef]
- Wahlquist, H.D.; Estabrook, F.B. Bäcklund transformation for solutions of the Korteweg-de Vries equation. Phys. Rev. Lett. 1973, 31, 1386–1390. [Google Scholar] [CrossRef]
- Guo, Y. Nonlinear Evolution Equations and Their Solitary Wave Solutions, 1st ed.; Beijing University of Posts and Telecommunications Press: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Wadati, M.; Sanuki, H.; Konno, K. Relationships among inverse method, Bäcklund transformation and an infinite number of conservation laws. Prog. Theor. Phys. 1975, 53, 419–436. [Google Scholar] [CrossRef]
- Satsuma, J. Higher conservation laws for the Korteweg-de Vries equation through Bäcklund transformation. Prog. Theor. Phys. 1974, 52, 1396–1397. [Google Scholar] [CrossRef]
- Li, J.; Xu, T.; Meng, X.H.; Yang, Z.C.; Zhu, H.W.; Tian, B. Symbolic Computation on Integrable Properties of a Variable-Coefficient Korteweg–de Vries Equation from Arterial Mechanics and Bose–Einstein Condensates. Phys. Scr. 2007, 75, 278–283. [Google Scholar] [CrossRef]
- Wadati, M.; Toda, M. The exact N-soliton solution of the Korteweg-de Vries equation. J. Phys. Soc. Jpn. 1972, 32, 1403–1411. [Google Scholar] [CrossRef]
- Tian, B.; Gao, Y.T. Soliton-like solutions to the (2 + 1)-dimensional integrable dispersive long wave equations. Phys. Scr. 1996, 53, 641. [Google Scholar] [CrossRef]
- Tian, B.; Gao, Y.T. Extension of generalized tanh method and soliton-like solutions for a set of nonlinear evolution equations. Chaos Solitons Fractals 1997, 8, 1651–1653. [Google Scholar] [CrossRef]
| Change in the Perturbed Coefficient | Change in the Inhomogeneity Coefficient | Change in the Nonlinearity Coefficient | Change in the Forcing Term | |
|---|---|---|---|---|
| Solitonic amplitude | Not affected | Affected | Affected | Not affected |
| Solitonic velocity | Affected | Affected | Affected | Affected |
| Solitonic background | Affected | Affected | Affected | Affected |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Wang, Z.; Wang, K.; Jiang, N.; Wei, G. Analytic Investigation of a Generalized Variable-Coefficient KdV Equation with External-Force Term. Mathematics 2025, 13, 1642. https://doi.org/10.3390/math13101642
Li G, Wang Z, Wang K, Jiang N, Wei G. Analytic Investigation of a Generalized Variable-Coefficient KdV Equation with External-Force Term. Mathematics. 2025; 13(10):1642. https://doi.org/10.3390/math13101642
Chicago/Turabian StyleLi, Gongxun, Zhiyan Wang, Ke Wang, Nianqin Jiang, and Guangmei Wei. 2025. "Analytic Investigation of a Generalized Variable-Coefficient KdV Equation with External-Force Term" Mathematics 13, no. 10: 1642. https://doi.org/10.3390/math13101642
APA StyleLi, G., Wang, Z., Wang, K., Jiang, N., & Wei, G. (2025). Analytic Investigation of a Generalized Variable-Coefficient KdV Equation with External-Force Term. Mathematics, 13(10), 1642. https://doi.org/10.3390/math13101642





