Abstract
In this paper, we address the problem of obtaining bias-free and complete finite size approximations of the solution sets (Pareto fronts) of multi-objective optimization problems (MOPs). Such approximations are, in particular, required for the fair usage of distance-based performance indicators, which are frequently used in evolutionary multi-objective optimization (EMO). If the Pareto front approximations are biased or incomplete, the use of these performance indicators can lead to misleading or false information. To address this issue, we propose the Reference Set Generator (RSG), which can, in principle, be applied to Pareto fronts of any shape and dimension. We finally demonstrate the strength of the novel approach on several benchmark problems.
Keywords:
multi-objective optimization; Pareto front approximation; performance indicators; benchmarking MSC:
68W50
1. Introduction
Multi-objective optimization has become an integral part of the decision making for many real-world problems. In a multi-objective optimization problem (MOP), one is faced with the issue of concurrently optimizing k individual objectives. The set of optimal solutions is called the Pareto set, and its image is the Pareto front. The latter set is, in many cases, most important for the decision maker (DM), since it provides him/her with an overview of the optimal performances for his/her project. What makes MOPs hard to deal with is that one can expect that both the Pareto set and front form—at least locally and under certain assumptions on the model—objects of dimension [1]. For the numerical treatment of MOPs, specialized evolutionary algorithms, called multi-objective evolutionary algorithms (MOEAs), have caught the interest of many researchers and practitioners during the last three decades [2]. MOEAs are population-based and hence allow one to obtain a finite approximation of the entire solution set in one run of the algorithm. For the performance assessment of the outcome sets, several different indicators have been proposed so far (e.g., [3,4,5,6,7,8]). Some of these performance indicators are distance-based and require a “suitable” finite-size representation of the Pareto front. While until now, a vast variety of different MOEAs have been proposed and analyzed, it is fair to say that the generation of suitable reference sets has played a rather minor role in the evolutionary multi-objective optimization (EMO) community. It is evident that such reference sets should be complete. Furthermore, as we show in this work, a biased representation can lead to misleading or even false information.
To fill this gap, we propose in this work the Reference Set Generator (RSG). The main steps of RSG are as follows: (i) A first approximation of the Pareto front is either taken or generated. This set can be, in principle, of arbitrary size, and the elements can be non-uniformly distributed along the Pareto front (i.e., biased). However, all of these elements have to be “close enough” to the set of interest. In order to obtain a bias-free approximation, (ii) component detection and (iii) a filling step are applied to . Finally, (iv) a reduction step is applied. The RSG is applicable to MOPs with Pareto fronts of, in principle, any shape and dimension. This is in contrast to existing methods that generate such reference sets that require an analytic expression of either the Pareto front or the Pareto set (or a tight superset of it). Furthermore, the resulting reference set is of any desired magnitude. We will show the strength of the novel method on several benchmark problems.
The remainder of this paper is organized as follows: in Section 2, we briefly recall the background for the understanding of this work. We further discuss the related work and the performance indicators that benefit from our approach. In Section 3, we motivate the need for bias-free complete finite-size Pareto front approximations. In Section 4, we propose the Reference Set Generator (RSG) that aims for such sets. In Section 5, we present some numerical results on selected benchmark problems and compare the RSG to related algorithms. Finally, we draw our conclusions in Section 6 and give possible paths for future research.
2. Background and Related Work
We consider multi-objective optimization problems (MOPs) that can be mathematically expressed via
Hereby, the map F is defined as
where we assume each of the individual objectives, , , to be continuous. We stress, however, that the method we propose in the sequel, RSG, can, in principle, also be applied to discrete problems. Q is the domain of the objective functions that is typically expressed by equality and inequality constraints.
In order to define the optimality of a MOP, one can use the concept of dominance [9].
Definition 1.
- (a)
- Let . Then, the vector v is less than w () if for all . The relation is defined analogously.
- (b)
- is dominated by a point () with respect to (Equation (MOP)) if and .
- (c)
- is called a Pareto point or Pareto optimal if there is no that dominates x.
- (d)
- The set of Pareto optimal solutionsis called the Pareto set.
- (e)
- The image of the Pareto set is called the Pareto front.
One can expect that both the Pareto set and the Pareto front form, under certain conditions and at least locally, objects of dimension . For details, we refer to [1]. Due to this “curse of dimensionality”, it is, hence, not possible for an evolutionary multi-objective optimization algorithm (MOEA) to keep all promising candidate solutions (e.g., all non-dominated ones) during the algorithm run. It is hence inevitable—at least for continuous problems—to select which of the promising solutions should be kept in order to obtain a “suitable” approximation of the solution set (in most cases, the Pareto front of the given MOP). Within MOEAs, this process is termed “selection”. Another term, which can be used synonymously, is “archiving”. The latter is typically used when the MOEA is equipped with an external archive.
Most of the existing MOEAs can be divided into three main classes: First, there exist MOEAs that are based on the concept of dominance (e.g., [10,11,12,13]). Second, there exist MOEAs that are based on decompositions (e.g., [14,15,16,17,18]), and third, there are MOEAs that make use of an indicator function (e.g., [19,20,21]). The selection strategies of the first generation of MOEAs of the first class are based on a combination of non-dominated sorting and niching (e.g., [22,23,24]). Later, elite preservation was included, leading to increased overall performance (and, as a consequence, better Pareto front approximations). This holds, e.g., for SPEA [25], PAES [13], SPEA-II [11], and NSGA-II [10]. Theoretical studies on selection mechanisms have been done by the groups of Rudolph [26,27,28,29] and Hanne [30,31,32,33]. All of these selection mechanisms deal with the abilities of the populations to reach the Pareto set/front. On the other hand, the distributions of the individuals along the Pareto sets/fronts have not been considered. The selection mechanisms of the MOEAs within the second and third class follow directly from the construction of the algorithms: selection in a decomposition-based MOEA is done by considering the values of the chosen scalarization functions. Analogously, the selection in an indicator-based MOEA is done by considering the indicator contributions.
Existing (external) archiving strategies can also be divided into three classes: (a) unbounded archivers, (b) implicitly bounded archivers, and (c) bounded archivers. Unbounded archivers store all promising solutions during the algorithm run. The magnitudes of such archives can exceed any given threshold if the algorithm is run long enough. Unbounded archivers have, e.g., been used and analyzed in [34,35,36,37,38,39,40]. -dominance [41] can be viewed as a weaker concept of dominance. This relation allows single solutions to “cover” entire parts of the Pareto front of a given MOP, which is the basis for most implicitly bounded archivers. Such strategies have first been considered in the context of evolutionary multi-objective optimization (EMO) by Laumanns et al. [42]. Later works proposed and analyzed different approximations (such as gap-free approximations of the Pareto front) and dealt with different sets of interest (e.g., the consideration of all nearly optimal or all -locally optimal solutions) [38,39,43]. Finally, bounded archivers have, e.g., been proposed in [44,45], where adaptive grid selections have been utilized. Bounded archivers tailored to the use of the hypervolume indicator have been suggested in [46,47]. In ref. [48], a bounded archiver aiming for Hausdorff approximations of the Pareto front is presented and analyzed. Laumanns and Zenklusen have proposed two bounded archivers that aim for -approximations of the Pareto front [49].
All of the selection/archiving strategies mentioned above have in common that they aim for a “best approximation” of the Pareto front out of the given (finite) data. A related but slightly different problem is to generate a “suitable” (in particular, complete and bias-free) finite-size approximation of the set of interest S for the sake of comparisons, even if S is known approximately or even analytically but is not “trivial” (e.g., a line segment, a simplex, or perfectly spherical). It is known that most selection mechanisms have a non-monotonic behavior, which may result in the fact that entire regions of the Pareto front are not covered. Some of the external archives have monotonic behavior and even aim for gap-free approximations. On the other hand, uniformity of the final archive cannot be guaranteed. Both issues are, e.g., discussed in [43]. The evolutionary multi-objective optimization platform PlatEMO [50] provides reference sets for many benchmark problems. The underyling method was proposed in Tian et al. It uses uniform sampling on the simplex and then maps these points to the particular Pareto fronts of each problem. However, an analytical expression or characterization of the Pareto front is required, and in some cases, the obtained set is not completely uniform. Furthermore, in pymoo [51]—a multi-objective optimization framework in Python—built-in functions to obtain reference sets of the Pareto fronts for selected MOPs are provided. This is mainly the case for problems where the fronts are given analytically. Some other reference sets are provided with fixed magnitude; however, no direct information is provided as to how they have been obtained. A method related to RSG can be found in [52], which has the aim of guiding the iterates of a particular Newton method toward the Pareto front. In this work, we extend this idea for the purpose of generating complete and bias-free Pareto front approximations of relatively large magnitudes (in particular, compared to population sizes used in EMO). RSG is, in principle, applicable to Pareto fronts of any shape or dimension. For this, however, an initial reference set has to be given. The retrieval of this set is problem-dependent, and it is not always clear how to obtain a suitable approximation (though we give some guidelines as to which method may be most promising for a given MOP).
Finally, reference sets such as the ones generated by RSG are helpful for the evaluation of the performance qualities of candidate sets (populations) in EMO. More precisely, such sets are required for all distance-based indicators. The earliest of such indicators are the Generational Distance (GD, [3]) and the Inverted Generational Distance. (IGD, [5]). Later, the indicator [6] was proposed, which is a combination of slight variants of the GD and IGD and can be viewed as an averaged version of the Hausdorff distance . So far, there exist several extensions of these performance indicators. For instance, the consideration of continuous sets—either only the Pareto front or also the candidate solution set—has been done in [8,53], leading to modifications of and . The indicators IGD+ [7] and DOA [54] are modifications of the IGD that are Pareto-compliant.
3. Motivation
Here, we motivate the need for complete and bias-free finite-size Pareto front approximations and propose the Reference Set Generator (RSG) that targets such sets in the next section.
Distance-based indicators require a “suitable” finite-size approximation of the Pareto front in order to give a “correct” value for the approximation quality of the considered candidate solution set. In particular, this holds for the abovementioned indicators GD, IGD, and , together with their variants. Such representations are ideally uniformly spread along the entire Pareto front [53]. This, however, is a non-trivial task, unless the Pareto front is given analytically and has a relatively simple form (e.g., linear or perfectly spherical). Regrettably, this is the case for only a few test problems (e.g., DTLZ1 and DTLZ2). On the other hand, there exist quite a few benchmark MOPs where the shape of the Pareto set is relatively simple. For such problems, it is tempting to choose uniform samples from the Pareto set (i.e., , where all ) and to use the respective image to represent of the Pareto front. The following discussion shows, however, that this approach has to be handled with care, since it can induce unwanted biases in the approximations that, in turn, may result in misleading indicator values.
As the first example, consider the one-dimensional bi-objective problem
Let the domain be given by ; then, the Pareto set is identical to Q, and the Pareto front is the line segment that connects the points and . Figure 1 shows the result when using N equally spaced points along the Pareto set. As can be seen for and , there is a clear bias of the images toward the right lower end of the Pareto front. For , the Pareto front approximation is “complete” (at least from the practical point of view) and appears to be perfect. However, it possesses the same bias. To see the impact of the reference set on the performance indicators, consider the two hypothetical outcomes (e.g., possible results from different MOP solvers):
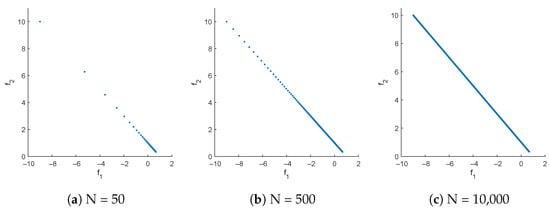
Figure 1.
Pareto front representations of MOP (3) when using , 500, and equally distributed samples along the Pareto set.
Figure 2 shows the two sets together with the Pareto front. Note that A is the perfect five-element approximation of the Pareto front: the elements are equally distributed along the Pareto front, and the extreme points are shifted “halfway in” [53]. The set B is certainly not perfect, as it, e.g., fails to “cover” more than half of the front. Table 1 shows values for different distance-based indicators, the outcomes , and different representations R of the Pareto front. For (the one shown in Figure 1c), all indicators—except —yield lower values for B than for A, indicating (erroneously) that B is better than A. This is not the case for , since the Hausdorff distance is determined by the maximum of the considered distances and not by an average of those (however, has other disadvantages in the context of EMO in that it most prominently punishes single outliers [6]). The situation changes when selecting as a representation of the front. This representation also contains N = 10,000 elements, but these are chosen uniformly along the Pareto front. Now, there is a tie for the two GD variants, and for all other indicators, A leads to better values than B. These values are indeed very close to the “correct” values: all exact GD values are equal to zero, since A and B are contained in the Pareto front. In order to compute the exact IGD values, a particular integral has to be solved [53]. When using as representation, the computation of the IGD values can be interpreted as a Riemann sum with N = 10,000 equally sized sub-intervals leading to perfect solutions—at least from the practical point of view.
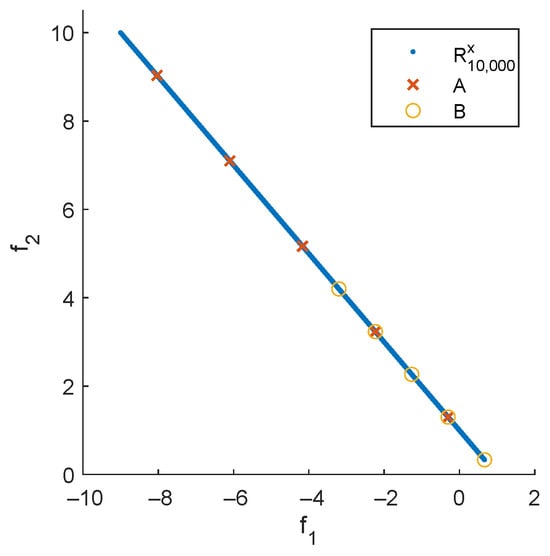
Figure 2.
Representation of the Pareto front of MOP (3), together with the two hypothetical outcomes A and B.

Table 1.
Indicator values for different indicators, the outcomes , and the representations of the Pareto front. Better indicator values are diplayed in bold font.
We repeat the process, but now using only elements for the representation (see Table 1). We can see the same trend, i.e., that B appears to be better for , while A appears to be better when using . Furthermore, we see that the indicator values for are already quite close to the exact values (i.e., when using ). While the proper choice of N may not be an issue for bi-objective problems (), this may become important for a larger number of objectives due to the “curse of dimensionality”: at least for continuous problems, one can expect that the Pareto front forms under certain (mild) assumptions a manifold of dimension [1].
We next consider further test problems. Figure 3, Figure 4, Figure 5 and Figure 6 show the Pareto front approximations for the commonly used test problems DTLZ1, DTLZ2, ZDT1, and ZDT3, respectively, where the representation has been obtained via uniform sampling in the decision variable space along the Pareto set. In all cases, the Pareto front representations appear to be perfect for large enough values of N. However, certain biases can be observed for lower values of N. For all test problems, we selected two points out of the representation and show the distances to their nearest neighbors (denoted by ). These distances differ by one order of magnitude, which confirms that the solutions are not uniformly distributed along the fronts. Using such representations, the same issues can arise as the one discussed above.
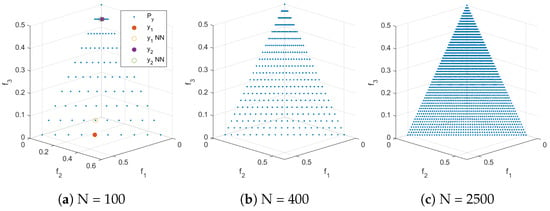
Figure 3.
Pareto front approximations for DTLZ1 resulting from uniformly sampling the Pareto set with N points. Distances to the nearest neighbors in (a): ; .
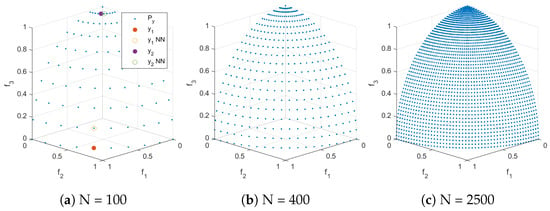
Figure 4.
Pareto front approximations for DTLZ2 resulting from uniformly sampling the Pareto set with N points. Distances to the nearest neighbors in (a): , .
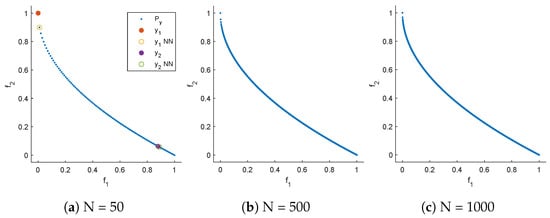
Figure 5.
Pareto front approximations for ZDT1 resulting from uniformly sampling the Pareto set with N points. Distances to the nearest neighbors in (a): ; .
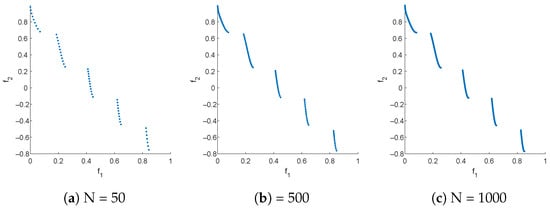
Figure 6.
Pareto front approximations for ZDT3 resulting from uniformly sampling the Pareto set with N points. Distances to the nearest neighbors in (a): ; .
To conclude, the suitable representation of the Pareto front of a given MOP is crucial when considering distance-based performance indicators that use an average of the distances considered. Such representations are ideally equally distributed over the front. If the representation contains a bias, this may result in misleading indicator values, leading, in turn, to a wrong evaluation of the obtained results. In particular, the approach to performing the sampling along the Pareto set is, though tempting, not appropriate for such indicator-based indicators. In the sequel, we will propose a method that aims to achieve uniform Pareto front representations.
4. Reference Set Generator (RSG)
In the following, we will present the RSG, which is a method that aims to generate complete and bias-free Pareto front approximations. We will first present the general idea of the method and further on discuss the steps in detail.
4.1. General Idea
We assume in the following that we are interested in a Pareto front approximation of size N for a given MOP. Furthermore, we assume that we are given a set of (in principle) arbitrary size ℓ of non-dominated, possibly non-uniformly distributed points that are “close enough” to the PF. The computation of is in general a non-trivial task. Below, we will discuss different strategies to obtain suitable approximations. Given these data, the Reference Set Generator (RSG) consists of three main steps: component detection, filling, and reduction. More precisely, given that may have imperfections or biases in the approximation, the idea is to fill the gaps between the points within each connected point of . This leads to a more complete set F with a higher cardinality than , which can then be reduced to obtain a uniform reference set of size N. Note that PFs can be disconnected, and if we simply fill the gaps in , we may introduce points that do not belong to the PF (see Figure 7b for such an example). Therefore, component detection must be performed before applying the filling process to each detected component (Figure 7a).
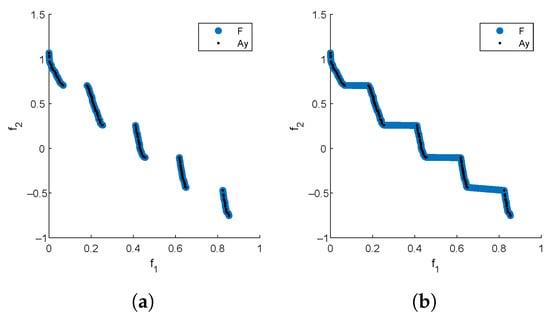
Figure 7.
Filling with (a) and without (b) component detection for ZDT3. Note that points not in the PF are included if the component detection step is omitted (b).
The general procedure of the RSG is presented in Algorithm 1, and each of the main steps will be explained in the following subsections.
Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show all the steps of RSG on the test problems ZDT3, DTLZ7, WFG2, CONV3, CONV3-4, and CONV4-2F (we will discuss these examples in more detail in Section 5).
| Algorithm 1 Reference Set Generator (RSG) |
|
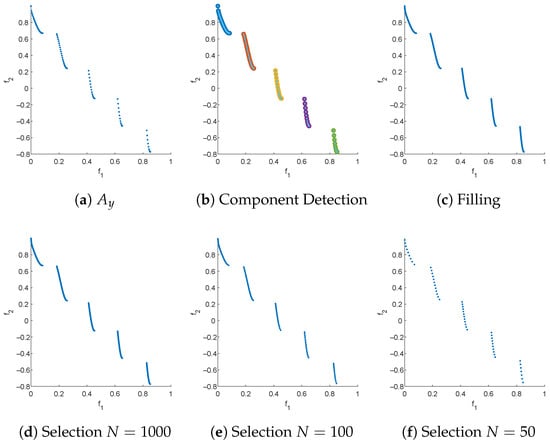
Figure 8.
The main steps of RSG on ZDT3 as well as three reference sets for , 100, and 50. For this problem, we have taken the starting set from PlatEMO and have set . In (b), detected connected components are represented by different colors.
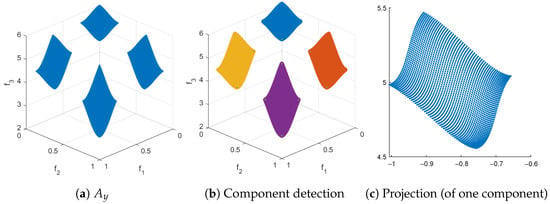
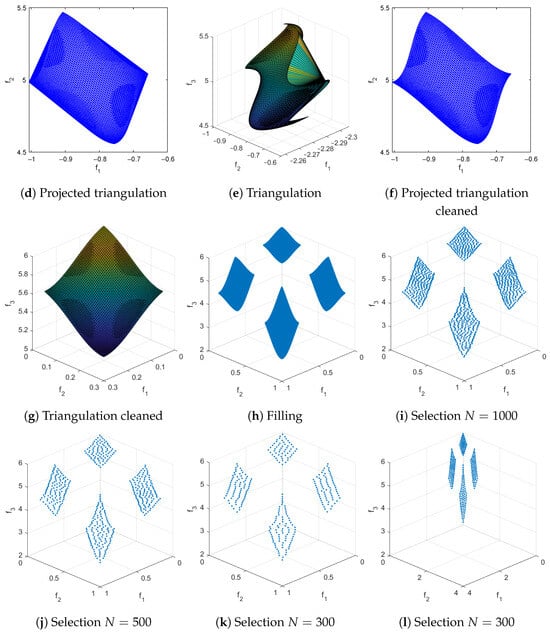
Figure 9.
The main steps of RSG on DTLZ7 as well as three reference sets for , and 300. We have taken from pymoo and have set . (k,l) show the same results, but (l) uses the same range for all variables, indicating uniformity of the solution set. In (b), detected connected components are represented by different colors.
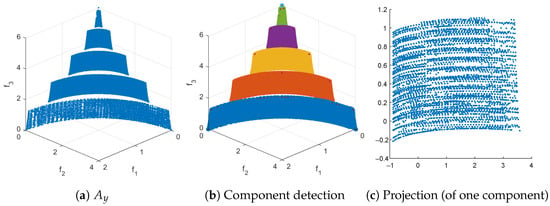
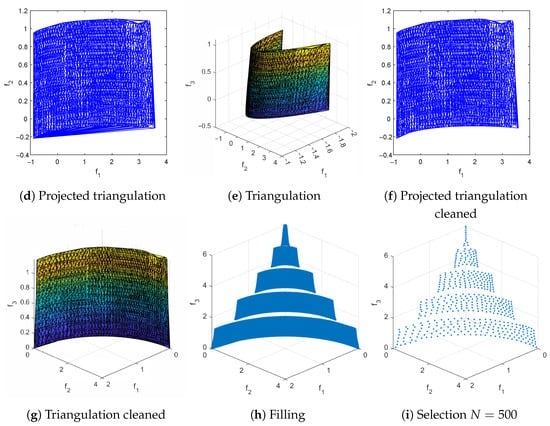
Figure 10.
The main steps of RSG on WFG2 as well as the reference set for . We have obtained from PT (together with a non-dominance test) and have set . In (b), detected connected components are represented by different colors.
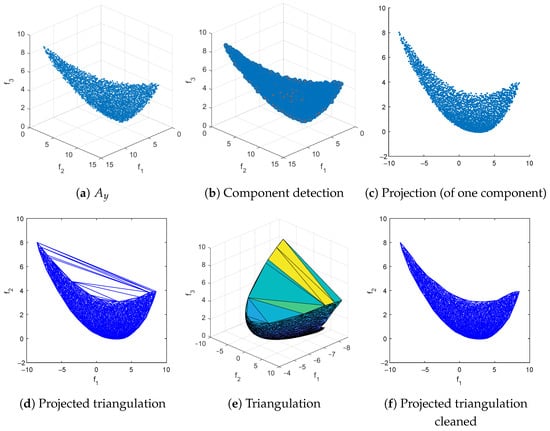
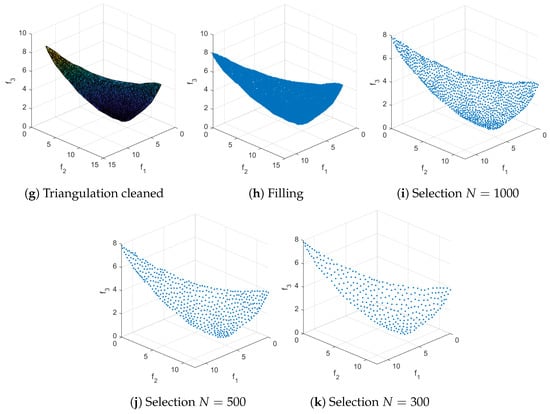
Figure 11.
The main steps of RSG on CONV3 as well as reference sets for and 300. We have obtained via uniform sampling along the PS (together with a non-dominance test) and have set .
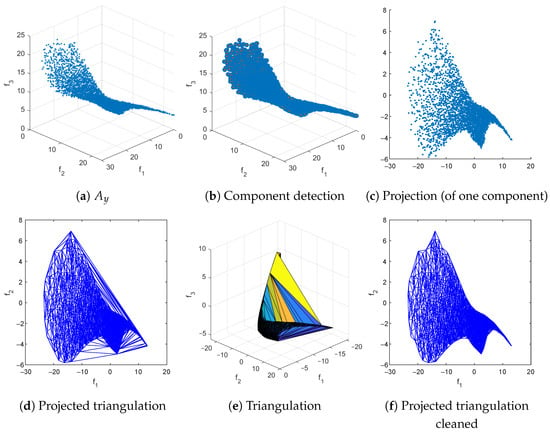
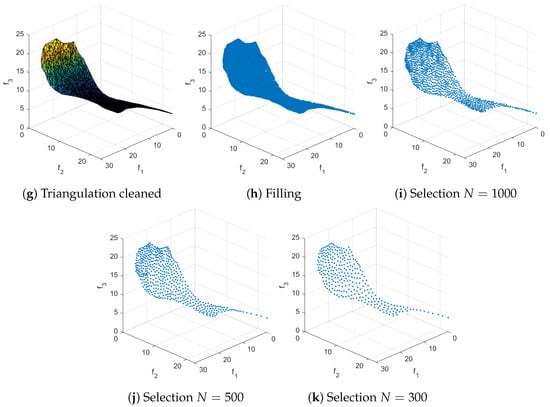
Figure 12.
The main steps of RSG on CONV3-4 as well as reference sets for and 300. We have obtained via uniform sampling along the PS (together with a non-dominance test) and have set .
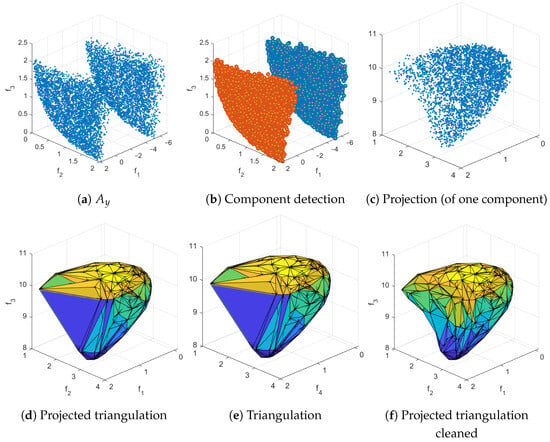
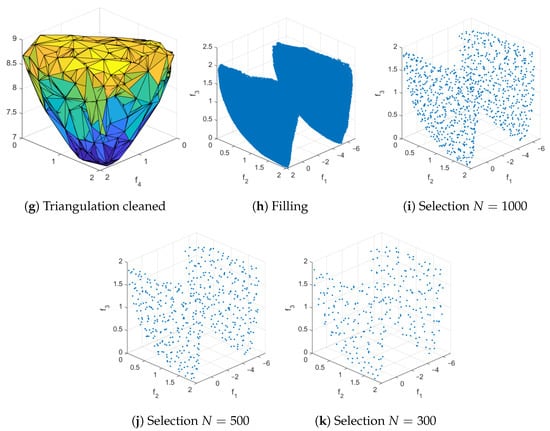
Figure 13.
The main steps of RSG on CONV4-2F as well as reference sets for and 300. We have obtained via merging final populations from 30 independent runs of NSGA-III (population size 500, 400 generations), together with a non-dominance test. We and have set . In (b), detected connected components are represented by different colors.
4.2. Component Detection
Since the Pareto front might be disconnected, a component detection on is needed. We use DBSCAN [55] in objective space for this purpose for three main reasons: (i) the number of components does not need to be known a priori, (ii) the method detects outliers, and (iii) we have observed that a density-based approach works better than a distance-based one (e.g., k-means) for component detection. DBSCAN has two parameters: and r. The selection of these parameters is problem-dependent. Depending on the information available about the Pareto front, we suggest the following values:
- If it is known that the PF is connected, this step can simply be omitted. Note that the main application of RSG is in the approximation of Pareto fronts of known benchmark functions, where the shapes of the PFs are at least known roughly.
- If the range of the PF is roughly known or normalized and the PF is disconnected (or at least suspected to be), r can be set to 10% of the range and to 10% of when few components are expected. Alternatively, r can be set to a smaller value (e.g., 2–3%) and to 1–2% of when several components are anticipated.
- No information of the PF is known a priori. To make the component detection process “parameter-free”, we compute a small grid search to find the optimal values of and r based on the weakest link function defined in [56]. Based on our experiments, we suggest setting the parameter values to and for bi-objective problems and to and otherwise, where is the average pairwise distance between all points and .
A summary of the component detection process is presented in Algorithm 2. r and have to be given as grid search ranges: and are the input variables containing the lower and upper bounds of the grid search for r and , respectively. The step size for r is also needed, and it is given in the input variable . For , it is not needed, as this variable is an integer. With these values, the grid search values are defined as and . If the grid search is not needed, simply set as and as , using the desired values for r and , and the component detection will be performed only once with those values. In the following, we describe the remaining steps for a single connected component. If multiple components exist, the procedures must be repeated analogously for each component identified by Algorithm 2.
| Algorithm 2 Component Detection |
|
4.3. Filling
Even if we know the PS a priori, a uniform sampling of the PS will not result in a uniform sampling of the PF. We assume that we have a set of points that is not uniformly distributed. However, if we fill the gaps and select N points from the filled set, we can obtain a more uniform set, leading to better IGD approximations when selecting points from these filled sets. The idea behind the filling step is to create a set that is as uniform as possible so that the reduction step (in particular, k-means) does not become stuck in non-uniform local optima, which would lead to non-uniform final sets. The next task is, therefore, to compute solutions that are ideally uniformly distributed along .
This process is performed differently for and objectives:
- For , we sort the points of in increasing order of , i.e., the first objective. Then, we consider the piecewise linear curve formed by the segments between and , and , and so on. The total length of this curve is given by , where . To perform the filling, we arrange the desired points along the curve L such that the first point is and the subsequent points are distributed equidistantly along L. This is achieved by placing each point at a distance of from the previous one along L. See Algorithm 3 for details.
- The filling process for consists of several intermediate steps that must be described first; see Algorithm 4 for a general outline of the procedure. The procedure is as follows: First, to better represent (particularly for the filling step), we triangulate this set in dimensional space. This is done because the PF for continuous MOPs forms a set whose dimension is at most . To achieve this, we compute a “normal vector” to using Equation (8), and then we project it onto the hyperplane normal to , obtaining the projected set . After this, we compute the Delaunay triangulation [57] of , which provides a triangulation that can be used in the original k-dimensional space. For some PFs, the triangulation may include triangles (or simplex for ) that extend beyond (Figure 12d), so a removal strategy is applied to eliminate these triangles and obtain the final triangulation T. Finally, each triangle is uniformly filled at random with a number of points proportional to its area (or volume for ), resulting in the filled set F of size .We will now describe each step in more detail in the following:
- -
- Computing “normal vector” : Since the front is not known, we compute the normal direction orthogonal to the convex hull defined by the minimal elements of . More precisely, we compute as follows: if , choosewhere denotes the i-th element of , and setNext, compute a QR factorization of M, i.e.,where is an orthogonal matrix with column vectors , and is a right upper triangular matrix. Then, the vectoris the desired shifting direction. Since Q is orthogonal, the vectors form an orthonormal basis of the hyperplane that is orthogonal to . That is, these vectors can be used for the construction of .
- -
- Projection : We use as the first axis of a new coordinate system , where the vectors are defined as above. In this coordinate system, the orthonormal vectors form the basis of a hyperplane orthogonal to . , and the projection of the points of onto this hyperplane is achieved by first expressing the points in this new coordinate system as and then removing the first coordinate, yielding . Finally, .
- -
- Delaunay Triangulation : Compute the Delaunay triangulation of . This returns , which is a list of size containing the indices of that form the triangles (or simplices for ). The list serves as the triangulation for the k-dimensional set , which is possible because consists of indices, making it independent of the dimension. We use to denote the number of triangles obtained, to denote the indices of the vertices forming triangle i, and to denote the corresponding vertices of triangle i.
- -
- Triangle Cleaning : We identify three types of unwanted triangles: those with large sides, those with large areas, and those where the matrix containing the coordinates of the vertices has a large condition number. The type of cleaning applied depends on the problem; however, the procedure remains the same for any problematic triangle case and is outlined in Algorithm 5. First, the property (area, largest side, or condition number) is computed for all the triangles . Next, triangles i with are removed.
- -
- Triangle Filling : For each triangle with area , we generate points uniformly at random inside triangle , following the procedure described in [58]. That is, the number of points is proportional to the area (or volume) of each triangle (or simplex). Here, is the total area of the triangulation.
| Algorithm 3 Filling ( Objectives) |
|
| Algorithm 4 Filling ( Objectives) |
|
| Algorithm 5 Triangle Cleaning |
|
4.4. Reduction
Once we have computed the filled set F, we need to select N points that are ideally evenly distributed along F. To this end, we use k-means clustering with N clusters, as there is a strong relationship between k-means and the optimal IGD subset selection [59,60]. The resulting N cluster centroids form the PF reference set Z. The use of k-means for reduction can be modified in the RSG code; alternatives such as k-medoids and spectral clustering are also supported (this is an input parameter in the code). Note that this reduction step can be further adapted to generate reference sets tailored to other types of indicators (i.e., those that are not distance-based), since one of the output of RSG the raw filled set F.
4.5. Obtaining
The RSG requires an initial approximation of the Pareto front. Note that by construction of the algorithm, this set can have small imperfections (which can be removed by the filling step) and can also have biases in the approximation (reduction step). However, it is desired that “captures” the shape of the entire Pareto front. In particular, the RSG is not capable of detecting if an entire region of the Pareto front is missing in . The computation of such an approximation is certainly problem-dependent. For our computations, we have used the following three main procedures to obtain , depending on the complexity of the PF shape:
- -
- Sampling: In the easiest case, either the PS or the PF is given analytically, which is indeed given for several benchmark problems. If a sampling can be performed directly in objective space (e.g., for linear fronts), the remaining steps of the RSG may not be needed to further improve the quality of the solution set. If the sampling is performed in decision variable space, the elements of the resulting image are not necessarily uniformly distributed along the Pareto front as discussed above. However, in that case, the filling and reduction steps may help to remove biases. We have used sampling, e.g., for the test problems DTLZ1, CONV3, and CONV3-4.
- -
- Continuation: If neither the PS nor the PF has an “easy” shape, one alternative is to make use of multi-objective continuation methods, probably in combination with the use of several different starting points and with a non-dominance test. In particular, we have used the Pareto Tracer (PT, [61,62]), which is a state-of-the-art continuation method that is able to treat problems of, in principle, any dimensions (both n and k), can handle general constraints, and that can even detect local degeneration of the solution set. Continuation is advisable if the PS/PF consists of relatively few connected components and if the gradient information can at least be approximated. We have used PT, e.g., for the test problems WFG2, DTLZ5, and DTLZ6.
- -
- Archiving: The result of an MOEA or any other MOP solver can, of course, be taken. This could be either the final archive of the population, via merging several populations of the same or several runs [52], or via using external (unbounded) archives [43]. Note that this includes taking a reference set from a given repository. Archiving is advisable if none of the above techniques can be applied successfully.We have used archiving, e.g., for the test problems DTLZ1-4, DTLZ7, ZDT1-6, CONV3, CONV3-4, and CONV4-2F.
4.6. Complexity Analysis
The overall time complexity is for (regardless of the number of components) and for , where ℓ is the size of the initial approximation , k is the number of objectives, is the number of triangles in the Delaunay triangulation, is the number of iterations of k-means (bounded to 500 in this work), N is the desired size of the reference set Z, and is the size of the filling. This assumes that and that the triangle-cleaning method used is based on the longest side (which was the method applied to all the references presented in this work). Typically, obtaining a decent approximation requires a large value of , making the clustering step the dominant one and thus reducing the overall complexity to for any k. We now present the time complexity analysis in detail for each step separately, considering a single component:
- Component Detection: The time complexity is , which accounts for the computation of the average distance plus the size of the grid search () multiplied by the sum of the complexities of DBSCAN and the WeakestLink computation. Here, ℓ is the size of , and represents the number of parameter combinations of the grid search, with for and for using the suggested values for the case where no information about the PF is known a priori. If it is previously known that the Pareto front is connected, then the parameters of DBSCAN can be correctly adjusted, and can be set to 1.
- Filling: The time complexity depends on the number of objectives:
- -
- For , the time complexity is , which accounts for sorting and placing the points along the line segments.
- -
- For , the time complexity is due to the computations involved in determining the normal vector , changing coordinates and projecting, performing the Delaunay triangulation, and filling the triangles. Here, represents the size of the cleaned Delaunay triangulation, i.e., the number of triangles. Additionally, triangle cleaning must be considered, though its complexity depends on the method used. It is given by when the cleaning is based on area or the condition number (due to determinant computation) or when the cleaning is based on the longest side.
- Select Reference Set T: The time complexity is due to the k-means clustering algorithm. Here, is the number of iterations of k-means.
The space complexity of RSG is dominated by the reduction step (i.e., k-means) and is given by , where k is the number of objectives, is the size of the filling set, and N is the desired reference set size. Since typically , the complexity simplifies to .
5. Numerical Results
In this section, we show the strength of the novel approach on selected benchmark test problems. We further show—as far as possible—comparisons to related methods. See Appendix A for the definitions of the test problems CONV3, CONV3-4, and CONV4-2F.
First, we demonstrate the working principle of the RSG on selected test problems with different characteristics (number of objectives, choice of the initial set , and shape of the Pareto front). For all problems, we show all the main steps of the RSG: initial solution, component detection, filling, and the selection. For the latter, we show the obtained reference sets for different values of N to show the effect of the new method. In particular, we have used the following six test problems (refer to Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13): ZDT3 ( objectives, disconnected, and convex–concave Pareto front), DTLZ7 (, disconnected, and convex–concave PF), WFG2 (, disconnected, and convex PF, where the latter refers to each connected component), CONV3 (, connected, and convex PF), CONV3-4 (, connected, and convex PF, where one part of the PF is nearly degenerated), and CONV4-2F (, disconnected, and convex PF). Note that the starting sets for ZDT3 and DTLZ7 contain (slight) biases that were removed by the RSG. The applicability to CONV3, CONV3-4, and CONV4-2F show the universality of the RSG: in contrast to other methods that generate reference sets, the RSG does not, in principle, need any analytical information of the PF. It requires, however, a “suitable” initial solution , which is a non-trivial task and is problem-dependent. Refer to Section 4.5 for general guidelines. In the captions of Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, we describe how we obtained this set for each problem.
Figure 14 shows some numerical results of the RSG on DTLZ1 and DTLZ2 with and without the filling step. As can be seen, the candidate solutions are more evenly distributed when using the filling. Without filling, a bias can be observed on the top end of the fronts similar to uniform sampling along the Pareto set (refer to Figure 3 and Figure 4 and the related discussion).
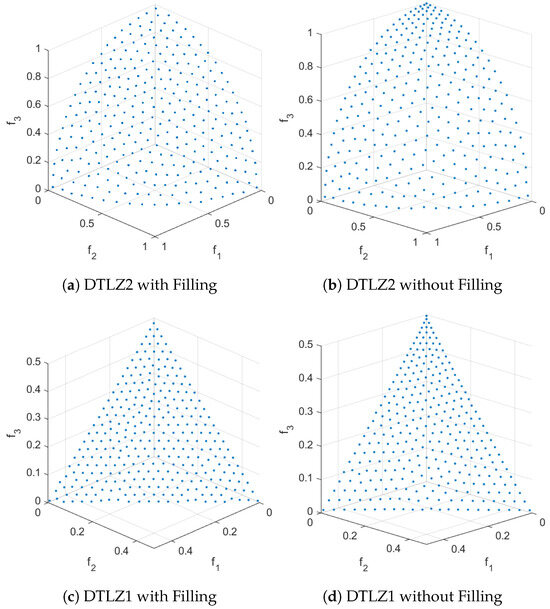
Figure 14.
Effect of the filling step shown on DTLZ2 (above) and DTLZ1 (below). The left-side references were obtained using RSG with a starting set of size 300, which was filled with points and then reduced to a reference set of points using k-means. The right-side references were obtained without filling by uniformly sampling 1,000,000 points on the Pareto set and then reducing the obtained front to using k-means. Bias can be observed on the upper part of the Pareto front in both cases without filling (right side), around for DTLZ2 and for DTLZ1.
Table 2 and Table 3 show the running times (in seconds) of the RSG on selected bi-objective and three-objective problems for different filling sizes. We used for the starting set the reference provided by PlatEMO, with a size of 100 for bi-objective problems and a problem-dependent size for three-objective problems. The size of the final reference set was fixed at 100 for bi-objective and 300 for three-objective problems. Naturally, the larger the filling size, the longer the runtime of the RSG. However, reference sizes of 100 and 300 are typically standard for comparisons, meaning that, in general, the RSG only needs to be run once per problem.

Table 2.
RSG running time (in seconds) for bi-objective problems varying the size of the filling set (). The size of was fixed at 100 for all problems, and the size of the final reference set was set to .

Table 3.
RSG running time (in seconds) for problems with objectives varying the size of the filling set (). The size of was set to 300, 1024, 1134, and 990 for DTLZ2, DTLZ7, C2_DTLZ2, and CDTLZ2, respectively. The size of the final reference set was fixed at .
Additionally, a comparison between the RSG, PlatEMO [50], pymoo, and filling step is presented in Figure 15 and Figure 16 for the WFG2, ZDT1, ZDT3, DTLZ2, Convex DTLZ2 (CDTLZ2), C2-DTLZ2, and DTLZ7 test problems. Although the reference sets provided by PlatEMO and pymoo are of high quality, they still exhibit some bias in certain bi-objective problems (such as ZDT1 and ZDT3) and especially in three-objective problems such as WFG2, and CDTLZ2. Furthermore, for problems like WFG2 and DTLZ7, the number of points in the reference sets of PlatEMO and pymoo is limited to a fixed set in contrast to the RSG, which can generate any desired number of points.
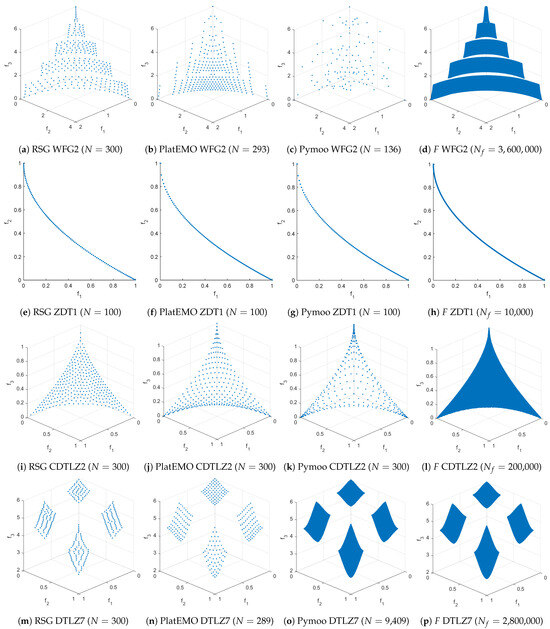
Figure 15.
The first part of the comparisons between RSG (first column), PlatEMO (second column), pymoo (third column), and the filling step F of RSG (fourth column) are shown. A reference set of size 100 was used for bi-objective problems and 300 for three-objective problems. For bi-objective problems, all methods produced exactly 100 points. However, for three-objective problems, PlatEMO and pymoo did not always yield exactly 300 points—for example, PlatEMO in WFG2 and DTLZ7 and pymoo in WFG2, DTLZ7, and IDTLZ2.
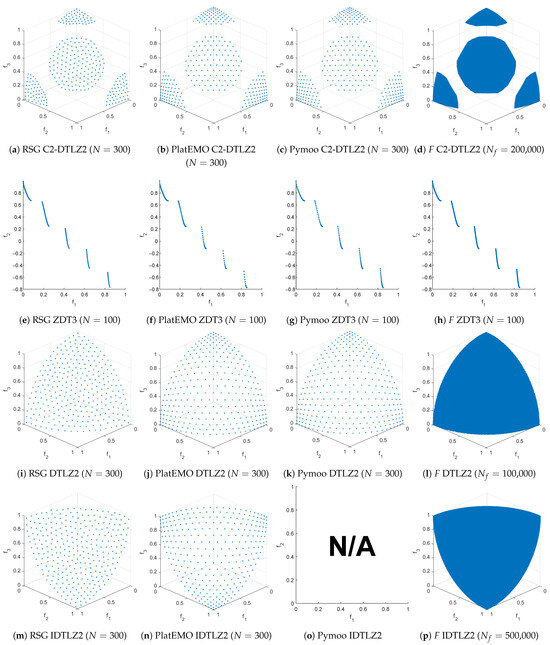
Figure 16.
The second part of the comparisons between RSG (first column), PlatEMO (second column), pymoo (third column), and the filling step F of RSG (fourth column) are shown. A reference set of size 100 was used for bi-objective problems and 300 for three-objective problems. For bi-objective problems, all methods produced exactly 100 points. However, for three-objective problems, PlatEMO and pymoo did not always yield exactly 300 points—for example, PlatEMO in WFG2 and DTLZ7 and pymoo in WFG2, DTLZ7, and IDTLZ2. Figure marked as N/A indicates that no reference set was provided.
6. Conclusions and Future Work
In this paper, we have addressed the problem of obtaining bias-free and complete finite-size approximations of the solution sets (Pareto fronts) of multi-objective optimization problems (MOPs). Such approximations are, in particular, required for the fair usage of distance-based performance indicators, which are frequently used in evolutionary multi-objective optimization (EMO). If the Pareto front approximations are biased or incomplete, the use of these performance indicators can lead to misleading or false information. To address this issue, we have proposed the Reference Set Generator (RSG). This method starts with an initial (probably biased) approximation of the Pareto front. An unbiased approximation is then computed via component detection, filling, and a reduction to the desired size. The RSG can be applied to Pareto fronts of any shape and dimension. We have finally demonstrated the strength of the novel approach on several benchmark problems.
In the future, we intend to use the RSG on the Pareto fronts of all commonly used continuous test problems. Special attention has to be paid to problems with degenerated fronts (i.e., problems where the Pareto front does locally not form an object of dimension ). In the current approach, we handled degeneracy using the Pareto Tracer (PT) to obtain a filled set and, from there, used the reduction step. For future work, we will explore if the projection can be modified to fill such sets, which may lead to a more general approach to handling degeneration.
Another important aspect is scalability. In order to apply the method to higher dimensional problems, variants have to be considered that are less costly. For example, to avoid performing a grid search, alternative parameter selection methods can be explored. Similarly, for the reduction step, a faster k-means variant or a different subset selection method could be used. A study on the effect of k-means initialization is also left as future work. Next, we stress that we have designed the RSG for Pareto front approximations. There are, however, other interesting sets of interest in the context of multi-objective optimization that may be worth investigating. This may include the entire Pareto set or locally optimal solutions, as considered in multi-objective multi-modal optimization (e.g., [38,63]) or the families of Pareto sets/fronts in the context of dynamic multi-objective optimization [64].
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
O. Schütze acknowledges support from the CONAHCYT, project CBF2023-2024-1463.
Data Availability Statement
The code and data presented in the study are openly available in GitHub at https://github.com/aerfangel/RSG (accessed on 24 April 2025). See also the website of the third author for more information about the RSG (https://neo.cinvestav.mx/Group/)(accessed on 24 April 2025).
Acknowledgments
Angel E. Rodriguez-Fernandez acknowledges support from the SECIHTI to pursue his postdoc fellowship at the CINVESTAV-IPN.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Current PF approximation | |
| ℓ | Size of , the starting PF approximation |
| N | Desired size of approximation |
| Z | RSG result: reference set of size N |
| F | Filled set |
| Size of filling | |
| i-th detected component | |
| C | Set of all detected components |
| L | Total length of 2D curve |
| Delaunay triangulation | |
| Number of triangles in | |
| T | Cleaned triangulation |
| Number of triangles in T | |
| Normal vector | |
| Projected | |
| Selected cleaning property (area/volume, largest side, or condition number) | |
| Value of property for triangle i | |
| Threshold for removing triangles | |
| Area/volume of triangle/simplex i | |
| A | Total area/volume of the triangulation |
| r | Radius of DBSCAN |
Appendix A. Function Definitions
- CONV3
- CONV3-4
- CONV4-2F
References
- Hillermeier, C. Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 135. [Google Scholar]
- Coello Coello, C.A.; Goodman, E.; Miettinen, K.; Saxena, D.; Schütze, O.; Thiele, L. Interview: Kalyanmoy Deb Talks about Formation, Development and Challenges of the EMO Community, Important Positions in His Career, and Issues Faced Getting His Works Published. Math. Comput. Appl. 2023, 28, 34. [Google Scholar] [CrossRef]
- Veldhuizen, D.A.V. Multiobjective Evolutionary Algorithms: Classifications, Analyses, and New Innovations; Technical Report; Air Force Institute of Technology: Dayton, OH, USA, 1999. [Google Scholar]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Grunert, V.D.F. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Cruz, N.C. Solving Multiobjective Optimization Problems Using an Artificial Immune System. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- Schütze, O.; Esquivel, X.; Lara, A.; Coello Coello, C.A. Using the averaged Hausdorff distance as a performance measure in evolutionary multi-objective optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Masuda, H.; Nojima, Y. A Study on Performance Evaluation Ability of a Modified Inverted Generational Distance Indicator. In Proceedings of the GECCO’15: Genetic and Evolutionary Computation Conference, Madrid, Spain, 11–15 July 2015; pp. 695–702. [Google Scholar] [CrossRef]
- Bogoya, J.M.; Vargas, A.; Cuate, O.; Schütze, O. A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets. Math. Comput. Appl. 2018, 23, 51. [Google Scholar] [CrossRef]
- Deb, K.; Ehrgott, M. On Generalized Dominance Structures for Multi-Objective Optimization. Math. Comput. Appl. 2023, 28, 100. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Sameer, S.A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evol. Comput. IEEE Trans. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization. In Proceedings of the Evolutionary Methods for Design, Optimisation and Control with Application to Industrial Problems (EUROGEN 2001), Athens, Greece, 19–21 September 2002; Giannakoglou, K., Tsahalis, D., Periaux, J., Papailiou, K., Eds.; International Center for Numerical Methods in Engineering (CIMNE): Barcelona, Spain, 2002; pp. 95–100. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. An overview of evolutionary algorithms in multiobjective optimization. Evol. Comput. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto Archived Evolution Strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multi-objective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Zuiani, F.; Vasile, M. Multi Agent Collaborative Search based on Tchebycheff decomposition. Comput. Optim. Appl. 2013, 56, 189–208. [Google Scholar] [CrossRef]
- Moubayed, N.A.; Petrovski, A.; McCall, J. (DMOPSO)-M-2: MOPSO Based on Decomposition and Dominance with Archiving Using Crowding Distance in Objective and Solution Spaces. Evol. Comput. 2014, 22, 47–77. [Google Scholar] [CrossRef]
- Beume, N.; Naujoks, B.; Emmerich, M.T.M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Bader, J. SPAM: Set Preference Algorithm for multiobjective optimization. In Proceedings of the Parallel Problem Solving From Nature PPSN X, Dortmund, Germany, 13–17 September 2008; pp. 847–858. [Google Scholar]
- Wagner, T.; Trautmann, H. Integration of Preferences in Hypervolume-based multiobjective evolutionary algorithms by means of desirability functions. IEEE Trans. Evol. Comput. 2010, 14, 688–701. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic algorithms for multiobjective optimization: Formulation, discussion, and generalization. In Proceedings of the 5-th International Conference on Genetic Algorithms, Champaign, IL, USA, 17–21 July 1993; pp. 416–423. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multiobjective optimization. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Computation, Orlando, FL, USA, 27–29 June 1994; IEEE Press: Piscataway, NJ, USA, 1994; pp. 82–87. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Rudolph, G. Finite Markov Chain results in evolutionary computation: A Tour d’Horizon. Fundam. Inform. 1998, 35, 67–89. [Google Scholar] [CrossRef]
- Rudolph, G. On a multi-objective evolutionary algorithm and its convergence to the Pareto set. In Proceedings of the IEEE International Conference on Evolutionary Computation (ICEC 1998), Anchorage, AK, USA, 4–9 May 1998; IEEE Press: Piscataway, NJ, USA, 1998; pp. 511–516. [Google Scholar]
- Rudolph, G.; Agapie, A. Convergence Properties of Some Multi-Objective Evolutionary Algorithms. In Proceedings of the Evolutionary Computation (CEC), La Jolla, CA, USA, 16–19 July 2000; IEEE Press: Piscataway, NJ, USA, 2000. [Google Scholar]
- Rudolph, G. Evolutionary Search under Partially Ordered Fitness Sets. In Proceedings of the International NAISO Congress on Information Science Innovations (ISI 2001), Dubai, United Arab Emirates, 17–21 March 2001; ICSC Academic Press: Sliedrecht, The Netherlands, 2001; pp. 818–822. [Google Scholar]
- Hanne, T. On the convergence of multiobjective evolutionary algorithms. Eur. J. Oper. Res. 1999, 117, 553–564. [Google Scholar] [CrossRef]
- Hanne, T. Global multiobjective optimization with evolutionary algorithms: Selection mechanisms and mutation control. In Proceedings of the First International Conference on Evolutionary Multi-Criterion Optimization, EMO 2001, Zurich, Switzerland, 7–9 March 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 197–212. [Google Scholar]
- Hanne, T. A multiobjective evolutionary algorithm for approximating the efficient set. Eur. J. Oper. Res. 2007, 176, 1723–1734. [Google Scholar] [CrossRef]
- Hanne, T. A Primal-Dual Multiobjective Evolutionary Algorithm for Approximating the Efficient Set. In Proceedings of the Evolutionary Computation (CEC), Singapore, 25–28 September 2007; IEEE Press: Piscataway, NJ, USA, 2007; pp. 3127–3134. [Google Scholar]
- Brockhoff, D.; Tran, T.D.; Hansen, N. Benchmarking numerical multiobjective optimizers revisited. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 639–646. [Google Scholar]
- Wang, R.; Zhou, Z.; Ishibuchi, H.; Liao, T.; Zhang, T. Localized weighted sum method for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 22, 3–18. [Google Scholar] [CrossRef]
- Pang, L.M.; Ishibuchi, H.; Shang, K. Algorithm Configurations of MOEA/D with an Unbounded External Archive. arXiv 2020, arXiv:2007.13352. [Google Scholar]
- Nan, Y.; Shu, T.; Ishibuchi, H. Effects of External Archives on the Performance of Multi-Objective Evolutionary Algorithms on Real-World Problems. In Proceedings of the 2023 IEEE Congress on Evolutionary Computation (CEC), Chicago, IL, USA, 1–5 July 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, A.E.; Schäpermeier, L.; Hernández, C.; Kerschke, P.; Trautmann, H.; Schütze, O. Finding ϵ-Locally Optimal Solutions for Multi-Objective Multimodal Optimization. IEEE Trans. Evol. Comput. 2024. [Google Scholar] [CrossRef]
- Schütze, O.; Rodriguez-Fernandez, A.E.; Segura, C.; Hernández, C. Finding the Set of Nearly Optimal Solutions of a Multi-Objective Optimization Problem. IEEE Trans. Evol. Comput. 2024, 29, 145–157. [Google Scholar] [CrossRef]
- Nan, Y.; Ishibuchi, H.; Pang, L.M. Small Population Size is Enough in Many Cases with External Archives. In Evolutionary Multi-Criterion Optimization, Proceedings of the 13th International Conference, EMO 2025, Canberra, ACT, Australia, 4–7 March 2025; Singh, H., Ray, T., Knowles, J., Li, X., Branke, J., Wang, B., Oyama, A., Eds.; Springer Nature: Singapore, 2025; pp. 99–113. [Google Scholar]
- Loridan, P. ϵ-Solutions in Vector Minimization Problems. J. Optim. Theory Appl. 1984, 42, 265–276. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef] [PubMed]
- Schütze, O.; Hernández, C. Archiving Strategies for Evolutionary Multi-Objective Optimization Algorithms; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Knowles, J.D.; Corne, D.W. Properties of an adaptive archiving algorithm for storing nondominated vectors. IEEE Trans. Evol. Comput. 2003, 7, 100–116. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Bounded Pareto archiving: Theory and practice. In Metaheuristics for Multiobjective Optimisation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 39–64. [Google Scholar]
- Knowles, J.D.; Corne, D.W.; Fleischer, M. Bounded archiving using the Lebesgue measure. In Proceedings of the IEEE Congress on Evolutionary Computation, Canberra, ACT, Australia, 8–12 December 2003; IEEE Press: IEEE, NJ, USA, 2003; pp. 2490–2497. [Google Scholar]
- López-Ibáñez, M.; Knowles, J.D.; Laumanns, M. On Sequential Online Archiving of Objective Vectors. In Evolutionary Multi-Criterion Optimization (EMO 2011), Proceedings of the 6th International Conference, EMO 2011, Ouro Preto, Brazil, 5–8 April 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 46–60. [Google Scholar]
- Castellanos, C.I.H.; Schütze, O. A Bounded Archiver for Hausdorff Approximations of the Pareto Front for Multi-Objective Evolutionary Algorithms. Math. Comput. Appl. 2022, 27, 48. [Google Scholar] [CrossRef]
- Laumanns, M.; Zenklusen, R. Stochastic convergence of random search methods to fixed size Pareto front approximations. Eur. J. Oper. Res. 2011, 213, 414–421. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Wang, H.; Rodriguez-Fernandez, A.E.; Uribe, L.; Deutz, A.; Cortés-Piña, O.; Schütze, O. A Newton Method for Hausdorff Approximations of the Pareto Front Within Multi-objective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2024. [Google Scholar] [CrossRef]
- Rudolph, G.; Schütze, O.; Grimme, C.; Domínguez-Medina, C.; Trautmann, H. Optimal averaged Hausdorff archives for bi-objective problems: Theoretical and numerical results. Comput. Optim. Appl. 2016, 64, 589–618. [Google Scholar] [CrossRef]
- Dilettoso, E.; Rizzo, S.A.; Salerno, N. A Weakly Pareto Compliant Quality Indicator. Math. Comput. Appl. 2017, 22, 25. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD, Portland, OR, USA, 2–4 August 1996; Simoudis, S., Han, J., Fayyad, U., Eds.; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Ben-David, S.; Ackerman, M. Measures of Clustering Quality: A Working Set of Axioms for Clustering. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; Koller, D., Schuurmans, D., Bengio, Y., Bottou, L., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2008; Volume 21. [Google Scholar]
- Delaunay, B. Sur la sphère vide. Bull. L’AcadeÉmie Des Sci. L’URSS Cl. Des Sci. MathÉmatiques 1934, 1934, 793–800. [Google Scholar]
- Smith, N.A.; Tromble, R.W. Sampling Uniformly from the Unit Simplex; Johns Hopkins University: Baltimore, MD, USA, 2004. [Google Scholar]
- Uribe, L.; Bogoya, J.M.; Vargas, A.; Lara, A.; Rudolph, G.; Schütze, O. A Set Based Newton Method for the Averaged Hausdorff Distance for Multi-Objective Reference Set Problems. Mathematics 2020, 8, 1822. [Google Scholar] [CrossRef]
- Chen, W.; Ishibuchi, H.; Shang, K. Clustering-Based Subset Selection in Evolutionary Multiobjective Optimization. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 468–475. [Google Scholar] [CrossRef]
- Martín, A.; Schütze, O. Pareto Tracer: A predictor-corrector method for multi-objective optimization problems. Eng. Optim. 2018, 50, 516–536. [Google Scholar] [CrossRef]
- Schütze, O.; Cuate, O. The Pareto Tracer for the treatment of degenerated multi-objective optimization problems. Eng. Optim. 2024, 57, 261–286. [Google Scholar] [CrossRef]
- Li, W.; Yao, X.; Zhang, T.; Wang, R.; Wang, L. Hierarchy ranking method for multimodal multiobjective optimization with local Pareto fronts. IEEE Trans. Evol. Comput. 2022, 27, 98–110. [Google Scholar] [CrossRef]
- Cai, X.; Wu, L.; Zhao, T.; Wu, D.; Zhang, W.; Chen, J. Dynamic adaptive multi-objective optimization algorithm based on type detection. Inf. Sci. 2024, 654, 119867. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).