Bayesian Tapered Narrowband Least Squares for Fractional Cointegration Testing in Panel Data
Abstract
1. Introduction
2. Related Work
3. Bayesian Tapered Narrowband Least Squares
- -
- and are independent innovation processes.
- -
- and are memory parameters satisfying under fractional cointegration.
3.1. Likelihood Construction
- -
- is the tapered spectral density of .
- -
- is the error spectral density.
3.2. Hierarchical Prior Specification
3.2.1. Unit-Specific Cointegrating Vectors
3.2.2. Memory Parameters
3.2.3. Tapering Hyperparameters
3.3. Posterior Computation
Gibbs–Metropolis–Hastings Algorithm
- Proposal Distribution:
- Acceptance Ratio:
- A1 (Stationarity): The memory parameters satisfy , ensuring the process is nonstationary but mean-reverting.
- A2 (Spectral Smoothness): The tapered spectral density is twice continuously differentiable with respect to ν.
- A3 (Prior Dominance): The hyperparameters satisfy , , and , ensuring that the prior does not asymptotically dominate the likelihood.
- A4 (Ergodicity): For each unit i, the process is ergodic, with cross-sectional and temporal independence.
- Within-group variance: ,
- Between-group variance: .
- BTNBLS:
- TNBLS:
- 1
- Bias Reduction: Hierarchical shrinkage accelerates convergence to .
- 2
- Variance Reduction: Pooling information across units tightens posterior uncertainty.
- 3
- MSE Dominance: Squared bias decays faster than variance.
- 4
- Coverage: Credible intervals align with frequentist confidence intervals asymptotically. These properties make BTNBLS indispensable for fractional cointegration analysis in heterogeneous panels.
4. Bayesian Chen–Hurvich Panel Fractional Cointegration Test
- Likelihood: For each unit i, the tapered periodogram follows:where denotes the complex normal distribution.
- Priors:
- Tapering: The taper order p is fixed or assigned a categorical prior.
5. Simulation Study
- Finite-sample properties of cointegrating parameter estimators.
- Empirical Type 1 error and power of the Bayesian (), Modified (), and Original () Chen–Hurvich tests.
5.1. Finite-Sample Properties of Long-Memory Parameter Estimators
5.1.1. Simulation Design
- Simulated panel data with units and time periods, yielding total sample sizes . This aligns with empirical studies analyzing sectoral or country-level panels [34].
5.1.2. Bayesian MCMC Parameters
- Weakly Informative Priors for Hierarchical Parameters:
- –
- (prior variance of ): A scale of 1 balances flexibility and shrinkage, avoiding overfitting in panels with –50 units. Sensitivity analyses show robustness across .
- –
- , (shape/rate for ): These values induce a weakly informative prior with mean and variance , favoring moderate shrinkage. This aligns with Polson and Scott’s [41] recommendations for variance parameters in hierarchical models.
- Moderately Informative Priors for Memory Parameters:
- –
- (prior SD for ): A standard deviation of 0.1 reflects plausible ranges for long-memory parameters () in macroeconomic series [40]. Sensitivity checks confirm stability for .
- Convergence-Stabilizing Hyperparameters:
- –
- (scaling factor for ): A unit scale standardizes the identifiability constraint under , ensuring MCMC proposals remain in the stationary distribution [42].
- –
- : Directly enforces the theoretical requirement under , with to prevent boundary issues.
5.1.3. Bootstrap Procedure for Finite-Sample Metrics
- Resample Units: Draw units with replacement.
- Recompute Estimates:
- Metrics:
- Bias:
- Variance:
- MSE:
- Coverage Probability:where and is the standard normal quantile.
5.2. Empirical Type 1 Error and Power of Hypothesis Tests
Test Design
- Null Hypothesis (): .
- Alternative Hypothesis (): .
- Data Structure: , , .
5.3. Bootstrap-Based Test Metrics
- Type 1 Error Rate:
- Power:
5.4. Finite Sample Properties Simulation Results
5.5. Empirical Type I Error and Power Simulation Results
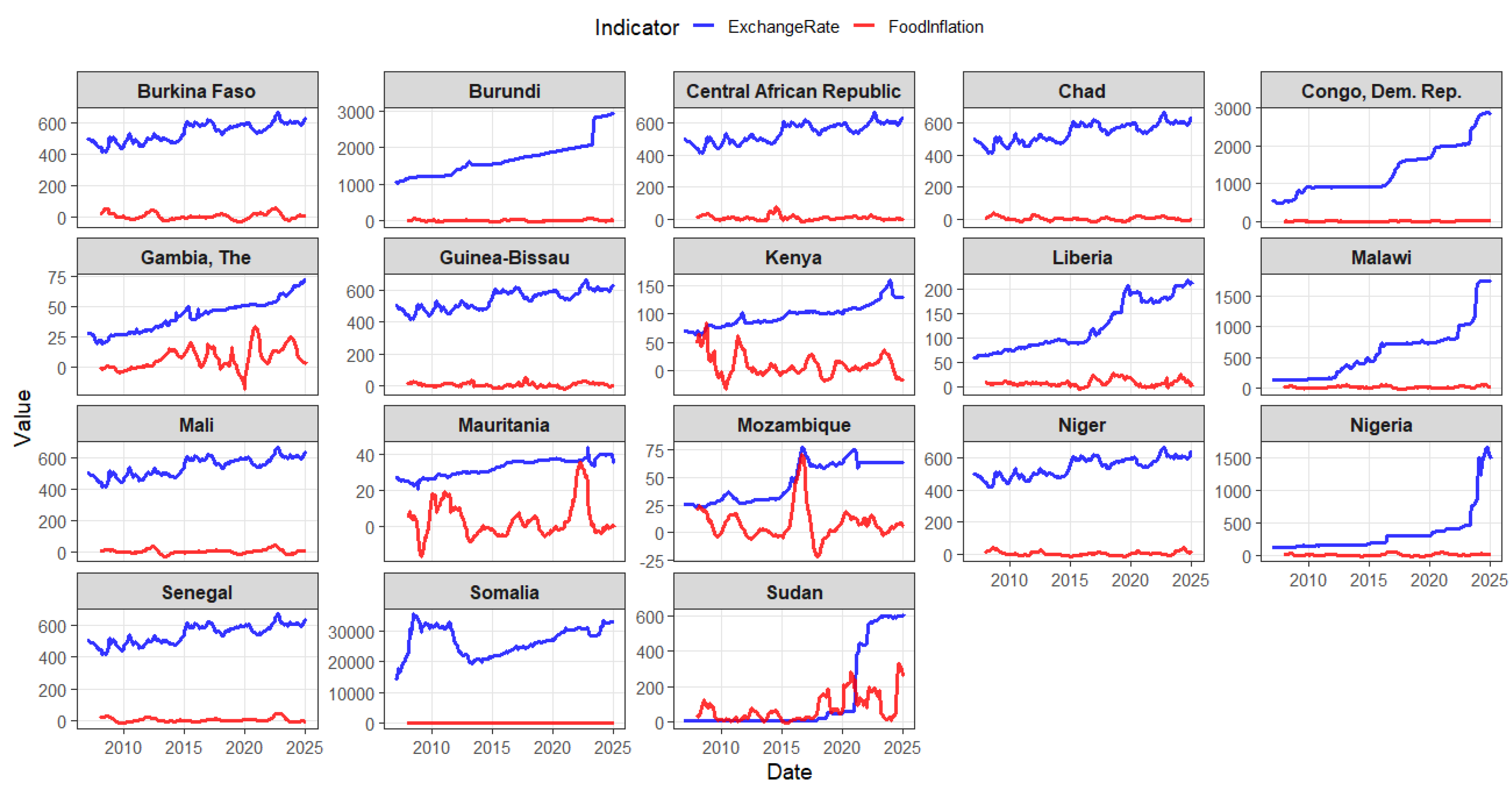
6. Testing Purchasing Power Parity in 18 Fragile Sub-Saharan Africa Countries
6.1. Data Description and Countries
6.2. PPP Fractional Cointegration Model
- -
- : USD exchange rate for country i at month t.
- -
- : Food price ratio for country i at month t.
- -
- : Country-specific fixed effects, capturing structural heterogeneity (e.g., trade policies).
- -
- : Fractional differencing operators with memory parameters (persistence of food price) and (exchange rate adjustment speed).
- -
- : Independent Gaussian errors with zero mean and finite variance.
6.3. Hypotheses
- -
- : No fractional cointegration (). Food price shocks permanently disrupt exchange rates, violating PPP.
- -
- : Fractional cointegration (). Exchange rates adjust to correct transient deviations from PPP caused by food inflation.
6.4. Estimation
- Bandwidth Selection: A bandwidth parameter defines the spectral window , optimizing the bias-variance trade-off in fractional parameter estimation [47].
- Memory Parameters: and are estimated via the proposed Bayesian tapered narrowband least squares (BTNBLS), which mitigates spectral leakage by downweighting endpoint distortions in Fourier transforms as well as parameter uncertainty.
7. Discussion of Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johansen, S.; Nielsen, M.Ø. Likelihood Inference for a Fractionally Cointegrated Vector Autoregressive Model. Econometrica 2012, 80, 2667–2732. [Google Scholar] [CrossRef]
- Khodamoradi, T.; Salahi, M.; Najafi, A.R. A Note on CCMV Portfolio Optimization Model with Short Selling and Risk-neutral Interest Rate. Stat. Optim. Inf. Comput. 2020, 8, 740–748. [Google Scholar] [CrossRef]
- Olaniran, S.F.; Ismail, M.T. A Comparative Analysis of Semiparametric Tests for Fractional Cointegration in Panel Data Models. Austrian J. Stat. 2022, 51, 96–119. [Google Scholar] [CrossRef]
- Olaniran, S.F.; Olaniran, O.R.; Allohibi, J.; Alharbi, A.A.; Ismail, M.T. A Generalized Residual-Based Test for Fractional Cointegration in Panel Data with Fixed Effects. Mathematics 2024, 12, 1172. [Google Scholar] [CrossRef]
- Olaniran, S.F.; Olaniran, O.R.; Allohibi, J.; Alharbi, A.A. A Novel Approach for Testing Fractional Cointegration in Panel Data Models with Fixed Effects. Fractal Fract. 2024, 8, 527. [Google Scholar] [CrossRef]
- Robinson, P.M. Diagnostic Testing for Cointegration. J. Econom. 2008, 143, 206–225. [Google Scholar] [CrossRef]
- Souza, I.V.M.; Reisen, V.A.; Franco, G.d.C.; Bondon, P. The Estimation and Testing of the Cointegration Order based on the Frequency Domain. J. Bus. Econ. Stat. 2018, 36, 695–704. [Google Scholar] [CrossRef]
- Leschinski, C.; Voges, M.; Sibbertsen, P. A Comparison of Semiparametric Tests for Fractional Cointegration. Stat. Pap. 2020, 62, 1997–2030. [Google Scholar] [CrossRef]
- Chen, W.W.; Hurvich, C.M. Semiparametric Estimation of Fractional Cointegrating Subspaces. Ann. Stat. 2006, 34, 2939–2979. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W. Co-integration and Error correction: Representation, Estimation, and Testing. Econom. J. Econom. Soc. 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Gujarati, D.N. Basic Econometrics, 4th ed.; McGraw-Hill: Singapore, 2003. [Google Scholar]
- Robinson, P.M. Efficient tests of nonstationary hypotheses. J. Am. Stat. Assoc. 1994, 89, 1420–1437. [Google Scholar] [CrossRef]
- Marinucci, D.; Robinson, P.M. Narrow-band analysis of nonstationary processes. Ann. Stat. 2001, 29, 947–986. [Google Scholar] [CrossRef]
- Chen, W.W.; Hurvich, C.M. Estimating fractional cointegration in the presence of polynomial trends. J. Econom. 2003, 117, 95–121. [Google Scholar] [CrossRef]
- Ergemen, Y.E.; Velasco, C. Estimation of Fractionally Integrated Panels with Fixed Effects and Cross-section Dependence. J. Econom. 2017, 196, 248–258. [Google Scholar] [CrossRef]
- Monge, M.; Lazcano, A.; Infante, J. Monetary policy and inflation rate in the behavior of consumer sentiment in the us. A fractional integration and cointegration analysis. Res. Econ. 2024, 78, 100981. [Google Scholar] [CrossRef]
- Malmierca-Ordoqui, M.; Gil-Alana, L.A.; Bermejo, L. Private and public debt convergence: A fractional cointegration approach. Empirica 2024, 51, 161–183. [Google Scholar] [CrossRef]
- Diakodimitriou, D.; Papageorgiou, T.; Tsioutsios, A. Fractional Long-Run Equilibrium of Education Expenditure and Economic Growth: The Case of the USA. J. Knowl. Econ. 2025, 4, 1–12. [Google Scholar] [CrossRef]
- Koop, G.; Strachan, R.; Van Dijk, H.; Villani, M. Bayesian approaches to cointegration. In The Palgrave Handbook of Theoretical Econometrics; Palgrave Macmillan Ltd.: London, UK, 2006; pp. 871–898. ISBN 1403941556. [Google Scholar]
- Koop, G.; Leon-Gonzalez, R.; Strachan, R. Bayesian inference in a cointegrating panel data model. In Bayesian Econometrics; Emerald Group Publishing Limited: Leeds, UK, 2008; Volume 23, pp. 433–469. [Google Scholar]
- Shaby, B.; Ruppert, D. Tapered covariance: Bayesian estimation and asymptotics. J. Comput. Graph. Stat. 2012, 21, 433–452. [Google Scholar] [CrossRef]
- Selvaraj, V.; Vairavasundaram, I.; Pranav, D.O.; Shukla, S.; Ashok, B. Implementation of Discrete Wavelet combined Bayesian-optimized Gaussian Process Regression based SOC prediction of EV battery. IEEE Access 2024, 12, 184052–184070. [Google Scholar] [CrossRef]
- Caporale, G.M.; Gil-Alana, L.A. Fractional cointegration and tests of present value models. Rev. Financ. Econ. 2004, 13, 245–258. [Google Scholar] [CrossRef]
- Caporale, G.M.; Gil-Alana, L.A. Fractional Integration and Cointegration in US Financial Time Series Data. Empir. Econ. 2014, 47, 1389–1410. [Google Scholar] [CrossRef]
- Wang, B.; Wang, M.; Chan, N.H. Residual-Based Test for Fractional Cointegration. Econ. Lett. 2015, 126, 43–46. [Google Scholar] [CrossRef]
- Olayeni, R.O.; Tiwari, A.K.; Wohar, M.E. Fractional frequency flexible Fourier form (FFFFF) for panel cointegration test. Appl. Econ. Lett. 2021, 28, 482–486. [Google Scholar] [CrossRef]
- Pata, U.K.; Yilanci, V. Financial development, globalization and ecological footprint in G7: Further evidence from threshold cointegration and fractional frequency causality tests. Environ. Ecol. Stat. 2020, 27, 803–825. [Google Scholar] [CrossRef]
- Demetrescu, M.; Kusin, V.; Salish, N. Testing for no cointegration in vector autoregressions with estimated degree of fractional integration. Econ. Model. 2022, 108, 105694. [Google Scholar] [CrossRef]
- Caporale, G.M.; Gil-Alana, L.A.; You, K. Stock market linkages between the ASEAN countries, China and the US: A fractional integration/cointegration approach. Emerging Mark. Financ. Trade 2022, 58, 1502–1514. [Google Scholar] [CrossRef]
- Uche, E.; Yağiş, O.; Al-Faryan, M.A.S. Exploring Saudi Arabia’s 2060 net zero-emission paths via fractional frequency Fourier procedures. The imperatives of resource efficiency, energy efficiency, and digitalization. Int. J. Green Energy 2025, 22, 168–182. [Google Scholar] [CrossRef]
- Ergemen, Y.E. System estimation of panel data models under long-range dependence. J. Bus. Econ. Stat. 2019, 37, 13–26. [Google Scholar] [CrossRef]
- Panov, M.; Spokoiny, V. Finite sample Bernstein–von Mises theorem for semiparametric problems. Bayesian Anal. 2015, 10, 665–710. [Google Scholar] [CrossRef]
- Delbaen, F. A remark on Slutsky’s theorem. In Proceedings of the Séminaire de Probabilités XXXII; Springer: Berlin/Heidelberg, Germany, 1998; pp. 313–315. [Google Scholar]
- Pesaran, M.H. Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 2006, 74, 967–1012. [Google Scholar] [CrossRef]
- Johansen, S.; Nielsen, M.Ø. Nonstationary Cointegration in the Fractionally Cointegrated VAR Model. J. Time Ser. Anal. 2019, 40, 519–543. [Google Scholar] [CrossRef]
- Hsiao, C. Analysis of Panel Data; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Baltagi, B.H.; Baltagi, B.H. Econometric Analysis of Panel Data; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4. [Google Scholar]
- Baillie, R.T. Long memory processes and fractional integration in econometrics. J. Econom. 1996, 73, 5–59. [Google Scholar] [CrossRef]
- Gelman, A.; Shalizi, C.R. Philosophy and the practice of Bayesian statistics. Br. J. Math. Stat. Psychol. 2013, 66, 8–38. [Google Scholar] [CrossRef]
- Koop, G.; Osiewalski, J.; Steel, M.F. Bayesian efficiency analysis through individual effects: Hospital cost frontiers. J. Econom. 1997, 76, 77–105. [Google Scholar] [CrossRef]
- Polson, N.G.; Scott, J.G. Good, great, or lucky? Screening for firms with sustained superior performance using heavy-tailed priors. Ann. Appl. Stat. 2012, 161–185. [Google Scholar] [CrossRef]
- Hoff, P.D. A First Course in Bayesian Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2009; Volume 580. [Google Scholar]
- Geweke, J. Evaluating the accuracy of sampling-based approaches to the calculations of posterior moments. Bayesian Stat. 1992, 4, 641–649. [Google Scholar]
- Kapetanios, G. A bootstrap procedure for panel data sets with many cross-sectional units. Econom. J. 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Development Data Group. Monthly food price estimates by product and market. WLD_2021_RTFP_v02_M; World Bank Microdata Library: Washington, DC, USA, 2021; Version 2025/03/11; Available online: https://microdata.worldbank.org/index.php/catalog/4483 (accessed on 11 March 2025).
- Algieri, B.; Kornher, L.; von Braun, J. The Changing Drivers of Food Inflation–Macroeconomics, Inflation, and War. 2024. Available online: https://ageconsearch.umn.edu/record/340561 (accessed on 11 March 2025).
- Robinson, P.M.; Yajima, Y. Determination of Cointegrating Rank in Fractional Systems. J. Econom. 2002, 106, 217–241. [Google Scholar] [CrossRef]
- Olaniran, S.F.; Ismail, M.T. Testing absolute purchasing power parity in West Africa using fractional cointegration panel approach. Sci. Afr. 2023, 20, e01615. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Beltrao, K.I. Asymptotics for the low-frequency ordinates of the periodogram of a long-memory time series. J. Time Ser. Anal. 1993, 14, 455–472. [Google Scholar] [CrossRef]


| (%) | (%) | (%) | ||
|---|---|---|---|---|
| 0.5 | 0.05 | +1.3 | +2.1 | +1.8 |
| 0.5 | 0.10 | +1.5 | +3.8 | +2.4 |
| 0.5 | 0.20 | +2.9 | +4.7 | +3.1 |
| 1.0 | 0.05 | −0.2 | +0.7 | −0.4 |
| 1.0 | 0.10 | Baseline | Baseline | Baseline |
| 1.0 | 0.20 | +1.1 | +2.3 | +1.6 |
| 2.0 | 0.05 | +3.4 | +1.9 | +2.8 |
| 2.0 | 0.10 | +4.1 | +3.3 | +3.5 |
| 2.0 | 0.20 | +4.9 | +4.2 | +4.6 |
| Under | Under | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimator | Coverage | Coverage | |||||||||
| OLS | 1.006 | 0.006 | 0.016 | 0.016 | 0.94 | 1.431 | 0.431 | 0.029 | 0.215 | 0.87 | |
| NBLS | 1.175 | 0.175 | 1.496 | 1.526 | 0.88 | 1.692 | 0.692 | 0.991 | 1.469 | 0.89 | |
| TNBLS | 1.167 | 0.167 | 1.684 | 1.712 | 0.85 | 1.741 | 0.741 | 1.137 | 1.686 | 0.89 | |
| BTNBLS | 1.074 | 0.074 | 0.017 | 0.023 | 0.93 | 1.041 | 0.041 | 0.025 | 0.027 | 0.94 | |
| OLS | 1.369 | 0.369 | 0.018 | 0.154 | 0.92 | 1.624 | 0.624 | 0.031 | 0.420 | 0.80 | |
| NBLS | 1.265 | 0.265 | 1.648 | 1.719 | 0.85 | 1.855 | 0.855 | 1.061 | 1.791 | 0.90 | |
| TNBLS | 1.292 | 0.292 | 1.924 | 2.010 | 0.82 | 1.929 | 0.929 | 1.269 | 2.132 | 0.87 | |
| BTNBLS | 1.199 | 0.199 | 0.019 | 0.059 | 0.93 | 1.103 | 0.103 | 0.028 | 0.038 | 0.91 | |
| OLS | 1.554 | 0.554 | 0.018 | 0.325 | 0.88 | 1.817 | 0.817 | 0.033 | 0.700 | 0.01 | |
| NBLS | 1.294 | 0.294 | 1.697 | 1.783 | 0.85 | 1.987 | 0.987 | 1.133 | 2.107 | 0.85 | |
| TNBLS | 1.341 | 0.341 | 2.029 | 2.146 | 0.82 | 2.094 | 1.094 | 1.419 | 2.616 | 0.87 | |
| BTNBLS | 1.229 | 0.229 | 0.020 | 0.072 | 0.92 | 1.138 | 0.138 | 0.031 | 0.050 | 0.88 | |
| OLS | 1.741 | 0.741 | 0.019 | 0.569 | 0.85 | 1.955 | 0.955 | 0.035 | 0.946 | 0.00 | |
| NBLS | 1.290 | 0.290 | 1.707 | 1.791 | 0.85 | 2.007 | 1.007 | 1.165 | 2.179 | 0.85 | |
| TNBLS | 1.360 | 0.360 | 2.106 | 2.236 | 0.82 | 2.151 | 1.151 | 1.526 | 2.850 | 0.85 | |
| BTNBLS | 1.256 | 0.256 | 0.021 | 0.087 | 0.92 | 1.161 | 0.161 | 0.038 | 0.064 | 0.87 | |
| Method/ | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.02 | 0.01 | 0.07 | 0.06 | 0.05 | 0.08 | 0.06 | 0.11 | |||
| 0.6 | 0.02 | 0.09 | 0.11 | 0.02 | 0.06 | 0.09 | 0.03 | 0.09 | 0.12 | ||
| 0.27 | 0.48 | 0.63 | 0.40 | 0.65 | 0.74 | 0.06 | 0.25 | 0.35 | |||
| 0.03 | 0.02 | 0.01 | 0.06 | 0.06 | 0.05 | 0.07 | 0.09 | 0.11 | |||
| 0.8 | 0.02 | 0.06 | 0.13 | 0.02 | 0.08 | 0.10 | 0.07 | 0.11 | 0.14 | ||
| 0.07 | 0.14 | 0.25 | 0.03 | 0.15 | 0.26 | 0.02 | 0.08 | 0.11 | |||
| 0.01 | 0.01 | 0.01 | 0.05 | 0.05 | 0.05 | 0.09 | 0.09 | 0.10 | |||
| 1.0 | 0.01 | 0.02 | 0.05 | 0.01 | 0.04 | 0.05 | 0.00 | 0.03 | 0.07 | ||
| 0.01 | 0.05 | 0.07 | 0.00 | 0.01 | 0.04 | 0.00 | 0.03 | 0.08 | |||
| 0.01 | 0.02 | 0.01 | 0.06 | 0.06 | 0.06 | 0.11 | 0.10 | 0.10 | |||
| 1.2 | 0.00 | 0.01 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 0.00 | 0.01 | 0.03 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.03 | |||
| 0.02 | 0.01 | 0.01 | 0.07 | 0.06 | 0.05 | 0.10 | 0.09 | 0.10 | |||
| 0.6 | 0.01 | 0.09 | 0.11 | 0.03 | 0.06 | 0.07 | 0.04 | 0.08 | 0.11 | ||
| 0.20 | 0.44 | 0.55 | 0.18 | 0.41 | 0.54 | 0.00 | 0.00 | 0.01 | |||
| 0.03 | 0.02 | 0.02 | 0.08 | 0.06 | 0.06 | 0.09 | 0.09 | 0.10 | |||
| 0.8 | 0.01 | 0.05 | 0.11 | 0.02 | 0.05 | 0.09 | 0.05 | 0.09 | 0.14 | ||
| 0.06 | 0.13 | 0.19 | 0.03 | 0.08 | 0.13 | 0.00 | 0.01 | 0.04 | |||
| 0.01 | 0.02 | 0.01 | 0.08 | 0.07 | 0.06 | 0.10 | 0.11 | 0.11 | |||
| 1.0 | 0.00 | 0.02 | 0.04 | 0.01 | 0.02 | 0.04 | 0.00 | 0.03 | 0.06 | ||
| 0.02 | 0.05 | 0.07 | 0.00 | 0.00 | 0.02 | 0.01 | 0.02 | 0.08 | |||
| 0.01 | 0.02 | 0.01 | 0.05 | 0.05 | 0.05 | 0.08 | 0.09 | 0.10 | |||
| 1.2 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 0.00 | 0.01 | 0.04 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.03 | |||
| 0.01 | 0.01 | 0.01 | 0.09 | 0.06 | 0.05 | 0.09 | 0.09 | 0.11 | |||
| 0.6 | 0.01 | 0.10 | 0.12 | 0.03 | 0.06 | 0.07 | 0.04 | 0.07 | 0.10 | ||
| 0.17 | 0.37 | 0.45 | 0.09 | 0.21 | 0.32 | 0.00 | 0.00 | 0.00 | |||
| 0.01 | 0.02 | 0.01 | 0.04 | 0.05 | 0.05 | 0.09 | 0.09 | 0.12 | |||
| 0.8 | 0.01 | 0.05 | 0.11 | 0.03 | 0.05 | 0.06 | 0.05 | 0.08 | 0.12 | ||
| 0.01 | 0.12 | 0.16 | 0.02 | 0.05 | 0.07 | 0.00 | 0.00 | 0.00 | |||
| 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.11 | 0.12 | 0.11 | |||
| 1.0 | 0.00 | 0.02 | 0.04 | 0.01 | 0.02 | 0.04 | 0.00 | 0.03 | 0.06 | ||
| 0.02 | 0.03 | 0.08 | 0.00 | 0.01 | 0.02 | 0.01 | 0.04 | 0.08 | |||
| 0.01 | 0.01 | 0.01 | 0.04 | 0.05 | 0.05 | 0.11 | 0.12 | 0.11 | |||
| 1.2 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 0.01 | 0.03 | 0.06 | 0.00 | 0.01 | 0.05 | 0.02 | 0.06 | 0.09 | |||
| Method/T | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.96 | 0.96 | 0.98 | 0.97 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | ||
| 0.30 | 0.68 | 0.70 | 0.63 | 0.77 | 0.82 | 0.74 | 0.84 | 0.85 | |||
| 0.42 | 0.63 | 0.65 | 0.52 | 0.63 | 0.68 | 0.59 | 0.63 | 0.68 | |||
| 0.4 | 0.96 | 0.96 | 0.98 | 0.97 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | ||
| 0.31 | 0.61 | 0.67 | 0.58 | 0.74 | 0.79 | 0.71 | 0.76 | 0.83 | |||
| 0.22 | 0.48 | 0.61 | 0.40 | 0.60 | 0.65 | 0.47 | 0.62 | 0.66 | |||
| 0.2 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | ||
| 0.19 | 0.50 | 0.76 | 0.49 | 0.78 | 0.83 | 0.66 | 0.84 | 0.88 | |||
| 0.32 | 0.59 | 0.78 | 0.50 | 0.71 | 0.78 | 0.63 | 0.73 | 0.79 | |||
| 0.6 | 0.96 | 0.96 | 0.98 | 0.97 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | ||
| 0.48 | 0.54 | 0.66 | 0.48 | 0.55 | 0.67 | 0.49 | 0.55 | 0.67 | |||
| 0.24 | 0.37 | 0.51 | 0.42 | 0.64 | 0.65 | 0.56 | 0.68 | 0.73 | |||
| 0.8 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | ||
| 0.32 | 0.34 | 0.44 | 0.32 | 0.35 | 0.44 | 0.33 | 0.35 | 0.44 | |||
| 0.05 | 0.07 | 0.15 | 0.07 | 0.09 | 0.16 | 0.09 | 0.10 | 0.17 | |||
| 0.6 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 1.00 | ||
| 0.23 | 0.24 | 0.27 | 0.23 | 0.25 | 0.28 | 0.23 | 0.25 | 0.28 | |||
| 0.03 | 0.04 | 0.10 | 0.04 | 0.07 | 0.10 | 0.05 | 0.09 | 0.11 | |||
| Exchange Rate | Price Ratio | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Country | Currency Code | 25% | 50% | 75% | IQR | 25% | 50% | 75% | IQR | |
| Burkina Faso | BFA | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.90 | 2.61 | 6.00 | 8.90 |
| Burundi | BDI | 218 | 1248.47 | 1631.54 | 1922.16 | 673.69 | −2.41 | 2.22 | 7.46 | 9.87 |
| Central African Republic | CAF | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −0.18 | 2.20 | 4.96 | 5.14 |
| Chad | TCD | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.63 | 1.20 | 3.80 | 6.42 |
| Congo, Dem. Rep. | COD | 218 | 917.99 | 929.14 | 1956.30 | 1038.31 | −0.91 | 2.21 | 6.74 | 7.64 |
| Gambia, The | GMB | 218 | 29.51 | 44.09 | 51.18 | 21.67 | 0.11 | 2.08 | 6.20 | 6.10 |
| Guinea-Bissau | GNB | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.37 | 1.21 | 3.36 | 5.72 |
| Kenya | KEN | 218 | 84.10 | 100.81 | 107.39 | 23.30 | −1.18 | 1.46 | 7.86 | 9.04 |
| Liberia | LBR | 218 | 83.36 | 96.03 | 177.18 | 93.82 | 0.78 | 2.40 | 5.02 | 4.24 |
| Malawi | MWI | 218 | 153.59 | 696.21 | 758.54 | 604.96 | 1.38 | 4.31 | 12.02 | 10.64 |
| Mali | MLI | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.15 | 1.17 | 3.95 | 6.11 |
| Mauritania | MRT | 218 | 28.51 | 33.89 | 36.22 | 7.71 | −1.99 | −0.02 | 2.48 | 4.47 |
| Mozambique | MOZ | 218 | 29.76 | 49.84 | 63.86 | 34.10 | −0.35 | 1.77 | 4.06 | 4.42 |
| Niger | NER | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.24 | 0.99 | 4.66 | 6.91 |
| Nigeria | NGA | 218 | 154.54 | 197.00 | 372.72 | 218.18 | −2.51 | 1.71 | 5.31 | 7.82 |
| Senegal | SEN | 218 | 491.12 | 554.17 | 593.12 | 102.00 | −2.05 | 0.60 | 3.63 | 5.68 |
| Somalia | SOM | 218 | 22,518.83 | 26,841.31 | 30,777.96 | 8259.13 | −3.03 | 1.31 | 5.22 | 8.25 |
| Sudan | SDN | 218 | 2.68 | 6.09 | 55.00 | 52.32 | 6.38 | 17.25 | 36.10 | 29.72 |
| USA (Baseline) | USD | 218 | 1.00 | 1.00 | 1.00 | 1.00 | 1.40 | 2.20 | 4.00 | 2.60 |
| Country | T | Reject H0 ? | |||||
|---|---|---|---|---|---|---|---|
| Burkina Faso | 218 | 0.00 | 1.00 | 0.93 | 0.516 | 0.3030 | No |
| Burundi | 218 | 0.02 | 0.95 | 0.63 | 2.366 | 0.0090 | Yes |
| Central African Republic | 218 | −0.01 | 0.99 | 0.61 | 2.889 | 0.0020 | Yes |
| Chad | 218 | −0.01 | 0.96 | 0.63 | 2.496 | 0.0060 | Yes |
| Congo, Dem. Rep. | 218 | 0.07 | 0.98 | 0.58 | 3.075 | 0.0010 | Yes |
| Gambia, The | 218 | 0.05 | 0.95 | 0.60 | 2.601 | 0.0050 | Yes |
| Guinea-Bissau | 218 | −0.01 | 0.92 | 0.45 | 3.565 | 0.0000 | Yes |
| Kenya | 218 | −0.01 | 1.00 | 0.74 | 1.933 | 0.0270 | Yes |
| Liberia | 218 | 0.02 | 0.95 | 0.50 | 3.403 | 0.0000 | Yes |
| Malawi | 218 | 0.04 | 0.94 | 0.60 | 2.610 | 0.0050 | Yes |
| Mali | 218 | 0.00 | 1.00 | 0.75 | 1.909 | 0.0280 | Yes |
| Mauritania | 218 | 0.00 | 1.00 | 0.54 | 3.479 | 0.0000 | Yes |
| Mozambique | 218 | −0.01 | 1.00 | 0.57 | 3.275 | 0.0010 | Yes |
| Niger | 218 | 0.00 | 1.00 | 0.59 | 3.095 | 0.0010 | Yes |
| Nigeria | 218 | 0.06 | 0.99 | 0.67 | 2.447 | 0.0070 | Yes |
| Senegal | 218 | −0.01 | 0.99 | 0.63 | 2.664 | 0.0040 | Yes |
| Somalia | 218 | 0.03 | 0.81 | 0.77 | 0.308 | 0.3790 | No |
| Sudan | 218 | 0.31 | 0.85 | 0.76 | 0.688 | 0.2460 | No |
| Pooled Panel | 3906 | 0.33 | 0.93 | 0.34 | 13.064 | 0.0000 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olaniran, O.R.; Olaniran, S.F.; Alzahrani, A.R.R.; Alharbi, N.M.; Alzahrani, A.A. Bayesian Tapered Narrowband Least Squares for Fractional Cointegration Testing in Panel Data. Mathematics 2025, 13, 1615. https://doi.org/10.3390/math13101615
Olaniran OR, Olaniran SF, Alzahrani ARR, Alharbi NM, Alzahrani AA. Bayesian Tapered Narrowband Least Squares for Fractional Cointegration Testing in Panel Data. Mathematics. 2025; 13(10):1615. https://doi.org/10.3390/math13101615
Chicago/Turabian StyleOlaniran, Oyebayo Ridwan, Saidat Fehintola Olaniran, Ali Rashash R. Alzahrani, Nada MohammedSaeed Alharbi, and Asma Ahmad Alzahrani. 2025. "Bayesian Tapered Narrowband Least Squares for Fractional Cointegration Testing in Panel Data" Mathematics 13, no. 10: 1615. https://doi.org/10.3390/math13101615
APA StyleOlaniran, O. R., Olaniran, S. F., Alzahrani, A. R. R., Alharbi, N. M., & Alzahrani, A. A. (2025). Bayesian Tapered Narrowband Least Squares for Fractional Cointegration Testing in Panel Data. Mathematics, 13(10), 1615. https://doi.org/10.3390/math13101615





