Inequalities of a Class of Analytic Functions Involving Multiplicative Derivative

Abstract

Using the concepts of multiplicative calculus and subordination of analytic functions, we define a new class of starlike bi-univalent functions based on a symmetric operator, which involved the three parameter Mittag-Leffler function. Estimates for the initial coefficients and Fekete–Szegő inequalities of the defined function classes are determined. Moreover, special cases of the classes have been discussed and stated as corollaries, which have not been discussed previously.

1. Introduction

For $\mathbb{U}=\left\{\xi \in \mathbb{C};\left|\xi \right|<1\right\}$, we let

$${\mathcal{A}}_n=\{\xi \in \mathbb{U};\phi \left(\xi \right)=\xi +a_{n+1}{\xi }^{n+1}+a_{n+2}{\xi }^{n+2}+\dots \}$$

and let $\mathcal{A}={\mathcal{A}}_1$. Throughout this paper, we let $\mathbb{C},{\mathbb{Z}}^{-}$ and $\mathbb{N}$ denote the sets of complex numbers, negative integers and natural numbers, respectively.

Mittag-Leffler function is a special function that gained prominence for its role in fractional calculus. Indeed, the Mittag–Leffler function appears in the kernels of most of the fractional derivative operators. The Mittag–Leffler function $E_{\theta }\left(z\right)$ (see [1] Equation (21)) and its two-parameter extension $E_{\theta ,\vartheta }\left(z\right)$ are defined, respectively, by

$$E_{\theta }\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{\Gamma \left(\theta n+1\right)}}\mathrm{and}{E}_{\theta ,\vartheta }\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{\Gamma \left(\theta n+\vartheta \right)}}(z,\theta ,\vartheta ,\in \mathbb{C},Re\left(\theta \right)>0),$$

and thesewere first considered by Gösta Mittag-Leffler in [2] and Wiman in [3]. Srivastava et al. [4] introduced the following multi-index Mittag-Leffler functions:

$$E_{{({\theta }_j,{\vartheta }_j)}_m}^{\gamma ,k,\delta ,ϵ}\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\rho \right)}_{kn}{\left(\delta \right)}_{ϵn}}{{\prod }_{j=1}^m\Gamma \left({\theta }_{j}n+{\vartheta }_j\right)}}{\displaystyle \frac{z^n}{n!}},$$

$$\left(\theta j,{\vartheta }_j,\gamma ,k,\delta ,ϵ\in \mathbb{C};Re\left({\theta }_j\right)>0,(j=1,\dots ,m);Re\left(\sum _{j=1}^m{\theta }_j\right)>Re(k+ϵ)-1\right).$$

The special case of the multi-index Mittag-Leffler functions $E_{\theta ,\vartheta }^{\rho }\left(\omega \right)$, known as the Prabhakar function ([5] Equation (1.3)) or the generalized Mittag-Leffler three-parameter function, is very popular among researchers. Explicitly, the generalized Mittag-Leffler three-parameter function is defined by

$$E_{\theta ,\vartheta }^{\rho }\left(\omega \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\rho \right)}_n{\xi }^n}{\Gamma \left(\theta n+\vartheta \right)n!}},(\omega ,\theta ,\vartheta ,\rho \in \mathbb{C},Re\left(\theta \right)>0).$$

Using the Mittag-Leffler function, Murat et al. [6] defined the operator $D_r^m(\theta ,\vartheta ,\rho )\phi :\mathbb{U}⟶\mathbb{U}$ by

$$\begin{array}{c}\hfill D_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)=\xi +\sum _{n=2}^{\infty }{\left[n+{\displaystyle \frac{r}{2}}(1+{(-1)}^{n+1})\right]}^m{\displaystyle \frac{\Gamma \left(\vartheta \right){\left(\rho \right)}_{n-1}}{\Gamma \left(\vartheta +\theta (n-1)\right)(n-1)!}}{a}_n{\xi }^n,\end{array}$$

(1)

where $m,r\in {\mathbb{N}}_0=\{0,1,2,\dots \},\xi ,\theta ,\vartheta ,\rho \in \mathbb{C},Re\left(\theta \right)>0.$ The operator $D_r^m(\theta ,\vartheta ,\rho )\phi$ was motivated by the operator $D_r^m\phi \left(\xi \right)$ defined by Ibrahim and Darus [7,8]. The operator $D_r^m(\theta ,\vartheta ,\rho )\phi$ defined in (1) is closely related to the operator recently studied by Umadevi and Karthikeyan [9].

Let $\mathcal{P}$ denote family of analytic functions with normalization $p\left(0\right)=1$ and also maps the unit disc onto a right half plane. We denote the classes of the starlike and convex functions by ${\mathcal{S}}^{*}$ and $\mathcal{C}$, respectively. For ${\phi }_1,{\phi }_2\in \mathcal{A}$, we say that ${\phi }_1$ is subordinate to ${\varphi }_2$ if ${\phi }_1\left(\xi \right)={\phi }_2\left(w\left(\xi \right)\right)$ holds true, where $w\left(z\right)$ is analytic if $\mathbb{U}$ satisfies $w\left(0\right)=0$ and $\left|w\left(\xi \right)\right|<1$. We will denote it as ${\phi }_1\left(\xi \right)\prec {\phi }_2\left(\xi \right)$.

Using the concept of the subordination of the analytic function, the classes ${\mathcal{S}}^{*}\left(\psi \right)$ and $\mathcal{C}\left(\psi \right)$ are defined, respectively, by

$${\displaystyle \frac{\xi {\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}\prec \psi \left(\xi \right)\mathrm{and}1+{\displaystyle \frac{\xi {\phi }^{″}\left(\xi \right)}{{\phi }^{\prime }\left(\xi \right)}}\prec \psi \left(\xi \right),$$

(2)

where $\psi \in \mathcal{P}$. Various authors have studied interesting subclasses of starlike and convex functions by specializing $\psi$ to be some functions that map the domain onto the regions like lune-shaped, cardioid, leaf-like, lemniscate of Bernoulli, and leaf-like in the right-half of the complex plane. Another important class that will be denoted as ${\mathcal{K}}^{\tau }\left(\psi \right)$, which is very useful in obtaining the properties of univalence, is defined by

$${\left({\phi }^{\prime }\left(\xi \right)\right)}^{\tau }\prec \psi \left(\xi \right),\psi \in \mathcal{P}.$$

We let $\mathcal{S}$ denote the class of functions univalent in $\mathbb{U}$. Note that $\phi \left(\xi \right)=\xi +{\sum }_{n=2}^{\infty }{a}_n{\xi }^n$ in $\mathcal{S}$ has an inverse ${\phi }^{-1}$, defined by ${\phi }^{-1}\left(\phi \left(\xi \right)\right)=\xi ,\xi \in \mathbb{U}$ and $\phi \left({\phi }^{-1}\left(w\right)\right)=w,\left(\right|w|<r;r\ge 1/4)$, where

$$\chi \left(w\right)={\phi }^{-1}\left(w\right)=w-a_2{w}^2+(2a_2^2-a_3)w^3-\left(5a_2^2-5a_2{a}_3+a_4\right)w^3+\dots .$$

(3)

A function $\phi$ defined on $\mathcal{A}$ is said to be bi-univalent if both $\phi$ and its inverse $\chi$ are one-to-one in $\mathbb{U}$. In practice, we call a class a subclass of bi-univalent if $\phi$ and its inverse satisfy the same conditions. We review a number of functions in the $\mathsf{\Sigma }$ family shown in Srivastava et al. [10] as follows:

$${\displaystyle \frac{\xi }{1-\xi }},-log(1-\xi )\mathrm{and}{\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+\xi }{1-\xi }}\right),$$

with the inverses that relate to them being

$${\displaystyle \frac{w}{1+w}},{\displaystyle \frac{e^w-1}{e^w}}\mathrm{and}{\displaystyle \frac{e^{2w}-1}{e^{2w}+1}}.$$

The known extremal function in class $\mathcal{S}$ does not belong to the family $\mathsf{\Sigma }$, but note that the class is not empty. Also, the functions $\xi -{\displaystyle \frac{{\xi }^2}{2}}$ and ${\displaystyle \frac{\xi }{1-{\xi }^2}}$ are not bi-univalent. Bi-starlike functions of order $\alpha (0<\alpha \le 1)$ denoted by ${\mathcal{S}}_{\mathsf{\Sigma }}^{*}\left(\alpha \right)$ and bi-convex functions of order $\alpha$ denoted by ${\mathcal{CV}}_{\mathsf{\Sigma }}\left(\alpha \right)$ were presented, and the bounds of coefficients of bi-univalent functions have been studied by many authors. Here, we let ${\mathcal{BK}}^{\tau }\left(\psi \right)$ ([11] Definition 2) denote the class of functions in $\mathcal{A}$ satisfying the conditions

$${\left({\phi }^{\prime }\left(\xi \right)\right)}^{\tau }\prec \psi \left(\xi \right)\mathrm{and}{\left({\chi }^{\prime }\left(w\right)\right)}^{\tau }\prec \psi \left(w\right),(\xi ,w\in \mathbb{U};\psi \in \mathcal{P}).$$

The class ${\mathcal{BK}}^0\left(\psi \right)$ was studied by Ali et al. [12]. Further, they obtained the coefficient inequalities (see [12] Corollary 2.1) for functions in ${\mathcal{ST}}_{\sum }\left(\psi \right)$ that satisfy the subordination conditions

$${\displaystyle \frac{\xi {\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}\prec \psi \left(\xi \right)\mathrm{and}{\displaystyle \frac{w{\chi }^{\prime }\left(w\right)}{\chi \left(w\right)}}\prec \psi \left(w\right),(\xi ,w\in \mathbb{U};\chi ={\phi }^{-1}).$$

1.1. Motivation and Novelty

Recently, researchers have introduced and studied various subclasses of analytic function by replacing the classical derivative with quantum derivatives or fractional-order derivatives. The study of univalent function theory in combination with multiplicative calculus was initiated recently by Karthikeyan and Murugusundaramoorthy in [13] when they replaced ${\phi }^{\prime }$ with $e^{{\displaystyle \frac{{\xi }^2{\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}}$ in the analytic characterization of ${\mathcal{S}}^{*}\left(\psi \right)$. Further, recently, Breaz et al. in [14] studied a new family of meromorphic functions involving the multiplicative derivative. Here, in this paper, we will introduce two new subclasses by replacing the ordinary derivatives involved in ${\mathcal{BK}}^{\tau }\left(\psi \right)$ and ${\mathcal{ST}}_{\sum }\left(\psi \right)$ with a multiplicative derivative.

1.2. A Brief Introduction to Multiplicative Calculus

Bashirov, Kurpinar and Özyapıin ([15] p. 37) (also see [16,17,18]) studied a restrictive calculus titled Multiplicative calculus that has proved its usefulness in economics and mathematical finance. For ${\phi }^{*}:\mathbb{R}⟶\mathbb{R}$, the multiplicative derivative is given by

$${\phi }^{*}\left(x\right)=\underset{h\to 0}{lim}{\left({\displaystyle \frac{\phi (x+h)}{\phi \left(x\right)}}\right)}^{{\displaystyle \frac{1}{h}}}=e^{{\displaystyle \frac{{\phi }^{\prime }\left(x\right)}{\phi \left(x\right)}}}=e^{{[ln\phi \left(x\right)]}^{\prime }},$$

where ${\phi }^{\prime }\left(x\right)$ is the classical derivative. The multiplicative derivative of $\phi$ at $\xi$ belonging to a domain in a complex plane where $\phi$ is non-vanishing and differentiable is given by

$${\phi }^{*}\left(\xi \right)=e^{{\phi }^{\prime }\left(\xi \right)/\phi \left(\xi \right)}\mathrm{and}{\phi }^{*\left(n\right)}\left(\xi \right)=e^{{\left[{\phi }^{\prime }\left(\xi \right)/\phi \left(\xi \right)\right]}^{\left(n\right)}},n=1,2,\dots .$$

Recently, Karthikeyan and Murugusundaramoorthy in [13] (also see [14,19]) introduced and studied a class of analytic functions $\mathcal{R}\left(\psi \right)$ motivated by the definition of ${\phi }^{*}\left(\xi \right)$, satisfying the subordination condition

$${\displaystyle \frac{\xi e^{\frac{{\xi }^2{\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}}{\phi \left(\xi \right)}}\prec \psi \left(\xi \right),$$

(4)

where $\psi \in \mathcal{P}$ has a series expansion in the form

$$\psi \left(\xi \right)=1+L_1\xi +L_2{\xi }^2+L_3{\xi }^3+\dots ,(L_1>0;\xi \in \mathbb{U}).$$

(5)

The class $\mathcal{R}\left(\psi \right)$ is defined by replacing ${\phi }^{\prime }\left(\xi \right)$ with $e^{\xi {[ln\phi \left(\xi \right)]}^{\prime }}$ in the definition of ${\mathcal{S}}^{*}\left(\psi \right)$ (see (2)). Notice that we did not use the multiplicative derivative explicitly in (4). The repercussions of using multiplicative derivative explicitly in ${\mathcal{S}}^{*}\left(\psi \right)$ would have left us working outside the existing framework of geometric function theory. Such a class would not be well defined, as $L_1\ne 0$ is a prerequisite.

Further, by replacing the classical derivative in ${\mathcal{K}}^{\tau }\left(\psi \right)$ with the multiplicative derivative, we define the class ${\mathcal{MK}}^{\tau }\left(\psi \right)$ as the class of functions satisfying

$${\left(e^{{[ln\phi \left(\xi \right)]}^{\prime }-1}\right)}^{\tau }\prec \psi \left(\xi \right),\left(0<\tau \le 1;\psi \in \mathcal{P}\right).$$

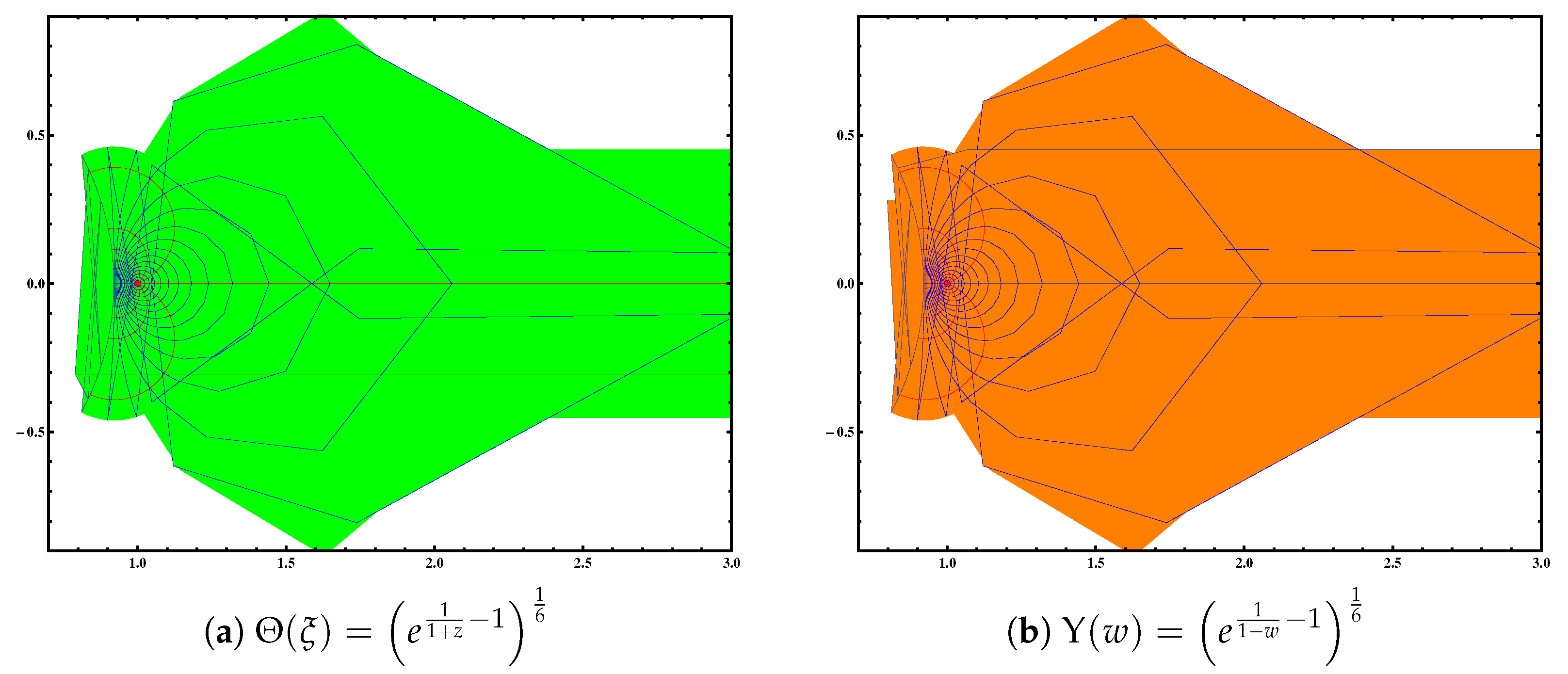
1.3. Definitions

Motivated by the study of Bi-starlike functions and the definition of the multiplicative derivative, we will now define ${\mathcal{BM}}^{\tau }\left(\psi \right)$ to denote the collections of functions in $\mathcal{A}$ satisfying the conditions

$${\left(e^{{[ln\phi \left(\xi \right)]}^{\prime }-1}\right)}^{\tau }\prec \psi \left(\xi \right)\mathrm{and}{\left(e^{{[ln\chi \left(w\right)]}^{\prime }-1}\right)}^{\tau }\prec \psi \left(w\right),$$

where $\chi ={\phi }^{-1}$, $0<\tau \le 1$ and $\psi \in \mathcal{P}$.

Example 1.

In this example, we will show that the class ${\mathcal{BM}}^{\tau }\left(\psi \right)$ is non-empty. Let $\phi \left(\xi \right)={\displaystyle \frac{\xi }{\xi +1}}$; then, the inverse function of φ is given by $\chi \left(w\right)={\displaystyle \frac{w}{1-w}}$. The function $\phi \left(\xi \right)={\displaystyle \frac{\xi }{\xi +1}}$ satisfies the normalization $f\left(0\right)=f^{\prime }\left(\xi \right)-1=0$ and maps the unit disc onto region $\left\{w:Re\left(w\right)<{\displaystyle \frac{1}{2}}\right\}$ (see Figure 1a). And the inverse function χ maps the unit disc onto region $\left\{z:Re\left(z\right)>-{\displaystyle \frac{1}{2}}\right\}$ (see Figure 1b). In contrast, the function $\mathsf{\Theta }\left(\xi \right)={\left(e^{{[ln\phi \left(\xi \right)]}^{\prime }-1}\right)}^{{\displaystyle \frac{1}{6}}}={\left(e^{{\displaystyle \frac{\xi {\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}-1}\right)}^{{\displaystyle \frac{1}{6}}}={\left(e^{{\displaystyle \frac{1}{1+z}}-1}\right)}^{{\displaystyle \frac{1}{6}}}$ maps the unit disc onto a region in the right half plane (see Figure 2a). Also, the inverse function satisfies ${\rm Y}\left(w\right)={\left(e^{{\displaystyle \frac{w{\chi }^{\prime }\left(w\right)}{\chi \left(w\right)}}-1}\right)}^{{\displaystyle \frac{1}{6}}}={\left(e^{{\displaystyle \frac{1}{1-w}}-1}\right)}^{{\displaystyle \frac{1}{6}}}$ and maps the unit disc onto a region in the right half place (see Figure 2b). Hence, the function $\phi \left(\xi \right)={\displaystyle \frac{\xi }{1+\xi }}$ is in class ${\mathcal{BM}}^{\tau }\left(\psi \right)$ for $\tau ={\displaystyle \frac{1}{6}}$.

Motivated by ${\mathcal{BK}}^{\tau }\left(\psi \right)$ and the recent study [20], we now define the new subclasses using a symmetric operator that involved a three-parameter Mittag-Leffler function.

Definition 1.

For $m,r\in {\mathbb{N}}_0=\{0,1,2,\dots \},\xi ,\theta ,\vartheta ,\rho \in \mathbb{C},Re\left(\theta \right)>0$, $0<\tau \le 1$ and $\chi ={\phi }^{-1}$ is defined as in (3), and we will denote the class of analytic functions φ to be in ${\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ if the following conditions are satisfied:

$${\left({\displaystyle \frac{D_r^m(\theta ,\vartheta ,\rho )F^{*}\left(\xi \right)}{e}}\right)}^{\tau }\prec \psi \left(\xi \right),$$

and

$${\left({\displaystyle \frac{D_r^m(\theta ,\vartheta ,\rho )G^{*}\left(w\right)}{e}}\right)}^{\tau }\prec \psi \left(w\right),$$

where $D_r^m(\theta ,\vartheta ,\rho )F^{*}\left(\xi \right)=e^{{\left[ln{D}_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)\right]}^{\prime }}$, $D_r^m(\theta ,\vartheta ,\rho )G^{*}\left(\xi \right)=e^{{\left[ln{D}_r^m(\theta ,\vartheta ,\rho )\chi \left(w\right)\right]}^{\prime }}$, $e=exp1$ and $\psi \in \mathcal{P}$ is defined as in (5).

Analogous to $\mathcal{R}\left(\psi \right)$, we now define the following:

Definition 2.

For $m,r\in {\mathbb{N}}_0=\{0,1,2,\dots \},\xi ,\theta ,\vartheta ,\rho \in \mathbb{C},Re\left(\theta \right)>0$, $0<\tau \le 1$ and $\chi ={\phi }^{-1}$ is defined as in (3), and we will denote the class of analytic functions to be in ${\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$ if the following conditions are satisfied:

$${\displaystyle \frac{\xi e^{\frac{{\xi }^2{D}_r^m(\theta ,\vartheta ,\rho ){\phi }^{\prime }\left(\xi \right)}{D_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)}}}{\left[D_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)\right]}}\prec \psi \left(\xi \right),$$

and

$${\displaystyle \frac{w{e}^{\frac{w^2{D}_r^m(\theta ,\vartheta ,\rho ){\chi }^{\prime }\left(w\right)}{D_r^m(\theta ,\vartheta ,\rho )\chi \left(w\right)}}}{\left[D_r^m(\theta ,\vartheta ,\rho )\chi \left(w\right)\right]}}\prec \psi \left(w\right),$$

where $\psi \in \mathcal{P}$ is defined as in (5).

Remark 1.

Example 1 illustrates that class ${\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ is non-empty. Similarly, the function $\phi \left(\xi \right)={\displaystyle \frac{3\xi }{3-\xi }}$ and its corresponding inverse function $\chi \left(w\right)={\displaystyle \frac{3w}{3+w}}$ can be used to illustrate that the class ${\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$ is non-empty.

Estimates for the initial coefficients and Fekete–Szegő inequalities of the defined function classes are investigated. Moreover, special cases of the classes ${\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ and ${\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$ are discussed and stated to be corollaries.

2. Coefficient Estimates for the Class ${\mathcal{BK}}_{\mathbf{r}}^{\mathbf{m}}(\theta ,\vartheta ,\rho ;\tau ,\psi )$

To begin with, we will obtain the coefficient bounds for functions belonging to the class ${\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$.

Lemma 1

([21]). Let $\mathcal{P}$ be the family of all functions $h,$ which are analytic in $\mathbb{U}$ with $\Re \left(h\right(\xi \left)\right)>0$ and given by

$$h\left(\xi \right)=1+p_1\xi +p_2{\xi }^2+\dots ,(\xi \in \mathbb{U})$$

then

$$|p_k|\le 2,\forall k\ge 1.$$

Theorem 1.

Let $\phi \in {\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ and let χ be the inverse of φ defined by

$${\phi }^{-1}\left(w\right)=w+\sum _{k=2}^{\infty }{d}_k{w}^k,\left(\right|w|<r;r\ge 1/4),$$

then

$$\begin{array}{c}\left|a_2\right|\le min\left\{{\displaystyle \frac{L_1}{\tau \left|{\mathsf{\Lambda }}_2\right|}},\sqrt{{\displaystyle \frac{4\left[L_1+\left|L_2-L_1\right|\right]}{\tau \left|{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right|}}},\right.\\ \left.{\displaystyle \frac{L_1\sqrt{2L_1}}{\sqrt{\tau \left|\left\{{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right\}{L}_1^2+2(L_1-L_2)\tau {\mathsf{\Lambda }}_2^2\right|}}}\right\}\end{array}$$

(6)

and

$$\begin{array}{c}\left|a_3\right|\le min\left\{{\displaystyle \frac{L_1}{2\left|{\mathsf{\Lambda }}_3\right|}}+{\displaystyle \frac{L_1^2}{{\tau }^2{\left|{\mathsf{\Lambda }}_2\right|}^2}},{\displaystyle \frac{\tau L_1+2\left|L_2-L_1\right|}{\left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]}}\right\},\end{array}$$

(7)

where ${\mathsf{\Lambda }}_n={\left[n+{\displaystyle \frac{r}{2}}(1+{(-1)}^{n+1})\right]}^m{\displaystyle \frac{\Gamma \left(\vartheta \right){\left(\rho \right)}_{n-1}}{\Gamma \left(\vartheta +\theta (n-1)\right)(n-1)!}}$.

Proof. 

Let $\phi \in {\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$; then, we have

$${\left({\displaystyle \frac{D_r^m(\theta ,\vartheta ,\rho )F^{*}\left(\xi \right)}{e}}\right)}^{\tau }=\psi \left[{\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}}\right]$$

(8)

and

$${\left({\displaystyle \frac{D_r^m(\theta ,\vartheta ,\rho )G^{*}\left(w\right)}{e}}\right)}^{\tau }=\psi \left[{\displaystyle \frac{q\left(w\right)-1}{q\left(w\right)+1}}\right],$$

(9)

where $\xi$ and w belong to $\mathbb{U}$. The functions $r\left(\xi \right)$ and $s\left(w\right)$ are Schwartz functions and have the following respective series expansion: $r\left(\xi \right)={\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}}=1+{\sum }_{n=1}^{\infty }{p}_n{\xi }^n$ and $s\left(w\right)={\displaystyle \frac{q\left(w\right)-1}{q\left(w\right)+1}}=1+{\sum }_{n=1}^{\infty }{q}_n{w}^n$ with $p\left(\xi \right),q\left(w\right)\in \mathcal{P}$.

Equating the coefficients of $\xi ,{\xi }^2,w$ and $w^2$ in (8) and (9), we have

$$a_2\tau {\mathsf{\Lambda }}_2={\displaystyle \frac{1}{2}}{L}_1{p}_1,$$

(10)

$${\displaystyle \frac{\tau }{2}}\left[4a_3{\mathsf{\Lambda }}_2+a_2^2{\mathsf{\Lambda }}_2^2\left(\tau -2\right)\right]={\displaystyle \frac{1}{2}}{L}_1\left(p_2-{\displaystyle \frac{p_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{L}_2{p}_1^2.$$

(11)

$$-a_2\tau {\mathsf{\Lambda }}_2={\displaystyle \frac{1}{2}}{L}_1{q}_1,$$

(12)

and

$${\displaystyle \frac{\tau }{2}}\left[-4a_3{\mathsf{\Lambda }}_3+a_2^2\left(\tau -2\right){\mathsf{\Lambda }}_2^2+8a_2^2{\mathsf{\Lambda }}_3\right]={\displaystyle \frac{1}{2}}{L}_1\left(q_2-{\displaystyle \frac{q_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{L}_2{q}_1^2.$$

(13)

From (10) and (12), we have

$$p_1=-q_1$$

and

$$8a_2^2{\tau }^2{\mathsf{\Lambda }}_2^2=L_1^2\left(p_1^2+q_1^2\right).$$

(14)

Adding Equations (11) and (13) and then using (14) in the resulting equation, we have

$$\begin{array}{c}{a}_2^2={\displaystyle \frac{L_1^3\left(p_2+q_2\right)}{2\tau \left[\left\{{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right\}{L}_1^2+2(L_1-L_2)\tau {\mathsf{\Lambda }}_2^2\right]}}.\end{array}$$

(15)

In light of the known inequalities $\left|p_n\right|\le 2$ and $\left|q_n\right|\le 2$ for all $n\ge 2$, (15) reduces to the result (6). To obtain (7), by subtracting (13) with (11), we obtain

$$a_3=a_2^2+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}.$$

(16)

Using (14) in (16), we obtain

$$a_3={\displaystyle \frac{L_1^2{p}_1^2}{4{\mathsf{\Lambda }}_2^2{\tau }^2}}+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}.$$

(17)

Similarly, applying (15) in (16), we obtain

$$a_3={\displaystyle \frac{L_1\left(p_2+q_2\right)+\left(L_2-L_1\right)p_1^2}{2\tau \left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]}}+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}.$$

(18)

Simplifying the expression (18), we have

$$\begin{array}{c}{a}_3={\displaystyle \frac{\left(L_2-L_1\right)p_1^2}{2\tau \left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]}}\\ +{\displaystyle \frac{L_1\left[p_2\left\{8{\mathsf{\Lambda }}_3+2\tau \left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]\right\}+q_2\left\{8{\mathsf{\Lambda }}_3-2\tau \left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]\right\}\right]}{16{\mathsf{\Lambda }}_3\tau \left[{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right]}}.\end{array}$$

(19)

In view of (17) and (19), we can obtain the result (7) using the well-known inequalities $\left|p_n\right|\le 2$ and $\left|q_n\right|\le 2$ for all $n\ge 2$. Hence, the proof of the theorem is found. □

Corollary 1.

Let $\phi \in \mathcal{A}$ and let χ be the inverse of φ defined by

$${\phi }^{-1}\left(w\right)=w+\sum _{k=2}^{\infty }{b}_k{w}^k,\left(\right|w|<r;r\ge 1/4),$$

satisfying the conditions

$$Re\left\{{\displaystyle \frac{F^{*}\left(\xi \right)}{e}}\right\}>0\mathrm{and}Re\left\{{\displaystyle \frac{G^{*}\left(\xi \right)}{e}}\right\}>0,$$

where $F^{*}\left(\xi \right)=e^{{\left[ln\phi \left(\xi \right)\right]}^{\prime }}$, $G^{*}\left(\xi \right)=e^{{\left[ln\chi \left(w\right)\right]}^{\prime }}$. Then, $\left|a_2\right|\le {\displaystyle \frac{2}{\sqrt{3}}}\mathrm{and}\left|a_3\right|\le {\displaystyle \frac{2}{3}}.$

Proof. 

In Theorem 1, taking $m=\theta =0$, $\rho =1$, $\psi \left(\xi \right)={\displaystyle \frac{1+\xi }{1-\xi }}$ and $\psi \left(w\right)={\displaystyle \frac{1+w}{1-w}}$, we can obtain $L_1=L_2=2$ and ${\mathsf{\Lambda }}_2={\mathsf{\Lambda }}_3=1$. Substituting these values in Equations (6) and (7), we obtain the assertion of the corollary. □

3. Fekete-Szegő Inequalities

Making use of the values of $a_2^2$ and $a_3$ and motivated by the recent work of Zaprawa [22], we prove the following Fekete–Szegő result for $f\in {\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$. We recall the following lemma to discuss Fekete-Szegő results:

Lemma 2

([22,23]). Let $l_1,l_2\in \mathbb{R}$ and $p_1,p_2\in \mathbb{C}$. If $|p_1|,|p_2|<\zeta$, then

$$\left|(l_1+l_2)p_1+(l_1-l_2)p_2\right|\le \left\{\begin{array}{ccc}2|l_1|\zeta & ,& |l_1|\ge |l_2|\\ 2|l_2|\zeta & ,& |l_1|\le |l_2|.\end{array}\right.$$

Theorem 2.

Let $f\in {\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ and $\aleph \in \mathbb{C}$, then

$$|a_3-\aleph a_2^2|\le \left\{\begin{array}{ccc}4L_1\left|\mathsf{\Theta }(\wp ,\tau ,\kappa )\right|& ,& \left|\mathsf{\Theta }(\wp ,\tau ,\kappa )\right|\ge |{\displaystyle \frac{L_1}{8{\mathsf{\Lambda }}_3}}|\\ {\displaystyle \frac{L_1}{2{\mathsf{\Lambda }}_3}}& ,& \left|\mathsf{\Theta }(\wp ,\tau ,\kappa )\right|\le |{\displaystyle \frac{L_1}{8{\mathsf{\Lambda }}_3}}|\end{array}\right.$$

where

$$\mathsf{\Theta }(\wp ,\tau ,\kappa )={\displaystyle \frac{(1-\aleph )L_1^2}{2\tau \left[\left\{{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right\}{L}_1^2+2(L_1-L_2)\tau {\mathsf{\Lambda }}_2^2\right]}}.$$

Proof. 

From (16), we have

$$a_3=a_2^2+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}.$$

Using (15), by simple calculation, we obtain

$$\begin{array}{ccc}\hfill a_3-\aleph a_2^2& =& {\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}+(1-\aleph )a_2^2\hfill \\ & =& {\displaystyle \frac{L_1\left(p_2-q_2\right)}{8{\mathsf{\Lambda }}_3}}+{\displaystyle \frac{(1-\aleph )L_1^3\left(p_2+q_2\right)}{2\tau \left[\left\{{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right\}{L}_1^2+2(L_1-L_2)\tau {\mathsf{\Lambda }}_2^2\right]}}\hfill \\ & =& L_1\left[\mathsf{\Theta }(\wp ,\tau ,\kappa )+{\displaystyle \frac{1}{8{\mathsf{\Lambda }}_3}}\right]p_2+L_1\left[\mathsf{\Theta }(\wp ,\tau ,\kappa )-{\displaystyle \frac{1}{8{\mathsf{\Lambda }}_3}}\right]q_2,\hfill \end{array}$$

where

$$\mathsf{\Theta }(\wp ,\tau ,\kappa )={\displaystyle \frac{(1-\aleph )L_1^2}{2\tau \left[\left\{{\mathsf{\Lambda }}_2^2(\tau -2)+4{\mathsf{\Lambda }}_3\right\}{L}_1^2+2(L_1-L_2)\tau {\mathsf{\Lambda }}_2^2\right]}}.$$

Now applying Lemma 2, we can obtain the desired result directly. Thus, we complete the proof. □

Remark 2.

Let the function $f\in {\mathcal{BK}}_r^m(\theta ,\vartheta ,\rho ;\tau ,\psi )$ and $\aleph =1$, then

$$|a_3-a_2^2|\le {\displaystyle \frac{L_1}{2{\mathsf{\Lambda }}_3}}.$$

4. Coefficient Estimates for the Class ${\displaystyle {\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )}$

Theorem 3.

Let ψ be defined as in (5) with $\left|L_1\right|\ge 1$ and let χ be the inverse of φ defined by

$${\phi }^{-1}\left(w\right)=w+\sum _{k=2}^{\infty }{b}_k{w}^k,\left(\right|w|<r;r\ge 1/4).$$

If $\phi \in {\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$, then

$$\begin{array}{c}\left|a_2\right|\le min\left\{{\displaystyle \frac{\left|L_1\right|+1}{\left|{\mathsf{\Lambda }}_2\right|}},\sqrt{{\displaystyle \frac{\left|L_1\right|+\left|L_2-L_1\right|+\frac{1}{2}}{\left|{\mathsf{\Lambda }}_2^2-{\mathsf{\Lambda }}_3\right|}}}\right.\\ \left.\sqrt{{\displaystyle \frac{{\left|L_1\right|}^3+\left(2\left|L_1\right|+1\right)\left|L_2-L_1\right|+{\left|L_1\right|}^2}{\left|{\mathsf{\Lambda }}_2^2(L_1^2+L_1-L_2)-{\mathsf{\Lambda }}_3{L}_1^2\right|}}}\right\}\end{array}$$

(20)

and

$$\begin{array}{c}\left|a_3\right|\le min\left\{{\left({\displaystyle \frac{\left|L_1\right|+1}{\left|{\mathsf{\Lambda }}_2\right|}}\right)}^2+\left|{\displaystyle \frac{L_1}{{\mathsf{\Lambda }}_3}}\right|+{\displaystyle \frac{2\left|L_2-L_1\right|}{\left|{\mathsf{\Lambda }}_3{L}_1\right|}}\left(1+{\displaystyle \frac{8}{\left|L_1\right|}}\right),\right.\\ \left.\left|{\displaystyle \frac{L_1}{{\mathsf{\Lambda }}_3}}\right|+{\displaystyle \frac{2\left|L_2-L_1\right|}{\left|{\mathsf{\Lambda }}_3{L}_1\right|}}\left(1+{\displaystyle \frac{8}{\left|L_1\right|}}\right)+{\displaystyle \frac{2{\left|L_1\right|}^2+\left|L_1\right|+2}{{\left|{\mathsf{\Lambda }}_2\right|}^2}}\right\},\end{array}$$

(21)

where ${\mathsf{\Lambda }}_n={\left[n+{\displaystyle \frac{r}{2}}(1+{(-1)}^{n+1})\right]}^m{\displaystyle \frac{\Gamma \left(\vartheta \right){\left(\rho \right)}_{n-1}}{\Gamma \left(\vartheta +\theta (n-1)\right)(n-1)!}}$.

Proof. 

$\phi \in {\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$; then, we have

$${\displaystyle \frac{\xi e^{\frac{{\xi }^2{D}_r^m(\theta ,\vartheta ,\rho ){\phi }^{\prime }\left(\xi \right)}{D_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)}}}{\left[D_r^m(\theta ,\vartheta ,\rho )\phi \left(\xi \right)\right]}}=\psi \left[{\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}}\right]$$

(22)

and

$${\displaystyle \frac{w{e}^{\frac{w^2{D}_r^m(\theta ,\vartheta ,\rho ){\chi }^{\prime }\left(w\right)}{D_r^m(\theta ,\vartheta ,\rho )\chi \left(w\right)}}}{\left[D_r^m(\theta ,\vartheta ,\rho )\chi \left(w\right)\right]}}=\psi \left[s\left(w\right)\right]=\psi \left[{\displaystyle \frac{q\left(w\right)-1}{q\left(w\right)+1}}\right],$$

(23)

where $\xi$ and w belong to $\mathbb{U}$. The functions $r\left(\xi \right)$ and $s\left(w\right)$ are Schwartz functions and have the respective series expansions $r\left(\xi \right)={\displaystyle \frac{p\left(\xi \right)-1}{p\left(\xi \right)+1}}=1+{\sum }_{n=1}^{\infty }{p}_n{\xi }^n$ and $s\left(w\right)={\displaystyle \frac{q\left(w\right)-1}{q\left(w\right)+1}}=1+{\sum }_{n=1}^{\infty }{q}_n{w}^n$ with $p\left(\xi \right),q\left(w\right)\in \mathcal{P}$.

Equating the coefficients of $\xi ,{\xi }^2,w$ and $w^2$ in (22) and (23), we have

$$\left[1-a_2{\mathsf{\Lambda }}_2\right]={\displaystyle \frac{1}{2}}{L}_1{p}_1,$$

(24)

$$\left[{\displaystyle \frac{1}{2}}+{\mathsf{\Lambda }}_2^2{a}_2^2-{\mathsf{\Lambda }}_3{a}_3\right]={\displaystyle \frac{1}{2}}{L}_1\left(p_2-{\displaystyle \frac{p_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{L}_2{p}_1^2,$$

(25)

$$\left[1+a_2{\mathsf{\Lambda }}_2\right]={\displaystyle \frac{1}{2}}{L}_1{q}_1,$$

(26)

and

$$\left[{\displaystyle \frac{1}{2}}+{\mathsf{\Lambda }}_2^2{a}_2^2-{\mathsf{\Lambda }}_3(2a_2^2-a_3)\right]={\displaystyle \frac{1}{2}}{L}_1\left(q_2-{\displaystyle \frac{q_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{L}_2{q}_1^2.$$

(27)

From (24) and (26), we have

$$p_1={\displaystyle \frac{4}{L_1}}-q_1$$

and

$$8{\mathsf{\Lambda }}_2^2{a}_2^2=L_1^2\left(p_1^2+q_1^2\right)-4L_1\left(p_1+q_1\right)+8.$$

(28)

Adding Equations (25) and (27) and then by using (28) in the resulting equation, we have

$$\begin{array}{c}{a}_2^2={\displaystyle \frac{1}{\left[{\mathsf{\Lambda }}_2^2(L_1^2+L_1-L_2)-{\mathsf{\Lambda }}_3{L}_1^2\right]}}\left[{\displaystyle \frac{L_1^3\left(p_2+q_2\right)}{4}}+{\displaystyle \frac{L_1\left(p_1+q_1\right)\left(L_2-L_1\right)}{2}}\right.\\ \left.-\left(L_2-L_1\right)-{\displaystyle \frac{L_1^2}{2}}\right].\end{array}$$

(29)

In light of the known inequalities $\left|p_n\right|\le 2$ and $\left|q_n\right|\le 2$ for all $n\ge 2$, (29) reduces to the result (20). To obtain (21), subtracting (27) with (25), we have

$$\begin{array}{cc}\hfill a_3& =a_2^2+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{4{\mathsf{\Lambda }}_3}}+{\displaystyle \frac{\left(L_2-L_1\right)}{{\mathsf{\Lambda }}_3{L}_1}}\left(p_1-{\displaystyle \frac{16}{L_1}}\right)\hfill \\ \hfill & ={\displaystyle \frac{L_1^2\left(p_1^2+q_1^2\right)}{8{\mathsf{\Lambda }}_2^2}}-{\displaystyle \frac{L_1}{2{\mathsf{\Lambda }}_2^2}}+{\displaystyle \frac{1}{{\mathsf{\Lambda }}_2^2}}+{\displaystyle \frac{L_1\left(p_2-q_2\right)}{4{\mathsf{\Lambda }}_3}}+{\displaystyle \frac{\left(L_2-L_1\right)}{{\mathsf{\Lambda }}_3{L}_1}}\left(p_1-{\displaystyle \frac{16}{L_1}}\right).\hfill \end{array}$$

Now using (28) in the above equality, we can obtain the result for (21). Hence, the proof of the theorem is found. □

Taking $m=\theta =0$ and $\rho =1$ in Theorem 3, we obtain the following result:

Corollary 2.

Let $\phi \in \mathcal{A}$ and let χ be the inverse of φ defined by

$${\phi }^{-1}\left(w\right)=w+\sum _{k=2}^{\infty }{b}_k{w}^k,\left(\right|w|<r;r\ge 1/4),$$

satisfying the conditions

$${\displaystyle \frac{\xi e^{\frac{{\xi }^2{\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}}{\phi \left(\xi \right)}}\prec \psi \left(\xi \right)\mathrm{and}{\displaystyle \frac{w{e}^{\frac{w^2{\chi }^{\prime }\left(w\right)}{\chi \left(w\right)}}}{\chi \left(w\right)}}\prec \psi \left(w\right),$$

then

$$\begin{array}{c}\left|a_2\right|\le min\left\{\left|L_1\right|+1,\sqrt{{\displaystyle \frac{{\left|L_1\right|}^3+\left(2\left|L_1\right|+1\right)\left|L_2-L_1\right|+{\left|L_1\right|}^2}{\left|L_1-L_2\right|}}}\right\}\end{array}$$

and

$$\begin{array}{c}\left|a_3\right|\le min\left\{{\left(\left|L_1\right|+1\right)}^2+\left|L_1\right|+{\displaystyle \frac{2\left|L_2-L_1\right|}{\left|L_1\right|}}\left(1+{\displaystyle \frac{8}{\left|L_1\right|}}\right),\right.\\ \left.\left|L_1\right|+{\displaystyle \frac{2\left|L_2-L_1\right|}{\left|L_1\right|}}\left(1+{\displaystyle \frac{8}{\left|L_1\right|}}\right)+2{\left|L_1\right|}^2+\left|L_1\right|+2\right\}.\end{array}$$

Letting $\psi \left(\xi \right)={\displaystyle \frac{1+\xi }{1-\xi }}$ and $\varphi \left(w\right)={\displaystyle \frac{1+w}{1-w}}$ in the Corollary 2, we can obtain the following result:

Corollary 3.

Let $\phi \in \mathcal{A}$ and let χ be the inverse of φ defined by

$${\phi }^{-1}\left(w\right)=w+\sum _{k=2}^{\infty }{b}_k{w}^k,\left(\right|w|<r;r\ge 1/4),$$

satisfying the conditions

$$Re\left\{{\displaystyle \frac{\xi e^{\frac{{\xi }^2{\phi }^{\prime }\left(\xi \right)}{\phi \left(\xi \right)}}}{\phi \left(\xi \right)}}\right\}>0\mathrm{and}Re\left\{{\displaystyle \frac{w{e}^{\frac{w^2{\chi }^{\prime }\left(w\right)}{\chi \left(w\right)}}}{\chi \left(w\right)}}\right\}>0,$$

then $\left|a_2\right|\le 3\mathrm{and}\left|a_3\right|\le 11.$

5. Conclusions

The classes studied in this paper are neither a subclass nor a generalization of the well-known classes like spirallike, starlike and convex. The present study is an extension of new class studied by Karthikeyan and Murugusundaramoorthy in [13], where we can find detailed the properties and applications of the defined function class. Specializing the parameters involved in Definitions 1 and 2, the introduced function classes reduce to classes with good geometrical implications. So, the results that we have obtained have lots of applications other than those that were pointed out here.

If we let $L_1={\displaystyle \frac{4}{5}}$ in (4), then it would lead to $p_1+q_1=5$, which is absurd. Now the question arises regarding how the definition ${\mathcal{BR}}_r^m(\theta ,\vartheta ,\rho ;\psi )$ should be reformulated so that the inequalities remain valid for all values of $L_1$. Further, could the classes be extended by replacing the ordinary derivative with a higher-order multiplicative derivative in the analytic characterization of the well-known geometrically defined subclasses of univalent functions?