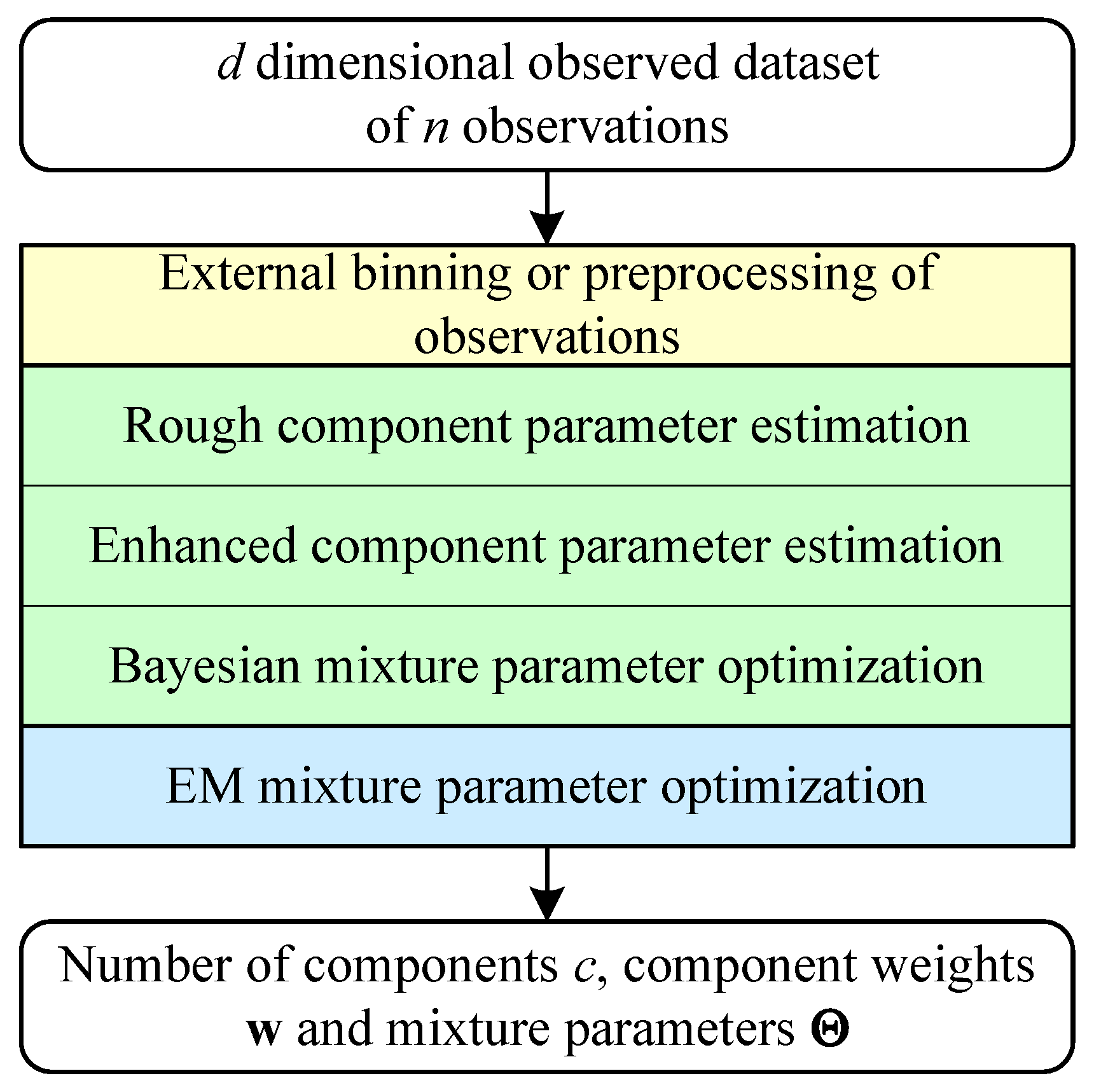
Nevertheless, the introduction of the EM algorithm into the estimation procedure did not solve the problems of optimising the spurious optima with overlapping components in the FMM. We have found that the main problems lie in the rough parameter estimation step and the Bayesian mixture parameter optimisation step, which we will discuss in more detail in the following text.
2.2.1. Rough Parameter Estimation
The rough parameter estimation phase is the most important step in the REBMIX algorithm. In this phase, rough parameters for the
lth component are estimated based on the global mode position
and its probability density
. These parameters are then used to cluster observations between the
lth component and the residue, as detailed in [
35,
37]. Unlike algorithms such as
k-means, which depends exclusively on the positions of observations and their distances, REBMIX utilizes additional information from the data set. It not only considers the positions of observations but also identifies the global mode, a distinctive feature of the data set. The determination of the empirical densities
by histogram preprocessing or external binning of the observations into
nonempty bins also substantially reduces computational time, especially for large data sets. For small data sets, kernel density estimation or
k-nearest neighbour may be preferable for preprocessing the observations.
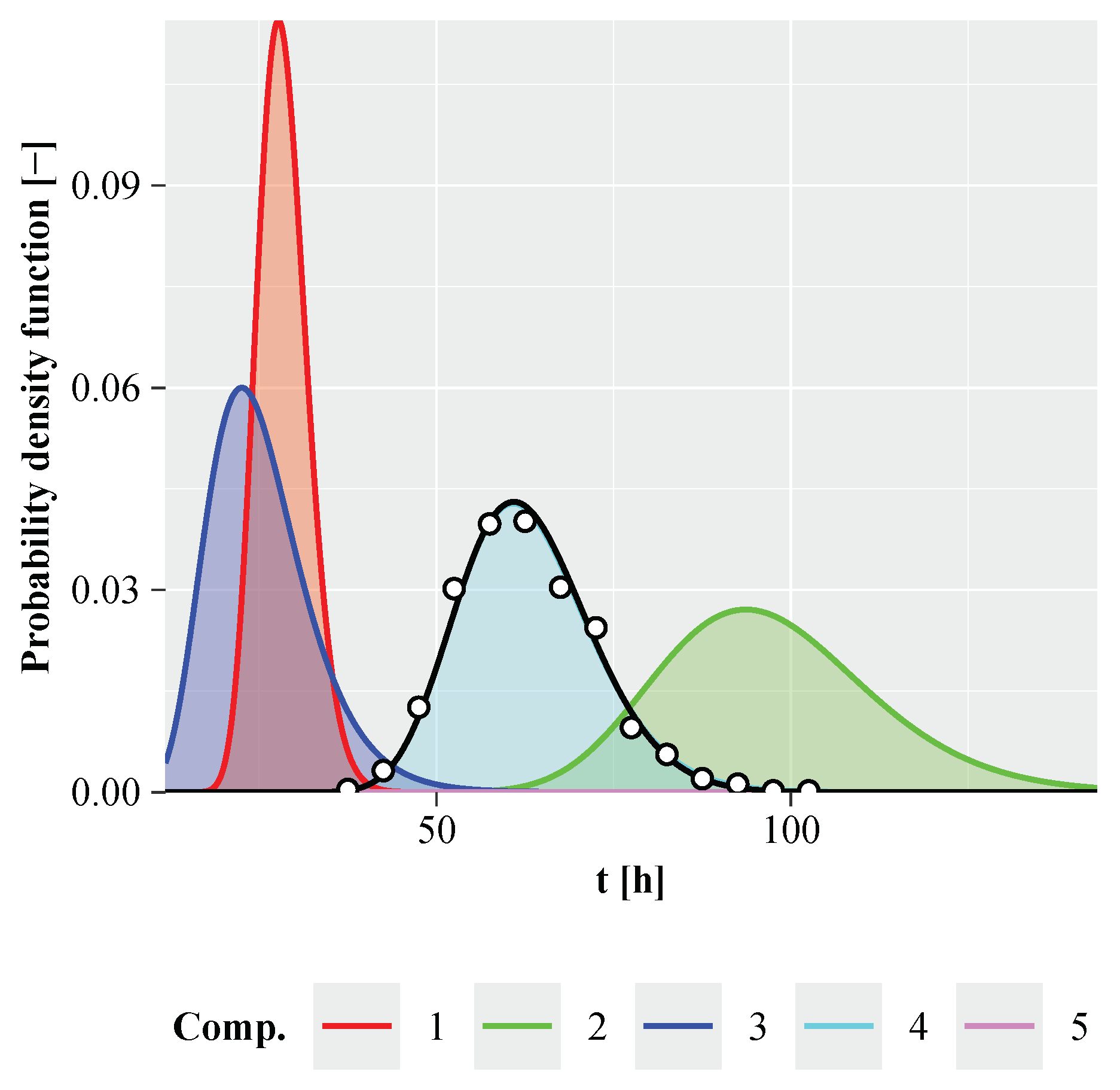
However, a fundamental problem, illustrated in
Figure 2, remains unresolved.
Figure 2 presents three plots, where rough component parameter estimation is depicted on three different estimation cases, namely a FMM with non-overlapping components (the plot on the left), moderately (the middle plot) and heavy overlapping components (the plot on the right). In all three plots, the residue is shown in green, the
lth component in red and the FMM probability density as a black line. The global mode is indicated by a black circle, while the mode of the true
lth component is indicated by a red circle. The true residue probability density at the global mode is shown by a green circle. The left and right global minima are represented by a black triangle pointing upwards and a triangle pointing downwards, respectively. The rough probability density of the
lth component is depicted by a thin red solid line, and the loose probability density of the
lth component is shown by a thin blue line.
The empirical density of the global mode
belongs exclusively to the
lth component only if the components are well separated (see red circle in left plot of
Figure 2), which overlaps the black circle. This is generally not the case for moderately or heavily overlapping components, as shown in the middle and right plots of
Figure 2. In these cases, the red and black circles are misaligned. The approach proposed in [
38], which is implemented in the package
rebmix version 2.15.0 and older remains accurate only under conditions where components are well separated, as shown in the left plot of the
Figure 2, or if a single component of the residue contributes to
, as shown in the middle plot of the
Figure 2. Cases where multiple components contribute to the
lth component, as illustrated in the right plot of the
Figure 2, may lead to estimation errors in
. According to [
38], the wider component of the residue in the middle plot of the
Figure 2 (mean
, standard deviation
) is extracted before the dominant
lth narrower component (
,
), which is suboptimal. Ideally, the dominant component in red, centred on
, should be extracted first. The refined rough parameter estimation, which addresses the the aforementioned issues, is outlined below.
After preprocessing or external binning of observations, the empirical probability densities
(black solid line) are obtained, from which the global mode position
and the corresponding value
can be readily identified. The true component probability density
, marked by the red circle, and the true probability density of the residue
marked by the green circle, are not available at this stage. Assume that the weight of the
lth component is
and that
. In other words, the thin red line representing the envelope under which the entire
lth component is believed to be contained can be calculated and visualised. The component parameters
of the red thin lines in
Figure 2 were connected to rigid restraints for the first time in [
38]. It was further demonstrated in [
38] that the rigid restraints alone are not sufficient to accurately restore the components of the residue when they overlap. Furthermore, an iterative procedure for defining the rough component parameters based on loose restraints was proposed in [
38].
If we carefully observe the area between the red thin lines and the black lines in
Figure 2, we can see that there is a global minimum
(triangle pointing upwards) to the left of
and another
(triangle pointing downwards) to the right of the global mode. At the beginning let
or equivalently
. Then
The sum of the differences between the empirical densities and the corresponding probability densities of the
lth component
is also calculated, where
h stands for the bin widths. Next, the number
and the density
are both initialised to zero. If
and
,
is incremented and
is increased by
. Similarly, if
and
,
and
. Finally, if
,
. The loose restraints then lead to
from which the loose rough component parameters,
, are calculated as explained in
Appendix A.1. For simpler notation, let
and
. In
Figure 2, the probability densities of the
lth component associated with the loose restraints are shown as thin blue lines.
Equation (
8) is valid only for non-overlapping bins. For kernel density estimation, the histogram is constructed with one bin aligned with
. Similarly, for
k-nearest neighbour, the histogram is constructed with one bin aligned with
. Here,
, where
denotes the mean Euclidean distance to the first non-coincident nearest neighbour. Further details on the estimation of the rough component parameters can be found in [
35,
37].
2.2.2. Bayesian Mixture Parameter Optimisation
The REBMIX algorithm clusters an observed data set of size n into c clusters of sizes associated with component probability densities and component weights . The clustering is designed to minimise both the sum of the positive relative deviations and the information criterion. As a result, the sum of the component weights satisfies , meaning that some observations may remain unassigned.
At the beginning, the number of outliers
N is set to zero and the initial first moments
and second moments
are taken from
Appendix A.3. The remaining observations are then allocated to the existing components based on the Bayes decision rule
For each observation, it is also determined whether it is an outlier. Outliers are identified as those that fall into the left or right tail of the probability density with a probability of
. If the observation is recognised as an outlier, then
. Otherwise
This ensures that the outliers do not influence
and
. A detailed explanation of the frequencies
associated with the densities
can be found in [
35].
After processing
v bins or
n observations, depending on the type of preprocessing, the component weights are recalculated
to fulfil
. The initial FMM parameters for the EM are finally obtained by inverting Equations (
A22)–(
A27). The lognormal parameters result from
The Weibull parameters are a solution of
To avoid numerical problems, the minimum value of
was set to
. If Equation (
17) returns a value less than or equal to zero, then
is set to
. Otherwise,
is used as the initial estimate. The gamma parameters are given by
This section introduces an important improvement with the inclusion of outliers, as compared to [
14].