A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks

Abstract

At the end of the 20th century, the rapid development of brain-like dynamics was attributed to the excellent modeling of numerous neurons and neural systems, which effectively simulated biological behaviors observed in the human brain. With the continuous advancement of research, memristive neural networks (MNNs) have been extensively studied. In recent years, the exploration of fractional-order MNNs (FMNNs) has attracted research interest, leading to the discovery of the system’s dynamical phenomena, including transient chaos, hyperchaos, multi-stability, and the coexistence of attractors. To facilitate comparative research and learning, a review of the newly proposed fractional-order chaotic system models in recent years is urgently needed. In this review, we first introduce the basic theoretical knowledge of chaotic dynamics, artificial neural networks, fractional order, and memristors. Then, we mathematically describe the fractional-order systems and detail the highly regarded FMNNs in recent years, making comparative discussions and studies. Finally, we discuss the application of these models across diverse domains and propose thought-provoking questions and future research directions.

1. Introduction

Chaotic dynamics [1,2,3], as an important branch of complexity science, has been gradually confirmed to be widely present in various fields since the 1970s [4,5,6,7,8,9,10,11,12,13,14]. Research shows that the human brain’s neuronal activities exhibit chaotic characteristics, which are sensitive to initial conditions [15,16,17,18,19,20]. Over the last few decades, mathematical models such as Hodgkin–Huxley (HH) [21], FitzHugh–Nagumo (FHN) [22,23], Hindmarsh–Rose (HR) [24] neurons, well-known Hopfield neural networks (HNNs) [25], cellular neural networks (CNNs) [26], and heterogeneous neural networks [27,28,29,30] have been established to capture the dynamical behaviors of biological neurons and networks. Through the analysis of these models, many brain-like dynamic characteristics such as chaos, hyperchaos [31,32,33,34], transient chaos [35,36,37], coexistence of attractors [38,39,40], and multi-stability [41,42,43] have been discovered. With the progress of research, people hope to find more accurate and complete methods to simulate the nervous system.

So far, fractional calculus has been widely applied in deep learning [44,45], image processing [46,47], biomedicine [48,49], and other fields. Given the complexity of the human brain system, fractional calculus has been introduced to enhance the accuracy of modeling neuronal discharge behavior and synaptic connectivity [50,51,52,53]. There are mainly three definitions of fractional calculus operations: Riemann–Liouville [54], Caputo [55], and Grunwald–Letnikov [56] definitions. The R-L operator and the G-L operator were proposed successively and widely applied in theoretical mathematical research. In applied mathematics, the Caputo operator is widely used due to its ease of computation and the property of carrying initial values, this characteristic of being sensitive to initial values not only facilitates its numerical calculation but also makes chaotic phenomena such as the multi-stability of the system more likely to occur. As early as the early 21st century, it was confirmed that fractional-order systems can generate chaos, such as fractional-order Chua [57], fractional-order Duffing [58], fractional-order Chen [59], and fractional-order Lu systems [60], which provides the possibility of introducing fractional operators into neural networks to construct chaotic systems.

Fractional-order neural networks (FNNs) can more accurately describe the cross-time-scale dynamic responses of neurons by introducing time memory kernel functions [61,62,63]. Fractional calculus was first applied in CNNs to generate chaotic phenomena. In 1998, P. Arena systematically discussed the chaotic and bifurcation behaviors of non-integer-order CNNs of less than the third order [64]. Two years later, he studied a second-order non-integer-order CNN system and discovered strange attractors in this system [65]. In 2006, I. Petras first proposed a three-neuron fractional-order CNN (FCNN) and confirmed the existence of solutions (attractors) in FCNNs [66]. With its complex and excellent dynamic characteristics, HNNs have been widely applied in the research of chaotic systems. Since A. Boroomand first studied a fractional-order HNN (FHNN) in 2009 [67], recent research on continuous-time FHNNs has flourished [50,51,68,69,70,71,72,73,74,75]. Xu et al. compared two parts of an integer-order coupled FHNN and concluded that the chaotic effect of an FHNN is better [76]. The continuous-time dynamic characteristics of traditional HNNs are easily disturbed by noise in hardware implementation. However, discrete fractional-order systems have the characteristics of strong stability and easy hardware implementation, so people have gradually turned their attention to the research of discrete-time FHNNs (DFHNNs) [77,78,79,80,81,82,83]. In 2022, Abbes et al. studied a three-neuron DFHNN and discovered chaos [80]. In the same year, Rabia et al. extended the concept of non-integer-order neural networks by proposing a polynomial-order DFHNN [81]. Additionally, many scholars have investigated the characteristics of systems such as HR [84,85], FHN [86], and other fractional-order systems [87,88,89,90,91]. These extended models offer novel insights into the mechanisms of memory storage dynamics in the nervous system through fractional-order analysis.

As the fourth fundamental circuit element that was theoretically predicted by Leon Chua in 1971 [92] and first physically realized by Hewlett–Packard Laboratories in 2008 [93], the memristor’s hysteresis property is highly consistent with the weight plasticity of biological synapses [94,95,96,97,98,99,100,101]. Moreover, its hardware-friendly nature enables MNNs to exhibit unique advantages in fields such as brain-inspired computing [102,103] and chaotic encryption [104,105,106]. Numerous researchers have conducted chaos studies in fractional-order memristive systems [107,108,109,110,111]. In 2023, Lin et al. systematically reviewed the latest research progress of MNNs and provided a general method for memristor-coupled neural networks [112], making it possible to construct FMNNs. Over the last few years, numerous MNNs have been studied in both continuous-time fractional-order [113,114,115,116,117,118,119,120,121,122,123] and discrete-time fractional-order [124,125,126] domains. Yu [118], Li [119], and Ding [120], respectively, investigated fractional-order memristive HR neural systems and discovered chaotic attractors existing in the systems. Ding studied a chaotic fractional-order memristive HNN (FMHNN) in 2022 and ultimately implemented it systematically using the ADM decomposition method [121]. Yao et al. studied fractional-order memristive FHN neural networks and confirmed the non-periodicity of the fractional-order system. In a discrete fractional-order domain, Lu implemented a discrete fractional-order memristive Rulkov neural system in 2022 [124]. Li et al. recently implemented a discrete FMHNN and provided the first FPGA implementation method [126]. Meanwhile, research on fractional-order in chaotic mappings is also steadily progressing [127,128]. Through these studies, scholars are moving towards more precise brain-like models.

According to our investigation, there are currently only three reviews on the fractional-order direction, namely the application of fractional-order operators in the modeling and control of robot manipulators [129], the application of fractional calculus in mathematical economics [130], and a review on the digital implementation of continuous-time fractional-order chaotic systems using FPGA and embedded hardware [131]. Although ref. [131] mentioned some fractional-order chaotic systems, it focused on introducing the hardware implementation methods of the circuits and did not classify and analyze the fractional-order systems and their chaotic behaviors. This paper summarizes most of the existing fractional-order chaotic neural networks, and in Section 2, it presents the methods for constructing continuous and discrete-time fractional-order networks using fractional-order operators. In Section 3, the popular models in recent years are classified and introduced, respectively, by dividing the network into continuous-time systems and discrete-time systems. In Section 4, it presents the current problems and future development directions of fractional-order systems. Finally, in Section 5, the conclusions are presented.

2. The Construction Theory of FMNNs

In this section, we will focus on introducing the general methods for constructing continuous-time and discrete-time FMNNs using fractional-order operators. For continuous-time fractional calculus, we have defined the three common calculus operators, namely G-L, R-L, and Caputo, and presented the methods for calculating the approximate solutions of continuous fractional-order systems. For discrete-time fractional differences, we only discuss the most common discrete fractional Caputo operator.

2.1. Continuous-Time Fractional Differential Theory

Fractional operators are an important component of the fractional calculus theory, and their definition is as follows [132]:

$${}_{t_0}\mathit{D}_t^{\alpha }f\left(t\right)=\left\{\begin{array}{c}{\displaystyle \frac{{\mathrm{d}}^q}{\mathrm{d}{t}^q}}q>0\hfill \\ 1q=0\hfill \\ {\int }_{t_0}^t{\left(\mathrm{d}t\right)}^{-q}q<0\hfill \end{array}\right.$$

(1)

Among them, the parameter q is the order of the fractional derivative, $t_0$ is the lower limit of the fractional calculus, and t is the upper limit of the fractional calculus. Next, we introduce the three definitions of fractional calculus.

2.1.1. G-L Definition

If the function $f\left(t\right)$ has an nth derivative on the interval $[t_0,t]$, when $q>0$, n should be at least q, then the definition of the fractional derivative of order $q\in [n,n+1)$ is [56]

$${}_{t_0}\mathit{D}_{\mathit{GL}}^{q}f\left(t\right)=\underset{h\to 0}{lim}{h}^{-q}\sum _{i=0}^{\left[\right(t-q)/h]}{\omega }_i^{q}f(t-ih)$$

(2)

where h is the sampling step size, and $t_0$ and t in (1) represent the same. $\left[\right]$ denotes the symbol for the integer part and ${\omega }_i^q$ is the polynomial coefficient, where

$${\omega }_i^q={(-1)}^i\left(\begin{array}{c}q\\ i\end{array}\right),\left(\begin{array}{c}q\\ i\end{array}\right)={\displaystyle \frac{q(q-1)(q-2)...(q-i+1)}{i!}}$$

(3)

A simple algorithm for ${\omega }_i^q$ is given as shown in (4):

$${\omega }_0^q=1,{\omega }_i^q=(1-{\displaystyle \frac{q+1}{i}}){\omega }_{i-1}^q,i=1,2,...,n$$

(4)

Taking the limit of Equation (2) again leads to the fractional calculus defined by G-L, as defined below:

$$\begin{array}{c}\hfill {}_{t_0}\mathit{D}_{\mathit{GL}}^{q}f\left(t\right)=\underset{h\to 0,nh=t-t_0}{lim}{h}^{-q}\left(\begin{array}{c}q\\ i\end{array}\right)f(t-ih)\\ \hfill =\sum _{i=0}^n{\displaystyle \frac{f^i\left(t_0\right){(t-t_0)}^{-q+i}}{\Gamma (-q+i+1)}}+{\displaystyle \frac{1}{\Gamma (-q+i+1)}}{\int }_{t_0}^t(t-\xi )f^{n-q}\left(\xi \right)\mathrm{d}\xi \end{array}$$

(5)

The gamma function is denoted by $\Gamma (.)$ and its expression is as follows:

$$\Gamma \left(w\right)={\int }_0^{\infty }{e}^{-\xi }{\xi }^{w-1}\mathrm{d}\xi$$

(6)

2.1.2. R-L Definition

The definition of the R-L fractional differential can be referred to [61,62], and its specific mathematical expression is

$${}_{t_0}\mathit{D}_{\mathit{RL}}^{q}f\left(t\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\Gamma (n-q)}}{\displaystyle \frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}}{\int }_{t_0}^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{q+1-n}}}\mathrm{d}\tau n-1\le q<n\hfill \\ {\displaystyle \frac{{\mathrm{d}}^{n}f\left(t\right)}{\mathrm{d}{t}^n}}q=n,\hfill \end{array}\right.$$

(7)

The meaning of each quantity in the formula can be referred to (1); for the convenience of organization and calculation, it is usually necessary to perform a Laplace transform on (7), for which the result is

$$L\left\{{}_{t_0}\mathit{D}_{\mathit{RL}}^{q}f\left(t\right)\right\}=s^{q}F\left(s\right)-\sum _{i=0}^{n-1}{}_{t_0}\mathit{D}_{\mathit{t}}^{\mathit{q-i-1}}f\left(t\right){|}_{t=0^{+}}$$

(8)

Equation (8) is presented in a form that is easy to accept and calculate. Since its independent variable is s in the frequency domain, it is often used for the frequency domain analysis of fractional-order equations.

2.1.3. Caputo Definition

Since the G-L definition and R-L definition do not involve initial values, they are not conducive to a direct calculation. However, in actual engineering, it is often necessary to set an interface for initial values to facilitate iterative calculation. Therefore, a more practical fractional operation definition method is needed. The Caputo definition is suitable for systems that require the use of initial values. At the same time, the Laplace transform of the Caputo derivative can be explained using known physics [132], which makes the Caputo definition more widely accepted by scholars and used in actual mathematical operations and engineering applications. The following is the definition of Caputo fractional calculus [133]: the Caputo fractional derivative of $f\left(t\right)$ is defined as

$${}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}f\left(t\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{\Gamma (n-q)}}{\int }_{t_0}^t{\displaystyle \frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{q+1-n}}}\mathrm{d}\tau n-1\le q<n\hfill \\ {\displaystyle \frac{{\mathrm{d}}^{n}f\left(t\right)}{\mathrm{d}{t}^n}}\hspace{1em}q=n.\hfill \end{array}\right.$$

(9)

The expression of $\Gamma (.)$ is given by (6). From (9), it can be seen that when the fractional order q approaches n infinitely, the Caputo fractional calculus can be regarded as the nth derivative of the function $f\left(t\right)$.

By observation, (7) and (9) are structurally similar because (9) interchanges the order of integration and differentiation in (7), thereby forming a new fractional operator. When the initial value $t_0=0$, the error between the two can be expressed by [56,134]

$$D_{Ca}^{q}f\left(t\right)=D_{RL}^{q}f\left(t\right)-\sum _{i=0}^{n-1}{r}_i^q\left(t\right)f^{\left(i\right)}\left(0\right),r_i^q\left(t\right)={\displaystyle \frac{t^{i-q}}{\Gamma (i+1-q)}}.$$

(10)

2.2. Continuous Fractional Approximate Solution Methods

The approximate solution methods for fractional calculus can be roughly classified into time-domain methods and frequency-domain methods. Research has found that the Adams–Bashforth–Moulton (ABM) algorithm has higher solution accuracy and faster solution speed. In [135], it was proved to be a simple and error-controllable prediction estimation algorithm, and it has better fitting characteristics compared with other estimation algorithms. Therefore, in this paper, we will introduce this fractional-operation numerical solution prediction-iteration algorithm, and use the Caputo calculus operator as an example to show the results and calculate the error. The reason for choosing the Caputo operator is that when dealing with specific physical applications, the unknown quantities usually have certain physical meanings, but sometimes, we are not sure what the physical meaning of the fractional derivative of the unknown is, which makes it difficult to handle the data. However, when we deal with fractional equations defined by the Caputo operator, we can specify the initial values, the function values themselves, and the integer-order derivatives [136], and these data usually have easily understandable physical meanings and can be measured through practical operations.

First, let us introduce two integral approximation methods, which will be used in numerical calculations, namely the product trapezoidal rule approximation equation and the product rectangular rule approximation equation, which are (11) and (12), respectively:

$${\int }_a^{b}g\left(z\right)dz\approx {\displaystyle \frac{b-a}{2}}\left(g\left(a\right)+g\left(b\right)\right)$$

(11)

$${\int }_a^{b}g\left(z\right)dz\approx (b-a)g\left(a\right)$$

(12)

Next, based on [135], we assume that the fractional operation of the Caputo operator on $f\left(t\right)$ is a function with t as the independent variable, which is specifically expressed as

$${}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}f\left(t\right)=x(t,f\left(t\right))$$

(13)

where $f\left(0\right)=f_0,q\in (0,1),t_0=0$. Let us use $f_h\left(t\right)$ to represent the numerical value of $f\left(t\right)$, and we can simultaneously represent (13) in a computable form with initial values as follows:

$$f_h\left(t\right)=\sum _{k=0}^{\lceil q\rceil -1}{f}_0^{\left(k\right)}{\displaystyle \frac{t^k}{k!}}+{\displaystyle \frac{1}{\Gamma \left(q\right)}}{\int }_0^t{(t-\tau )}^{q-1}x(\tau ,f_h\left(\tau \right))\mathrm{d}\tau$$

(14)

Since $q\in (0,1)$, the initial-value part is equal to $f_0$. Thus, (14) can be rewritten in a simpler form:

$$f_h\left(t\right)=f_0+{\displaystyle \frac{1}{\Gamma \left(q\right)}}{\int }_0^t{(t-\tau )}^{q-1}x(\tau ,f_h\left(\tau \right))d\tau$$

(15)

The range of $t\in [0,T]$ has a step size of $h=T/N$, where $t_n=nh,n=0,1,...,N,$ and N is a positive integer greater than 0. For the integral part on the right side of the equation, we approximate its value:

$${\int }_0^{t_{n+1}}{(t_{n+1}-\tau )}^{q-1}x\left(\tau \right)\mathrm{d}\tau \approx {\int }_0^{t_{n+1}}{(t_{n+1}-\tau )}^{q-1}{\tilde{x}}_{n+1}\left(\tau \right)\mathrm{d}\tau$$

(16)

Here, ${\tilde{x}}_{n+1}\left(t\right)$ is the piecewise linear interpolation of $x\left(t\right)$, with nodes and knots chosen at $t_j$, $j=0,1,2,\dots ,n+1$. Using the standard techniques of the quadrature theory [137], we find that the integral on the right-hand side of (16) can be written as

$${\int }_0^{t_{n+1}}{(t_{n+1}-\tau )}^{q-1}{\tilde{x}}_{n+1}\left(\tau \right)\mathrm{d}\tau ={\displaystyle \frac{h^q}{q(q+1)}}\sum _{j=0}^{n+1}{\beta }_{j,n+1}x\left(t_j\right)$$

(17)

By substituting (17) into (15), and according to $\Gamma \left(q\right)q(q+1)=\Gamma (q+2)$, we can obtain

$$f_h\left(t_{n+1}\right)=f_0+{\displaystyle \frac{h^q}{\Gamma (q+2)}}\sum _{j=0}^{n+1}{\beta }_{j,n+1}x\left(t_j\right)$$

(18)

among which

$${\beta }_{j,n+1}=\left\{\begin{array}{c}{n}^{q+1}-(n-q){(n+1)}^q,j=0\hfill \\ {(n-j+2)}^{q+1}+{(n-j)}^{q+1}-2(n-j+1),1\le j\le n\hfill \\ 1,j=n+1\hfill \end{array}\right.$$

(19)

According to the the fractional variant of the one-step Adams–Moulton method, if we take the case where $j=n+1$ separately, we can obtain

$$f_h\left(t_{n+1}\right)=f_0+{\displaystyle \frac{h^q}{\Gamma (q+2)}}x(t_{n+1},f_h^p\left(t_{n+1}\right))+{\displaystyle \frac{h^q}{\Gamma (q+2)}}\sum _{j=0}^n{\beta }_{j,n+1}x(t_j,f_h\left(t_j\right))$$

(20)

We only need to calculate the predicted value $f^p\left(t_{n+1}\right)$. Based on Equation (12), we again replace the integral part on the right side of (15) with

$$f_h^p\left(t_{n+1}\right)=f_0+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=0}^n{\alpha }_{j,n+1}x(t_j,f_h\left(t_j\right)),{\alpha }_{j,n+1}={\displaystyle \frac{h^q}{q}}({(n+1-j)}^q-{(n-j)}^q)$$

(21)

Then, the corrected result can be obtained:

$$\left\{\begin{array}{c}{f}_h^p\left(t_{n+1}\right)=f_0+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=0}^{n+1}{\beta }_{j,n+1}x(t_j,f_h\left(t_j\right))\hfill \\ f_h\left(t_{n+1}\right)=f_0+{\displaystyle \frac{h^q}{\Gamma (q+2)}}x(t_{n+1},f_h^p\left(t_{n+1}\right))+{\displaystyle \frac{h^q}{\Gamma (q+2)}}\sum _{j=0}^{n+1}{\alpha }_{j,n+1}x(t_j,f_h\left(t_j\right))\hfill \end{array}\right.$$

(22)

At this point, the approximate solution of $f\left(t_{n+1}\right)$ has been obtained. According to [135], the error between $f_h\left(t_{n+1}\right)$ and $f\left(t_{n+1}\right)$ is

$$\underset{j=0,1,...,N}{max}|f\left(t_j\right)-f_h\left(t_j\right)|=O\left(h^P\right),$$

(23)

where

$$P=min(2,1+q)$$

(24)

2.3. Discrete-Time Fractional Differential Theory and Numerical Calculation

Research on the discrete fractional difference field is not as extensive as that of the former. So far, most researchers have focused on the discretization study of the Caputo operator. Therefore, the discrete Caputo fractional difference operation is defined as follows:

Definition 1.

([55]). Given a relation $f:N_{n_0}\to R$, for a discrete function $f\left(n\right)$ with forward difference $\Delta f\left(n\right)$, the fractional sum of the fractional system can be obtained as

$${\Delta }_{n_0}^{-q}f\left(n\right)={\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{i=n_0}^{n-q}{\left(n-\sigma \left(i\right)\right)}^{(q-1)}f\left(i\right)$$

(25)

Then, the discrete-time fractional Caputo difference operator is defined as follows:

$$C{\Delta }_{n_0}^{q}f\left(n\right)={\displaystyle \frac{1}{\Gamma (m-q)}}\sum _{i=n_0}^{n-(m-q)}{(n-\sigma \left(i\right))}^{(m-q-1)}{\Delta }^{m}f\left(i\right)$$

(26)

where $n\in N_{n_0+m-q}$ is a time scalar and takes discrete values $(n_0,n_0+1,n_0+2...)$; n is a discrete time; $n_0$ is the initial point; and $\Gamma (.)$ is the Gamma function. $\sigma \left(i\right)=i+1$, $m=\lceil q\rceil$, and

$$n^{\left(q\right)}={\displaystyle \frac{\Gamma (n+1)}{\Gamma (n+1-q)}}$$

(27)

Definition 2.

([133]). The Caputo difference operator can be used to construct the Caputo difference equation:

$$\begin{array}{c}\hfill C{\Delta }_{n_0}^{q}f\left(n\right)=x(n+q-1,f(n+q-1)),{\Delta }^{k}f\left(p\right)=c_k,k=0,1,\dots ,m-1\end{array}$$

(28)

Definition 3.

([133]). Converting the differential Equation (28) into a solution form for a single element gives

$$f\left(n\right)=f\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{i=n_0+m-q}^{n-q}\left({(n-\sigma \left(i\right))}^{(q-1)}\right)x((i+q-1),f(i+q-1))$$

(29)

Setting $i+q=j$, the fractional-order equation with initial value can be obtained as follows:

$$f\left(n\right)=f\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}x((j-1),f(j-1))$$

(30)

3. Fractional-Order Memristive Neural Networks

In this section, we will introduce several classic FMNNs. First, the fractional-order memristor model is presented, followed by the mathematical expression of the final model of the fractional-order memristor-coupled neural network. We will provide the mathematical models of the fractional-order memristor-coupled continuous and discrete-time neurons (FMNNs).

3.1. Continuous-Time Fractional-Order Memristor Neural Networks

We will specifically explain how the fractional-order operator works by using systems composed of fractional-order memristor neural networks. Existing neural networks include HR, FHN, heterogeneous, HNNs, CNNs, etc. First, we introduce the continuous-time memristor model.

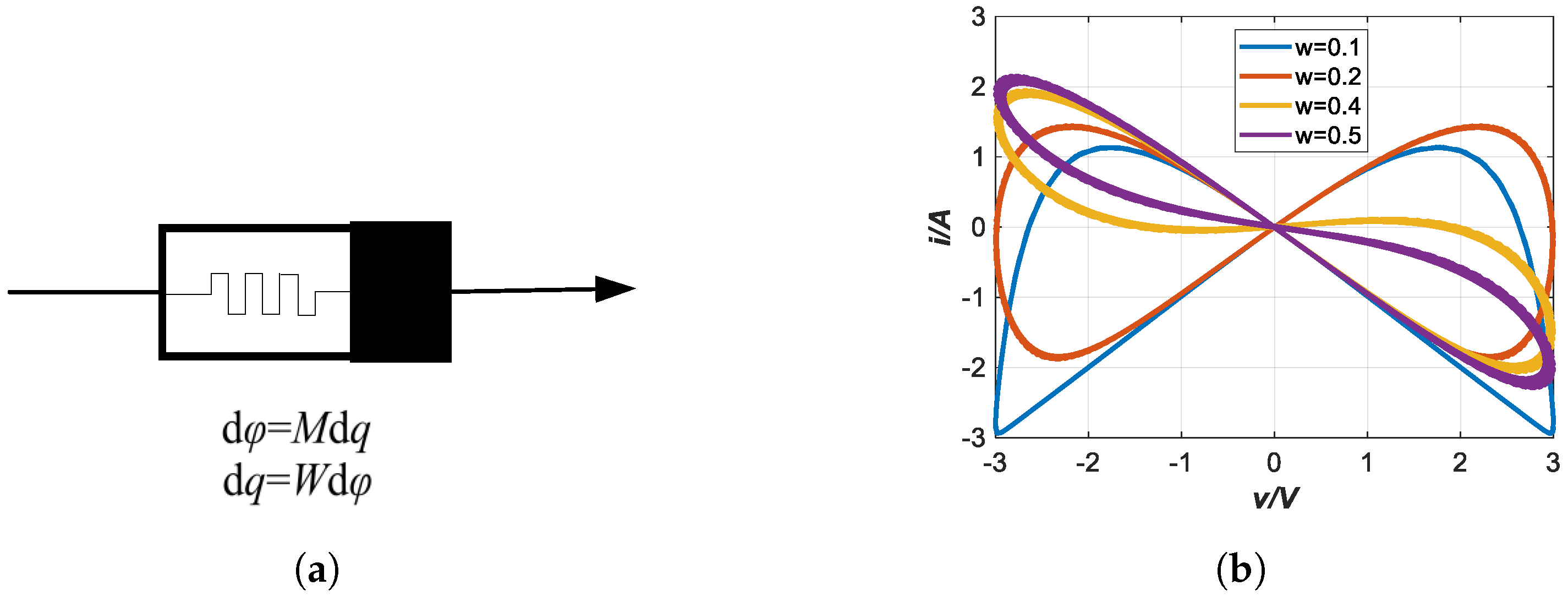
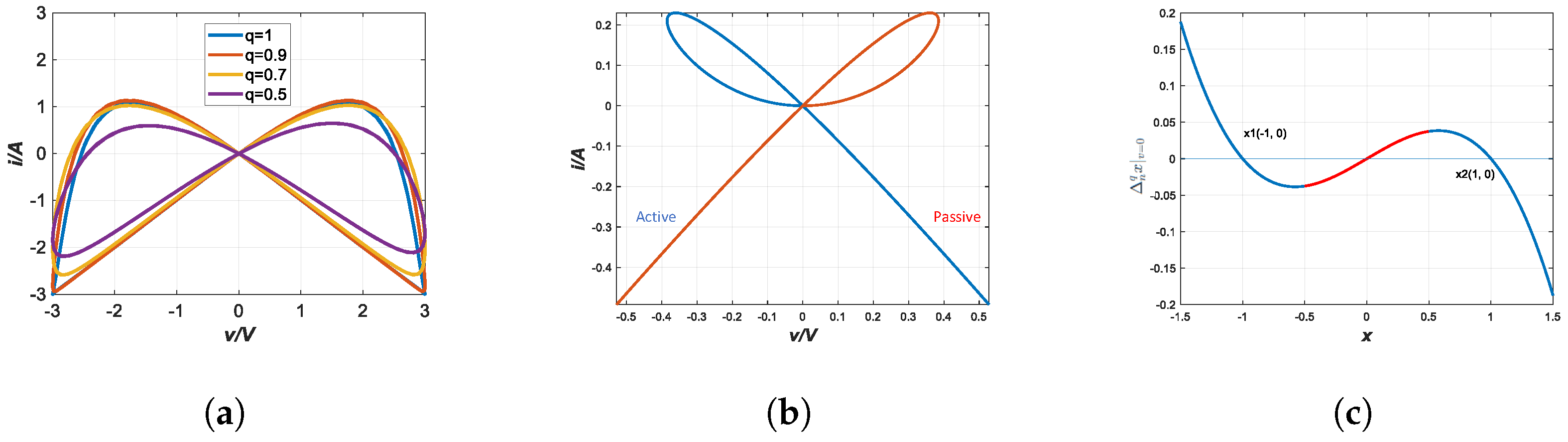
3.1.1. Continuous-Time Memristor Model

The contemporary definition of a memristor is a device with pinched hysteresis loops at both ends, such that when driven by any periodic voltage or current signal, the hysteresis loop always passes through the origin of the voltage-current plane, and as the input frequency increases to infinity, the $i-v$ curve degenerates into a straight line passing through the origin, thereby generating a periodic response of the same frequency [138,139,140]. The memristor symbol and the relationship between the physical quantities that it characterizes are shown in Figure 1a, where M and W represent memristance and memconductance, respectively, $\varphi$ is the magnetic flux, and q is the charge. Figure 1b characterizes its hysteresis loop characteristics; here, the memristor is the hysteresis loop of the fractional-order memristor in [126]. It can be seen that the fractional-order memristor still satisfies the two characteristics of passing through the origin and gradually degenerating into a straight line while passing through the origin as the input frequency increases.

From the definition of memristors, we can know that there are usually two types of memristor models, namely flux-type and charge-type. Among them, the flux-type memristor is used more frequently. Equation (31) is the mathematical expression form of the memristor definition:

$$\left\{\begin{array}{c}i=W\left(\varphi \right)v\hfill \\ \mathrm{d}\varphi /\mathrm{d}t=f(\varphi ,v)\hfill \end{array}\right.$$

(31)

Here, i and v, respectively, represent the current and voltage flowing through the memristor, and W is a function of the magnetic flux $\varphi$. The variation in $\varphi$ over time is characterized by the second equation, and f is a function of the magnetic flux and voltage. For instance, in [121], W is expressed as $a-btanh\left(\varphi \right)$, and f is characterized as $2\alpha tanh\left({\varphi }^3\right)-\beta \varphi -v$.

The fractional-order memristor is specifically manifested by applying the fractional-order operator from the second part to the differential or difference part of the original integer-order memristor, thereby obtaining the fractional-order differential equation. For the second-dimension equation of (31), it is the differential of the magnetic flux x with respect to time. Therefore, after applying the Caputo fractional-order operator, we can obtain

$$\left\{\begin{array}{c}i=W\left(\varphi \right)v\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^q\varphi =f(\varphi ,v)\hfill \end{array}\right.$$

(32)

The numerical calculation method for (32) can be referred to Section 2.2.

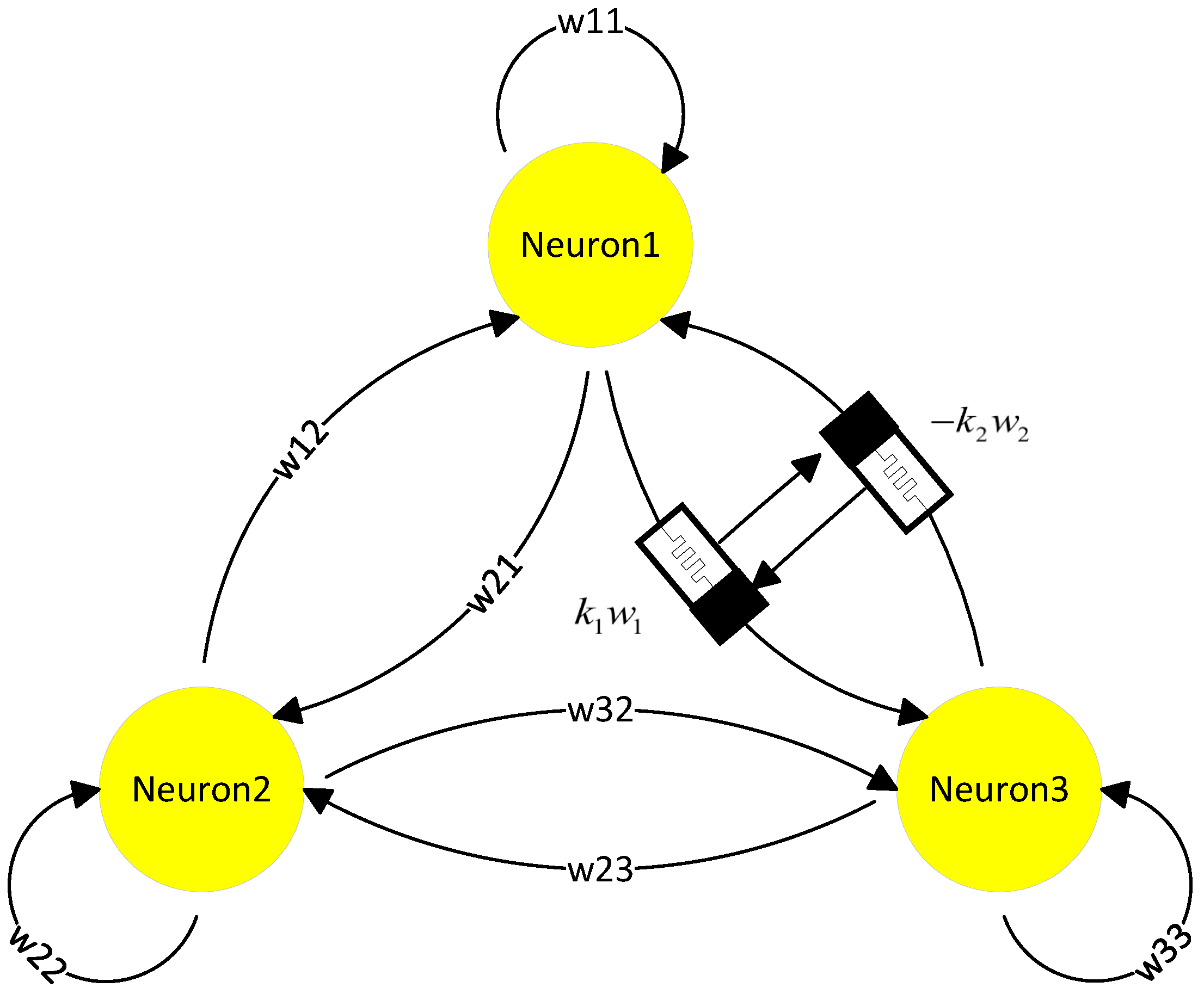
3.1.2. Continuous-Time FMNNs

(1) Continuous-time HR FMNNs

As is well known, the 2D and 3D HR neurons are, respectively, shown in (33) and (34):

$$\left\{\begin{array}{c}\mathrm{d}x/\mathrm{d}t=y-a{x}^3+b{x}^2+I\hfill \\ \mathrm{d}y/\mathrm{d}t=c-d{x}^2-y\hfill \end{array}\right.$$

(33)

where x represents the membrane potential, y is the spike or recovery variable, and I is the external excitation current.

$$\left\{\begin{array}{c}\mathrm{d}x/\mathrm{d}t=y-a{x}^3+b{x}^2-z+I\hfill \\ \mathrm{d}y/\mathrm{d}t=c-d{x}^2-y\hfill \\ \mathrm{d}z/\mathrm{d}t=\tau (s(x-x_1)-z)\hfill \end{array}\right.$$

(34)

In (34), x and y are referred to as fast variables; the parameter s is an adjustment parameter; r is typically on the order of ${10}^{-3}$; and $\tau$ is known as a small parameter. z is called the slow variable, representing the current through the slow channel, and $x_1$ is the resting state of the membrane potential x. In [119], Yu replaced the slow variable z in the HR neuron with a fractional-order memristor similar to (34). At this point, the input voltage of the memristor is x; so, the final fractional-order HR neuron formed is

$$\left\{\begin{array}{c}{}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}x=y-a{x}^3+b{x}^2+W\left(\varphi \right)x\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}y=c-d{x}^2-y\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^q\varphi =f(\varphi ,x)\hfill \end{array}\right.$$

(35)

$W\left(\varphi \right)=-tanh\left(\varphi \right),f(\varphi ,x)=-\tau x$, where $\tau$ is known as a small parameter.

Research on HR and other neural networks is also gradually advancing [141,142]. Yu et al. studied the HR neuron alone in 2020 and found hidden dynamic phenomena [118]. K. Rajagopal et al. discovered scrolls in the fractional-order HR MNN [143]. Li et al. coupled HR neurons with a multi-stable memristor in [119] and found complex chaotic phenomena. Ding et al. also studied the HR neuron and discovered chaotic phenomena, and implemented it on an ARM platform [120]. In 2024, Zhao et al. studied a network composed of FHN neurons coupled with fractional-order memristors and discovered chaos [123].

(2) Continuous-time heterogeneous FMNNs

The model of an FHN neuron is shown as Equation (36):

$$\left\{\begin{array}{c}\mathrm{d}z/\mathrm{d}t=z(z-1)(1-mz)-u,\hfill \\ \mathrm{d}n/\mathrm{d}t=nz,\hfill \end{array}\right.$$

(36)

The final heterogeneous neural network composed of HR neuron and FHN neuron is shown in Figure 2, and its expression after fractional-order operation is

$$\left\{\begin{array}{c}{}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}x=y-x^3+3x^2+w_{11}G\left(x\right)-k_{2}G\left(x\right)W_1(w,v),\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}y=1-5x^2-y,\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}z=z(z-1)(1-mz)-u+w_{22}G\left(z\right)+k_{1}G\left(x\right)W_2(w,v),\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}u=nz,\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^q\nu =f({\varphi }_1,\nu ),\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}w=f({\varphi }_2,w),\hfill \end{array}\right.$$

(37)

Among them, the $G\left(x\right)$ function serves as the activation function for two neurons, $w_1=W_1(w,v)$ and $w_2=W_2(w,v)$.

Over the last few years, the application of fractional-order memristor-coupled continuous-time neuron models has been increasingly common. Besides the coupling of heterogeneous neural networks mentioned in [121], Ding also studied heterogeneous memristor neural networks composed of other neurons in [144,145] and discovered chaos.

(3) Continuous-time Hopfield FMNNs

HNNs are composed of neurons capable of generating complex dynamic behaviors. An HNN can be regarded as a system that can transmit information, formed by the interconnection and mutual influence of several neurons. Memristors are often used as the synapses of HNNs and coupled with electromagnetic radiation [112]. A single Hopfield neuron is represented by Equation (38):

$$C_i\mathrm{d}{x}_i/\mathrm{d}t=-{\displaystyle \frac{x_i}{R_i}}+\sum _{j=1}^n{w}_{ij}G\left(x_j\right)+I_i$$

(38)

where $x_i$ represents the voltage across $C_i$; $R_i$ and $I_i$, respectively, denote the membrane resistance inside and outside the neuron and the input bias current. $G\left(x_j\right)$ represents the neuron activation function, which is typically the hyperbolic tangent function $tanh$ or the sine function $sin$. The synaptic weight $w_{ij}$ is a resistance. In [120], an FMHNN was reported, and its specific model is shown in Figure 3.

This is an HNN composed of three Hopfield neurons. It can be noted that this model employs two locally active memristors as the mutual synapses of the network, whereby the two memristors interact with each other, which can significantly enhance the dynamic characteristics of the model. Therefore, the MHNN after the action of the fractional-order operator can be expressed as

$$\left\{\begin{array}{c}{}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}x=-x+w_{11}G\left(x\right)+w_{12}G\left(y\right)-k_2{w}_{2}G\left(z\right)\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}y=-y+w_{21}G\left(x\right)+w_{22}G\left(y\right)+w_{23}G\left(z\right)\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^{q}z=-z+k_1{w}_{1}G\left(x\right)+w_{32}G\left(y\right)+w_{33}G\left(z\right)\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^q{\varphi }_1=f({\varphi }_1,x)\hfill \\ {}_{t_0}\mathit{D}_{\mathit{Ca}}^q{\varphi }_2=f({\varphi }_2,z)\hfill \end{array}\right.$$

(39)

In (31), $k_1$ and $k_2$ represent the coupling strength. $w_1$ and $w_2$ should be $W_1\left({\varphi }_1\right)$ and $W_2\left({\varphi }_2\right)$, but in this system, $w_1=W_1({\varphi }_1,{\varphi }_2),w_2=W_2({\varphi }_1,{\varphi }_2)$. Since the two memristors are in contact with each other, the corresponding magnetic fluxes will affect each other. $w_1$ and $w_2$ represent the interaction results of the magnetic fluxes between the two memristors. The author has thoughtfully considered this point.

HNNs have been widely applied in the study of chaotic dynamics due to their excellent neuron modeling and prominent fully connected characteristics. In 2019, K. Rajagopal investigated the chaotic and synchronous behaviors of the parameter uncertainties of FMHNN and discovered hyperchaos. Eventually, the author only provided the non-fractional-order FPGA implementation of this system [146]. In 2022, Yu studied a high-dimensional FMHNN and deeply analyzed its dynamic characteristics [122]. In 2024, Arsene investigated a continuous-time FMHNN and discovered symmetric multi-scroll chaotic attractors and double bubble bifurcations [115]. In the same year, Kong studied an FMHNN and discovered hyperchaos. Eventually, he applied this system to image encryption [116]. Li used a continuous-time FMHNN to solve the traveling salesman problem in [147]. Ramakrishnan studied a neural network composed of two Hopfield neurons in [148] and explored the influence of memristors and fractional-order operators on this system.

3.2. Discrete-Time Fractional-Order Memristor Neural Networks

Discrete-time FMNNs have become a research hotspot in the fields of neuromorphic computing and nonlinear systems due to their unique dynamic characteristics and innovative multidisciplinary intersections. In terms of hardware implementation, discrete-time FMNNs have the potential for high-density integration. Meanwhile, discrete-time modeling not only meets the engineering requirements of digital signal processing systems but also reveals the control mechanisms of complex bifurcations, chaotic synchronization, and other nonlinear phenomena through fractional-order difference equations. These features have attracted extensive attention from researchers in multiple disciplines.

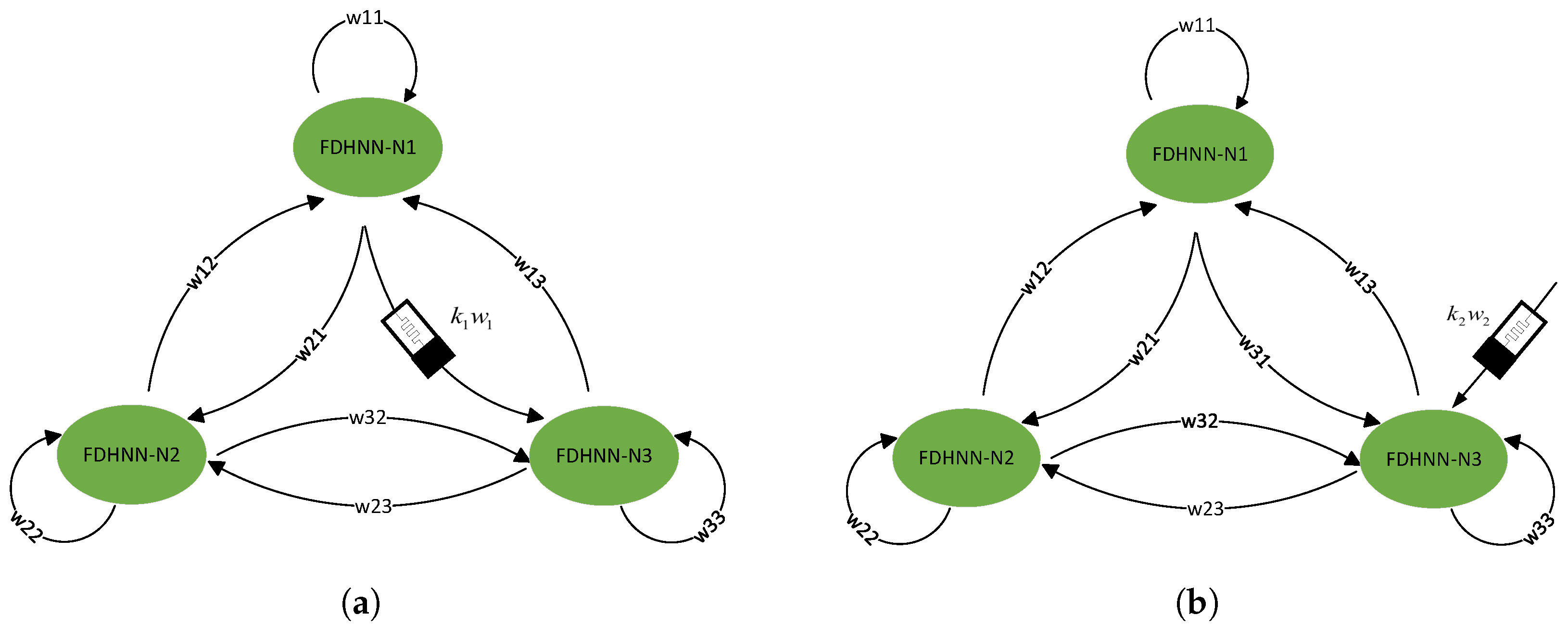
3.2.1. Discrete-Time Memristor Model

Discrete-time fractional-order memristors exhibit multiple advantages over continuous-time fractional-order memristors in both theoretical and application aspects, such as stronger engineering feasibility and digital compatibility, as well as richer dynamic behaviors and control flexibility. Therefore, they are highly worthy of research. In [124], Lu analyzed the hysteresis loop characteristics of a simple discrete fractional-order memristor and found that as the fractional order increases, the area of the memristor’s hysteresis loop gradually increases. In [126], Li proposed a discrete fractional-order local active memristor and presented its hysteresis loop. When applied to HNN, it generated chaos.

The equation of the discrete-time memristor is

$$\left\{\begin{array}{c}i\left(n\right)=W\left(\varphi \right(n\left)\right)v\left(n\right)\hfill \\ \varphi (n+1)-\varphi \left(n\right)=f\left(\varphi \right(n),v)\hfill \end{array}\right.$$

(40)

After applying the fractional difference operator, Equation (40) becomes

$$\left\{\begin{array}{c}i\left(n\right)=W\left(\varphi \right(n\left)\right)v\left(n\right)\hfill \\ {}_{n_0}\mathit{D}_{\mathit{Ca}}^q\varphi \left(n\right)=f(\varphi \left(n\right),v)\hfill \end{array}\right.$$

(41)

Discrete fractional-order examples can be obtained from Figure 4, where Figure 4a–c are the hysteresis loop diagrams, DC V-I diagrams, and POP diagrams of the discrete fractional-order local active memristor in [126] varying with the fractional order. Through observation, it can be seen that this memristor has rich dynamic characteristics and can be used to construct complex chaotic systems.

3.2.2. Discrete-Time FMNNs

(1) Discrete-Time Rulkov FMNNs

It is well known that most neuron models are continuous-time models, but some scholars have created discrete-time neuron models, such as the well-known Rulkov model [149], or some scholars have discretized the original continuous-time neuron models to form discrete neuron models, such as discrete-time HR and FHN neurons. The research on discrete memristive fractional-order neurons mainly focuses on the construction of the Rulkov neuron model, and its integer-order model is

$$\left\{\begin{array}{c}x(n+1)={\displaystyle \frac{\alpha }{1+x^2\left(n\right)}}+y\left(n\right)\hfill \\ y(n+1)=y\left(n\right)-\delta x\left(n\right)-\beta \hfill \end{array}\right.$$

(42)

where n represents discrete time, x is the fast variable representing the transmembrane voltage of a single neuron, and y is the slow variable representing the slow gating process. The time-scale difference between the two variables is determined by a sufficiently small value of the parameter $\delta$, and $\alpha ,\beta$ are both parameters. In [124], Lu replaced the slow variable y in (41) with a discrete fractional-order memristor, and the discrete fractional-order memristor Rulkov neuron model formed by using the memristor (41) and the Caputo discretization method in Section 2.3 is as follows:

$$\left\{\begin{array}{c}x\left(n\right)=x\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}({\displaystyle \frac{\alpha }{1+x^2(j-1)}}+\gamma +pW\left(\varphi \left(n\right)\right)x(j-1)-x(j-1))\hfill \\ y\left(n\right)=y\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}\left(f(\varphi (j-1),v)\right)\hfill \end{array}\right.$$

(43)

where p is the coupling strength and $\gamma$ is the constant.

Besides the simple Rulkov discrete memristor neural network model mentioned in [124], Ma et al. studied the dynamic phenomena of Rulkov neurons under electromagnetic radiation in 2023 and discovered hidden dynamic phenomena [150]. Tang et al. studied the chaotic synchronization phenomenon in Rulkov MNN [151]. In 2024, M. Ghasemi also studied chaos and synchronization in Rulkov neurons and observed various behaviors in the system, including tonic firing, periodic firing, and chaotic firing [152].

(2) Discrete-time Hopfield FMNNs

A single discrete-time Hopfield neuron is represented by Equation (44):

$$C_i\Delta x_i\left(n\right)=-{\displaystyle \frac{x_i\left(n\right)}{R_i}}+\sum _{j=1}^m{w}_{ij}G\left(x_j\left(n\right)\right)+I_i$$

(44)

Through [112], it is found that memristors can not only be used as synapses (both auto-synapses and inter-synapses), but also as a form of electromagnetic radiation of internal and external electric fields. In [126], Li constructed a model in which discrete fractional-order local active memristors are coupled with HNN synapses and electromagnetic radiation. Local activity is the origin of complexity, and thus, local active memristors are considered as circuit components that are more prone to generating chaotic systems. The model is specifically illustrated in Figure 5.

The fractional-order equations of Figure 5a and Figure 5b are, respectively, represented by (45) and (46). The specific application of the discrete method with initial values that can be computed is referred to in Section 2.3.

$$\left\{\begin{array}{c}x\left(n\right)=x\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-x(j-1)+w_{11}G\left(x(j-1)\right)+w_{12}G\left(y(j-1)\right)\hfill \\ +w_{13}G\left(z(j-1)\right))\hfill \\ y\left(n\right)=y\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-y(j-1)+w_{21}G\left(x(j-1)\right)+w_{22}G\left(y(j-1)\right)\hfill \\ +w_{23}G\left(z(j-1)\right))\hfill \\ z\left(n\right)=z\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-z(j-1)+k_{1}W\left(\varphi (j-1)\right)G\left(x(j-1)\right)\hfill \\ +w_{32}G\left(y(j-1)\right)+w_{33}G\left(z(j-1)\right))\hfill \\ \varphi \left(n\right)=\varphi \left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}\left(f(\varphi (j-1),x(j-1))\right)\hfill \end{array}\right.$$

(45)

$$\left\{\begin{array}{c}x\left(n\right)=x\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-x(j-1)+w_{11}G\left(x(j-1)\right)+w_{12}G\left(y(j-1)\right)\hfill \\ +w_{13}G\left(z(j-1)\right))\hfill \\ y\left(n\right)=y\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-y(j-1)+w_{21}G\left(x(j-1)\right)+w_{22}G\left(y(j-1)\right)\hfill \\ +w_{23}G\left(z(j-1)\right))\hfill \\ z\left(n\right)=z\left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}(-z(j-1)+w_{31}G\left(x(j-1)\right)+w_{32}G\left(y(j-1)\right)\hfill \\ +w_{33}G\left(z(j-1)\right)+k_{2}W\left(\varphi (j-1)\right)z(j-1))\hfill \\ \varphi \left(n\right)=\varphi \left(0\right)+{\displaystyle \frac{1}{\Gamma \left(q\right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+q)}{\Gamma (n-j+1)}}\left(f(\varphi (j-1),v(j-1))\right)\hfill \end{array}\right.$$

(46)

To facilitate readers’ understanding, we have summarized the applications of fractional-order memristors in both continuous-time and discrete-time neural network systems, as shown in

Table 1. Continuous- and discrete-time fractional-order memristor coupling neurons.

Neuron Systems	Continuous-Time	Discrete-Time
FM-HR	[118,119,120,143,153]	∖
FM-FHN	[123]	∖
FM-Heterogeneous	[121,144,145,154]	∖
FM-CNNs	[155,156]	∖
FM-ANNs	[157]	∖
FM-SNNs	∖	[158]
FM-ASNNs	[123]	[125]
FM-HNNs	[114,115,116,117,122,146,147,148,159,160,161,162,163,164,165]	[126]
FM-Rulkov	[144]	[124,150,151,152]

.

4. Recent Advances and Prospects

Fractional-order systems have now been widely used to solve practical problems in real life. Recently, there have been breakthroughs in the research of fractional-order systems in various fields: In the field of finance, Diabi et al. studied a three-dimensional discrete fractional financial mapping and analyzed its nonlinear dynamical system under commensurate and incommensurate orders, suggesting that economists can use it to determine the best time to buy and sell in the commercial market and create financial stability and economic strategies to promote economic growth [166]. In 2025, Farman [167] utilized fractional operators to predict the dynamics of financial risks under different random economic factors and discovered a series of chaotic phenomena. In the field of biology, Gupta et al. recently studied the fractional-order sunflower equation and discovered multi-scroll attractors within it [168]. In the field of cybersecurity, Jose F. in 2024 studied the chaos and stability of fractional-order network ecosystem models and proposed a three-dimensional cybernetic model to illustrate the interactions among users, hackers, and cybersecurity professionals [169]. In theoretical mathematics, Salah explored the stability of chaotic autonomous systems using the Atangana–Baleanu–Caputo fractional derivative, proving the existence of at least one solution and deriving the results of Ulam–Hyers stability [170]. In the field of engineering control, Zhang et al. applied the fractional-order adaptive sliding-mode controller (FASMC) to the unsolved problem of predefined-time stability [171].

In the field of neural networks, FNNs and FMNNs also exhibit excellent chaotic dynamic characteristics. Xu [50] proposed a four-element FHNN and, based on this network, designed a new multi-hash encryption algorithm. Security analysis indicates that this design algorithm has high security performance. Xie et al. studied a fractional-order multi-stable local active memristor and a chaotic system with transient transitions and state jumps [108]. In 2020, Yu investigated the hidden dynamics in the fractional-order memristor HR model [118]. Li [119] studied the discharge activity of a fractional-order HR neuron with a multi-stable memristor and found that the system exhibited chaotic phenomena with changes in coupling strength, fractional order, and excitation current. Ding [120] discovered transient chaos and the coexistence of attractors in FHNN and applied it to image encryption, achieving remarkable results. Zhou processed a CNN with fractional order and applied it to image encryption. Through various indicators, the superiority of the system was highlighted [156]. Yu [114] studied the chaotic dynamics of a new continuous-time FHNN under electromagnetic radiation and implemented it systematically on an FPGA. In 2025, Li [126] studied a three-element memristor-coupled DFHNN, discovered the coexistence of attractors and multi-stability, and for the first time, provided an FPGA implementation method for discrete fractional-order systems.

Despite the long development of fractional calculus, there are still some issues that need to be studied and resolved:

• Large numerical values of LEs have not yet been observed in fractional-order chaotic systems. Although the occurrence of hyperchaotic phenomena in existing FNNs and fractional-order chaotic systems is rare, the Lyapunov exponents (LEs) of discrete-time systems are often larger than those of continuous-time systems, which may provide some ideas for researchers.
• In recent years, fractional incommensurate-order systems have gradually become a research hotspot. In 2025, Diabi et al. studied a discrete fractional incommensurate-order Ueba system, proved its dynamical complexity, and proposed a control scheme for stabilization and synchronization [172]. Such an unbalanced fractional-order system may have higher adaptability in depicting the real world. Meanwhile, converting the fractional order into a parameterized polynomial is also a good choice. Future researchers should focus on this direction and conduct further studies.
• Similar to [112], it is well known that the nervous system is composed of a large number of neurons. However, the existing FNNs still only consider a few neurons. Even though they have made significant progress compared to integer-order models and are closer to reality, they still have significant limitations. Therefore, more extensive FNNs need to be further developed and studied.
• The hardware implementation methods of fractional-order systems have always been discussed and studied by people. Ref. [131] systematically described the FPGA implementation methods of most continuous-time FNNs. However, for the hardware implementation methods of discrete FNNs, only ref. [126] has provided a solution so far, and the method it offers is also a truncated approximation method with significant limitations. Therefore, the hardware implementation methods of discrete FNNs still need to be widely researched and discussed.

Here, we finally address a controversial topic regarding fractional calculus equations. In [123], it was demonstrated that fractional order exhibits more realistic asymmetric phenomena, which is attributed to the loss of periodic characteristics in periodic functions after fractional differentiation, causing curve distortion. Therefore, when analyzing the “periodic” phenomena in fractional-order systems, we should make more accurate descriptions. For instance, in [108], Wang et al. described a similar periodic phenomena in fractional-order systems as “Asymptotically-periodic” and abbreviated it as “A-period”, while in [126], Li referred to this situation as “periodic-like”. However, articles such as [79,114,157] did not pay attention to this issue.

5. Conclusions

This article systematically reviews the research progress on the chaotic dynamics of FNNs, covering continuous-time and discrete-time models, memristive coupling mechanisms, and various typical network architectures (such as HNNs, CNNs, HR, etc.), while also reviewing some important recent papers related to these types. By integrating the theory of fractional calculus with the dynamic characteristics of neural networks, it reveals that fractional-order operators can more accurately describe the cross-time-scale memory effects and nonlinear behaviors of neurons, providing methods for simulating the complex activities of biological neural systems (such as chaotic oscillations and multi-stable switching). At the same time, it indicates that discrete fractional-order models have advantages in suppressing noise sensitivity and other aspects, opening up new paths for applications such as chaotic encryption and brain-like hardware design. Subsequently, we present the methods of applying continuous-time and discrete-time fractional-order operators to differential equations. In the third section, we introduce some of the more classic FNN modeling mechanisms and methods in recent years. At the end of this article, we introduce the latest research progress of FNNs in different fields, including biology, finance, and cybersecurity. Finally, we raise four points for discussion and further research. Therefore, this review may help further research on chaotic systems based on FNNs, and we hope that this review can provide a good reference for researchers who want to delve deeper into this type of chaotic system.