A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks
Abstract
1. Introduction
2. The Construction Theory of FMNNs
2.1. Continuous-Time Fractional Differential Theory
2.1.1. G-L Definition
2.1.2. R-L Definition
2.1.3. Caputo Definition
2.2. Continuous Fractional Approximate Solution Methods
2.3. Discrete-Time Fractional Differential Theory and Numerical Calculation
3. Fractional-Order Memristive Neural Networks
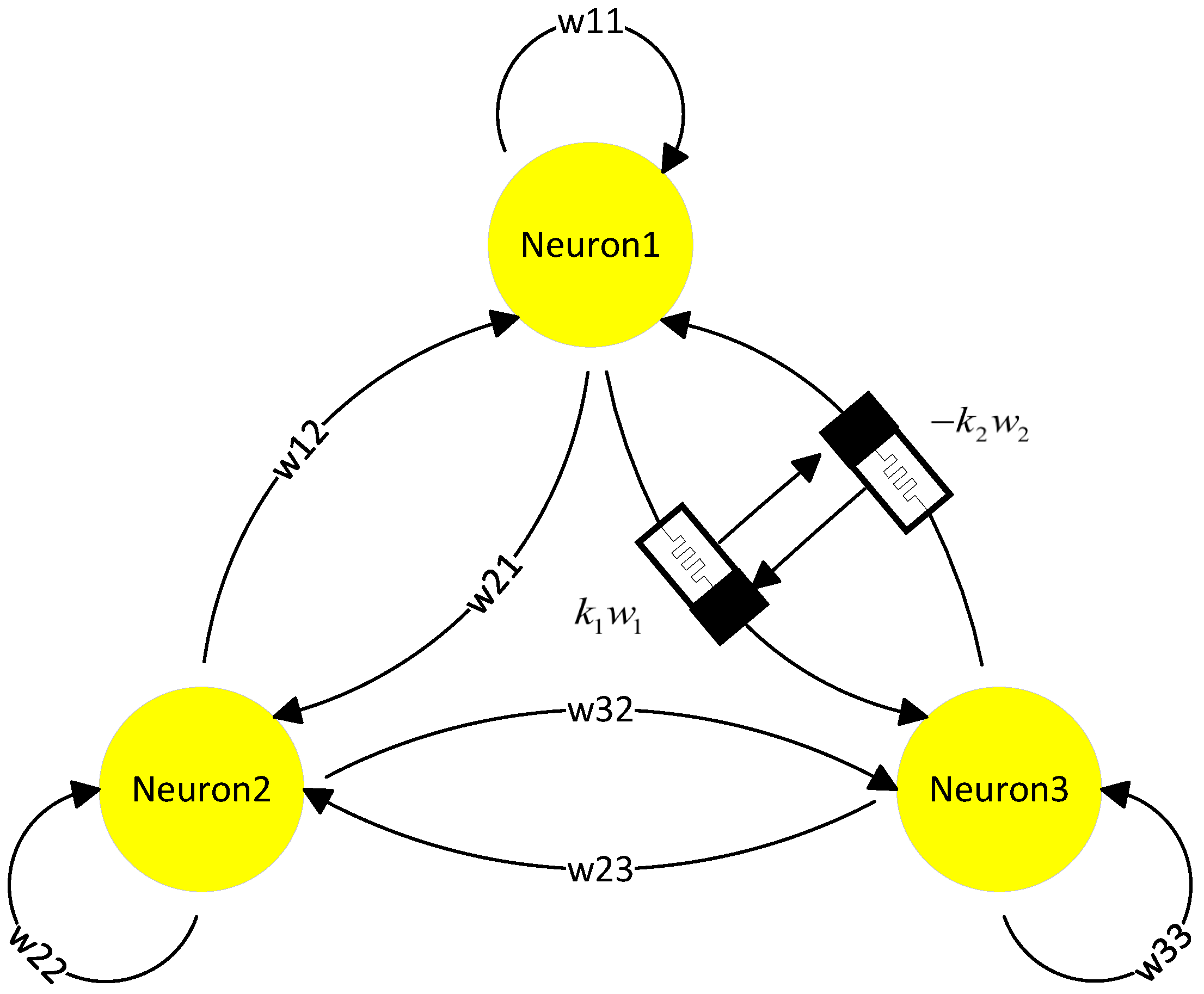
3.1. Continuous-Time Fractional-Order Memristor Neural Networks
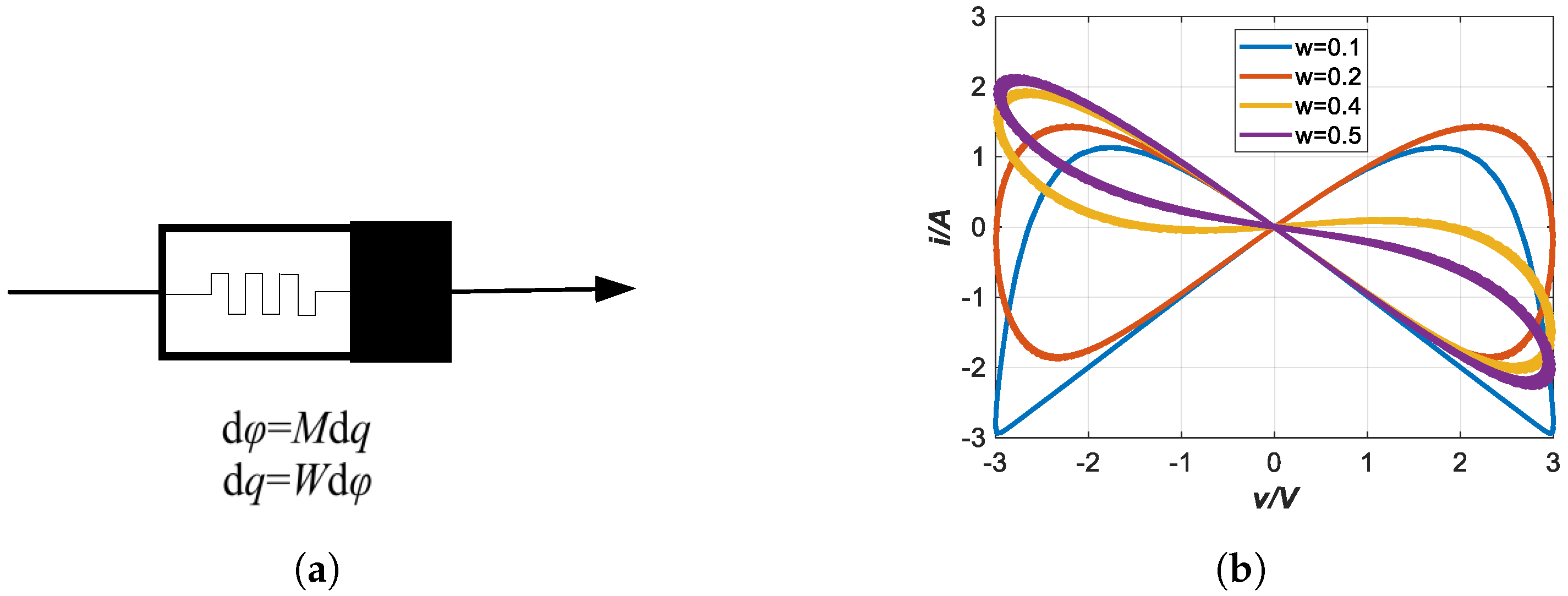
3.1.1. Continuous-Time Memristor Model
3.1.2. Continuous-Time FMNNs
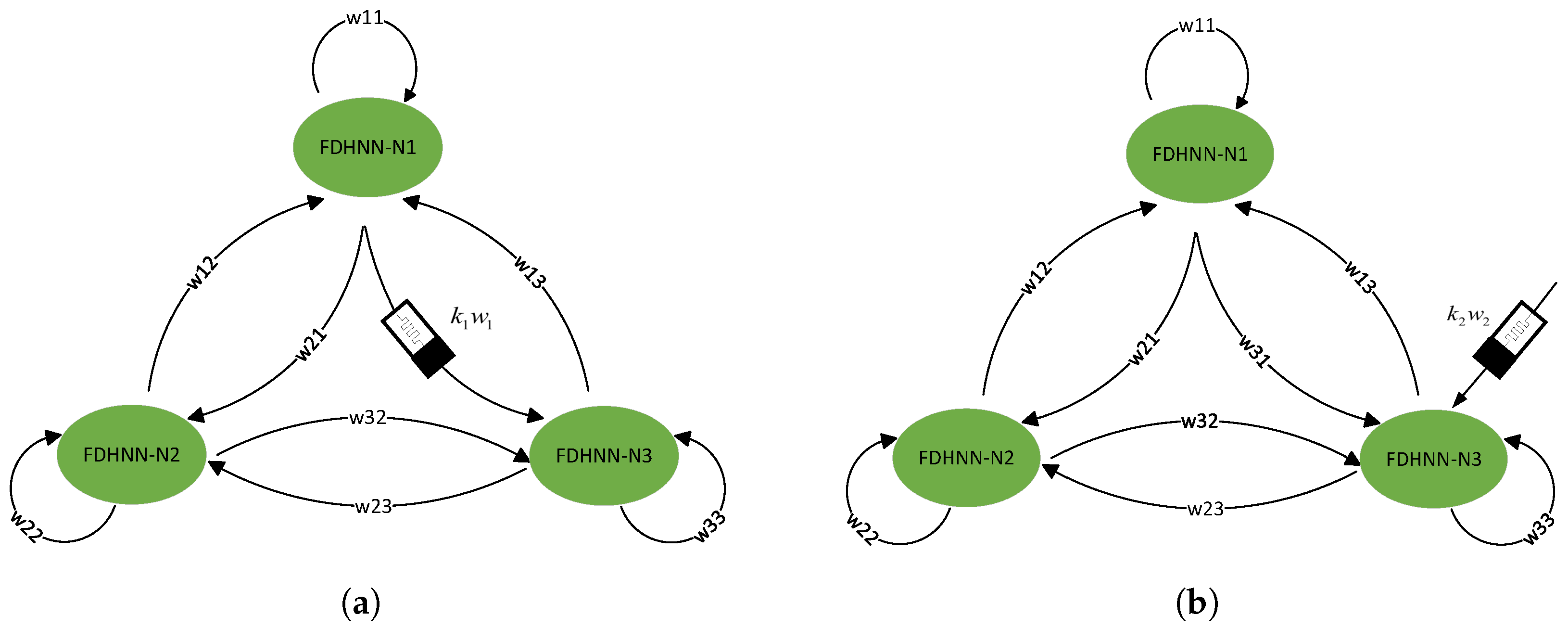
3.2. Discrete-Time Fractional-Order Memristor Neural Networks
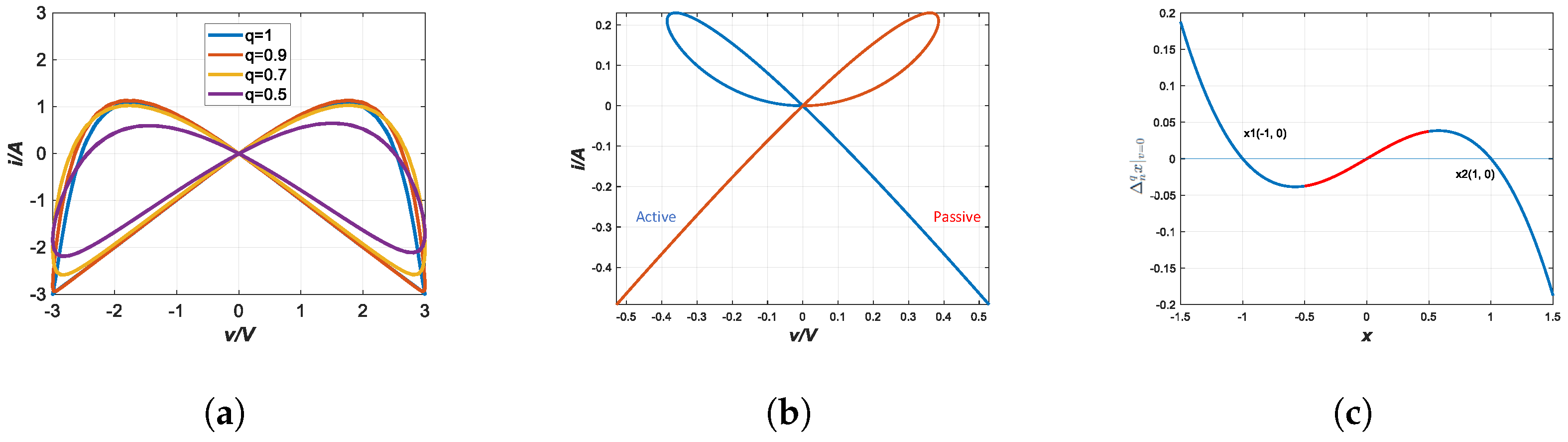
3.2.1. Discrete-Time Memristor Model
3.2.2. Discrete-Time FMNNs
4. Recent Advances and Prospects
- Large numerical values of LEs have not yet been observed in fractional-order chaotic systems. Although the occurrence of hyperchaotic phenomena in existing FNNs and fractional-order chaotic systems is rare, the Lyapunov exponents (LEs) of discrete-time systems are often larger than those of continuous-time systems, which may provide some ideas for researchers.
- In recent years, fractional incommensurate-order systems have gradually become a research hotspot. In 2025, Diabi et al. studied a discrete fractional incommensurate-order Ueba system, proved its dynamical complexity, and proposed a control scheme for stabilization and synchronization [172]. Such an unbalanced fractional-order system may have higher adaptability in depicting the real world. Meanwhile, converting the fractional order into a parameterized polynomial is also a good choice. Future researchers should focus on this direction and conduct further studies.
- Similar to [112], it is well known that the nervous system is composed of a large number of neurons. However, the existing FNNs still only consider a few neurons. Even though they have made significant progress compared to integer-order models and are closer to reality, they still have significant limitations. Therefore, more extensive FNNs need to be further developed and studied.
- The hardware implementation methods of fractional-order systems have always been discussed and studied by people. Ref. [131] systematically described the FPGA implementation methods of most continuous-time FNNs. However, for the hardware implementation methods of discrete FNNs, only ref. [126] has provided a solution so far, and the method it offers is also a truncated approximation method with significant limitations. Therefore, the hardware implementation methods of discrete FNNs still need to be widely researched and discussed.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Kumar, S.; Rani, S.; Mann, N. Analytical Soliton Solutions to a (2 + 1)-Dimensional Variable Coefficients Graphene Sheets Equation Using the Application of Lie Symmetry Approach: Bifurcation Theory, Sensitivity Analysis and Chaotic Behavior. Qual. Theory Dyn. Syst. 2025, 24, 80. [Google Scholar] [CrossRef]
- Kumar, S.; Rani, S. Lie symmetry reductions and dynamics of soliton solutions of (2+1)-dimensional Pavlov equation. Pramana J. Phys. 2020, 94, 116. [Google Scholar] [CrossRef]
- Faure, P.; Korn, H. Is there chaos in the brain? I. Concepts of nonlinear dynamics and methods of investigation. C. R. Acad. Sci. III 2001, 324, 773–793. [Google Scholar] [CrossRef] [PubMed]
- Korn, H.; Faure, P. Is there chaos in the brain? II. Experimental evidence and related models. C. R. Biol. 2003, 326, 787–840. [Google Scholar] [CrossRef] [PubMed]
- Khavrus’, V.A.; Farkas, H.; Strizhak, P.E. Conditions for mixed mode oscillations and deterministic chaos in nonlinear chemical systems. Theor. Exp. Chem. 2002, 38, 301–307. [Google Scholar] [CrossRef]
- Miyoshi, T.; Nitanai, T.; Inabe, N. Chaotic attractor with a characteristic of torus. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 944–948. [Google Scholar] [CrossRef]
- Majid, S.Z.; Asjad, M.I.; Kumar, S. Dynamical Study with Exact Travelling Waves with High Amplitude Solitons to Clannish Random Walker’s Parabolic Equation. Qual. Theory Dyn. Syst. 2025, 24, 14. [Google Scholar] [CrossRef]
- Kazem, A.; Sharifi, E.; Hussain, F.K.; Saberi, M.; Hussain, O.K. Support vector regression with chaos-based firefly algorithm for stock market price forecasting. Appl. Soft Comput. 2013, 13, 947–958. [Google Scholar] [CrossRef]
- Gu, H.; Li, C.; Li, Y.; Ge, X.; Lei, T. Various patterns of coexisting attractors in a hyperchaotic map. Nonlinear Dyn. 2023, 111, 7807–7818. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Quan, D.; Wang, C.; Yang, G.; Luo, D. Discrete Memristive Delay Feedback Rulkov Neuron Model: Chaotic Dynamics, Hardware Implementation and Application in Secure Communication. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Yu, F.; Su, D.; He, S.; Wu, Y.; Zhang, S.; Yin, H. Resonant tunneling diode cellular neural network with memristor coupling and its application in police forensic digital image protection. Chin. Phys. B 2025, 34, 050502. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, F.; Tan, B.; Huang, Y.; Yao, W.; Cai, S.; Lin, H. A class of n-D Hamiltonian conservative chaotic systems with three-terminal memristor: Modeling, dynamical analysis, and FPGA implementation. Chaos 2025, 35, 013121. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Wei, D.Q. Collective dynamics of neuronal network under synapse and field coupling. Nonlinear Dyn. 2021, 105, 753–765. [Google Scholar] [CrossRef]
- Pan, C.; Hong, Q.; Wang, X. A Novel Memristive Chaotic Neuron Circuit and Its Application in Chaotic Neural Networks for Associative Memory. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 521–532. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Ermentrout, G.B.; Terman, D.H. Mathematical Foundations of Neuroscience; Springer: New York, NY, USA, 2010. [Google Scholar]
- Babloyantz, A.; Destexhe, A. Low-dimensional chaos in an instance of epilepsy. Proc. Natl. Acad. Sci. USA 1986, 83, 3513–3517. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Fitzhugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef] [PubMed]
- Nagumo, J.; Arimoto, S.; Yoshizawa, S. An active pulse transmission line simulating nerve axon. Proc. IRE 1962, 50, 2061–2070. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R.M. A model of the nerve impulse using two first-order differential equations. Nature 1982, 296, 162–164. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, L. Cellular neural networks: Theory. IEEE Trans. Circuits Syst 1988, 35, 1257–1272. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, G. Chaotic dynamics of memristor-coupled tabu learning neuronal network. Int. J. Bifurc. Chaos 2025, 35, 2550053. [Google Scholar] [CrossRef]
- Ma, M.; Xiong, K.; Li, Z.; Sun, Y. Dynamic behavior analysis and synchronization of memristor-coupled heterogeneous discrete neural networks. Mathematics 2023, 11, 375. [Google Scholar] [CrossRef]
- Peng, C.; Li, Z.; Wang, M.; Ma, M. Dynamics in a memristor-coupled heterogeneous neuron network under electromagnetic radiation. Nonlinear Dyn. 2023, 111, 16527–16543. [Google Scholar] [CrossRef]
- Luo, D.; Wang, C.; Deng, Q. Dynamics in a memristive neural network with three discrete heterogeneous neurons and its application. Nonlinear Dyn. 2025, 113, 5811–5824. [Google Scholar] [CrossRef]
- Li, Q.; Tang, S.; Zeng, H.; Zhou, T. On hyperchaos in a small memristive neural network. Nonlinear Dyn. 2014, 78, 1087–1099. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, J.; Zhang, X.; Sun, Y.; Iu, H.H. Memristor-coupled asymmetric neural network, bionic modeling, chaotic dynamics analysis and encryption application. Chaos Solitons Fractals 2023, 166, 112905. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Tan, Y. Hidden extreme multistability with hyperchaos and transient chaos in a Hopfield neural network affected by electromagnetic radiation. Nonlinear Dyn. 2020, 99, 2369–2386. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Ni, J.; Yao, Y. Chaotic dynamics in a neural network under electromagnetic radiation. Nonlinear Dyn. 2018, 91, 1541–1554. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C. Influences of electromagnetic radiation distribution on chaotic dynamics of a neural network. Appl. Math. Comput. 2020, 91, 1541–1554. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Liu, J.; Chen, S. Multistable dynamics in a Hopfield neural network under electromagnetic radiation and dual bias currents. Nonlinear Dyn. 2022, 109, 2085–2101. [Google Scholar] [CrossRef]
- Wan, Q.; Yan, Z.; Li, F.; Chen, S.; Liu, J. Complex dynamics in a Hopfield neural network under electromagnetic induction and electromagnetic radiation. Chaos 2022, 32, 073107. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Kengne, J.; Fotsin, H.B. A plethora of behaviors in a memristor based Hopfield neural network. Int. J. Dyn. Syst. Cont. 2019, 7, 36–52. [Google Scholar] [CrossRef]
- Ding, S.; Wang, N.; Bao, H.; Chen, B.; Wu, H.; Xu, Q. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network, Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar] [CrossRef]
- Hua, M.; Bao, H.; Wu, H.; Xu, Q.; Bao, B. A single neuron model with memristive synaptic weight. Chin. J. Phys. 2022, 76, 217–227. [Google Scholar] [CrossRef]
- Chen, C.; Chen, J.; Bao, H.; Chen, M.; Bao, B. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons. Nonlinear Dyn. 2019, 95, 3385–3399. [Google Scholar] [CrossRef]
- Chen, C.; Min, F.; Zhang, Y.; Bao, B. Memristive electromagnetic induction effects on Hopfield neural network. Nonlinear Dyn. 2021, 106, 2559–2576. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Netw. 2017, 89, 19–30. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.; Zeng, G.; She, Q. Fractional-order convolutional neural networks with population extremal optimization. Neurocomputing 2022, 477, 36–45. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, D.; Zhao, T. Fractional calculus in image processing: A Review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef]
- Marazzato, R.; Sparavigna, A.C. Astronomical image processing based on fractional calculus: The AstroFracTool. arXiv 2009, arXiv:0910.4637. [Google Scholar]
- Wang, Z.; Ma, X. Application of fractional-order calculus approach to signal processing. In Proceedings of the 2011 6th IEEE Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 20–22 August 2011; pp. 220–222. [Google Scholar]
- Magin, R. Fractional calculus in bioengineering. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Emad, E.M.; Lone, S.J.; Pushali, T.; Omar, A. Almaghrabi. Analysis and control of the fractional chaotic Hopfield neural network. Adv. Differ. Equ. 2021, 126, 1–15. [Google Scholar]
- Pu, Y.; Yi, Z.; Zhou, J. Fractional hopfield neural networks: Fractional dynamic associative recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2319–2333. [Google Scholar] [CrossRef]
- Mohanasubha, R.; Suresh, K. Dynamical effects of hypergraph links in a network of fractional-order complex systems. Chaos 2022, 32, 123–128. [Google Scholar]
- Holm, M.T. The Laplace transform in discrete fractional calculus. Comput. Math. Appl. 2011, 62, 1591–1601. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Rudolf, S.; Shyam, L.K.; Tang, Y.; Huang, J. Almaghrabi, The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F.; Qammer, H.K. Chaos in a fractional order Chua’s system. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1995, 42, 485–490. [Google Scholar] [CrossRef]
- Ge, Z.; Ou, C. Chaos in a fractional order modified Duffing system. Chaos Solitons Fractals 2007, 34, 262–291. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 544–549. [Google Scholar] [CrossRef]
- Deng, W.; Li, C. Chaos synchronization of the fractional Lü system. Phys. A Stat. Mech. Its Appl. 2005, 353, 61–72. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999; 368p. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holl. Math. Stud. 2006, 204, 1–523. [Google Scholar]
- Lv, M.; Ma, J. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation. Neurocomputing 2016, 205, 375–381. [Google Scholar] [CrossRef]
- Arena, P.; Caponetto, R.; Fortuna, L.; Porto, D. Bifurcation and Chaos in Noninteger Order Cellular Neural Networks. Int. J. Bifurc. Chaos 1998, 8, 1527–1539. [Google Scholar] [CrossRef]
- Arena, P.; Fortuna, L.; Porto, D. Chaotic behavior in noninteger-order cellular neural networks. PhysRevE 2000, 61, 776–781. [Google Scholar] [CrossRef]
- Petras, I. A Note on the Fractional-Order Cellular Neural Networks. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 1021–1024. [Google Scholar]
- Boroomand, A.; Menhaj, M.B. Fractional-Order Hopfield Neural Networks. Adv.-Neuro-Inf. Process. 2009, 5506, 883–890. [Google Scholar]
- Eva, K.; Seenith, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar]
- Wang, M.; Wang, Y.; Chu, R. Dynamical Analysis of the Incommensurate Fractional-Order Hopfield Neural Network System and Its Digital Circuit Realization. Fractal Fract. 2023, 7, 474. [Google Scholar] [CrossRef]
- Li, N.; Xie, S.; Zhang, J. A color image encryption algorithm based on double fractional order chaotic neural network and convolution operation. Entropy 2022, 24, 933. [Google Scholar] [CrossRef]
- Zhang, R.; Qi, D.; Wang, Y. Dynamics analysis of fractional order three-dimensional Hopfield neural network. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 6, pp. 3037–3039. [Google Scholar]
- Batiha, I.M. Dynamics analysis of fractional-order Hopfield neural networks. Int. J. Biomath. 2020, 13, 2050083. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 1–16. [Google Scholar] [CrossRef]
- Fazzino, S.; Caponetto, R.; Patanè, L. A new model of Hopfield network with fractional-order neurons for parameter estimation. Nonlinear Dyn. 2021, 104, 2671–2685. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Li, B.; Banerjee, S.; Yan, H. Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation. Fractal Fract. 2022, 6, 637. [Google Scholar] [CrossRef]
- Xu, C.; Aouiti, C. Comparative analysis on Hopf bifurcation of integer-order and fractional-order two-neuron neural networks with delay. Int. J. Circuit Theory Appl. 2020, 48, 1459–1475. [Google Scholar] [CrossRef]
- Eva, K.; Stefan, B. Complex and chaotic dynamics in a discrete-time-delayed Hopfield neural network with ring architecture. Neural Netw. 2009, 22, 1411–1418. [Google Scholar]
- Chen, L. A novel color image encryption algorithm based on a fractional-order discrete chaotic neural network and DNA sequence operations. Front. Inform. Technol. Electron. Eng. 2020, 21, 866–879. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Huang, T. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Adel, O. Incommensurate Fractional Discrete Neural Network: Chaos and complexity. Eur. Phys. J. Plus. 2022, 137, 1–15. [Google Scholar]
- Rabia, C.K.; Adel, O. The Effect of Caputo Fractional Variable Difference Operator on a Discrete-Time Hopfield Neural Network with Non-Commensurate Order. Fractal Fract. 2022, 6, 1–13. [Google Scholar]
- Abdallah, A.; Rabia, C.K. Chaos in a two dimensional fractional discrete Hopfield neural network and its control. Alexandria Eng. J. 2023, 75, 627–638. [Google Scholar]
- He, S.; Vignesh, D.; Rondoni, L. Chaos and firing patterns in a discrete fractional Hopfield neural network model. Nonlinear Dyn. 2023, 111, 21307–21332. [Google Scholar] [CrossRef]
- Xie, Y.; Kang, Y.; Liu, Y. Firing properties and synchronization rate in fractional-order Hindmarsh-Rose model neurons. Sci. China Technol. Sci. 2014, 57, 914–922. [Google Scholar] [CrossRef]
- Meng, F.; Zeng, X.; Wang, Z. Dynamical behavior and synchronization in time-delay fractional-order coupled neurons under electromagnetic radiation. Nonlinear Dyn. 2019, 95, 1615–1625. [Google Scholar] [CrossRef]
- Alidousti, J.; Ghaziani, R.K. Spiking and bursting of a fractional order of the modified FitzHugh-Nagumo neuron model. Math. Models Comput. Simul. 2017, 9, 390–403. [Google Scholar] [CrossRef]
- Tripathi, D.; Pandey, S.K.; Das, S. Peristaltic flow of viscoelastic fluid with fractional Maxwell model through a channel. Appl. Math. Comput. 2010, 215, 3645–3654. [Google Scholar] [CrossRef]
- Lundstrom, B.; Higgs, M.; Spain, W. Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 2008, 11, 1335–1342. [Google Scholar] [CrossRef]
- He, Z.; Abbes, A.; Jahanshahi, H.; Alotaibi, N.D.; Wang, Y. Fractional-Order Discrete-Time SIR Epidemic Model with Vaccination: Chaos and Complexity. Mathematics 2022, 10, 165. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Liu, J.; Li, R.; Huang, D. Stability, bifurcation and characteristics of chaos in a new commensurate and incommensurate fractional-order ecological system. Math. Comput. Simul. 2025, 236, 248–269. [Google Scholar] [CrossRef]
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- He, J.; Xiao, M.; He, H.; Wang, Z.; Zheng, W.; Rutkowski, L. Facilitating and Determining Turing Patterns in 3-D Memristor Cellular Neural Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4131–4144. [Google Scholar] [CrossRef]
- Jo, S.H. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef]
- Yang, J.; Pickett, M.; Li, X. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nanotech. 2008, 3, 429–433. [Google Scholar] [CrossRef]
- Khan, M.U.; Hassan, B.; Alazzam, A. Brain inspired iontronic fluidic memristive and memcapacitive device for self-powered electronics. Microsyst. Nanoeng. 2025, 11, 37. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Biophysical neurons, energy, and synapse controllability: A review. J. Zhejiang Univ.-Sci. A 2023, 24, 109–129. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Jin, W.; Ma, J. Dynamical responses in a new neuron model subjected to electromagnetic induction and phase noise. Phys. A 2017, 469, 81–88. [Google Scholar] [CrossRef]
- Lv, M.; Wang, C.; Ren, G.; Ma, J.; Song, X. Model of electrical activity in a neuron under magnetic flow effect. Nonlinear Dyn. 2016, 85, 1479–1490. [Google Scholar] [CrossRef]
- Xiao, M.; Zheng, W.; Jiang, G.; Cao, J. Qualitative Analysis and Bifurcation in a Neuron System with Memristor Characteristics and Time Delay. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1974–1988. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Wang, Y.; He, Y.; Miao, X. Memristive brain-like computing. Acta Phys. Sin. 2022, 71, 140501. [Google Scholar] [CrossRef]
- Kuzum, D.; Yu, S.; Wong, H. Synaptic electronics: Materials, devices and applications. Nanotechnology 2013, 24, 382001. [Google Scholar] [CrossRef]
- Wang, B.; Zou, F.; Cheng, J. A memristor-based chaotic system and its application in image encryption. Optik 2018, 154, 538–544. [Google Scholar] [CrossRef]
- Aihara, K.; Takabe, T.; Toyoda, M. Chaotic neural networks. Phys. Lett. A 1990, 144, 333–340. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Yu, Y.; Bao, H.; Bao, B. Complex Dynamical Behaviors of a Fractional-Order System Based on a Locally Active Memristor. Complexity 2019, 2019, 051053. [Google Scholar] [CrossRef]
- Xie, W.; Wang, C.; Lin, H.; Mou, J. A fractional-order multistable locally active memristor and its chaotic system with transient transition, state jump. Nonlinear Dyn. 2021, 104, 4523–4541. [Google Scholar] [CrossRef]
- Fu, H.; Lei, T. Adomian Decomposition, Dynamic Analysis and Circuit Implementation of a 5D Fractional-Order Hyperchaotic System. Symmetry 2022, 14, 484. [Google Scholar] [CrossRef]
- Petras, I. Fractional-order memristor-based Chua’s circuit. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process 2010, 57, 975–979. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Cao, Y. An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int. J. Bifurc. Chaos 2022, 32, 2250035. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F. A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks. Mathematics 2023, 11, 1369. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. On the simplest fractional-order memristor-based chaotic system. Nonlinear Dyn. 2012, 70, 1185–1197. [Google Scholar] [CrossRef]
- Yu, F.; Lin, Y.; Xu, S.; Yao, W.; Gracia, Y.M.; Cai, S. Dynamic Analysis and FPGA Implementation of a New Fractional-Order Hopfield Neural Network System under Electromagnetic Radiation. Biomimetics 2023, 8, 559. [Google Scholar] [CrossRef]
- Arsene, L.M. Fractional-order-induced symmetric multi-scroll chaotic attractors and double bubble bifurcations in a memristive coupled Hopfield neural networks. Chaos Solitons Fractals 2024, 178, 114267. [Google Scholar]
- Kong, X.; Yu, F.; Yao, W. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Ding, D.; Xiao, H. Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption. Nonlinear Dyn. 2022, 108, 4433–4458. [Google Scholar] [CrossRef]
- Yu, Y.; Shi, M.; Kang, H. Hidden dynamics in a fractional-order memristive Hindmarsh-Rose model. Nonlinear Dyn. 2020, 100, 891–906. [Google Scholar] [CrossRef]
- Li, Z.; Xie, W. Firing activities in a fractional-order Hindmarsh–Rose neuron with multistable memristor as autapse. Chin. Phys. B 2023, 32, 010503. [Google Scholar] [CrossRef]
- Ding, D.; Jin, F.; Zhang, H. Coexisting multiple firing behaviors of fractional-order memristor-coupled HR neuron considering synaptic crosstalk and its ARM-based implementation. Chaos Solitons Fractals 2022, 158, 112014. [Google Scholar] [CrossRef]
- Ding, D.; Jin, F.; Zhang, H. Fractional-order heterogeneous neuron network based on coupled locally-active memristors and its application in image encryption and hiding. Chaos Solitons Fractals 2024, 187, 115397. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Yao, Z.; Sun, K.; Wang, H.; Mou, J. Collective behaviors of fractional-order FithzHugh–Nagumo network. Phys. A Stat. Mech. Its Appl. 2024, 639, 129673. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, C.; Deng, Q. The dynamics of a memristor-based Rulkov neuron with fractional-order difference. Chin. Phys. B 2022, 31, 060502. [Google Scholar] [CrossRef]
- He, S.; Vignesh, D. Chaos and multi-layer attractors in asymmetric neural networks coupled with discrete fractional memristor. Neural Netw. 2023, 167, 572–587. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Deng, Q. Discrete-time fractional-order local active memristor-based Hopfield neural network and its FPGA implementation. Chaos Solitons Fractals 2025, 193, 116053. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, D. A stable meaningful image encryption scheme using the newly-designed 2D discrete fractional-order chaotic map and Bayesian compressive sensing. Signal Process 2022, 195, 108489. [Google Scholar] [CrossRef]
- Alexan, W.; Alexan, N.; Gabr, M. Multiple-layer image encryption utilizing fractional-order chen hyperchaotic map and cryptographically secure prngs. Fractal Fract. 2023, 7, 287. [Google Scholar] [CrossRef]
- Bingi, K.; Rajanarayan, P.B.; Pal, S.A. A Review on Fractional-Order Modelling and Control of Robotic Manipulators. Fractal Fract. 2023, 7, 77. [Google Scholar] [CrossRef]
- Tarasov, V.E. On History of Mathematical Economics: Application of Fractional Calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Clemente-López, D.; Munoz-Pacheco, J.M.; Rangel-Magdaleno, J. A Review of the Digital Implementation of Continuous-Time Fractional-Order Chaotic Systems Using FPGAs and Embedded Hardware. Arch. Comput. Methods Eng. 2023, 30, 951–983. [Google Scholar] [CrossRef]
- Ndolane, S. Study of a Fractional-Order Chaotic System Represented by the Caputo Operator. Complexity 2021, 2021, 5534872. [Google Scholar]
- Miller, K.S.; Ross, B. Fractional Difference Calculus. Proceedings of the International Symposium on Univalent Functions. Fract. Calc. Their Appl. 1988, 145, 139–152. [Google Scholar]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The FracPECE subroutine for the numerical solution of differential equations of fractional order. Forsch. Und Wiss. Rechn. 1998, 145, 57–71. [Google Scholar]
- Adhikari, S.P.; Sah, M.P.; Kim, H. Three fingerprints of memristor. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Chua, L.O. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 89–157. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, C.; Deng, Q. Locally active memristor with three coexisting pinched hysteresis loops and its emulator circuit. Int. J. Bifurcat. Chaos 2020, 30, 2050184. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, X. Filippov Hindmarsh–Rose neuronal model with threshold policy control. IEEE Trans. Neural Netw. 2019, 30, 306–311. [Google Scholar] [CrossRef]
- Etémé, A.S.; Tabi, C.B.; Mohamadou, A. Longrange memory effects in a magnetized Hindmarsh–Rose neural network. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105208. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Jafari, S. Wave propagation and spiral wave formation in a Hindmarsh-Rose neuron model with fractional-order threshold memristor synaps. Int. J. Mod. Phys. B 2020, 34, 2050157. [Google Scholar] [CrossRef]
- Ding, D.; Niu, Y.; Zhang, H. Fractional-order heterogeneous memristive Rulkov neuronal network and its medical image watermarking application. Chin. Phys. B 2024, 33, 050503. [Google Scholar] [CrossRef]
- Ding, D.; Jiang, L.; Hu, Y.; Yang, Z.; Li, Q.; Zhang, Z.; Wu, Q. Hidden coexisting firings in fractional-order hyperchaotic memristor-coupled HR neural network with two heterogeneous neurons and its applications. Chaos 2021, 31, 083107. [Google Scholar] [CrossRef]
- Rajagopal, K.; Tuna, M.; Karthikeyan, A. Dynamical analysis, sliding mode synchronization of a fractional-order memristor Hopfield neural network with parameter uncertainties and its non-fractional-order FPGA implementation. Eur. Phys. J. Spec. Top. 2019, 228, 2065–2080. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, S.; Su, D.; Wu, Y.; Gracia, Y.M.; Yin, H. Dynamic Analysis and Implementation of FPGA for a New 4D Fractional-Order Memristive Hopfield Neural Network. Fractal Fract. 2025, 9, 115. [Google Scholar] [CrossRef]
- Balamurali, R.; Zhen, W.; Hayder, N. Dynamics of a two-neuron hopfield neural network: Memristive synapse and autapses and impact of fractional order. AEU Int. J. Electron. Commun. 2024, 187, 155506. [Google Scholar]
- Rulkov, F. Regularization of Synchronized Chaotic Bursts. Phys. Rev. Lett. 2001, 86, 183. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Mou, J.; Banerjee, S.; Cao, Y. Analysis of the functional behavior of fractional-order discrete neuron under electromagnetic radiation. Chaos Solitons Fractals 2023, 176, 114113. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, H.; Zhu, W.; Sun, K. Dynamics and synchronization of fractional-order Rulkov neuron coupled with discrete fracmemristor. Chaos Solitons Fractals 2025, 192, 116012. [Google Scholar] [CrossRef]
- Ghasemi, M.; Raeissi, Z.M.; Foroutannia, A.; Mohammadian, M.; Shakeriaski, F. Dynamic Effects Analysis in Fractional Memristor-Based Rulkov Neuron Model. Biomimetics 2024, 9, 543. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Mao, B.; Lei, T. Multistable Behaviors Analysis and Sliding Mode Control of Fractional-order Memristive Hindmarsh-Rose Neuron. In Proceedings of the 2023 35th Chinese Control and Decision Conference (CCDC), Yichang, China, 20–22 May 2023; pp. 397–402. [Google Scholar]
- Victor, K.T.; Arsene, L. Fractional-order bi-Hopfield neuron coupled via a multistable memristor: Complex neuronal dynamic analysis and implementation with microcontroller. AEU Int. J. Electron. Commun. 2025, 191, 155661. [Google Scholar]
- Xiu, C.; Li, X. Edge Extraction Based on Memristor Cell Neural Network with Fractional Order Template. IEEE Access 2019, 7, 90750–90759. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, D. Dynamics analysis and cryptographic implementation of a fractional-order memristive cellular neural network model. Chin. Phys. B 2024, 33, 040506. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Y.; Wang, H.; Nie, D. Quasi-synchronization of discrete-time tempered fractional-order memristive neural networks with time delays. Neurocomputing 2025, 619, 129146. [Google Scholar] [CrossRef]
- He, S.; Vignesh, D.; Banerjee, S. Dynamics of memristor coupled discrete fractional symmetric neural network model. Chin. J. Phys. 2024, 91, 698–711. [Google Scholar] [CrossRef]
- Liu, F.; Cai, G.; Zhou, F.; Wang, W.; Wang, H.; Yang, X. Dynamic Analysis and Control of Fractional Order Memristor Hopfield Neural Network. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 1–5. [Google Scholar]
- Yang, N.; Liang, J.; Wu, C.; Guo, Z. Dynamics and Implementation of FPGA for Memristor-Coupled Fractional-Order Hopfield Neural Networks. Int. J. Bifurc. Chaos 2024, 34, 2450106. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Ju, X.; Guo, Z. A novel fractional-order memristive Hopfield neural network for traveling salesman problem and its FPGA implementation. Neural Netw. 2024, 179, 106548. [Google Scholar] [CrossRef]
- Anzo-Hernández, A.; Zambrano-Serrano, E.; Platas-Garza, M.A.; Volos, C. Dynamic Analysis and FPGA Implementation of Fractional-Order Hopfield Networks with Memristive Synapse. Fractal Fract. 2024, 8, 628. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.; Cai, S.; Du, S. Dynamic Analysis and Audio Encryption Application in IoT of a Multi-Scroll Fractional-Order Memristive Hopfield Neural Network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Wang, M.; Deng, B. A Multistable Memristor and Its Application in Fractional-Order Hopfield Neural Network. Braz. J. Phys. 2022, 52, 205. [Google Scholar] [CrossRef]
- Venkatesh, J.; Pchelintsev, A.N.; Karthikeyan, A.; Parastesh, F.; Jafari, S. A Fractional-Order Memristive Two-Neuron-Based Hopfield Neuron Network: Dynamical Analysis and Application for Image Encryption. Mathematics 2023, 11, 4470. [Google Scholar] [CrossRef]
- Louiza, D.; Adel, O. On fractional discrete financial system: Bifurcation, chaos, and control. Chin. Phys. B 2024, 33, 100201. [Google Scholar]
- Farman, M.; Nisar, K.S.; Ali, M. Chaos and forecasting financial risk dynamics with different stochastic economic factors by using fractional operator. Model. Earth Syst. Environ. 2025, 11, 146. [Google Scholar] [CrossRef]
- Gupta, D.; Bhalekar, S. Fractional order sunflower equation: Stability, bifurcation and chaos. Eur. Phys. J. Spec. Top. 2024, 11, 4470. [Google Scholar] [CrossRef]
- José, F.; Manisha, K.N. Chaos and stability of a fractional model of the cyber ecosystem. AIMS Math. 2024, 9, 22146–22173. [Google Scholar]
- Salah, B.; Sabarinathan, S. Chaos and stability analysis of the nonlinear fractional-order autonomous system. Alex. Eng. J. 2025, 118, 278–291. [Google Scholar]
- Zhang, M.; Zang, H.; Liu, Z. Fractional-order adaptive sliding mode control based on predefined-time stability for chaos synchronization. Chaos Solitons Fractals 2025, 191, 115921. [Google Scholar] [CrossRef]
- Diabi, L.; Ouannas, A. The Discrete Ueda System and Its Fractional Order Version: Chaos, Stabilization and Synchronization. Mathematics 2025, 13, 239. [Google Scholar] [CrossRef]

| Neuron Systems | Continuous-Time | Discrete-Time |
|---|---|---|
| FM-HR | [118,119,120,143,153] | ∖ |
| FM-FHN | [123] | ∖ |
| FM-Heterogeneous | [121,144,145,154] | ∖ |
| FM-CNNs | [155,156] | ∖ |
| FM-ANNs | [157] | ∖ |
| FM-SNNs | ∖ | [158] |
| FM-ASNNs | [123] | [125] |
| FM-HNNs | [114,115,116,117,122,146,147,148,159,160,161,162,163,164,165] | [126] |
| FM-Rulkov | [144] | [124,150,151,152] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, Y.; Yang, G.; Deng, Q. A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks. Mathematics 2025, 13, 1600. https://doi.org/10.3390/math13101600
Wang C, Li Y, Yang G, Deng Q. A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks. Mathematics. 2025; 13(10):1600. https://doi.org/10.3390/math13101600
Chicago/Turabian StyleWang, Chunhua, Yufei Li, Gang Yang, and Quanli Deng. 2025. "A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks" Mathematics 13, no. 10: 1600. https://doi.org/10.3390/math13101600
APA StyleWang, C., Li, Y., Yang, G., & Deng, Q. (2025). A Review of Fractional-Order Chaotic Systems of Memristive Neural Networks. Mathematics, 13(10), 1600. https://doi.org/10.3390/math13101600







