Robustness Study of Unit Elasticity of Intertemporal Substitution Assumption and Preference Misspecification
Abstract
1. Introduction
2. Materials and Methods
2.1. Motivations
2.1.1. The Elasticity of Intertemporal Substitution and the Challenges
2.1.2. The Unit EIS Assumption and the Modeling Issues
- a.
- The EIS in Epstein–Zin Preferences
- b.
- The Empirical Evidence of Non-Unit EIS
- c.
- The Rationale and Limitations of the Unit EIS Assumption
2.1.3. The Rationale for Robustness Analysis on Christensen 2017 Model
2.1.4. Monte Carlo Simulation Connect Preference Parameters with Asset Prices
2.2. Robustness Study Framework
2.2.1. Stochastic Discount Factor and Decomposition
2.2.2. Sieve Estimation Setup
2.2.3. Data-Generating Process
3. Results
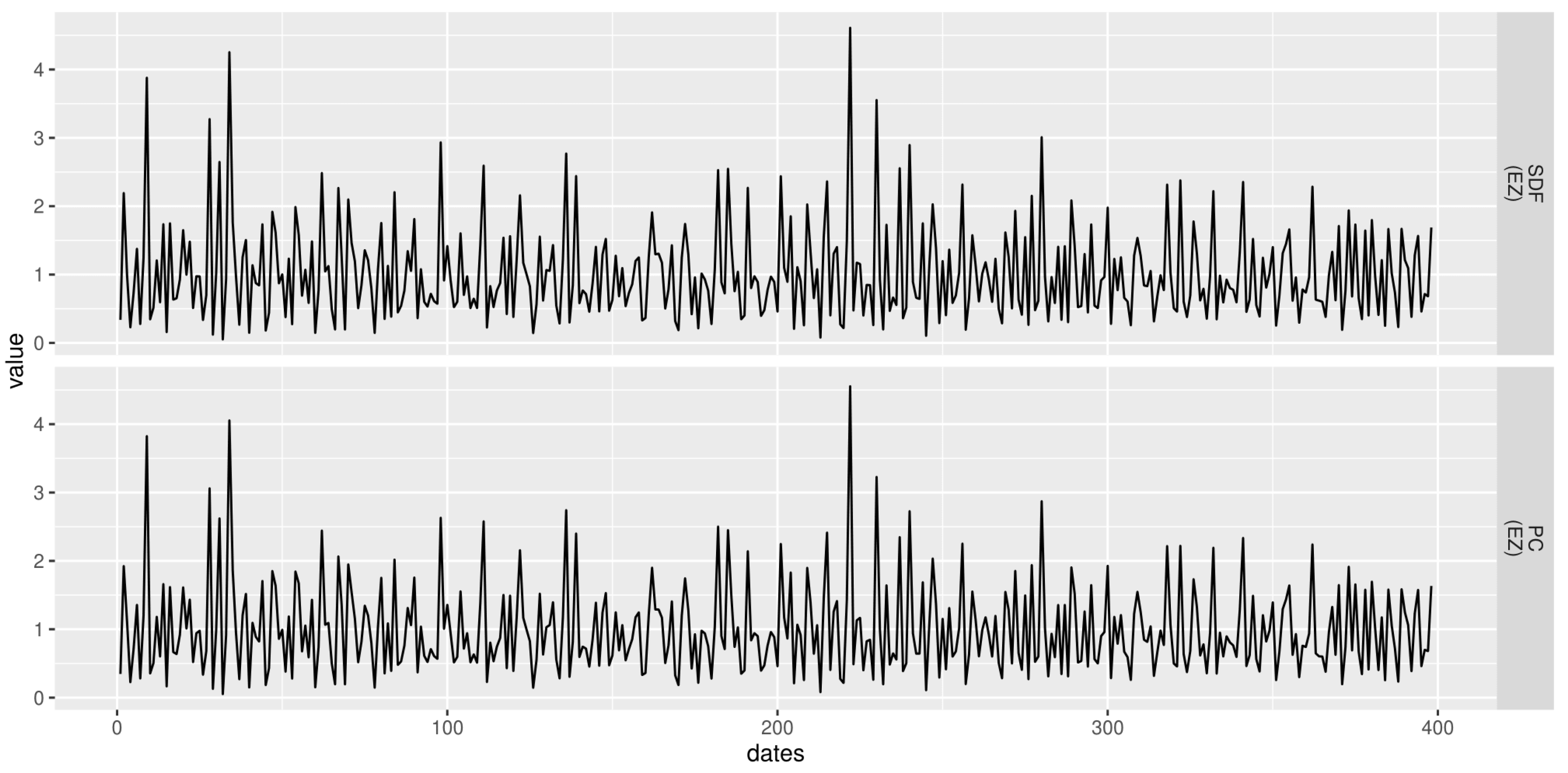
3.1. Study with the Generated Dividend and Consumption Growth Rates
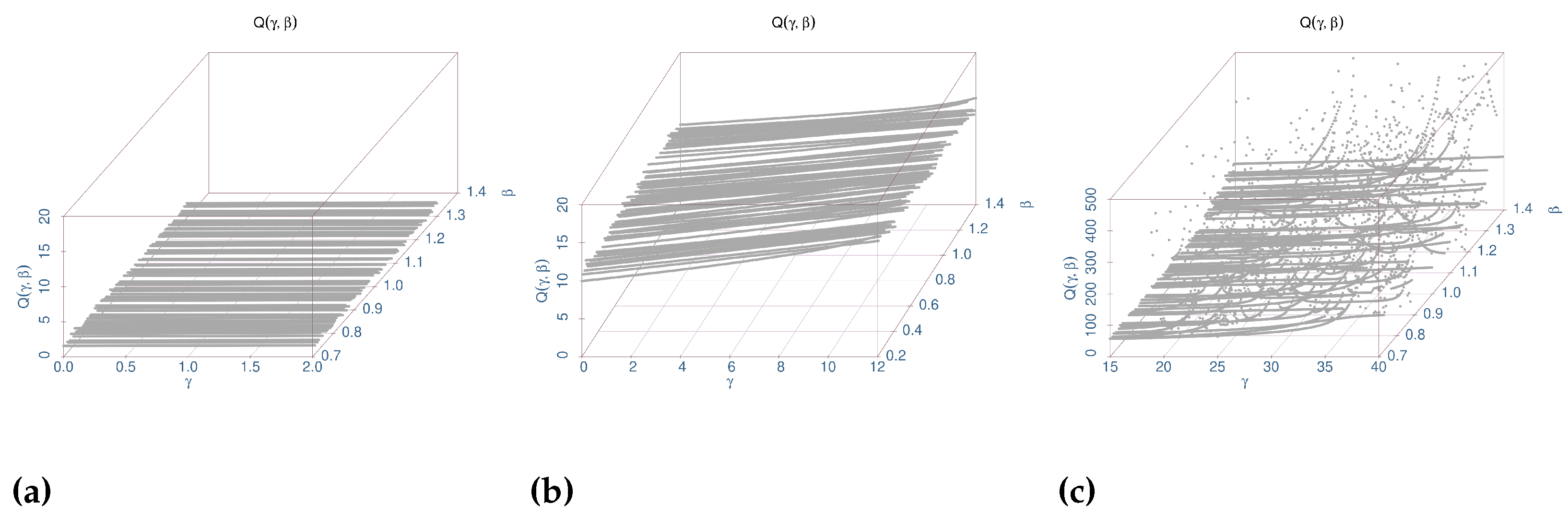
3.2. Estimation Surface Study
4. Discussion
4.1. The Efficiency of the Robustness Framework
4.2. The Insights of Christensen 2017 Robustness Study
4.3. Implications for Broader Asset Pricing Models
4.3.1. The Revealed Absorption Effect and Justification
4.3.2. Connection to Asset Pricing Models
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
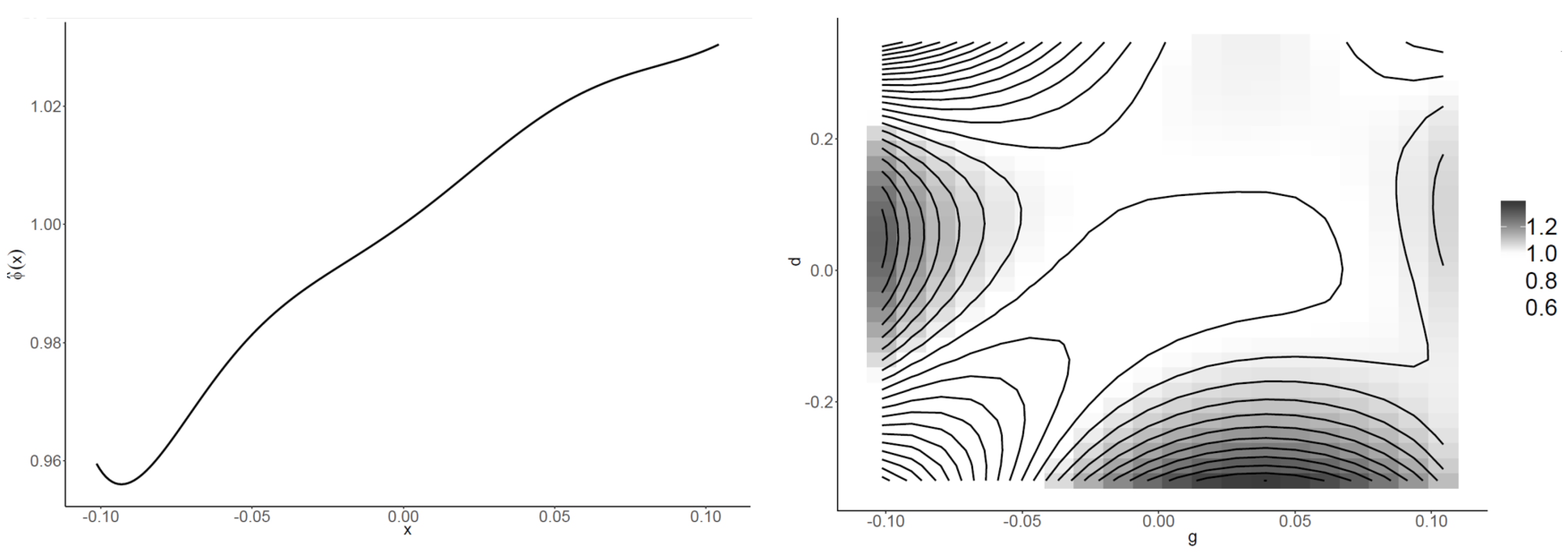
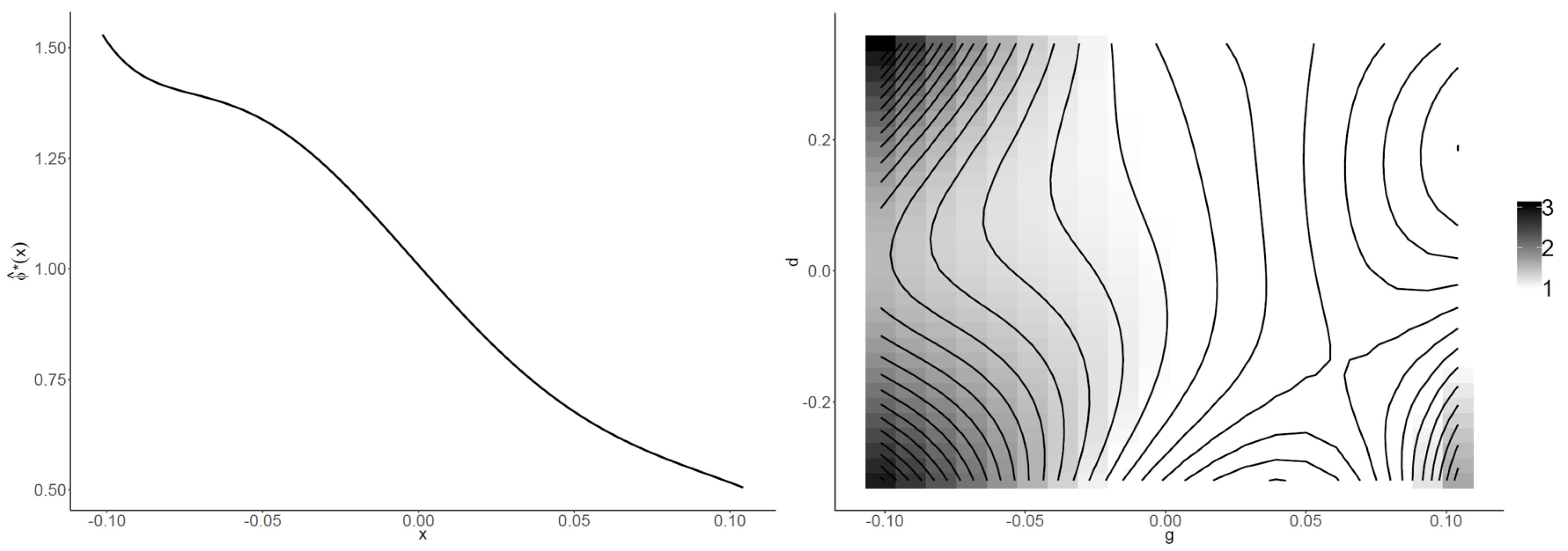

| 0.9616 | 0.9633 | 0.9888 | 0.9888 | 0.9889 | |
| (0.9533, 0.9667) | (0.9562, 0.9706) | (0.9876, 0.9898) | (0.9876, 0.9899) | (0.9877, 0.9899) | |
| 0.0391 | 0.0374 | 0.0113 | 0.0112 | 0.0112 | |
| (0.0339, 0.0477) | (0.0298, 0.0447) | (0.0102, 0.0125) | (0.0102, 0.0125) | (0.0101, 0.0124) | |
| 0.4039 | 0.1316 | 0.0002 | 0.0003 | 0.0003 | |
| (0.1640, 0.7158) | (−0.1750, 0.1724) | (0.0002, 0.0003) | (0.0002, 0.0003) | (0.0002, 0.0004) | |
| 0.9375 | 0.9492 | 0.99 | 0.99 | 0.99 | |
| (0.9208, 0.9513) | (0.9429, 0.9700) | ||||
| 33.7604 | 19.119 | 0.7 | 0.8 | 0.9 | |
| (31.3992, 53.6258) | (8.2750, 24.6641) | ||||
| 1.426 | 1.1010 | 1.0004 | 1.0002 | 1.0001 | |
| (1.0347, 1.7873) | (0.7365, 1.1395) | (1.0000, 1.0007) | (1.0001, 1.0005) | (1.0000, 1.0003) | |
| 0.8944 | 0.8974 | 0.9912 | 0.9919 | 0.9926 | |
| (0.8877, 0.8972) | (0.8928, 0.9021) | (0.9876, 0.9898) | (0.9896, 0.9922) | (0.9900,0.9928) | |
| 0.1116 | 0.1082 | 0.0089 | 0.0081 | 0.0074 | |
| (0.1085, 0.1190) | (0.1030, 0.1134) | (0.0084, 0.0109) | (0.0078, 0.0104) | (0.0072,0.0100) | |
| 0.154 | 0.0999 | 0.0058 | 0.0091 | 0.0132 | |
| (−0.0449, 0.2820) | (0.0935, 0.1931) | (0.0030, 0.0050) | (0.0047, 0.0078) | (0.0068,0.0112) | |
| 0.8804 | 0.8857 | 0.99 | 0.99 | 0.99 | |
| (0.8652, 0.8934) | (0.8725, 0.8991) | ||||
| 19.1893 | 15.8118 | 4 | 5 | 6 | |
| (13.0482, 31.2515) | (8.3206, 27.8645) | ||||
| 1.1376 | 1.0797 | 0.9993 | 1.0005 | 1.0025 | |
| (0.9030, 1.2622) | (0.8705, 1.1592) | (1.0000, 1.0007) | (0.9936, 1.0034) | (0.9934,1.0057) | |
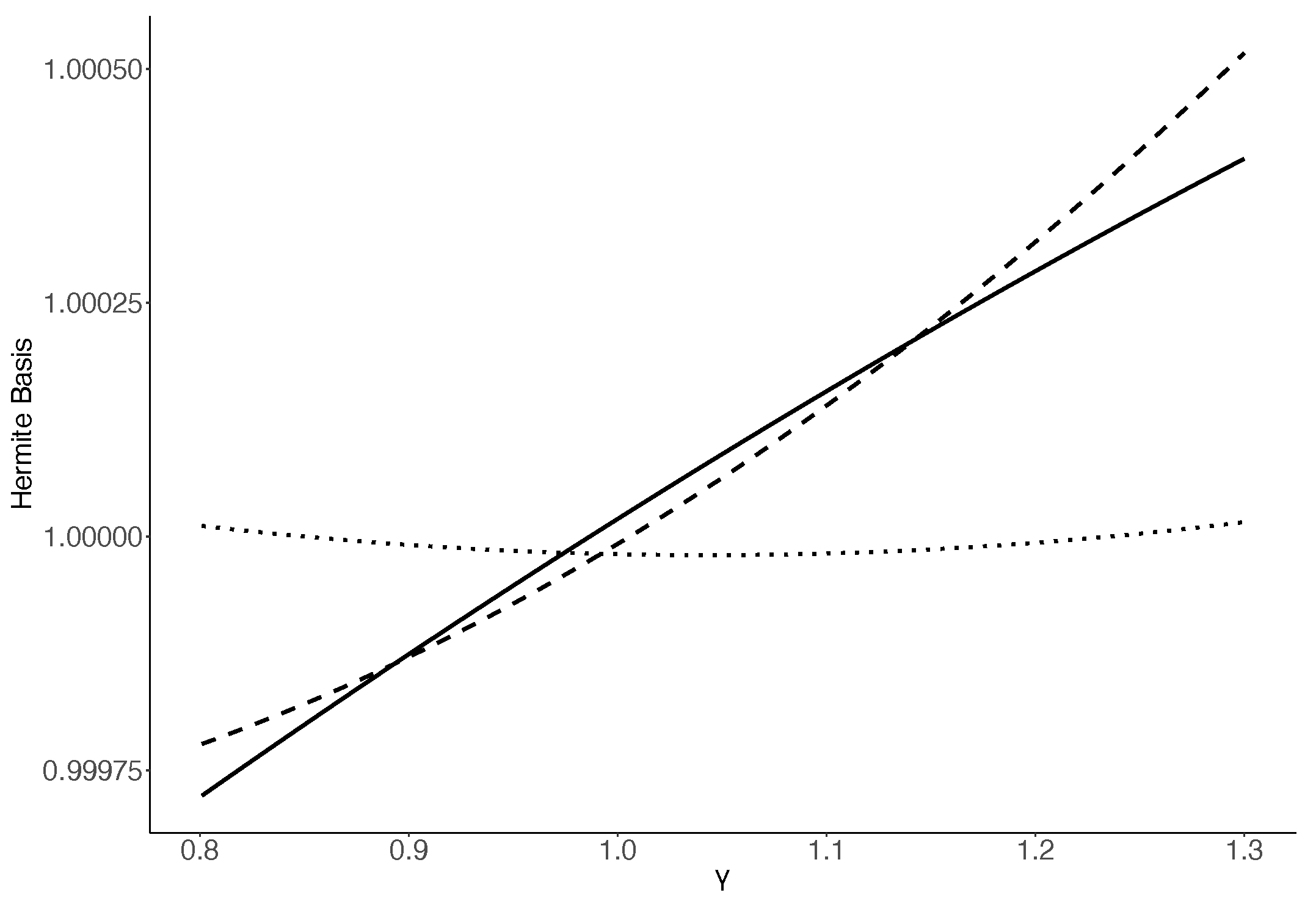
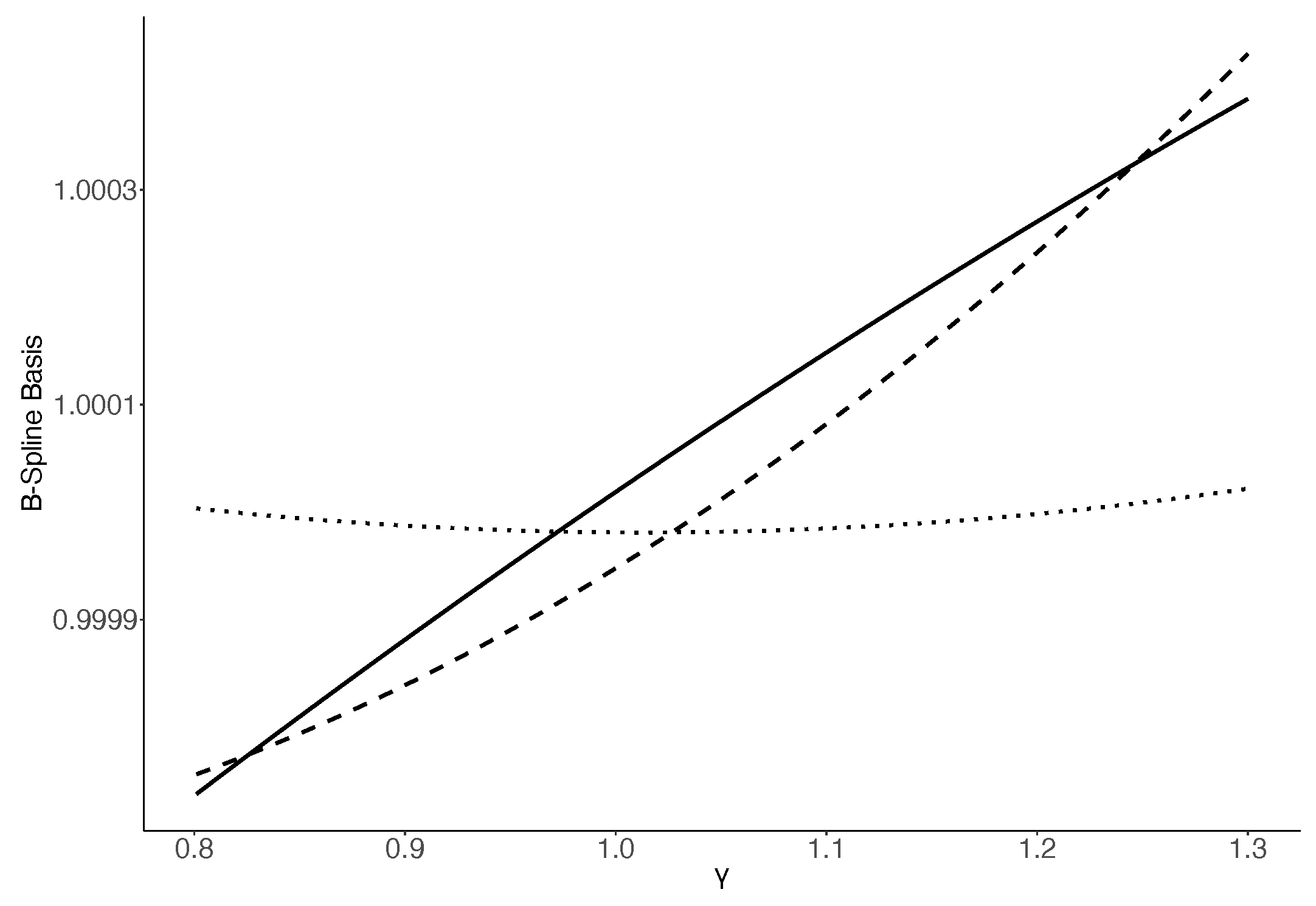
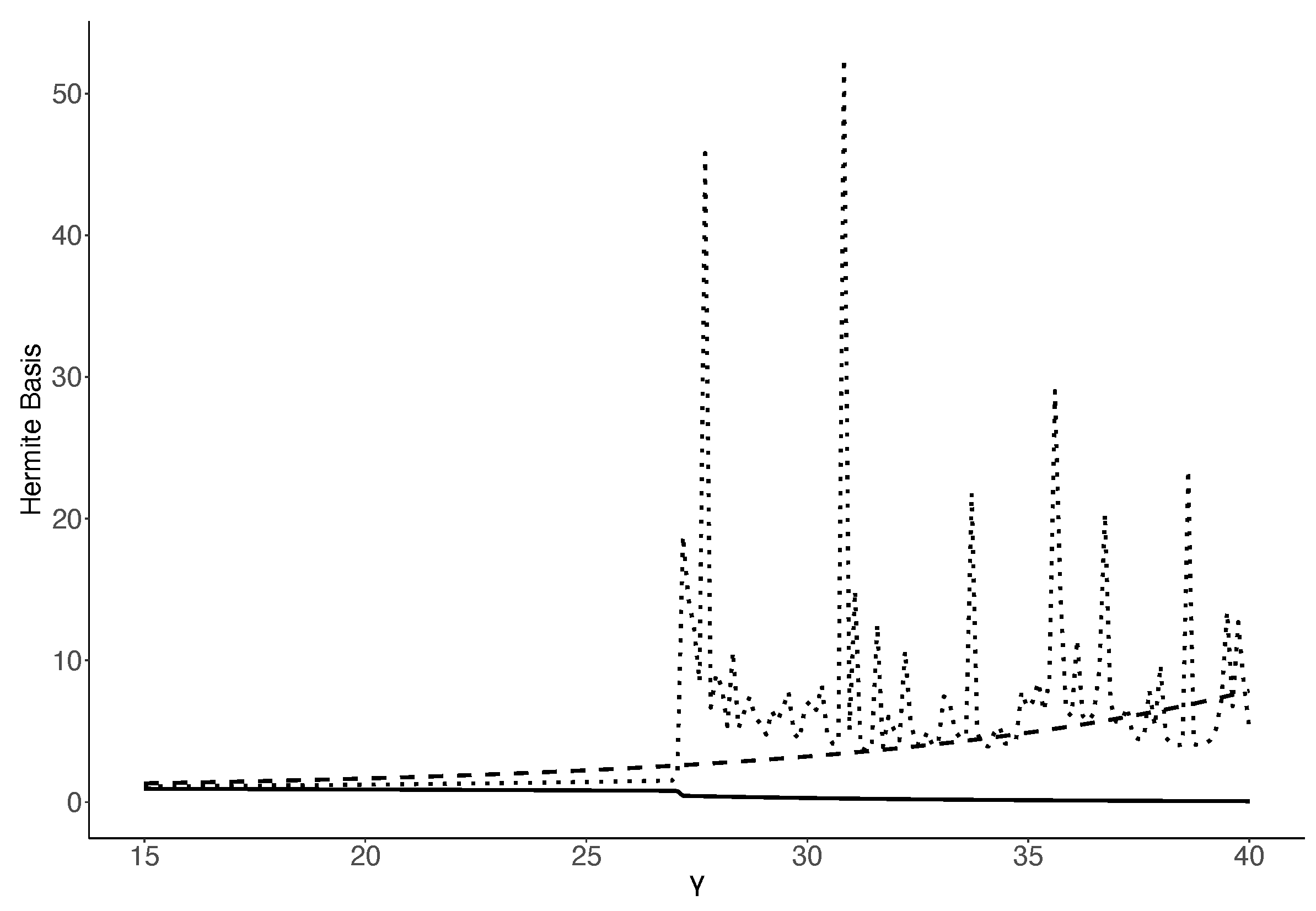

References
- Epstein, L.G.; Zin, S.E. Substitution, Risk Aversion, and the Temporal Behavior of Consumption and Asset Returns: A Theoretical Framework. Econometrica 1989, 57, 937–969. [Google Scholar] [CrossRef]
- Bansal, R.; Yaron, A. Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles. J. Financ. 2004, 59, 1481–1509. [Google Scholar] [CrossRef]
- Hansen, L.P.; Scheinkman, J.A. Long-Term Risk: An Operator Approach. Econometrica 2009, 77, 177–234. [Google Scholar]
- Christensen, T.M. Nonparametric Stochastic Discount Factor Decomposition. Econometrica 2017, 85, 1501–1536. [Google Scholar] [CrossRef]
- Tauchen, G.; Hussey, R. Quadrature-Based Methods for Obtaining Approximate Solutions to Nonlinear Asset Pricing Models. Econometrica 1991, 59, 371–396. [Google Scholar] [CrossRef]
- Smith, D.C. Finite sample properties of tests of the Epstein-Zin asset pricing model. J. Econom. 1999, 93, 113–148. [Google Scholar] [CrossRef]
- Moskowitz, T.J.; Vissing-Jorgensen, A. The Returns to Entrepreneurial Investment: A Private Equity Premium Puzzle? Am. Econ. Rev. 2002, 92, 745–778. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Viceira, L.M. Consumption and Portfolio Decisions when Expected Returns are Time Varying. Q. J. Econ. 1999, 114, 433–495. [Google Scholar] [CrossRef]
- Browning, M.; Crossley, T.F. The Life-Cycle Model of Consumption and Saving. J. Econ. Perspect. 2001, 15, 3–22. [Google Scholar] [CrossRef]
- Campbell, J.Y. Consumption-based asset pricing. In Handbook of the Economics of Finance; Elsevier: Amsterdam, The Netherlands, 2003; Volume 1, Part 2; pp. 803–887. [Google Scholar]
- Hall, R.E. Intertemporal substitution in consumption. J. Political Econ. 1988, 96, 339–357. [Google Scholar] [CrossRef]
- Runkle, D.E. Liquidity constraints and the permanent-income hypothesis: Evidence from panel data. J. Monet. Econ. 1991, 27, 73–98. [Google Scholar] [CrossRef]
- Breeden, D.T. An intertemporal asset pricing model with stochastic consumption and investment opportunities. J. Financ. Econ. 1979, 7, 265–296. [Google Scholar] [CrossRef]
- Ferson, W.E.; Constantinides, G.M. Habit persistence and durability in aggregate consumption: Empirical tests. J. Financ. Econ. 1991, 29, 199–240. [Google Scholar] [CrossRef]
- Hansen, L.P.; Singleton, K.J. Generalized Instrumental Variables Estimation of Nonlinear Rational Expectations Models. Econometrica 1982, 50, 1269–1286. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Mankiw, N.G. Consumption, income, and interest rates: Reinterpreting the time series evidence. Nber Macroecon. Annu. 1989, 4, 185–216. [Google Scholar] [CrossRef]
- Attanasio, O.P.; Weber, G. Consumption growth, the interest rate and aggregation. Rev. Econ. Stud. 1993, 60, 631–649. [Google Scholar] [CrossRef]
- Attanasio, O.P.; Weber, G. Is consumption growth consistent with intertemporal optimization? Evidence from the consumer expenditure survey. J. Political Econ. 1995, 103, 1121–1157. [Google Scholar] [CrossRef]
- Vissing-Jørgensen, A. Limited asset market participation and the elasticity of intertemporal substitution. J. Political Econ. 2002, 110, 825–853. [Google Scholar] [CrossRef]
- Vissing-Jørgensen, A.; Attanasio, O.P. Stock-market participation, intertemporal substitution, and risk-aversion. Am. Econ. Rev. 2003, 93, 383–391. [Google Scholar] [CrossRef]
- Lucas, R.E. Asset Prices in an Exchange Economy. Econometrica 1978, 46, 1429–1445. [Google Scholar] [CrossRef]
- Kydland, F.E.; Prescott, E.C. Time to build and aggregate fluctuations. Econometrica 1982, 50, 1345–1370. [Google Scholar] [CrossRef]
- King, R.G.; Plosser, C.I.; Rebelo, S.T. Production, growth and business cycles: I. The basic neoclassical model. J. Monet. Econ. 1988, 21, 195–232. [Google Scholar] [CrossRef]
- Mehra, R.; Prescott, E.C. The equity premium: A puzzle. J. Monet. Econ. 1985, 15, 145–161. [Google Scholar] [CrossRef]
- Weil, P. The equity premium puzzle and the risk-free rate puzzle. J. Monet. Econ. 1989, 24, 401–421. [Google Scholar] [CrossRef]
- Hansen, L.P.; Sargent, T.J. Robustness; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Giuliano, P.; Turnovsky, S.J. Intertemporal substitution, risk aversion, and economic performance in a stochastically growing open economy. J. Int. Money Financ. 2003, 22, 529–556. [Google Scholar] [CrossRef]
- Hansen, L.P.; Sargent, T.J. Robust control and model uncertainty. Am. Econ. Rev. 2001, 91, 60–66. [Google Scholar] [CrossRef]
- Lucas, R.E. Supply-Side Economics: An Analytical Review. Oxf. Econ. Pap. 1990, 42, 293–316. [Google Scholar] [CrossRef]
- Jones, L.; Manuelli, R.; Siu, H. Growth and Business Cycles; Working Paper 7633; National Bureau of Economic Research: Cambridge, MA, USA, 2000. [Google Scholar] [CrossRef]
- Cont, R.; Hansen, L.P.; Renault, E. Pricing Kernels; Wiley: Chichester, UK, 2010. [Google Scholar]
- Alvarez, F.; Jermann, U.J. Using Asset Prices to Measure the Persistence of the Marginal Utility of Wealth. Econometrica 2005, 73, 1977–2016. [Google Scholar] [CrossRef]
- Hansen, L.P.; Heaton, J.C.; Li, N. Consumption Strikes Back? Measuring Long Run Risk. J. Political Econ. 2008, 116, 260–302. [Google Scholar] [CrossRef]
- Kocherlakota, N. On tests of representative consumer asset pricing models. J. Monet. Econ. 1990, 26, 285–304. [Google Scholar] [CrossRef]
- Kandel, S.; Stambaugh, R.F. On the Predictability of Stock Returns: An Asset-Allocation Perspective. J. Financ. 1996, 51, 385–424. [Google Scholar]
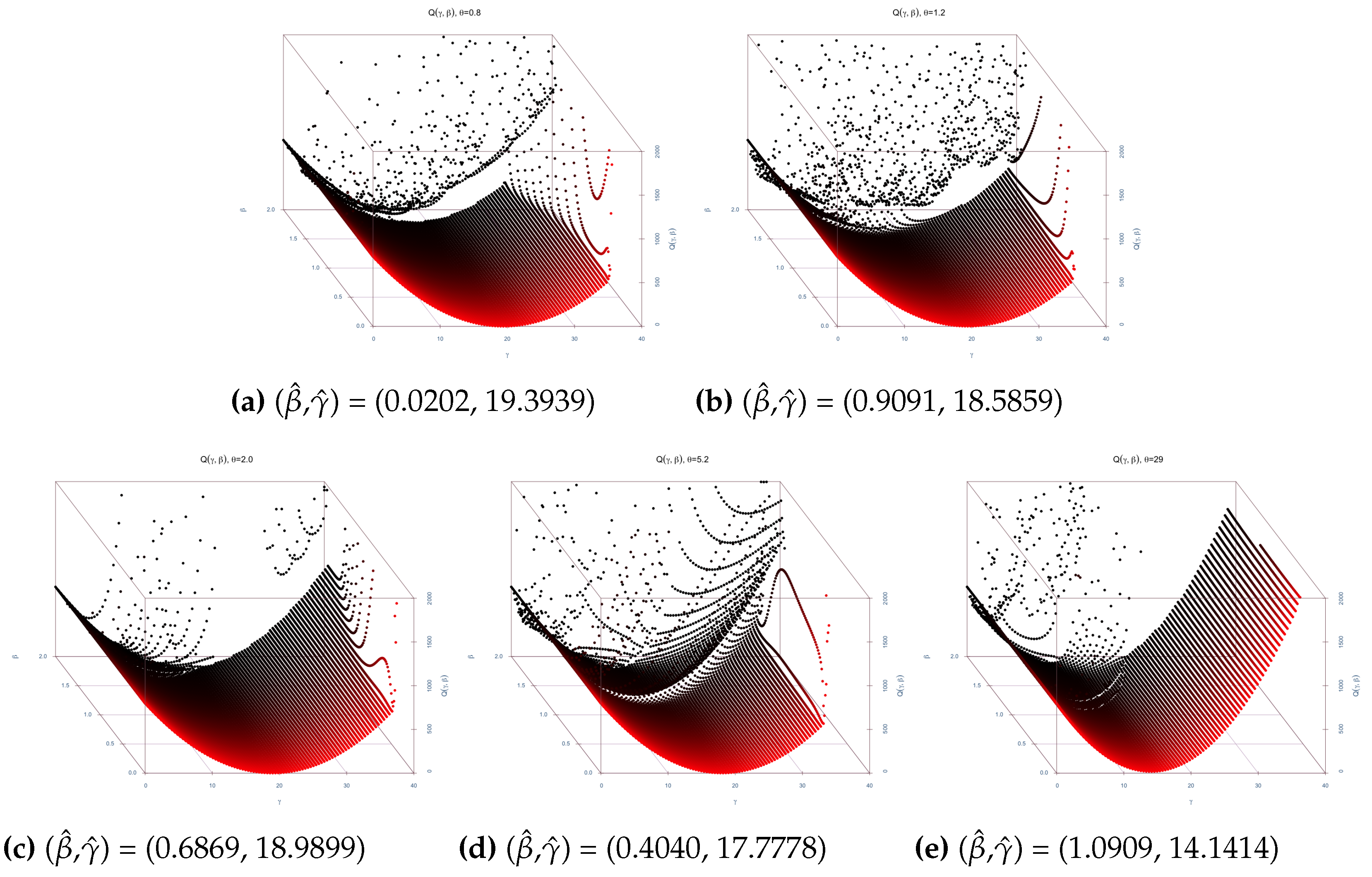
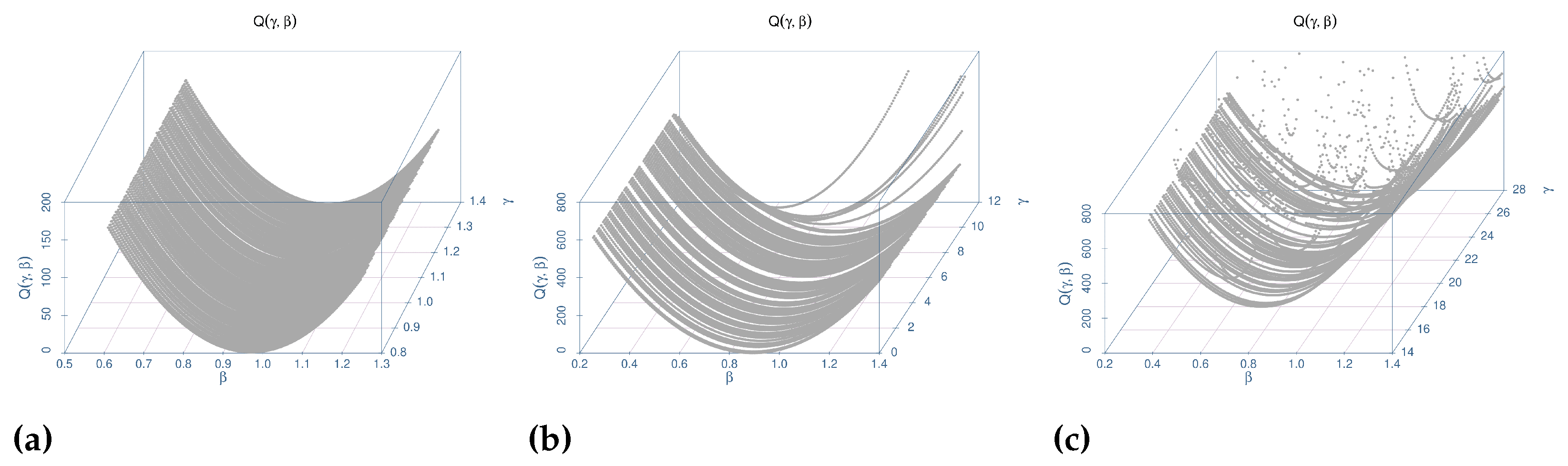

| Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | Intercept | Var () | Cov () | |||
| dt | Mean Point Estimate | 0.004 | 0.111 | 0.416 | 0.014 | 0.002 |
| Standard Error | 0.007 | 0.054 | 0.186 | |||
| gt | Mean Point Estimate | 0.021 | 0.017 | −0.161 | 0.001 | 0.002 |
| Standard Error | 0.002 | 0.016 | 0.054 |
| , | Equity Premium | ||||
|---|---|---|---|---|---|
| 0.8, 0.8 | Mean of estimates | 0.036 | 0.038 | 0.035 | 0.003 |
| Std. dev. Of estimates | 0.035 | 0.125 | 0.004 | ||
| 5.2, 5.2 | Mean of estimates | 0.114 | 0.116 | 0.104 | 0.012 |
| Std. dev. Of estimates | 0.063 | 0.136 | 0.030 | ||
| 25, 29 | Mean of estimates | 0.268 | 0.265 | 0.137 | 0.128 |
| Std. dev. Of estimates | 0.254 | 0.262 | 0.170 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, H. Robustness Study of Unit Elasticity of Intertemporal Substitution Assumption and Preference Misspecification. Mathematics 2025, 13, 1593. https://doi.org/10.3390/math13101593
Jing H. Robustness Study of Unit Elasticity of Intertemporal Substitution Assumption and Preference Misspecification. Mathematics. 2025; 13(10):1593. https://doi.org/10.3390/math13101593
Chicago/Turabian StyleJing, Huarui. 2025. "Robustness Study of Unit Elasticity of Intertemporal Substitution Assumption and Preference Misspecification" Mathematics 13, no. 10: 1593. https://doi.org/10.3390/math13101593
APA StyleJing, H. (2025). Robustness Study of Unit Elasticity of Intertemporal Substitution Assumption and Preference Misspecification. Mathematics, 13(10), 1593. https://doi.org/10.3390/math13101593






