1. Introduction
The automated storage system with four-way shuttles is a densely packed storage system that has been booming in recent years. With its many remarkable advantages, it is deeply integrated into various aspects of the modern logistics system.
In the field of e-commerce warehousing, in the face of the need for rapid processing of a large number of orders, four-way shuttles can operate stably even under high-intensity operations due to their strong robustness, ensuring the accurate storage and retrieval of goods. In cold chain logistics, their good adaptability to low-temperature environments effectively guarantees the storage and circulation quality of fresh products, pharmaceuticals, and other items. Moreover, because this system has a very high space utilization rate, it can greatly increase storage capacity within limited warehouse space, meeting the warehousing needs of cities with tight land resources. In terms of the efficiency of inbound and outbound operations, four-way shuttles perform excellently, being able to quickly complete the handling of goods and significantly enhancing the overall rhythm of logistics operations.
As the core handling units of the automated storage system with four-way shuttles, four-way shuttles have the characteristic of flexible movement in main passages and storage lanes. Their operational efficiency has a decisive impact on the overall efficiency of goods inbound and outbound operations of the system. In the scenario of multiple four-way shuttles working collaboratively, path planning faces many complex challenges.
The warehousing environment is significantly dynamic. Factors such as the real-time adjustment of the goods storage layout and random changes in the operation status of equipment all pose stringent requirements for the dynamic adaptability of path planning. At the same time, when multiple shuttles are operating in parallel, it is necessary to achieve a reasonable arrangement of the operation trajectories of the vehicles under the constraints of limited space and time resources to avoid path conflicts and congestion. In addition, due to the diversity of the operation tasks of each four-way shuttle and the differences in task priorities, how to establish an efficient task allocation and collaborative scheduling mechanism to ensure the overall smoothness and efficiency of the operations of multiple shuttles is also a key issue that urgently needs to be solved in the path planning process.
At present, in the field of path planning for storage four-way shuttles, a large number of research achievements have emerged. Borovinšek M et al. [
1] took the minimization of the average throughput time, power consumption, and total investment cost of the shuttle vehicle system as the objective function, carried out multi-objective optimization for the design of the shuttle vehicle system, and solved it with the NSGA-II genetic algorithm. Koenig et al. [
2] proposed the Lifelong Planning A* algorithm (LPA), which reuses the search results to achieve efficient search and can quickly respond to environmental changes. Manny Shankar et al. [
3] proposed a path planning method that combines the artificial potential field method and the particle swarm optimization algorithm, which takes less time than the pure particle swarm optimization algorithm. Harshal S. Dewang et al. [
4] proposed a path planning method for mobile robots based on the Adaptive Particle Swarm Optimization (APSO) algorithm, which has a good obstacle avoidance effect and a short time to reach the target. Chaymaa Lamini et al. [
5] used the Genetic Algorithm (GA) to solve the path planning problem in a static environment, and the improved algorithm has a better effect. Shiwei Lin et al. [
6] improved the particle swarm optimization algorithm with the help of the Simulated Annealing (SA) algorithm, and the hybrid PSO-SA algorithm has better performance. Jing designed an improved A* obstacle avoidance algorithm based on real-time information in reference [
7]. Guo et al. [
8] proposed the TTE method and verified the real-time information sharing mechanism. Aline Sandip et al. [
9] proposed the Control Based A* (CBA*) path planning algorithm and the improved DCBA* algorithm to make it more flexible and robust.
The above-mentioned studies mostly take a single handling device as the research object, providing research references for solving multi-objective optimization problems and improving the efficiency of path planning. However, these studies are all conducted in static environments, focusing on enhancing the path planning ability and algorithm efficiency of a single shuttle vehicle. They do not take into account the impact of storage location occupation and the passability of the roadway during inbound and outbound operations when multiple tasks are being executed.
In their study on solving the conflicts in the multi-four-way shuttle system, Eren C et al. [
10] proposed a multi-agent path planning method based on a bilateral negotiation strategy. Compared with the advanced centralized method, in a large search space and high density, it can find a conflict-free path solution with a higher success rate, and the path cost difference is small. Wei et al. [
11] proposed a method based on an altruistic strategy. When there is a conflict, the robot adjusts its local path first and sends adjustment information to surrounding robots to prevent collisions. Pianpak et al. [
12] proposed the ros-dmapf algorithm based on a distributed structure, which is implemented by multiple sub-solvers through the question-answer set programming. Experiments show that it has obvious performance advantages over algorithms such as WHA*. K.J.C. Fransen et al. [
13] proposed a dynamic path planning method suitable for grid systems and simulated four practical problems under two AGV densities by dynamically updating the graphical representation of vertex weights. LEE et al. [
14] constructed a storage detection system based on the Cyber-Physical system, used the shortest path algorithm to plan the path of the shuttle vehicle, and used the time window method to detect and adjust conflicts, ultimately achieving conflict-free scheduling. Felipe Garcia Lopez et al. [
15] adopted a collaborative trajectory optimization method for the path intersection of multiple devices, obtained a smooth collision avoidance path, and solved the difficult problem of smooth collision avoidance path planning for multiple devices at close range. Jinyu Cao [
16] conducted research on path planning in dynamic environments based on reinforcement learning. He proposed a pedestrian perception enhancement algorithm and improved the SAC algorithm. By designing a multi-step proxy reward function and using distributed soft policy iteration, he optimized the path decision-making process. Experiments have verified that these methods effectively improve the path planning performance of mobile robots. Fuqin D et al. [
17] designed a distributed deep reinforcement learning path planning method named DCAMAPF based on the actor-critic deep reinforcement learning framework. Through the request and response communication mechanism and the local attention mechanism, this method enables robots to plan paths collaboratively. Compared with methods such as D*Lite, this method significantly reduces the blocking rate and the occupation of computing cache in both discrete and centralized initialization environments. Yu, L et al. [
18] proposed the G2-rMAPPO method based on hierarchical reinforcement learning. By integrating the global guided path with the rMAPPO algorithm, this method is used to handle the dynamic path planning of multiple AGVs. Additionally, a dense reward function is designed, which enables AGVs to effectively avoid obstacles in dynamic environments and improves the efficiency of path planning.
In conclusion, some scholars have conducted relevant research on the path planning of four-way shuttles and the resolution of multi-agent conflicts. Regarding four-way shuttles, most of the research focuses on improving the path planning efficiency of single or multiple devices in static environments. Bionic heuristic algorithms are often selected and then integrated with and improve upon other algorithms.
For the issues of resolving multi-agent conflicts and path planning in dynamic environments, the methods mainly fall into two categories: distributed methods and centralized methods. Through various algorithm innovations, such as the improved A* algorithm, collaborative trajectory optimization, algorithms based on time windows and repulsive force fields, etc., and the formulation of diverse strategies, scholars have successfully addressed many problems faced by agents in path planning, such as collisions, deadlocks, and low efficiency.
However, most of these studies focus on AGVs and robots, and there are relatively few studies on four-way shuttle systems. In a four-way shuttle system, inbound and outbound tasks will change the status of storage locations and affect the passability of storage lanes. This study will take a single layer of the four-way shuttle system as the research object and investigate the path planning problem when multiple four-way shuttles operate simultaneously.
In the research of path planning, the A* algorithm integrates the efficient characteristics of the Breadth-First Search (BFS) and the greedy algorithm. It draws on the Dijkstra algorithm to accurately calculate the distances among the current position, the starting position, and the target position, and then determines the shortest path of the node. At the same time, it uses a heuristic function to guide the search direction. On the premise of ensuring the acquisition of the global optimal solution, it significantly improves the search efficiency. The A* algorithm has outstanding advantages in static path planning and provides an efficient solution for complex path searching.
The CBS algorithm has remarkable advantages in multi-vehicle path planning and has been widely recognized [
19]. This paper focuses on the path planning of multiple four-way shuttles in a dynamic warehouse environment. The dynamic changes and the multi-vehicle cooperation requirements in this scenario pose extremely high demands on the efficiency, accuracy, and real-time adaptability of the algorithm. The excellent performance of the A* algorithm in static path planning makes it suitable for constructing the basic framework of the path planning for four-way shuttles. The CBS algorithm, on the other hand, can effectively solve the problems of multi-vehicle path conflicts and coordination. Based on this, this paper deeply integrates the A* algorithm with the CBS algorithm, aiming to take advantage of their complementary strengths to achieve accurate and efficient path planning for multiple four-way shuttles in a dynamic environment and to provide assistance for the development of research and applications in this field.
To achieve this research goal, the following chapters are arranged in a systematic manner. In
Section 2, the main components of the four-way shuttle storage system will be introduced, which provides a fundamental understanding of the research object. In
Section 3, based on the working characteristics of the four-way shuttle system and according to the mode of the four-way shuttle’s compound operation, a mathematical model will be established with the objective of minimizing the time for the four-way shuttle to complete the operation task. This model serves as the basis for subsequent algorithm design. In
Section 4, an improvement method for the A* algorithm will be proposed, aiming to enhance its performance in the context of this research. In
Section 5, based on the improved A* algorithm, a path planning algorithm for dynamic environments based on the CBS will be designed. Finally, in
Section 6, according to the layout of the four-way shuttle system of an enterprise, a simulation experiment will be designed to verify the superiority of the improved A* algorithm and the effectiveness of the path planning algorithm for dynamic environments based on the CBS. Through these step-by-step research processes, we expect to contribute to the in-depth study of path planning in multi-vehicle dynamic storage systems.
2. Overview of System
Figure 1 shows a schematic diagram of a four-way shuttle vertical warehouse. The four-way shuttle vertical warehouse is an efficient and flexible automated storage system. Its main hardware components include four-way shuttles, elevators, and racks. The four-way shuttle is the core execution device of the system, responsible for the storage, retrieval, and handling of goods, as shown in
Figure 2. Equipped with two pairs of vertical drive wheels, the four-way shuttle can move in four directions. It is also equipped with various sensors (such as lidar, cameras, and ultrasonic sensors) for environmental perception, and can precisely execute handling tasks in combination with the motion control system. As shown in
Figure 3, the elevator achieves vertical handling through a cargo platform. The four-way shuttle can enter the cargo platform for handling operations and can also move with the elevator for inter-layer operations. The four-way shuttle rack (as shown in
Figure 4) is the main storage device of the system. It adopts a modular design and has high scalability. The rack is composed of columns and beams, and rails are laid between storage locations, forming the driving path for the four-way shuttle to move horizontally.
The software of the four-way shuttle system is mainly the warehouse management system (WMS), which integrates path planning algorithms to solve problems such as multi-vehicle collaboration and task scheduling, ensuring the efficient operation of the warehouse. Compared with the stacker storage system, the four-way shuttle system has a higher storage density and supports the simultaneous operation of multiple four-way shuttles, enabling rapid storage and retrieval, reducing the waiting time for goods, and thus improving the efficiency of inbound and outbound operations. In addition, the four-way shuttle system has good flexibility. It can increase or decrease the number of four-way shuttles according to requirements, adapt to future development, and can flexibly adapt to different warehouse layouts to optimize space utilization. The four-way shuttle system also has real-time monitoring and scheduling capabilities, which can dynamically adjust storage and retrieval strategies, quickly respond to inventory changes and market demands, and improve storage efficiency. The above characteristics make the four-way shuttle system an efficient solution for warehouse expansion and layout changes, meeting the flexibility requirements of modern logistics.
3. System Modeling
Based on the characteristics of the four-way shuttle system, the research in this paper is conducted based on the following assumptions:
The scene map is represented by a raster graph. Each four-way shuttle in the system has the same model and performance, and the size of one four-way shuttle just occupies one raster.
Time is represented in a discrete manner. Each four-way shuttle can only move one raster or stay in place within each unit of time. The acceleration of the four-way shuttle is regarded as infinite, and it takes one unit of time to pick and place goods and change directions.
The four-way shuttle adopts the operation mode of composite tasks. One four-way shuttle can receive multiple composite tasks, but these tasks need to be completed in sequence. Subsequent tasks cannot be executed before all operations of the previous composite task are completed.
Only the inbound and outbound tasks on a single-layer plane are considered, and the inbound and outbound locations of goods are known. The situation where the target goods in the warehouse need to be relocated during storage and retrieval is not considered.
When the system starts to operate, at t = 0, the WMS evenly distributes all composite tasks to all four-way shuttles at one time. It is assumed that the initial position of all four-way shuttles is at the elevator of the first inbound task. A composite task is composed of one inbound task bound to one outbound task. The four-way shuttle completes the inbound operation, the empty running operation, and the outbound operation in sequence according to the task order. The process of a composite operation is as follows:
Inbound operation: The four-way shuttle retrieves the pallet from the elevator docking port. Subsequently, it traverses through the main aisle and sub-aisles, reaching the entrance of the roadway corresponding to the target storage location. After entering the roadway, it arrives at the target storage location and deposits the pallet. If the roadways in columns of this layer are unoccupied and obstacle-free, the four-way shuttle can utilize these roadways as sub-aisles for longitudinal movement.
Unloaded operation: Upon completion of the inbound operation, the four-way shuttle enters an unloaded state. Based on the location of the goods specified in the outbound task of this composite task, a path from the termination point of the inbound task to the initiation point of the outbound task must be planned. Since the four-way shuttle is not carrying any cargo at this stage, it can pass beneath the storage locations. All roadways can serve as sub-aisles for longitudinal movement.
Outbound operation: The four-way shuttle picks up the pallet from the outbound storage location and moves to the roadway entrance. Then, it transports the pallet through the main aisle and sub-aisles to the target elevator docking port. Once the unloading process is finished, this composite task concludes. If there are unoccupied and obstacle-free roadways on this layer, the four-way shuttle can employ these roadways as sub-aisles for longitudinal movement.
When, among multiple composite tasks assigned by the warehouse management system (WMS), the elevator for the inbound task of a composite task is in a different position from the elevator for the outbound task of the previous composite task, an empty-running operation is required, and the four-way shuttle is commanded to move to the position of the elevator for the next inbound task.
Now, the representations of the constants, variables, etc. mentioned in the mathematical modeling stage are listed separately here for reference, as shown in
Table 1.
Based on the above assumptions, the path planning problem for multiple four-way shuttles can be described as follows: In the raster map Map, there is a set of obstacle coordinates B, and there are m four-way shuttles, denoted as
I = {1, 2, 3, …,
m}. The four-way shuttle
i needs to execute
Ni composite tasks, and E
i empty-running operations need to be inserted between the composite tasks. The task sequence is
Ti = {
W1,
W2,
W3, …,
W3Ni+Ei}. The execution of the nth operation
Wa by the four-way shuttle
i can be expressed as
Wa = {
Sa,
Da}, where
Sa and
Da represent the starting position and the end position of the nth operation respectively. The path of the four-way shuttle
i can be expressed as
Pi, which records the position of the four-way shuttle
i in the map Map at each unit of time.
Li(
t) represents the position of the four-way shuttle
i at time
t, expressed in coordinates (x, y).
c(
a) represents the cost value of the four-way shuttle executing the task
Wa, and
C(i) represents the cost value of the four-way shuttle
i after executing all tasks, which can be expressed as follows:
In the formula,
represents the start time of task a for the four-way shuttle, and
represents the end time of task a. For the path planning problem of multiple four-way shuttles, the optimization objective of the mathematical model is to minimize the total task completion time of all four-way shuttles:
Among the constraint conditions, Equation (4) indicates that the coordinate points of the path of the four-way shuttle must be within the map Map. Equation (5) shows that the path of the four-way shuttle cannot overlap with the obstacle points on the map. Equation (6) represents the movement constraints of the four-way shuttle, which can only move one raster horizontally or vertically per unit of time, or stay in place. Among them, and represent the coordinate positions of the four-way shuttle i at time t and (t + 1). Equations (7) and (8) indicate that the four-way shuttles cannot occupy one raster simultaneously and cannot exchange positions, respectively. Equations (9) and (10) represent the value range of the numbers of the four-way shuttles and the value range of the discrete time series.
By solving the above mathematical model, a conflict-free path set will be obtained, denoted as
P:
In this paper, a combination of the improved A* algorithm and the CBS algorithm will be adopted to solve this path planning problem. Subsequently, the influence of map state changes on the path will be considered, and a path planning method for dynamic environments will be proposed.
5. Optimization of the CBS Algorithm Based on the A* Algorithm
5.1. Basic Principle of the Conflict-Based Search Algorithm
The Conflict-Based Search (CBS) algorithm, as an efficient multi-agent path planning method, aims to find conflict-free paths for multiple agents through two key stages: high-level conflict search and low-level path planning.
In the low-level path planning stage, classic single-agent path planning algorithms such as the A* algorithm are used to plan paths for each agent separately. During this process, the existence of other agents is not considered. Instead, a path from the starting point to the end point is planned based only on the agent’s own starting and target positions.
The high-level conflict search stage focuses on resolving conflicts generated in the low-level path planning. It is achieved by constructing a constraint tree. Initially, each agent obtains a preliminary path through the low-level path planning algorithm. Then, the algorithm comprehensively checks the paths of all agents to identify existing conflicts. These conflicts usually occur when two or more agents are at the same position at the same time or use the same path edge at the same time.
After a conflict is detected, the algorithm decomposes it into specific constraints, mainly including time constraints and space constraints. These constraints are applied to the paths of the conflicting agents respectively. For example, if two agents will meet at the same position at a certain time, a constraint of “not being at this position at this time” will be added to one of the agents.
For agents affected by the constraints, their paths are re-planned in the low-level path planning according to the new constraints. This process still uses the single-agent path planning algorithm, but the newly added constraints are fully considered to avoid previously detected conflicts.
After each application of constraints and re-planning of paths, a new node is generated in the constraint tree. The algorithm continuously checks whether there are still conflicts in the new paths. If there are conflicts, the process of conflict decomposition, constraint application, and path update is repeated until a conflict-free path solution that meets all constraints is found.
5.2. Conflict Avoidance Strategy
In the problem of path planning for multiple four-way shuttles, the design of conflict avoidance strategies is an important part of ensuring the efficient operation of the system. During the task execution process of four-way shuttles, position conflicts or path conflicts often occur, and at this time, reasonable avoidance strategies must be adopted to solve these problems. This paper proposes two effective conflict avoidance strategies: the priority strategy for inbound and outbound tasks and the priority strategy for nearby tasks. These two strategies can optimize the conflict resolution process in different scenarios and improve the overall efficiency of the system.
5.2.1. The Priority Strategy for Inbound and Outbound Tasks
The core idea of the inbound and outbound task priority strategy is to determine the priority of four-way shuttles based on the types of tasks they are performing, mainly the impact of tasks on the storage location status. Since inbound tasks will occupy storage locations upon completion, they are given priority. For idle-load tasks, as an outbound task will start right after an idle-load task is finished, and the status of the storage location changes at the moment when the four-way shuttle picks up the goods, four-way shuttles performing idle-load tasks also have priority. The main process of the inbound and outbound task priority strategy algorithm is shown in Algorithm 2.
When a conflict occurs between two four-way shuttles, assume that the set of conflicts is “conflicts”, which includes specific conflict instances such as “conflict1” and “conflict2”. Each instance contains the time when the conflict occurs, the location of the conflict, and the numbers of the conflicting four-way shuttles. For each “conflict”, obtain the numbers of the two four-way shuttles involved, denoted as “FS1” and “FS2”. Use the function “DeterminePriority” to determine whether they have priority. This function first checks if they are performing tasks related to changes in the storage location status. If an idle-load task is detected, it further checks the validity of the inbound and outbound tasks before and after this idle-load task (whether the starting point and the ending point are the same) to determine if it is an idle-load task between two compound tasks. If not, it is given priority. After being judged by the function “DeterminePriority”, the priority statuses of FS1 and FS2 are denoted as “priority1” and “priority2” respectively.
Compare the priorities of the two conflicting four-way shuttles. If only one shuttle has priority, the other needs to give way. In the pseudo-code, if “priority1 > priority2”, apply constraints to FS2 using the function “ApplyConstraint(FS2, conflict)” and re-plan the path of FS2 using the A* algorithm. Conversely, if “priority2 > priority1”, apply constraints to FS1 using the function “ApplyConstraint(FS1, conflict)” and re-plan the path of FS1. If neither of the two four-way shuttles is involved in changes to the storage location status, or if both are performing inbound tasks or idle-load tasks, the nearby-task priority strategy is executed.
The advantage of this strategy is that it can flexibly determine the conflict priority according to the nature of tasks. Especially in situations where optimal utilization of storage location resources needs to be ensured, by prioritizing tasks that affect the storage location status, it effectively avoids the waste of storage location resources.
| Algorithm 2: Main function of the priority strategy for inbound and outbound tasks |
| Input: Map, conflict set conflicts = {conflict1, conflict2…}, path set P of four-way shuttle |
| Output: A set of conflict-free paths P |
Initialization: FS1, FS2
1: for each conflict in conflicts do
2: FS1 = conflict.shuttle1
3: FS2 = conflict.shuttle2
4: priority1 = DeterminePriority(FS1)
5: priority2 = DeterminePriority(FS2)
6: if priority1 > priority2 then
7: ApplyConstraint(FS2, conflict)
8: shuttle2.path = AStar(FS2, GetConstraints(FS2))
9: else if priority2 > priority1 then
10: ApplyConstraint(FS1, conflict)
11: shuttle1.path = AStar(FS1, GetConstraints(FS1))
12: else
13: NearbyTaskPriorityStrategy(FS1, FS2, conflict)
14: end if
15: end for
16: return P |
5.2.2. The Priority Strategy for Nearby Tasks
The nearby task priority strategy determines the priority in case of conflicts based on the distance between the four-way shuttle and the target location. When a conflict is detected, calculate the Manhattan distances between the two conflicting four-way shuttles and their respective targets. The shuttle with a shorter distance is given a higher priority. Apply constraints to the other four-way shuttle and re-plan its path to make it give way to the shuttle with higher priority. The pseudo-code of the nearby task priority strategy algorithm is shown in Algorithm 3.
First, use the “CalculateDistance” function to calculate the Manhattan distances between FS1, FS2 and their respective targets, and obtain “distance1” and “distance2”. Compare these two distance values. If “distance1” is less than “distance2”, it means FS1 is closer to its target. At this time, give FS1 a higher priority. In the pseudo-code, this is reflected in applying the constraint related to the conflict “conflict” to FS2 using the function “ApplyConstraint(FS2, conflict)”, and then re-planning the path of FS2 using the A* algorithm according to the constraints of FS2. Otherwise, apply the constraint “ApplyConstraint(FS1, conflict)” to FS1 and re-plan the path of FS1.
The underlying assumption of this strategy is that a four-way shuttle closer to its target is usually near the end of its task. If its progress is delayed, it may lead to an overall delay in the task, which in turn affects the system’s efficiency. Therefore, prioritizing the four-way shuttle closer to the target can ensure that the task is completed on time and reduce unnecessary time consumption.
| Algorithm 3: Algorithm of the priority strategy for nearby tasks |
| Input: Map, FS1, FS2, conflict, PFS1, PFS2 |
| Output: A set of conflict-free paths |
Initialization: distance1, distance2
1: distance1 = CalculateDistance(FS1.path, FS1.currentTask.end)
2: distance2 = CalculateDistance(FS2.path, FS2.currentTask.end)
3: if distance1 < distance2 then
4: ApplyConstraint(FS2, conflict)
5: FS2.path = AStar(FS2, GetConstraints(FS2))
6: else
7: ApplyConstraint(FS1, conflict)
8: FS1.path = AStar(FS1, GetConstraints(FS1))
9: end if
10: return PFS1, PFS2 |
In conclusion, the priority strategy for inbound and outbound tasks and the priority strategy for nearby tasks respectively provide different conflict resolution solutions from two perspectives: the impact of tasks on the status of storage locations and the physical distance between tasks and their targets. The former optimizes the use of resources by giving priority to tasks that affect the status of storage locations, while the latter reduces system delays by prioritizing the completion of tasks that are closer to their targets. By flexibly selecting these two strategies in practical applications, the scheduling efficiency and resource utilization rate of the multi-four-way shuttle system can be effectively improved.
5.3. Global Planning of CBS Based on the Dynamic Environment
In this study, the execution of inbound and outbound tasks will lead to changes in the situation of storage locations within the warehouse. There are specifically the following two situations:
After the inbound task is completed, the roadway that was originally unoccupied by goods is occupied. A four-way shuttle carrying goods can no longer use this roadway as a sub-channel for movement.
After the outbound task starts, the roadway that was originally occupied by only one storage location is released from occupation. There are no goods in this roadway, and a four-way shuttle carrying goods can use this roadway as a sub-channel for movement.
These two situations will cause the originally planned path to no longer be the optimal path. To solve this problem, this paper proposes a global planning of CBS based on the dynamic environment, and the basic principles are as follows:
Step 1: Combine the known task set into composite tasks in the form of inbound tasks, empty-running tasks, and outbound tasks, and evenly distribute them to all four-way shuttles. If the end position of the previous composite task of a four-way shuttle is different from the start position of the next composite task, add an empty-running task to move to the start position of the next composite task.
Step 2: Initialize the map and plan the path, and import two rasterized maps:
Import the information of the positions where goods are already stored in the warehouse and the obstacles into the rasterized map. When inbound and outbound tasks occur, the A* algorithm calls this map to plan the path for the four-way shuttle.
Only import the information of the obstacles in the warehouse into the rasterized map. When an empty-running task occurs, the A* algorithm calls this map to plan the path for the four-way shuttle.
Step 3: Establish a ChangeList. This list records, in ascending order of time points, the types of inbound and outbound tasks completed by all four-way shuttles, the time points when the map changes occur, the corresponding coordinates, and the numbers of the four-way shuttles.
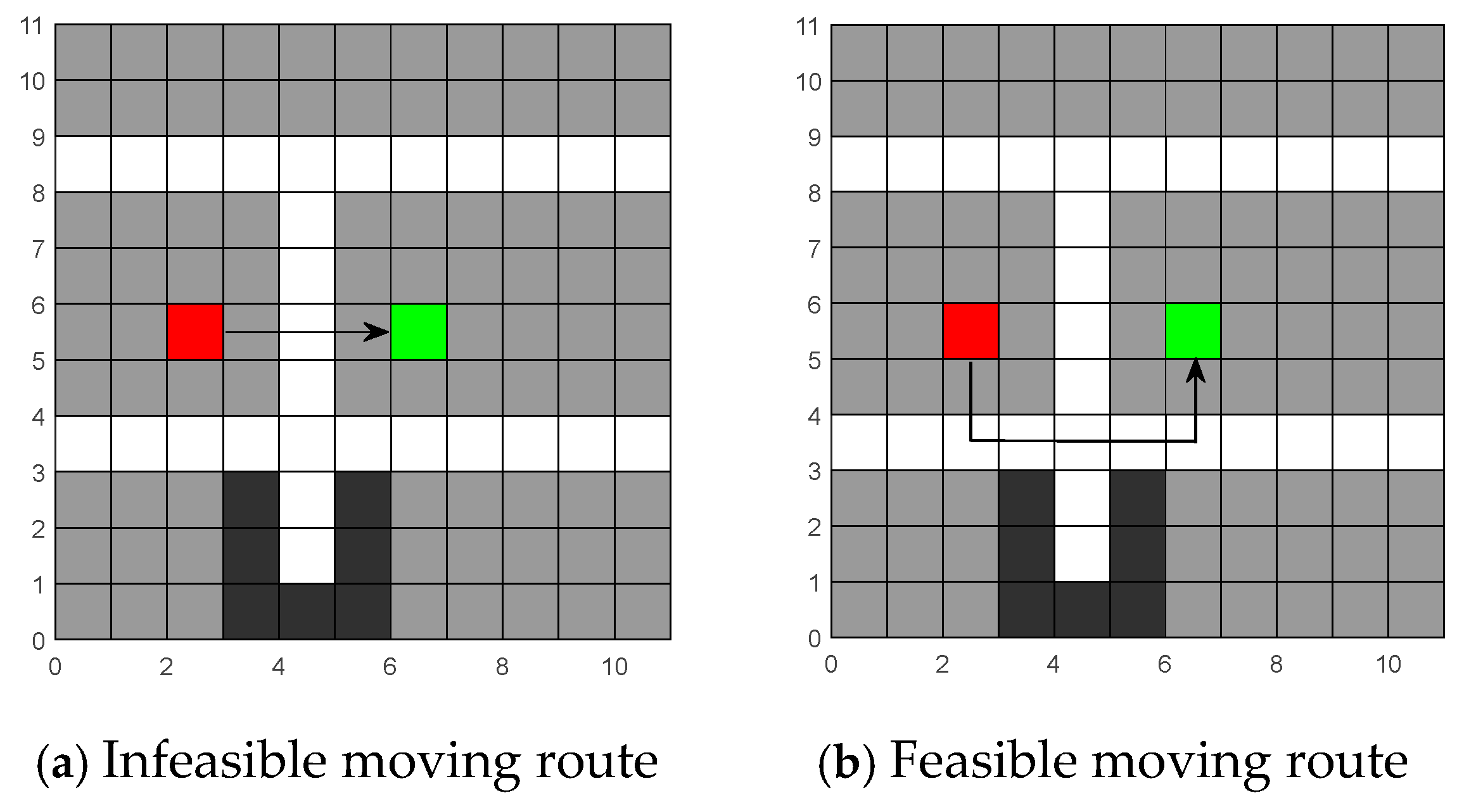
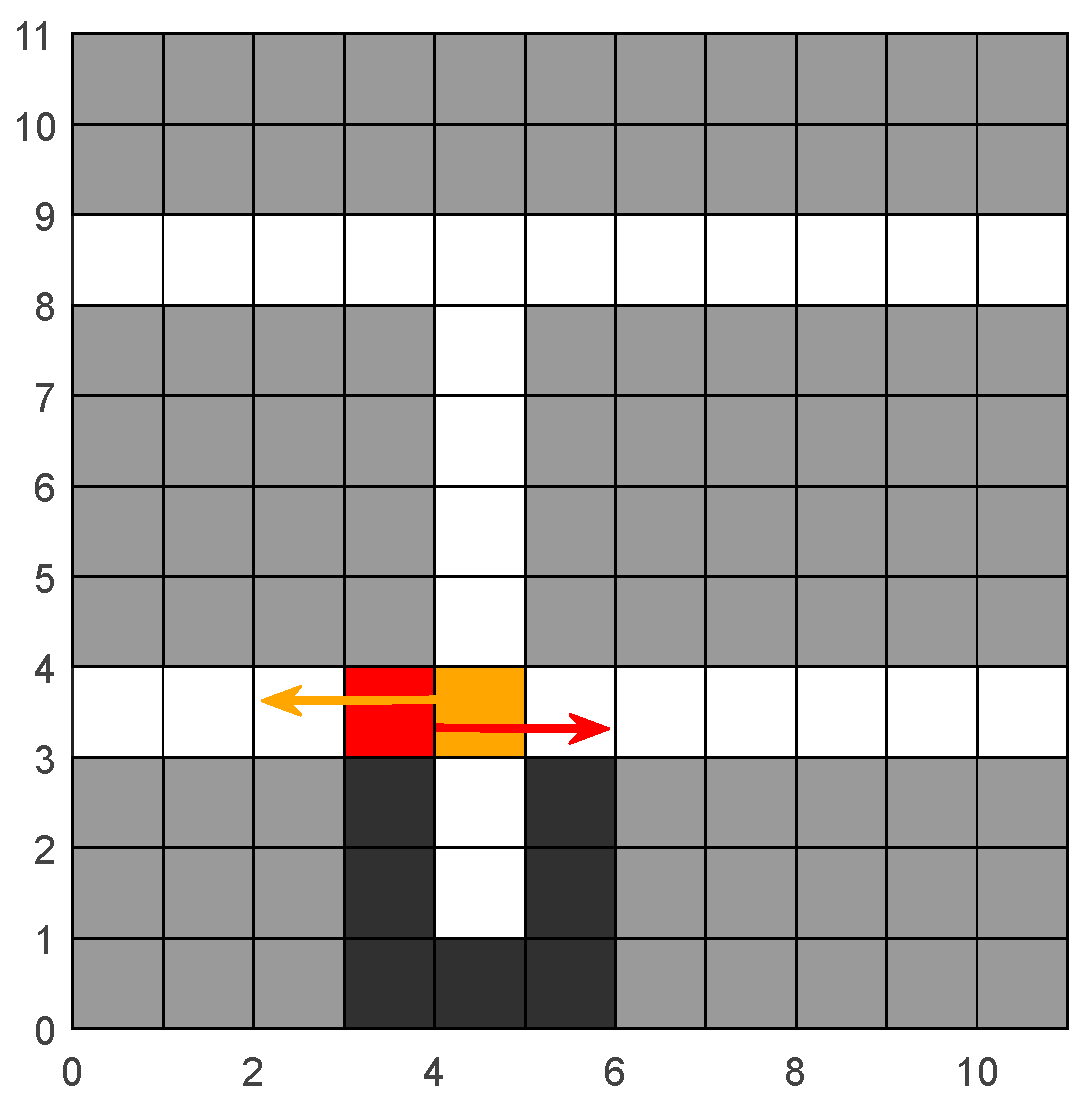
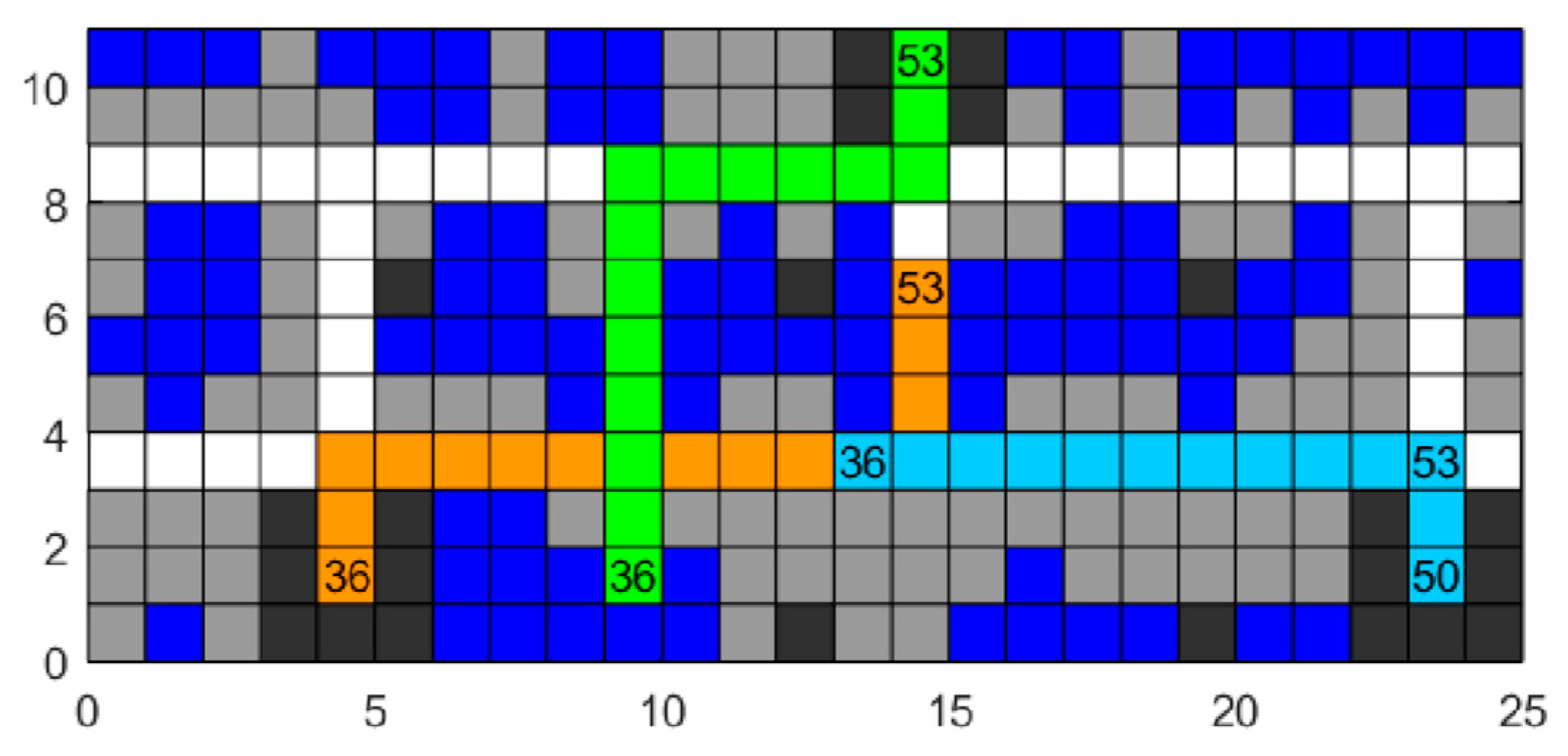
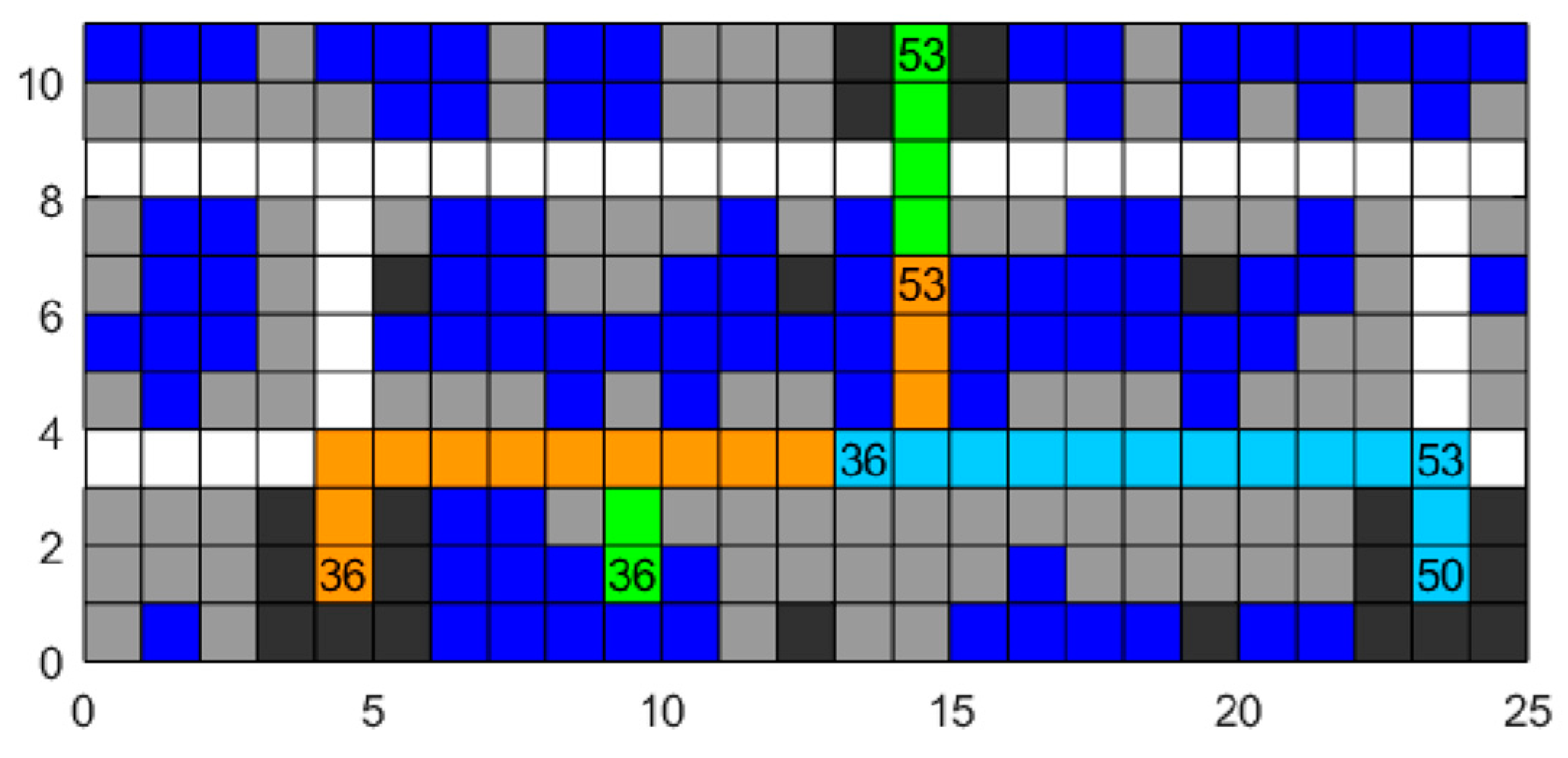
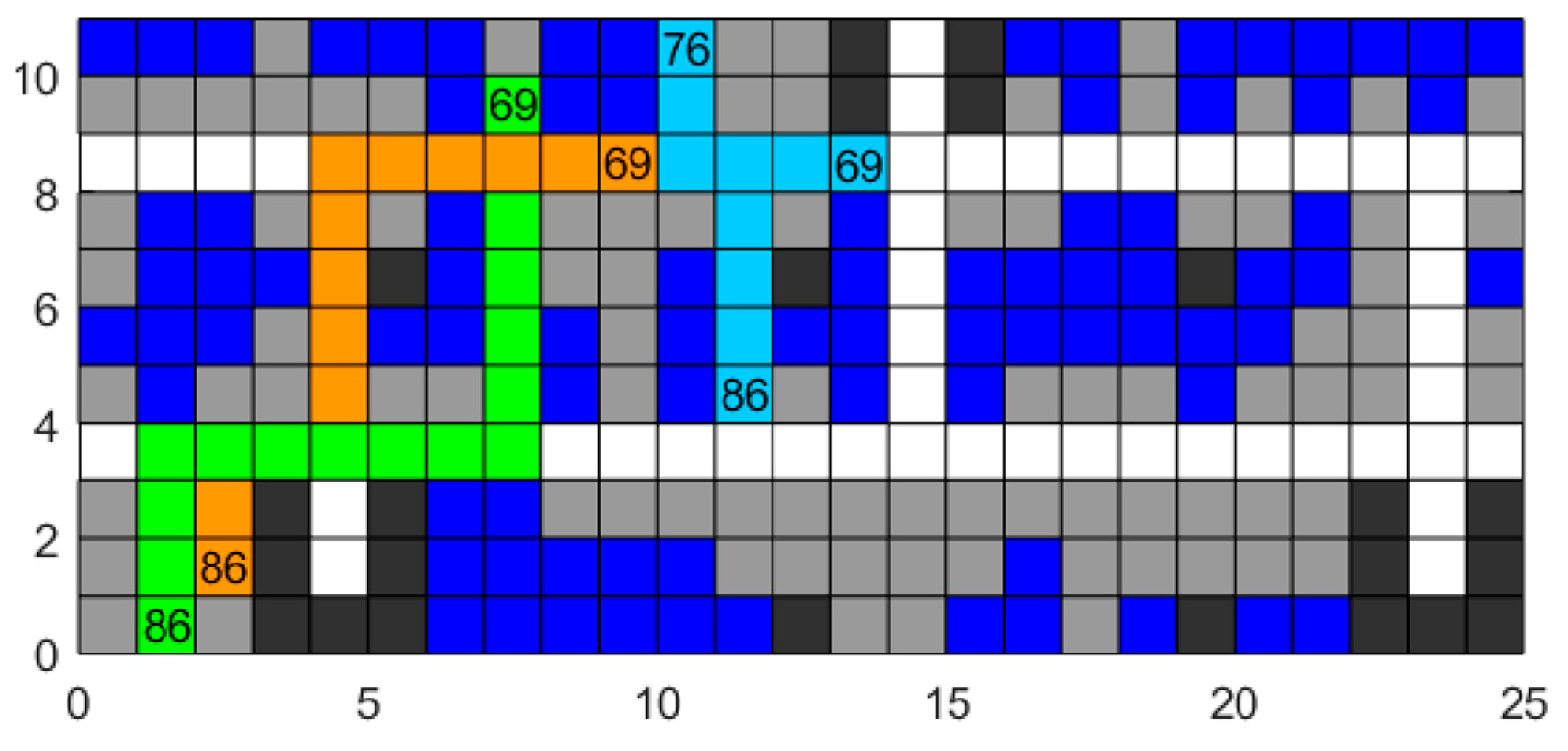
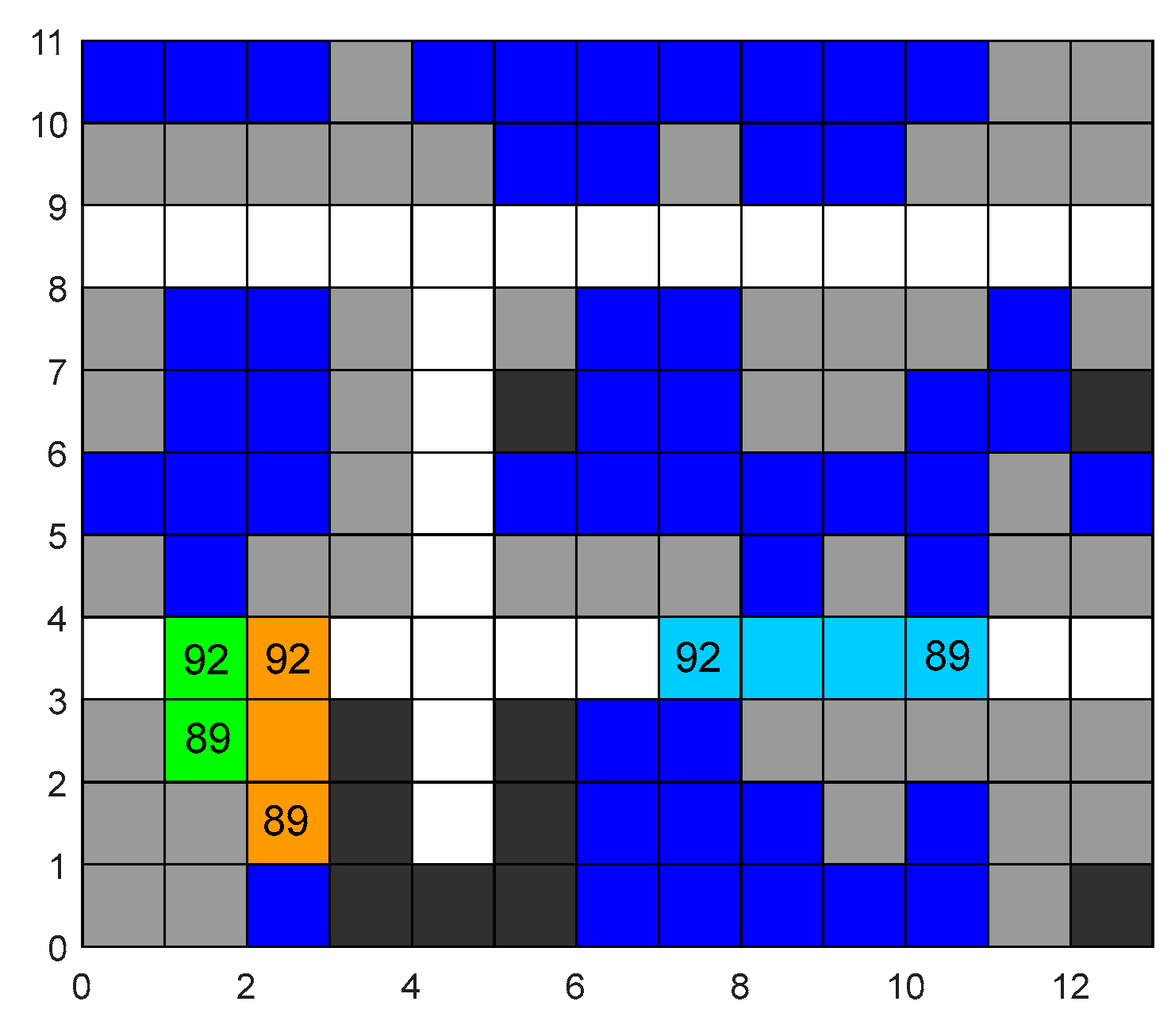
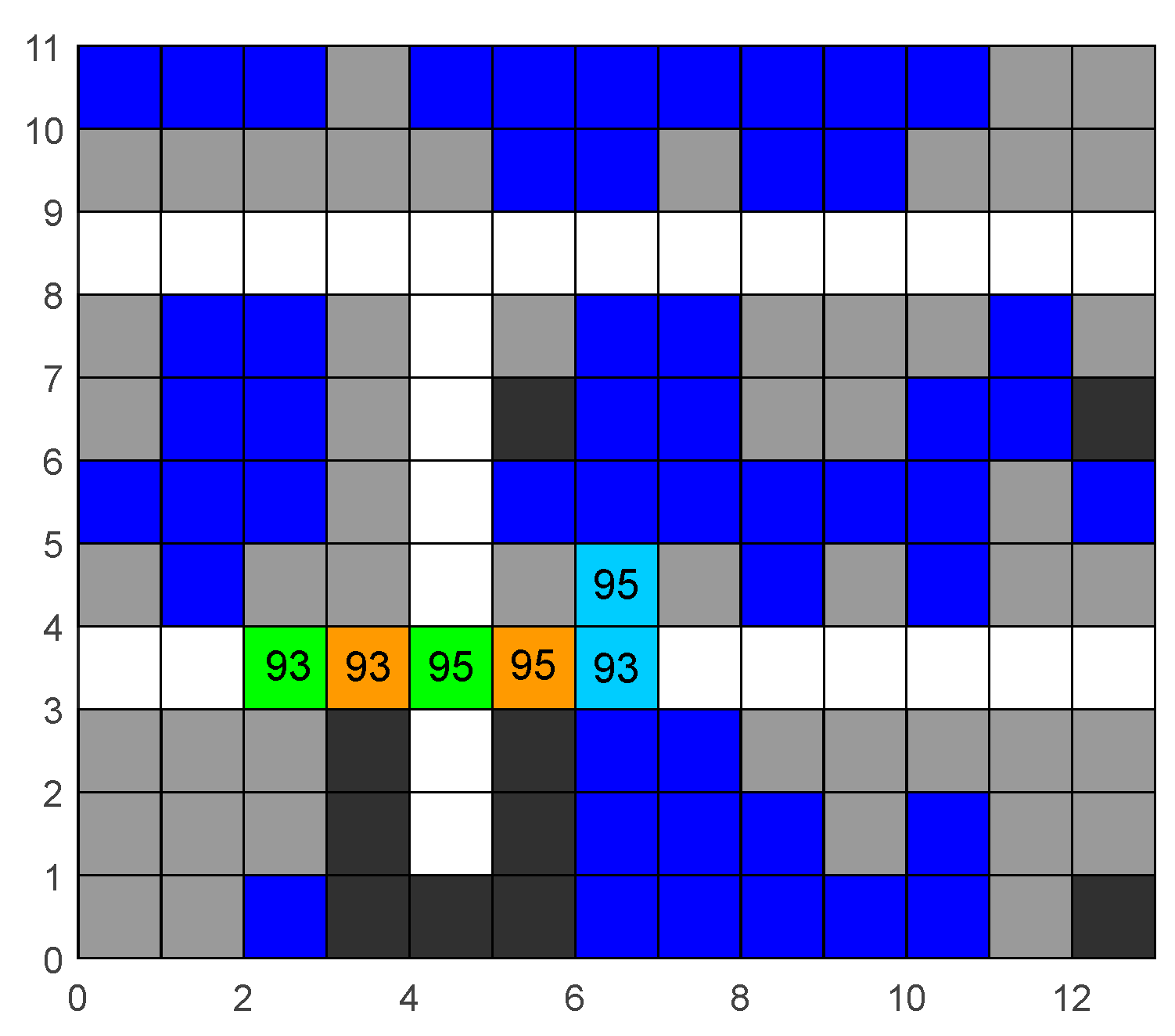
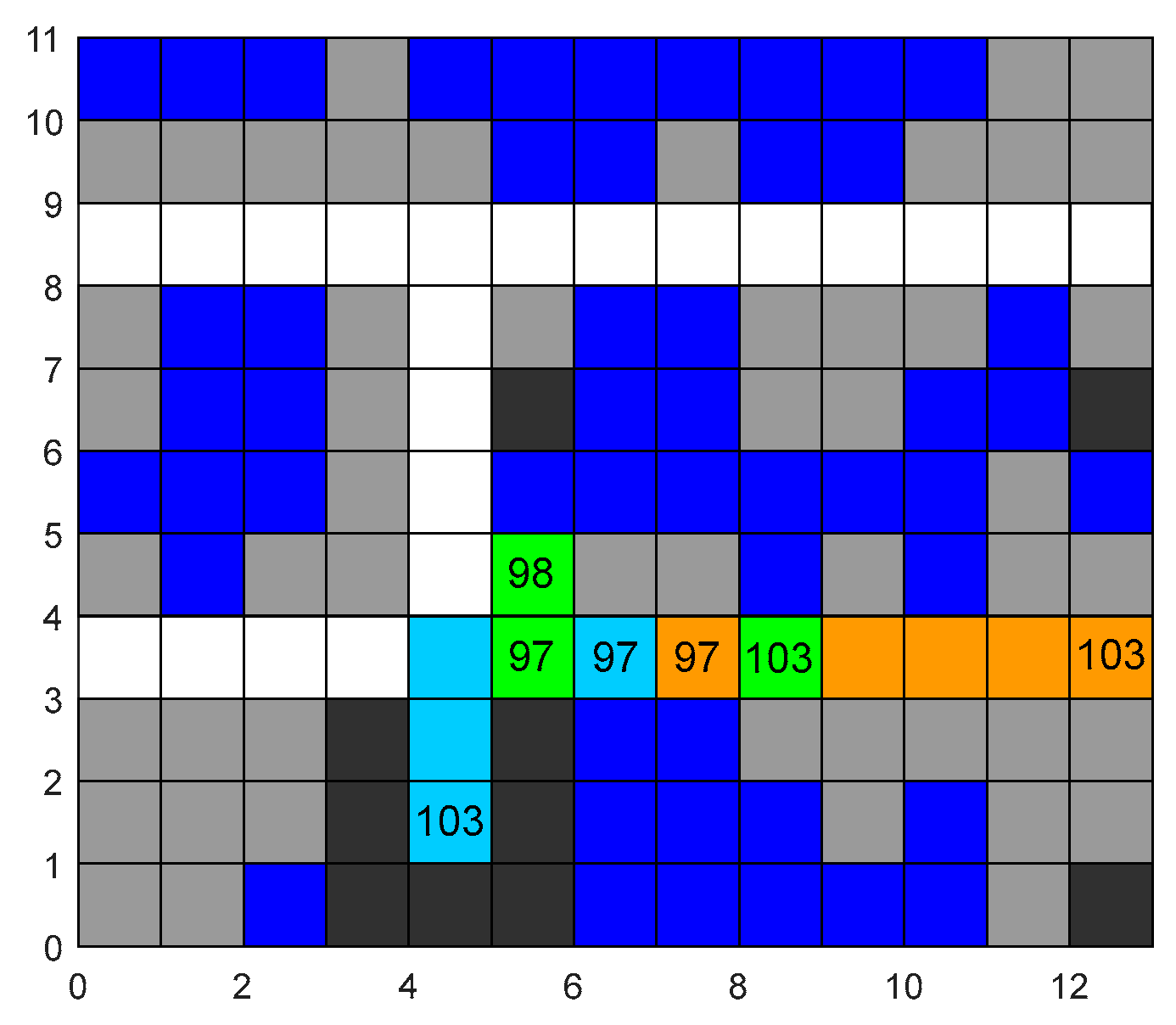
Step 4: Conflict detection. Conduct conflict detection according to the path of each obtained four-way shuttle. Check whether there are situations of position exchange (
Figure 7) or simultaneous occupation of one raster (
Figure 8) on the path. Record the obtained first conflict position, time point, and the number of the four-way shuttle, and proceed to Step 5. If no conflict is detected, proceed to Step 8.
Step 5: Compare the conflict time with the time recorded in the first set of data in the ChangeList. If the conflict time is less than the time in the list, it indicates that the conflict occurred before the map state changed. At this time, check whether the number of the four-way shuttle recorded in the first set of the list is the same as that of the four-way shuttle involved in the conflict. If it is, proceed to Step 6; if not, proceed to Step 7. If the conflict time is greater than the time in the list, proceed to Step 9.
Step 6: Adopt the priority strategy for inbound and outbound tasks. Add constraints to the non-priority four-way shuttle for avoidance and use the A* algorithm to replan the path to resolve the conflict. Return to Step 4.
Step 7: Adopt the priority strategy for nearby tasks. Assign priority to the four-way shuttle closer to the destination. Add constraints to the other four-way shuttle for avoidance and use the A* algorithm to replan the path. Then, return to Step 4.
Step 8: Check if the ChangeList is empty. If it is empty, it means that the map state has been fully changed and there are no conflicts in the paths of the four-way shuttles. The algorithm ends, and a conflict-free path solution set is obtained. If it is not empty, proceed to Step 9.
Step 9: Update the map and replan the paths. According to the task type and coordinates in the first set of data in the ChangeList, modify the distribution state of obstacles on the map. Due to the change in the occupancy of storage locations in the warehouse, replan the path for each four-way shuttle. Specifically, the four-way shuttle that causes the map change by completing a task replans the path for subsequent tasks using the new map, while the path before this task remains unchanged. For other four-way shuttles, take the position at the time point when the map changes as the starting point, and replan the path to complete the current task and subsequent tasks. Update the completion time points of subsequent tasks in the ChangeList and then delete the first set of data in the ChangeList and return to Step 4.
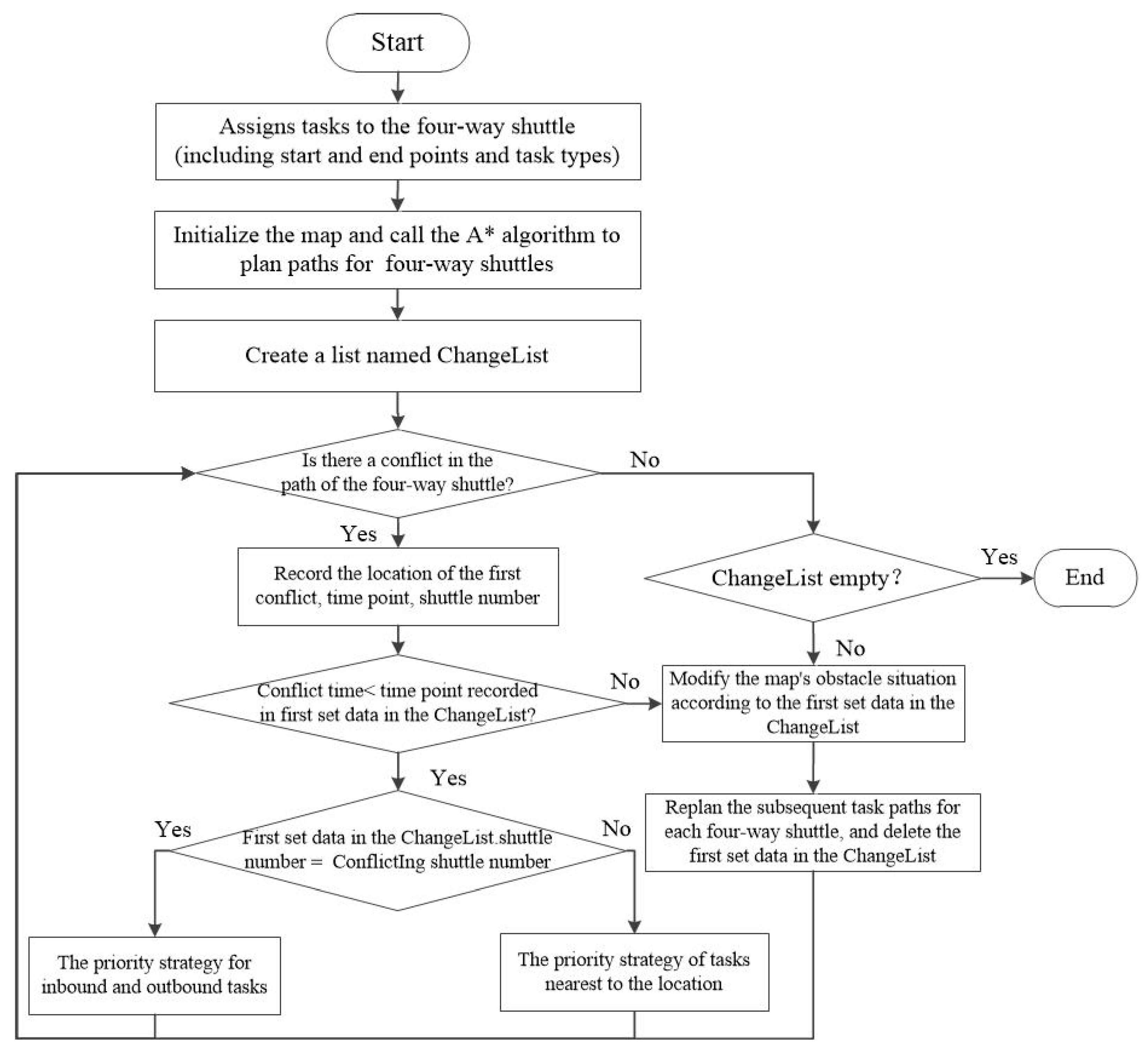
Figure 9 shows the flowchart of the global planning algorithm of CBS based on the dynamic environment.
7. Conclusions
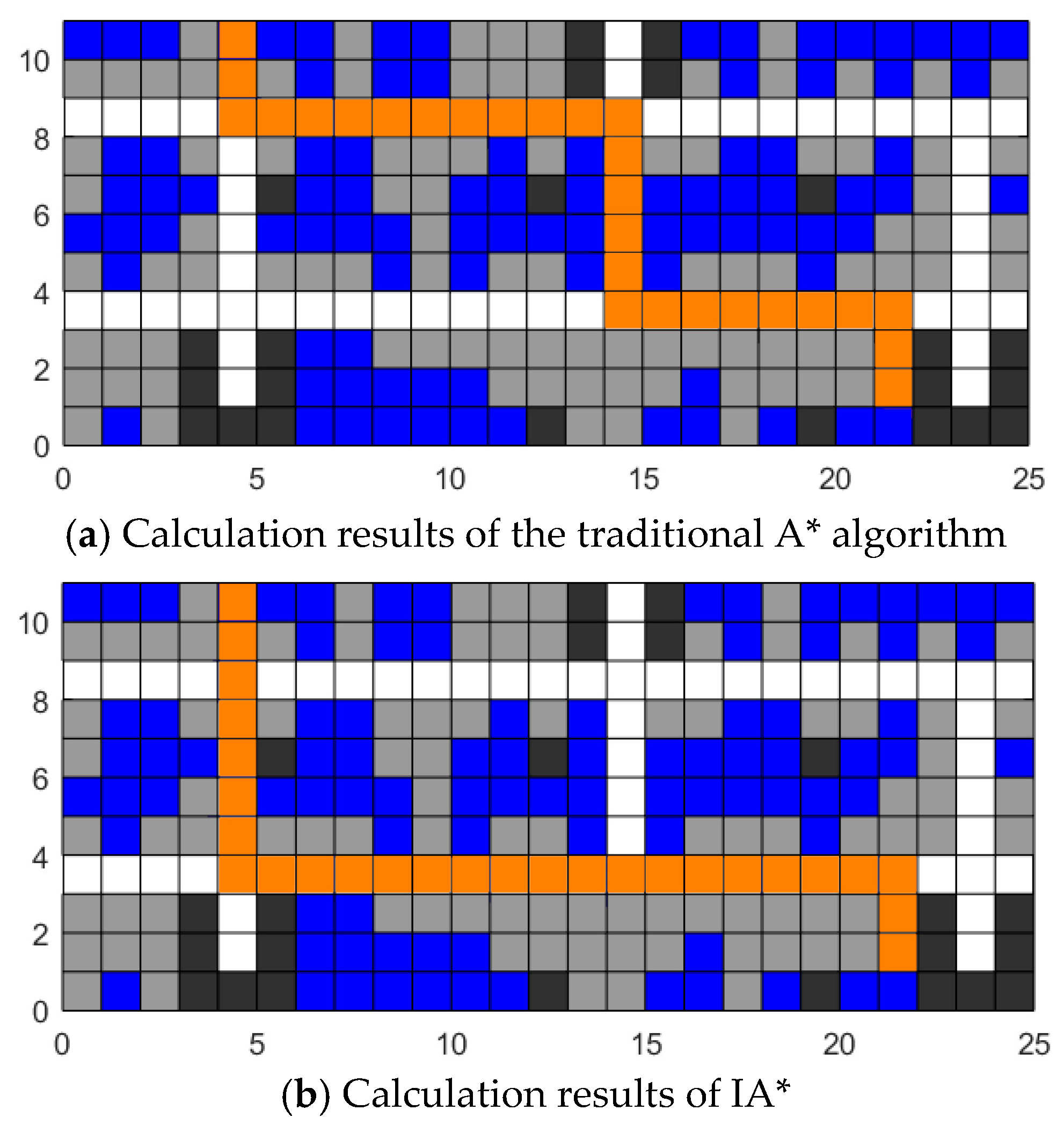
To address the multi-vehicle path planning problem in a four-way shuttle storage system within a dynamic environment, considering the map state changes caused by the inbound and outbound operations of four-way shuttles, a CBS global planning algorithm based on the dynamic environment is proposed. This algorithm improves the CBS obstacle-avoidance algorithm based on the A* algorithm. By adding direction constraints for expanding nodes and turning costs, the path search ability and computational efficiency of the A* algorithm are enhanced. A ChangeList is introduced to record the task type, time point, coordinates, and the number of the four-way shuttle for each task when the map state changes. By updating the ChangeList, the paths of other four-way shuttles after the map state change are re-planned, enabling the paths of four-way shuttles to be updated according to environmental changes.
In terms of conflict resolution, the inbound-outbound task priority strategy and the nearby-task priority strategy are incorporated into the CBS algorithm, resulting in a set of conflict-free paths that take into account both dynamic map changes and obstacle avoidance for multiple four-way shuttles. By referencing the layout of a four-way shuttle warehouse of a certain company and conducting simulation analysis, a conflict-free path set is obtained when three four-way shuttles operate simultaneously, each with two sets of composite tasks. The effectiveness of the algorithm is verified by analyzing the path status of four-way shuttles during specific time periods.
In the comparative experiments with algorithms such as DCBS-PFM and RRT-A, the IA*-CBS algorithm proposed in this paper demonstrated excellent performance. It performed outstandingly in key indicators such as the average task completion time, the average number of conflicts, and the average number of direction changes. It is capable of efficiently planning paths, effectively reducing vehicle conflicts, and decreasing vehicle energy consumption, which reflects its strong competitiveness and practical application potential.
This study did not consider the acceleration and deceleration issues of four-way shuttles, as well as the collaborative scheduling problems with elevators. To conform to the actual operation situation of the system, further research can incorporate more rigorous equipment parameters into the calculation of equipment path costs, such as acceleration and deceleration rates, direction change time, pallet lifting time, etc., and conduct scheduling research on the entire four-way shuttle system in combination with the connection between the elevators and the four-way shuttles. At the same time, considering that there is still room for optimization in the computational efficiency of the current algorithm, it is necessary to further explore optimization strategies to improve the algorithm’s operation efficiency, so as to better meet the practical needs of the actual warehouse system.