Ion Channel Memory Drives Cardiac Early Afterdepolarizations in Fractional Models
Abstract
1. Introduction
2. Mathematical Methods
2.1. Fractional Calculus Preliminaries
2.2. Delay Kernels
2.3. Delays in Hodgkin-Huxley’s Equation Type
2.4. Fractional Cardiac Models
3. Fractional FitzHugh-Nagumo, Mitchell-Schaeffer and Karma Models, and the Emergence of EADs
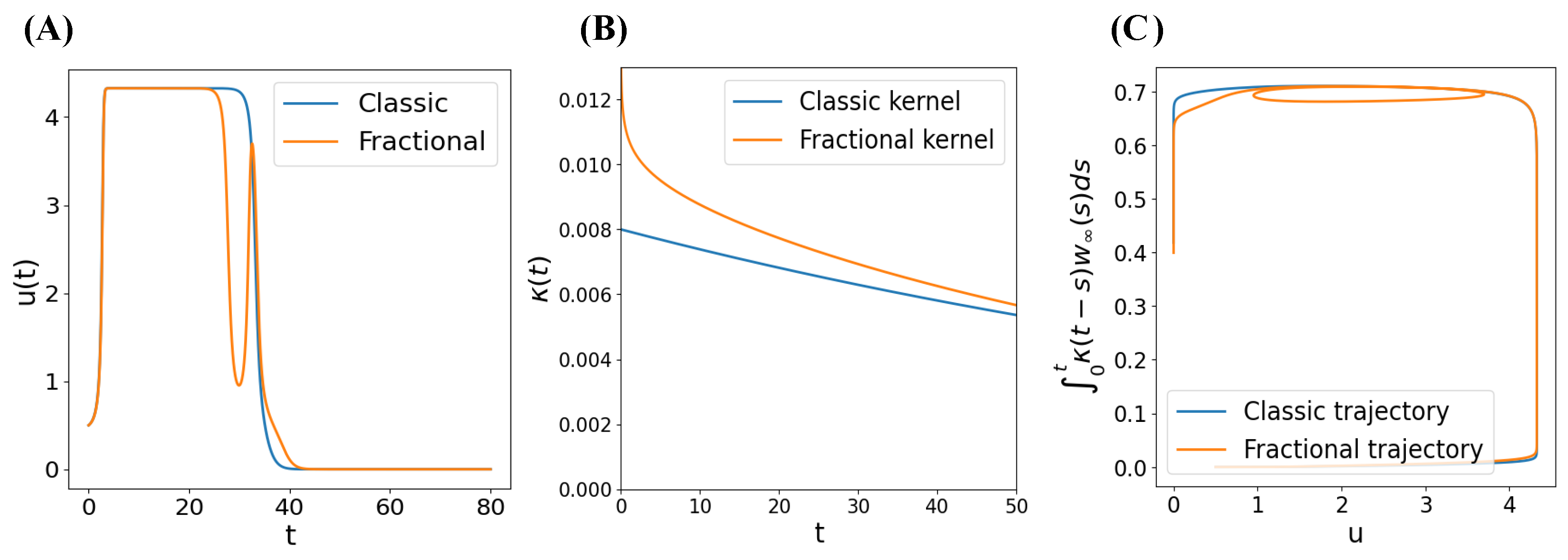
3.1. Fractional FitzHugh-Nagumo Model
3.2. Fractional Adapted Mitchell-Schaeffer Model
3.3. Fractional Adapted Karma Model
4. Discussion of Earlyafterdepolarizations’ Emergence
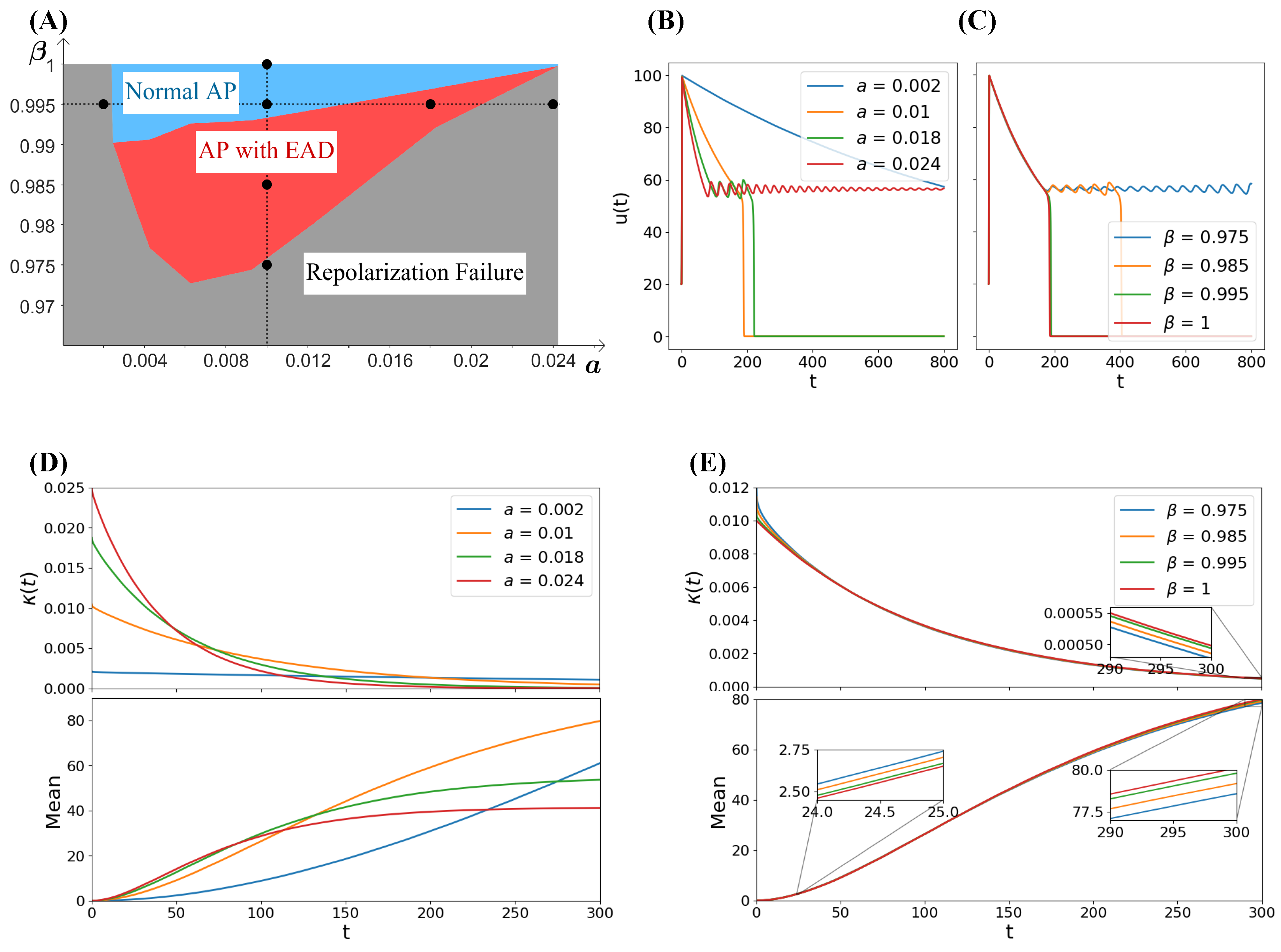
4.1. Sensitivity Analysis
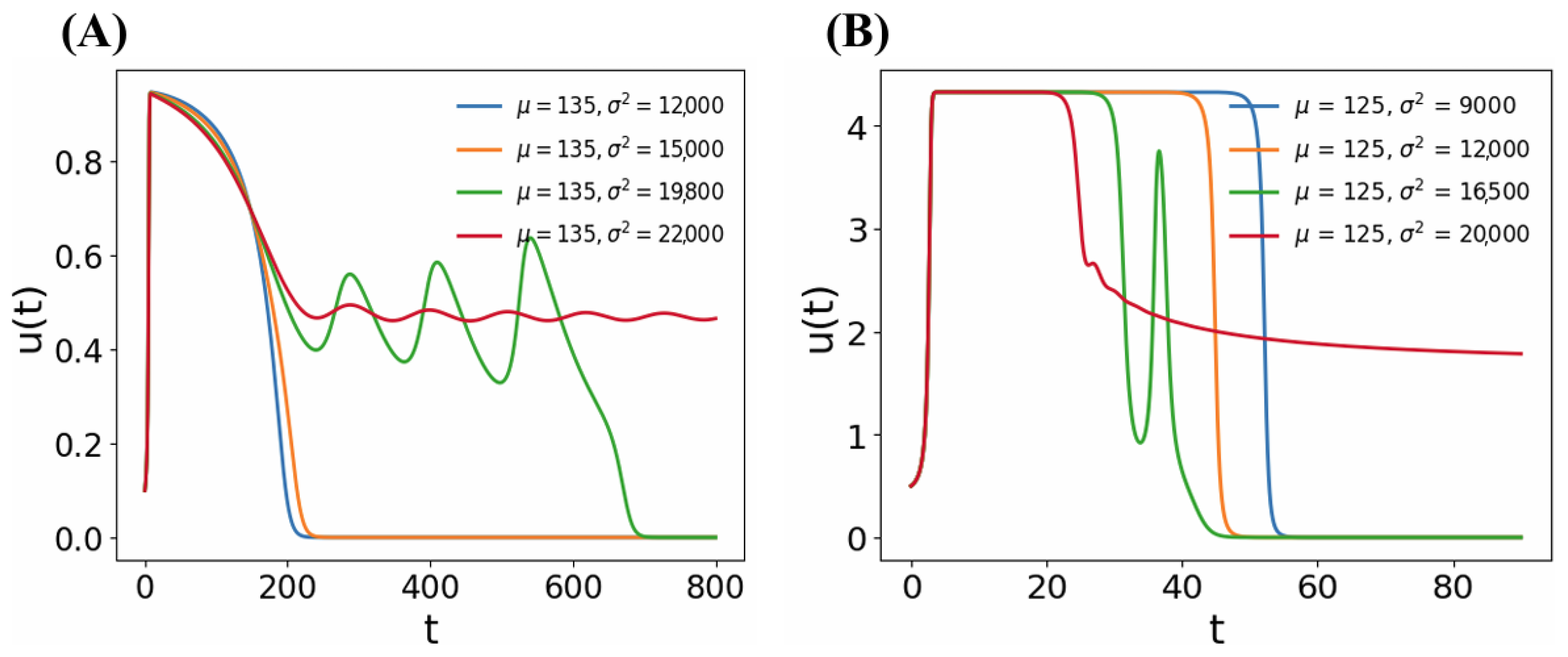
4.2. The Emergence of EADs in Terms of Mean and Variance
4.3. Stability Analysis
4.3.1. Equilibrium Points
4.3.2. Stability
4.3.3. Emergence of EADs
5. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Study of the Gamma Mittag-Leffler PDF Kernel

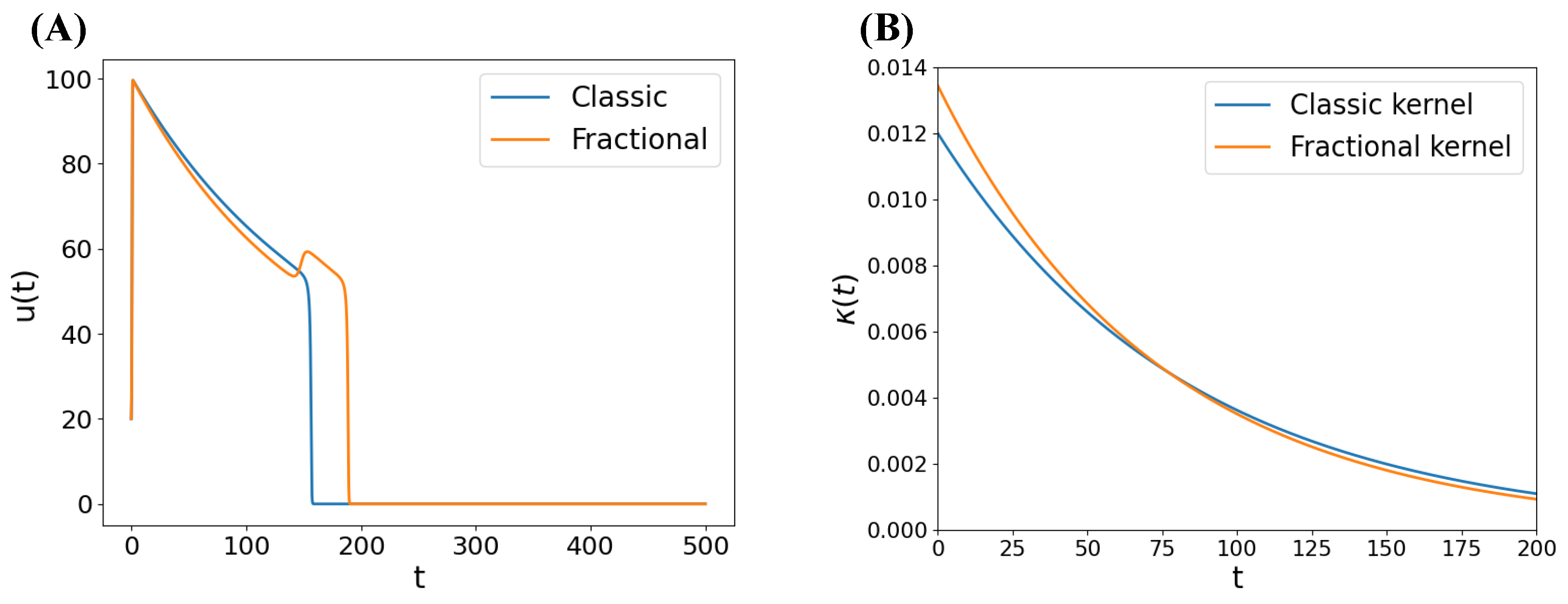
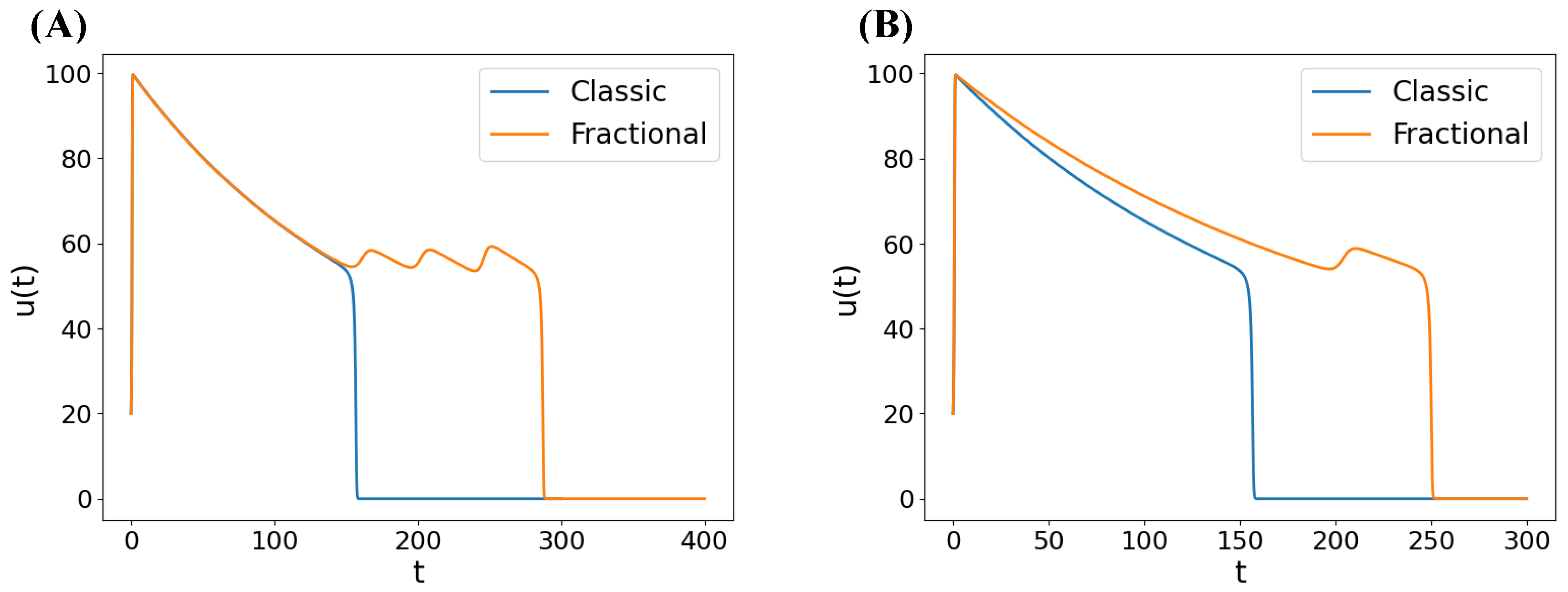
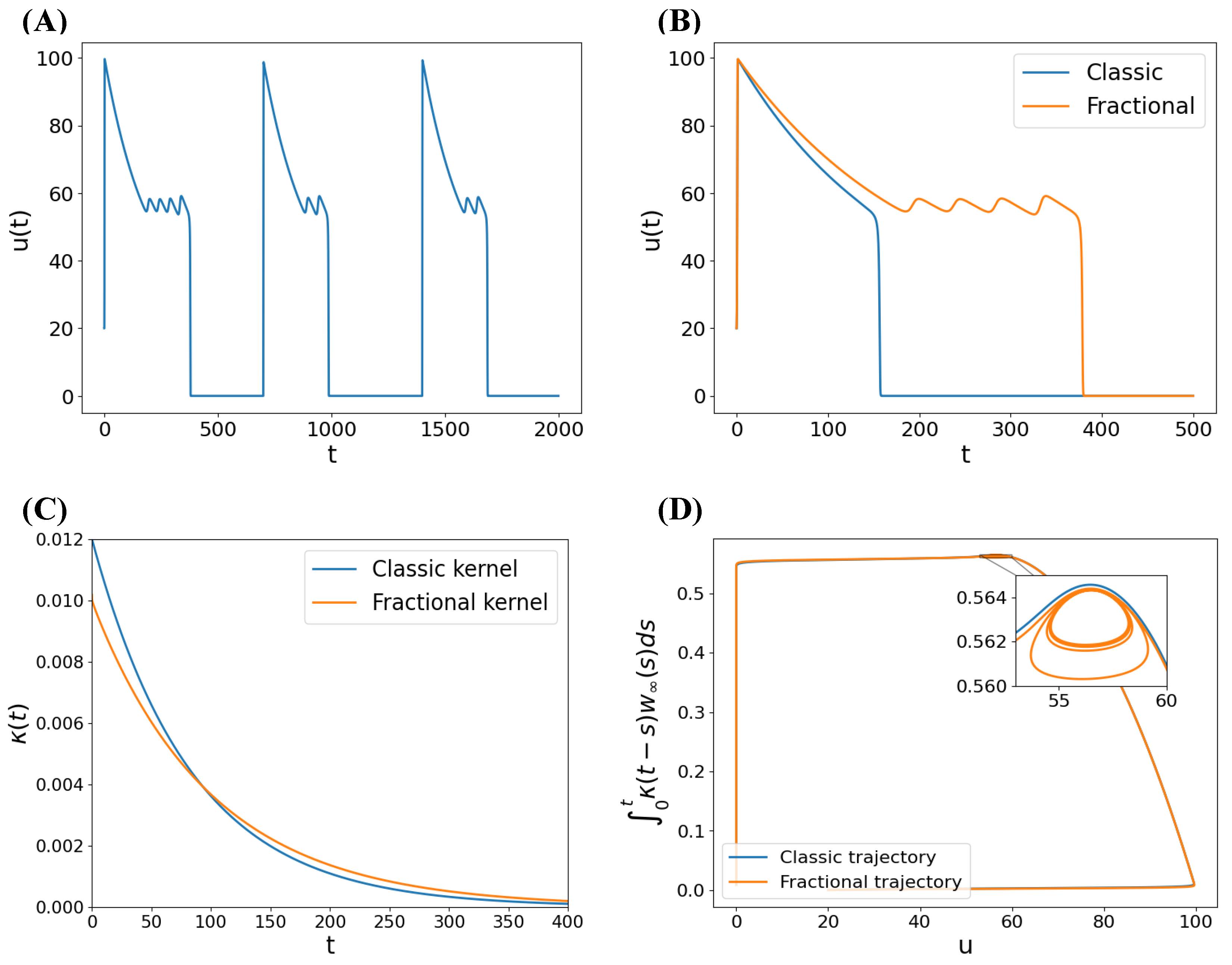
Appendix B. EADs Examples in the Fractional FHN Model

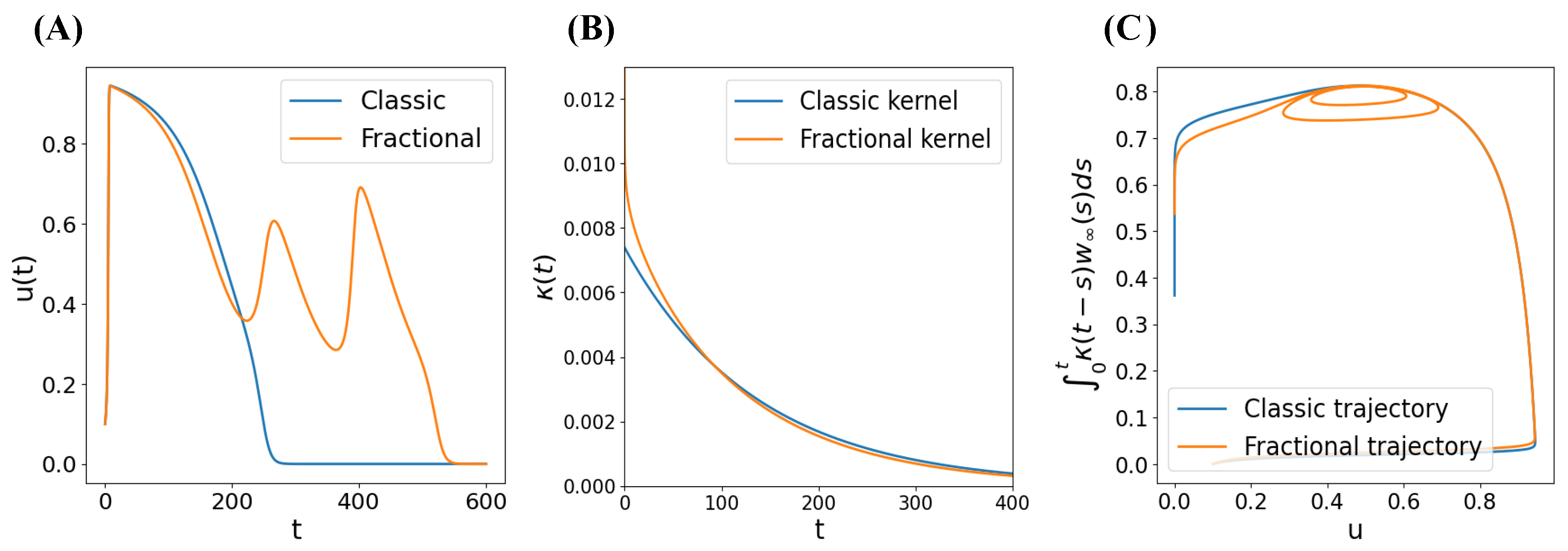
Appendix C. Justification of Our Adaptations in the MS and Karma Models

References
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef] [PubMed]
- Cranefield, P.F. Action potentials, afterpotentials, and arrhythmias. Circ. Res. 1977, 41, 415–423. [Google Scholar] [CrossRef]
- Charpentier, F.; Drouin, E.; Gauthier, C.; Marec, H.L. Early after/depolarizations and triggered activity: Mechanisms and autonomic regulation. Fundam. Clin. Pharmacol. 1993, 7, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Song, Z.; Qu, Z. Determinants of early afterdepolarization properties in ventricular myocyte models. PLoS Comput. Biol. 2018, 14, e1006382. [Google Scholar] [CrossRef]
- Stein, J.; Greene, D.; Fenton, F.; Shiferaw, Y. Mechanism of Arrhythmogenesis Driven by Early After Depolarizations in Cardiac Tissue. PLoS Comput. Biol. 2025, 21, e1012635. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Qu, Z.; Huang, X. Dissecting the roles of calcium cycling and its coupling with voltage in the genesis of early afterdepolarizations in cardiac myocyte models. PLoS Comput. Biol. 2024, 20, e1011930. [Google Scholar] [CrossRef]
- Barrio, R.; Jover-Galtier, J.A.; Martínez, M.; Pérez, L.; Serrano, S. Mathematical birth of Early Afterdepolarizations in a cardiomyocyte model. Math. Biosci. 2023, 366, 109088. [Google Scholar] [CrossRef]
- Kügler, P.; Erhardt, A.H.; Bulelzai, M. Early afterdepolarizations in cardiac action potentials as mixed mode oscillations due to a folded node singularity. PLoS ONE 2018, 13, e0209498. [Google Scholar] [CrossRef]
- de Barros, L.C.; Lopes, M.M.; Santo Pedro, F.; Esmi, E.; dos Santos, J.P.C.; Sánchez, D.E. The memory effect on Fractional Calculus: An application in the spread of COVID-19. Comput. Appl. Math. 2021, 40, 72. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef]
- Ngueuteu, G.; Yamapi, R.; Woafo, P. Quasi-static transient and mixed mode oscillations induced by fractional derivatives effect on the slow flow near folded singularity. Nonlinear Dyn. 2014, 78, 2717–2729. [Google Scholar] [CrossRef]
- Abdelouahab, M.S.; Lozi, R. Hopf-like bifurcation and mixed mode oscillation in a fractional-order FitzHugh-Nagumo model. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2183. [Google Scholar]
- Teka, W.W.; Upadhyay, R.K.; Mondal, A. Spiking and bursting patterns of fractional-order Izhikevich model. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 161–176. [Google Scholar] [CrossRef]
- Lozi, R.; Abdelouahab, M.S.; Chen, G. Mixed-Mode Oscillations Based on Complex Canard Explosion in a Fractional-Order Fitzhugh-Nagumo Model. Appl. Math. Nonlinear Sci. 2020, 5, 239–256. [Google Scholar] [CrossRef]
- Mbouna, S.G.N. Fractional Calculus-Based Generalization of the FitzHugh-Nagumo Model: Biophysical Justification, Dynamical Analysis and Neurocomputational Implications. In Nonlinear Systems-Recent Developments and Advances; IntechOpen: London, UK, 2022. [Google Scholar]
- Gao, X.L.; Zhang, H.L.; Wang, Y.L.; Li, Z.Y. Research on pattern dynamics behavior of a fractional vegetation-water model in arid flat environment. Fractal Fract. 2024, 8, 264. [Google Scholar] [CrossRef]
- He, K.; Song, J.; Zhao, N.; Liu, S. Hopf bifurcation and dynamical transitions in a fractional-order FitzHugh-Rinzel model with multiple time delays. Commun. Nonlinear Sci. Numer. Simul. 2025, 141, 108471. [Google Scholar] [CrossRef]
- Monteiro, N.Z.; dos Santos, R.W.; Mazorche, S.R. Bridging the gap between models based on ordinary, delayed, and fractional differentials equations through integral kernels. Proc. Natl. Acad. Sci. USA 2024, 121, e2322424121. [Google Scholar] [CrossRef]
- Monteiro, N.Z.; dos Santos, R.W.; Mazorche, S.R. Constructive fractional models through Mittag-Leffler functions. Comput. Appl. Math. 2024, 43, 177. [Google Scholar] [CrossRef]
- Colli Franzone, P.; Pavarino, L.F. A parallel solver for reaction–diffusion systems in computational electrocardiology. Math. Model. Methods Appl. Sci. 2004, 14, 883–911. [Google Scholar] [CrossRef]
- Rogers, J.M.; McCulloch, A.D. A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Trans. Biomed. Eng. 1994, 41, 743–757. [Google Scholar] [CrossRef]
- Mitchell, C.C.; Schaeffer, D.G. A two-current model for the dynamics of cardiac membrane. Bull. Math. Biol. 2003, 65, 767–793. [Google Scholar] [CrossRef]
- Karma, A. Spiral breakup in model equations of action potential propagation in cardiac tissue. Phys. Rev. Lett. 1993, 71, 1103. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.; Tarasov, V.E. Trends, directions for further research, and some open problems of Fractional Calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional integrals and derivatives; Gordon and Breach Science Publishers: Yverdon Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: San Diego, CA, USA, 1998. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Heidelberg, Germany, 2004. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014; Volume 2. [Google Scholar]
- Cushing, J.M. Integrodifferential Equations and Delay Models in Population Dynamics; Springer Science & Business Media: New York, NY, USA, 2013; Volume 20. [Google Scholar]
- Nair, S.S. An Overview of Generalized Gamma Mittag–Leffler Model and Its Applications. Axioms 2015, 4, 365. [Google Scholar] [CrossRef]
- Rameh, R.B.; Cherry, E.M.; dos Santos, R.W. Single-variable delay-differential equation approximations of the Fitzhugh-Nagumo and Hodgkin-Huxley models. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105066. [Google Scholar] [CrossRef]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Fenton, F.H.; Cherry, E.M. Models of cardiac cell. Scholarpedia 2008, 3, 1868. [Google Scholar] [CrossRef]
- Weiss, J.N.; Garfinkel, A.; Karagueuzian, H.S.; Chen, P.S.; Qu, Z. Early afterdepolarizations and cardiac arrhythmias. Heart Rhythm 2010, 7, 1891–1899. [Google Scholar] [CrossRef]
- Monteiro, N.Z.; Mazorche, S.R.; dos Santos, R.W. Positivity and equilibrium in a fractional SIR model with Mittag-Leffler memory. Trends Comput. Appl. Math. 2024, 25, e01789. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.; El-Saka, H.A. Equilibrium points, stability and numerical solutions of fractional-order predator–prey and rabies models. J. Math. Anal. Appl. 2007, 325, 542–553. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A proof for non existence of periodic solutions in time invariant fractional order systems. Automatica 2009, 45, 1886–1890. [Google Scholar] [CrossRef]
- Mazorche, S.R.; Monteiro, N.Z. Modelos epidemiológicos fracionários: O que se perde, o que se ganha, o que se transforma? In Proceeding Series of the Brazilian Society of Computational and Applied Mathematics; SBMAC: São Carlos, Brazil, 2021; Volume 8. [Google Scholar]
- Calatayud, J.; Jornet, M.; Pinto, C.M. On the interpretation of Caputo fractional compartmental models. Chaos, Solitons Fractals 2024, 186, 115263. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Erickson, A.M.; Henry, B.I.; McGann, A.V.; Murray, J.M.; Nichols, J.A. A General Framework for Fractional Order Compartment Models. SIAM Rev. 2021, 63, 375–392. [Google Scholar] [CrossRef]
- Tran, D.X.; Sato, D.; Yochelis, A.; Weiss, J.N.; Garfinkel, A.; Qu, Z. Bifurcation and chaos in a model of cardiac early afterdepolarizations. Phys. Rev. Lett. 2009, 102, 258103. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, N.Z.; Mazorche, S.R. Fractional Derivatives Applied to Epidemiology. Trends Comput. Appl. Math. 2021, 22, 157–177. [Google Scholar] [CrossRef]
- Diethelm, K. Monotonicity of functions and sign changes of their Caputo derivatives. Fract. Calc. Appl. Anal. 2016, 19, 561–566. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. J. Pharmacokinet. Pharmacodyn. 2010, 37, 203–207. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteiro, N.Z.; dos Santos, R.W.; Mazorche, S.R. Ion Channel Memory Drives Cardiac Early Afterdepolarizations in Fractional Models. Mathematics 2025, 13, 1585. https://doi.org/10.3390/math13101585
Monteiro NZ, dos Santos RW, Mazorche SR. Ion Channel Memory Drives Cardiac Early Afterdepolarizations in Fractional Models. Mathematics. 2025; 13(10):1585. https://doi.org/10.3390/math13101585
Chicago/Turabian StyleMonteiro, Noemi Zeraick, Rodrigo Weber dos Santos, and Sandro Rodrigues Mazorche. 2025. "Ion Channel Memory Drives Cardiac Early Afterdepolarizations in Fractional Models" Mathematics 13, no. 10: 1585. https://doi.org/10.3390/math13101585
APA StyleMonteiro, N. Z., dos Santos, R. W., & Mazorche, S. R. (2025). Ion Channel Memory Drives Cardiac Early Afterdepolarizations in Fractional Models. Mathematics, 13(10), 1585. https://doi.org/10.3390/math13101585





