Abstract
Physics-informed neural networks (PINNs) offer a mesh-free approach to solving partial differential equations (PDEs) with embedded physical constraints. Although PINNs have gained traction in various engineering fields, their adoption for railway bridge analysis remains under-explored. To address this gap, a systematic review was conducted across Scopus and Web of Science (2020–2025), filtering records by relevance, journal impact, and language. From an initial pool, 120 articles were selected and categorised into nine thematic clusters that encompass computational frameworks, hybrid integration with conventional solvers, and domain decomposition strategies. Through natural language processing (NLP) and trend mapping, this review evidences a growing but fragmented research landscape. PINNs demonstrate promising capabilities in load distribution modelling, structural health monitoring, and failure prediction, particularly under dynamic train loads on multi-span bridges. However, methodological gaps persist in large-scale simulations, plasticity modelling, and experimental validation. Future work should focus on scalable PINN architectures, refined modelling of inelastic behaviours, and real-time data assimilation, ensuring robustness and generalisability through interdisciplinary collaboration.
Keywords:
physics-informed neural networks (PINNs); partial differential equations (PDEs); scientific machine learning; domain decomposition; inverse problems; computational mechanics MSC:
74-10; 00A69
1. Introduction
Railway bridges are fundamental components of transport networks; they ensure the continuity and efficiency of rail traffic and thus support economic development and operational safety. Their economic relevance and structural safety are emphasised because of this strategic role. These bridges are subjected to constant and variable loads, which render them vulnerable to structural failure; the possible consequences range from service interruptions to collapse, with attendant economic losses and safety risks. Therefore, a timely and accurate analysis is indispensable because inadequate or delayed evaluations can lead to prolonged closures and increased maintenance costs.
Physics-informed neural networks (PINNs) have been proposed as an innovative alternative to traditional numerical simulation and structural monitoring methods. Unlike conventional approaches, a PINN integrates the physical laws that govern structural behaviour, namely the conservation of mass, momentum, and energy, directly into its loss function. This integration yields more accurate and physically consistent solutions while reducing computational effort. Consequently, PINNs are regarded as powerful tools for the early and efficient analysis of railway bridges; their use is expected to optimise maintenance decisions, lower operating costs, and enhance long-term structural safety.
During the last decade, deep learning techniques for solving partial differential equations (PDEs) have gained prominence in engineering and the physical sciences. In particular, PINNs have been established as a promising approach for problems in fluid mechanics [1], solid mechanics [2], thermal processes [3], and non-linear or multi-scale phenomena [4]. By incorporating loss terms that penalise deviations from governing PDEs and boundary conditions, PINNs embed prior physical knowledge and yield numerical solutions of increased accuracy and robustness [5,6].
Several systematic reviews of PINN research have been published. Dieva et al. [7] concentrate on non-Newtonian flows in porous media and omit structural applications, underscoring the need to explore PINNs within infrastructure systems such as railway bridges. Farea et al. [8] present a broad survey of current PINN techniques and trends, but their scope remains limited to general physics and computational challenges, omitting civil engineering applications.
Cai et al. [9] investigate wind engineering problems, demonstrating the ability of PINNs to manage complex geometries and boundary conditions; nevertheless, structural systems such as railway bridges are not examined. Yang et al. [10] introduce a framework for chase–evasion tasks in aerospace, but their study is confined to control and space dynamics contexts. Lino et al. [11] classify deep learning methods for flow simulation, yet do not explore structural monitoring or railway infrastructure applications.
Lawal et al. [12] and Abdulkadirov et al. [13] discuss methodological advances and optimisation algorithms but do not address railway bridges. Chen et al. [14] focus on geoengineering applications, whereas Khalid et al. [15] analyse laminated composites; in both cases, bridge monitoring is not considered. Hou et al. [16] study propeller wakes, while Hu et al. [17] integrate constitutive models in solid mechanics; neither work discusses railway infrastructure.
Although PINNs have achieved notable success in many engineering domains, their application to railway bridges—where complex dynamic loads, intricate geometries, and long-term degradation are prevalent—remains under-explored. Most studies continue to rely on the finite element method (FEM) or finite difference method (FDM). A comparative summary of the strengths and limitations of both approaches in this context is presented in Table 1.

Table 1.
Comparative overview: PINNs vs. traditional numerical methods (TNM; e.g., FEM/FDM) for railway bridge engineering applications.
The present study, therefore, evaluates whether PINNs can improve the structural analysis of railway bridges relative to traditional methods. Two research questions are addressed: (i) how do PINN results compare with classical numerical methods in terms of accuracy and computational efficiency? (ii) What advantages and limitations arise when PINNs model complex phenomena such as vibration, deformation, and stress propagation in railway bridges?
The main contributions of the article are as follows:
- A systematic bibliographic analysis of PINN research applied to railway bridge structures is presented; 120 studies (2020–2025) were selected according to relevance, journal ranking, and methodological rigour.
- A hybrid methodology is employed, combining natural language processing, semantic analysis, and citation mapping to classify contributions.
- The potential of PINNs to improve load distribution modelling, failure prediction, and real-time monitoring is demonstrated. Their advantages over TNM in accuracy, efficiency, and adaptability are highlighted.
- Research gaps are identified: large-scale simulation, plasticity modelling, and real-time data integration.
- Deployment challenges are discussed, including the need for parallelisation, GPU acceleration, and error-bounding frameworks.
- Future research directions are proposed, encouraging interdisciplinary collaboration and experimental validation.
The article proceeds as follows. Section 2 presents the theoretical foundations of PINNs and their relevance to structural problems. The methodology is then detailed, followed by an analysis of the results. The implications are discussed, and conclusions are drawn regarding the potential of PINNs for monitoring and maintaining railway bridges.
This review first reports the identified trends and applications (Section 3); it then analyses key findings (Section 3 and Section 5); finally, it offers conclusions and future perspectives (Section 6). The synthesis focuses on performance metrics, computational efficiency, and PINN capabilities relative to traditional methods. Bibliographic details, study characteristics, and methodological aspects were extracted; missing values were recorded, and no data were imputed. Funding sources were not systematically collected.
2. Methodology
This systematic review was conducted and reported in accordance with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 statement [18]. A brief overview of the procedure is provided first, followed by a stage-by-stage description. The review commenced with a comprehensive search of the Scopus and Web of Science (WoS) databases; predefined filters were then applied to refine the initial set of records. Inclusion and exclusion criteria were used to ensure relevance and methodological rigour. The workflow is summarised in Figure 1. After retrieval, the references were merged and cleaned to remove duplicates and low-quality items, and a full-text review with quality checks was carried out. Expert validation was included to assess the coherence of the dataset. Once the corpus had been validated, thematic clustering was performed with natural language processing (NLP) techniques to identify key research topics and emerging trends.
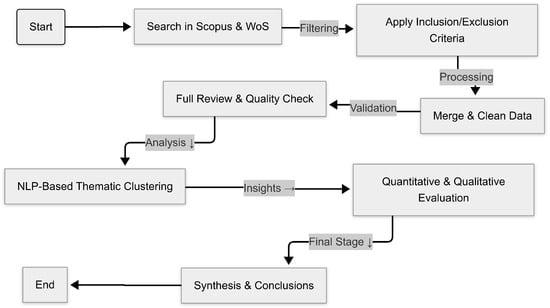
Figure 1.
Semi-automated literature review methodology, showing the process and key steps.
A combined quantitative–qualitative evaluation was then completed to examine topic distribution, reveal research gaps, and assess methodological contributions. The final step synthesised the principal findings and formulated the conclusions. This structured, transparent, and reproducible approach ensured a robust and comprehensive literature assessment.
2.1. Document Search and Retrieval
Searches were executed in Scopus and WoS under the predefined criteria. This process included systematic refinement of search terms, combining established keywords (e.g., physics-informed neural networks, PDEs, and computational mechanics) with emerging concepts (e.g., railway bridges and structural health monitoring). The database search was last conducted on [18 February 2025], and the final query was as follows:
(“physics-informed neural network*” OR “PINN*” OR “physics-guided neural network*” OR “physics-based machine learning*” OR “computational mechanics*” OR “finite element*” OR “numerical simulation*”) AND (“railway bridge*” OR “structural health monitoring*” OR “SHM” OR “topology optimisation*” OR “fatigue analysis*” OR “damage detection*” OR “bridge assessment*” OR “vibration analysis*” OR “residual stress*” OR “cyclic loading*”)
The following search-enhancement strategies were adopted:
- Semantic expansion and synonym analysis: A thesaurus of related terms was used to identify synonyms and equivalent expressions, widening coverage across differing terminologies.
- Temporal and quality filters: Documents published between 2015 and 2025, written in English, and indexed in Scopus or WoS under Q1/Q2 journals were prioritised.
- Iterative Boolean refinement: Core terms were used initially, followed by dynamic refinement that incorporated emerging keywords, maintaining dataset coherence while accommodating evolving terminology.
2.2. Document Fusion and Cleaning
The Scopus and WoS results were merged into a single database. Duplicates were removed on the basis of DOI, title, and authorship. No additional data transformations were required before the qualitative, thematic, and bibliometric synthesis.
The following criteria were then applied:
- Inclusion: publications of methodological rigour, appearing in Q1/Q2 outlets, written in English, and focused on PINNs, PDEs, SHM, or bridge engineering.
- Exclusion: items without verifiable access, lacking explicit PINN–PDE content, or unrelated to mechanical or structural engineering.
A preliminary corpus was obtained. Eligible studies were selected through independent screening by two reviewers; disagreements were resolved by discussion or, if needed, by a third reviewer. No automation tools were employed.
Because the review is qualitative and not a meta-analysis, tests for heterogeneity, sensitivity, reporting bias, or certainty assessment (e.g., GRADE) were beyond scope and therefore omitted.
2.3. Thematic Analysis Using NLP and Expert Review
Text mining and semantic analysis techniques were applied to identify the main research lines. These included unsupervised topic modelling and frequent term extraction, combined with expert validation. The workflow comprised the following:
- Text preprocessing: tokenisation, stop-word removal, lexical normalisation, and lemmatisation.
- Topic modelling and clustering: latent dirichlet allocation (LDA) and BERT-based clustering.
- Expert validation: examination and adjustment of preliminary themes by specialists in structural engineering and computational science.
- Cluster consolidation: establishment of final thematic areas, including PINNs in computational mechanics, railway bridge applications, vibration analysis, and structural health monitoring.
This approach combined the scalability of NLP with expert oversight and produced a robust thematic classification aligned with the PINN research landscape.
2.4. Full Review and Validated Inclusion
Each clustered document was assessed for relevance to the study objectives. The assessment considered the following:
- Methodological quality: experimental design, PDE formulation, and network architecture.
- Applicability: suitability for SHM and bridge mechanics, with attention to cyclic loading, fatigue, and dynamic predictions.
- Validation: presence of numerical or experimental corroboration and the generalisability of conclusions.
Only items satisfying both the NLP-based classification and expert review were retained. No author contact or automation tools were used during data extraction.
Formal risk-of-bias instruments were not applied because most studies were computational; instead, domain experts appraised methodological quality, as described in Section 2.3.
2.5. Quantitative Analysis: Metrics, Visualisations, and Key Indicators
A bibliometric analysis was carried out to examine temporal evolution, impact, and thematic concentration:
- Temporal distribution: publication trends since 2018, with acceleration after 2022.
- Sources and impact: distribution by journal, h index, citation counts, and ranking.
- Term clouds and co-occurrence networks: visualisation of topic prevalence and interrelations with simulation methods and structural analysis approaches.
These analyses supplied a temporal and thematic map of the field and revealed gaps for future exploration. Links between the quantitative results and the discussion in Section 5 informed further reflection on emerging questions.
Standardised effect-size measures were not applicable, owing to the descriptive nature of the synthesis.
2.6. Qualitative Analysis: Descriptive Review and Meta-Thesis
A qualitative appraisal was then performed to compare the most significant approaches in bridge engineering, structural design, and fatigue analysis, and to examine theoretical advances in PINNs. The review proceeded along three axes:
- Structured synthesis of findings.
- Identification of research gaps and opportunities.
- Discussion and meta-synthesis.
The narrative review, underpinned by the NLP-based classification, provided a cohesive perspective and outlined future projections for PINNs in structural engineering. A summary of the qualitative phases and their methodological contributions is presented in Table 2.

Table 2.
Summary of the qualitative approach and its methodological contribution.
The qualitative process thus transcended descriptive reviews: it integrated multiple perspectives, highlighted convergences, and identified future potential. Under-explored domains, such as weld fatigue or PINNs customised for composite materials, were flagged for further study. The ensuing discussion promotes technology transfer to industry and continuous improvement in bridge design, maintenance, and monitoring.
Figure 2 details the sequence of NLP analysis and expert validation, expanding one of the key stages in Figure 1. Unsupervised topic modelling, iterative expert review, and final consolidation are illustrated step by step. This description clarifies how NLP and expert judgement were combined to obtain a reliable thematic classification.
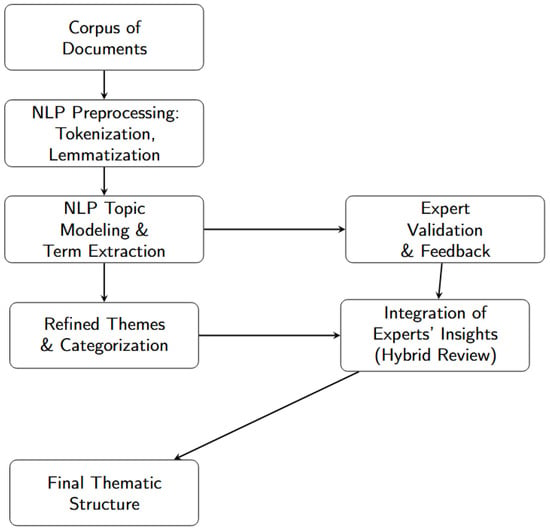
Figure 2.
Detailed flowchart of the NLP-based thematic analysis with expert evaluations.
2.7. Final Synthesis
At this stage, the quantitative and qualitative findings were integrated. Connections were established between research trends, methodological approaches, and thematic clusters. Emphasis was placed on potential applications of PINNs to the structural analysis of railway bridges.
The results were also linked with broader insights from Section 5, including challenges such as real-time SHM, fatigue under cyclic loading, and multi-scale modelling. By aligning bibliometric trends with engineering needs, this synthesis provides a coherent roadmap for advancing PINN-based approaches.
Table 3 summarises each methodological phase. It complements Figure 1 by listing the NLP techniques, clustering algorithms, and validation strategies employed.

Table 3.
Description of methodological phases for NLP-based thematic analysis with expert validation.
3. Findings and Discussions
3.1. From Differential Operators to Neural Approximators in Railway Bridge Structural Analysis
To motivate the use of physics-informed neural networks (PINNs) from a mathematical perspective, the general framework of partial differential equations (PDEs) and their boundary and initial conditions is recalled. Let denote a domain in a d-dimensional space (typically , or 3), and let be a time horizon. A PDE of order m in strong form is written as follows:
where is the unknown field, is a differential operator (linear or non-linear), and f is a known source term, which may be zero or defined in suitable function spaces.
This general PDE framework allows the modelling of stress, strain, and dynamic responses in railway bridge components subjected to moving train loads. It also supports vibration analysis from wheel–rail impacts, where represents displacement, velocity, or acceleration. Thermo-mechanical behaviours in critical zones such as gusset plates can be modelled by embedding multi-physics operators in . Realistic boundary conditions, such as bolted joints or elastomeric supports, may be incorporated using sensor data during PINN training.
By approximating while satisfying physical laws, boundary conditions, and sensor data, PINNs offer a flexible approach, particularly under incomplete or sparse datasets, as often found in railway bridge structural health monitoring.
Boundary and Initial Conditions in Railway Bridge Modelling
For the PDE in Equation (1), initial and boundary conditions must be imposed. A time-dependent initial condition is expressed as follows:
and, for , higher-order temporal derivatives may also be required. A boundary condition is specified on :
where may be a Dirichlet, Neumann, Robin, or non-linear operator.
In railway bridge modelling, initial conditions represent residual stresses, geometric imperfections, or effects from seismic or construction processes. Boundary conditions describe support types (e.g., pinned, roller, or elastomeric) that govern force transmission. Time-dependent boundary terms capture dynamic loads such as train-induced forces.
While classical methods such as FEM and FDM approximate through discretisation, they may face limitations in meshing and computational cost when applied to complex geometries or high-dimensional problems, especially in components like gusset plates or composite bearings.
PINNs, introduced by Raissi et al. [19], overcome these challenges by embedding the governing PDEs and boundary/initial conditions directly into the network’s loss function, enabling mesh-free, accurate modelling under uncertain or variable conditions.
3.2. Artificial Neural Networks: Approximation Perspective in Railway Bridge Analysis
3.2.1. Universal Approximation Theorem
Artificial neural networks (ANNs) offer a flexible framework for approximating real-valued functions using compositions of affine transformations and non-linear activations. A standard depth-L network with neurons per layer defines a mapping , where collects all trainable parameters. According to the universal approximation theorem, ANNs can approximate continuous functions on compact subsets of to arbitrary accuracy, given sufficient depth or width [2].
The general neural approximation is written as follows:
where and are weights and biases, and is a non-linear activation (e.g., ReLU, tanh, and sine). The goal is to construct a representation that approximates the PDE solution accurately.
In railway bridge analysis, neural networks act as surrogate models to approximate displacement fields, stress states, and modal properties. This is useful when analytical solutions are unavailable or traditional numerical methods are computationally expensive [16,17]. In PINNs, training involves minimising a composite loss that incorporates PDE constraints and optionally, sensor data (e.g., strain gauges and accelerometers) [15]. This allows structural prediction under dynamic loads, reducing mesh dependence and improving generalisability [20,21].
3.2.2. ANNs for PDE Approximation: Traditional Approaches in Railway Bridge Applications
The use of ANNs to solve PDEs began with Lagaris et al. [22], where is constructed to satisfy boundary conditions by design:
with A and B chosen to enforce the boundary conditions for all , and is a neural network.
This method ensures boundary conditions are inherently satisfied, simplifying training by focusing on minimising the PDE residual .
In railway bridge problems involving complex supports, e.g., bolted joints or elastomeric isolators, traditional numerical methods often face limitations due to discontinuities or geometric singularities. Classical approaches require manually constructed ansatz functions (A, B), which become impractical in high-dimensional or multi-physics settings [23,24].
To address this, PINNs have emerged by embedding physical laws into the loss function, avoiding handcrafted forms and enabling scalable modelling across complex structural domains [2,20,25].
3.3. Physics-Informed Neural Networks
3.3.1. Conceptual Framework
Physics-informed neural networks (PINNs) [19,26] provide an alternative to mesh-based PDE solvers, especially when data are sparse or partially observed. Their core principle is to embed the governing physics directly into training by penalising PDE residuals. For a PDE as in (1), the approximation is as follows:
where denotes the trainable network parameters. Automatic differentiation enables the exact computation of derivatives like , , and . The residual is as follows:
which is included in the loss function.
It is noteworthy that while the term physics-informed neural network (PINN), as predominantly used in the literature reviewed herein and following the seminal work of Raissi et al. [19], typically refers to methodologies integrating physical laws primarily through penalty terms in the loss function (enforcing PDE residuals and boundary/initial conditions via automatic differentiation), the broader field of integrating physics with deep learning encompasses other related paradigms. For example, approaches termed physics-guided deep learning (PGDL) may leverage physical principles more broadly, potentially guiding network architecture design, informing feature engineering, or incorporating physics-based models alongside data-driven components, sometimes using physics-informed loss functions derived from simplified physical models or consistency requirements rather than direct PDE residuals [27]. While potentially distinct in their specific integration mechanisms, both PINN and PGDL paradigms share the common goal of enhancing model accuracy, data efficiency, and generalisation by embedding domain knowledge, thereby moving beyond purely data-driven “black box” models. This review focuses specifically on the PINN approach characterised by the loss-based enforcement of governing equations, reflecting the predominant methodology found in the selected corpus for structural analysis.
In railway bridge analysis, where dynamic loads and complex geometries limit conventional solvers, PINNs offer a mesh-free, physics-based framework for modelling structural responses. Constitutive laws, boundary conditions, and in situ data can all be embedded in a unified learning architecture, enabling simulation under realistic operational scenarios [1,15,21].
3.3.2. PDE Loss Term
The physical fidelity of a physics-informed neural network (PINN) is achieved by enforcing the governing PDE through a residual-based loss:
where denotes collocation points in .
This loss minimises the discrepancy between the network prediction and the physical law encoded in and f. No meshing is needed; collocation points may be chosen uniformly, adaptively, or randomly.
This formulation is especially effective for modelling wave propagation, thermal diffusion, or stress concentrations in railway bridge components such as gusset plates, diaphragms, or bearings, where non-linear and transient behaviours arise under cyclic train loads. By focusing directly on the PDE at selected points, PINNs can estimate dynamic responses without explicit numerical integration [2].
3.3.3. Boundary and Initial Condition Loss
In railway bridges, accurate modelling of initial states, due to pre-stress, prior load history, or temperature, is crucial. In PINNs, boundary and initial conditions are embedded as additional loss terms. The boundary condition loss is as follows:
where is the boundary operator, and g represents imposed conditions, such as support reactions or measured displacements.
For instance, implementing boundary conditions for specific structural features like truss joints within the PINN framework requires careful formulation of the term based on structural mechanics principles. For an idealised pin joint connecting multiple members at a node , the loss could penalise deviations from zero moment transfer and enforce displacement continuity ( being identical for all connected member ends approached from different elements). For semi-rigid or complex bolted joints, the loss might incorporate penalty terms representing non-linear rotational stiffness or force–displacement relationships derived from detailed component models or experimental data, effectively embedding the joint’s specific mechanical behaviour directly into the network’s training objective. Handling such complex BCs often relies on precise sampling of collocation points around the joint and appropriate weighting within the overall loss function .
Similarly, the initial condition loss is as follows:
with defining the initial field. This is critical for transient dynamics, such as train-induced vibrations or thermal effects, improving predictive accuracy [2].
Together, these loss components ensure that the predicted solution satisfies both the governing equations and realistic structural constraints, without requiring mesh-based enforcement or predefined ansatz functions.
3.3.4. Combined Loss and Optimisation Problem
The total loss function used for training is as follows:
where , , and balance the importance of each term [28,29]. The optimisation goal is as follows:
Gradient computation is performed via backpropagation, using optimisers such as Adam or L-BFGS. Once trained, the network provides a high-fidelity solution suitable for real-time monitoring or structural health evaluation of railway bridges.
3.4. Role of Automatic Differentiation
A major advantage of PINNs is the ability to compute high-order derivatives with machine precision using automatic differentiation (AD) [19]. This eliminates the need for numerical discretisation schemes like finite differences or finite elements.
In structural mechanics, AD supports the accurate calculation of spatial and temporal derivatives relevant to stress, strain, and vibration modelling. For railway bridges, this allows direct resolution of strain concentrations or modal variations near features like gusset plates or support bearings [2,30].
However, AD introduces some limitations. Computational cost increases with the number of derivatives or in complex PDE systems, such as 3D thermo-mechanical problems with anisotropy and dynamic loads. Chiu et al. reported that even advanced hybrid methods like CAN-PINN must balance derivative precision and training stability [31].
AD does not resolve numerical stiffness or gradient pathologies, which may affect PINN performance in highly dynamic or multi-scale structural problems [32]. In long-span steel bridges under repeated loading, PINNs may require tailored loss-balancing or domain decomposition strategies for stable training [28,29].
3.5. Error Estimates and Convergence
Although PINNs deliver strong empirical results, rigorous convergence proofs are still scarce, particularly for structural applications subjected to realistic loads and boundary conditions. A typical goal is to bound the physical error by the following:
where is the representation error, and is the optimisation error. Here, C is a stability constant: it encapsulates the sensitivity of the PDE solution to perturbations and depends only on the governing equations, material coefficients, domain geometry, and boundary/initial conditions; it never depends on the errors themselves. Moreover, denotes the Sobolev norm, which quantifies both the error in the solution and its first-order weak derivatives. Specifically, for any function , this norm is defined as follows:
This formulation reflects the regularity required of solutions in PDE error analysis, especially for time-dependent problems, and is widely used when analysing the convergence of PINNs under physically realistic constraints [6].
For railway bridges, convergence can be sensitive to initialisation, loss balancing, and sampling strategies, particularly when modelling multi-scale stress gradients, thermal effects, or local damage. For example, convergence may fail in thin or curved components with stiff constraints if adaptive sampling is not used or if the network lacks capacity.
Recent methods mitigate these limitations by incorporating constitutive laws or modifying the loss function, especially in solid mechanics [17]. These methods are promising for real infrastructure components, like trusses and bridge decks, where FEM may struggle due to meshing issues or numerical locking.
Therefore, despite theoretical progress, practical convergence in bridge analysis still depends on domain-specific strategies, requiring further methodological innovation.
3.6. Inverse and Data-Driven Extensions
In structural mechanics, particularly for railway bridges, governing equations are often only partially known, and data may be noisy or limited. This motivates inverse PINN formulations, where observational data are integrated with the PDE residual in the loss function:
allowing the network to learn hidden parameters such as degradation, diffusion, or loading profiles.
This is particularly useful for SHM, where full-field sensing is infeasible. PINNs have been applied to detect damage and infer properties from sparse sensor data, combining physical models and observations [17,19]. Applications include laminated composites and truss elements, where damage is inferred from boundary or strain data.
For railway bridges, inverse PINNs help model internal stress, corrosion, or thermal fields not directly measurable. However, stability and identifiability can be compromised when data are sparse or noisy, especially under coupled or non-linear dynamics [8].
3.7. Chronological Evolution of PINNs
PINNs provide a mesh-free framework for solving PDEs by integrating neural networks, automatic differentiation, and physics-based loss terms. Key features include the following:
- Universal approximation: ANNs represent PDE solutions over continuous domains.
- Physics enforcement: PDEs and constraints are encoded via loss penalties.
- Automatic differentiation: Enables precise derivative computation without finite differences or elements.
- Inverse problem solving: Latent parameters can be inferred via embedded optimisation.
Despite challenges like non-convex loss landscapes and hyperparameter sensitivity, PINNs have become popular for high-dimensional and irregular domains. Advances in optimisation, adaptive weighting, and domain decomposition continue to expand their capabilities [12,29,33].
As summarised in Table 4, PINNs have evolved through distinct stages. Early attempts in the 1990s, such as those by Lagaris et al. [22], embedded boundary conditions in neural representations but were limited by computational power. Progress continued through the 2000s, leading to the formal PINN framework by Raissi et al. [19] between 2017–2019. This development was enabled by advances in automatic differentiation, which allowed efficient integration of PDEs into neural training.

Table 4.
Chronological evolution of physics-informed neural networks (PINNs). This timeline highlights key methodological and computational milestones from their early inception to modern-day applications.
3.8. Thematic Analysis
From 2020 to 2021, research on PINNs focused on addressing core challenges such as gradient pathologies and spectral bias. These issues were mitigated by developing new activation functions and applying domain decomposition techniques [12,26]. Such improvements enhanced training stability, especially for structural systems described by stiff PDEs, like stress wave propagation or dynamic responses in bridge joints.
During the same period, hybrid and hierarchical architectures, like XPINNs and hp-VPINNs, were introduced to improve scalability and efficiency [7]. These models are well-suited for railway bridges, where subcomponents (e.g., bearings, decks, and trusses) exhibit heterogeneous behaviours. Localised learning and domain partitioning allow these architectures to handle complexity more effectively.
Between 2022 and 2023, architectural advances focused on integrating transfer learning, operator learning, and evolutionary optimisers [8,29]. These developments enabled PINNs to perform real-time data assimilation. In railway applications, this supports adaptive modelling, which is useful for vibration-based damage detection or uncertain boundary conditions. Efforts to introduce a posteriori error estimates also improved model reliability [6], which is vital for safety-critical applications like fatigue and maintenance planning.
More recently, attention has shifted toward GPU/TPU-accelerated PINNs for high-dimensional multi-physics problems with limited or nonuniform data [9]. PINNs are now being explored not just as complements to FEM or FDM but as hybrid tools that combine data-driven learning with physical modelling, particularly relevant for railway bridges affected by uncertainty in loading, materials, and geometry.
3.8.1. Score Distribution of Studies
Figure 3 shows the score assigned to each reviewed study based on conceptual focus and methodological rigour. The top-ranked study scored 10.0, reflecting a strong combination of differential modelling, neural approximation, and SHM integration. Four other studies achieved a score of 8.0, indicating solid methodological quality.
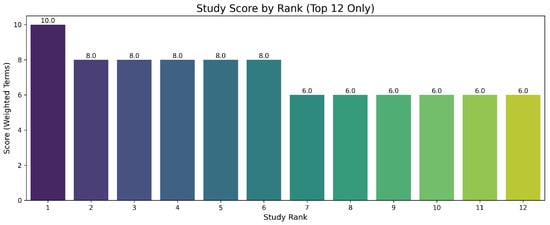
Figure 3.
Score distribution identifying the top 12 most relevant studies based on weighted terms, publication quality, and alignment with PINN applications for structural engineering challenges pertinent to railway bridges. This highlights foundational works addressing relevant physical phenomena and computational approaches.
Scores drop significantly beyond the fifth-ranked study, with many clustering around 6.0. This indicates a methodological bottleneck. Under-explored areas include fatigue in metallic bridges, inverse calibration under noisy conditions, and integration with FEM/FVM solvers. These aspects are critical for real-world applications like retrofitting and performance monitoring in railway bridges.
The clustering of highly ranked studies in a few institutions suggests a need for wider collaboration across disciplines. Areas like damage localisation in pin-connected trusses or thermo-mechanical effects in bearings would benefit from more diverse contributions.
In summary, while PINNs are maturing into powerful tools, their successful application to railway bridge mechanics requires further advances in methodological diversity, validation practices, and scalable training strategies.
3.8.2. Top Journals
Figure 4 shows the distribution of leading journals that have published articles on physics-informed neural networks (PINNs) within the analysed corpus. The horizontal axis indicates the number of contributions per journal, while the vertical axis lists the journal titles. Notably, Computer Methods in Applied Mechanics and Engineering and the Journal of Computational Physics stand out with 13 and 9 publications, respectively. This concentration underscores the central role of journals rooted in computational mechanics and numerical methods in advancing PINN methodologies.
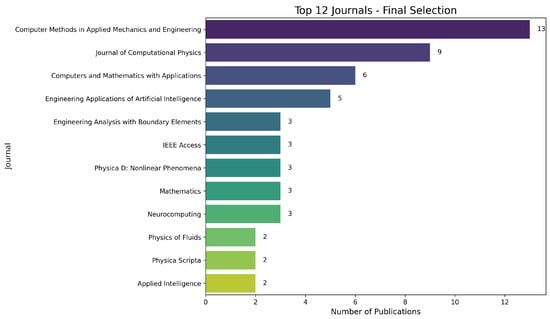
Figure 4.
Leading publication venues for PINN research relevant to structural analysis, ranked by article count within our corpus. The prominence of computational mechanics and applied mathematics journals indicates the primary sources for foundational methods applicable to railway bridge modelling.
These two journals serve as methodological anchors in the field, offering rigorous frameworks for integrating differential equation solvers with neural architectures. Their editorial orientation aligns well with the core challenges addressed by PINNs: modelling non-linear, multi-physics systems with sparse or noisy data. In the context of railway bridge mechanics, the tools and theories disseminated through these venues are critical for advancing fatigue modelling, modal identification, and hybrid physics–data-driven simulation strategies.
Other key contributors include Computers and Mathematics with Applications and Engineering Applications of Artificial Intelligence, with six and five publications, respectively. Their presence highlights a possible growing interdisciplinary work between applied mathematics, computational intelligence, and engineering mechanics. This intersection is particularly valuable in domains where predictive accuracy, robustness under uncertainty, and adaptive learning are essential, such as structural health monitoring (SHM) of trusses, support zones, and long-span decks in rail infrastructure.
Journals such as Engineering Analysis with Boundary Elements, IEEE Access, and Physica D: Nonlinear Phenomena, each contributing three publications, reflect the diversity of scientific communities engaging with PINNs. From high-frequency vibration modelling to non-linear damage propagation, this cross-domain interest affirms the potential of PINNs to unify approaches traditionally separated by methodological boundaries.
The strong presence of engineering-focused outlets (e.g., Applied Intelligence and Engineering Applications of Artificial Intelligence) suggests increasing momentum toward real-world implementation. Applications cited within these publications include data assimilation for load estimation, topology optimisation, and online failure detection, all of which are directly applicable to the evolving needs of railway bridge maintenance and resilience modelling.
3.8.3. Word Cloud
Figure 5 illustrates the word cloud generated from the titles and abstracts of the studies included in this review. The size of each word is proportional to its frequency of occurrence, providing a visual summary of dominant themes and recurring concepts in the PINN literature. Notably, terms such as “informed”, “neural”, “differential”, “equation”, and “pinn” appear prominently, reaffirming the centrality of partial differential equation (PDE) modelling and its fusion with machine learning architectures.

Figure 5.
Word cloud illustrating dominant concepts in the reviewed PINN literature applicable to structural analysis. Prominent terms like ‘physics informed’, ‘neural network’, ‘differential equation’, ‘solving’, ‘inverse problem’, and ‘boundary condition’ highlight core technical themes, while terms like ‘dynamic’, ‘parameter’, ‘structural’, and ‘optimisation’ point towards specific challenges relevant to modelling complex railway bridge behaviour and health monitoring.
The presence of words like “optimisation”, “accuracy”, “parameter”, and “framework” reveals a methodological orientation toward increasing model precision, training stability, and computational efficiency. These elements are particularly critical in structural engineering contexts, such as railway bridge analysis, where complex geometries, heterogeneous materials, and uncertain boundary conditions challenge conventional solvers.
Likewise, the frequent mention of terms such as “boundary condition”, “inverse problem”, “residual”, and “gradient” signals a sustained focus on integrating classical numerical mechanics (e.g., FEM and FDM) with data-driven approaches. This hybridisation allows PINNs to address challenges in fatigue diagnosis, damage localisation, and real-time monitoring, especially in long-span or pin-connected railway bridges, where internal states are difficult to access directly.
The inclusion of terms like “adaptive”, “solving”, “learning”, and “simulation” points to the dynamic evolution of the field. These concepts reflect ongoing efforts to generalise PINNs across high-dimensional, time-dependent, and multi-physics problems. In structural mechanics, this facilitates modelling scenarios such as temperature-induced deformation, vibration modes, or stress redistribution following mechanical failure.
Hence, the word cloud acts as a qualitative lens through which the key scientific intersections of the PINN field become visible: physics-based modelling, numerical analysis, machine learning, and computational intelligence. This convergence could define the methodological backbone of contemporary research and highlights future opportunities in structural applications, including predictive maintenance of railway bridges, where interpretability, accuracy, and adaptability remain fundamental requirements.
3.8.4. Production over Time
Figure 6 displays the annual distribution of the selected articles from 2020 to early 2025. A clear inflexion point is observed from 2022 onwards, with a substantial surge in 2023 (43 articles) and sustained high output in 2024 (35 articles). This upward trajectory reflects the accelerated integration of physics-informed neural networks (PINNs) into the computational sciences, particularly in domains requiring the solution of complex partial differential equations (PDEs).
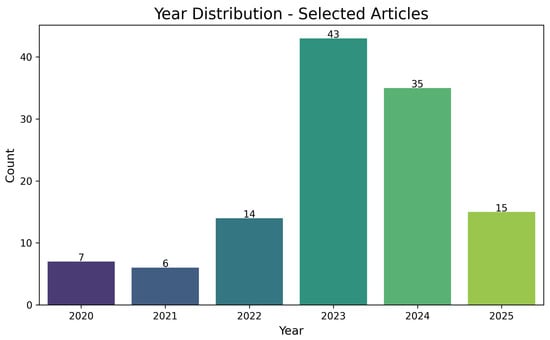
Figure 6.
Temporal distribution (2015–2025) of the selected publications relevant to PINNs in structural analysis, showing accelerated interest from 2022 onwards. This trend reflects the increasing exploration of PINNs for complex engineering problems, including those pertinent to railway bridge infrastructure integrity and monitoring.
The sharp growth between 2022 and 2024 aligns with key developments in automatic differentiation libraries, deep learning architectures, and hybrid numerical solvers, technologies that have enhanced the scalability, robustness, and interpretability of PINNs. These characteristics are particularly relevant in structural engineering contexts, such as railway bridge assessment, where complex boundary conditions, multi-material interactions, and limited measurement access pose persistent modelling challenges.
Despite a modest decline in 2024 compared to the 2023 peak, the number of publications remains markedly higher than pre-2022 levels. The continued production of articles in early 2025 (15 studies) suggests a stable research momentum. This reflects both a maturation of core methodologies and the emergence of new applications, including parameter inference, damage detection, and adaptive simulation in structural health monitoring (SHM).
For railway bridges in particular, the current research trajectory suggests that PINNs are increasingly viewed not only as theoretical tools but also as viable engineering solutions. Their capacity to assimilate sparse sensor data, encode known physics, and generalise across structural configurations makes them attractive for predictive maintenance and safety assessment under operational uncertainty.
Therefore, the year-wise distribution reveals a rapidly consolidating research area, driven by technological enablers and application demand. PINNs are transitioning from algorithmic novelty to a core modelling strategy in structural mechanics. Future efforts will likely emphasise domain-specific adaptations, such as interface handling in jointed systems, thermal–mechanical coupling in metallic elements, and reliability quantification under real-time constraints, all highly relevant for next-generation railway bridge management.
4. Clusters Analysis
Semantic vector embeddings extracted from article titles and abstracts enabled the classification of studies into thematic clusters, as illustrated in Figure 7. The distribution shows a strong concentration in clusters 2 and 3, with 26 and 23 articles, respectively, indicating that the dominant research interest lies in direct PDE solving and PINN architecture optimisation. These clusters largely correspond to foundational studies emphasising mathematical formulations and neural approximator design, which, while methodologically rich, remain general-purpose and often detached from specific structural engineering applications.
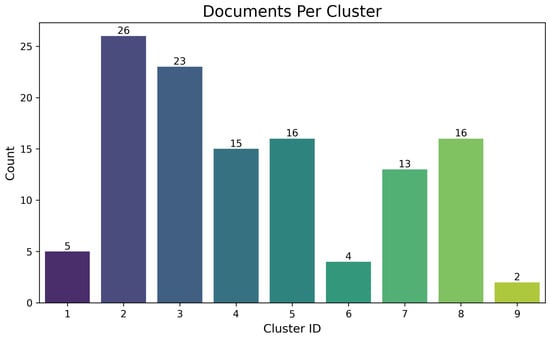
Figure 7.
Distribution of the 120 selected articles across the nine thematic clusters derived from semantic analysis. This visualises the concentration of research in foundational methods (e.g., Clusters 2 and 3) versus application-focused areas directly relevant to specific railway bridge challenges (e.g., symmetry in Cluster 1, solid mechanics/optimisation in Cluster 8, and inverse problems/noisy data in Cluster 9).
In contrast, clusters 6 and 9 show significantly lower representation (4 and 2 articles, respectively), reflecting emerging or underdeveloped areas in the literature. These groups are particularly relevant for structural health monitoring (SHM), fatigue modelling, and data-driven discovery of governing equations, fields with direct implications for the assessment and preservation of railway bridge infrastructure. As outlined in Table 5, their limited presence suggests a missed opportunity to exploit PINNs for tasks such as fatigue prediction in gusset plates, inverse stress reconstruction in truss elements, or real-time evaluation of damage accumulation in riveted joints.

Table 5.
Cluster-wise summary of PINN applications and their relevance to railway bridge analysis.
To provide an overview of these identified thematic areas before delving into individual cluster details, Table 5 summarises the key characteristics of each cluster. For each of the nine identified clusters (referenced hereafter by their ID), the table presents the assigned descriptive title, highlights potential application areas relevant to railway bridge analysis, and offers a concise outline of the primary advantages and limitations associated with the methodologies grouped within that theme. This table serves as a roadmap for the subsequent detailed discussion of each cluster presented in Section 4.
From an applied perspective, this clustering reveals that the literature has yet to fully explore physics-informed strategies for modelling multiaxial degradation in steel lattice bridges or long-span girders. Recent contributions demonstrate that PINNs can effectively incorporate damage mechanics formulations into the loss function, enabling residual stress estimation and lifetime prediction under non-trivial boundary and loading conditions. Such approaches are highly promising for analysing railway bridge components subjected to repeated thermal cycling and operational vibrations.
Additionally, applied studies in pedestrian or steel-frame bridges have shown that combining PINNs with physical simulations and experimental data enables accurate damage localisation, even in noisy or incomplete datasets. In this regard, the under-represented clusters may offer a methodological reservoir for advancing digital twin technologies for railway bridges, especially when fused with sensor-driven monitoring and hybrid numerical validation.
Therefore, the thematic segmentation of the literature not only reveals gaps in the current state of research but also provides a strategic roadmap for future work in structural mechanics. The fact that the most populated clusters do not directly address railway bridge problems reinforces the core premise of this review: the application of PINNs to structural analysis in rail infrastructure remains incipient and must be strengthened through physics-guided, data-informed, and numerically robust approaches, particularly for real-time performance prediction, maintenance planning, and safety assurance under operational uncertainty.
4.1. Cluster 1: Incorporation of Continuous and Conditional Symmetries in PINNs
This cluster emphasises the integration of symmetry-based formulations, both continuous and conditional, into physics-informed neural networks (PINNs) to improve their performance in solving non-linear partial differential equations (PDEs). These advancements, collectively referred to as symmetry-enhanced PINNs (SEPINNs), demonstrate notable improvements in numerical accuracy and generalisation, especially in regimes characterised by non-linear diffusion or wave propagation [35,36].
From a structural engineering perspective, the relevance of SEPINNs becomes particularly significant when addressing dynamic phenomena in railway bridges, such as resonance-induced stresses or wave propagation in steel trusses. For instance, railway bridge components often exhibit inherent symmetries, either geometric or boundary-induced, that can be exploited to reduce the solution space and improve learning efficiency. Incorporating continuous invariants (e.g., for vibration modes) or conditional symmetries (e.g., for segmental boundary conditions) enables more stable learning trajectories and fewer training data requirements [35,37].
Moreover, the application of generalised symmetry-enhanced PINNs (gsPINNs) in inverse problems, such as damage localisation or residual stress identification, holds potential for addressing under-instrumented scenarios typical in real-world monitoring of ageing bridges. These networks demonstrate strong performance even when trained on sparse datasets, making them particularly well-suited for infrastructure where sensor coverage is limited or expensive [35].
One particularly promising avenue is the use of symmetry groups to synthetically augment training datasets without relying on additional physical measurements. In bridge systems exhibiting repeatable substructures (e.g., repeated gusset plate assemblies or symmetric support conditions), this approach can enrich the training process and improve generalisation in zones of high stress concentration or non-linear behaviour near boundaries.
However, a critical limitation arises when such symmetries are only partially present or disrupted by retrofitting, corrosion, or material degradation. In these cases, enforcing incorrect symmetry assumptions may bias the solution or obscure localised pathologies. Hence, symmetry-enhanced strategies should be accompanied by diagnostic tools that evaluate the validity of symmetry conditions in specific structural configurations.
Hence, the findings from this cluster suggest that SEPINNs and gsPINNs can play a pivotal role in extending PINN applicability to dynamic and inverse problems in railway bridge analysis. By harnessing geometric or physical symmetries inherent in structural configurations, these models offer enhanced learning efficiency, robustness under data scarcity, and better predictive stability under complex boundary conditions, all essential traits for advancing real-time structural health monitoring and predictive maintenance in railway infrastructure [35,36,37].
4.2. Cluster 2: Methodological Advances in PINNs and Optimisation for PDEs
This cluster centres on the development of enhanced architectures and training strategies for PINNs, particularly focused on structural reliability, multi-scale physics, and inverse problem solving. The growing sophistication of these frameworks holds clear implications for improving the structural analysis of railway bridges, especially in terms of computational efficiency, parameter identification, and handling of spatial heterogeneities.
For instance, the introduction of PINN-FORM as a reliability-oriented framework directly contributes to fatigue and failure assessment in structural elements under stochastic loading, such as bridge gussets or pinned connections subjected to cyclic train loads [38]. This is especially valuable when dealing with complex constitutive behaviour or hidden damage mechanisms embedded within implicit state equations.
The NH-PINN framework, integrating neural homogenisation across three levels, enhances the resolution of multi-scale problems by bridging macro-scale bridge behaviour with localised stress responses at bolts or welds, often affected by microstructural inconsistencies or material degradation [39]. This capacity for multi-resolution modelling could greatly benefit long-span bridges where local failures might compromise global stability.
In the realm of inverse modelling, H-PINNs and PIRBNs have shown strong capabilities in identifying hidden parameters and local behaviours from sparse data [20,24]. In railway bridge applications, these models could be deployed to detect changes in stiffness or damping from limited sensor data, potentially enabling early detection of degradation in metallic bearings or riveted joints.
From a dynamic perspective, Bolandi et al.’s PINN-based stress prediction offers a promising route for real-time evaluation of dynamic load paths as trains traverse the bridge, especially under high-frequency or resonant conditions [40]. Such modelling is critical for evaluating fatigue accumulation in repetitive structural configurations.
Furthermore, hybridised training schemes (e.g., GA + L-BFGS), adaptive learning stages, and NAS-PINNs demonstrate significant improvements in training convergence and robustness under complex boundary conditions or non-linearities [32,41,42]. These traits are particularly desirable when modelling bridge response under mixed boundary conditions, such as fixed supports at one end and elastomeric bearings at the other.
However, the practical deployment of these methods faces several technical challenges. Many of the architectures, while computationally efficient in reduced problems, require substantial tuning when applied to real-scale bridge models with mixed materials, geometric irregularities, and multiple interacting components. Moreover, advanced optimisers or neural search methods (e.g., cat-and-mouse algorithms or CPINN-AIC) may incur overheads incompatible with time-sensitive tasks such as live structural health monitoring or rapid post-event assessments [32,43].
Nevertheless, these methodological innovations significantly extend the potential of PINNs beyond academic benchmarks, offering realistic pathways toward solving full-scale PDE systems in engineering practice. For railway bridges, this could translate into enhanced model fidelity, lower computational costs, and adaptive learning strategies robust to real-world uncertainties. As such, the advances in this cluster contribute critically to the overall objective of improving structural analysis accuracy compared to traditional numerical methods like FEM or FDM.
4.3. Cluster 3: General Reviews and In-Depth Methods on PINNs for PDEs
This cluster synthesises foundational reviews and methodological refinements of PINNs that collectively deepen our understanding of their theoretical structure, while outlining critical pathways for practical engineering deployment. A key contribution is the classification of PINNs into three major methodological categories, offering a structured roadmap to guide implementation across complex PDE-driven systems [34].
In the context of railway bridge analysis, these reviews help establish a theoretical framework that bridges machine learning with classical mechanics. Specifically, the explicit incorporation of physical constraints into deep learning models, e.g., stress–strain relationships or boundary condition consistency, emerges as a decisive factor in enhancing numerical fidelity for solid mechanics applications [44]. For instance, when analysing stress distribution across gusset plates or predicting localised fatigue zones in steel girders, the enforcement of boundary conditions through auxiliary terms can drastically improve convergence and accuracy under real-world loading scenarios [45].
Operator splitting and algebraic–differential structure integration [46] stand out as particularly useful for complex bridge systems, where multiple physics (e.g., thermal, dynamic, and mechanical fields) interact non-linearly. This is especially relevant in long-span railway bridges subjected to seasonal thermal gradients and vibrational loads induced by passing trains.
Notably, frameworks such as VINO and VC-PINN [4,47] introduce variational and variable-coefficient-based extensions of traditional PINNs, offering enhanced modelling capabilities for heterogeneous materials or assemblies with spatially varying stiffness, features frequently encountered in retrofitted or mixed-material bridges.
Recent advances in handling high-dimensionality and multi-physics coupling [48,49] also align well with the challenges posed by full-scale bridge modelling, particularly when assessing the behaviour of structures under combined thermal–mechanical loading or during transient dynamic events like train braking.
Other contributions, including the use of convolutional layers, generative adversarial networks (GANs), and surrogate model integration [50,51,52], may also offer benefits for real-time monitoring tasks, where PINNs can be trained to infer structural states from indirect measurements, reducing reliance on dense sensor networks. These architectures enable robust data-driven approximation of system behaviour under limited or noisy input, a condition commonly observed in railway bridge monitoring under operational loads.
However, despite their conceptual promise, many of the reviewed approaches remain under-explored in structural applications involving boundary discontinuities, geometric irregularities, or long-term degradation phenomena. As such, adapting them to the idiosyncrasies of railway infrastructure will require further tailoring, especially in terms of training stability and physical interpretability.
Therefore, this cluster establishes the epistemological foundation for applying PINNs to structural analysis. By critically assembling key techniques, including NTK analysis, variational PINNs, auxiliary-based boundary enforcement, and deep generative surrogates, it provides a solid base for the systematic integration of AI-driven solvers into railway bridge diagnostics and simulation.
4.4. Cluster 4: Domain Decomposition, Parametric Analysis, and Innovations in Hybrid Modelling
The studies within this cluster explore advanced techniques that aim to resolve the intrinsic complexity of solving differential equations (partial, fractional, and integro-differential) by bridging artificial intelligence and physics-based modelling. These innovations bear considerable potential for the structural analysis of railway bridges, especially in scenarios involving discontinuities, geometric singularities, or parametric variability.
The cv-PINN framework, which integrates domain decomposition with variational learning, enables localised training and accurate boundary condition handling [21]. For railway bridges with heterogeneous structural components, such as composite spans or retrofitted gussets, this localised learning approach allows independent subdomain optimisation, facilitating parallel computation and improved scalability.
Similarly, A-PINN and PGD-PINN architectures extend the reach of PINNs to integro-differential and parametric PDEs [53,54]. These capabilities are particularly relevant when modelling time-dependent cumulative effects like thermal fatigue, creep, or corrosion propagation in long-span bridges subjected to environmental fluctuations.
Frameworks designed for optimal control under parameter uncertainty, such as those introduced by Demo et al. [25], offer new perspectives for maintenance scheduling and load redistribution strategies in railway infrastructure. In this context, railway bridge models can benefit from parametric sensitivity analysis to inform reinforcement planning or isolation system calibration.
Innovative strategies for handling heterogeneity and high-dimensional variability, such as DaPINN, stochastic projection schemes, and fuzzy logic-based training environments [55,56,57], expand the modelling frontier in cases where deterministic parameter estimation is unreliable. These methods may aid in simulating bridge responses under unknown soil–structure interaction conditions or fluctuating thermal loads.
Moreover, approaches like waveform inversion in viscoelastic media [58] and PIBI-Nets [59] point to powerful tools for interpreting structural health data, especially in layered or non-homogeneous materials often found in old railway bridges. By reconstructing mechanical parameters from limited surface data, these techniques could improve internal damage localisation and assessment of degradation hidden within large metallic or composite assemblies.
Architectural innovations (multi-output configurations with spatio-temporal adaptation [60], NSGA-PINNs for noisy data environments [61], and multi-fidelity approaches [62]) enhance the flexibility and robustness of PINNs in settings characterised by sparse or low-resolution sensor data. These strategies align well with current challenges in bridge monitoring systems, where data irregularity and sensor drift are common.
Lastly, parameter-sharing-based transfer learning [63] may offer efficient adaptation of pre-trained models to new bridge configurations or to post-damage states after seismic events or heavy load incursions. This contributes to developing resilient, reconfigurable digital twins of railway bridges.
Overall, this cluster signals a significant methodological advance. The versatility, modularity, and adaptability of the hybrid and decomposed approaches reviewed here align closely with the demands of railway bridge analysis, particularly where localised degradation, complex support conditions, or parametric uncertainty hinder the effectiveness of conventional numerical methods.
4.5. Cluster 5: Transformations, Hybrid Methods, and New Application Scenarios in PINNs
This fifth cluster presents a wide array of methodologies that challenge conventional paradigms for solving PDEs through physics-informed neural networks. Particularly, this group emphasises enhancing stability and precision when dealing with non-linearities and discontinuities, core challenges in structural models of railway bridges exposed to variable loading, fatigue, or material degradation.
Variable transformation schemes such as VT-PINN have shown to improve approximation accuracy under strong gradients or complex topologies [64]. In railway bridge analysis, these strategies could be adapted to account for stress concentrations near support zones, gusset plate connections, or damaged regions, where abrupt changes in mechanical response are common.
The adoption of hybrid frameworks, merging neural networks with numerical solvers, represents a pivotal step toward ensuring physical consistency while reducing computational burden. For instance, combining neural networks with finite difference or finite volume techniques allows accurate modelling of discontinuities in bolted or riveted joints [65], which are typical in older steel truss bridges.
The incorporation of smoothing phase fields into PINN training processes contributes to stabilising the learning in systems governed by discontinuous material parameters [66]. This could be highly beneficial for simulating interfaces between corrosion-damaged and intact zones in bridge components, where material stiffness may change non-linearly.
The stepwise time-discretised approach proposed in [67] simplifies the modelling of long-term sustainability phenomena. Such time-advancing schemes could be directly translatable to the modelling of creep or cyclic degradation in elastomeric bearings or metallic joints under repeated thermal expansion.
From a fluid–structure interaction perspective, the neural particle method [68] and PINNs adapted to dynamic data [69] support the simulation of transient aerodynamic or hydrodynamic effects on bridges, scenarios relevant to wind-induced vibrations or flood impact loading. These methods offer alternatives to traditional Lagrangian solvers with the added advantage of online adaptability.
Innovative contributions such as the two-stage training for wave localisation [70] and the use of interior point algorithms in thermo-fluidic models [71] reveal new avenues for identifying localised vibrational modes or transient thermal gradients in bridges, enhancing the prediction of fatigue-critical regions.
More broadly, models integrating Hausdorff fractional derivatives [72], polynomial interpolation [73], and liquid time-constant neural dynamics [74] offer methodological flexibility for addressing multi-scale or fractal-like behaviour in materials, potentially relevant in assessing micro-crack propagation or paint layer degradation in steel structures.
Data assimilation strategies across fluid and structural domains [75] and techniques for preserving homotopy [76] further exemplify how real-time updating of digital twin models could be achieved, particularly in environments characterised by non-linearity, uncertainty, and evolving boundary conditions.
Altogether, the cluster reveals an impressive breadth of tools that, while often developed in generalised or fluid-centric contexts, carry high translational potential for the structural analysis of railway bridges. Their integration could lead to more robust, physically grounded, and interpretable models capable of handling the discontinuities, complex interactions, and dynamic loads inherent to railway infrastructure.
4.6. Cluster 6: Control, Error Certification, and Wavelet-Based Methods for PDEs
This sixth cluster contributes fundamentally to the reliability of PINN-based solvers by introducing tools for error quantification and control enforcement, both of which are essential in structural engineering applications involving safety-critical systems such as railway bridges. A key advancement is the establishment of a posteriori error bounds, which allow practitioners to estimate the deviation of PINN approximations from true physical solutions without requiring ground truth data [6]. This is particularly useful in railway bridge diagnostics, where full-field stress or displacement data are rarely available, and where certifiable approximations are required to inform maintenance or retrofitting decisions.
Complementarily, wavelet-enhanced PINNs improve both computational efficiency and error detectability [77]. By incorporating wavelet-based diagnostics into the loss function, these models allow localised tracking of error concentrations, useful, for example, in identifying early stage fatigue damage or stress risers in gusset plates or truss joints.
Moreover, recent studies have extended PINNs to act as controllable systems [5], capable of learning and enforcing physical constraints dynamically. In railway bridge applications, such control-aware architectures could support smart actuation strategies in vibration mitigation systems or real-time adjustment of boundary conditions under variable loads. Ultimately, the combination of robust error quantification and adaptive control elevates the potential of PINNs as not only predictive tools but also as reliable decision-making frameworks in structural health monitoring and design optimisation.
4.7. Cluster 7: Temporal Decomposition, Free Edge Methodologies, and Multi-Network Strategies in PINNs
The seventh cluster introduces sophisticated decomposition strategies to tackle complex PDEs over large domains or extended simulation times. These innovations are highly relevant to railway bridge analysis, particularly in simulating transient dynamic responses (e.g., train passage, wind gusts, or seismic excitation) where causality and time-dependent boundary conditions must be respected.
The adoption of temporally aware PINNs such as CEENs [78], which prioritise early stage temporal learning, can help model propagating stress waves across bridge decks or truss systems more consistently with initial loading conditions. Similarly, characteristic-based splitting of Navier–Stokes equations [1] and heat-flow solvers without prior simulations [3] open the door to hybrid fluid–structure simulations involving airflow over bridge girders or thermal expansion of metal bearings under solar radiation.
The integration of dynamic meshing and pre-trained submodels, exemplified by Trans-Net [79], provides computational scalability, particularly suitable for simulating high-fidelity models of long-span bridges with localised non-linearities. Likewise, multi-domain architectures such as UFV-PINN [80] and subdomain partitioning strategies [81] allow for the modular simulation of bridge components, e.g., modelling piers, decks, and expansion joints independently yet coherently.
Moreover, techniques for solving PDEs over complex 3D geometries [82], the parareal temporal extension scheme [83], and the Multi-Net strategy [84] all support high-resolution modelling while mitigating training time, an essential aspect when developing real-time digital twins of railway infrastructure.
The inclusion of finite difference methods in loss terms [85] also enhances optimisation convergence, making PINNs competitive with traditional FEM-based workflows in stationary problems such as stress analysis under constant dead loads.
In sum, the methods in Cluster 7 underscore how decomposable, parallelisable, and temporally aware PINNs can bring both speed and interpretability to simulations of railway bridges under operational and extreme events. Their compatibility with large-scale, irregular domains and their potential for real-time deployment make them prime candidates for structural diagnostics and decision support in modern railway networks.
4.8. Cluster 8: Innovations in Solid Mechanics, Structural Optimisation, and Design of Complex Physical Behaviours
This eighth cluster offers promising advancements in solid mechanics and structural optimisation, providing a relevant foundation for improving the modelling and analysis of railway bridges. High-order PDE solvers for aerospace structures [2] and parameter estimation techniques for biharmonic elasticity equations [23] showcase the versatility of PINNs in dealing with complex stress fields and elastic behaviour. These capabilities can be directly transferred to gusset plates and joint regions in metallic railway trusses, where high-order stress gradients and boundary complexities are common.
In scenarios involving dynamic loads, such as vibrations induced by repeated train passages, PINN variants with advanced temporal discretisation (e.g., AT-PINN [86] and AT-PINN-HC [87]) prove particularly beneficial. These architectures enhance temporal resolution while preserving boundary conditions exactly [88,89], enabling accurate simulation of time-dependent structural responses, including fatigue cycles and resonance in bridge spans.
Additionally, the application of PINNs in modelling hyperelastic and contact behaviours [90,91] has potential implications for components like elastomeric bearings, expansion joints, and concrete-encased steel members, where non-linearity and contact interactions must be captured precisely. The use of hard constraint enforcement strategies [86] allows for the inclusion of operational and design restrictions directly into the model, a necessary step for railway bridges operating under strict safety codes.
Of particular interest is the integration of PINNs with topology optimisation methods (PINNTO) [33], which opens new avenues for lightweight and performance-driven structural design in railway bridge components, especially in modular bridge decks or prefabricated truss systems. Such methods may enable optimal material distribution in components subjected to multi-axial loading, reducing weight while maintaining structural integrity.
Variational PINN formulations have also demonstrated utility in identifying heterogeneous material properties [21], applicable to ageing infrastructure where degradation patterns are spatially variable. Likewise, mesh-free schemes like Runge–Kutta PINNs [92] offer robust alternatives to finite element discretisations, particularly in regions where complex geometries or discontinuities challenge traditional meshing strategies.
Furthermore, the emergence of neural models tailored to civil materials, such as cement rheology prediction [37], expands the applicability of PINNs to reinforced concrete elements, prevalent in bridge abutments, decks, and foundations, allowing better simulation of creep, shrinkage, and non-linear stiffness behaviour.
In sum, this cluster exemplifies a methodological maturation of PINNs in structural mechanics, providing a valuable toolbox for modelling the full spectrum of mechanical behaviour in railway bridges, from dynamic vibration analysis to advanced material modelling and optimal structural design.
4.9. Cluster 9: Inverse Modelling and Robust Discovery of PDEs from Noisy Data
This final cluster presents significant potential for the structural analysis of railway bridges by addressing one of the most common limitations in field applications: data incompleteness and measurement noise. The integration of lasso regression within PINNs [93] provides a parsimonious yet effective strategy for estimating PDE coefficients, enabling interpretable and data-adaptive models. Such capabilities are highly relevant when attempting to infer mechanical properties or damage evolution from sparse or indirect measurements in real bridge structures, especially where high-fidelity sensor networks are not available.
The adoption of noise-aware learning frameworks [94] further enhances the resilience of PINNs against operational disturbances and measurement inaccuracies, which are typical in railway environments due to vibrations, weather exposure, or limited sensor calibration. These frameworks allow the selective filtering of non-physical data components, strengthening the identification of plausible governing equations that describe real-time structural behaviour under uncertainty.
In practical terms, these methods facilitate inverse modelling of key variables such as stress distribution, damage progression, or boundary compliance from partially observed displacement or strain fields. This is particularly useful in the context of bridge inspection campaigns or in the design of digital twins, where the full field solution is often reconstructed from limited instrumentation.
By transforming incomplete datasets into physically consistent models, this cluster aligns with the future of data-driven structural health monitoring (SHM), offering a robust path for implementing PINNs in railway bridge diagnostics. The ability to extract governing dynamics under uncertainty not only increases model reliability but also enhances decision-making for maintenance prioritisation and long-term asset management.
To provide a more actionable comparison beyond the thematic clusters identified in Table 5, Table 6 summarises prominent PINN architectural variants discussed within the reviewed literature. This table highlights their core concepts, typical strengths, and associated limitations relevant to the challenges encountered in railway bridge analysis.

Table 6.
Summary and comparison of key PINN architectural variants relevant to railway bridge analysis.
Table 6 provides a comparative overview aimed at making the findings of this review more actionable for researchers selecting appropriate methodologies. While foundational MLP-based PINNs offer versatility [19], addressing the specific demands of railway bridge analysis often benefits from specialised architectures. For instance, domain decomposition approaches [21,96] demonstrably improve scalability for large or complex structures, though requiring careful handling of subdomain interfaces. Variational formulations like VPINNs offer potential advantages in stability and error estimation [47,95], whereas hybrid methods seek to combine the robustness of traditional solvers with PINN flexibility [65,97]. For SHM applications involving noisy field data or requiring real-time updates, noise-aware frameworks [94] and transfer/sequential learning approaches [63,98] are particularly relevant. Ultimately, the optimal architectural choice involves considering the specific physical problem, data availability, computational resources, and the trade-offs between factors such as implementation complexity, training stability, scalability, and accuracy required for the target railway bridge application.
5. Final Discussion
As illustrated by the evolution milestones in Table 4, physics-informed neural networks (PINNs) have transitioned from simple trial-based neural approximators into a sophisticated, interdisciplinary framework that merges physics, mathematics, and computational science. This evolution, from early efforts embedding boundary conditions into network architectures [22] to the development of symmetry-enhanced models, hybrid solvers, and adaptive learning mechanisms, has significantly expanded their domain of applicability. Notably, recent advances allow PINNs to address a broad array of real-world engineering problems under conditions where classical numerical methods, such as FEM, FVM, or FDM, often face computational or modelling limitations, especially in highly non-linear, noisy, or data-scarce scenarios.
The temporal analysis of publication trends (Figure 6) evidences a sharp increase in scholarly attention from 2022 onward, peaking in 2023 and 2024. This surge corresponds with the proliferation of multi-physics modelling needs and the maturity of automatic differentiation libraries, catalysing the development of scalable PINN architectures. However, as visualised in Figure 3 and Figure 4, the concentration of research remains heavily focused on general PDE solvers and computational fluid/solid mechanics, with limited exploration in structural applications tailored to railway infrastructure. This knowledge gap becomes more pronounced in the cluster distribution (Figure 7), where thematic clusters directly linked to structural health monitoring (SHM) and bridge analysis are under-represented.
Cluster-based synthesis offers a roadmap for understanding how PINNs can fill this void. Symmetry-based approaches (Cluster 1) have demonstrated enhanced extrapolation capabilities and reduced training complexity by enforcing physical invariants, which is crucial for capturing stress wave propagation and fatigue in high-gradient regions such as gusset plates or longitudinal beams in steel bridges [35,37]. These architectures allow for more robust modelling of non-linear behaviours without requiring excessively dense sampling, thereby reducing the dependence on destructive testing.
In tandem, optimisation-driven methods and hybrid models (Cluster 2) such as EPINNs and PIRBNs have proven effective in resolving complex boundary interactions, for instance, in metallic joints and embedded connections of railway bridges [24,88]. Rather than displacing traditional solvers, PINNs complement them, offering mesh-free alternatives that reduce computational costs and allow higher flexibility in geometry.
Mathematically rigorous formulations (Cluster 3), including operator splitting, variational constraints, and tangent kernel analysis, further improve predictive stability. These tools are instrumental for applications like finite strain plasticity modelling [99], which supports fatigue and life-cycle analysis of bridge components subject to cyclic and dynamic loading.
Mathematically rigorous formulations (Cluster 3), including operator splitting, variational constraints, and tangent kernel analysis, offer pathways to improve predictive stability, especially for complex applications. One such critical application demanding enhanced modelling is finite-strain plasticity, vital for fatigue and life cycle analysis of railway bridge components under cyclic loading; work such as Niu et al. [99] highlights both the feasibility and current challenges of tackling this with PINNs. Building upon such foundations, further enhancing plasticity modelling capabilities could involve several specific strategies aimed at capturing these complex, history-dependent, inelastic behaviours. These include tailoring network architectures (e.g., depth and activation functions) to accurately represent intricate yield surfaces and hardening laws inherent in structural metals, and explicitly incorporating internal state variables (e.g., equivalent plastic strain and back-stress tensors) to correctly handle path-dependency under cyclic or complex loading. Furthermore, leveraging variational formulations like VPINNs [47,95] might offer advantages in robustly enforcing plasticity constraints or handling non-smooth yield criteria. Additionally, advanced training strategies, such as adaptive sampling concentrating on regions undergoing plastic flow or sophisticated loss weighting schemes balancing elastic/plastic residuals, alongside potential hybrid approaches coupling PINNs with established computational plasticity algorithms (e.g., return mapping), represent promising research directions for achieving improved convergence and accuracy necessary for reliable structural integrity assessments.
From a modelling standpoint, spatial–temporal domain decomposition and parametric hybridisation (Cluster 4) have opened pathways for simulating multi-scale and multi-physics processes under operational variability. In railway bridge analysis, such capabilities enable dynamic response modelling under mixed traffic conditions or thermal expansion events [87]. These architectures, often employing PGD representations or fuzzy modelling, ensure global continuity while reducing computational overhead.
Discontinuity management and variable transformation techniques (Cluster 5), such as VT-PINN and smoothing phase fields, further equip PINNs to handle abrupt parameter transitions, typical in steel–concrete interfaces or corrosion zones in bridge elements. The integration of topology optimisation via PINNTO exemplifies how such methods can optimise stiffener configurations or mass distribution in railway bridges, improving both performance and resource efficiency [33].
Clusters 6 and 7 push the boundaries toward real-world readiness. Error certification strategies, e.g., upper error bounds [6], increase trust in predictions, essential for safety-critical infrastructure monitoring. Likewise, parareal PINNs and subdomain training techniques allow real-time simulations and adaptive SHM systems to operate efficiently, even in large-scale infrastructures with changing boundary conditions [79,80]. These advances directly address the need for predictive models capable of evolving with operational states.
Expanding further, applications in solid mechanics and structural optimisation (Cluster 8) demonstrate that PINNs can resolve problems involving hyperelasticity, damped vibrations, and plastic deformation in complex geometries. Coupled with hard boundary enforcement and sequential learning, these models rival classical solvers in accuracy while allowing faster adaptation and integration with data sources [92]. Additionally, RheologyNet [37] illustrates how domain-specific PINNs are being used to evaluate concrete and mortar formulations for railway bridge repair, thereby reducing adhesion failures and extending structural durability.
Addressing the challenges inherent in large-scale simulations is crucial for practical PINN deployment in railway bridge analysis. Several promising avenues for optimising scalability were identified in the reviewed literature. Domain decomposition methods (such as XPINNs, cv-PINN, and UFV-PINN) [7,21,33,80] effectively tackle large computational domains by partitioning them into smaller, coupled subdomains suitable for parallel training. Concurrently, hybrid methods that integrate PINNs with traditional solvers (e.g., FEM/FVM), along with temporal decomposition techniques like Parareal PINNs [68,83], leverage the strengths of different approaches to reduce the overall computational burden. Furthermore, advancements in hardware acceleration via enhanced parallelisation on GPUs/TPUs [9,31,83], combined with optimised network architectures (e.g., through NAS-PINN [32]) and efficient training algorithms, are fundamental for enabling simulations of real-world, geometrically complex railway bridges.
These scalability enhancements, in turn, underpin the potential for integrating PINNs with real-time sensor data for monitoring, a task which presents its own set of challenges and requires specific strategies. PINNs inherently facilitate data assimilation by incorporating an observational data term () into the loss function, constraining the model with live measurements [19]. For effective real-time updates, sequential learning or transfer learning approaches can be employed, where pre-trained models are rapidly fine-tuned as new data batches arrive, mitigating the need for complete retraining [63,98]. Adaptive sampling techniques may also optimise computational focus during updates [100]. Significant challenges remain, however, including the computational latency of frequent model evaluations, the robust handling of potentially noisy, incomplete, or asynchronous sensor streams [93,94], maintaining model stability against drift during continuous updates, and managing high-dimensional parameter spaces. Potential solutions involve developing robust noise-aware learning frameworks [94], implementing adaptive loss weighting schemes [101], leveraging reduced-order modelling for efficiency [102], and potentially utilising edge computing paradigms to process data closer to the source.
Finally, Cluster 9 introduces robust inverse modelling strategies that are vital for scenarios with incomplete or noisy data. Techniques integrating lasso regression or noise-aware learning frameworks [93,94] facilitate the discovery of governing equations from in situ monitoring systems or partial datasets, enabling data-driven diagnostics of structural degradation and failure mechanisms in ageing bridges.
Beyond the qualitative advantages discussed, several studies within our review corpus provide explicit quantitative or comparative assessments highlighting the performance trade-offs between PINNs and traditional numerical methods (TNM) for specific railway bridge-relevant scenarios. For instance, in solving inverse problems for parameter identification or damage detection using sparse data, PINN approaches integrating techniques like lasso regression or noise-aware frameworks reportedly achieve robust results even with limited or noisy inputs where traditional iterative methods might struggle [93,94]. While direct speed comparisons vary, the fast inference times of trained PINNs are frequently cited as advantageous for potential real-time assessment derived from inverse solutions or as surrogate models [103]. In forward simulations, such as dynamic response or vibration analysis, studies indicate PINNs can reach high accuracy levels, sometimes comparable to high-fidelity FEM for specific setups [2,89], particularly demonstrating strength in handling complex geometries or boundary conditions without mesh constraints, as seen in topology optimisation applications [33]. However, this accuracy often comes at the cost of significant training time; the challenge of high computational expense during training is frequently noted, with some PINN implementations requiring substantial resources, especially compared to optimised TNM solvers for simpler linear or stationary problems [28,83]. These quantitative examples underscore that while PINNs offer compelling advantages, particularly for data assimilation, inverse problems, and geometric flexibility, their computational efficiency, especially during the training phase, remains a critical consideration compared to mature TNM solvers for many standard forward simulation tasks in structural mechanics.
Collectively, the findings from these clusters not only respond to the research questions proposed, but also establish that PINNs can improve the structural analysis of railway bridges as follows:
- Enhancing the accuracy and interpretability of stress, vibration, and deformation predictions through physically grounded architectures.
- Offering meshless and adaptive alternatives that integrate seamlessly with real-time sensor data.
- Surpassing traditional methods in handling high-dimensional, non-linear, and poorly constrained systems.
- Reducing computational cost and uncertainty in structural life-cycle simulations.
Nevertheless, challenges persist. PINNs still exhibit sensitivity to hyperparameter tuning, require long training times for large domains, and lack standardised protocols for validation in structural applications. These limitations highlight the importance of interdisciplinary efforts and benchmarking frameworks.
Furthermore, whilst this review focused specifically on the advancements within PINN methodologies, it is important to acknowledge the significant role of established probabilistic approaches in structural analysis and health monitoring. Techniques such as Bayesian networks (BNs) offer robust frameworks for reliability assessment by integrating probabilistic models with monitoring data for dynamic updates [104]. Similarly, Gaussian processes (GPs) and hierarchical Bayesian models have demonstrated high accuracy in modelling, uncertainty quantification, and forecasting for complex SHM datasets, particularly under challenging conditions like extreme weather events [105,106]. A promising direction for future research lies in exploring the synergy between PINNs and these probabilistic methods. For instance, integrating PINNs with BNs could enhance reliability assessments, whilst hybrid PINN-GP models might offer improved uncertainty quantification capabilities alongside physics-informed predictions. Comparative studies evaluating the strengths and weaknesses of PINNs versus these established probabilistic techniques for specific railway bridge monitoring tasks would also be highly valuable.
Addressing the critical gap in experimental validation could involve several strategies. Firstly, developing benchmark problems based on simplified laboratory-scale physical models of bridge components or connections would allow for controlled validation of PINN predictions against measured data. Secondly, leveraging sparse sensor data already available from existing railway bridge monitoring systems, combined with inverse PINN formulations [1,19,93,94], can provide partial validation and model calibration even without full-field measurements. Thirdly, adopting multi-fidelity approaches [62], where high-fidelity simulations or targeted experiments validate specific aspects of lower-fidelity PINN models used for broader analysis, could offer a pragmatic path forward. Fostering collaboration between computational researchers and experimentalists is paramount to designing meaningful validation campaigns.
In tandem with the historical progression underlined in Table 4, a pronounced interdisciplinary synergy has emerged. Mathematics underpins the formulation and convergence of PINNs, physics informs the governing equations and boundary constraints, and computational sciences contribute the requisite automatic differentiation and large-scale training capabilities. As the field moves forward, it is anticipated that PINNs will further incorporate uncertainty quantification, high-performance computing strategies, and sophisticated model-order reduction techniques. This convergence is poised to unlock real-time predictive solutions, particularly in mission-critical domains where data and physical laws coexist in complex feedback loops, such as live monitoring of structural health or predictive maintenance in large-scale infrastructure systems.
In summary, PINNs represent an alternative for structural analysis in railway engineering. By uniting domain knowledge, mathematical rigour, and algorithmic flexibility, they offer a scalable and interpretable approach that not only complements but, in key areas, outperforms traditional numerical techniques. Unlocking their full potential will depend on future collaborations across disciplines, bridging theory with application in the evolving landscape of structural engineering.
5.1. Limitations and Remaining Challenges
Despite the significant advancements presented, several limitations concerning both the current state of PINN technology for railway bridge applications and the scope of this systematic review should be acknowledged to contextualise the findings and guide future efforts.
Regarding PINN methodologies themselves, critical challenges persist that hinder widespread adoption in this safety-critical domain. These include the following:
- Scalability and computational cost: While techniques like domain decomposition and GPU acceleration show promise, simulating large-scale, geometrically complex 3D bridge models under realistic dynamic loads often remains computationally prohibitive or requires extensive tuning.
- Modelling complex physics: Accurately capturing history-dependent inelastic behaviours like plasticity and fatigue, crucial for long-term bridge assessment, remains a significant hurdle for many current PINN formulations.
- Experimental validation: A major gap identified throughout this review is the lack of rigorous experimental validation against field data from actual railway bridges, which is essential for building confidence and understanding model performance under real-world conditions and uncertainties.
- Data scarcity and quality: While PINNs can leverage sparse data, their performance in inverse problems or data assimilation is still sensitive to the quantity, quality (noise levels), and distribution of available sensor measurements.
- Training stability and hyperparameters: PINN training can be sensitive to network architecture choices, initialisation, loss weight balancing, and optimiser selection, often requiring considerable expertise and computational resources for effective tuning.
- Theoretical guarantees: Formal error bounds and robust uncertainty quantification frameworks tailored specifically for complex structural mechanics problems solved via PINNs are still under development.
Furthermore, this systematic review has its own limitations. The search was confined to the Scopus and Web of Science databases, potentially excluding relevant contributions from grey literature, pre-print servers, or regional databases. The specific search terms used might not have captured all pertinent studies due to variations in terminology. Additionally, formal assessments of publication bias or the certainty of the evidence body using standardised tools (like GRADE) were not performed as part of the review’s scope. These limitations collectively underscore the need for continued, focused research and development to mature PINN technology for reliable, practical deployment in railway engineering.
5.2. Experimental Validation: Current Status and Challenges
A recurring and critical theme identified throughout this systematic review is the significant gap concerning the experimental validation of PINNs for real-world railway bridge monitoring and analysis. While PINNs demonstrate considerable theoretical promise and success in benchmark or simulated scenarios, their credibility and path towards practical adoption heavily depend on rigorous validation against physical experiments, whether in controlled laboratory settings or challenging field conditions.
Our review found that studies incorporating substantial experimental validation remain scarce within the specific context of railway bridges. The few investigations attempting validation often rely on simplified structural components, idealised loading conditions, or laboratory-scale models [3,107]. While valuable as initial steps, these studies typically do not capture the full complexity of large-scale bridge behaviour, environmental variability (e.g., temperature effects and humidity), operational noise, and the intricacies of real sensor data (e.g., sparsity, noise, drift, and asynchronous measurements). Key challenges hindering more extensive validation include the high cost associated with instrumenting and testing full-scale bridges or representative components under realistic dynamic loads, the difficulty in obtaining ground truth data for internal states (like stress fields or damage progression), and the lack of standardised benchmark datasets and protocols for comparing PINN performance in structural applications [108,109].
Bridging this critical theory–practice gap requires concerted effort. As previously discussed (Section 5), strategies such as developing standardised laboratory benchmarks, leveraging sparse field data through advanced inverse problem formulations [19,93,94], adopting multi-fidelity approaches combining simulation and targeted experiments [62], and fostering close collaboration between computational modelling experts and experimental structural engineers are essential pathways forward. Without robust experimental validation demonstrating reliable performance under realistic conditions, the transition of PINNs from academic tools to trusted engineering solutions for railway bridge management will remain significantly constrained.
6. Conclusions
This study demonstrates that PINNs have evolved from basic neural approximators into robust frameworks capable of solving large-scale, non-linear problems in computational mechanics. Their integration into the structural analysis and maintenance of railway bridges offers advanced capabilities in predictive modelling, structural health monitoring, and optimisation. However, challenges remain regarding experimental validation, scalability, and real-world implementation.
This systematic review synthesised the current state of knowledge regarding physics-informed neural networks (PINNs) for railway bridge analysis by employing a structured methodology detailed in Section 2. Following the PRISMA 2020 guidelines [18], relevant literature published between 2015 and 2025 was retrieved from Scopus and Web of Science databases using a defined search strategy and subjected to rigorous filtering based on relevance and quality criteria (Q1/Q2). The final corpus of 120 articles was analysed using a hybrid approach combining natural language processing (NLP) for thematic clustering, quantitative bibliometric analysis, expert validation, and qualitative synthesis to identify key trends, capabilities, challenges, and future research directions discussed herein.
As highlighted in Table 7, PINNs provide reliable modelling of dynamic loads and fatigue phenomena, as well as detailed non-linear assessments of welded joints and composite structures. Their incorporation into structured methodological frameworks (Section 2) suggests that PINNs are not merely supplementary tools but have the potential to transform infrastructure analysis and maintenance workflows.

Table 7.
Key conclusions on the application of PINNs in structural problems of railway bridges, relevant references, and potential benefits.
Advancements in error estimation, domain decomposition, and optimisation strategies (Table 4 and Section 5) further strengthen their interpretability, robustness, and applicability. These developments position PINNs as a promising alternative to traditional solvers, enhancing accuracy, computational efficiency, and real-time monitoring capabilities in railway bridge engineering.
PINNs have evolved from basic neural approximators into robust, physics-integrated frameworks capable of handling complex PDEs in railway bridge mechanics. Their multi-physics capabilities allow the accurate modelling of structural behaviours under cyclic loading and dynamic forces, surpassing and complementing traditional numerical methods. Additionally, their integration with in situ sensor data and machine learning enables real-time structural health monitoring (SHM), enhancing early fault detection and predictive maintenance strategies in railway bridges. Moreover, exploring synergies between PINNs and established probabilistic methods like Bayesian networks and Gaussian processes presents a key opportunity for future advancements in robust structural assessment and monitoring under uncertainty.
Despite these advancements, experimental validation and large-scale implementation remain limited, particularly in pre-stressed connections, fatigue analysis, and composite material modelling. The scarcity of publicly available structural datasets hampers model generalisation, reinforcing the need for collaboration between academia, industry, and regulatory agencies. The integration of PINNs with FEM, FVM, and FDM has improved numerical stability in railway bridges with complex geometries, while advances in exact dirichlet boundary PINNs (EPINNs) enhance boundary treatment precision, particularly in metallic joint assessments.
In infrastructure design, PINN-based topology optimisation (PINNTO) presents a promising approach to improving weight-to-strength ratios in bridge reinforcement, ensuring structural efficiency. The development of error estimation techniques and control enforcement mechanisms is a crucial step toward industrial adoption, ensuring reliability in safety-critical applications such as fatigue prediction and dynamic response evaluation. Additionally, advances in domain decomposition and multi-scale modelling suggest that PINNs can optimise large-scale railway bridge simulations while maintaining computational efficiency. Their capability to infer governing equations from sparse or noisy data further enhances their adaptability to real-world applications.
From a methodological perspective, PINNs’ mesh-free adaptability and ability to enforce physics-based constraints make them invaluable for structural assessment. Their automatic differentiation framework effectively handles boundary and initial conditions, overcoming limitations of traditional grid-based techniques. By mapping high-frequency stress variations and structural deformations, PINNs reduce reliance on destructive testing, advancing predictive maintenance in railway bridge diagnostics.
Looking ahead, unlocking the full potential of PINNs for reliable deployment in railway infrastructure hinges on addressing several critical research frontiers. Firstly, significant advancements in computational performance are necessary for real-time, large-scale applications, primarily through enhanced parallelisation strategies and effective GPU/TPU acceleration of both training and inference. Secondly, the development and adoption of rigorous error-bounding frameworks and uncertainty quantification techniques tailored for PINN-based structural analysis are essential to bolster confidence and enable certification for use in safety-critical systems. Finally, and perhaps most crucially, bridging the gap between theoretical promise and widespread industrial implementation requires a concerted effort towards increased experimental validation using standardised benchmarks and field data, fostered by strong cross-disciplinary collaboration between computational scientists, structural engineers, and infrastructure owners.
Taken together, these findings confirm that PINNs are a transformative tool for railway bridge analysis, redefining accuracy, sustainability, and safety in future infrastructure design and assessment. The methodological framework outlined in Section 2 not only clarifies their potential but also serves as a systematic template for ongoing research in computational mechanics, data assimilation, and digital-twin frameworks in engineering.
Funding
This research was supported by the VINCI-DI initiative at Pontificia Universidad Católica de Valparaíso (PUCV), under project number 039.706/2025.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors express their gratitude to the institutions and funding bodies that supported this research. Special thanks to the Pontificia Universidad Católica de Valparaíso (PUCV) for its continuous academic support, particularly through the Doctorate in Intelligent Industry program.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AT-PINN | Advanced Time-Marching Physics-Informed Neural Network |
| DaPINN | Dimension-Augmented Physics-Informed Neural Network |
| DOAJ | Directory of Open Access Journals |
| EPINN | Exact Dirichlet Boundary Physics-Informed Neural Network |
| GPU | Graphics Processing Unit |
| L-BFGS | Limited-memory Broyden–Fletcher–Goldfarb–Shanno Optimiser |
| LD | Linear Dichroism |
| NH-PINN | Neural Homogenisation-Based Physics-Informed Neural Network |
| PDE | Partial Differential Equation |
| PDEs | Partial Differential Equations |
| PINN | Physics-Informed Neural Network |
| PINNs | Physics-Informed Neural Networks |
| Q1 | Quartile 1 (top-ranked journal classification) |
| TLA | Three Letter Acronym |
| WoS | Web of Science |
References
- Hu, S.; Liu, M.; Zhang, S.; Dong, S.; Zheng, R. Physics-informed neural network combined with characteristic-based split for solving Navier–Stokes equations. Eng. Appl. Artif. Intell. 2024, 128, 107453. [Google Scholar] [CrossRef]
- Singh, V.; Harursampath, D.; Dhawan, S.; Sahni, M.; Saxena, S.; Mallick, R. Physics-Informed Neural Network for Solving a One-Dimensional Solid Mechanics Problem. Modelling 2024, 5, 1532–1549. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, X.; Chen, X.; Xu, C.; Liu, J. PINN-FFHT: A physics-informed neural network for solving fluid flow and heat transfer problems without simulation data. Int. J. Mod. Phys. C 2022, 33, 2250166. [Google Scholar] [CrossRef]
- Miao, Z.; Chen, Y. VC-PINN: Variable coefficient physics-informed neural network for forward and inverse problems of PDEs with variable coefficient. Phys. D Nonlinear Phenom. 2023, 456, 133945. [Google Scholar] [CrossRef]
- García-Cervera, C.J.; Kessler, M.; Periago, F. Control of Partial Differential Equations via Physics-Informed Neural Networks. J. Optim. Theory Appl. 2023, 196, 391–414. [Google Scholar] [CrossRef]
- Hillebrecht, B.; Unger, B. Rigorous a Posteriori Error Bounds for PDE-Defined PINNs. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 1583–1593. [Google Scholar] [CrossRef]
- Dieva, N.; Aminev, D.; Kravchenko, M.; Smirnov, N. Overview of the Application of Physically Informed Neural Networks to the Problems of Nonlinear Fluid Flow in Porous Media. Computation 2024, 12, 69. [Google Scholar] [CrossRef]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding Physics-Informed Neural Networks: Techniques, Applications, Trends, and Challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- Cai, K.; Wang, J. Physics-informed neural networks for solving incompressible Navier–Stokes equations in wind engineering. Phys. Fluids 2024, 36, 121303. [Google Scholar] [CrossRef]
- Yang, F.; Yang, L.; Zhu, Y. A physics-informed deep learning framework for spacecraft pursuit-evasion task assessment. Chin. J. Aeronaut. 2024, 37, 363–376. [Google Scholar] [CrossRef]
- Lino, M.; Fotiadis, S.; Bharath, A.A.; Cantwell, C.D. Current and emerging deep-learning methods for the simulation of fluid dynamics. Proc. R. Soc. A 2023, 479, 20230058. [Google Scholar] [CrossRef]
- Lawal, Z.K.; Yassin, H.; Lai, D.T.C.; Idris, A.C. Physics-Informed Neural Network (PINN) Evolution and Beyond: A Systematic Literature Review and Bibliometric Analysis. Big Data Cogn. Comput. 2022, 6, 140. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of Optimization Algorithms in Modern Neural Networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Chen, X.X.; Zhang, P.; Yin, Z.Y. Physics-Informed neural network solver for numerical analysis in geoengineering. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 18, 33–51. [Google Scholar] [CrossRef]
- Khalid, S.; Yazdani, M.H.; Azad, M.M.; Elahi, M.U.; Raouf, I.; Kim, H.S. Advancements in Physics-Informed Neural Networks for Laminated Composites: A Comprehensive Review. Mathematics 2025, 13, 17. [Google Scholar] [CrossRef]
- Hou, X.; Zhou, X.; Liu, Y. Reconstruction of ship propeller wake field based on self-adaptive loss balanced physics-informed neural networks. Ocean. Eng. 2024, 309, 118341. [Google Scholar] [CrossRef]
- Hu, H.; Qi, L.; Chao, X. Physics-informed Neural Networks (PINN) for computational solid mechanics: Numerical frameworks and applications. Thin-Walled Struct. 2024, 205, 112495. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Chandrasukmana, Y.; Margaretha, H.; Van Ivanky Saputra, K. The Hadamard-PINN for PDE inverse problems: Convergence with distant initial guesses. Examples Counterexamples 2025, 7, 100175. [Google Scholar] [CrossRef]
- Liu, C.; Wu, H. cv-PINN: Efficient learning of variational physics-informed neural network with domain decomposition. Extrem. Mech. Lett. 2023, 63, 102051. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef]
- Vahab, M.; Haghighat, E.; Khaleghi, M.; Khalili, N. A Physics-Informed Neural Network Approach to Solution and Identification of Biharmonic Equations of Elasticity. J. Eng. Mech. 2022, 148, 04021154. [Google Scholar] [CrossRef]
- Bai, J.; Jeong, H.; Batuwatta-Gamage, C.P.; Xiao, S.; Wang, Q.; Rathnayaka, C.M.; Alzubaidi, L.; Liu, G.R.; Gu, Y. An Introduction to Programming Physics-Informed Neural Network-Based Computational Solid Mechanics. Int. J. Comput. Methods 2023, 20, 2350013. [Google Scholar] [CrossRef]
- Demo, N.; Strazzullo, M.; Rozza, G. An extended physics informed neural network for preliminary analysis of parametric optimal control problems. Comput. Math. Appl. 2023, 143, 383–396. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Xu, X.; Liu, C. Physics-guided deep learning for damage detection in CFRP composite structures. Compos. Struct. 2024, 331, 117889. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Luo, K.; Liao, S.; Guan, Z.; Liu, B. An enhanced hybrid adaptive physics-informed neural network for forward and inverse PDE problems. Appl. Intell. 2025, 55, 255. [Google Scholar] [CrossRef]
- Hu, Z.; Jagtap, A.D.; Karniadakis, G.E.; Kawaguchi, K. Augmented Physics-Informed Neural Networks (APINNs): A gating network-based soft domain decomposition methodology. Eng. Appl. Artif. Intell. 2023, 126, 107183. [Google Scholar] [CrossRef]
- Chiu, P.H.; Wong, J.C.; Ooi, C.; Dao, M.H.; Ong, Y.S. CAN-PINN: A fast physics-informed neural network based on coupled-automatic–numerical differentiation method. Comput. Methods Appl. Mech. Eng. 2022, 395, 114909. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, L. NAS-PINN: Neural architecture search-guided physics-informed neural network for solving PDEs. J. Comput. Phys. 2024, 496, 112603. [Google Scholar] [CrossRef]
- Jeong, H.; Bai, J.; Batuwatta-Gamage, C.P.; Rathnayaka, C.; Zhou, Y.; Gu, Y. A Physics-Informed Neural Network-based Topology Optimization (PINNTO) framework for structural optimization. Eng. Struct. 2023, 278, 115484. [Google Scholar] [CrossRef]
- Blechschmidt, J.; Ernst, O.G. Three ways to solve partial differential equations with neural networks—A review. GAMM Mitteilungen 2021, 44, e202100006. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhang, H.; Liu, Y.; Li, J.Y.; Liu, C.B. Generalized conditional symmetry enhanced physics-informed neural network and application to the forward and inverse problems of nonlinear diffusion equations. Chaos Solitons Fractals 2023, 168, 113169. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhang, H.; Liu, Y.; Guo, L.L.; Zhang, L.S.; Zhang, Z.Y. Utilizing symmetry-enhanced physics-informed neural network to obtain the solution beyond sampling domain for partial differential equations. Nonlinear Dyn. 2023, 111, 21861–21876. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, S.J.; Li, J.Y.; Liu, Y.; Zhang, Z.Y. Enforcing generalized conditional symmetry in physics-informed neural network for solving the KdV-like equation with Robin initial/boundary conditions. Nonlinear Dyn. 2023, 111, 10381–10392. [Google Scholar] [CrossRef]
- Meng, Z.; Qian, Q.; Xu, M.; Yu, B.; Yıldız, A.R.; Mirjalili, S. PINN-FORM: A new physics-informed neural network for reliability analysis with partial differential equation. Comput. Methods Appl. Mech. Eng. 2023, 414, 116172. [Google Scholar] [CrossRef]
- Leung, W.T.; Lin, G.; Zhang, Z. NH-PINN: Neural homogenization-based physics-informed neural network for multiscale problems. J. Comput. Phys. 2022, 470, 111539. [Google Scholar] [CrossRef]
- Bolandi, H.; Sreekumar, G.; Li, X.; Lajnef, N.; Boddeti, V.N. Physics informed neural network for dynamic stress prediction. Appl. Intell. 2023, 53, 26313–26328. [Google Scholar] [CrossRef]
- Pratama, D.A.; Abo-Alsabeh, R.R.; Bakar, M.A.; Salhi, A.; Ibrahim, N.F. Solving partial differential equations with hybridized physic-informed neural network and optimization approach: Incorporating genetic algorithms and L-BFGS for improved accuracy. Alex. Eng. J. 2023, 77, 205–226. [Google Scholar] [CrossRef]
- Ji, R.; Shi, S.; Han, Y.; Liu, D. An Adaptive Physics-Informed Neural Network with Two-Stage Learning Strategy to Solve Partial Differential Equations. Numer. Math. 2022, 16, 298–322. [Google Scholar] [CrossRef]
- Irsalinda, N.; Bakar, M.A.; Harun, F.N.; Surono, S.; Pratama, D.A. A new hybrid approach for solving partial differential equations: Combining Physics-Informed Neural Networks with Cat-and-Mouse based Optimization. Results Appl. Math. 2025, 25, 100539. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving partial differential equations using deep learning and physical constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Manavi, S.; Fattahi, E.; Becker, T. A trial solution for imposing boundary conditions of partial differential equations in physics-informed neural networks. Eng. Appl. Artif. Intell. 2024, 127, 107236. [Google Scholar] [CrossRef]
- Vu-Quoc, L.; Humer, A. Partial-differential-algebraic equations of nonlinear dynamics by physics-informed neural-network: (I) Operator splitting and framework assessment. Int. J. Numer. Methods Eng. 2024, 125, e7586. [Google Scholar] [CrossRef]
- Eshaghi, M.S.; Anitescu, C.; Thombre, M.; Wang, Y.; Zhuang, X.; Rabczuk, T. Variational Physics-informed Neural Operator (VINO) for solving partial differential equations. Comput. Methods Appl. Mech. Eng. 2025, 437, 117785. [Google Scholar] [CrossRef]
- Cheung, K.C.; See, S. Recent advance in machine learning for partial differential equation. CCF Trans. High Perform. Comput. 2021, 3, 298–310. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, Z. Is the neural tangent kernel of PINNs deep learning general partial differential equations always convergent? Phys. D Nonlinear Phenom. 2024, 457, 133987. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, Y.Y.; Liu, W.; Dai, C.Q. Data-driven prediction of soliton solutions of the higher-order NLSE via the strongly-constrained PINN method. Comput. Math. Appl. 2022, 127, 144–153. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.; Guan, H.; Wang, J.; Yang, J.; Zhang, C.; Tao, D. Generative adversarial physics-informed neural networks for solving forward and inverse problem with small labeled samples. Comput. Math. Appl. 2025, 183, 98–120. [Google Scholar] [CrossRef]
- Zhi, P.; Wu, Y.; Qi, C.; Zhu, T.; Wu, X.; Wu, H. Surrogate-Based Physics-Informed Neural Networks for Elliptic Partial Differential Equations. Mathematics 2023, 11, 2723. [Google Scholar] [CrossRef]
- Yuan, L.; Ni, Y.Q.; Deng, X.Y.; Hao, S. A-PINN: Auxiliary physics informed neural networks for forward and inverse problems of nonlinear integro-differential equations. J. Comput. Phys. 2022, 462, 111260. [Google Scholar] [CrossRef]
- Ghnatios, C.; Chinesta, F. A Parsimonious Separated Representation Empowering PINN–PGD-Based Solutions for Parametrized Partial Differential Equations. Mathematics 2024, 12, 2365. [Google Scholar] [CrossRef]
- Guan, W.; Yang, K.; Chen, Y.; Liao, S.; Guan, Z. A dimension-augmented physics-informed neural network (DaPINN) with high level accuracy and efficiency. J. Comput. Phys. 2023, 491, 112360. [Google Scholar] [CrossRef]
- N., N.; Chakraborty, S. Stochastic projection based approach for gradient free physics informed learning. Comput. Methods Appl. Mech. Eng. 2023, 406, 115842. [Google Scholar] [CrossRef]
- Wu, W.; Duan, S.; Sun, Y.; Yu, Y.; Liu, D.; Peng, D. Deep fuzzy physics-informed neural networks for forward and inverse PDE problems. Neural Netw. 2025, 181, 106750. [Google Scholar] [CrossRef]
- Pakravan, A. One-Dimensional Elastic and Viscoelastic Full-Waveform Inversion in Heterogeneous Media Using Physics-Informed Neural Networks. IEEE Access 2024, 12, 69922–69940. [Google Scholar] [CrossRef]
- Nagy-Huber, M.; Roth, V. Physics-informed boundary integral networks (PIBI-Nets): A data-driven approach for solving partial differential equations. J. Comput. Sci. 2024, 81, 102355. [Google Scholar] [CrossRef]
- Hao, T.T.; Yan, W.J.; Chen, J.B.; Sun, T.T.; Yuen, K.V. Multi-output multi-physics-informed neural network for learning dimension-reduced probability density evolution equation with unknown spatio-temporal-dependent coefficients. Mech. Syst. Signal Process. 2024, 220, 111683. [Google Scholar] [CrossRef]
- Lu, B.; Moya, C.; Lin, G. NSGA-PINN: A Multi-Objective Optimization Method for Physics-Informed Neural Network Training. Algorithms 2023, 16, 194. [Google Scholar] [CrossRef]
- Regazzoni, F.; Pagani, S.; Cosenza, A.; Lombardi, A.; Quarteroni, A. A physics-informed multi-fidelity approach for the estimation of differential equations parameters in low-data or large-noise regimes. Atti Della Accad. Naz. Dei Lincei, Cl. Sci. Fis. Mat. Nat. Rend. Lincei Mat. Appl. 2021, 32, 437–470. [Google Scholar] [CrossRef]
- Manikkan, S.; Srinivasan, B. Transfer physics informed neural network: A new framework for distributed physics informed neural networks via parameter sharing. Eng. Comput. 2023, 39, 2961–2988. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, Y. VT-PINN:Variable transformation improves physics-informed neural networks for approximating partial differential equations. Appl. Soft Comput. 2024, 167, 112370. [Google Scholar] [CrossRef]
- Lv, C.; Wang, L.; Xie, C. A hybrid physics-informed neural network for nonlinear partial differential equation. Int. J. Mod. Phys. C 2023, 34, 2350082. [Google Scholar] [CrossRef]
- He, R.; Chen, Y.; Yang, Z.; Huang, J.; Guan, X. Phase field smoothing-PINN: A neural network solver for partial differential equations with discontinuous coefficients. Comput. Math. Appl. 2024, 171, 188–203. [Google Scholar] [CrossRef]
- Valentino, C.; Pagano, G.; Conte, D.; Paternoster, B.; Colace, F.; Casillo, M. Step-by-step time discrete Physics-Informed Neural Networks with application to a sustainability PDE model. Math. Comput. Simul. 2025, 230, 541–558. [Google Scholar] [CrossRef]
- Wessels, H.; Weißenfels, C.; Wriggers, P. The neural particle method—An updated Lagrangian physics informed neural network for computational fluid dynamics. Comput. Methods Appl. Mech. Eng. 2020, 368, 113127. [Google Scholar] [CrossRef]
- Tarkhov, D.; Lazovskaya, T.; Antonov, V. Adapting PINN Models of Physical Entities to Dynamical Data. Computation 2023, 11, 168. [Google Scholar] [CrossRef]
- Lin, S.; Chen, Y. A two-stage physics-informed neural network method based on conserved quantities and applications in localized wave solutions. J. Comput. Phys. 2022, 457, 111053. [Google Scholar] [CrossRef]
- Chandra, P.; Das, R. Design of a unified physics-informed neural network using interior point algorithm to study the bioconvection nanofluid flow via stretching surface. Eng. Appl. Artif. Intell. 2024, 133, 108647. [Google Scholar] [CrossRef]
- Wu, G.; Wang, F.; Qiu, L. Physics-Informed Neural Network for solving Hausdorff derivative Poisson equations. Fractals 2023, 31, 2340103. [Google Scholar] [CrossRef]
- Tang, S.; Feng, X.; Wu, W.; Xu, H. Physics-informed neural networks combined with polynomial interpolation to solve nonlinear partial differential equations. Comput. Math. Appl. 2023, 132, 48–62. [Google Scholar] [CrossRef]
- Sun, R.; Jeong, H.; Zhao, J.; Gou, Y.; Sauret, E.; Li, Z.; Gu, Y. A physics-informed neural network framework for multi-physics coupling microfluidic problems. Comput. Fluids 2024, 284, 106421. [Google Scholar] [CrossRef]
- Bai, X.D.; Wang, Y.; Zhang, W. Applying physics informed neural network for flow data assimilation. J. Hydrodyn. 2020, 32, 1050–1058. [Google Scholar] [CrossRef]
- Thabet, H.; Kendre, S.; Peters, J. Numerical solutions for space–time conformable nonlinear partial differential equations via a scientific machine learning technique. Neurocomputing 2025, 620, 129134. [Google Scholar] [CrossRef]
- Ernst, L.; Urban, K. A certified wavelet-based physics-informed neural network for the solution of parameterized partial differential equations. IMA J. Numer. Anal. 2025, 45, 494–515. [Google Scholar] [CrossRef]
- Jung, J.; Kim, H.; Shin, H.; Choi, M. CEENs: Causality-enforced evolutional networks for solving time-dependent partial differential equations. Comput. Methods Appl. Mech. Eng. 2024, 427, 117036. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, C. Discovering physics-informed neural networks model for solving partial differential equations through evolutionary computation. Swarm Evol. Comput. 2024, 88, 101589. [Google Scholar] [CrossRef]
- Mei, D.; Zhou, K.; Liu, C.H. Unified finite-volume physics informed neural networks to solve the heterogeneous partial differential equations. Knowl. Based Syst. 2024, 295, 111831. [Google Scholar] [CrossRef]
- Khademi, A.; Dufour, S. A novel discretized physics-informed neural network model applied to the Navier-Stokes equations. Phys. Scr. 2024, 99, 076016. [Google Scholar] [CrossRef]
- Fang, Z.; Zhan, J. A Physics-Informed Neural Network Framework for PDEs on 3D Surfaces: Time Independent Problems. IEEE Access 2020, 8, 26328–26335. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Zhou, L.; Sun, J.; Sun, G. Multi-Net strategy: Accelerating physics-informed neural networks for solving partial differential equations. Softw. Pract. Exp. 2022, 52, 2513–2536. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, L.M.; Shu, C.; Dong, H.; Du, Y.J.; Song, Y.X. Least-square finite difference-based physics-informed neural network for steady incompressible flows. Comput. Math. Appl. 2024, 175, 33–48. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Zhang, W.; Yang, J. A Hard-Constraint Wide-Body Physics-Informed Neural Network Model for Solving Multiple Cases in Forward Problems for Partial Differential Equations. Appl. Sci. 2024, 14, 189. [Google Scholar] [CrossRef]
- Chen, Z.; Lai, S.K.; Yang, Z.; Ni, Y.Q.; Yang, Z.; Cheung, K.C. AT-PINN-HC: A refined time-sequential method incorporating hard-constraint strategies for predicting structural behavior under dynamic loads. Comput. Methods Appl. Mech. Eng. 2025, 436, 117691. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Jiang, X. Physics-informed neural network algorithm for solving forward and inverse problems of variable-order space-fractional advection-diffusion equations. Neurocomputing 2023, 535, 64–82. [Google Scholar] [CrossRef]
- Söyleyici, C.; Ünver, H.O. A Physics-Informed Deep Neural Network based beam vibration framework for simulation and parameter identification. Eng. Appl. Artif. Intell. 2025, 141, 109804. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Enhanced physics-informed neural networks for hyperelasticity. Int. J. Numer. Methods Eng. 2023, 124, 1585–1601. [Google Scholar] [CrossRef]
- Muradova, A.D.; Stavroulakis, G.E. Physics-Informed Neural Networks for elastic plate problems with bending and winkler-type contact effects. J. Serbian Soc. Comput. Mech. 2021, 15, 46–55. [Google Scholar] [CrossRef]
- Xiao, S.; Bai, J.; Jeong, H.; Alzubaidi, L.; Gu, Y. A meshless Runge-Kutta-based Physics-Informed Neural Network framework for structural vibration analysis. Eng. Anal. Bound. Elem. 2025, 170, 106054. [Google Scholar] [CrossRef]
- Ma, M.; Fu, L.; Guo, X.; Zhai, Z. Incorporating Lasso Regression to Physics-Informed Neural Network for Inverse PDE Problem. CMES Comput. Model. Eng. Sci. 2024, 141, 385–399. [Google Scholar] [CrossRef]
- Thanasutives, P.; Morita, T.; Numao, M.; Fukui, K.I. Noise-aware physics-informed machine learning for robust PDE discovery. Mach. Learn. Sci. Technol. 2023, 4, 015009. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E.M. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Hu, Z.; Jagtap, A.D.; Karniadakis, G.E.; Kawaguchi, K. When do extended Physics-Informed Neural Networks (XPINNS) improve generalization? SIAM J. Sci. Comput. 2022, 44, A3158–A3182. [Google Scholar] [CrossRef]
- Mitusch, S.K.; Funke, S.W.; Kuchta, M. Hybrid FEM-NN models: Combining artificial neural networks with the finite element method. J. Comput. Phys. 2021, 446, 110651. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Chakraborty, S.; Rabczuk, T. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theor. Appl. Fract. Mech. 2020, 106, 102447. [Google Scholar] [CrossRef]
- Niu, S.; Zhang, E.; Bazilevs, Y.; Srivastava, V. Modeling finite-strain plasticity using physics-informed neural network and assessment of the network performance. J. Mech. Phys. Solids 2023, 172, 105177. [Google Scholar] [CrossRef]
- Aikawa, Y.; Ueda, N.; Tanaka, T. Improving the Efficiency of Training Physics-Informed Neural Networks Using Active Learning. New Gener. Comput. 2024, 42, 739–760. [Google Scholar] [CrossRef]
- van der Meer, R.; Oosterlee, C.W.; Borovykh, A. Optimally weighted loss functions for solving PDEs with Neural Networks. J. Comput. Appl. Math. 2022, 405, 113887. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Q.; Hesthaven, J.S.; Zhang, C. Physics-informed machine learning for reduced-order modeling of nonlinear problems. J. Comput. Phys. 2021, 446, 110666. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Physics-Informed Deep Learning for Computational Elastodynamics without Labeled Data. J. Eng. Mech. 2021, 147, 04021043. [Google Scholar] [CrossRef]
- Wang, Q.A.; Chen, J.; Ni, Y.; Xiao, Y.; Liu, N.; Liu, S.; Feng, W. Application of Bayesian networks in reliability assessment: A systematic literature review. Structures 2025, 71, 108098. [Google Scholar] [CrossRef]
- Wang, Q.A.; Wang, H.B.; Ma, Z.G.; Ni, Y.Q.; Liu, Z.J.; Jiang, J.; Sun, R.; Zhu, H.W. Towards high-accuracy data modelling, uncertainty quantification and correlation analysis for SHM measurements during typhoon events using an improved most likely heteroscedastic Gaussian process. Smart Struct. Syst. 2023, 32, 267–279. [Google Scholar] [CrossRef]
- Wang, Q.A.; Liu, Q.; Ma, Z.G.; Wang, J.F.; Ni, Y.Q.; Ren, W.X.; Wang, H.B. Data interpretation and forecasting of SHM heteroscedastic measurements under typhoon conditions enabled by an enhanced Hierarchical Sparse Bayesian Learning model with high robustness. Measurement 2024, 230, 114509. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, Q.; Qin, K. Physics-based deep learning for flow problems. Energies 2021, 14, 7760. [Google Scholar] [CrossRef]
- Haghighat, E.; Juanes, R. SciANN: A Keras/TensorFlow wrapper for scientific computations and physics-informed deep learning using artificial neural networks. Comput. Methods Appl. Mech. Eng. 2021, 373, 113552. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).