Dynamics of an Impulsive Predator–Prey Model with a Seasonally Mass Migrating Prey Population
Abstract
1. Introduction
2. The Model
3. Lemmas and Definition
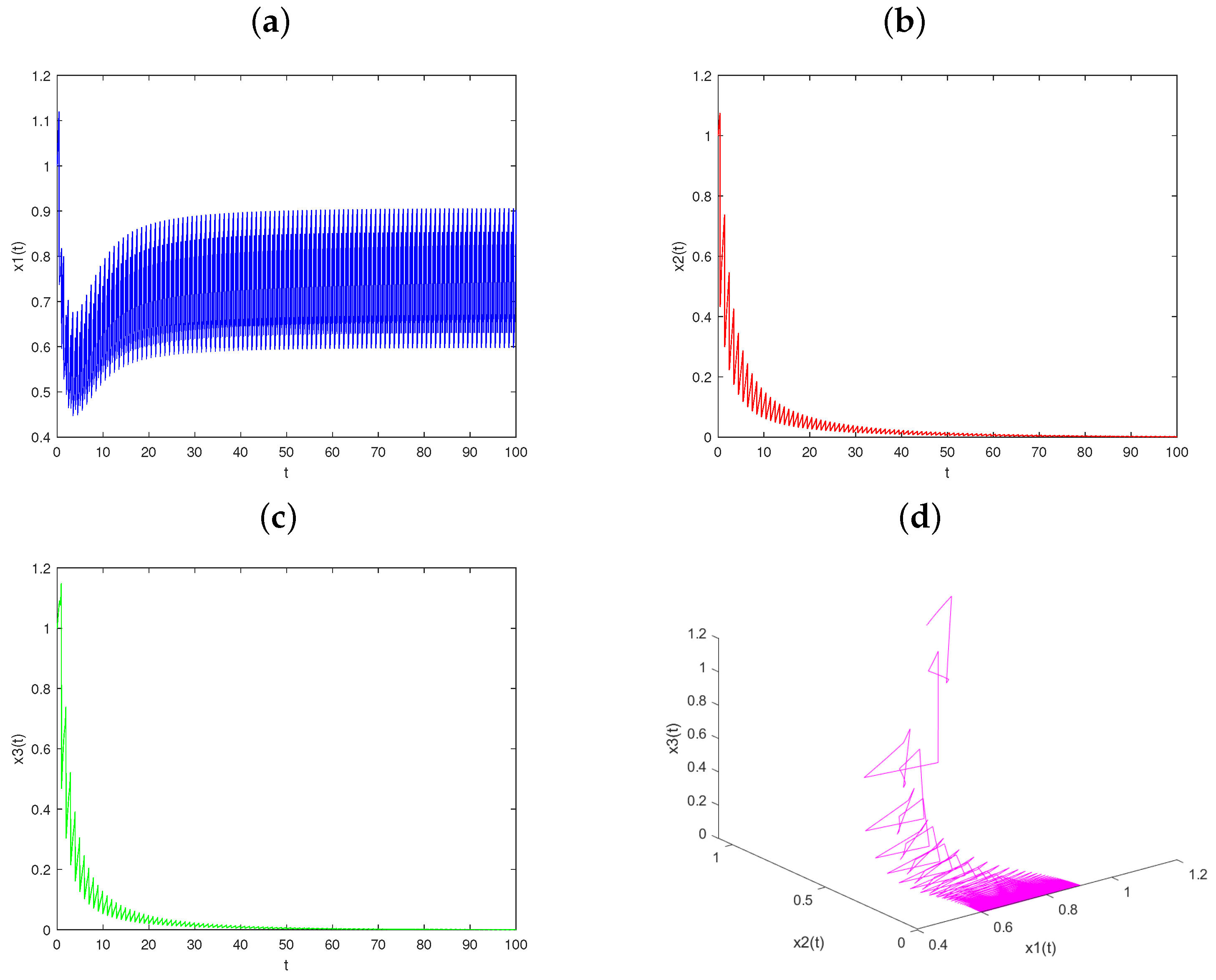
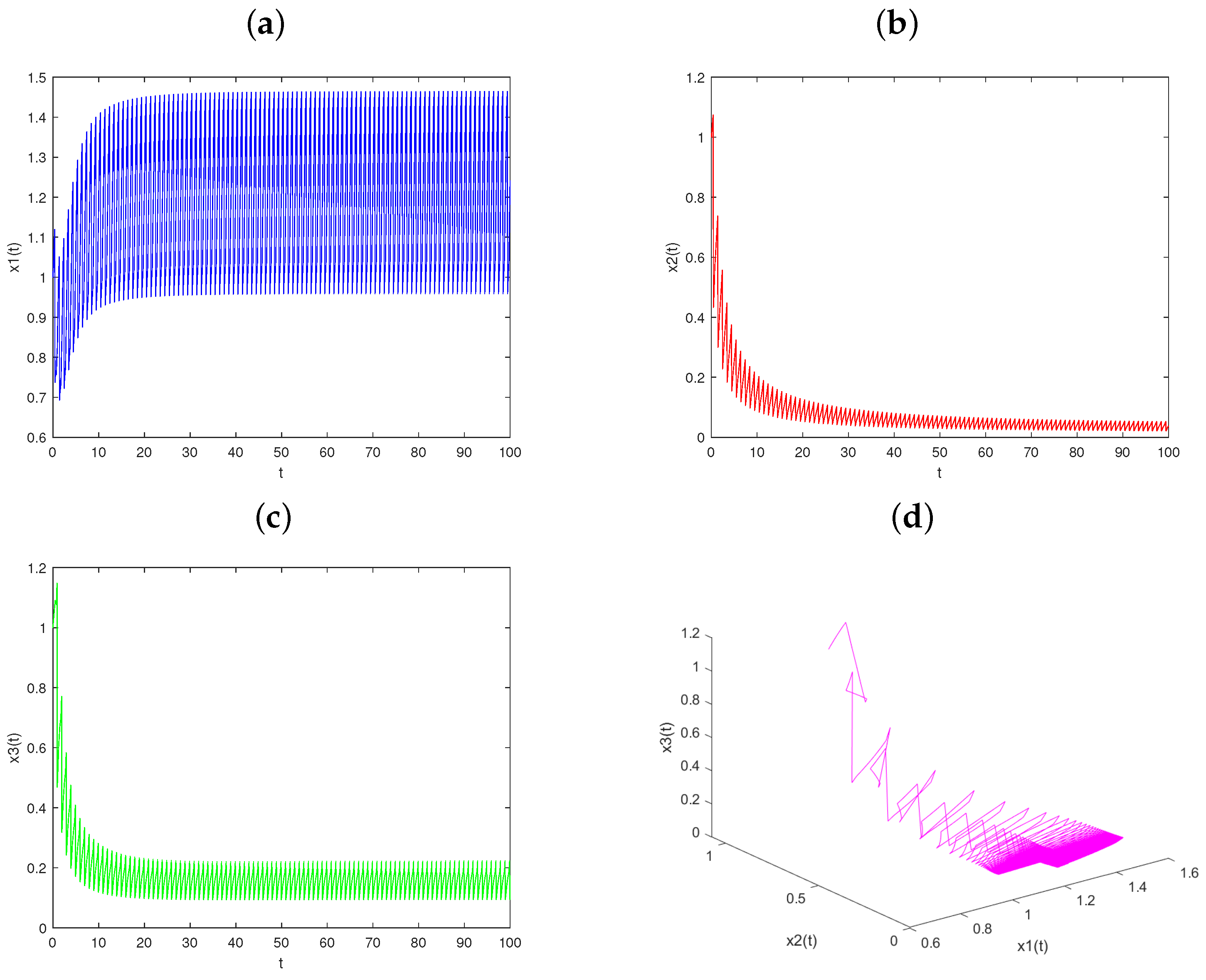
4. The Dynamics
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Huang, Y. Biodiversity and stability mechanism: Understanding and future reseach. Acta Ecol. Sinaca 2016, 36, 1–12. (In Chinese) [Google Scholar]
- O’Regan, S.M.; Kelly, T.C.; Korobeinikov, A.; O’Callaghan, M.J.; Pokrovskii, A.V.; Rachinskii, D. Chaos in a seasonally perturbed SIR model: Avian influenza in a seabird colony as a paradigm. J. Math. Biol. 2013, 67, 293–327. [Google Scholar] [CrossRef] [PubMed]
- Dingle, H. Migration strategies of insects. Science 1972, 175, 1327–1335. [Google Scholar] [CrossRef] [PubMed]
- Dixon, A.F.C.; Horth, S.; Kindlmann, P. Migration in in insect:cost and strategies. J. Anim. Ecol. 1993, 63, 182–190. [Google Scholar] [CrossRef]
- Matthiopoulos, J.; Harwood, J.; Thomas, L.E.N. Metapopulation consequences of site fidelity for colonially breeding mammals and birds. J. Anim. Ecol. 2005, 74, 716–727. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology II Spatial Models and Biomedical Applications; Springer: New York, NY, USA, 2000. [Google Scholar]
- Hassel, M.P.; Comins, N.H.; May, R.M. Spatial structure and chaos in insect population dynamics. Nature 1991, 353, 255–258. [Google Scholar] [CrossRef]
- Stone, L.; Hart, D. Effects of Immigration on the Dynamics of Simple Population Models. Theor. Popul. Biol. 1999, 55, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Pal, N.; Samanta, S.; Chattopadhyay, J. The impact of diffusive migration on ecosystem stability. Chaos Solitons Fractals 2015, 78, 317–328. [Google Scholar] [CrossRef]
- Hobson, K.A.; Wassenaar, L.I. Tracking Animal Migration with Stable Isotopes, 2nd ed.; Academic Press-Elsevier: New York, NY, USA, 2019. [Google Scholar]
- Levin, S.A. Dispersal and population interactions. Am. Nat. 1974, 108, 207–228. [Google Scholar] [CrossRef]
- Holt, R.D. Population Dynamics in two-patch environments: Some anomalous consequences of an optimal habitat distribution. Theor. Popul. Biol. 1985, 28, 181–208. [Google Scholar] [CrossRef]
- Jiao, J.; Cai, S.; Chen, L. Analysis of a stage-structured predator-prey system with birth pulse and impulsive harvesting at different moments. Nonlinear Anal. Real World Appl. 2011, 12, 2232–2244. [Google Scholar] [CrossRef]
- Jiao, J.; Cai, S.; Li, L. Impulsive vaccination and dispersal on dynamics of an SIR epidemic model with restricting infected individuals boarding transports. Phys. Stat. Mech. Its Appl. 2016, 449, 145–159. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Quan, Q.; Dai, X. Dynamics of a pest-nature enemy model for IPM with repeatedly releasing natural enemy and impulsively spraying pesticides. Adv. Contin. Discret. Model. 2025, 52, 1–13. [Google Scholar] [CrossRef]
- Lakshmikantham, V. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Jiao, J.; Cai, S.; Li, L. Dynamics of a periodic switched predator-prey system with impulsive harvesting and hibernation of prey population. J. Frankl. Inst. 2016, 353, 3818–3834. [Google Scholar] [CrossRef]
- Jiao, J.; Liu, Z.; Li, L.; Nie, X. Threshold dynamics of a stage-structured single population model with non-transient and transient impulsive effects. Appl. Math. Lett. 2019, 97, 88–92. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Hui, J.; Chen, L. Impulsive diffusion in single species model. Chaos Solitons Fractals 2007, 33, 1213–1219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Jiao, J. Dynamics of an Impulsive Predator–Prey Model with a Seasonally Mass Migrating Prey Population. Mathematics 2025, 13, 1550. https://doi.org/10.3390/math13101550
Xiao Y, Jiao J. Dynamics of an Impulsive Predator–Prey Model with a Seasonally Mass Migrating Prey Population. Mathematics. 2025; 13(10):1550. https://doi.org/10.3390/math13101550
Chicago/Turabian StyleXiao, Yunpeng, and Jianjun Jiao. 2025. "Dynamics of an Impulsive Predator–Prey Model with a Seasonally Mass Migrating Prey Population" Mathematics 13, no. 10: 1550. https://doi.org/10.3390/math13101550
APA StyleXiao, Y., & Jiao, J. (2025). Dynamics of an Impulsive Predator–Prey Model with a Seasonally Mass Migrating Prey Population. Mathematics, 13(10), 1550. https://doi.org/10.3390/math13101550




