Multi-Subject Decision-Making Analysis in the Public Opinion of Emergencies: From an Evolutionary Game Perspective

Abstract

This study employs evolutionary game theory to analyze the tripartite interaction among government regulators, media publishers, and self-media participants in emergency public opinion management. We establish an evolutionary game model incorporating strategic motivations and key influencing factors; then, we validate the model through systematic simulations. Key findings demonstrate the following: ① the system exhibits dual stable equilibria: regulated equilibrium and autonomous equilibrium. ② Sensitivity analysis identifies critical dynamics: ① self-media behavior is primarily driven by penalty avoidance ($g_3$) and losses ($w_2$); ② media participation hinges on revenue incentives ($m_2$) versus regulatory burdens ($k$); ③ government intervention efficacy diminishes on emergencies when resistance ($v_1$ + $v_3$) exceeds control benefits. The study reveals that effective governance requires the following: ① adaptive parameter tuning of punishment–reward mechanisms; ② dynamic coordination between information control and market incentives. This framework advances emergency management by quantifying how micro-level interactions shape macro-level opinion evolution, providing actionable insights for balancing stability and information freedom in digital governance.

1. Introduction

The digital revolution has fundamentally transformed crisis communication, with social media platforms emerging as dominant conduits for information dissemination during public emergencies [1,2,3,4]. High-profile incidents such as the Tianjin Port Explosion and Changchung Changsheng Vaccine Scandal demonstrate how digital platforms can rapidly escalate localized events into nationwide public opinion crises through viral propagation. This phenomenon is further exacerbated by the algorithmic amplification of sensational content by self-media actors, significantly complicating crisis containment efforts.

Understanding the tripartite dynamics between the media, self-media, and government during such events provides critical insights for ① crisis mitigation: developing mechanisms to counter misinformation cascades; ② urban governance: enhancing sentiment analysis and response frameworks; ③ social stability: balancing free expression with responsible communication.

Our study employs evolutionary game theory to model these complex interactions, offering a novel perspective on multi-stakeholder decision-making in digital crisis environments. This approach reveals how platform architecture, economic incentives, and regulatory policies collectively shape the evolution of online public opinion.

2. Literature Review

The study of multi-subject decision-making in the context of public opinion during emergencies has gained significant attention in recent years, particularly due to the increasing complexity of information dissemination and the interplay between the government, media, and self-media. This literature review synthesizes existing research from the perspective of evolutionary game theory, highlighting the dynamics and interactions among these key stakeholders.

2.1. Public Opinion and Emergencies

Public opinion during emergencies is a critical area of study, as it significantly influences societal stability and crisis management [5,6]. Victor et al. [7] purposed two Brazilian Portuguese corpora collected from different media concerning public security issues in a specific location. Guo et al. [8] developed a new GSPN model to analyze the evolution of online public opinion on emergencies. De Carvalho et al. [9] analyzed a space and time topic of the Brazilian immunization program and public trust through Twitter information. Wang et al. [10] established an indicator system utilizing the K-means text clustering model, public prediction, and expectation, and their evolution underlying public concern was elucidated employing TF–IDF text mining models. Zhou et al. [11] designed a self-distillation contrastive learning method for analyzing online public opinion. Zhai et al. [12] constructed a logic map of online public opinion events through the microblog information of “rainstorm in Henan”. Research by Jiang et al. [13] emphasizes the importance of timely and accurate information dissemination in shaping public perception and behavior during crises. The role of traditional media and, more recently, self-media platforms has been pivotal in this process [14]. The rapid spread of information, coupled with the potential for misinformation, underscores the need for effective multi-subject decision-making frameworks.

2.2. Multi-Subject Decision-Making

The concept of multi-subject decision-making involves collaboration. The participants in public opinion are usually divided into three categories: government, media, and netizens [15,16,17]. The traditional public opinion governance model is based on the social governance model of information resource monopoly, and the government, as a single entity, achieves public opinion governance through information asymmetry [5,18]. The media is beginning to influence the government’s public opinion governance and gradually participating in public opinion governance [5]. Zhang and Feng [19] explored how these entities interact and influence each other’s strategies during public opinion crises. Their work highlights the necessity of understanding the decision-making processes of each stakeholder to develop comprehensive crisis management strategies.

2.3. Evolutionary Game Theory

Evolutionary game theory provides a robust framework for analyzing strategic interactions among multiple decision-makers. Unlike classical game theory, which assumes static and fully rational players, evolutionary game theory considers the dynamic and adaptive nature of decision-making. Wang et al. [20] combined traditional evolutionary and complex network theories to implement the network communication game model of competitive public opinion information. Qiu et al. [21] constructed a three-party evolutionary game model and proposed public opinion communication management strategies and critical intervention points. Based on the “situation response” model, Wei et al. [22] used evolutionary game theory to study the evolutionary process of the group strategy selection of network public opinion communicators and network public opinion guides in sudden network public opinion events. This approach is particularly useful in the context of public opinion, where stakeholders continuously adapt their strategies based on the evolving information landscape and the actions of others.

2.4. Applications in Public Opinion Management

Zhang and Wang [23] considered the behavioral impact of different government measures and analyzed the coupling mechanism between negative information and government information. Similarly, Rou and Fiscutean [24] examined the role of self-media in shaping public opinion and found that the credibility and timeliness of information shared by self-media influences significantly impact public trust and behavior. Their findings [25,26,27,28] suggest that cooperative strategies can lead to more effective public opinion management, while competitive strategies may exacerbate misinformation and public panic.

2.5. Conclusions

From our above analysis, we discern that scholars have performed much research on disseminating and supervising online public opinion. However, the first one is a relatively little in-depth exploration of multi-subject collaborative decision-making from an experimental perspective and not a summary of the evolution laws of public opinion in multi-subject decision-making; the second is more research is needed on the impact of the self-media on disseminating online public opinion. The media and self-media are essential participants in online public opinion communication, and they can promote the spread of public opinion. Based on this, we built a three-party “government–media–self-media” evolutionary game model to discuss the stability strategies of the network public opinion supervision system under different circumstances. This study invoked game theory through a Matlab 2023a software simulation to dynamically analyze the evolution of the three major subjects’ behaviors—the government’s, the media’s, and the self-media’s—in the process of the development of the event; analyze the interaction between the subjects’ behaviors and the evolution of the event; explore in-depth how the government, the media, and the self-media can promote and influence the evolution of the event as well as the evolution of the subjects’ behaviors during the event and the game process of the subjects’ behavior during the event’s evolution; and draw relevant conclusions.

3. Methods

3.1. Analysis of the Leading Players of the Game

The game’s subject, also known as the participant or bureau participant, is the decision-making subject, i.e., the individual who makes decisions in the game. Game theory is the primary method to study decision-making when the behaviors of the decision-making subjects are directly interacting with each other and to solve the decision-making equilibrium problem, i.e., the decision-making problem and equilibrium problem when a subject’s choice is affected by the choices of the different subjects, and its own choices affect the choices of the other subjects in turn. In the game’s process, the game’s subject should be able to adjust their decision-making behavior, interact with different subjects, and impact the decision-making behavior of other subjects.

In the evolution of public opinion, the media refers to organizations that officially collect and report public opinion information. Self-media is the disseminator and governing party of public opinion information, running through the entire process of public opinion evolution. It is the main driving force for sudden events to generate public opinion in the network, spread public opinion, and further ferment it. Self-media entities will exercise their supervisory power over government entities to a certain extent and have a particular impact on the behavior of government entities. The government is a service-oriented institution that safeguards national security and maintains social stability, playing the roles of guide and governance in the evolution of online public opinion. Generally speaking, the views of media subjects are fairer and objective than those of netizens, and the government can also use the media to expand its influence and better guide and govern the evolution of public opinion. Some self-media may release radical comments or false information due to their knowledge, background, or interests, which may hurt the evolution of public opinion.

The previous analysis can be seen in the main body of the event, which mainly consists of the government as a representative of the controller, the media as a representative of the publisher, and the self-media as a representative of the disseminator. The three parts of the evolution of emergencies will be affected by the behavior of the government, media, and self-media, and the behavioral strategies adopted by the three emergencies’ game subjects determine the direction of emergencies. The government’s behavioral strategies include intervention and non-intervention; the self-media’s behavioral strategies include participation and non-participation; and the media’s behavioral strategies include reporting and non-reporting.

In this paper, from the perspective of the main body of emergencies, we take the multiple subjects of event evolution and scenario evolution game equilibrium solution as the object and construct the game model of strategy selection of the government, media, and self-media in the evolution of emergencies.

3.2. Analysis of the Dynamics of the Game’s Leading Players

In the evolution of emergencies, all kinds of game subjects’ internal state changes and external-environment changes will affect the subject between each other’s choice of strategy, drawing on game theory in economics, management, and other disciplines in the use of mature, practical experience according to its determination of the effect factors, combined with the emergencies in the field of the unique characteristics inherent in this paper that the main body of the game is the finite rationality of the participants in the game to find the most favorable options for themselves in the process of searching for the optimal strategy over time. In the process of searching for the most advantageous plan for themselves, their strategy selection gradually evolves to converge on the optimal strategy, in which the degree of psychological satisfaction is one of the main motives driving their decision-making: the government, media platforms, and self-media, the three subjects in the higher degree of psychological satisfaction driven to maximize their interests as the goal of their behavioral strategy selection. Psychological satisfaction is the subject’s satisfaction with the benefits of the behavioral strategy, and an improvement in the government’s credibility will increase its satisfaction with the strategy. Similarly, online media companies are committed to adopting strategies that can help promote their platforms, increase the number of users’ followers, and improve the reputation of their companies; for the self-media, this is reflected in their psychological satisfaction, sense of identity, and realized traffic monetization. On the other hand, other factors can also affect the decision-making of the game’s subjects to different degrees.

This paper considers that the critical factors affecting the evolution of the event game mainly include three parts, i.e., the evolution of the event heat, the reward and punishment mechanism of the governmental departments, and the deterioration of the negative impacts. The heat of event evolution refers to the degree of people’s attention to emergencies, mainly reflected by the heat of event public opinion. The interaction between the heat of the event and the subject’s behavior is an essential factor affecting the behavioral choices of the three parties, i.e., the change in the heat of the event will have a more significant impact on the dynamic influence of the subject’s decision-making behavior and vice versa. A change in the subject’s behavioral strategy will also affect the heat of the emergencies, and the subject of the game will continuously adjust his game strategy according to the different stages of the event evolution to maximize the game gain. The government’s reward and punishment mechanism generally refers to the relevant policies and regulations issued by the government to cope with emergencies, which will motivate some of the behaviors of the self-media and media while restraining some of the behaviors of the other part of the media, thus influencing the behaviors of the leading players of the event game, such as the self-media and the press. The continuous deterioration of the event’s negative impact involves the nature of the event itself and the effect on the external environment during the event’s evolution, etc. In the continuous deterioration of the negative impact of the emergencies, the game’s leading players will actively or passively change their game strategies.

Therefore, this paper proposes a dynamic game model of the government, media, and self-media, which is mainly composed of three types of essential influences affecting the government, media, and self-media; the factors affecting the degree of satisfaction of each subject; and the three types of crucial influences affecting the evolution process of the event game, as shown in Figure 1.

4. Model Construction

4.1. Game Assumptions

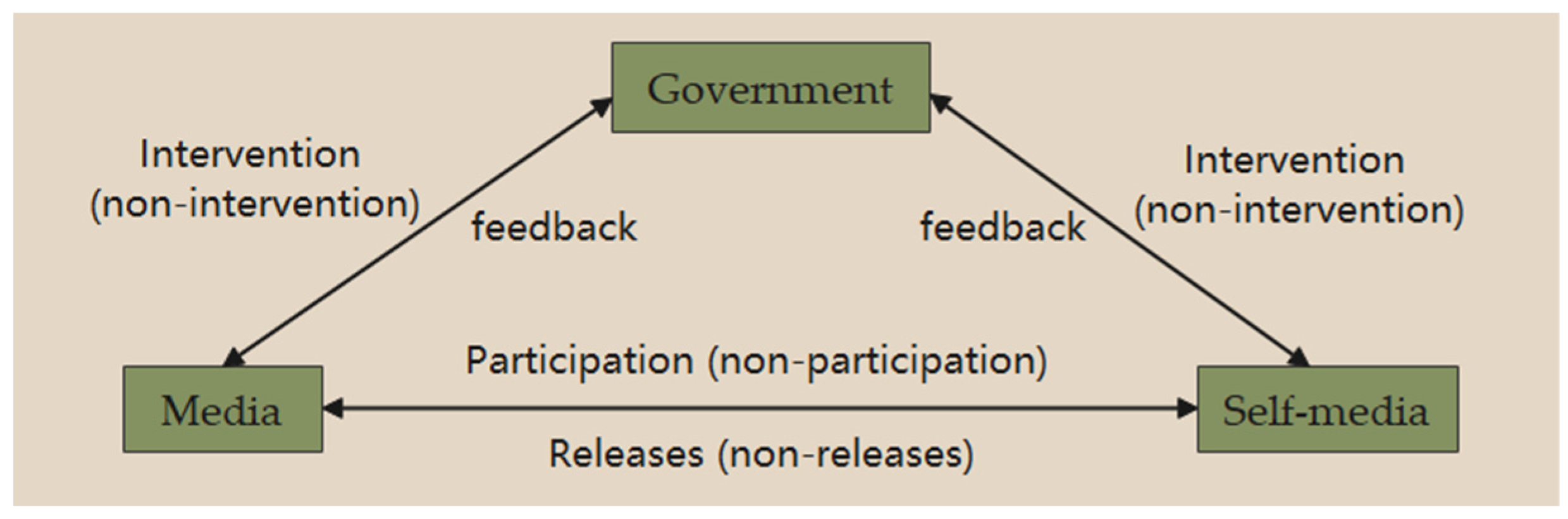
There are many factors affecting the game strategy of the three parties, and a variety of internal and external factors will constrain the choice of game strategy of the three parties in the evolution of the game, in which the behavioral strategy of the subjects is constrained by each other’s and weighed against each other’s, and at the same time, they aim to maximize the sense of identity and benefits in their hearts. Therefore, in the study of the evolution of emergencies in the process of the behavior of the self-media, the media, and the government, the three participants should be taken into account.

Therefore, when studying the behavior of the self-media, media, and government during the evolution of emergencies, we should fully consider the costs and benefits of the three participants in choosing different strategies and formulating coping strategies based on the game in various scenarios. In this paper, the general assumptions of the model are set as follows:

Hypothesis 1.

Participants in the evolution of emergencies in the government, media, self-media, and other game subjects are rational economic people; that is, to maximize their interests as the goal, the subjects are to consider their benefits and pay the cost of making changes in the game process of their strategies.

Hypothesis 2.

The government, media, and self-media constitute the main body of the game of emergencies. During the evolution of emergencies, the government can choose “intervention” and “non-intervention” strategies, the media can choose “reporting” and “non-reporting” strategies, and the self-media can choose “participation” and “non-participation” strategies. The media can choose to “report” or “not report”, and the self-media can choose to “participate” or “not participate”. When an emergency breaks out, the government’s strategy set is $a_1$ and $a_2$, and $a_1$ represents the intervention strategy while $a_2$ represents the strategy of non-intervention; the set of media reporting strategies are $b_1$ and $b_2$, and ${ b}_1$ represents adopting the reporting strategy while${ b}_2$ represents adopting the non-reporting strategy; the strategies of the self-media participation in the event discussion are $c_1$ and $c_2$. $c_1$ represents choosing to participate in the strategy, while $c_2$ represents choosing not to participate in the strategy.

Hypothesis 3.

The government is the central perspective to develop the hypothesis; when there is an emergency, the government’s timely choice of active strategy will be effective in mitigating the risk of emergency loss and brings benefits $m_1$. In the process of actively responding to emergencies, the government needs to pay for the cost of time, workforce, and resources $n_1$. The cost of time, workforce resources, etc., that the government has to pay for in the process of actively responding to the emergencies and the loss caused by the suppression of public opinion by the self-media is $v_1.$ The negative impact of the evolution of the subjective behaviors of emergencies forwarded to the government by the media is $v_3.$ The adverse effects of the government’s negative response. The suppression of public opinion by the self-media is $v_2.$ The loss brought by the media to the government is $v_4$. The negative impact of the government’s negative response, such as the decrease in credibility of the government, is $g_1$.

Hypothesis 4.

The media is the central perspective to develop the hypothesis; the media chooses to forward and report on emergencies; in the case of the self-media not participating in the case, the media’s information will not be concerned, assuming that its revenue is 0, but it will pay for a certain amount of time and energy and other costs $h_3$. In the case of self-media participation, the media’s gain from reporting on the event of concern, such as the promotion of the platform, the increase in the number of users’ fans, the enhancement of reputation and other aspects of self-media attention, is 0, but it will pay for a specific cost of time and energy $m_2$. The cost of time and energy is the same as the cost of time and energy $n_2$. When the government chooses to respond positively, the reputation and fines incurred by the media as a result of the government’s constraints are$l$, the rewards given by the government to the media are $k$. If the media does not forward the information about emergencies, the self-media participation in the situation will cause an inevitable loss of $g_2$.

Hypothesis 5.

Taking the self-media as the central perspective, the self-media participation in the discussion of the emergencies will obtain psychological satisfaction or sense of identity and other benefits $m_3$. The time cost for the media to report and reprint the information on emergencies so that the self-media can obtain more information is $n_3$. When the media does not report and reprint the information, the time cost for the self-media to obtain more information through other ways is $w_3$, that is, $w_3>n_3.$ When the government responds positively, the self-media will obtain positive psychological benefits $w_1$. When the government chooses a negative response strategy, the self-media will lose the psychological gap caused by their dissatisfaction with society and the government ${ w}_2$ and the potential loss caused by participation in the discussion of the event ${ g}_3$.

Hypothesis 6.

Self-media (disseminator) behavioral strategies are assumed to be divided into participation and non-participation. If the self-media’s involvement in public opinion dissemination obtains higher benefits, they will participate, and vice versa, they will not participate. Suppose their probability of participation is set as x and the non-participation probability is set as $1-x$. When $x=1$, when the probability of involvement is x, the probability of non-participation is x. When the probability of non-participation is $x=0$, it means the self-media must not participate. The media’s (publisher’s) behavioral strategies are divided into reporting and non-reporting. Suppose the benefit of reporting the speech of critical-incident online public opinion is greater than the reporting cost. In that case, the media chooses to report, and vice versa, it decides not to report. The probability of reporting is set as $y$, and the probability of not reporting is set as $1-y$. When $y=1$, it means that the media will report it; when $y=0$, it means the media must not report. Government (controller) behavioral strategies are divided into intervention and non-intervention. The government does not intervene for various reasons, such as not obtaining the risk and cost of public opinion intervention due to pre-preparation. The intervention probability is set as$z$, and the probability of non-intervention is set as $1-z$. When $z=1$, the government intervene; when the government will not intervene, $z=0$.

Hypothesis 7.

This paper further analyzes the behavioral decision-making of the government, media, and self-media in-depth and systematically, and based on the interactions between the three subjects in the evolution of emergencies, the relationship between the three subjects and the factors affecting them, the parameters of the interactions between the three subjects are derived, as shown in

Table 1. Influence parameters of the three-party subject game.

Parameter Symbol	Parameter Meaning
${\mathrm{m}}_1$	Gains when governments choose to intervene positively, e.g., increased trust and improved public image
${\mathrm{m}}_2$	Benefits gained from the media choosing to take an active interest in emergencies, e.g., advertising revenue, reputation, enhanced credibility, and high attention
${\mathrm{m}}_3$	Benefits accruing to self-media who choose to participate actively, e.g., high attention, high traffic, advertising
${\mathrm{n}}_1$	The cost to the government of choosing to intervene actively, e.g., monitoring public opinion, collecting information, time, manpower, and material resources
${\mathrm{n}}_2$	The cost of the media choosing to take an active interest in emergencies, e.g., human and material resources costs for collecting information, following up, marketing
${\mathrm{n}}_3$	The cost to the self-media of choosing to participate actively, e.g., losses caused by information collection, criticism for incorrect statements, online violence
$\mathrm{k}$	Media revenue under active government response
$\mathrm{l}$	Media losses under negative government response
${\mathrm{h}}_3$	The cost of the media choosing to pay attention and report when the self-media does not participate
${\mathrm{g}}_1$	Losses arising from the government’s non-intervention
${\mathrm{g}}_2$	Losses arising from lack of media coverage
${\mathrm{g}}_3$	Losses arising from the non-participation of the self-media in the discussion
${\mathrm{w}}_1$	Positive benefits when governments respond positively
${\mathrm{w}}_2$	Losses of the self-media in negative government response
${\mathrm{w}}_3$	Costs such as time and effort to the self-media when the media does not publish
${\mathrm{v}}_1$	Negative public opinion from the self-media when the government actively responds to emergencies
${\mathrm{v}}_2$	Negative public opinion from the self-media when the government passively responds to emergencies
${\mathrm{v}}_3$	Negative impact of the media reposting when the government actively responds to emergencies
${\mathrm{v}}_4$	Negative impact of the media reposting when the government passively responds to emergencies
$\mathrm{x}$	The probability that the government will use an active intervention strategy
$\mathrm{y}$	The probability of the media choosing to report attention
$\mathrm{z}$	The probability of the self-media choosing to participate in the event

below.

4.2. Mixed-Strategy Game Matrix

From the above, it can be seen that the game combination structure of the government, media, and self-media; the government’s intervention and non-intervention strategies; the media’s reporting and non-reporting strategy; and the self-media participation and non-participation and other behavioral combinations form a total of 8 types of game strategies, covering all the possible forms of random combinations of the subject’s behavioral choices. The game-specific combinations are shown in

Table 2. Combination of the interaction relationships of the three-party subject game.

Strategic Combination	Self-Media (Disseminator)	Media (Publisher)	Government (Regulator)
1	participate (in sth)	propagate	interventions
2	participate (in sth)	propagate	non-intervention
3	participate (in sth)	non-communication	interventions
4	participate (in sth)	non-communication	non-intervention
5	non-participation	propagate	interventions
6	non-participation	propagate	non-intervention
7	non-participation	non-communication	interventions
8	non-participation	non-communication	non-intervention

.

According to the above assumptions and the random combination of the three-party game, this paper constructs the mixed-strategy game matrix of the self-media (disseminator), media (publisher), and government (regulator), as shown in

Table 3. Mixed-strategy game matrix.

Media (Publisher)		Government (Regulator)
			$\mathbf{Interventions}\mathit{z}$	$\mathbf{\text{Non-Intervention}} 1-\mathit{z}$
Self-media (Disseminator)	participate (in sth) $x$	$\mathrm{Report} \left(\mathrm{news}\right) y$ Non-reporting $1-y$	$m_3-n_3+w_1$, $m_2-n_2+k$, $m_1-n_1-v_1-v_3$. $m_3-w_3+w_1,$ ${-g}_2+l$, $m_1-n_1$.	$m_3-n_3-w_2,$ $m_2-n_2,$ ${-g}_1-v_4-v_2$. $m_3-w_3-w_2,$ ${-g}_2,$ $g_1-v_2$.
	$\text{non-participation} 1-x$	$\mathrm{report} \left(\mathrm{news}\right) y$ No coverage 1 − y	${-g}_3,$ $k-h_3,$ $m_1-n_1-v_3$. ${-g}_3,$ $l,$ $m_1-n_1-v_1$	${-g}_3,$ ${-h}_3$, ${-g}_1{-v}_4.$ ${-g}_3,$ 0, ${-g}_1$.

below.

4.3. Modeling Analysis

1. Strategic stability analysis of self-media (disseminator)

The expected benefits of the self-media (disseminator) participation or non-participation in online opinion outbreaks and the average expected benefits (${\mathrm{E}}_{11}$, ${\mathrm{E}}_{12}$, and ${\mathrm{E}}_1$), respectively:

$$\begin{gathered} {\mathrm{E}}_{11}=\mathrm{y}\mathrm{z}\left[{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1\right]+\mathrm{y}\left(1-\mathrm{z}\right)\left[{\mathrm{m}}_3-{\mathrm{n}}_3-{\mathrm{w}}_2\right]+\left(1-\mathrm{y}\right)\mathrm{z}\left[{\mathrm{m}}_3-{\mathrm{w}}_3+{\mathrm{w}}_1\right]+\left(1-\mathrm{y}\right)\left(1-\mathrm{z}\right)\left[{\mathrm{m}}_3-{\mathrm{w}}_3-{\mathrm{w}}_2\right] \\ {\mathrm{E}}_{12}={-\mathrm{g}}_3 \\ {\mathrm{E}}_1={\mathrm{x}\mathrm{E}}_{11}+{\left(1-\mathrm{x}\right)\mathrm{E}}_{12} \end{gathered}$$

(1)

The equation for the replication dynamics chosen by the self-media (disseminator) is:

$$\mathrm{F}\left(\mathrm{x}\right)={\displaystyle \frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}}}=\mathrm{x}\left({\mathrm{E}}_{11}-{\mathrm{E}}_1\right)=\mathrm{x}\left(\mathrm{x}-1\right)\left[\right({\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2)-\mathrm{y}{\mathrm{g}}_3-{\mathrm{z}\mathrm{g}}_3]$$

(2)

The first derivative of $\mathrm{x}$ and the set $\mathrm{G}\left(\mathrm{y}\right)$ are:

$${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}=\left(2\mathrm{x}-1\right)[{(\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2)-{\mathrm{y}\mathrm{g}}_3-{\mathrm{z}\mathrm{g}}_3]$$

(3)

$$\mathrm{G}\left(\mathrm{y}\right)=[{(\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2)-{\mathrm{y}\mathrm{g}}_3-{\mathrm{z}\mathrm{g}}_3]$$

(4)

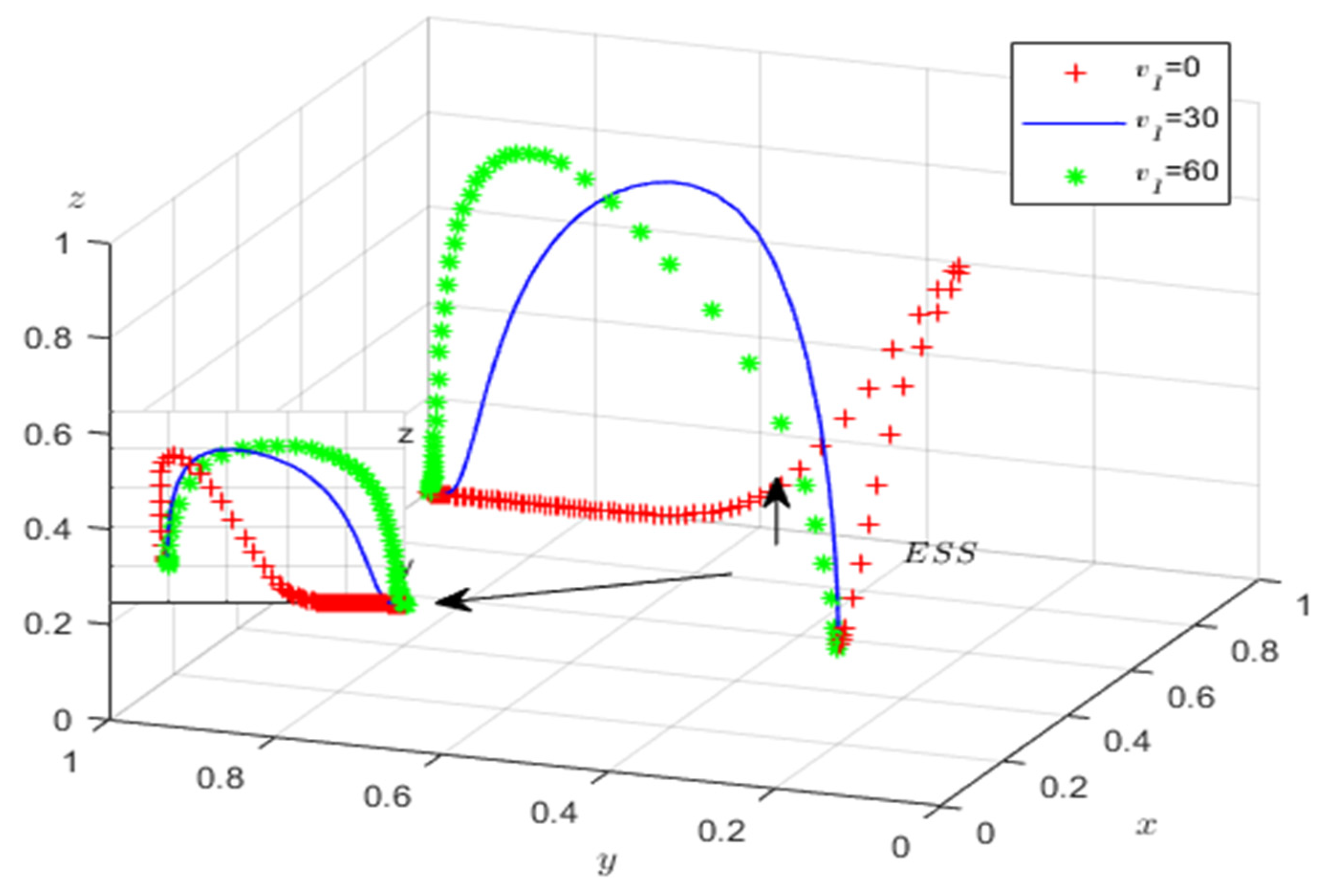
According to the stability theorem of differential equations, the probability of the self-media (disseminator) choosing to participate in the discussion of public opinion on emergencies in a stable state must be satisfied: $\mathrm{F}\left(\mathrm{x}\right)=0$ and ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}<0$. Since ${\displaystyle \frac{\mathrm{G}\left(\mathrm{y}\right)}{\mathrm{y}}}<0$, $\mathrm{G}\left(\mathrm{y}\right)$ is the probability of participating in the public opinion discussion of a critical incident with respect to $\mathrm{y}$, the reduced function. Therefore, when $\mathrm{y}={\displaystyle \raisebox{1ex}{$[{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-{\mathrm{z}\mathrm{g}}_3]$}\!\left/ \!\raisebox{-1ex}{${\mathrm{g}}_3$}\right.}={\mathrm{y}}^{*},$ $\mathrm{G}\left(\mathrm{y}\right)=0,$ currently, ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}$ is a constant equal to 0; the self-media (propagator) cannot determine the stabilization strategy. When $\mathrm{y}<{\mathrm{y}}^{*}$, $\mathrm{G}\left(\mathrm{y}\right)>0$, currently, ${{\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}|}_{\mathrm{x}=0}<0$, and $\mathrm{x}=0$ is the evolutionary stable strategy (ESS) of the self-media (propagator); vice versa. $\mathrm{x}=1$ is the ESS. ${\mathrm{y}}^{*}$ represents the critical probability of self-media strategy selection. ${\mathrm{y}}^{*}$ represents the critical probability of strategic choices made by other relevant groups, such as governments or media.

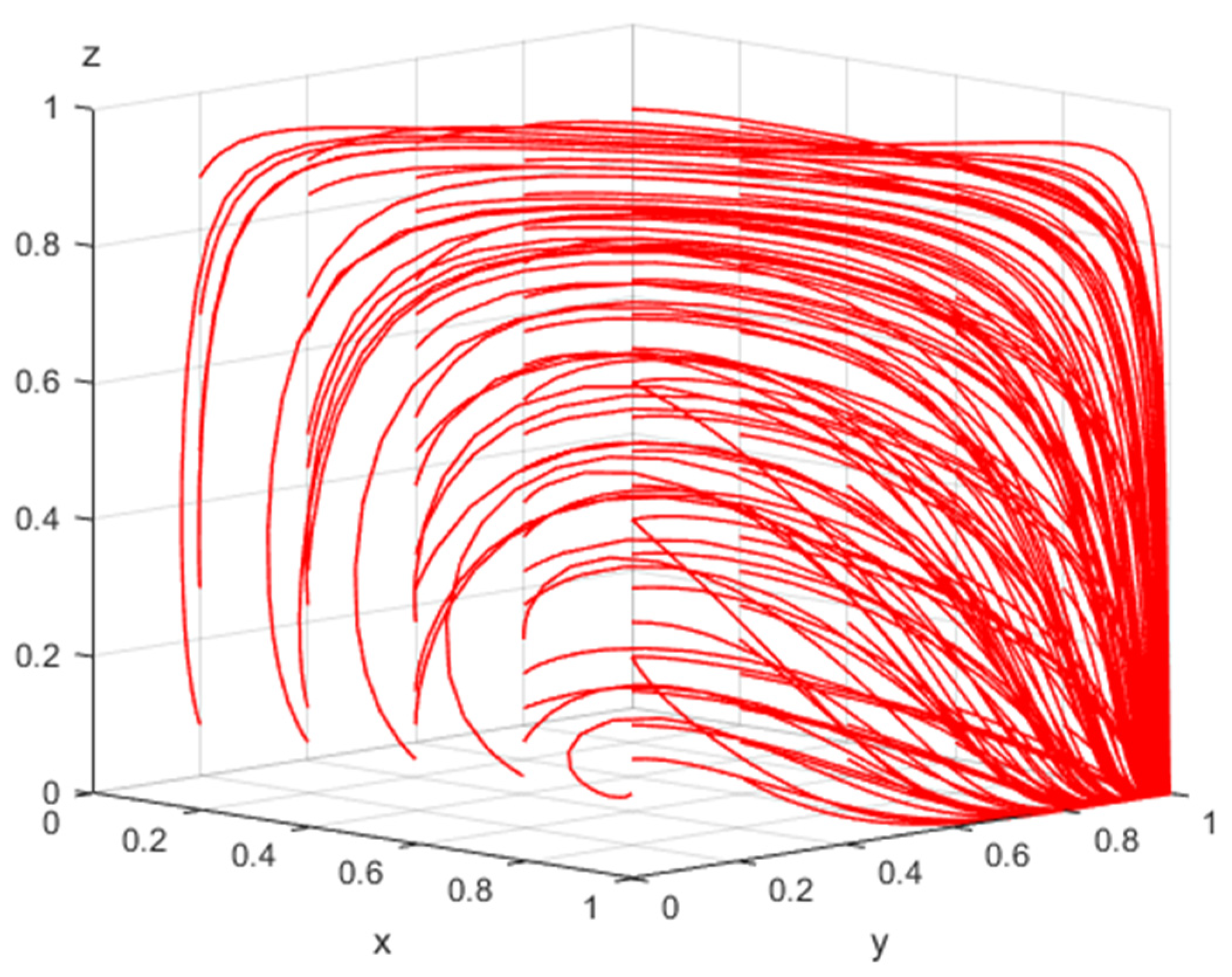
The phase diagram of the strategy evolution of the self-media (disseminator) is shown in Figure 2 below:

From Figure 2, the probability of the self-media (disseminator) not participating in the dissemination of public opinion on emergencies is ${\mathrm{A}}_1$. The volume of ${\mathrm{V}}_{\mathrm{A}1}$ and the likelihood of participating in the dissemination of public opinion on emergencies is ${\mathrm{A}}_2$; the volume of ${\mathrm{V}}_{\mathrm{A}2}$ is calculated as follows:

$$\begin{gathered} {\mathrm{V}}_{\mathrm{A}1}={\iint }_0^1{\displaystyle \frac{{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-\mathrm{z}{\mathrm{g}}_3}{\mathrm{g}3}}\mathrm{d}\mathrm{z}\mathrm{d}\mathrm{x}={\displaystyle \frac{2{(\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2)-\mathrm{g}3}{2\mathrm{g}3}}, \\ {\mathrm{V}}_{\mathrm{A}2}=1-{\mathrm{V}}_{\mathrm{A}1}. \end{gathered}$$

Corollary 1.

The probability of the self-media (disseminator) participating in the dissemination of public opinion on emergencies is positively correlated with the gains the self-media gain by choosing to participate, the positive psychological gains the self-media gain when the government responds positively, the losses the self-media incur when they respond negatively to emergencies, the damaging psychological losses the self-media incur when the government reacts negatively, and the costs the self-media pay when they participate in public opinion.

Proof. 

According to the probability of the self-media (disseminator) participating in the dissemination of public opinion on emergencies ${\mathrm{V}}_{\mathrm{A}2}$, calculating the first partial derivatives of each element. Conclusion: An increase in ${\mathrm{m}}_3$, ${\mathrm{w}}_1$ and ${\mathrm{g}}_3$, as well as a decrease in ${\mathrm{w}}_2$, and ${\mathrm{n}}_3$, will increase the probability of self-media participating in online opinion discussions. □

Corollary 1 shows a positive correlation between whether the self-media will participate in the discussion of public opinion on emergencies and whether they can benefit from it, which is consistent with the rational broker hypothesis in the previous section. Usually, the self-media need to gain a sense of identity and practical benefits from participating in online public opinion on emergencies, which is the main reason that drives the self-media to disseminate their views. On the other hand, the government’s behavior mainly influences whether the self-media participates. Suppose the government responds positively and introduces reward and punishment policies and incentives. In that case, the self-media will be motivated to participate in the discussion so that the self-media will obtain additional positive benefits, and the possibility of participating in the debate will be increased accordingly; on the other hand, if the government responds negatively, it will bring adverse losses to the self-media, and the self-media will reduce their participation in the discussion. On the contrary, the government’s negative response will bring adverse losses to the self-media, and the self-media will consciously reduce their involvement in public opinion, which shows that the government’s adjustment of its intervention strategy can influence the self-media’s game choices. In this process, the self-media’s negative response to emergencies may also cause losses in their interests, and the more significant these losses are, the more the self-media will actively participate in the discussion of public opinion on emergencies, which is consistent with the previous hypothesis.

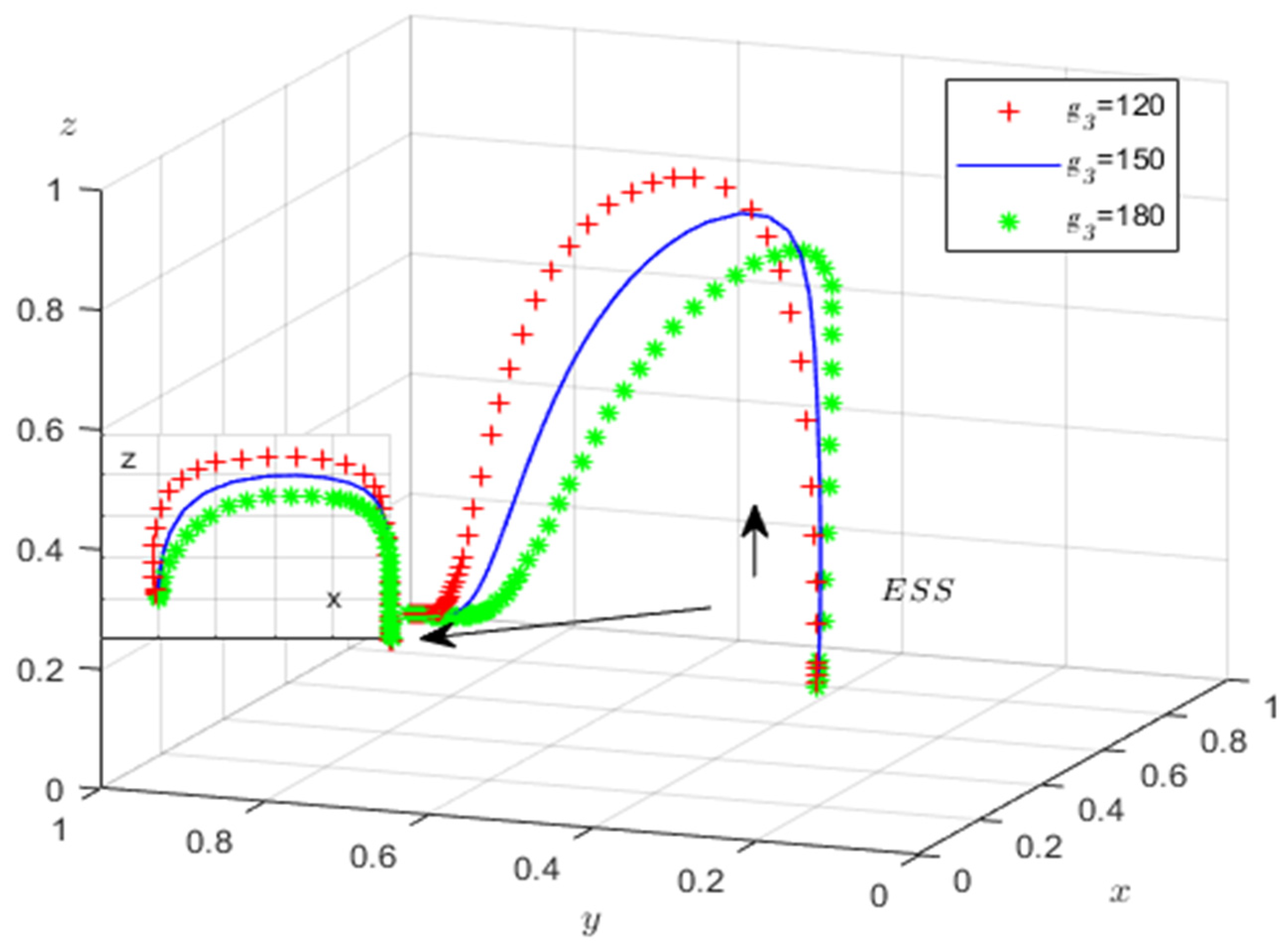
Corollary 2.

The probability of the self-media (disseminator) disseminating public opinion on emergencies rises with the media reporting on emergencies and the likelihood of government intervention in public opinion on emergencies.

The proof, from the analysis of the stability of the self-media’s (disseminator’s) curation, is that when $\mathrm{z}<\left[{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-{\mathrm{y}\mathrm{g}}_3\right]/{\mathrm{g}}_3$, $\mathrm{y}<{\mathrm{y}}^{*}$, $\mathrm{G}\left(\mathrm{y}\right)>0$. ${{\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{x}\right)\right)}{\mathrm{d}\mathrm{x}}}|}_{\mathrm{x}=0}<0$, then $\mathrm{x}=0$ is an evolutionary equilibrium strategy; conversely, $\mathrm{x}=1$ is the evolutionary equilibrium strategy. Therefore, as $\mathrm{y}$, $\mathrm{z}$ gradually increase, the stabilization strategy of the self-media (participants) increases from $\mathrm{x}=0$ (not participating in critical-incident online public opinion discussion) to $\mathrm{x}=1$ (participating in critical-incident online public opinion discussion).

Corollary 2 shows that media reports have positive incentives for the self-media to participate in public opinion discussions, media reports will reduce the cost of the self-media searching for information on their own, and truthful reports will reduce the likelihood of propagating false information among the population. Therefore, ensuring positive guidance of public opinion by the media can effectively enhance the truthfulness of public opinion dissemination in emergencies. Similarly, appropriate government intervention is also necessary to guide public opinion to the right path and provide confidence and support for the self-media to spread positive public opinion. Thus, when an emergency needs to be solved by the power of the self-media’s public opinion, positive media reports and timely and appropriate government guidance can encourage self-media participation.

2. Strategic stability analysis of the media (publisher)

Expected benefits of the media (publisher) reporting or not reporting on online opinion outbreaks and the average expected benefits (${\mathrm{E}}_{21}$,${\mathrm{E}}_{22}, {\mathrm{E}}_2$), respectively:

$$\begin{gathered} {\mathrm{E}}_{21}=\mathrm{x}\mathrm{z}\left[{\mathrm{m}}_2-{\mathrm{n}}_2+\mathrm{k}\right]+\mathrm{x}\left(1-\mathrm{z}\right)\left[{\mathrm{m}}_2-{\mathrm{n}}_2\right]+\left(1-\mathrm{x}\right)\mathrm{z}\left[\mathrm{k}-{\mathrm{h}}_3\right]+\left(1-\mathrm{x}\right)\left(1-\mathrm{z}\right)[-{\mathrm{h}}_3] \\ {\mathrm{E}}_{22}=\mathrm{x}\mathrm{z}\left[{-\mathrm{g}}_2+\mathrm{l}\right]+\mathrm{x}\left(1-\mathrm{z}\right)\left[-{\mathrm{g}}_2\right]+\left(1-\mathrm{x}\right)\mathrm{z}\mathrm{l} \\ {\mathrm{E}}_2=\mathrm{y}{\mathrm{E}}_{21}+(1-\mathrm{y}){\mathrm{E}}_{21} \end{gathered}$$

(5)

The equation for the replication dynamics chosen by the media (publisher) is

$$\mathrm{F}\left(\mathrm{y}\right)={\displaystyle \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{t}}}=\mathrm{y}\left({\mathrm{E}}_{21}-{\mathrm{E}}_2\right)=\mathrm{y}\left(\mathrm{y}-1\right)[\left(1-\mathrm{x}\right)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-\mathrm{z}\left(\mathrm{k}-{\mathrm{h}}_3\right)-{\mathrm{g}}_2+\mathrm{l}]$$

(6)

The first-order derivative $\mathrm{x}$ and the settings of $\mathrm{G}\left(\mathrm{y}\right)$, respectively:

$${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{y}\right)\right)}{\mathrm{d}\mathrm{y}}}=\left(2\mathrm{y}-1\right)[\left(1-\mathrm{x}\right)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-\mathrm{z}\left(\mathrm{k}-{\mathrm{h}}_3\right)-{\mathrm{g}}_2+\mathrm{l}]$$

(7)

$$\mathrm{J}\left(\mathrm{z}\right)=[\left(1-\mathrm{x}\right)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-\mathrm{z}\left(\mathrm{k}-{\mathrm{h}}_3\right)-{\mathrm{g}}_2+\mathrm{l}]$$

(8)

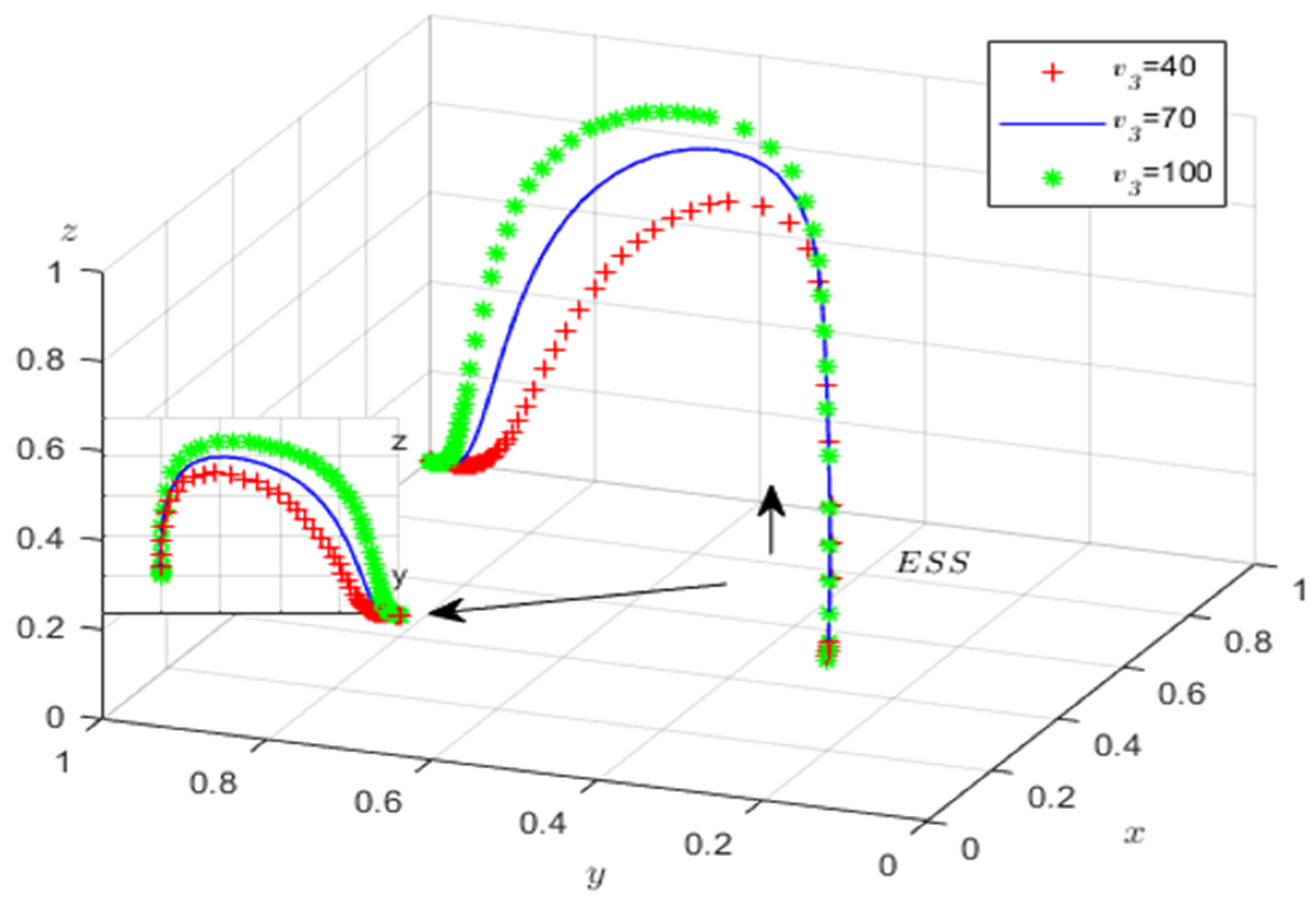
According to the stability theorem of differential equations, the probability that the media (publisher) chooses to participate in the discussion of public opinion on critical incidents is in a steady state must be satisfied: $\mathrm{F}\left(\mathrm{y}\right)=0$ and ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{y}\right)\right)}{\mathrm{d}\mathrm{y}}}<0$. Since ${\displaystyle \frac{\mathrm{J}\left(\mathrm{z}\right)}{\mathrm{z}}}<0$, $\mathrm{J}\left(\mathrm{z}\right)$ is a decreasing function with respect to $\mathrm{y}$, the reduced function. Therefore, when $\mathrm{z}={\displaystyle \raisebox{1ex}{$[\left(1-\mathrm{x}\right)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-\mathrm{z}\left(\mathrm{k}-{\mathrm{h}}_3\right)-{\mathrm{g}}_2+\mathrm{l}]$}\!\left/ \!\raisebox{-1ex}{$(\mathrm{k}-{\mathrm{h}}_3)$}\right.}={\mathrm{z}}^{*}$, $\mathrm{J}\left(\mathrm{z}\right)=0$; at this time, ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{y}\right)\right)}{\mathrm{d}\mathrm{y}}}$ is constant equal to 0; the media (publisher) cannot determine a stabilization strategy when $\mathrm{z}<{\mathrm{z}}^{*}$;$\mathrm{J}\left(\mathrm{z}\right)>0$. Currently, ${{\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{y}\right)\right)}{\mathrm{d}\mathrm{y}}}|}_{\mathrm{y}=0}<0,\mathrm{y}=0$ is the evolutionarily stable strategy (ESS) of the media (publisher) when $\mathrm{z}>{\mathrm{z}}^{*},$ $\mathrm{y}=1$ is the ESS. ${\mathrm{z}}^{*}$ represents the critical probability of government (regulator) strategy selection.

The phase diagram of strategy evolution for the media (publisher) is shown in Figure 3 below:

From Figure 3, the tangent crosses the point ${\left(\right[\mathrm{m}}_2$ − ${\mathrm{n}}_2-({\mathrm{g}}_2-\mathrm{l})]/{\mathrm{m}}_2-{\mathrm{n}}_2,0,0)$, where ${\mathrm{V}}_{\mathrm{B}1}$ is the volume of $B_1$, which is the probability that the media (publisher) chooses not to publish the critical-incident public opinion. $B_2$ is the volume of ${\mathrm{V}}_{\mathrm{B}2}$, the probability that the media (publisher) choose to publish the breaking-news public opinion, which is calculated as follows:

$${\mathrm{V}}_{\mathrm{B}2}={\int }_1^1{\int }_0^{{\displaystyle \frac{{\mathrm{m}}_{2-}{\mathrm{n}}_2-({\mathrm{g}}_2-\mathrm{l})}{{\mathrm{m}}_2-{\mathrm{n}}_2}}}{\displaystyle \frac{\left(1-\mathrm{x}\right)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-{\mathrm{g}}_2+\mathrm{l}}{\mathrm{k}-{\mathrm{h}}_3}}\mathrm{d}\mathrm{x}\mathrm{d}\mathrm{y}={\displaystyle \frac{[{\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-{\mathrm{g}}_2+\mathrm{l}]}^2}{2(\mathrm{k}-{\mathrm{h}}_3)\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)}}.{\mathrm{V}}_{\mathrm{B}1}=1-{\mathrm{V}}_{\mathrm{B}2}.$$

Corollary 3.

The probability of the media (publisher) participating in the dissemination of public opinion on emergencies is positively correlated with the benefits of self-media participation in positive media reporting, the incentives given by the government when the media responds positively, and the reputational damage and fines faced by the government when it responds positively but the media does not pay attention to the report. It is negatively correlated with the losses incurred by the media’s passive response and the costs of the media’s choice to pay attention to the report and the government’s positive response. The costs of time and effort paid by the media when the self-media do not participate and the reputational damage and fines faced by the government when it responds positively and the media does not pay attention to the reports are negatively correlated.

Proof. 

According to the probability of the media (publisher) to publish the online opinion of a critical incident ${\mathrm{V}}_{\mathrm{B}2}$, a conclusion is drawn by finding the first-order partial derivatives of each element of the expression of ${\mathrm{m}}_2$, $\mathrm{k}$, and $\mathrm{l}$ increasing and ${\mathrm{n}}_2$, ${\mathrm{g}}_2$, and ${\mathrm{h}}_3$ decreasing, leading to an increase in the probability of self-media participation in online opinion discussions. □

Inference 3 shows that whether the media (publisher) will participate in the publication of critical-incident online public opinion is positively correlated with the gain gained from positive reporting and negatively correlated with the loss incurred from the negative response, which is consistent with the assumption of the rational broker in the previous section that the media will choose the path of maximizing their interest in their decision-making. Both the government and self-media play a role in the media’s choice of whether to report on critical-incident online public opinion. On the one hand, the probability of media reporting is positively correlated with the policy incentives given by the government, i.e., the higher the level of government incentives and support, the more proactively the media will participate in the reporting of online public opinion, and on the contrary, the stronger the government-based punitive measures are when the media responds negatively, the more proactively the media will report on public opinion as well. On the other hand, the higher the cost of time and energy paid by the media when the self-media does not participate in disseminating public opinion, the less likely the media will choose to report it. Encouraging the self-media to actively join in the discussion of public opinion on emergencies can share the pressure of the media’s cost in reporting emergencies and make them more motivated to participate in releasing public opinion on emergencies on the Internet.

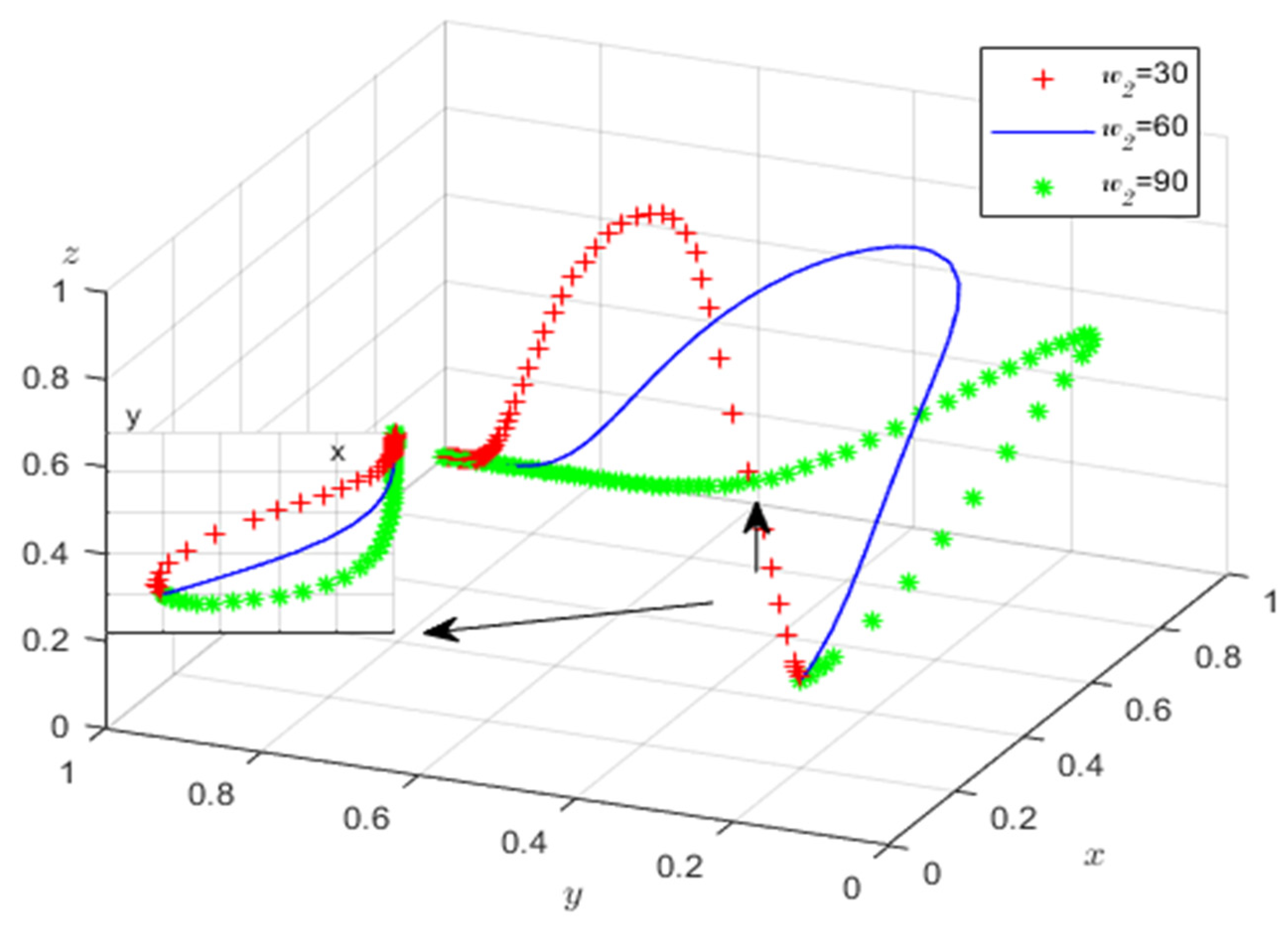
Corollary 4.

The probability of the media (publisher) reporting on critical-incident online public opinion during the evolutionary process increases with the self-media’s participation in critical-incident online public opinion or the probability of government intervention in critical-incident online public opinion.

Proof. 

From the analysis of the curatorial stability of the media (publisher), when $\mathrm{z}<{\mathrm{z}}^{*}$, $\mathrm{x}<{\displaystyle \raisebox{1ex}{$\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)-\mathrm{z}\left(\mathrm{k}-{\mathrm{h}}_3\right)-{\mathrm{g}}_2+\mathrm{l}$}\!\left/ \!\raisebox{-1ex}{$\left({\mathrm{m}}_2-{\mathrm{n}}_2\right)$}\right.}<{\mathrm{x}}^{*}$ when $\mathrm{y}=0$ is the ESS; when $\mathrm{z}>{\mathrm{z}}^{*}$, $\mathrm{x}>{\mathrm{x}}^{*}$ when $\mathrm{y}=1$ is the ESS. □

Therefore, as $\mathrm{x}/\mathrm{z}$ increases, the probability that the media (publisher) will engage in critical-incident online opinion reporting increases.

Corollary 4 shows that the participation of the self-media in the dissemination of online public opinion on emergencies will have positive incentives for the media to publish relevant reports; the more the self-media participate in the discussion, the more the media gain when publishing news, the lower the average cost of dealing with matters in the process of publishing news, the higher the sense of identity the media can obtain, and the more they will take the action of positively publishing news, which is in line with the conclusions of Corollary Three. This is consistent with the conclusion of Corollary Three. The more the government actively adopts the strategy of intervening in the online public opinion of emergencies, the more the media will actively report the relevant events. As an intervener and regulator, the government’s movement can significantly impact the evolution of emergencies. At the same time, the government’s rewards and punishments are also closely related to the self-interests of the relevant media. Therefore, this paper concludes that when it is necessary to utilize the power of the media to positively guide the online public opinion of emergencies, the government’s active intervention and the enhancement of the self-media’s attention to the events are effective measures.

3. Analysis of the strategic stability of the government (regulator)

The expected benefits of the government’s (regulator’s) intervention or non-intervention in online public opinion emergencies and the average expected benefits (${\mathrm{E}}_{31}$, ${\mathrm{E}}_{32}$, ${\mathrm{E}}_3$), respectively:

$$\begin{gathered} {\mathrm{E}}_{31}=\mathrm{x}\mathrm{y}\left[{\mathrm{m}}_1-{\mathrm{n}}_1-{\mathrm{v}}_3-{\mathrm{v}}_1\right]+\mathrm{y}\left(1-\mathrm{x}\right)\left[{\mathrm{m}}_1-{\mathrm{n}}_1-{\mathrm{v}}_3\right]+\left(1-\mathrm{y}\right)\mathrm{x}\left[{\mathrm{m}}_1-{\mathrm{n}}_1\right]+\left(1-\mathrm{y}\right)\left(1-\mathrm{x}\right)\left[{\mathrm{m}}_1-{\mathrm{n}}_1-{\mathrm{v}}_1\right] \\ {\mathrm{E}}_{32}=\mathrm{x}\mathrm{y}\left[-{\mathrm{g}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right]+\mathrm{y}\left(1-\mathrm{x}\right)\left[-{\mathrm{g}}_1-{\mathrm{v}}_4\right]+\left(1-\mathrm{y}\right)\mathrm{x}\left[-{\mathrm{g}}_1-{\mathrm{v}}_2\right]+\left(1-\mathrm{y}\right)\left(1-\mathrm{x}\right)[-{\mathrm{g}}_1] \\ {\mathrm{E}}_3=\mathrm{z}{\mathrm{E}}_{11}+(1-\mathrm{z}){\mathrm{E}}_{12} \end{gathered}$$

(9)

The replication dynamic equation chosen by the government (controller) is

$$\mathrm{F}\left(\mathrm{z}\right)={\displaystyle \frac{\mathrm{d}\mathrm{z}}{\mathrm{d}\mathrm{t}}}=\mathrm{z}\left({\mathrm{E}}_{31}-{\mathrm{E}}_3\right)=\mathrm{z}\left(\mathrm{z}-1\right)[-2\left({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right)-\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1)-\mathrm{y}{\mathrm{g}}_1]$$

(10)

The first-order derivative $\mathrm{z}$ and the settings of $\mathrm{H}\left(\mathrm{y}\right)$, respectively:

$${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{z}\right)\right)}{\mathrm{d}\mathrm{z}}}=\left(2\mathrm{z}-1\right)[-2\left({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right)-\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1)-\mathrm{y}{\mathrm{g}}_1]$$

(11)

$$\mathrm{H}\left(\mathrm{y}\right)=[-2\left({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right)-\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1)-\mathrm{y}{\mathrm{g}}_1]$$

(12)

According to the stability theorem of differential equations, the probability that the government (controller) chooses to participate in the discussion of public opinion on emergencies is in a steady state must be satisfied: $\mathrm{F}\left(\mathrm{z}\right)=0$ and ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{z}\right)\right)}{\mathrm{d}\mathrm{z}}}<0$. Since ${\displaystyle \frac{\mathrm{H}\left(\mathrm{y}\right)}{\mathrm{y}}}<0$, then $\mathrm{H}\left(\mathrm{y}\right)$ is a function with respect to $\mathrm{y}$, the reduced function. Therefore, when $\mathrm{y}={\displaystyle \raisebox{1ex}{$[2\left({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right)+\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1\left)\right]$}\!\left/ \!\raisebox{-1ex}{${\mathrm{g}}_1$}\right.}={\mathrm{y}}^{**}$, $\mathrm{H}\left(\mathrm{y}\right)=0$; at this time, ${\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{z}\right)\right)}{\mathrm{d}\mathrm{z}}}$ is a constant equal to 0. The self-media (propagator) cannot determine a stabilization strategy when $\mathrm{y}<{\mathrm{y}}^{**}$, $\mathrm{H}\left(\mathrm{y}\right)=0$; at this time, ${{\displaystyle \frac{\mathrm{d}\left(\mathrm{F}\left(\mathrm{z}\right)\right)}{\mathrm{d}\mathrm{z}}}|}_{\mathrm{z}=0}<0,\mathrm{z}=0$ is the self-media’s (propagator’s) evolutionarily stable strategy (ESS); conversely, $\mathrm{z}=1$ is the ESS. ${\mathrm{y}}^{**}$ represents the critical probability of strategy selection by other relevant groups (such as self-media or the media), which determines whether the government chooses to participate in the evolution of stable strategies for controlling online public opinion events.

The phase diagram for the evolution of the government’s (regulator) strategy is shown in Figure 4 below:

From Figure 4, the probability that the government (regulator) is not involved in the dissemination of public opinion on emergencies is $\mathrm{C}1$, the volume of ${\mathrm{V}}_{\mathrm{C}1}$, and the probability of participating in the dissemination of public opinion on emergencies is $\mathrm{C}2$, the volume of ${\mathrm{V}}_{\mathrm{C}2}$, which is calculated as:

$${\mathrm{V}}_{\mathrm{C}1}={\iint }_0^1{\displaystyle \frac{-2({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2)-\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1)}{{\mathrm{g}}_1}}\mathrm{d}\mathrm{z}\mathrm{d}\mathrm{x}={\displaystyle \frac{-4({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2)-\mathrm{x}({\mathrm{n}}_1-{\mathrm{m}}_1)}{2{\mathrm{g}}_1}}, {\mathrm{V}}_{\mathrm{C}2}=1-{\mathrm{V}}_{\mathrm{C}1}.$$

Corollary 5.

The probability that the government (regulator) is involved in the dissemination of public opinion in emergencies is positively related to the gains gained from the government’s choice of a positive strategy, the losses incurred from the government’s negative response, the suppression of public opinion by the self-media for the government’s negative response, and the losses brought about by the adverse reaction of the government to the media forwarded to the government, and it is negatively correlated with the degree of the public opinion suppression of the government’s positive response by the self-media, the degree of negative impacts brought about by the positive response of the government, the negative impacts brought about by the positive reaction from the government, the positive response of the government, and the negative impacts forwarded to the government by the media. Negative correlation.

Proof. 

Based on the probability of government (regulator) involvement in the propagation of public opinion on emergencies ${\mathrm{V}}_{\mathrm{C}2}$, the conclusion is drawn by finding the first-order partial derivatives of each element of the expression of ${\mathrm{m}}_1$ and ${\mathrm{g}}_1$. ${\mathrm{v}}_1$, ${\mathrm{v}}_3$ increase; ${\mathrm{v}}_2$ and ${\mathrm{v}}_4$ decrease, all leading to an increase in the probability of self-media participation in online opinion discussions. □

Corollary 5 shows that whether the government (regulator) will intervene in a critical incident online, public opinion is positively correlated with the gains it gains from its actions and negatively correlated with the losses incurred from its negative response, which is consistent with the assumption of the rational broker in the previous section. The government (regulator) will decide to maximize its interests. When the government responds negatively to network public opinion emergencies, other parties involved will make corresponding decisions because of their interests: the self-media will disseminate negative remarks about the government controller, and the media will publish reports about the government’s inaction, which is not conducive to the increase in the psychological identity of the government controller. At the same time, it will reduce the credibility of the government to a certain degree, and the more the self-media and the media negatively pressure the government, the more the government will actively intervene in the situation. When negative pressure from the self-media and the media increases, the government will take a more active intervention, directly proportional to each other. On the other hand, the government’s intervention measures in the active response process still need to meet the expectations of the self-media and the media entirely. To a certain extent, they may harm the interests of other game subjects so that the self-media may suppress the government’s actions. The press may negatively affect the government when forwarding the relevant remarks. The stronger the social intervention, the less likely the government will actively take measures to control public opinion on emergencies. Therefore, whether the government can actively predict and control the negative impacts of its control actions is a crucial consideration for the government before taking control measures.

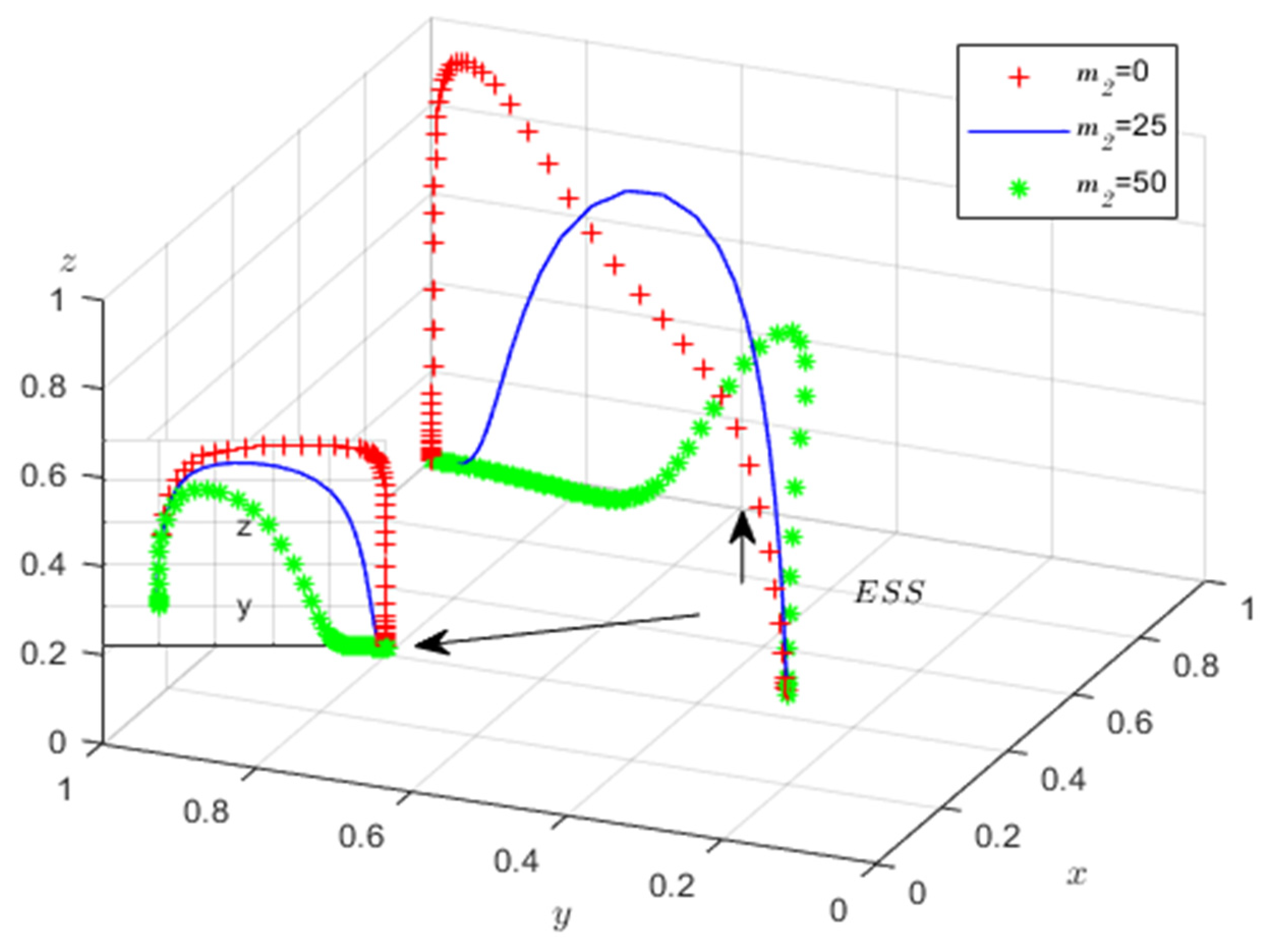
Corollary 6.

The probability that the government (regulator) is involved in disseminating public opinion on emergencies increases with the media’s reporting on emergencies and the likelihood of the self-media disseminating public opinion on emergencies.

Proof. 

From the stability analysis of the government’s (regulator’s) policy, when $\mathrm{z}<\left[-2\left({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2\right)\right]-\mathrm{x}\left({\mathrm{n}}_1-{\mathrm{m}}_1\right)]/{\mathrm{g}}_1$ and $\mathrm{y}<\mathrm{y}**$, $\mathrm{H}\left(\mathrm{y}\right)>0$ and $\mathrm{d}\left(\mathrm{F}\right(\mathrm{z}\left)\right)/\mathrm{d}\mathrm{z}|\mathrm{z}=0<0$, $\mathrm{z}=0$ is the evolutionary equilibrium strategy. On the contrary, z = 1 is the evolutionary equilibrium strategy. Therefore, as x, y gradually increases, the stabilization strategy of the government (controller) increases from $\mathrm{z}=0$ (intervening in critical-incident online public opinion) to $\mathrm{z}=1$ (not intervening in critical-incident online public opinion). □

Corollary 6 shows that when there are more self-media participants and media participants in the game environment, the probability that the government will participate in the game and intervene in the online public opinion of emergencies promptly will increase because the self-media and the media have a higher degree of autonomy in their speeches. When they express their views or release the news, they will disseminate information about emergencies from various perspectives, which is redundant. They may contain both truthful and distorted information, so the government will take control measures when the number of participants increases. Therefore, when the number of participants increases, the government will take control measures. On the other hand, considering the status of the self-media and media as rational brokers, the government should take control measures to prevent them from strolling false information for profit. Therefore, when the scope of online public opinion on emergencies is broad and the number of subjects involved is large, the government should participate promptly and take control measures to avoid the development of public opinion in an uncontrollable direction.

4.4. Equilibrium Points in a Tripartite Evolutionary Game Model

The system equilibrium points can be obtained from $\mathrm{F}\left(\mathrm{x}\right)=0, \mathrm{F}\left(\mathrm{y}\right)=0, \mathrm{F}\left(\mathrm{z}\right)=0: {\mathrm{E}}_1\left(0,0,0\right), {\mathrm{E}}_2\left(1,0,0\right), {\mathrm{E}}_3\left(0,1,0\right), {\mathrm{E}}_4\left(0,0,1\right), {\mathrm{E}}_5\left(1,1,0\right), {\mathrm{E}}_6\left(1,0,1\right), {\mathrm{E}}_7\left(0,1,1\right), {\mathrm{E}}_8\left(1,1,1\right),$${\mathrm{E}}_9(0,2({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2)/({\mathrm{n}}_1-{\mathrm{m}}_1),[{\mathrm{m}}_2-{\mathrm{n}}_2-{\mathrm{g}}_2+\mathrm{l}]/\mathrm{k}-{\mathrm{h}}_3),$${\mathrm{E}}_{10}\left(2\right({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2)/({\mathrm{n}}_1-{\mathrm{m}}_1),0,{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-{\mathrm{g}}_3/{\mathrm{g}}_3),$${\mathrm{E}}_{11}\left(2\right({\mathrm{v}}_3+{\mathrm{v}}_1-{\mathrm{v}}_4-{\mathrm{v}}_2)-({\mathrm{n}}_1-{\mathrm{m}}_1)/{\mathrm{g}}_1,1,{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-{\mathrm{g}}_3/{\mathrm{g}}_3),$${\mathrm{E}}_{12}({\mathrm{m}}_2-{\mathrm{n}}_2-({\mathrm{g}}_2-\mathrm{l}\left)\right]/{\mathrm{m}}_2-{\mathrm{n}}_2,{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2/{\mathrm{g}}_3,0),$${\mathrm{E}}_{13}({\mathrm{m}}_2-{\mathrm{n}}_2-{\mathrm{g}}_2+\mathrm{l}-\mathrm{k}+{\mathrm{h}}_3/({\mathrm{m}}_2-{\mathrm{n}}_2),{\mathrm{m}}_3-{\mathrm{n}}_3+{\mathrm{w}}_1-{\mathrm{w}}_2-{\mathrm{g}}_3/{\mathrm{g}}_3,1),1)$. The Jacobian matrix of the three-party evolutionary game is

$$\mathrm{y}=\left[\begin{array}{ccc}{\mathrm{J}}_1& {\mathrm{J}}_2& {\mathrm{J}}_3\\ {\mathrm{J}}_4& {\mathrm{J}}_5& {\mathrm{J}}_6\\ {\mathrm{J}}_7& {\mathrm{J}}_8& {\mathrm{J}}_9\end{array}\right]=\left[\begin{array}{ccc}\partial \mathrm{F}\left(\mathrm{x}\right)/\partial \mathrm{x}& \partial \mathrm{F}\left(\mathrm{x}\right)/\partial \mathrm{y}& \partial \mathrm{F}\left(\mathrm{x}\right)/\partial \mathrm{z}\\ \partial \mathrm{F}\left(\mathrm{y}\right)/\partial \mathrm{x}& \partial \mathrm{F}\left(\mathrm{y}\right)/\partial \mathrm{y}& \partial \mathrm{F}\left(\mathrm{y}\right)/\partial \mathrm{z}\\ \partial \mathrm{F}\left(\mathrm{z}\right)/\partial \mathrm{x}& \partial \mathrm{F}\left(\mathrm{z}\right)/\partial \mathrm{y}& \partial \mathrm{F}\left(\mathrm{z}\right)/\partial \mathrm{z}\end{array}\right]$$

According to Lyapuonv’s (Lyapuonv) first method, all eigenvalues of the Jacobi matrix have a negative fundamental part, and the equilibrium point is asymptotically stable; at least one of the eigenvalues of the Jacobi matrix has a positive fundamental part, and the equilibrium point is unstable; the eigenvalues of the Jacobi matrix, except for the eigenvalues with a natural part of zero, have negative genuine parts, the equilibrium point is in a critical state, and the eigenvalue sign cannot determine the stability. In the stability analysis of the equilibrium point, this paper puts forward some assumptions on the above variables, as shown in

Table 4. Jacobi matrix with selected assumptions.

	Jacobian Matrix Eigenvalues		Stability Conclusions	Hypothesis
	$\mathsf{\lambda }$	real symbol
$E_1$ (0,0,0)	${\mathsf{\lambda }}_{11},{ \mathsf{\lambda }}_{12},{ \mathsf{\lambda }}_{13}$	(−, −, +)	Point of instability	${\mathsf{\lambda }}_{13}>0$
$E_2$ (1,0,0)	${\mathsf{\lambda }}_{21},{ \mathsf{\lambda }}_{22},{ \mathsf{\lambda }}_{23}$	(+, +, uncertain)	Point of instability	${\mathsf{\lambda }}_{21}>0$
$E_3$ (0,1,0)	${\mathsf{\lambda }}_{31},{ \mathsf{\lambda }}_{32},{ \mathsf{\lambda }}_{33}$	(+, +, uncertain)	Point of instability	${\mathsf{\lambda }}_{32}>0$
$E_4$ (0,0,1)	${\mathsf{\lambda }}_{41},{ \mathsf{\lambda }}_{42},{ \mathsf{\lambda }}_{43}$	(−, −, −)	ESS	${\mathsf{\lambda }}_{41}<0,{ \mathsf{\lambda }}_{42}<0$
$E_5$ (1,1,0)	${\mathsf{\lambda }}_{51},{ \mathsf{\lambda }}_{52},{ \mathsf{\lambda }}_{53}$	(−, −, −)	ESS	/
$E_6$ (1,0,1)	${\mathsf{\lambda }}_{61},{ \mathsf{\lambda }}_{62},{ \mathsf{\lambda }}_{63}$	(not sure, +, not sure)	Point of instability	${\mathsf{\lambda }}_{62}>0$
$E_7$ (0,1,1)	${\mathsf{\lambda }}_{71},{ \mathsf{\lambda }}_{72},{ \mathsf{\lambda }}_{73}$	(+, indeterminate, uncertain)	Point of instability	${\mathsf{\lambda }}_{71}>0$
$E_8$ (1,1,1)	${\mathsf{\lambda }}_{81},{ \mathsf{\lambda }}_{82},{ \mathsf{\lambda }}_{83}$	(−, −, +)	Point of instability	${\mathsf{\lambda }}_{83>0}$
$E_9$$(0, y_1$$,z_1$)	${\mathsf{\lambda }}_{91},{ \mathsf{\lambda }}_{92}={\mathsf{\lambda }}_{93}$	(−, 0, 0)	inconclusive	${\mathsf{\lambda }}_{91}<0$
$E_{10}$$(x_1$$,0,z_2$)	${\mathsf{\lambda }}_{101},{ \mathsf{\lambda }}_{102}={\mathsf{\lambda }}_{103}$	(−, 0, 0)	inconclusive	${\mathsf{\lambda }}_{101}<0$
$E_{11}$$(x_2$$,1,z_2$)	${\mathsf{\lambda }}_{111},{ \mathsf{\lambda }}_{112}={\mathsf{\lambda }}_{113}$	(−, 0, 0)	inconclusive	${\mathsf{\lambda }}_{111}<0$
$E_{12}$$(x_2$$,y_2$,0)	${\mathsf{\lambda }}_{121},{ \mathsf{\lambda }}_{122}=-{\mathsf{\lambda }}_{123}$	(Uncertainty, +, −)	Point of instability	/
$E_{12}$$(x_3$$,y_3$,1)	${\mathsf{\lambda }}_{131},{ \mathsf{\lambda }}_{132}=-{\mathsf{\lambda }}_{133}$	(uncertainty, +, −)	Point of instability	/

Assumption conditions: 1. ${\mathsf{\lambda }}_{41}<0,{ \mathsf{\lambda }}_{42}<0$; 2. ${\mathsf{\lambda }}_{61}>0$; 3. ${\mathsf{\lambda }}_{23}>0$.

.

Corollary 7.

When the system satisfies the condition ${\lambda }_{41}<0$, i.e., $\left(m_3-n_3+w_1-w_2-2g_3\right)<0$, and ${\lambda }_{42}<0$, i.e.,$\left(m_2-n_2-g_2+l-k+h_3\right)<0$, there are two stable points $E_4$ (0,0,1) and $E_5$ (1,1,0) in the critical-incident network opinion replication dynamic system.

Corollary 7 shows that when the self-media and the government gain less in the game, the media and self-media pay more for each other’s participation. The psychological benefits of both are less, and the fines are more when the government responds positively; the strategy combinations will be stabilized in the combination of self-media non-participation, media non-publication, and government intervention and the combination of self-media participation, media publication, and government non-intervention strategies. Suppose the government takes intervention measures and chooses to use a combination of fewer rewards and more fines. In that case, the enthusiasm for the self-media and media will be significantly reduced. Finally, combining self-media, media non-participation, and government intervention will stabilize the game strategy to intervene in the development of online public opinion on emergencies. Another perspective of the same premise is that the government does not interfere with the online public opinion of emergencies, in which case the self-media and the media will play the game in another way to achieve a balanced state between the two sides. Both will seek benefits and reduce losses in the event to reach a balance point of netizen participation, media release, and government non-interference.

Corollary 8.

When $m_3+w_1>n_3+w_2+2g_3 and m_2+l+h_3>n_2+k+g_2$, there is one and only one stable point $E_5\left(1,1,0\right)$ for the critical-incident online opinion replication dynamic system.

Corollary 8 shows that the self-media’s and media’s psychological expectations of the government’s incentives and disincentives will influence their decision on whether to participate in the game of critical-incident online public opinion. When they anticipate that the government is more likely to take incentives and that they can benefit from the game, they will participate in the publication and discussion of online public opinion on emergencies, even if the government does not intervene in the current process. Therefore, there is some room for the government to maneuver in the gaming process. Whether the government formulates incentives and penalties, whether it adopts consecutive incentives and penalties for emergencies in the same area, and how it determines the strength of the incentives and penalties will all impact the current and future gaming events and patterns in the exact location.

5. Simulation Experiments

This section intends to verify the authenticity of evolutionary stability analysis to present the multi-agent game behavior of network public opinion in the above scenario. Based on the parameter constraint conditions, values were assigned and analyzed using Matlab 2023a for numerical simulation.

Firstly, to enhance the scientificity and traceability of parameter settings, regarding the definition of the simulation experiment parameters, this study took the following two steps:

(1) Define and assign values in combination with relevant literature research conclusions, the Statistical Report on Internet Development in China, data published by the Ministry of Industry and Information Technology and other databases, and parameter assignment based on the principle of equality balance;

(2) Using the parameter values obtained through the above methods as initial values and integrating the experience and judgment of 15 experts and scholars in the field of online public opinion (7 professors, 5 young teachers, and 3 PhDs), adopting multiple rounds of the Delphi method, fully demonstrate the rationality of the parameter assignment and determine the final experimental parameters.

The basic variable assignments are as follows:

Array 1: $\mathrm{g}3=180, \mathrm{w}2=60, \mathrm{m}2=20, \mathrm{v}3=70, \mathrm{v}1=30, \mathrm{n}2=100, \mathrm{k}=50, \mathrm{h}3=-15, \mathrm{w}1=-10, \mathrm{m}3=80, \mathrm{n}3=150, \mathrm{v}4=60, \mathrm{v}2=40, \mathrm{g}1=-75, \mathrm{m}1=100, \mathrm{n}1=20, \mathrm{l}=20, \mathrm{g}2=60$, consistent with Corollary 7’s condition.

Array 2: Increase the variable values m3, m2, and l, and decrease the variable value $\mathrm{g}3, \mathrm{n}3, \mathrm{n}2, \mathrm{k}, \mathrm{g}2$. This assignment satisfies the conditions in Corollary 8: g3 = 150, w2 = 60, m2 = 25, v3 = 70, v1 = 30, n2 = 20, k = 20, h3 = −15, w1 = −10, m3 = 180, n3 = 100, v4 = 60, v2 = 40, g1 = −75, m1 = 100, n1 = 20, l = 40, g2 = 30.

5.1. Model Validation

To reduce the error caused by the randomness of experimental results, this study conducted 50 evolutionary simulations of Array 1 with different initial variable values after assigning values to the essential variables. The results are shown in Figure 5:

Figure 5 shows that under the condition of satisfying Corollary 7, there are two stable points (0, 0, 1) and (1, 1, 0) in the evolution of the system, namely, the strategy combination of the self-media (participants), media (publishers), and government (regulators) (participation, reporting, non-intervention) and (non-participation, non-reporting, intervention), which are two stable combinations of evolution. This further confirms that the government should adjust its movements and strategies according to the different actions of the self-media and media. The simulation results conform to the assumption of Corollary 7 mentioned earlier.

① High-pressure control equilibrium (0, 0, 1): When the government adopts a strong intervention strategy, the self-media and media choose to withdraw from the public opinion arena due to risk avoidance ($g_3$↑) and insufficient returns ($m_2$↓). This result confirms the theoretical expectation of the “cicada effect” that excessive regulation can lead to the shrinkage of the public discourse space.

② Autonomous participation equilibrium (1,1,0): When the government withdraws intervention, the self-media and media achieve self-organizing equilibrium through market-oriented mechanisms ($m_3$↑, $m_2$↑), which is highly consistent with the “common based peer production” model proposed.

On this basis, this study conducted 50 evolutionary simulations of Array 2 with different initial variable values, and the results are shown in Figure 6:

It is worth noting that, as shown in Figure 6, all evolutionary paths converge to E5 (1, 1, 0) under the condition of Inference 8, which has important policy implications:

When the media revenue (m₂) exceeds the critical value ($m_2>n_2+k+g_2+l-h_3$), even if the government does not intervene (x = 0), the system can still maintain a stable information supply, indicating that market-oriented mechanisms can replace administrative regulation in certain fields.

The difference in convergence speed (initial value sensitivity) indicates a significant historical path-dependence effect, which provides a theoretical basis for “progressive governance reform”.

5.2. Sensitivity Analysis

To reveal the core roles of interest driven, psychological loss, external incentives, and policy resistance in multi-agent games, based on the assignment of Array 2, this paper is again based on analyzing the impact of changes in the values of ${\mathrm{g}}_3,{\mathrm{w}}_2,{\mathrm{m}}_2,\mathrm{k},{\mathrm{v}}_1,{ \mathrm{v}}_3$ on the process and outcome of the evolutionary game.

5.2.1. Self-Media Perspective

To gain a deeper understanding of the loss-driven mechanism and behavioral logic of the self-media, sensitivity analysis was conducted on ${ \mathrm{g}}_3$ and ${\mathrm{w}}_2$.

To analyze the impact of ${\mathrm{g}}_3$ changes on the evolutionary game process and results, we assigned “Losses arising from the non-participation of self-media in the discussion” ${ \mathrm{g}}_3$ as ${\mathrm{g}}_3=120,150,180$. It replicates the simulation results of the dynamic equation set evolving 50 times, as shown in Figure 7 below.

Figure 7 shows that the greater the non-participation loss of the self-media (such as loss of benefits), the higher the probability of accelerating its participation in the evolution of public opinion, but the evolution is not significant. As $g_3$ increases, the willingness for self-media participation z decreases, exhibiting a “loss sensitive” characteristic. As ${\mathrm{g}}_3$ increases, self-media interests are lost to a greater extent. The greater the loss suffered by the self-media when they do not participate in critical-incident online public opinion, the greater the probability that they will continue to participate in public opinion discussions. Under the assumption of rational brokers, they will find ways to reduce their losses, such as voicing their opinions on the network and seeking reasonable interests through media channels.

To analyze the impact of ${\mathrm{w}}_2$ changes on the evolutionary game process and results, we assigned “Losses of self-media in Negative Government Response” ${\mathrm{w}}_2$ as ${\mathrm{w}}_2=30,60,90$. It replicates the simulation results of the dynamic equation system evolving 50, times as shown in Figure 8 below:

Figure 8 shows that when the government intervenes passively, the greater the pressure on the self-media (${\mathrm{w}}_2$ increases), the slower the evolution speed of their participation in public opinion. Government response delay (w₂↑) will trigger preventive silence, causing a lag in public opinion response. Considering the risk of policy uncertainty, the preventive response of platform censorship, and the pressure of social public opinion backlash, the government’s failure to report emergencies will indeed systematically increase the pressure on the self-media to speak out.

5.2.2. Media Perspective

To gain a deeper understanding of the profit-driving mechanism and synergistic effects of the media, a sensitivity analysis was conducted on ${\mathrm{m}}_2$ and $\mathrm{k}$.

To analyze the impact of “Benefits gained from media choosing to take an active interest in emergencies” ${\mathrm{m}}_2$ changes on the evolutionary game process and results, ${\mathrm{m}}_2$ was set as ${\mathrm{m}}_2=0,25,50$, and the simulation results are as shown in Figure 9.

Figure 9 shows that the increase in benefits brought by the media choosing to focus on emergencies will significantly accelerate the evolution of the media’s participation in public opinion. The benefits brought by the media choosing to focus on emergencies $m_2$ needs to exceed the critical value ($m_2>n_2+k+g_2-l-h_3$) in order to activate sustained participation. Emergencies inherently attract widespread public attention due to their suddenness, impact, and relevance to societal safety. By prioritizing such events, media outlets can rapidly expand their audience reach, increasing engagement metrics (clicks, shares, views) and advertising revenue. This financial incentive drives media organizations to further refine their strategies for covering crises, reinforcing a cycle of heightened participation in public discourse.

To analyze the impact of “Media revenue under active government response” $\mathrm{k}$ on the process and results of the evolutionary game, $\mathrm{k}$ is assigned as $\mathrm{k}=0,20,40$. The simulation results are shown in Figure 10.

Figure 10 shows that the greater the government’s reward for positive reporting (with an increase in k), the faster the evolution of media participation in public opinion. The increase in k enhances media engagement by altering incentive structures, reducing operational risks, fostering competition, and gradually institutionalizing compliant reporting practices.

5.2.3. Government Perspective

To analyze the resistance and pressure mechanisms of the government, sensitivity analysis was conducted on ${\mathrm{v}}_1$ and ${\mathrm{v}}_3$.

To analyze the impact of “Negative public opinion from self-media when the government actively responds to emergencies” ${\mathrm{v}}_1$ on the process and results of the evolutionary game, ${\mathrm{v}}_1$ is assigned to ${\mathrm{v}}_1=0,30,60$. The simulation results are shown in Figure 11 as follows.

Figure 11 shows that when the government actively intervenes, the greater the resistance of the self-media (${\mathrm{v}}_1$ increases), the faster the evolution speed of the government stopping intervention. As ${\mathrm{v}}_1$ increases, the government faces greater resistance from netizens’ online public opinion when actively taking measures to solve emergencies. In this process, the government may invest a lot of manpower and material resources but still cannot achieve the expected results. Over time, the government will adopt more passive ways to respond to emergencies and no longer take active measures.

To analyze the impact of “Negative impact of media reposting when the government actively responds to emergencies” ${\mathrm{v}}_3$ on the process and results of the evolutionary game, ${\mathrm{v}}_3$ is assigned as ${\mathrm{v}}_3=40,70,100$, and the simulation results are shown in Figure 12 as follows.

Figure 12 shows that the stronger the negative impact of media coverage (with an increase in v3), the faster the evolution of government intervention. The accelerating effect of v3 on government exit conforms to the second-order communication model of “agenda setting”. The intensification of negative reports may weaken public trust in governance, and if the government cannot achieve the expected results due to public opposition, it will tend to respond passively in the long run.

6. Summary

This paper takes the evolutionary game theory as the theoretical basis and conducts a multi-subject evolutionary game analysis of emergencies. Firstly, it identifies the subjects as the three major subjects, namely, the controller represented by the government, the participant represented by self-media, and the publisher represented by the media; it analyzes the motivation of the game and the influencing factors, constructs an evolutionary game model, and finally carries out a simulation and analysis of the game model built between the subjects. In this study, we simulated the impacts of losses incurred by the self-media’s negative response to emergencies, the effects of adverse psychological losses brought about by the government’s negative response to the self-media, the impacts of gains from media attention and reporting on the self-media’s participation, the effects of rewards given by the government on the media when the media responds positively, the impact of public opinion suppression from the self-media on the government when the government responds positively, the impacts of the adverse effects of the media’s retransmission on the government when the government responds positively, and so on. The speed of the game model to reach the equilibrium point changes with variables such as the impact of the government’s positive response, the adverse effects of the government’s positive response to the media forwarding to the government, and the movement of each game subject.

Finally, this article concludes that:

The evolutionary game system will have two stable equilibrium states. ① Strict control balance (0, 0, 1): when the government implements high-intensity intervention ($g_3$↑) and the cost of media and self-media participation ($n_2 n_3$) is too high, the system converges to the state of “government led media self-discipline self-media silence”. This equilibrium is applicable to high-risk public opinion events, but it may lead to information rigidity in the long run. ② Autonomous participation equilibrium (1, 1, 0): when the government delegates power (x↓) and market incentives ($m_2 m_3$) are sufficient, the system forms a virtuous cycle of “media independent reporting–active participation of self-media–government non-intervention”. This balance is more sustainable in livelihood-related events. ③ Critical condition for phase transition: there is a threshold effect on the efficiency of government intervention: when the sum of the intensity of self-media confrontation ($v_1$) and negative media dissemination ($v_3$) exceeds government revenue ($m_1$), the system will inevitably jump from E4 to E5.

Sensitivity analysis revealed the core roles of interest driven, psychological losses, external incentives, and policy resistance in multi-agent games. The government needs to balance the participation motivations of the self-media and media through interest coordination, flexible incentives, and dynamic communication mechanisms to avoid the risk of public opinion losing control:

The logic of self-media behavior: risk avoidance and adversarial participation. The participation of the self-media in decision-making $z$ is highly sensitive to punishment costs $g_3$ and psychological losses $w_2$, which conforms to the assumption of “bounded rational economic agents”. When the government imposes high-intensity punishments ($g_3$↑) or negative responses trigger psychological distrust ($w_2$↑), the self-media tend to withdraw from the public opinion field ($z\to 0$), forming a “cicada effect”. However, if the self-media successfully increase the cost of government intervention through collective confrontation ($v_1$↑), they may force the government to withdraw from intervention (x → 0), thereby triggering a “retaliatory rebound” in self-media participation. This phenomenon confirms the existence of the “adversarial public sphere” in the digital age, where non-state actors can counteract the control of traditional authorities through technological empowerment.

Media strategy selection: the paradox of commercialization and responsibility. The media’s reporting behavior y is governed by the marginal substitution rate of revenue $m_2$ and regulatory costs $k$. Empirical evidence shows that when $m_2>n_2+k+g_2-l-h_3$, the media chooses to actively report ($y\to 1$), but its content production shows a “traffic priority” tendency, leading to a decline in the quality of public information, such as the emergence of clickbait headlines. It is worth noting that the inhibitory effect of negative media dissemination ($v_3$↑) on government intervention exhibits non-linear characteristics, which is in line with the classic argument of the media shaping policy priorities in agenda setting theory. However, excessive reliance on commercial profits $m_2$ may lead to “market failure”, and externalities need to be corrected through institutional subsidies k.

The dilemma of government governance: the decline of control effectiveness and credibility. Government intervention decisions x face a trade-off between punishment and credibility: increasing the severity of punishment ($g_3$↑) can suppress negative public opinion in the short term (E4 equilibrium), but it will intensify self-media confrontation ($v_1$↑) and negative media dissemination ($v_3$↑), leading to the “Tacitus Trap” in the long run, where the marginal utility of government intervention decreases as credibility is lost. This finding is consistent with research on the efficiency boundary of “digital authoritarianism”, indicating that excessive reliance on hard control ($g_3, k$) may backfire.

The practical significance of this article lies in the following: (1) it can help understand the efficiency and social impact of information dissemination under different combinations of strategies; (2) it can provide a reference for the government to formulate information control policies to balance social stability and credibility; (3) we can provide strategic recommendations for the media and self-media to optimize information dissemination and public trust.

This study did not consider the endogenous effects of platform algorithms, and in the future, algorithm transparency can be introduced as a moderating variable. And the model’s accuracy in describing the natural world still needs to be improved, as it only corresponds to actual events, which simply and inevitably has imperfections. A single simulation analysis also has significant limitations. We will consider further enhancing the systematic mapping between the model and the real world.